文档内容
2020年宁夏中考数学试卷(教师版)
一、选择题(本题共8小题,每小题3分,共24分.在每小题给出的四个选项中只有一个
是符合题目要求的)
1.(3分)下列各式中正确的是( )
A.a3•a2=a6 B.3ab﹣2ab=1
C. =2a+1 D.a(a﹣3)=a2﹣3a
【微点】合并同类项;同底数幂的乘法;单项式乘多项式.
【思路】利用整式的计算法则对四个选项一一验证即可得出答案.
【解析】解:A、a3•a2=a5,所以A错误;
B、3ab﹣2ab=ab,所以B错误;
C、 ,所以C错误;
D、a(a﹣3)=a2﹣3a,所以D正确;
故选:D.
【点拨】本题考查整式乘除法的简单计算,注意区分同底数幂相乘,底数不变,指数相
加,而幂的乘方是底数不变,指数相乘,这两个要区分清楚;合并同类项的时候字母部
分不变,系数进行计算,只有当系数计算结果为0时,整体为0.
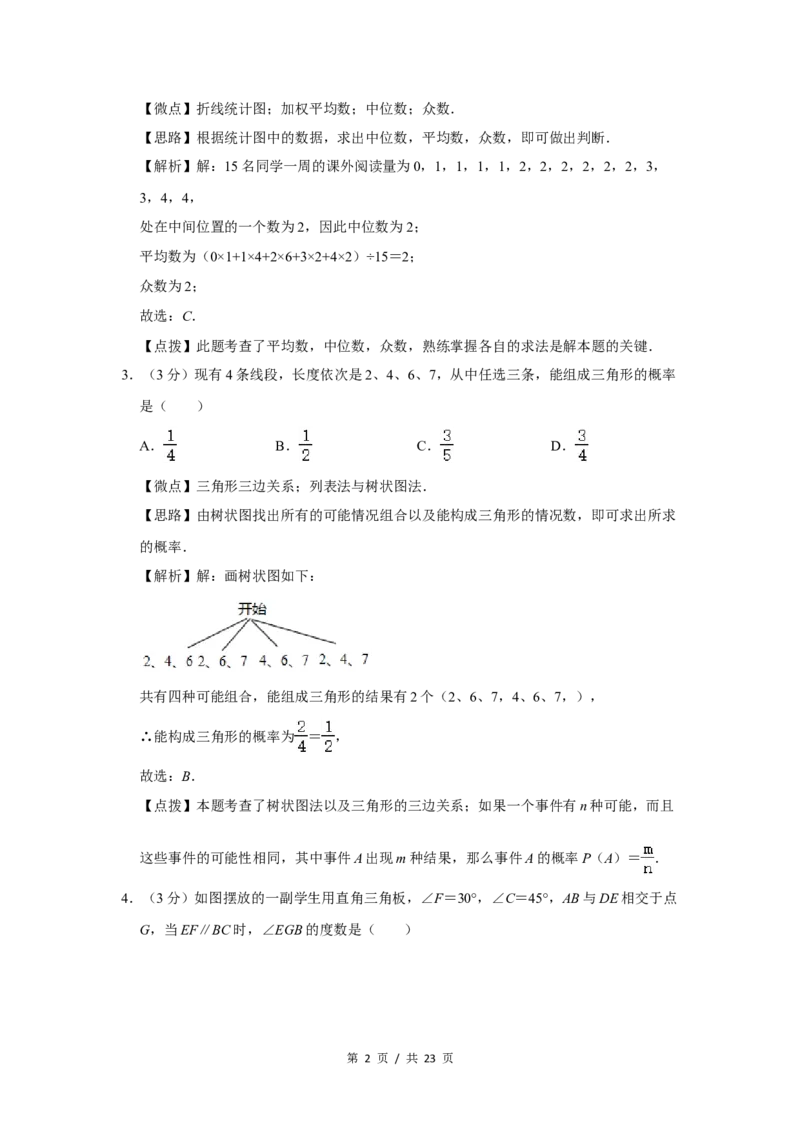
2.(3分)小明为了解本班同学一周的课外阅读量,随机抽取班上15名同学进行调查,
并将调查结果绘制成折线统计图(如图),则下列说法正确的是( )
A.中位数是3,众数是2
B.众数是1,平均数是2
C.中位数是2,众数是2
D.中位数是3,平均数是2.5
第 1 页 / 共 23 页【微点】折线统计图;加权平均数;中位数;众数.
【思路】根据统计图中的数据,求出中位数,平均数,众数,即可做出判断.
【解析】解:15名同学一周的课外阅读量为0,1,1,1,1,2,2,2,2,2,2,3,
3,4,4,
处在中间位置的一个数为2,因此中位数为2;
平均数为(0×1+1×4+2×6+3×2+4×2)÷15=2;
众数为2;
故选:C.
【点拨】此题考查了平均数,中位数,众数,熟练掌握各自的求法是解本题的关键.
3.(3分)现有4条线段,长度依次是2、4、6、7,从中任选三条,能组成三角形的概率
是( )
A. B. C. D.
【微点】三角形三边关系;列表法与树状图法.
【思路】由树状图找出所有的可能情况组合以及能构成三角形的情况数,即可求出所求
的概率.
【解析】解:画树状图如下:
共有四种可能组合,能组成三角形的结果有2个(2、6、7,4、6、7,),
∴能构成三角形的概率为 = ,
故选:B.
【点拨】本题考查了树状图法以及三角形的三边关系;如果一个事件有n种可能,而且
这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)= .
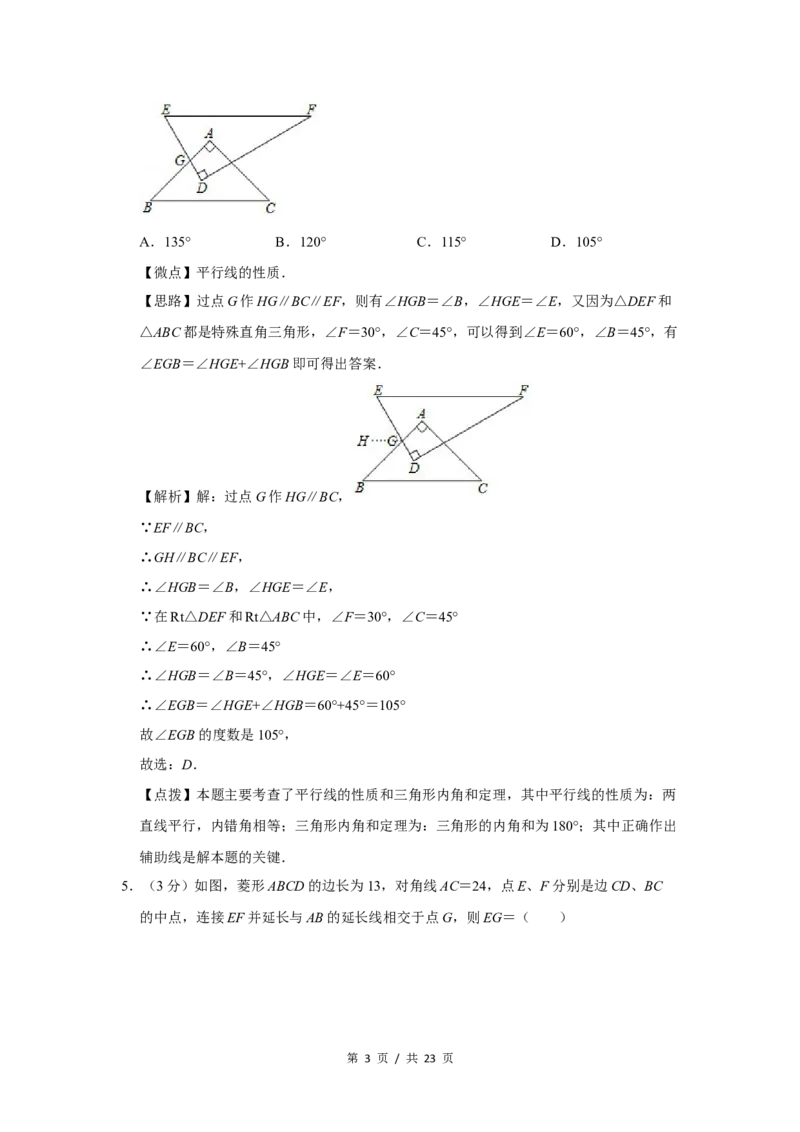
4.(3分)如图摆放的一副学生用直角三角板,∠F=30°,∠C=45°,AB与DE相交于点
G,当EF∥BC时,∠EGB的度数是( )
第 2 页 / 共 23 页A.135° B.120° C.115° D.105°
【微点】平行线的性质.
【思路】过点G作HG∥BC∥EF,则有∠HGB=∠B,∠HGE=∠E,又因为△DEF和
△ABC都是特殊直角三角形,∠F=30°,∠C=45°,可以得到∠E=60°,∠B=45°,有
∠EGB=∠HGE+∠HGB即可得出答案.
【解析】解:过点G作HG∥BC,
∵EF∥BC,
∴GH∥BC∥EF,
∴∠HGB=∠B,∠HGE=∠E,
∵在Rt△DEF和Rt△ABC中,∠F=30°,∠C=45°
∴∠E=60°,∠B=45°
∴∠HGB=∠B=45°,∠HGE=∠E=60°
∴∠EGB=∠HGE+∠HGB=60°+45°=105°
故∠EGB的度数是105°,
故选:D.
【点拨】本题主要考查了平行线的性质和三角形内角和定理,其中平行线的性质为:两
直线平行,内错角相等;三角形内角和定理为:三角形的内角和为180°;其中正确作出
辅助线是解本题的关键.
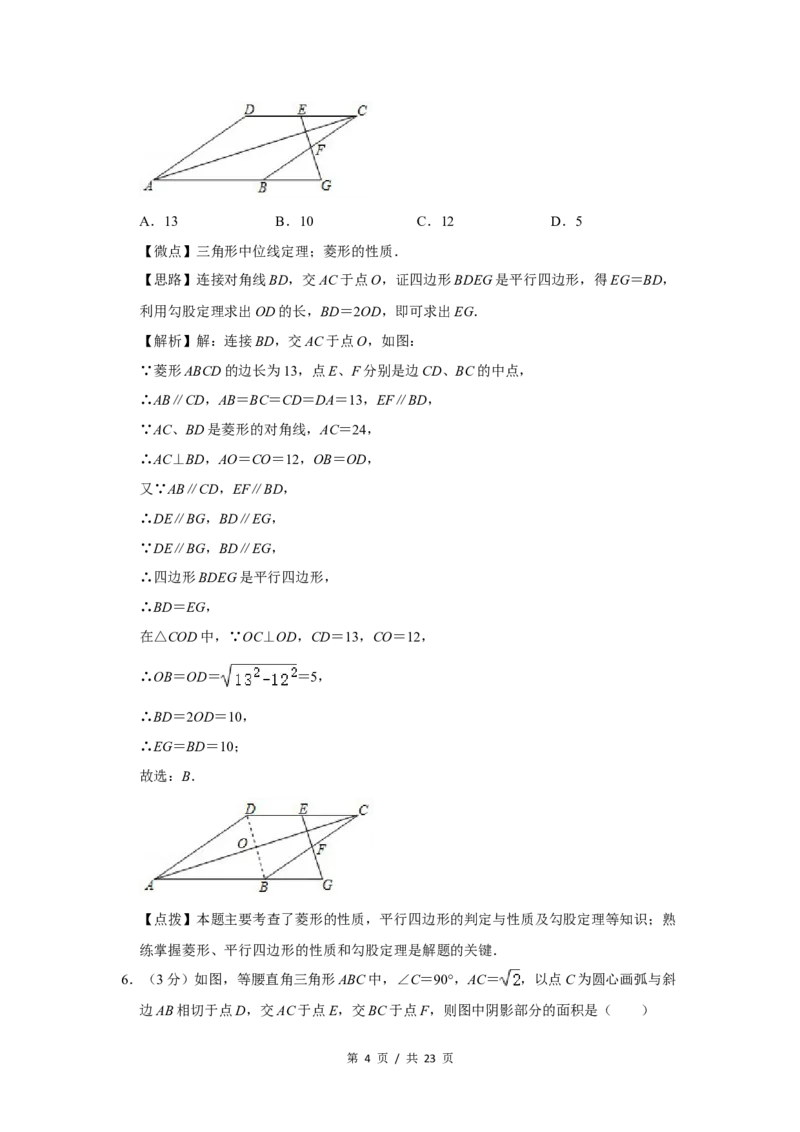
5.(3分)如图,菱形ABCD的边长为13,对角线AC=24,点E、F分别是边CD、BC
的中点,连接EF并延长与AB的延长线相交于点G,则EG=( )
第 3 页 / 共 23 页A.13 B.10 C.12 D.5
【微点】三角形中位线定理;菱形的性质.
【思路】连接对角线BD,交AC于点O,证四边形BDEG是平行四边形,得EG=BD,
利用勾股定理求出OD的长,BD=2OD,即可求出EG.
【解析】解:连接BD,交AC于点O,如图:
∵菱形ABCD的边长为13,点E、F分别是边CD、BC的中点,
∴AB∥CD,AB=BC=CD=DA=13,EF∥BD,
∵AC、BD是菱形的对角线,AC=24,
∴AC⊥BD,AO=CO=12,OB=OD,
又∵AB∥CD,EF∥BD,
∴DE∥BG,BD∥EG,
∵DE∥BG,BD∥EG,
∴四边形BDEG是平行四边形,
∴BD=EG,
在△COD中,∵OC⊥OD,CD=13,CO=12,
∴OB=OD= =5,
∴BD=2OD=10,
∴EG=BD=10;
故选:B.
【点拨】本题主要考查了菱形的性质,平行四边形的判定与性质及勾股定理等知识;熟
练掌握菱形、平行四边形的性质和勾股定理是解题的关键.
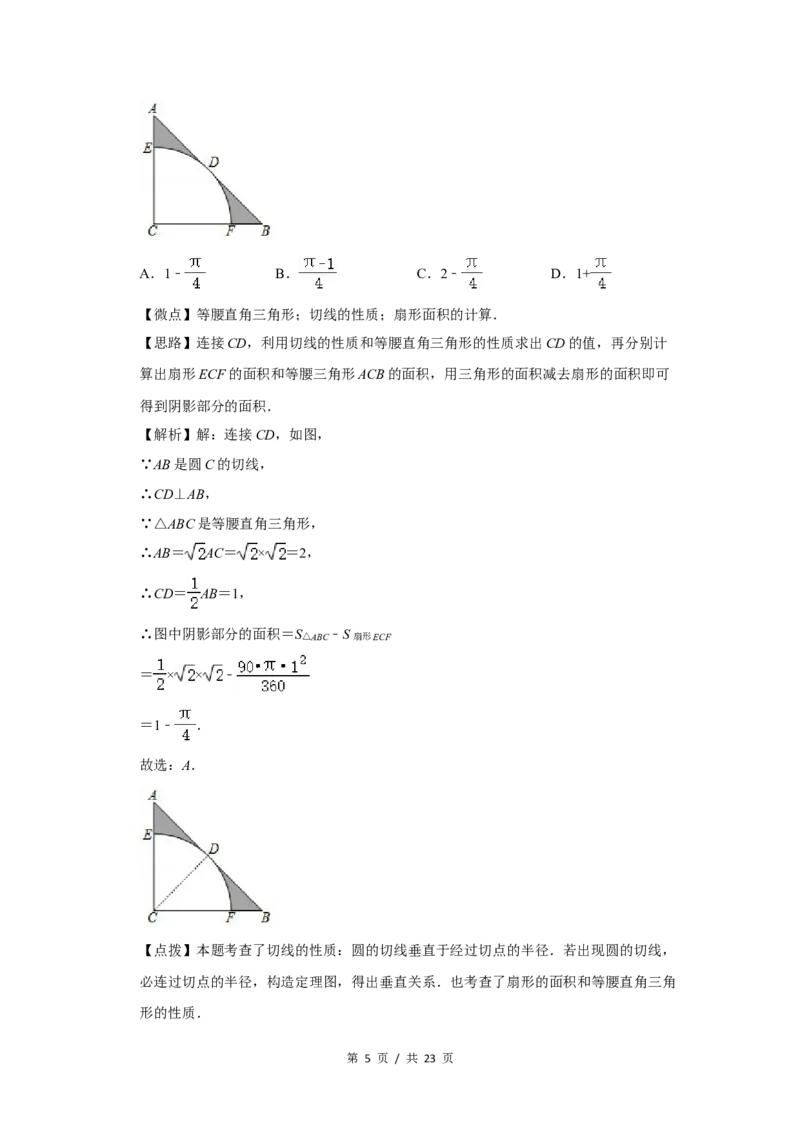
6.(3分)如图,等腰直角三角形ABC中,∠C=90°,AC= ,以点C为圆心画弧与斜
边AB相切于点D,交AC于点E,交BC于点F,则图中阴影部分的面积是( )
第 4 页 / 共 23 页A.1﹣ B. C.2﹣ D.1+
【微点】等腰直角三角形;切线的性质;扇形面积的计算.
【思路】连接CD,利用切线的性质和等腰直角三角形的性质求出CD的值,再分别计
算出扇形ECF的面积和等腰三角形ACB的面积,用三角形的面积减去扇形的面积即可
得到阴影部分的面积.
【解析】解:连接CD,如图,
∵AB是圆C的切线,
∴CD⊥AB,
∵△ABC是等腰直角三角形,
∴AB= AC= × =2,
∴CD= AB=1,
∴图中阴影部分的面积=S△ABC ﹣S扇形ECF
= × × ﹣
=1﹣ .
故选:A.
【点拨】本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,
必连过切点的半径,构造定理图,得出垂直关系.也考查了扇形的面积和等腰直角三角
形的性质.
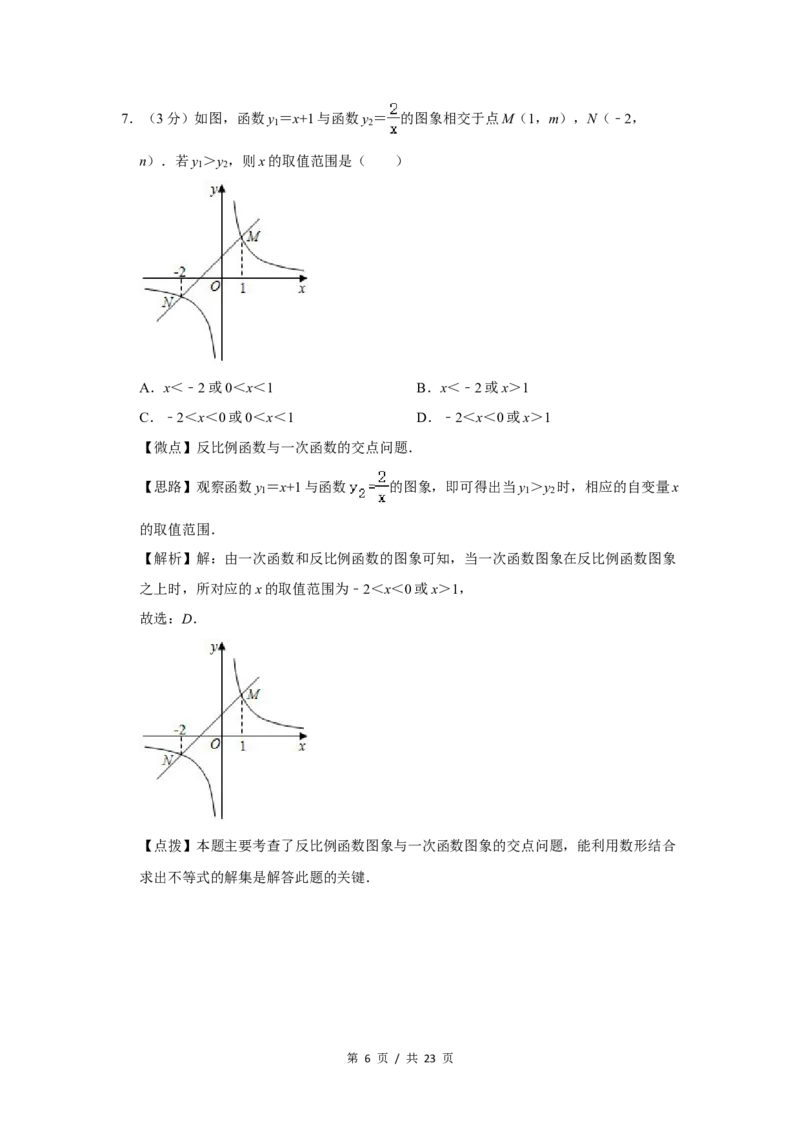
第 5 页 / 共 23 页7.(3分)如图,函数y =x+1与函数y = 的图象相交于点M(1,m),N(﹣2,
1 2
n).若y >y ,则x的取值范围是( )
1 2
A.x<﹣2或0<x<1 B.x<﹣2或x>1
C.﹣2<x<0或0<x<1 D.﹣2<x<0或x>1
【微点】反比例函数与一次函数的交点问题.
【思路】观察函数y =x+1与函数 的图象,即可得出当y >y 时,相应的自变量x
1 1 2
的取值范围.
【解析】解:由一次函数和反比例函数的图象可知,当一次函数图象在反比例函数图象
之上时,所对应的x的取值范围为﹣2<x<0或x>1,
故选:D.
【点拨】本题主要考查了反比例函数图象与一次函数图象的交点问题,能利用数形结合
求出不等式的解集是解答此题的关键.
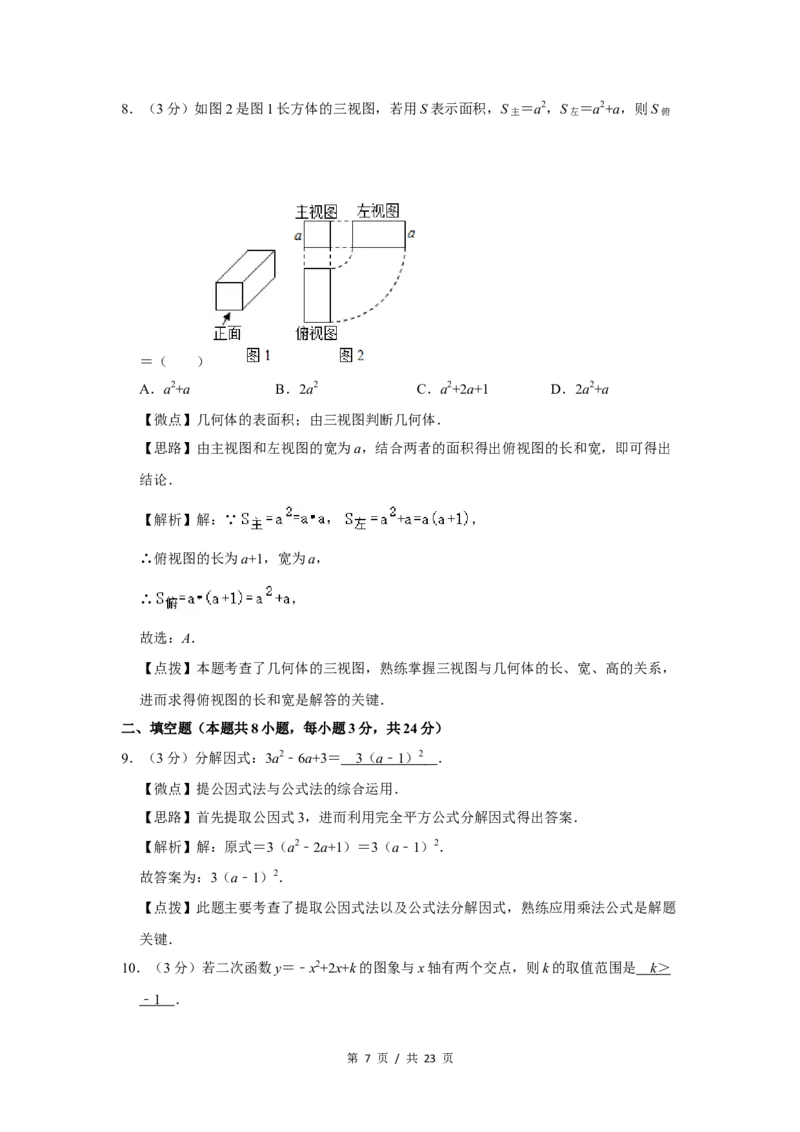
第 6 页 / 共 23 页8.(3分)如图2是图1长方体的三视图,若用S表示面积,S主 =a2,S左 =a2+a,则S俯
=( )
A.a2+a B.2a2 C.a2+2a+1 D.2a2+a
【微点】几何体的表面积;由三视图判断几何体.
【思路】由主视图和左视图的宽为a,结合两者的面积得出俯视图的长和宽,即可得出
结论.
【解析】解:∵ ,
∴俯视图的长为a+1,宽为a,
∴ ,
故选:A.
【点拨】本题考查了几何体的三视图,熟练掌握三视图与几何体的长、宽、高的关系,
进而求得俯视图的长和宽是解答的关键.
二、填空题(本题共8小题,每小题3分,共24分)
9.(3分)分解因式:3a2﹣6a+3= 3 ( a ﹣ 1 ) 2 .
【微点】提公因式法与公式法的综合运用.
【思路】首先提取公因式3,进而利用完全平方公式分解因式得出答案.
【解析】解:原式=3(a2﹣2a+1)=3(a﹣1)2.
故答案为:3(a﹣1)2.
【点拨】此题主要考查了提取公因式法以及公式法分解因式,熟练应用乘法公式是解题
关键.
10.(3分)若二次函数y=﹣x2+2x+k的图象与x轴有两个交点,则k的取值范围是 k >
﹣ 1 .
第 7 页 / 共 23 页【微点】抛物线与x轴的交点.
【思路】根据二次函数y=﹣x2+2x+k的图象与x轴有两个交点,可知判别式△>0,列
出不等式并解之即可求出k的取值范围.
【解析】解:∵二次函数y=﹣x2+2x+k的图象与x轴有两个交点,
∴△=4﹣4×(﹣1)•k>0,
解得:k>﹣1,
故答案为:k>﹣1.
【点拨】本题考查二次函数的判别式、解一元一次不等式,熟记二次函数的图象与判别
式的三种对应关系并熟练运用是解答的关键.
11.(3分)有三张大小、形状完全相同的卡片.卡片上分别写有数字4、5、6,从这三张
卡片中随机先后不放回地抽取两张,则两次抽出数字之和为奇数的概率是 .
【微点】列表法与树状图法.
【思路】列表得出所有情况,看取出的两张卡片上的数字之和为奇数的情况数占所有情
况数的多少即可.
【解析】解:列表得:
4 5 6
4 9 10
5 9 11
6 10 11
共有6种情况,取出的两张卡片上的数字之和为奇数的情况数为4种,
∴两次抽出数字之和为奇数的概率为 .
故答案为: .
【点拨】本题考查了列表法与列树状图法以及概率公式;得到取出的两张卡片上的数字
之和为奇数的情况数是解决本题的关键;用到的知识点为:概率等于所求情况数与总情
况数之比.
12.(3分)我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:
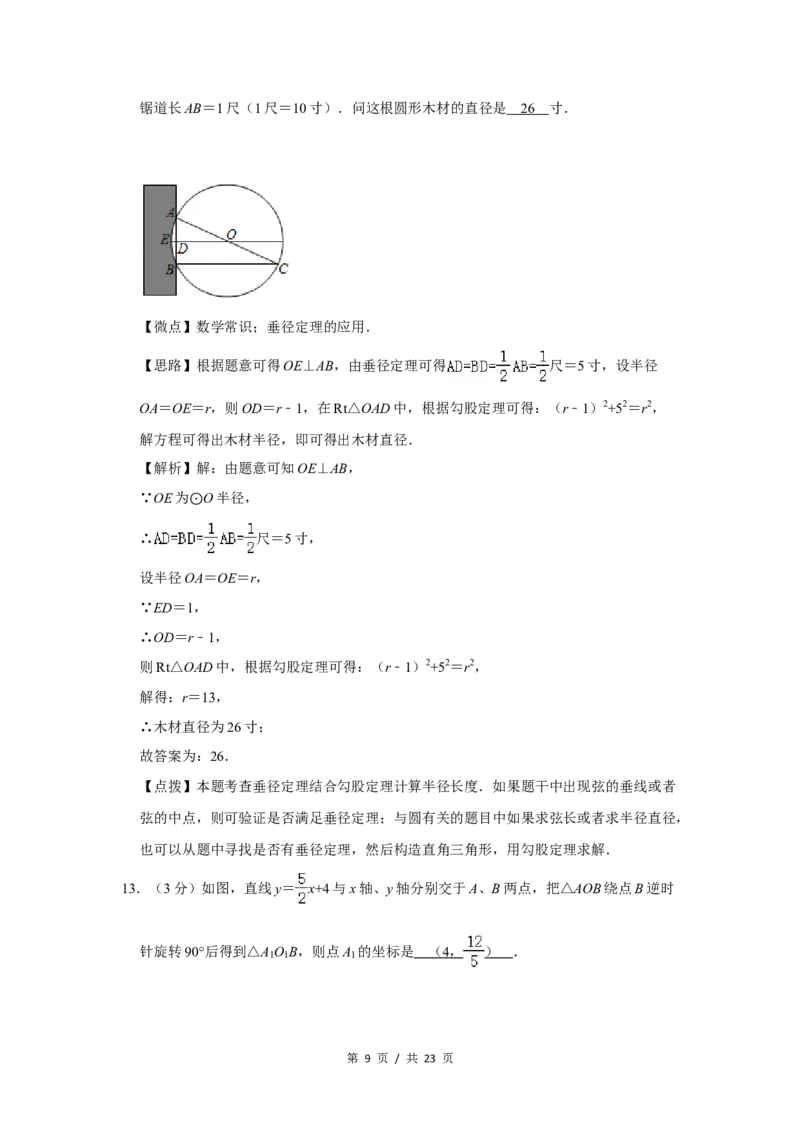
“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思
是:今有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深ED=1寸,
第 8 页 / 共 23 页锯道长AB=1尺(1尺=10寸).问这根圆形木材的直径是 2 6 寸.
【微点】数学常识;垂径定理的应用.
【思路】根据题意可得OE⊥AB,由垂径定理可得 尺=5寸,设半径
OA=OE=r,则OD=r﹣1,在Rt△OAD中,根据勾股定理可得:(r﹣1)2+52=r2,
解方程可得出木材半径,即可得出木材直径.
【解析】解:由题意可知OE⊥AB,
∵OE为 O半径,
⊙
∴ 尺=5寸,
设半径OA=OE=r,
∵ED=1,
∴OD=r﹣1,
则Rt△OAD中,根据勾股定理可得:(r﹣1)2+52=r2,
解得:r=13,
∴木材直径为26寸;
故答案为:26.
【点拨】本题考查垂径定理结合勾股定理计算半径长度.如果题干中出现弦的垂线或者
弦的中点,则可验证是否满足垂径定理;与圆有关的题目中如果求弦长或者求半径直径,
也可以从题中寻找是否有垂径定理,然后构造直角三角形,用勾股定理求解.
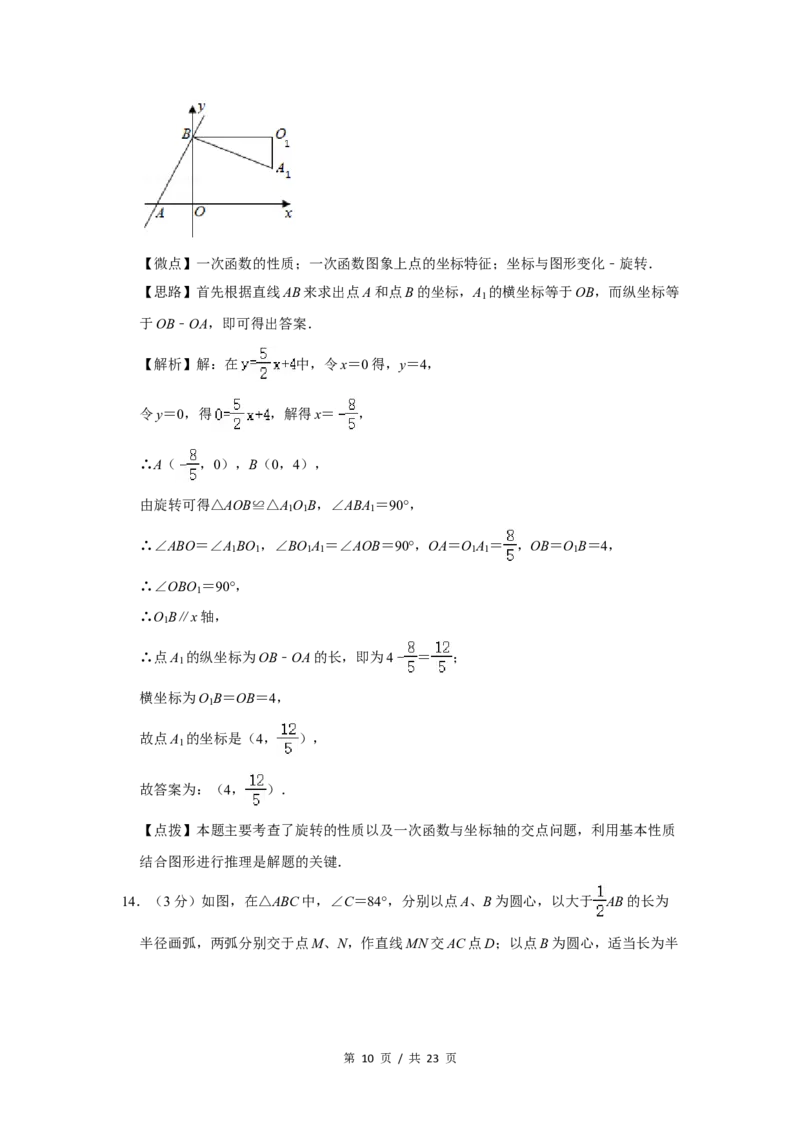
13.(3分)如图,直线y= x+4与x轴、y轴分别交于A、B两点,把△AOB绕点B逆时
针旋转90°后得到△A O B,则点A 的坐标是 ( 4 , ) .
1 1 1
第 9 页 / 共 23 页【微点】一次函数的性质;一次函数图象上点的坐标特征;坐标与图形变化﹣旋转.
【思路】首先根据直线AB来求出点A和点B的坐标,A 的横坐标等于OB,而纵坐标等
1
于OB﹣OA,即可得出答案.
【解析】解:在 中,令x=0得,y=4,
令y=0,得 ,解得x= ,
∴A( ,0),B(0,4),
由旋转可得△AOB≌△A O B,∠ABA =90°,
1 1 1
∴∠ABO=∠A BO ,∠BO A =∠AOB=90°,OA=O A = ,OB=O B=4,
1 1 1 1 1 1 1
∴∠OBO =90°,
1
∴O B∥x轴,
1
∴点A 的纵坐标为OB﹣OA的长,即为4 = ;
1
横坐标为O B=OB=4,
1
故点A 的坐标是(4, ),
1
故答案为:(4, ).
【点拨】本题主要考查了旋转的性质以及一次函数与坐标轴的交点问题,利用基本性质
结合图形进行推理是解题的关键.
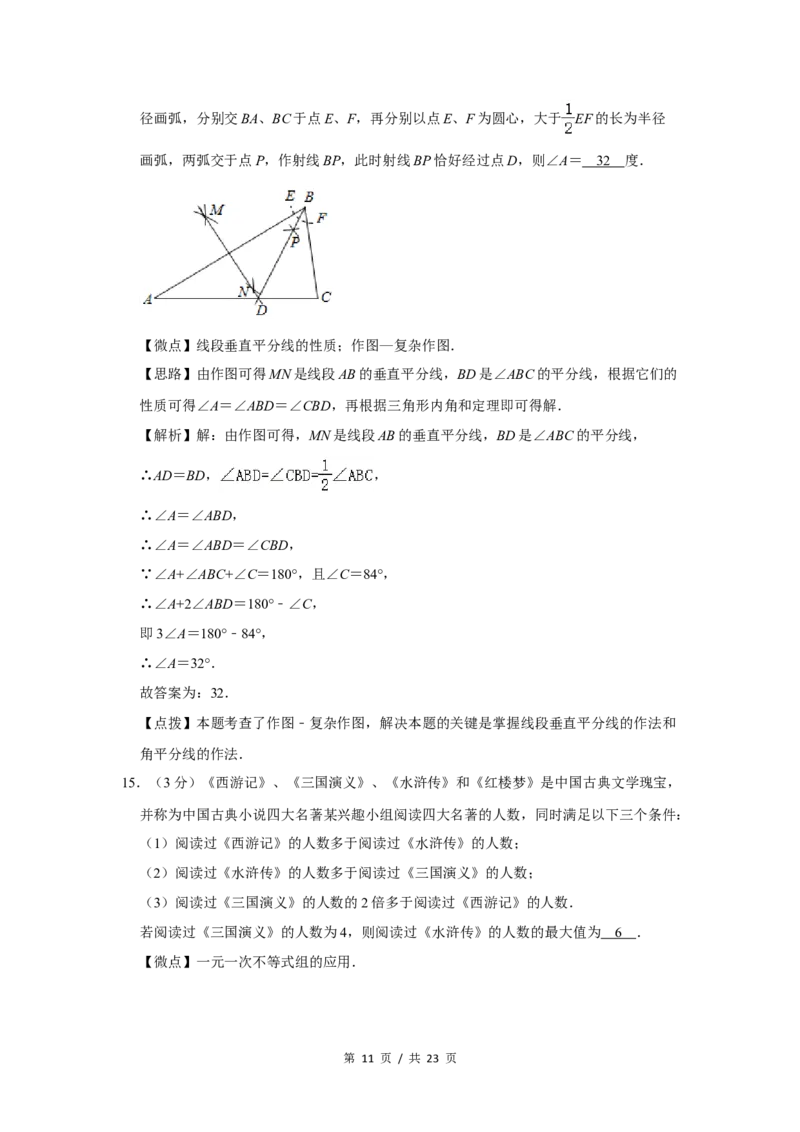
14.(3分)如图,在△ABC中,∠C=84°,分别以点A、B为圆心,以大于 AB的长为
半径画弧,两弧分别交于点M、N,作直线MN交AC点D;以点B为圆心,适当长为半
第 10 页 / 共 23 页径画弧,分别交BA、BC于点E、F,再分别以点E、F为圆心,大于 EF的长为半径
画弧,两弧交于点P,作射线BP,此时射线BP恰好经过点D,则∠A= 3 2 度.
【微点】线段垂直平分线的性质;作图—复杂作图.
【思路】由作图可得MN是线段AB的垂直平分线,BD是∠ABC的平分线,根据它们的
性质可得∠A=∠ABD=∠CBD,再根据三角形内角和定理即可得解.
【解析】解:由作图可得,MN是线段AB的垂直平分线,BD是∠ABC的平分线,
∴AD=BD, ,
∴∠A=∠ABD,
∴∠A=∠ABD=∠CBD,
∵∠A+∠ABC+∠C=180°,且∠C=84°,
∴∠A+2∠ABD=180°﹣∠C,
即3∠A=180°﹣84°,
∴∠A=32°.
故答案为:32.
【点拨】本题考查了作图﹣复杂作图,解决本题的关键是掌握线段垂直平分线的作法和
角平分线的作法.
15.(3分)《西游记》、《三国演义》、《水浒传》和《红楼梦》是中国古典文学瑰宝,
并称为中国古典小说四大名著某兴趣小组阅读四大名著的人数,同时满足以下三个条件:
(1)阅读过《西游记》的人数多于阅读过《水浒传》的人数;
(2)阅读过《水浒传》的人数多于阅读过《三国演义》的人数;
(3)阅读过《三国演义》的人数的2倍多于阅读过《西游记》的人数.
若阅读过《三国演义》的人数为4,则阅读过《水浒传》的人数的最大值为 6 .
【微点】一元一次不等式组的应用.
第 11 页 / 共 23 页【思路】设阅读过《西游记》的人数是a,阅读过《水浒传》的人数是b(a,b均为整
数),根据给定的三个条件,即可得出关于a,b的二元一次不等式组,结合a,b均为
整数即可得出b的取值范围,再取其中最大的整数值即可得出结论.
【解析】解:设阅读过《西游记》的人数是a,阅读过《水浒传》的人数是b(a,b均
为整数),
依题意,得: ,
∵a,b均为整数
∴4<b<7,
∴b最大可以取6.
故答案为:6.
【点拨】本题考查二元一次不等式组的应用,根据各数量之间的关系,正确列出二元一
次不等式组是解题的关键.
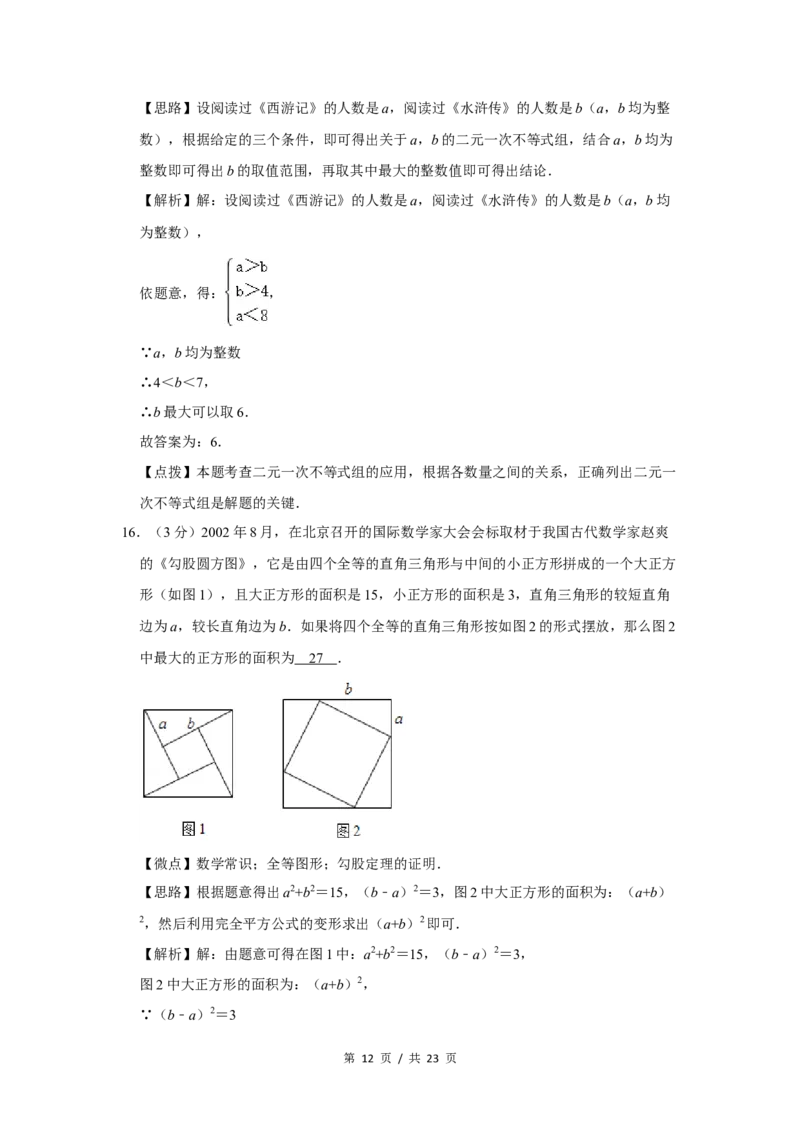
16.(3分)2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽
的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方
形(如图1),且大正方形的面积是15,小正方形的面积是3,直角三角形的较短直角
边为a,较长直角边为b.如果将四个全等的直角三角形按如图2的形式摆放,那么图2
中最大的正方形的面积为 2 7 .
【微点】数学常识;全等图形;勾股定理的证明.
【思路】根据题意得出a2+b2=15,(b﹣a)2=3,图2中大正方形的面积为:(a+b)
2,然后利用完全平方公式的变形求出(a+b)2即可.
【解析】解:由题意可得在图1中:a2+b2=15,(b﹣a)2=3,
图2中大正方形的面积为:(a+b)2,
∵(b﹣a)2=3
第 12 页 / 共 23 页a2﹣2ab+b2=3,
∴15﹣2ab=3
2ab=12,
∴(a+b)2=a2+2ab+b2=15+12=27,
故答案为:27.
【点拨】本题考查了完全平方公式在几何图形中的应用,熟知完全平方式的形式是解题
关键.
三、解答题(本题共有6个小题,每小题6分,共36分)
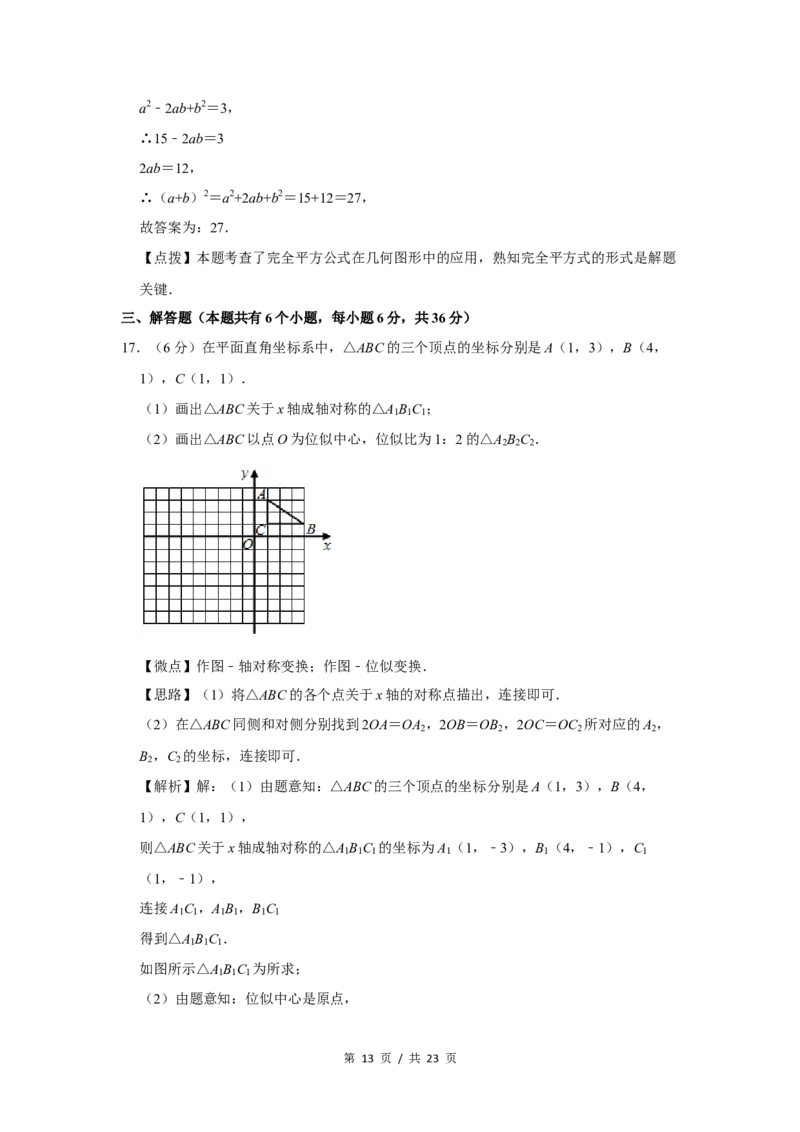
17.(6分)在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(1,3),B(4,
1),C(1,1).
(1)画出△ABC关于x轴成轴对称的△A B C ;
1 1 1
(2)画出△ABC以点O为位似中心,位似比为1:2的△A B C .
2 2 2
【微点】作图﹣轴对称变换;作图﹣位似变换.
【思路】(1)将△ABC的各个点关于x轴的对称点描出,连接即可.
(2)在△ABC同侧和对侧分别找到2OA=OA ,2OB=OB ,2OC=OC 所对应的A ,
2 2 2 2
B ,C 的坐标,连接即可.
2 2
【解析】解:(1)由题意知:△ABC的三个顶点的坐标分别是A(1,3),B(4,
1),C(1,1),
则△ABC关于x轴成轴对称的△A B C 的坐标为A (1,﹣3),B (4,﹣1),C
1 1 1 1 1 1
(1,﹣1),
连接A C ,A B ,B C
1 1 1 1 1 1
得到△A B C .
1 1 1
如图所示△A B C 为所求;
1 1 1
(2)由题意知:位似中心是原点,
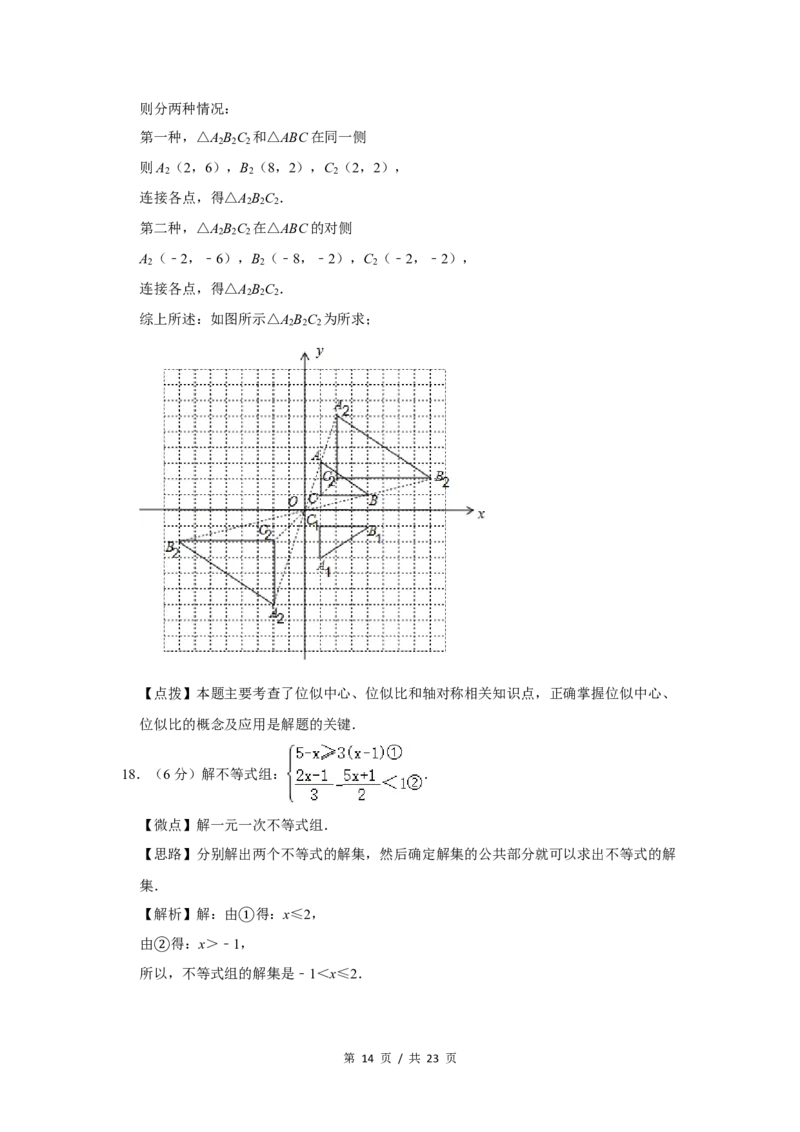
第 13 页 / 共 23 页则分两种情况:
第一种,△A B C 和△ABC在同一侧
2 2 2
则A (2,6),B (8,2),C (2,2),
2 2 2
连接各点,得△A B C .
2 2 2
第二种,△A B C 在△ABC的对侧
2 2 2
A (﹣2,﹣6),B (﹣8,﹣2),C (﹣2,﹣2),
2 2 2
连接各点,得△A B C .
2 2 2
综上所述:如图所示△A B C 为所求;
2 2 2
【点拨】本题主要考查了位似中心、位似比和轴对称相关知识点,正确掌握位似中心、
位似比的概念及应用是解题的关键.
18.(6分)解不等式组: .
【微点】解一元一次不等式组.
【思路】分别解出两个不等式的解集,然后确定解集的公共部分就可以求出不等式的解
集.
【解析】解:由 得:x≤2,
由 得:x>﹣1①,
所②以,不等式组的解集是﹣1<x≤2.
第 14 页 / 共 23 页【点拨】本题考查了不等式组的解法,关键是求出两个不等式的解,然后根据口诀求出
不等式组的解集.
19.(6分)先化简,再求值:( + )÷ ,其中a= .
【微点】分式的化简求值.
【思路】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变
形,约分得到最简结果,代入计算即可求出值.
【解析】解:原式=
=
=
当 时,原式= .
【点拨】本题考查了分式的化简求值,解题的关键是选择正确的计算方法,对通分、分
解因式、约分等知识点熟练掌握.
20.(6分)在“抗击疫情”期间,某学校工会号召广大教师积极开展了“献爱心捐款”
活动,学校拟用这笔捐款购买A、B两种防疫物品.如果购买A种物品60件,B种物品
45件,共需1140元;如果购买A种物品45件,B种物品30件,共需840元.
(1)求A、B两种防疫物品每件各多少元;
(2)现要购买A、B两种防疫物品共600件,总费用不超过7000元,那么A种防疫物
品最多购买多少件?
【微点】二元一次方程组的应用;一元一次不等式的应用.
【思路】(1)设A种防疫物品每件x元,B种防疫物品每件y元,根据“如果购买A种
物品60件,B种物品45件,共需1140元;如果购买A种物品45件,B种物品30件,
共需840元”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设购买A种防疫物品m件,则购买B种防疫物品(600﹣m)件,根据总价=单价
×购买数量结合总费用不超过7000元,即可得出关于m的一元一次不等式,解之取其中
最大的整数值即可得出结论.
【解析】解:(1)设A种防疫物品每件x元,B种防疫物品每件y元,
第 15 页 / 共 23 页依题意,得: ,
解得: .
答:A种防疫物品每件16元,B种防疫物品每件4元.
(2)设购买A种防疫物品m件,则购买B种防疫物品(600﹣m)件,
依题意,得:16m+4(600﹣m)≤7000,
解得:m≤383 ,
又∵m为正整数,
∴m的最大值为383.
答:A种防疫物品最多购买383件.
【点拨】本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:
(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列
出一元一次不等式.
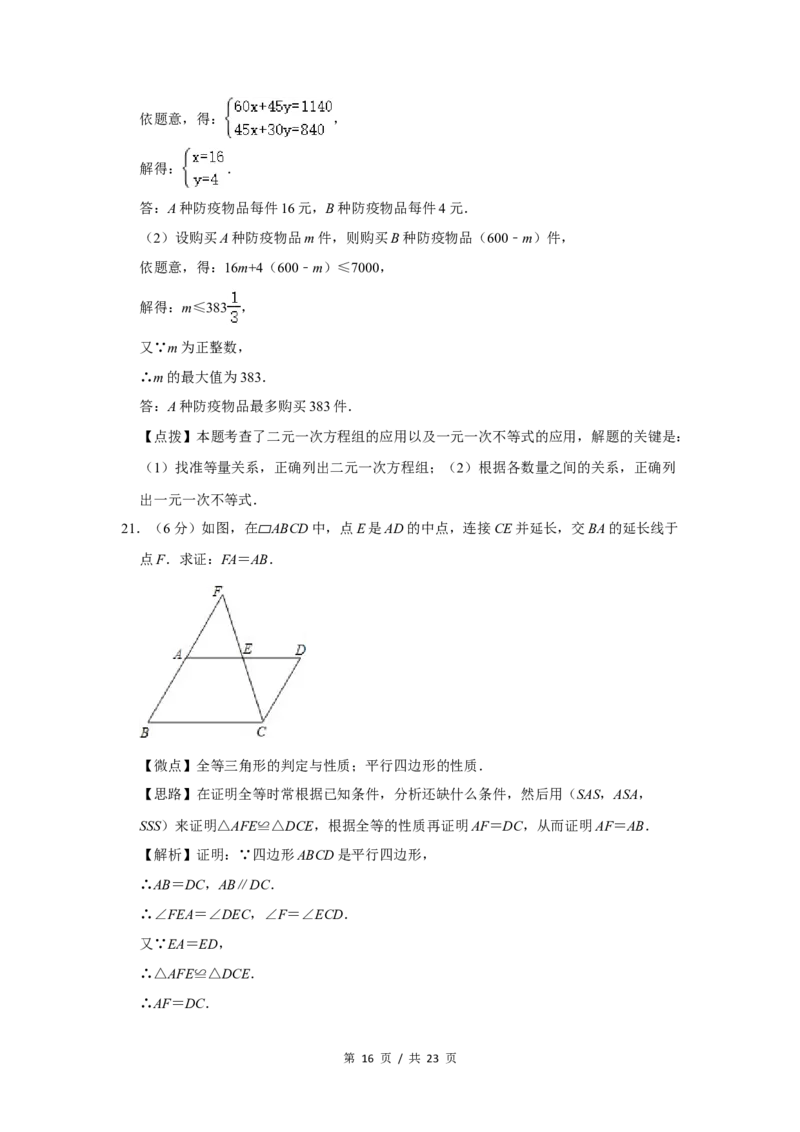
21.(6分)如图,在 ABCD中,点E是AD的中点,连接CE并延长,交BA的延长线于
点F.求证:FA=A▱B.
【微点】全等三角形的判定与性质;平行四边形的性质.
【思路】在证明全等时常根据已知条件,分析还缺什么条件,然后用(SAS,ASA,
SSS)来证明△AFE≌△DCE,根据全等的性质再证明AF=DC,从而证明AF=AB.
【解析】证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC.
∴∠FEA=∠DEC,∠F=∠ECD.
又∵EA=ED,
∴△AFE≌△DCE.
∴AF=DC.
第 16 页 / 共 23 页∴AF=AB.
【点拨】本题考查平行四边形的性质及全等三角形等知识,是比较基础的证明题.
22.(6分)某家庭记录了未使用节水龙头20天的日用水量数据(单位:m3)和使用了节
水龙头20天的日用水量数据,得到频数分布表如下:
未使用节水龙头20天的日用水量频数分布表:
日用水量/m3 0≤x<0.1 0.1≤x<0.2 0.2≤x<0.3 0.3≤x<0.4 0.4≤x<0.5
频数 0 4 2 4 10
使用了节水龙头20天的日用水量频数分布表:
日用水量/m3 0≤x<0.1 0.1≤x<0.2 0.2≤x<0.3 0.3≤x<0.4
频数 2 6 8 4
(1)计算未使用节水龙头20天的日平均用水量和使用了节水龙头20天的日平均用水
量;
(2)估计该家庭使用节水龙头后,一年能节省多少立方米水?(一年按365天计算)
【微点】用样本估计总体;频数(率)分布表;加权平均数.
【思路】(1)取组中值,运用加权平均数分别计算出未使用节水龙头20天的日平均用
水量和使用了节水龙头20天的日平均用水量即可;
(2)先计算平均一天节水量,再乘以365即可得到结果.
【解析】解:(1)未使用节水龙头20天的日平均用水量为: ×
(0×0.05+4×0.15+2×0.25+4×0.35+10×0.45)=0.35(m3),
使用了节水龙头20天的日平均用水量为: ×(2×0.05+6×0.15+8×0.25+4×0.35)=0.22
(m3);
(2)365×(0.35﹣0.22)=365×0.13=47.45(m3),
答:估计该家庭使用节水龙头后,一年能节省47.45m3水.
【点拨】此题主要考查节水量的估计值的求法,考查加权平均数等基础知识,考查运算
求解能力,是基础题.
四、解答题(本题共4道题,其中23、24题每题8分,25、26题每题10分,共36分)
23.(8分)如图,在△ABC中,∠B=90°,点D为AC上一点,以CD为直径的 O交
AB于点E,连接CE,且CE平分∠ACB. ⊙
(1)求证:AE是 O的切线;
⊙
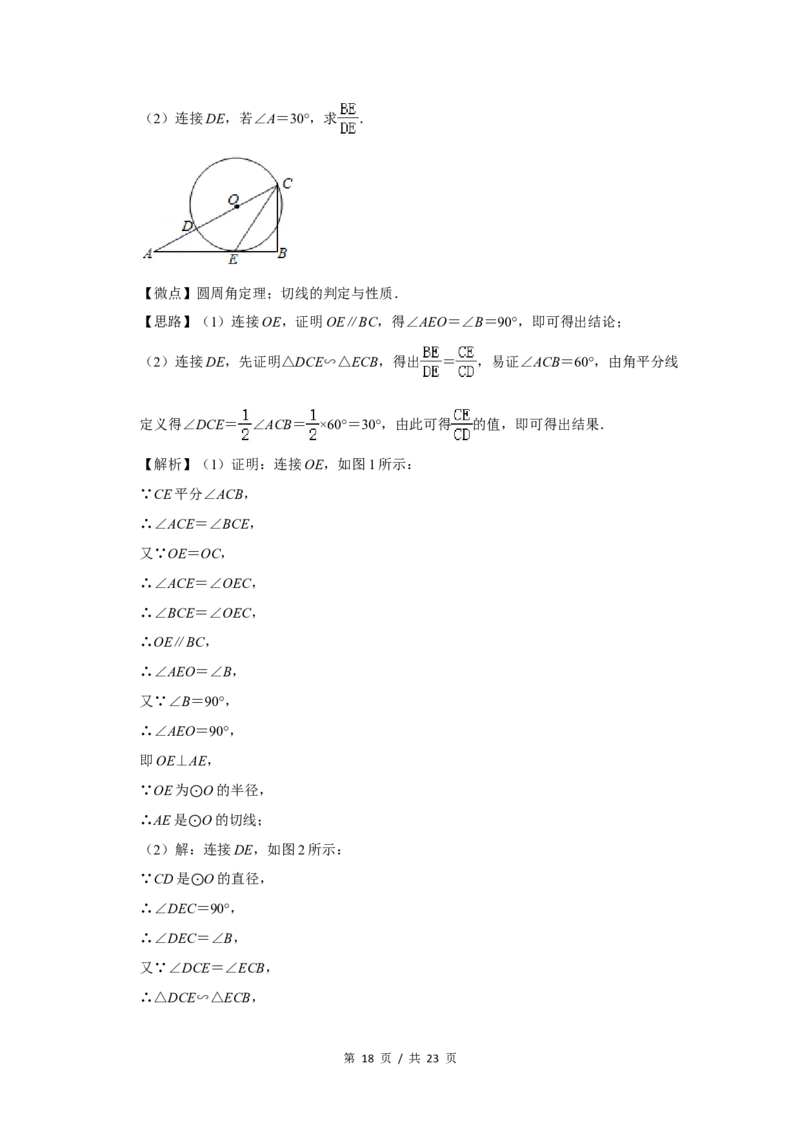
第 17 页 / 共 23 页(2)连接DE,若∠A=30°,求 .
【微点】圆周角定理;切线的判定与性质.
【思路】(1)连接OE,证明OE∥BC,得∠AEO=∠B=90°,即可得出结论;
(2)连接DE,先证明△DCE∽△ECB,得出 = ,易证∠ACB=60°,由角平分线
定义得∠DCE= ∠ACB= ×60°=30°,由此可得 的值,即可得出结果.
【解析】(1)证明:连接OE,如图1所示:
∵CE平分∠ACB,
∴∠ACE=∠BCE,
又∵OE=OC,
∴∠ACE=∠OEC,
∴∠BCE=∠OEC,
∴OE∥BC,
∴∠AEO=∠B,
又∵∠B=90°,
∴∠AEO=90°,
即OE⊥AE,
∵OE为 O的半径,
∴AE是⊙O的切线;
(2)解⊙:连接DE,如图2所示:
∵CD是 O的直径,
∴∠DEC⊙=90°,
∴∠DEC=∠B,
又∵∠DCE=∠ECB,
∴△DCE∽△ECB,
第 18 页 / 共 23 页∴ = ,
∵∠A=30°,∠B=90°,
∴∠ACB=60°,
∴∠DCE= ∠ACB= ×60°=30°,
∴ =cos∠DCE=cos30°= ,
∴ = .
【点拨】本题考查了平行线的判定与性质、角平分线定义、切线的判定、圆周角定理、
相似三角形的判定和性质、锐角三角函数等知识;结合题意灵活运用知识点是解题关键.
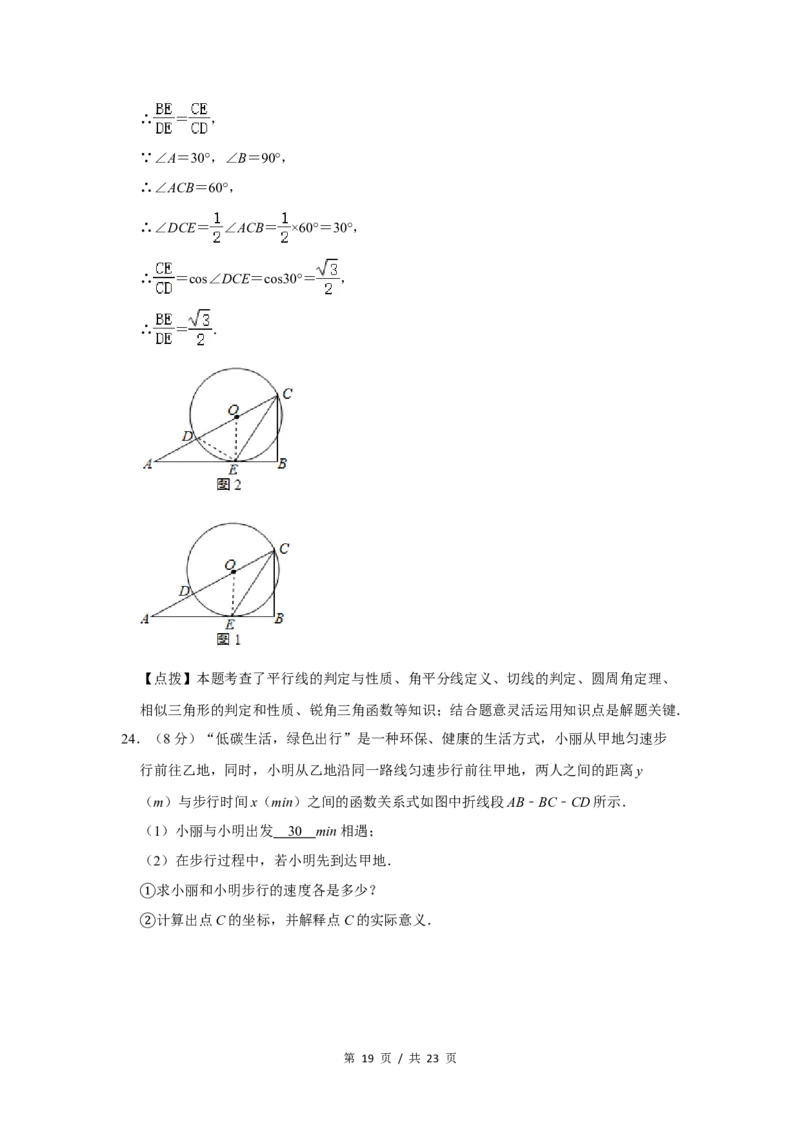
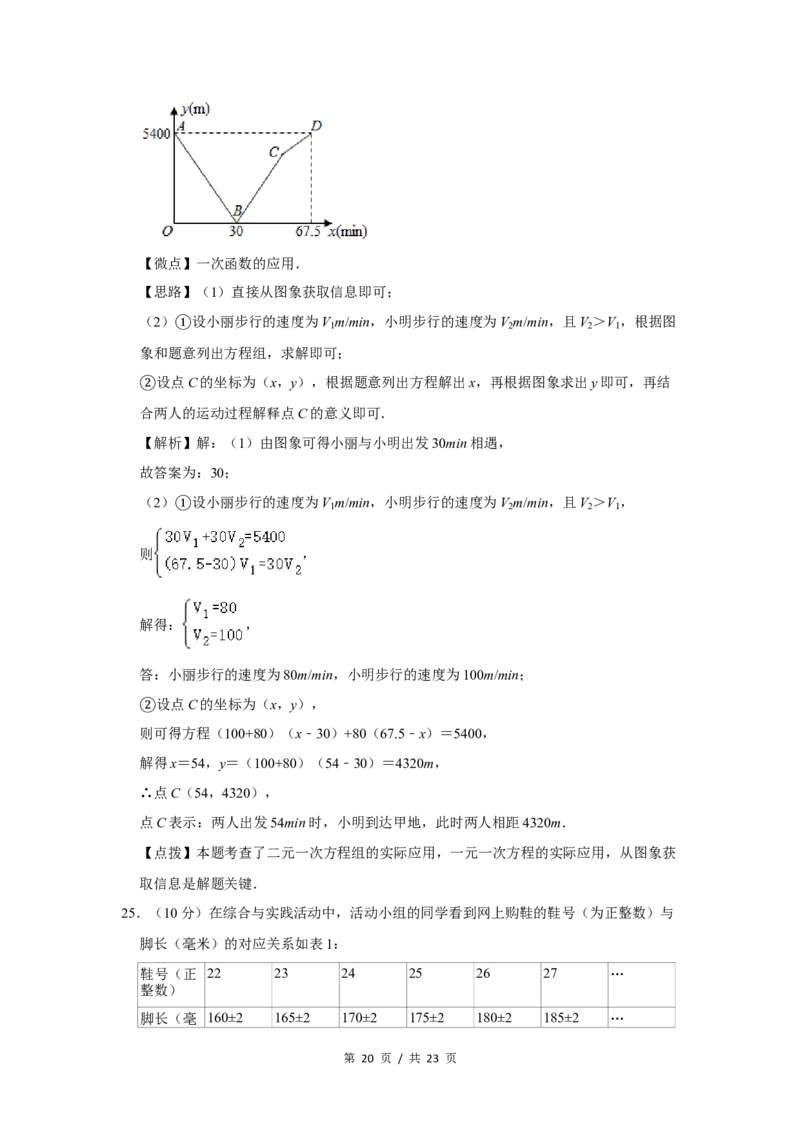
24.(8分)“低碳生活,绿色出行”是一种环保、健康的生活方式,小丽从甲地匀速步
行前往乙地,同时,小明从乙地沿同一路线匀速步行前往甲地,两人之间的距离y
(m)与步行时间x(min)之间的函数关系式如图中折线段AB﹣BC﹣CD所示.
(1)小丽与小明出发 3 0 min相遇;
(2)在步行过程中,若小明先到达甲地.
求小丽和小明步行的速度各是多少?
①计算出点C的坐标,并解释点C的实际意义.
②
第 19 页 / 共 23 页【微点】一次函数的应用.
【思路】(1)直接从图象获取信息即可;
(2) 设小丽步行的速度为V m/min,小明步行的速度为V m/min,且V >V ,根据图
1 2 2 1
象和题①意列出方程组,求解即可;
设点C的坐标为(x,y),根据题意列出方程解出x,再根据图象求出y即可,再结
②合两人的运动过程解释点C的意义即可.
【解析】解:(1)由图象可得小丽与小明出发30min相遇,
故答案为:30;
(2) 设小丽步行的速度为V m/min,小明步行的速度为V m/min,且V >V ,
1 2 2 1
①
则 ,
解得: ,
答:小丽步行的速度为80m/min,小明步行的速度为100m/min;
设点C的坐标为(x,y),
②则可得方程(100+80)(x﹣30)+80(67.5﹣x)=5400,
解得x=54,y=(100+80)(54﹣30)=4320m,
∴点C(54,4320),
点C表示:两人出发54min时,小明到达甲地,此时两人相距4320m.
【点拨】本题考查了二元一次方程组的实际应用,一元一次方程的实际应用,从图象获
取信息是解题关键.
25.(10分)在综合与实践活动中,活动小组的同学看到网上购鞋的鞋号(为正整数)与
脚长(毫米)的对应关系如表1:
鞋号(正 22 23 24 25 26 27 …
整数)
脚长(毫 160±2 165±2 170±2 175±2 180±2 185±2 …
第 20 页 / 共 23 页米)
为了方便对问题的研究,活动小组将表1中的数据进行了编号,并对脚长的数据b 定义
n
为[b ]如表2:
n
序号n 1 2 3 4 5 6 …
鞋号a 22 23 24 25 26 27 …
n
脚长b 160±2 165±2 170±2 175±2 180±2 185±2 …
n
脚长[b ] 160 165 170 175 180 185 …
n
定义:对于任意正整数m、n,其中m>2.若[b ]=m,则m﹣2≤b ≤m+2.
n n
如:[b ]=175表示175﹣2≤b ≤175+2,即173≤b ≤177.
4 4 4
(1)通过观察表2,猜想出a 与序号n之间的关系式,[b ]与序号n之间的关系式;
n n
(2)用含a 的代数式表示[b ];计算鞋号为42的鞋适合的脚长范围;
n n
(3)若脚长为271毫米,那么应购鞋的鞋号为多大?
【微点】一元一次方程的应用;一元一次不等式组的应用.
【思路】(1)观察表格里的数据,可直接得出结论;
(2)把n用含有a 的式子表示出来,代入[b ]=5n+155化简整理,再计算鞋号为42对
n n
应的n的值,代入[b ]=5n+155求解即可;
n
(3)首先计算[b ]=270,再代入[b ]=5a +50求出a 的值即可.
n n n n
【解析】解:(1)a =21+n;
n
[b ]=160+5(n﹣1)=5n+155;
n
(2)由a =21+n与[b ]=5n+155解得:[b ]=5a +50,
n n n n
把a =42代入a =21+n得n=21,
n n
所以[b ]=5×42+50=260,
21
则:260﹣2≤b ≤260+2,即258≤b ≤262.
21 21
答:鞋号为42的鞋适合的脚长范围是258mm~262mm;
(3)根据[b ]=5n+155可知[b ]能被5整除,
n n
∵270﹣2≤271≤270+2,
∴[b ]=270,
n
将[b ]=270代入[b ]=5a +50中得a =44.
n n n n
故应购买44号的鞋.
【点拨】此题主要考查了一元一次不等式组的应用,一元一次方程的应用,读懂题意是
解题的关键.
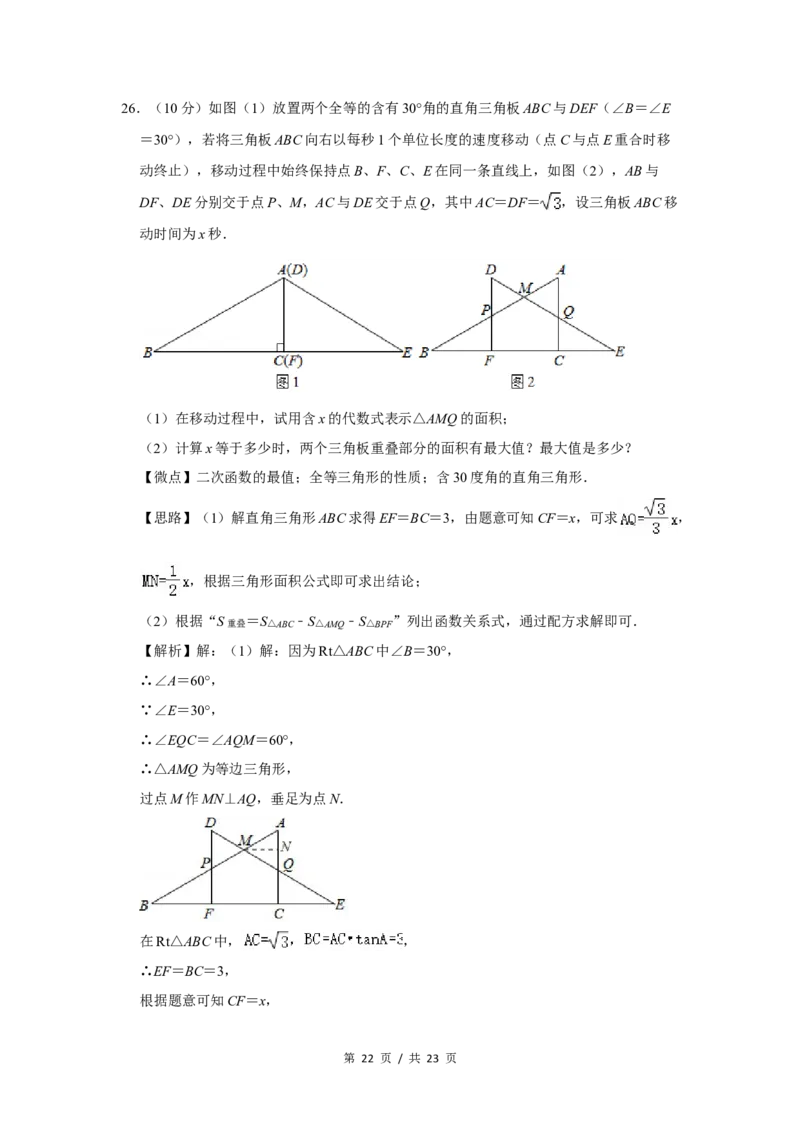
第 21 页 / 共 23 页26.(10分)如图(1)放置两个全等的含有30°角的直角三角板ABC与DEF(∠B=∠E
=30°),若将三角板ABC向右以每秒1个单位长度的速度移动(点C与点E重合时移
动终止),移动过程中始终保持点B、F、C、E在同一条直线上,如图(2),AB与
DF、DE分别交于点P、M,AC与DE交于点Q,其中AC=DF= ,设三角板ABC移
动时间为x秒.
(1)在移动过程中,试用含x的代数式表示△AMQ的面积;
(2)计算x等于多少时,两个三角板重叠部分的面积有最大值?最大值是多少?
【微点】二次函数的最值;全等三角形的性质;含30度角的直角三角形.
【思路】(1)解直角三角形ABC求得EF=BC=3,由题意可知CF=x,可求 ,
,根据三角形面积公式即可求出结论;
(2)根据“S重叠 =S△ABC ﹣S△AMQ ﹣S△BPF ”列出函数关系式,通过配方求解即可.
【解析】解:(1)解:因为Rt△ABC中∠B=30°,
∴∠A=60°,
∵∠E=30°,
∴∠EQC=∠AQM=60°,
∴△AMQ为等边三角形,
过点M作MN⊥AQ,垂足为点N.
在Rt△ABC中, ,
∴EF=BC=3,
根据题意可知CF=x,
第 22 页 / 共 23 页∴CE=EF﹣CF=3﹣x ,
∴ ,
∴ ,
而 ,
∴ ,
(2)由(1)知BF=CE=3﹣x ,
∴ =
= ,
所以当x=2时,重叠部分面积最大,最大面积是 .
【点拨】本题属于几何变换综合题,考查了平移变换,等边三角形的性质和判定,解直
角三角形,二次函数的性质等知识,解题的关键是灵活运用所学知识解决问题,学会用
分类讨论的思想思考问题,属于中考压轴题.
第 23 页 / 共 23 页