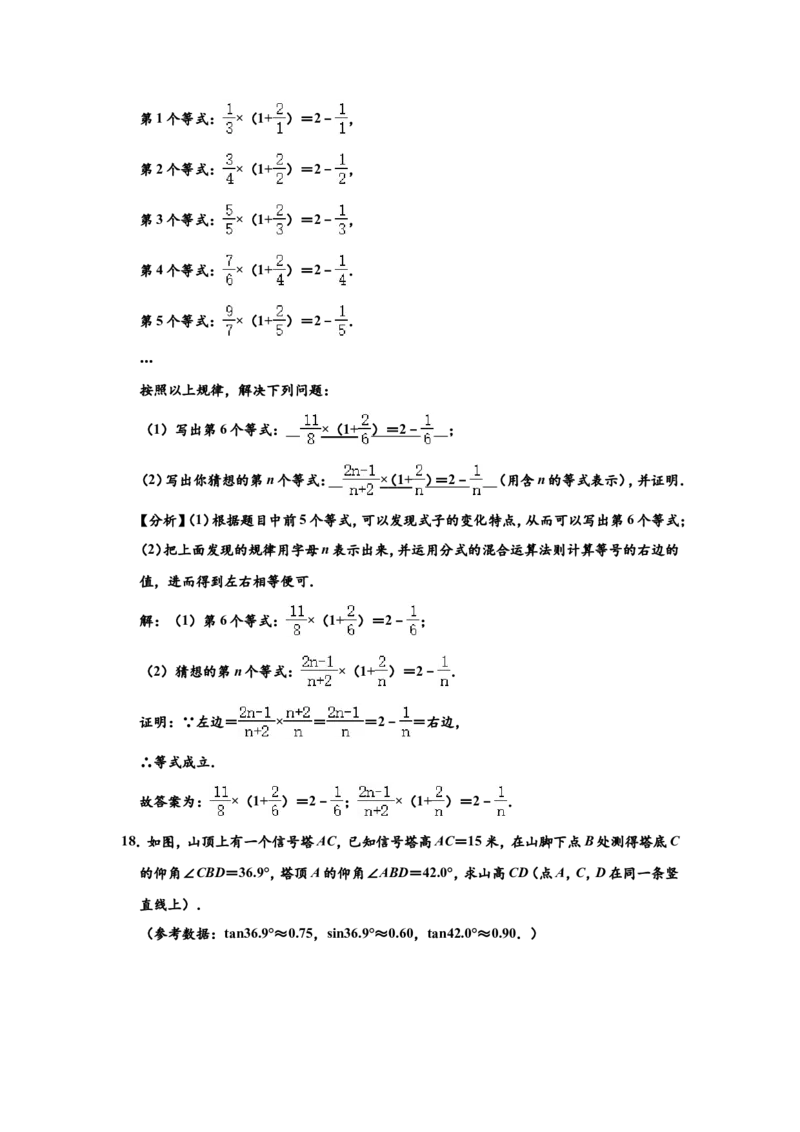文档内容
2020年安徽省中考数学试卷
一、选择题
1.下列各数中,比﹣2小的数是( )
A.﹣3 B.﹣1 C.0 D.2
2.计算(﹣a)6÷a3的结果是( )
A.﹣a3 B.﹣a2 C.a3 D.a2
3.下面四个几何体中,主视图为三角形的是( )
A. B.
C. D.
4.安徽省计划到2022年建成54700000亩高标准农田,其中54700000用科学记数法表示为(
)
A.5.47×108 B.0.547×108 C.547×105 D.5.47×107
5.下列方程中,有两个相等实数根的是( )
A.x2+1=2x B.x2+1=0 C.x2﹣2x=3 D.x2﹣2x=0
6.冉冉的妈妈在网上销售装饰品.最近一周,每天销售某种装饰品的个数为:11,10,11,13,
11,13,15.关于这组数据,冉冉得出如下结果,其中错误的是( )
A.众数是11 B.平均数是12 C.方差是 D.中位数是13
7.已知一次函数y=kx+3的图象经过点A,且y随x的增大而减小,则点A的坐标可以是(
)
A.(﹣1,2) B.(1,﹣2) C.(2,3) D.(3,4)
8.如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A.若AC=4,cosA= ,则BD的
长度为( )A. B. C. D.4
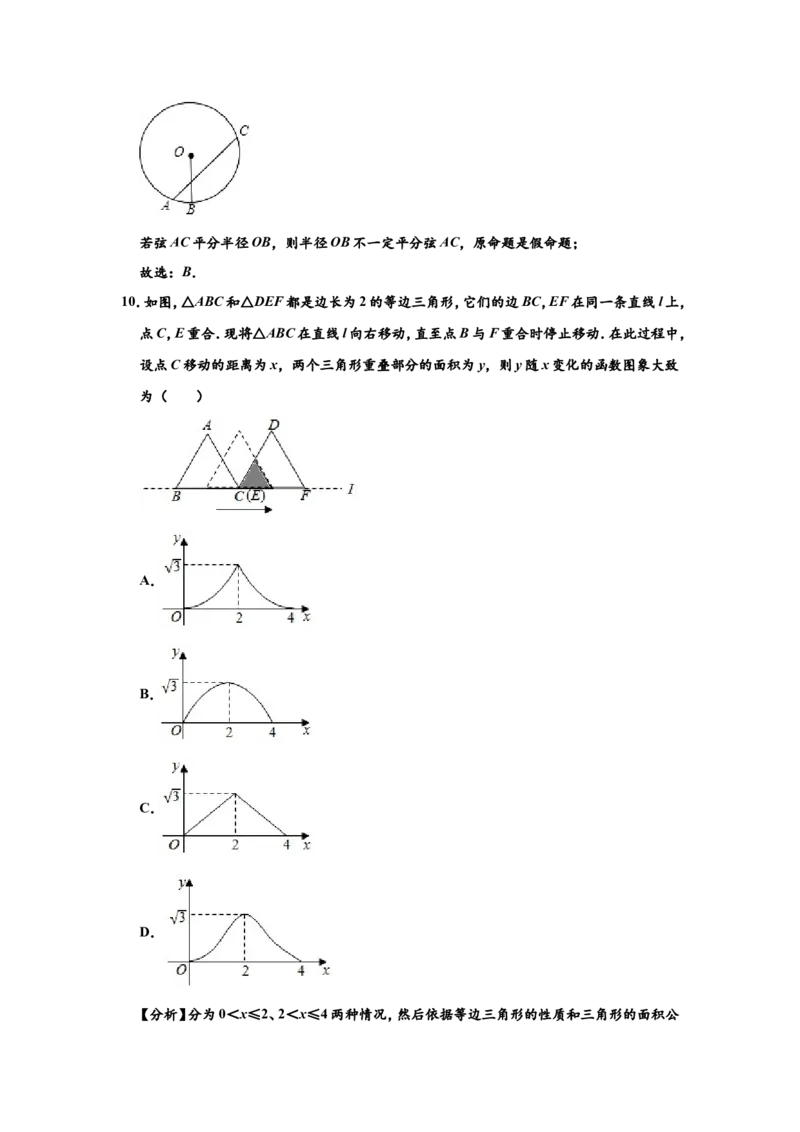
9.已知点A,B,C在 O上,则下列命题为真命题的是( )
A.若半径OB平分弦⊙AC,则四边形OABC是平行四边形
B.若四边形OABC是平行四边形,则∠ABC=120°
C.若∠ABC=120°,则弦AC平分半径OB
D.若弦AC平分半径OB,则半径OB平分弦AC
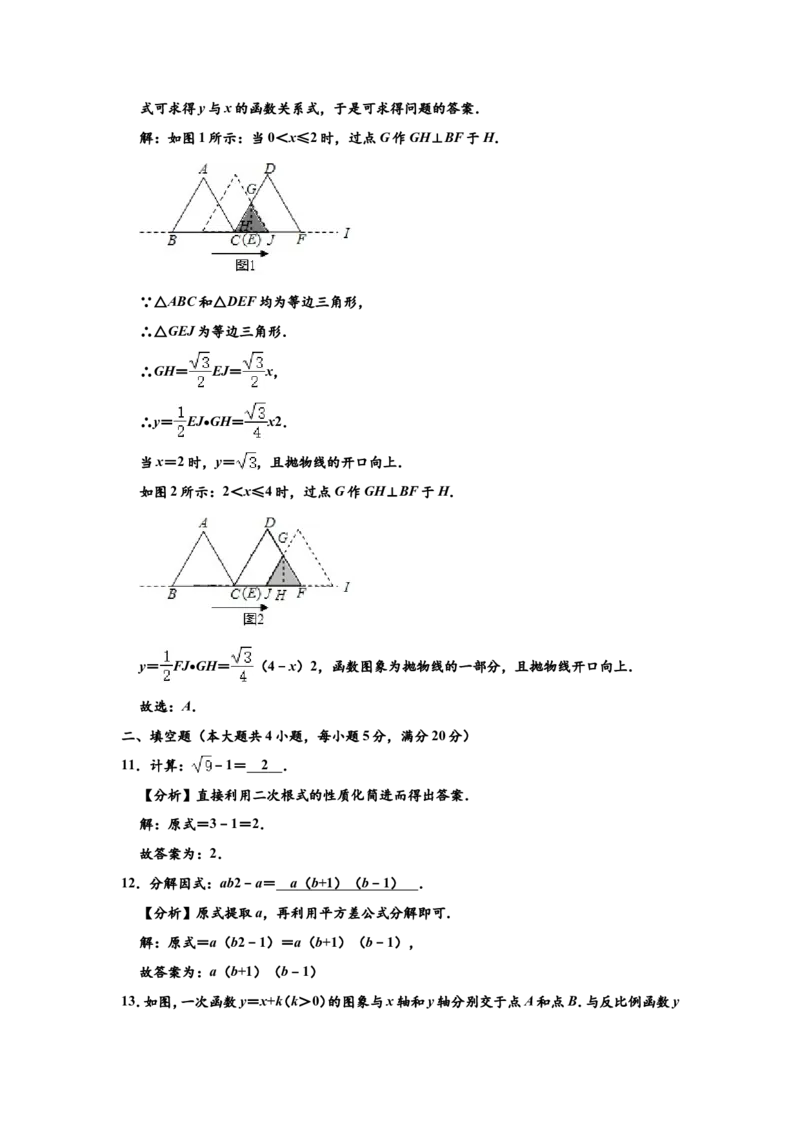
10.如图,△ABC和△DEF都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,
点C,E重合.现将△ABC在直线l向右移动,直至点B与F重合时停止移动.在此过程中,
设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为
( )
A.
B.
C.D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.计算: ﹣1= .
12.分解因式:ab2﹣a= .
13.如图,一次函数y=x+k(k>0)的图象与x轴和y轴分别交于点A和点B.与反比例函数y
= 的图象在第一象限内交于点C,CD⊥x轴,CE⊥y轴.垂足分别为点D,E.当矩形
ODCE与△OAB的面积相等时,k的值为 .
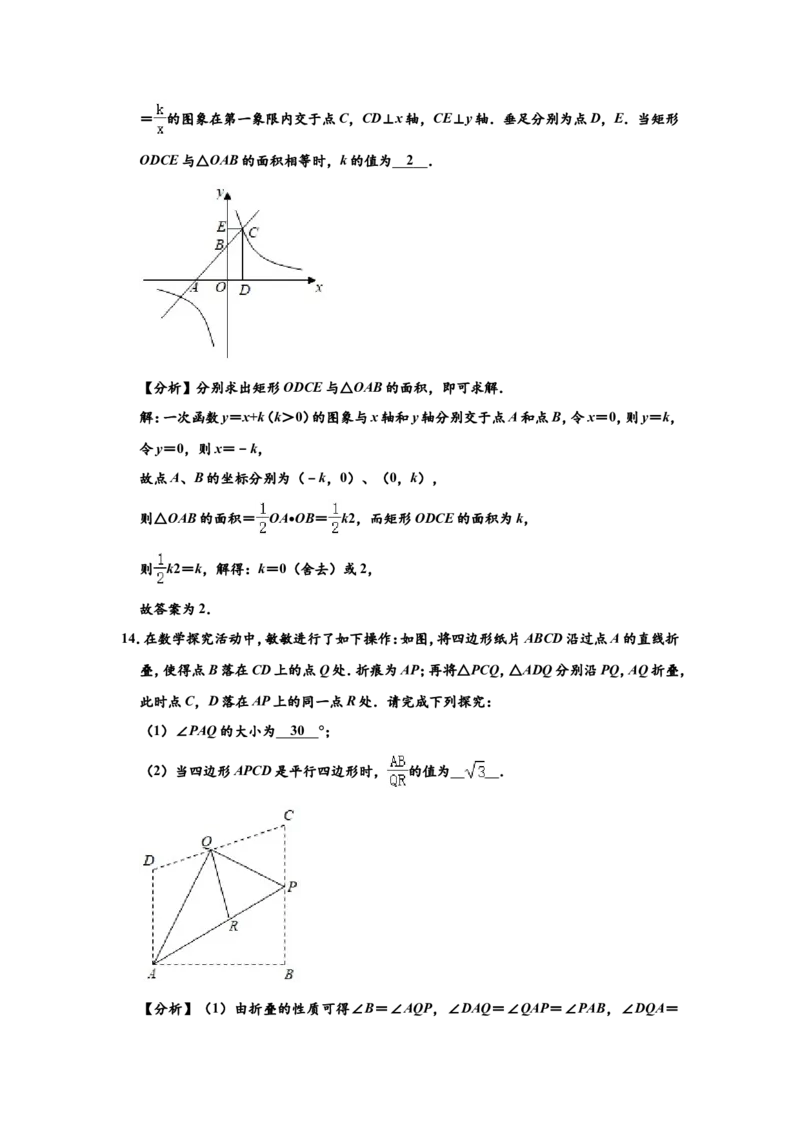
14.在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片ABCD沿过点A的直线折
叠,使得点B落在CD上的点Q处.折痕为AP;再将△PCQ,△ADQ分别沿PQ,AQ折叠,
此时点C,D落在AP上的同一点R处.请完成下列探究:
(1)∠PAQ的大小为 °;
(2)当四边形APCD是平行四边形时, 的值为 .
三、(本大题共2小题,每小题8分,满分16分)15.解不等式: >1.
16.如图,在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交
点)为端点的线段AB,线段MN在网格线上.
(1)画出线段AB关于线段MN所在直线对称的线段A1B1(点A1,B1分别为A,B的对应
点);
(2)将线段B1A1绕点B1顺时针旋转90°得到线段B1A2,画出线段B1A2.
四、(本大题共2小题,每小题8分,满分16分)
17.观察以下等式:
第1个等式: ×(1+ )=2﹣ ,
第2个等式: ×(1+ )=2﹣ ,
第3个等式: ×(1+ )=2﹣ ,
第4个等式: ×(1+ )=2﹣ .
第5个等式: ×(1+ )=2﹣ .
…
按照以上规律,解决下列问题:
(1)写出第6个等式: ;
(2)写出你猜想的第n个等式: (用含n的等式表示),并证明.
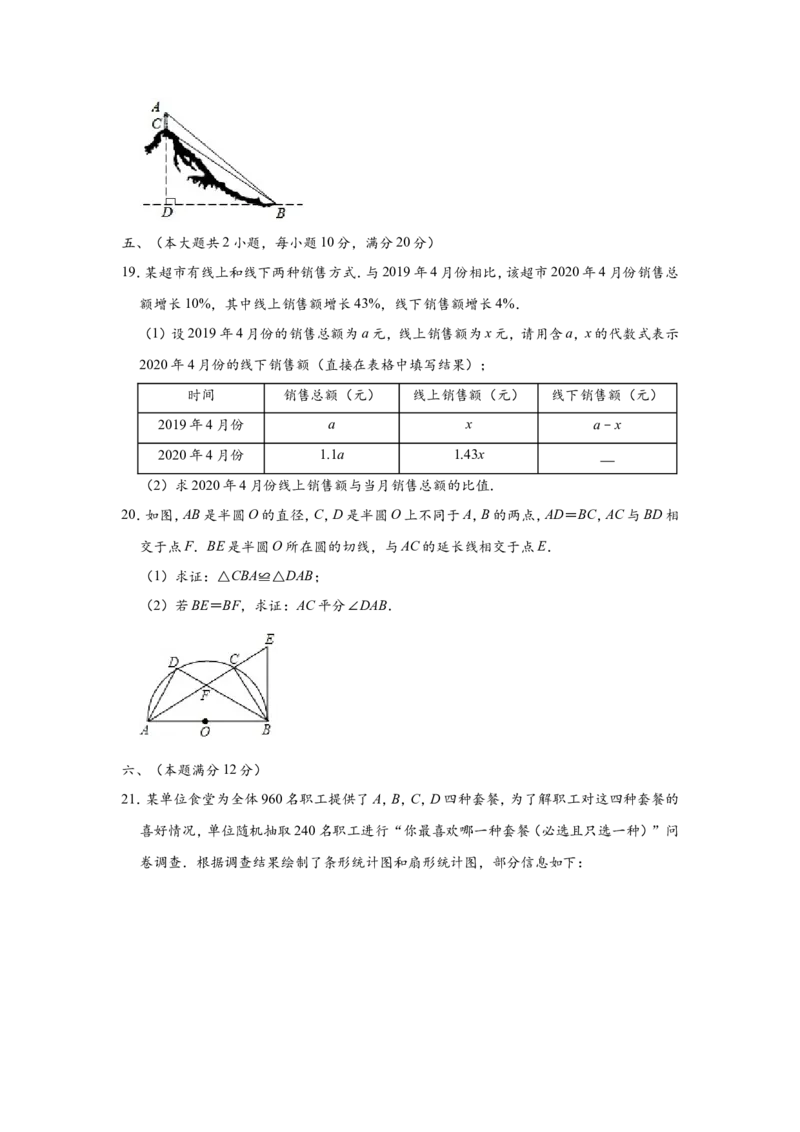
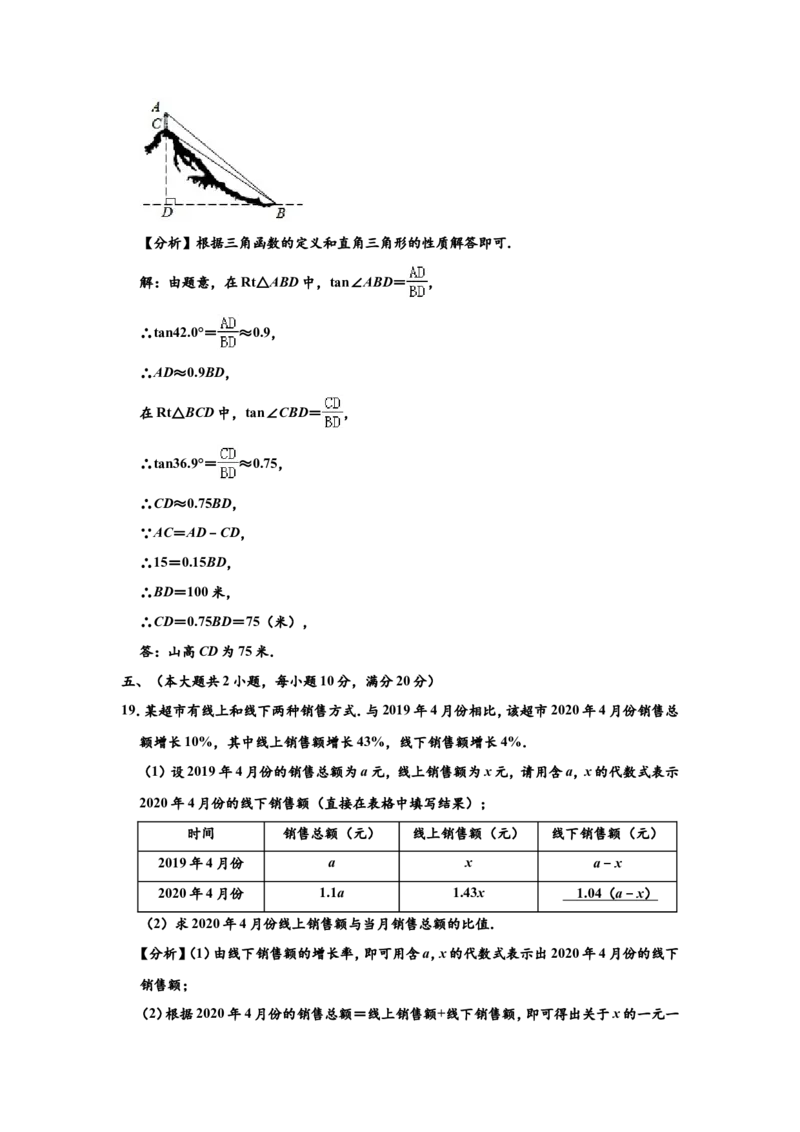
18.如图,山顶上有一个信号塔AC,已知信号塔高AC=15米,在山脚下点B处测得塔底C
的仰角∠CBD=36.9°,塔顶A的仰角∠ABD=42.0°,求山高CD(点A,C,D在同一条竖直
线上).
(参考数据:tan36.9°≈0.75,sin36.9°≈0.60,tan42.0°≈0.90.)五、(本大题共2小题,每小题10分,满分20分)
19.某超市有线上和线下两种销售方式.与2019年4月份相比,该超市2020年4月份销售总
额增长10%,其中线上销售额增长43%,线下销售额增长4%.
(1)设2019年4月份的销售总额为a元,线上销售额为x元,请用含a,x的代数式表示
2020年4月份的线下销售额(直接在表格中填写结果);
时间 销售总额(元) 线上销售额(元) 线下销售额(元)
2019年4月份 a x a﹣x
2020年4月份 1.1a 1.43x
(2)求2020年4月份线上销售额与当月销售总额的比值.
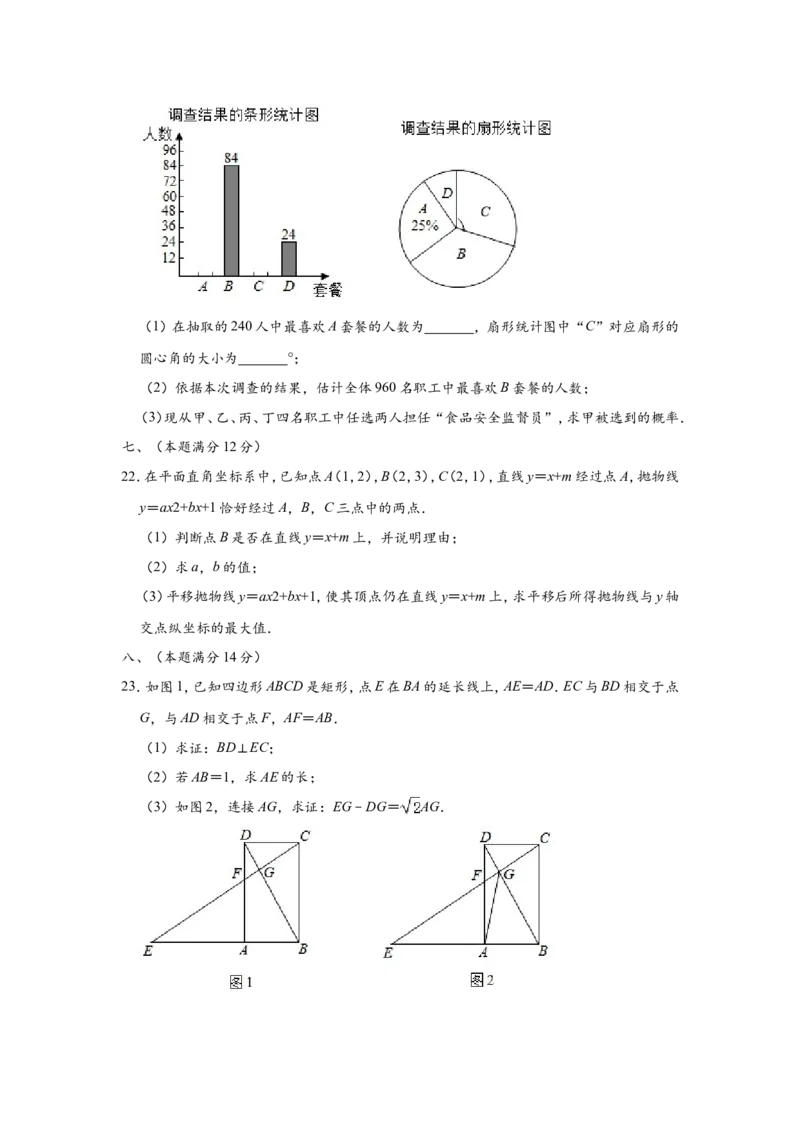
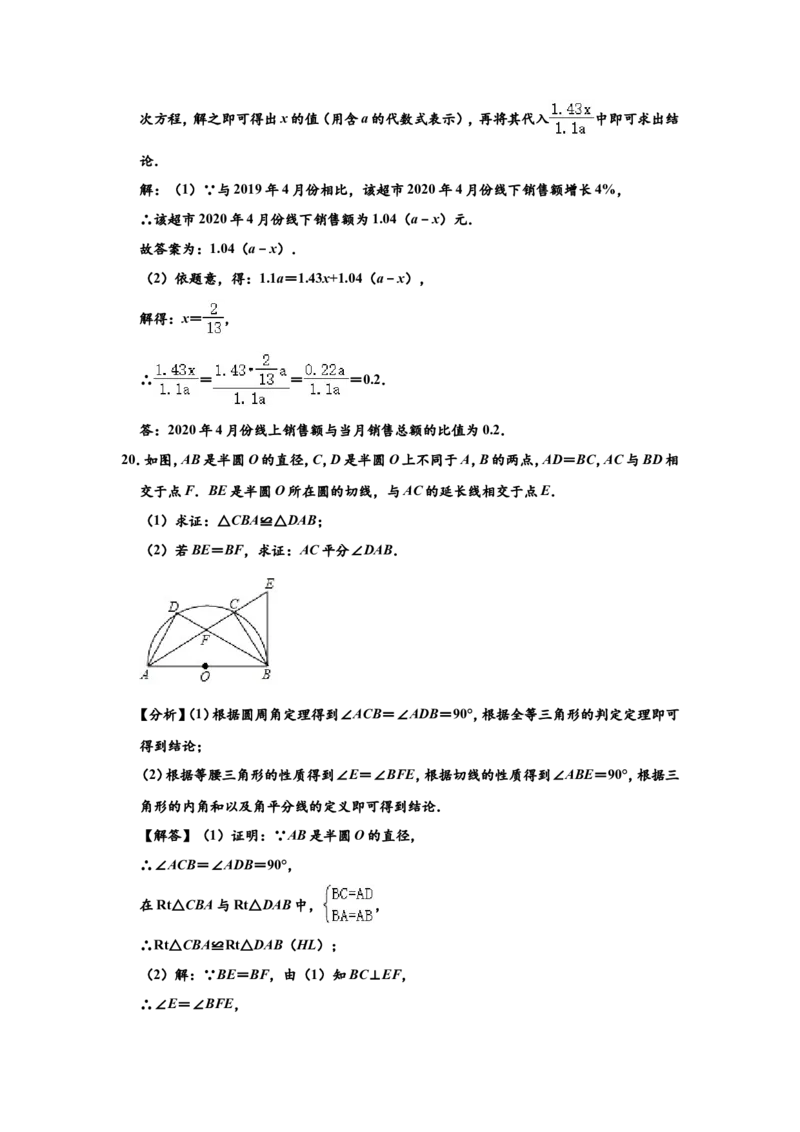
20.如图,AB是半圆O的直径,C,D是半圆O上不同于A,B的两点,AD=BC,AC与BD相
交于点F.BE是半圆O所在圆的切线,与AC的延长线相交于点E.
(1)求证:△CBA≌△DAB;
(2)若BE=BF,求证:AC平分∠DAB.
六、(本题满分12分)
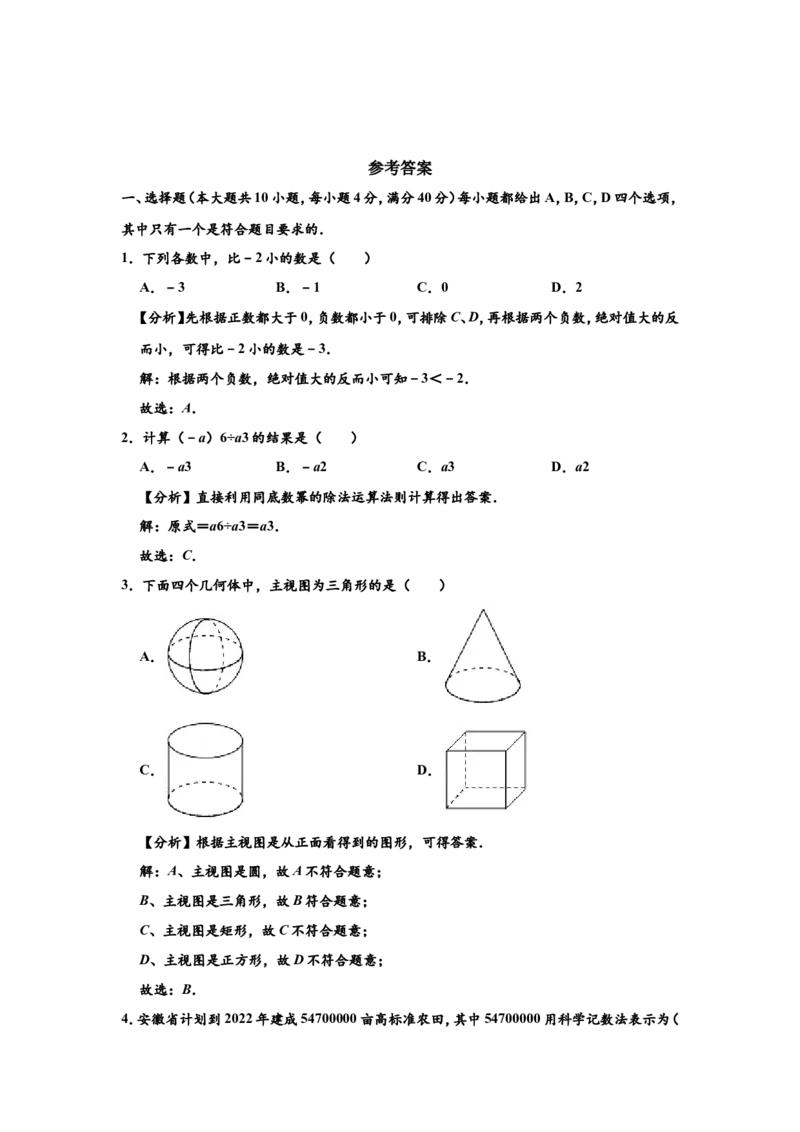
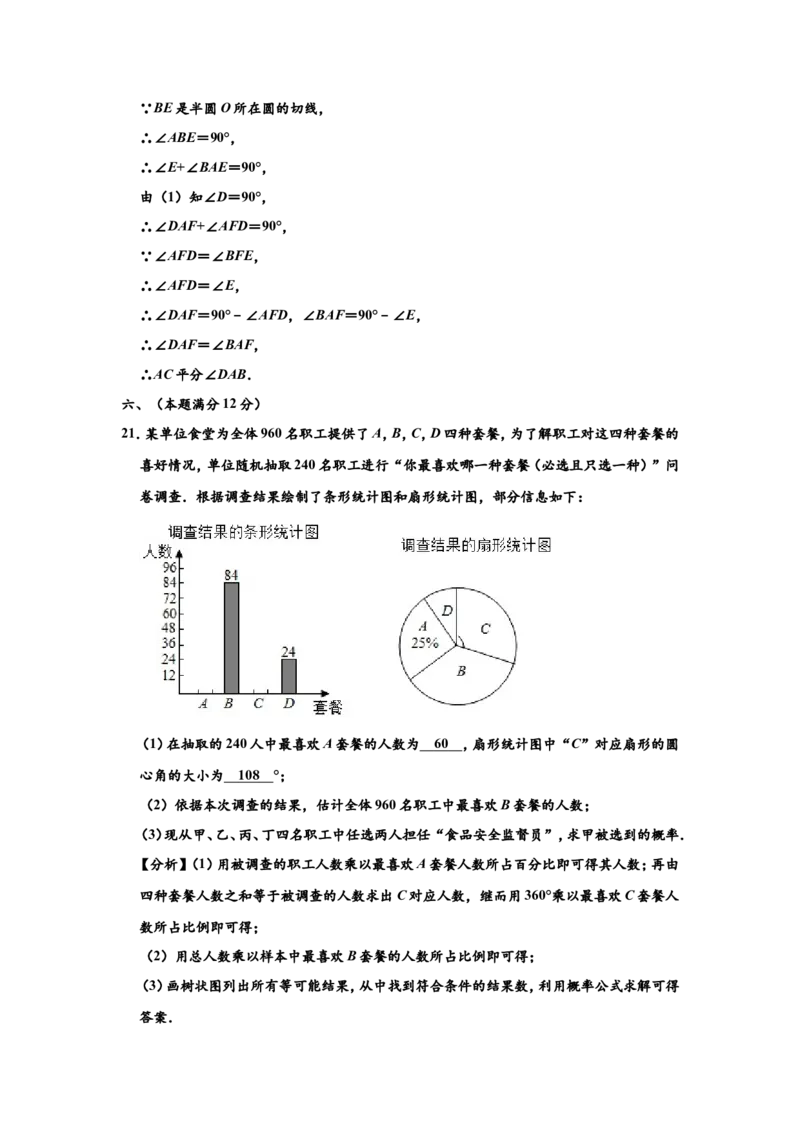
21.某单位食堂为全体960名职工提供了A,B,C,D四种套餐,为了解职工对这四种套餐的
喜好情况,单位随机抽取240名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问
卷调查.根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:(1)在抽取的240人中最喜欢A套餐的人数为 ,扇形统计图中“C”对应扇形的
圆心角的大小为 °;
(2)依据本次调查的结果,估计全体960名职工中最喜欢B套餐的人数;
(3)现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,求甲被选到的概率.
七、(本题满分12分)
22.在平面直角坐标系中,已知点A(1,2),B(2,3),C(2,1),直线y=x+m经过点A,抛物线
y=ax2+bx+1恰好经过A,B,C三点中的两点.
(1)判断点B是否在直线y=x+m上,并说明理由;
(2)求a,b的值;
(3)平移抛物线y=ax2+bx+1,使其顶点仍在直线y=x+m上,求平移后所得抛物线与y轴
交点纵坐标的最大值.
八、(本题满分14分)
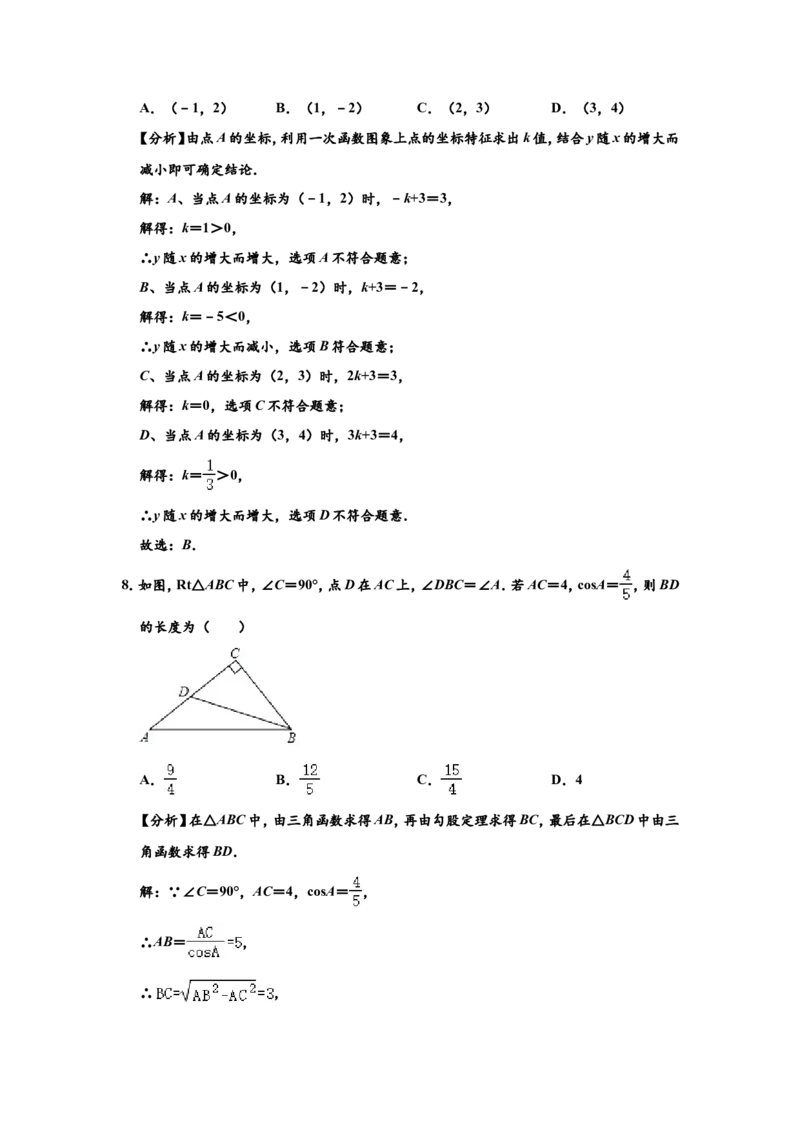
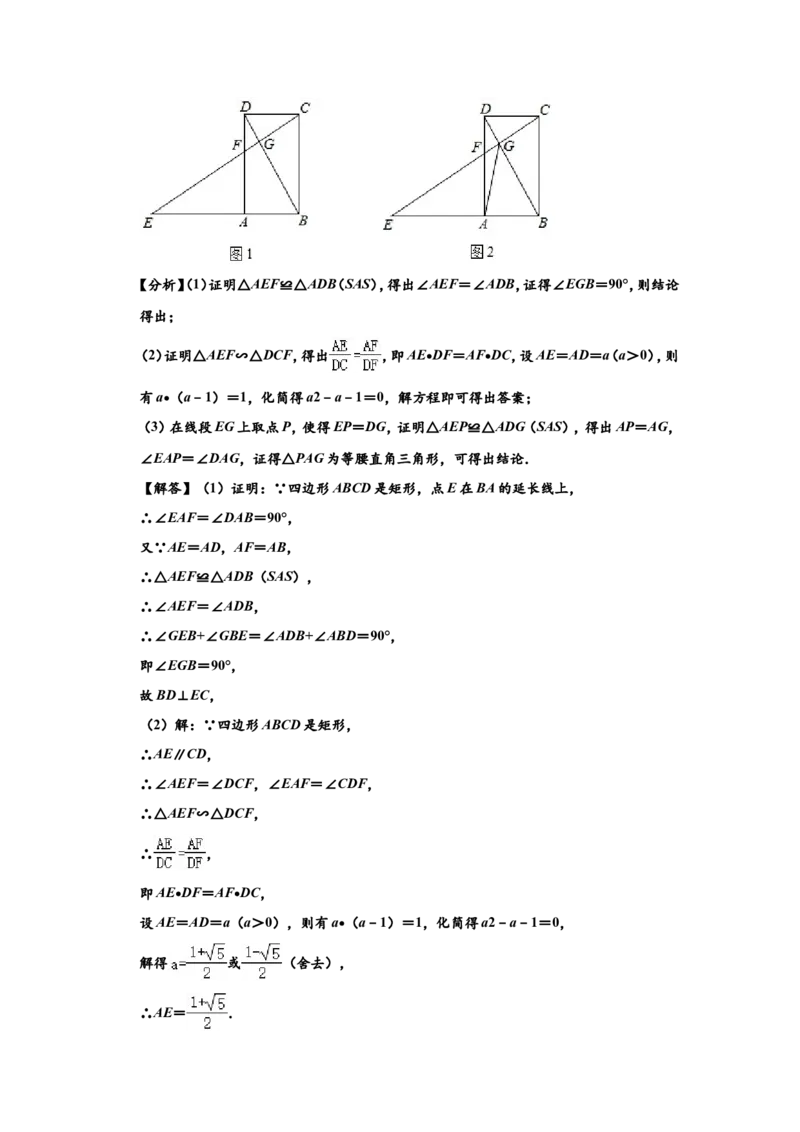
23.如图1,已知四边形ABCD是矩形,点E在BA的延长线上,AE=AD.EC与BD相交于点
G,与AD相交于点F,AF=AB.
(1)求证:BD⊥EC;
(2)若AB=1,求AE的长;
(3)如图2,连接AG,求证:EG﹣DG= AG.参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)每小题都给出A,B,C,D四个选项,
其中只有一个是符合题目要求的.
1.下列各数中,比﹣2小的数是( )
A.﹣3 B.﹣1 C.0 D.2
【分析】先根据正数都大于0,负数都小于0,可排除C、D,再根据两个负数,绝对值大的反
而小,可得比﹣2小的数是﹣3.
解:根据两个负数,绝对值大的反而小可知﹣3<﹣2.
故选:A.
2.计算(﹣a)6÷a3的结果是( )
A.﹣a3 B.﹣a2 C.a3 D.a2
【分析】直接利用同底数幂的除法运算法则计算得出答案.
解:原式=a6÷a3=a3.
故选:C.
3.下面四个几何体中,主视图为三角形的是( )
A. B.
C. D.
【分析】根据主视图是从正面看得到的图形,可得答案.
解:A、主视图是圆,故A不符合题意;
B、主视图是三角形,故B符合题意;
C、主视图是矩形,故C不符合题意;
D、主视图是正方形,故D不符合题意;
故选:B.
4.安徽省计划到2022年建成54700000亩高标准农田,其中54700000用科学记数法表示为()
A.5.47×108 B.0.547×108 C.547×105 D.5.47×107
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值
时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
解:54700000用科学记数法表示为:5.47×107.
故选:D.
5.下列方程中,有两个相等实数根的是( )
A.x2+1=2x B.x2+1=0 C.x2﹣2x=3 D.x2﹣2x=0
【分析】判断上述方程的根的情况,只要看根的判别式△=b2﹣4ac的值的符号就可以了.
有两个相等实数根的一元二次方程就是判别式的值是0的一元二次方程.
解:A、△=(﹣2)2﹣4×1×1=0,有两个相等实数根;
B、△=0﹣4=﹣4<0,没有实数根;
C、△=(﹣2)2﹣4×1×(﹣3)=16>0,有两个不相等实数根;
D、△=(﹣2)2﹣4×1×0=4>0,有两个不相等实数根.
故选:A.
6.冉冉的妈妈在网上销售装饰品.最近一周,每天销售某种装饰品的个数为:11,10,11,13,
11,13,15.关于这组数据,冉冉得出如下结果,其中错误的是( )
A.众数是11 B.平均数是12 C.方差是 D.中位数是13
【分析】根据平均数、众数、中位数、方差的计算方法分别计算这组数据的平均数、众数、中
位数、方差,最后做出选择.
解:数据11,10,11,13,11,13,15中,11出现的次数最多是3次,因此众数是11,于是A
选项不符合题意;
将这7个数据从小到大排列后,处在中间位置的一个数是11,因此中位数是11,于是D符
合题意;
=(11+10+11+13+11+13+15)÷7=12,即平均数是12,于是选项B不符合题意;
S2= [(10﹣12)2+(11﹣12)2×3+(13﹣12)2×2+(15﹣12)2]= ,因此方差为 ,于
是选项C不符合题意;
故选:D.
7.已知一次函数y=kx+3的图象经过点A,且y随x的增大而减小,则点A的坐标可以是(
)A.(﹣1,2) B.(1,﹣2) C.(2,3) D.(3,4)
【分析】由点A的坐标,利用一次函数图象上点的坐标特征求出k值,结合y随x的增大而
减小即可确定结论.
解:A、当点A的坐标为(﹣1,2)时,﹣k+3=3,
解得:k=1>0,
∴y随x的增大而增大,选项A不符合题意;
B、当点A的坐标为(1,﹣2)时,k+3=﹣2,
解得:k=﹣5<0,
∴y随x的增大而减小,选项B符合题意;
C、当点A的坐标为(2,3)时,2k+3=3,
解得:k=0,选项C不符合题意;
D、当点A的坐标为(3,4)时,3k+3=4,
解得:k= >0,
∴y随x的增大而增大,选项D不符合题意.
故选:B.
8.如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A.若AC=4,cosA= ,则BD
的长度为( )
A. B. C. D.4
【分析】在△ABC中,由三角函数求得AB,再由勾股定理求得BC,最后在△BCD中由三
角函数求得BD.
解:∵∠C=90°,AC=4,cosA= ,
∴AB= ,
∴ ,∵∠DBC=∠A.
∴cos∠DBC=cos∠A= ,
∴ ,
故选:C.
9.已知点A,B,C在 O上,则下列命题为真命题的是( )
A.若半径OB平分弦⊙AC,则四边形OABC是平行四边形
B.若四边形OABC是平行四边形,则∠ABC=120°
C.若∠ABC=120°,则弦AC平分半径OB
D.若弦AC平分半径OB,则半径OB平分弦AC
【分析】根据垂径定理,平行四边形的性质判断即可.
解:A、如图,
若半径OB平分弦AC,则四边形OABC不一定是平行四边形;原命题是假命题;
B、若四边形OABC是平行四边形,
则AB=OC,OA=BC,
∵OA=OB=OC,
∴AB=OA=OB=BC=OC,
∴∠ABO=∠OBC=60°,
∴∠ABC=120°,是真命题;
C、如图,
若∠ABC=120°,则弦AC不平分半径OB,原命题是假命题;
D、如图,若弦AC平分半径OB,则半径OB不一定平分弦AC,原命题是假命题;
故选:B.
10.如图,△ABC和△DEF都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,
点C,E重合.现将△ABC在直线l向右移动,直至点B与F重合时停止移动.在此过程中,
设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致
为( )
A.
B.
C.
D.
【分析】分为0<x≤2、2<x≤4两种情况,然后依据等边三角形的性质和三角形的面积公式可求得y与x的函数关系式,于是可求得问题的答案.
解:如图1所示:当0<x≤2时,过点G作GH⊥BF于H.
∵△ABC和△DEF均为等边三角形,
∴△GEJ为等边三角形.
∴GH= EJ= x,
∴y= EJ•GH= x2.
当x=2时,y= ,且抛物线的开口向上.
如图2所示:2<x≤4时,过点G作GH⊥BF于H.
y= FJ•GH= (4﹣x)2,函数图象为抛物线的一部分,且抛物线开口向上.
故选:A.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.计算: ﹣1= 2 .
【分析】直接利用二次根式的性质化简进而得出答案.
解:原式=3﹣1=2.
故答案为:2.
12.分解因式:ab2﹣a= a ( b + 1 )( b ﹣ 1 ) .
【分析】原式提取a,再利用平方差公式分解即可.
解:原式=a(b2﹣1)=a(b+1)(b﹣1),
故答案为:a(b+1)(b﹣1)
13.如图,一次函数y=x+k(k>0)的图象与x轴和y轴分别交于点A和点B.与反比例函数y= 的图象在第一象限内交于点C,CD⊥x轴,CE⊥y轴.垂足分别为点D,E.当矩形
ODCE与△OAB的面积相等时,k的值为 2 .
【分析】分别求出矩形ODCE与△OAB的面积,即可求解.
解:一次函数y=x+k(k>0)的图象与x轴和y轴分别交于点A和点B,令x=0,则y=k,
令y=0,则x=﹣k,
故点A、B的坐标分别为(﹣k,0)、(0,k),
则△OAB的面积= OA•OB= k2,而矩形ODCE的面积为k,
则 k2=k,解得:k=0(舍去)或2,
故答案为2.
14.在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片ABCD沿过点A的直线折
叠,使得点B落在CD上的点Q处.折痕为AP;再将△PCQ,△ADQ分别沿PQ,AQ折叠,
此时点C,D落在AP上的同一点R处.请完成下列探究:
(1)∠PAQ的大小为 3 0 °;
(2)当四边形APCD是平行四边形时, 的值为 .
【分析】(1)由折叠的性质可得∠B=∠AQP,∠DAQ=∠QAP=∠PAB,∠DQA=∠AQR,∠CQP=∠PQR,∠D=∠ARQ,∠C=∠QRP,由平角的性质可得∠D+∠C=
180°,∠AQP=90°,可证AD∥BC,由平行线的性质可得∠DAB=90°,即可求解;
(2)由平行四边形和折叠的性质可得AR=PR,由直角三角形的性质可得AP=2PB=
2QR,AB= PB,即可求解.
解:(1)由折叠的性质可得:∠B=∠AQP,∠DAQ=∠QAP=∠PAB,∠DQA=∠AQR,
∠CQP=∠PQR,∠D=∠ARQ,∠C=∠QRP,
∵∠QRA+∠QRP=180°,
∴∠D+∠C=180°,
∴AD∥BC,
∴∠B+∠DAB=180°,
∵∠DQR+∠CQR=180°,
∴∠DQA+∠CQP=90°,
∴∠AQP=90°,
∴∠B=∠AQP=90°,
∴∠DAB=90°,
∴∠DAQ=∠QAP=∠PAB=30°,
故答案为:30;
(2)由折叠的性质可得:AD=AR,CP=PR,
∵四边形APCD是平行四边形,
∴AD=PC,
∴AR=PR,
又∵∠AQP=90°,
∴QR= AP,
∵∠PAB=30°,∠B=90°,
∴AP=2PB,AB= PB,
∴PB=QR,
∴ = ,
故答案为: .
三、(本大题共2小题,每小题8分,满分16分)15.解不等式: >1.
【分析】根据解一元一次不等式基本步骤:去分母、移项、合并同类项、系数化为1可得.
解:去分母,得:2x﹣1>2,
移项,得:2x>2+1,
合并,得:2x>3,
系数化为1,得:x> .
16.如图,在由边长为1个单位长度的小正方形组成的网格中,给出了以格点(网格线的交
点)为端点的线段AB,线段MN在网格线上.
(1)画出线段AB关于线段MN所在直线对称的线段A1B1(点A1,B1分别为A,B的对应
点);
(2)将线段B1A1绕点B1顺时针旋转90°得到线段B1A2,画出线段B1A2.
【分析】(1)分别作出A,B的对应点A1,B2即可.
(2)作出点A1的对应点A2即可.
解:(1)如图线段A1B1即为所求.
(2)如图,线段B1A2即为所求.
四、(本大题共2小题,每小题8分,满分16分)
17.观察以下等式:第1个等式: ×(1+ )=2﹣ ,
第2个等式: ×(1+ )=2﹣ ,
第3个等式: ×(1+ )=2﹣ ,
第4个等式: ×(1+ )=2﹣ .
第5个等式: ×(1+ )=2﹣ .
…
按照以上规律,解决下列问题:
(1)写出第6个等式: × ( 1+ )= 2 ﹣ ;
(2)写出你猜想的第n个等式: ×( 1+ )= 2 ﹣ (用含n的等式表示),并证明.
【分析】(1)根据题目中前5个等式,可以发现式子的变化特点,从而可以写出第6个等式;
(2)把上面发现的规律用字母n表示出来,并运用分式的混合运算法则计算等号的右边的
值,进而得到左右相等便可.
解:(1)第6个等式: ×(1+ )=2﹣ ;
(2)猜想的第n个等式: ×(1+ )=2﹣ .
证明:∵左边= × = =2﹣ =右边,
∴等式成立.
故答案为: ×(1+ )=2﹣ ; ×(1+ )=2﹣ .
18.如图,山顶上有一个信号塔AC,已知信号塔高AC=15米,在山脚下点B处测得塔底C
的仰角∠CBD=36.9°,塔顶A的仰角∠ABD=42.0°,求山高CD(点A,C,D在同一条竖
直线上).
(参考数据:tan36.9°≈0.75,sin36.9°≈0.60,tan42.0°≈0.90.)【分析】根据三角函数的定义和直角三角形的性质解答即可.
解:由题意,在Rt△ABD中,tan∠ABD= ,
∴tan42.0°= ≈0.9,
∴AD≈0.9BD,
在Rt△BCD中,tan∠CBD= ,
∴tan36.9°= ≈0.75,
∴CD≈0.75BD,
∵AC=AD﹣CD,
∴15=0.15BD,
∴BD=100米,
∴CD=0.75BD=75(米),
答:山高CD为75米.
五、(本大题共2小题,每小题10分,满分20分)
19.某超市有线上和线下两种销售方式.与2019年4月份相比,该超市2020年4月份销售总
额增长10%,其中线上销售额增长43%,线下销售额增长4%.
(1)设2019年4月份的销售总额为a元,线上销售额为x元,请用含a,x的代数式表示
2020年4月份的线下销售额(直接在表格中填写结果);
时间 销售总额(元) 线上销售额(元) 线下销售额(元)
2019年4月份 a x a﹣x
2020年4月份 1.1a 1.43x 1.0 4 ( a ﹣ x )
(2)求2020年4月份线上销售额与当月销售总额的比值.
【分析】(1)由线下销售额的增长率,即可用含a,x的代数式表示出2020年4月份的线下
销售额;
(2)根据2020年4月份的销售总额=线上销售额+线下销售额,即可得出关于x的一元一次方程,解之即可得出x的值(用含a的代数式表示),再将其代入 中即可求出结
论.
解:(1)∵与2019年4月份相比,该超市2020年4月份线下销售额增长4%,
∴该超市2020年4月份线下销售额为1.04(a﹣x)元.
故答案为:1.04(a﹣x).
(2)依题意,得:1.1a=1.43x+1.04(a﹣x),
解得:x= ,
∴ = = =0.2.
答:2020年4月份线上销售额与当月销售总额的比值为0.2.
20.如图,AB是半圆O的直径,C,D是半圆O上不同于A,B的两点,AD=BC,AC与BD相
交于点F.BE是半圆O所在圆的切线,与AC的延长线相交于点E.
(1)求证:△CBA≌△DAB;
(2)若BE=BF,求证:AC平分∠DAB.
【分析】(1)根据圆周角定理得到∠ACB=∠ADB=90°,根据全等三角形的判定定理即可
得到结论;
(2)根据等腰三角形的性质得到∠E=∠BFE,根据切线的性质得到∠ABE=90°,根据三
角形的内角和以及角平分线的定义即可得到结论.
【解答】(1)证明:∵AB是半圆O的直径,
∴∠ACB=∠ADB=90°,
在Rt△CBA与Rt△DAB中, ,
∴Rt△CBA≌Rt△DAB(HL);
(2)解:∵BE=BF,由(1)知BC⊥EF,
∴∠E=∠BFE,∵BE是半圆O所在圆的切线,
∴∠ABE=90°,
∴∠E+∠BAE=90°,
由(1)知∠D=90°,
∴∠DAF+∠AFD=90°,
∵∠AFD=∠BFE,
∴∠AFD=∠E,
∴∠DAF=90°﹣∠AFD,∠BAF=90°﹣∠E,
∴∠DAF=∠BAF,
∴AC平分∠DAB.
六、(本题满分12分)
21.某单位食堂为全体960名职工提供了A,B,C,D四种套餐,为了解职工对这四种套餐的
喜好情况,单位随机抽取240名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问
卷调查.根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
(1)在抽取的240人中最喜欢A套餐的人数为 6 0 ,扇形统计图中“C”对应扇形的圆
心角的大小为 10 8 °;
(2)依据本次调查的结果,估计全体960名职工中最喜欢B套餐的人数;
(3)现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,求甲被选到的概率.
【分析】(1)用被调查的职工人数乘以最喜欢A套餐人数所占百分比即可得其人数;再由
四种套餐人数之和等于被调查的人数求出C对应人数,继而用360°乘以最喜欢C套餐人
数所占比例即可得;
(2)用总人数乘以样本中最喜欢B套餐的人数所占比例即可得;
(3)画树状图列出所有等可能结果,从中找到符合条件的结果数,利用概率公式求解可得
答案.解:(1)在抽取的240人中最喜欢A套餐的人数为240×25%=60(人),
则最喜欢C套餐的人数为240﹣(60+84+24)=72(人),
∴扇形统计图中“C”对应扇形的圆心角的大小为360°× =108°,
故答案为:60、108;
(2)估计全体960名职工中最喜欢B套餐的人数为960× =336(人);
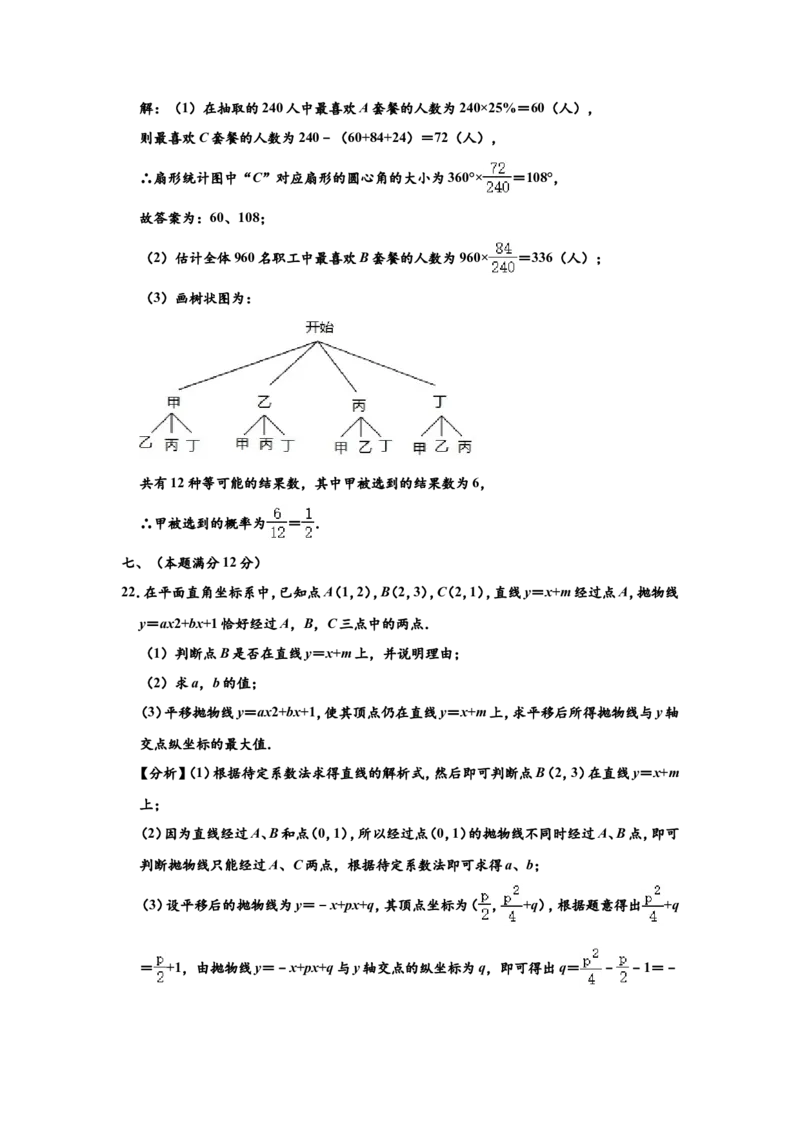
(3)画树状图为:
共有12种等可能的结果数,其中甲被选到的结果数为6,
∴甲被选到的概率为 = .
七、(本题满分12分)
22.在平面直角坐标系中,已知点A(1,2),B(2,3),C(2,1),直线y=x+m经过点A,抛物线
y=ax2+bx+1恰好经过A,B,C三点中的两点.
(1)判断点B是否在直线y=x+m上,并说明理由;
(2)求a,b的值;
(3)平移抛物线y=ax2+bx+1,使其顶点仍在直线y=x+m上,求平移后所得抛物线与y轴
交点纵坐标的最大值.
【分析】(1)根据待定系数法求得直线的解析式,然后即可判断点B(2,3)在直线y=x+m
上;
(2)因为直线经过A、B和点(0,1),所以经过点(0,1)的抛物线不同时经过A、B点,即可
判断抛物线只能经过A、C两点,根据待定系数法即可求得a、b;
(3)设平移后的抛物线为y=﹣x+px+q,其顶点坐标为( , +q),根据题意得出 +q
= +1,由抛物线y=﹣x+px+q与y轴交点的纵坐标为q,即可得出q= ﹣ ﹣1=﹣(p﹣1)2+ ,从而得出q的最大值.
解:(1)点B是在直线y=x+m上,理由如下:
∵直线y=x+m经过点A(1,2),
∴2=1+m,解得m=1,
∴直线为y=x+1,
把x=2代入y=x+1得y=3,
∴点B(2,3)在直线y=x+m上;
(2)∵直线y=x+1与抛物线y=ax2+bx+1都经过点(0,1),且B、C两点的横坐标相同,
∴抛物线只能经过A、C两点,
把A(1,2),C(2,1)代入y=ax2+bx+1得 ,
解得a=﹣1,b=2;
(3)由(2)知,抛物线为y=﹣x2+2x+1,
设平移后的抛物线为y=﹣x+px+q,其顶点坐标为( , +q),
∵顶点仍在直线y=x+1上,
∴ +q= +1,
∴q= ﹣ ﹣1,
∵抛物线y=﹣x+px+q与y轴的交点的纵坐标为q,
∴q= ﹣ ﹣1=﹣ (p﹣1)2+ ,
∴当p=1时,平移后所得抛物线与y轴交点纵坐标的最大值为 .
八、(本题满分14分)
23.如图1,已知四边形ABCD是矩形,点E在BA的延长线上,AE=AD.EC与BD相交于
点G,与AD相交于点F,AF=AB.
(1)求证:BD⊥EC;
(2)若AB=1,求AE的长;
(3)如图2,连接AG,求证:EG﹣DG= AG.【分析】(1)证明△AEF≌△ADB(SAS),得出∠AEF=∠ADB,证得∠EGB=90°,则结论
得出;
(2)证明△AEF∽△DCF,得出 ,即AE•DF=AF•DC,设AE=AD=a(a>0),则
有a•(a﹣1)=1,化简得a2﹣a﹣1=0,解方程即可得出答案;
(3)在线段EG上取点P,使得EP=DG,证明△AEP≌△ADG(SAS),得出AP=AG,
∠EAP=∠DAG,证得△PAG为等腰直角三角形,可得出结论.
【解答】(1)证明:∵四边形ABCD是矩形,点E在BA的延长线上,
∴∠EAF=∠DAB=90°,
又∵AE=AD,AF=AB,
∴△AEF≌△ADB(SAS),
∴∠AEF=∠ADB,
∴∠GEB+∠GBE=∠ADB+∠ABD=90°,
即∠EGB=90°,
故BD⊥EC,
(2)解:∵四边形ABCD是矩形,
∴AE∥CD,
∴∠AEF=∠DCF,∠EAF=∠CDF,
∴△AEF∽△DCF,
∴ ,
即AE•DF=AF•DC,
设AE=AD=a(a>0),则有a•(a﹣1)=1,化简得a2﹣a﹣1=0,
解得 或 (舍去),
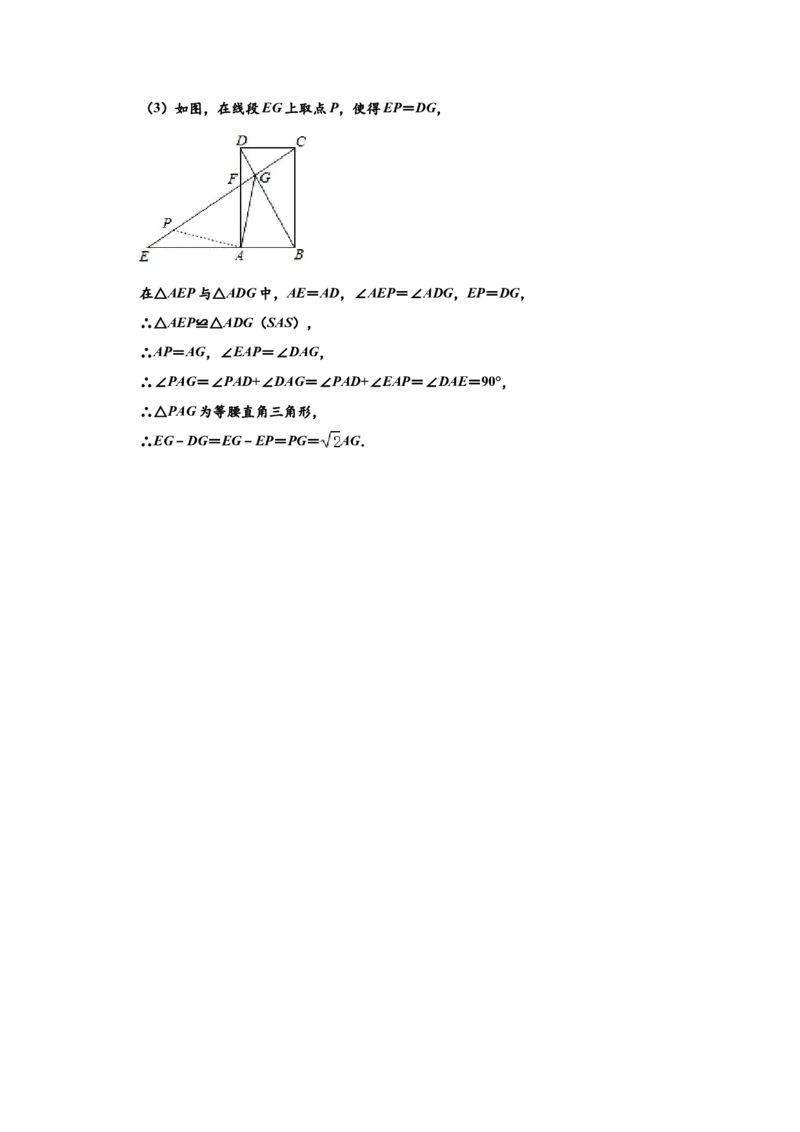
∴AE= .(3)如图,在线段EG上取点P,使得EP=DG,
在△AEP与△ADG中,AE=AD,∠AEP=∠ADG,EP=DG,
∴△AEP≌△ADG(SAS),
∴AP=AG,∠EAP=∠DAG,
∴∠PAG=∠PAD+∠DAG=∠PAD+∠EAP=∠DAE=90°,
∴△PAG为等腰直角三角形,
∴EG﹣DG=EG﹣EP=PG= AG.