文档内容
2020年河南省中考数学试卷
一、选择题
1.2的相反数是( )
A.﹣2 B.﹣ C. D.2
2.如图摆放的几何体中,主视图与左视图有可能不同的是( )
A. B. C. D.
3.要调查下列问题,适合采用全面调查(普查)的是( )
A.中央电视台《开学第一课》的收视率
B.某城市居民6月份人均网上购物的次数
C.即将发射的气象卫星的零部件质量
D.某品牌新能源汽车的最大续航里程
4.如图,l1∥l2,l3∥l4,若∠1=70°,则∠2的度数为( )
A.100° B.110° C.120° D.130°
5.电子文件的大小常用B,KB,MB,GB等作为单位,其中1GB=210MB,1MB=210KB,
1KB=210B.某视频文件的大小约为1GB,1GB等于( )
A.230B B.830B C.8×1010B D.2×1030B
6.若点A(﹣1,y1),B(2,y2),C(3,y3)在反比例函数y=﹣ 的图象上,则y1,y2,y3的大小
关系是( )
A.y1>y2>y3 B.y2>y3>y1 C.y1>y3>y2 D.y3>y2>y1
7.定义运算:m☆n=mn2﹣mn﹣1.例如:4☆2=4×22﹣4×2﹣1=7.则方程1☆x=0的根的
情况为( )
A.有两个不相等的实数根 B.有两个相等的实数根C.无实数根 D.只有一个实数根
8.国家统计局统计数据显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务
收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长
率为x,则可列方程为( )
A.500(1+2x)=7500
B.5000×2(1+x)=7500
C.5000(1+x)2=7500
D.5000+5000(1+x)+5000(1+x)2=7500
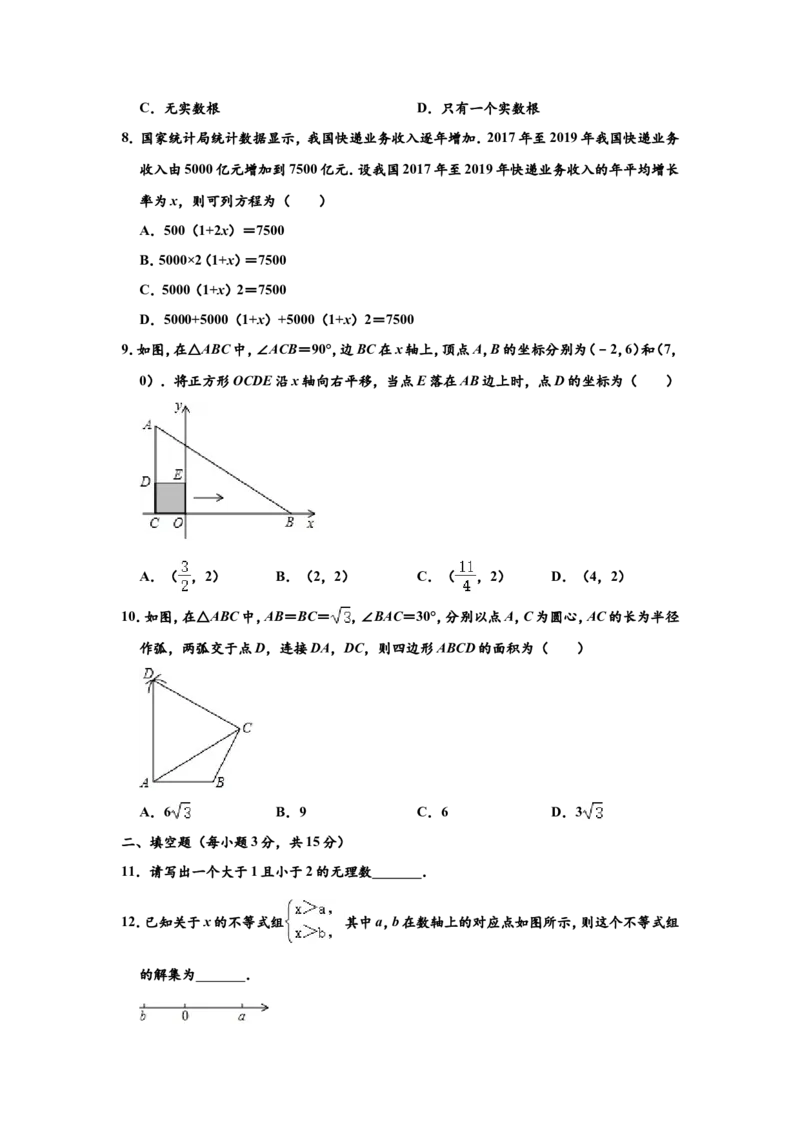
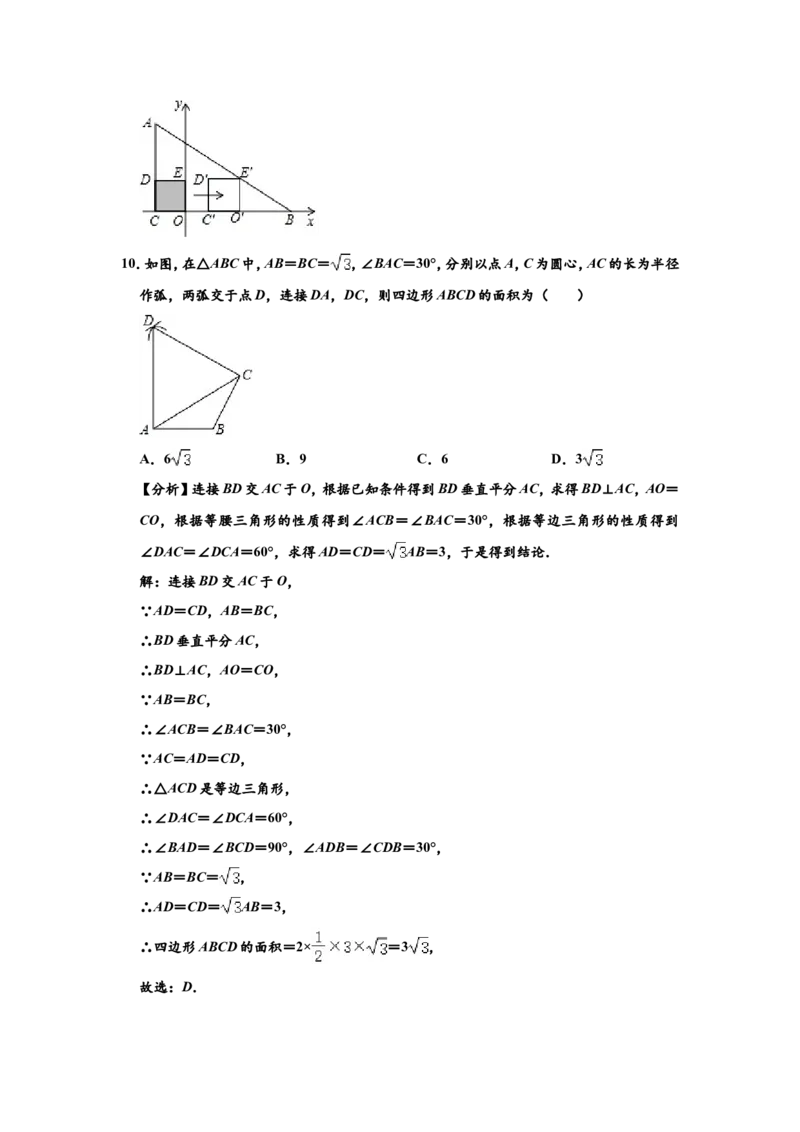
9.如图,在△ABC中,∠ACB=90°,边BC在x轴上,顶点A,B的坐标分别为(﹣2,6)和(7,
0).将正方形OCDE沿x轴向右平移,当点E落在AB边上时,点D的坐标为( )
A.( ,2) B.(2,2) C.( ,2) D.(4,2)
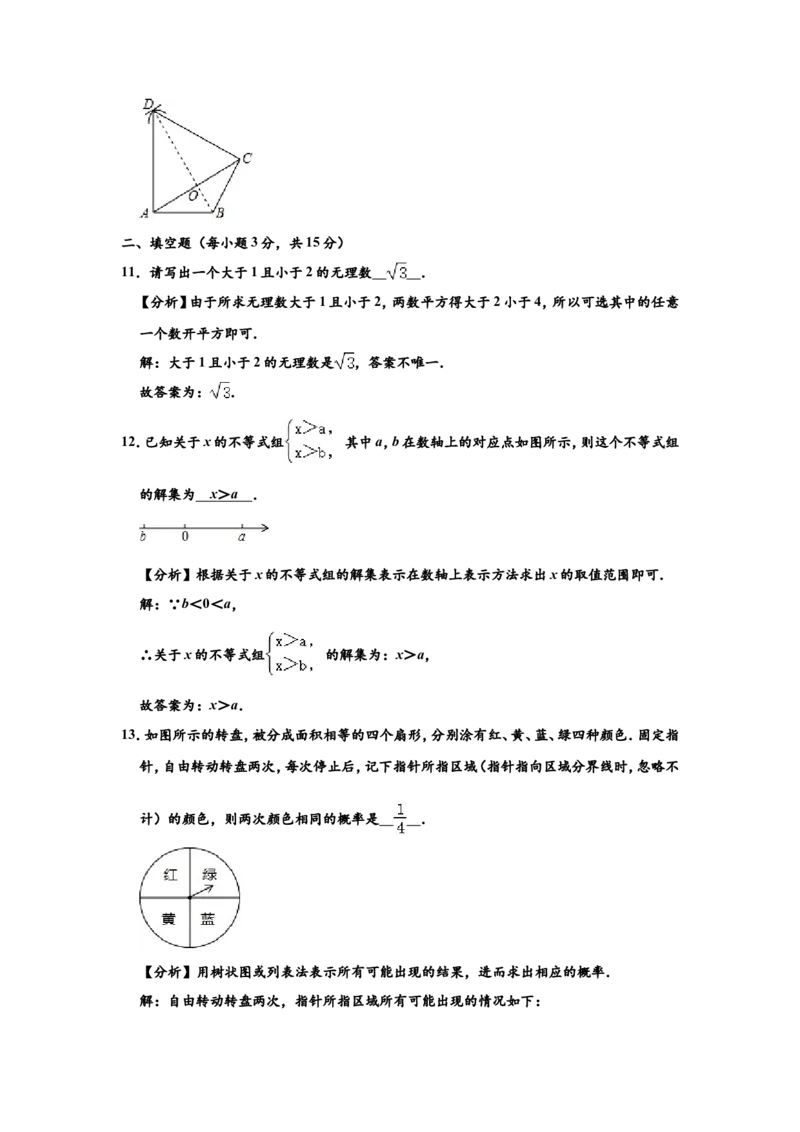
10.如图,在△ABC中,AB=BC= ,∠BAC=30°,分别以点A,C为圆心,AC的长为半径
作弧,两弧交于点D,连接DA,DC,则四边形ABCD的面积为( )
A.6 B.9 C.6 D.3
二、填空题(每小题3分,共15分)
11.请写出一个大于1且小于2的无理数 .
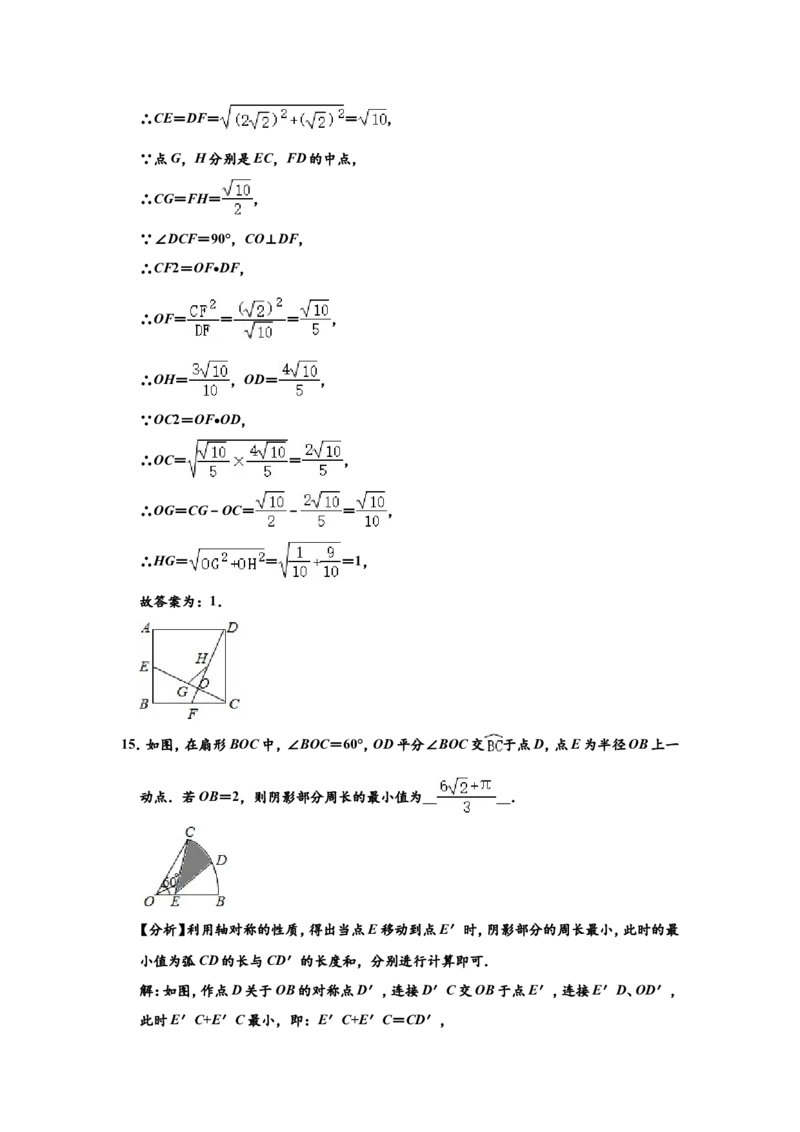
12.已知关于x的不等式组 其中a,b在数轴上的对应点如图所示,则这个不等式组
的解集为 .13.如图所示的转盘,被分成面积相等的四个扇形,分别涂有红、黄、蓝、绿四种颜色.固定指
针,自由转动转盘两次,每次停止后,记下指针所指区域(指针指向区域分界线时,忽略不
计)的颜色,则两次颜色相同的概率是 .
14.如图,在边长为2 的正方形ABCD中,点E,F分别是边AB,BC的中点,连接EC,
FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为 .
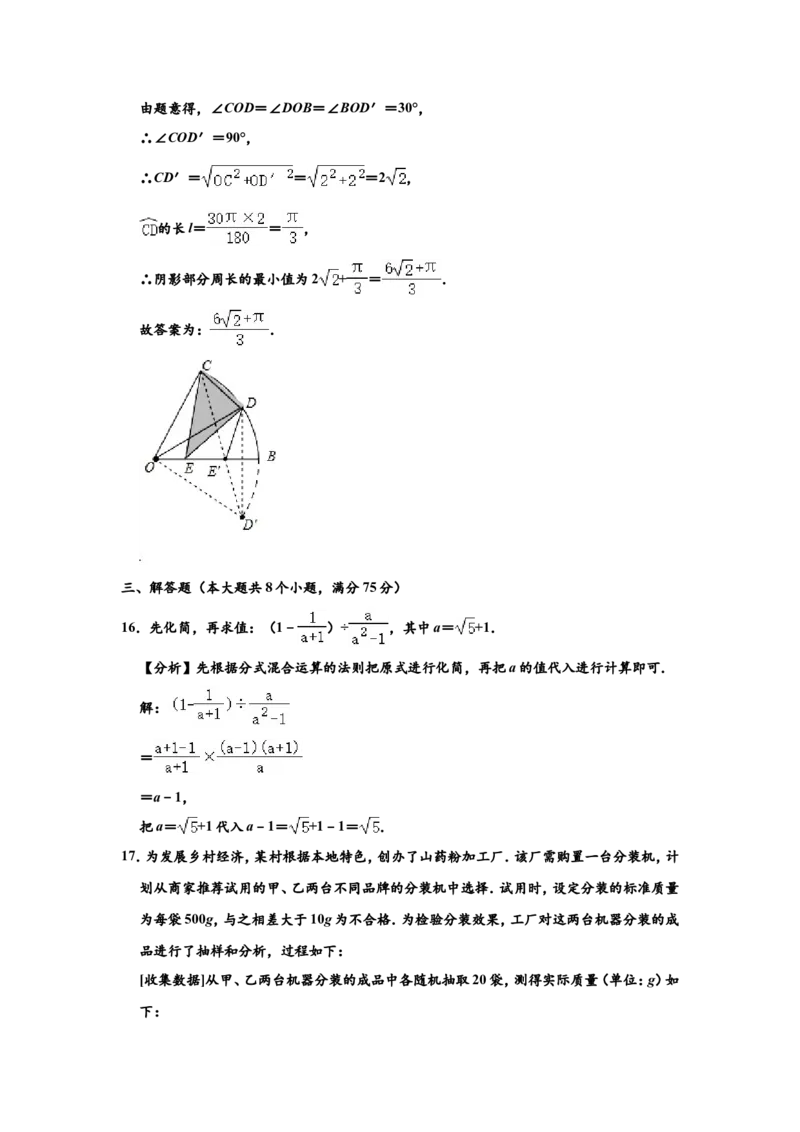
15.如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交 于点D,点E为半径OB上一
动点.若OB=2,则阴影部分周长的最小值为 .
三、解答题(本大题共8个小题,满分75分)
16.先化简,再求值:(1﹣ )÷ ,其中a= +1.
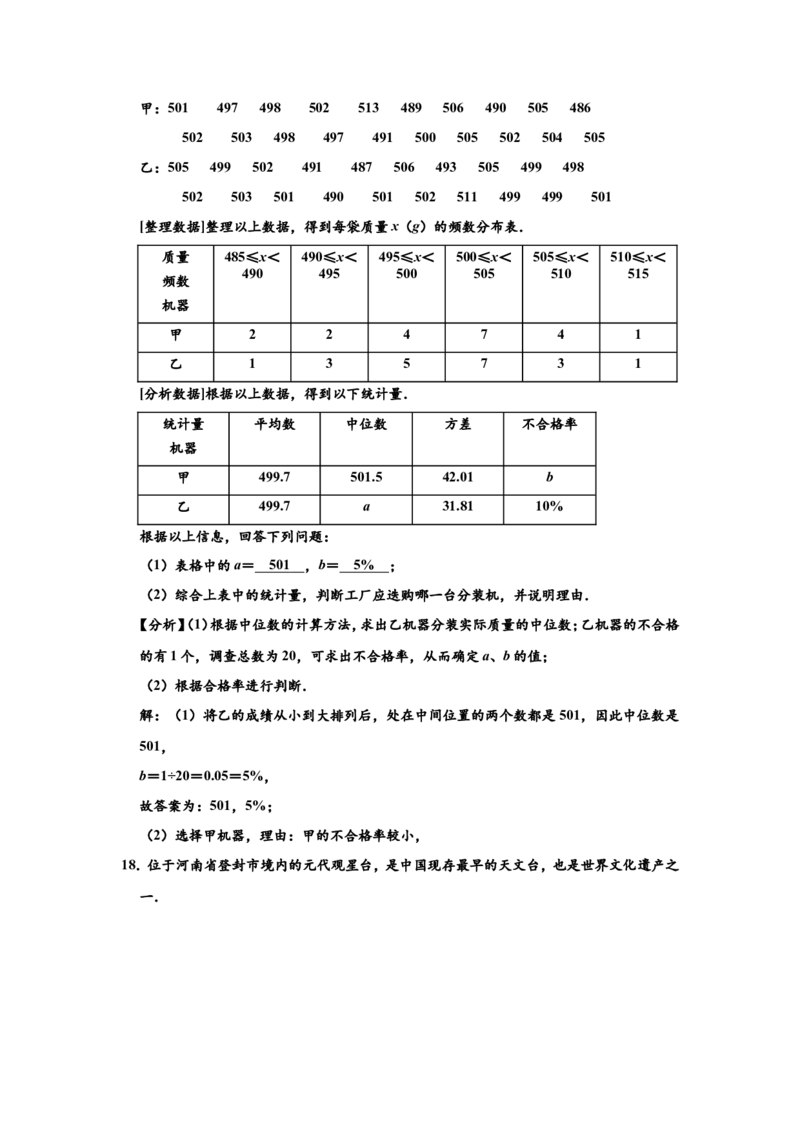
17.为发展乡村经济,某村根据本地特色,创办了山药粉加工厂.该厂需购置一台分装机,计
划从商家推荐试用的甲、乙两台不同品牌的分装机中选择.试用时,设定分装的标准质量
为每袋500g,与之相差大于10g为不合格.为检验分装效果,工厂对这两台机器分装的成
品进行了抽样和分析,过程如下:
[收集数据]从甲、乙两台机器分装的成品中各随机抽取20袋,测得实际质量(单位:g)如
下:
甲:501 497 498 502 513 489 506 490 505 486
502 503 498 497 491 500 505 502 504 505
乙:505 499 502 491 487 506 493 505 499 498
502 503 501 490 501 502 511 499 499 501
[整理数据]整理以上数据,得到每袋质量x(g)的频数分布表.质量 485≤x< 490≤x< 495≤x< 500≤x< 505≤x< 510≤x<
490 495 500 505 510 515
频数
机器
甲 2 2 4 7 4 1
乙 1 3 5 7 3 1
[分析数据]根据以上数据,得到以下统计量.
统计量 平均数 中位数 方差 不合格率
机器
甲 499.7 501.5 42.01 b
乙 499.7 a 31.81 10%
根据以上信息,回答下列问题:
(1)表格中的a= ,b= ;
(2)综合上表中的统计量,判断工厂应迭购哪一台分装机,并说明理由.
18.位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之
一.
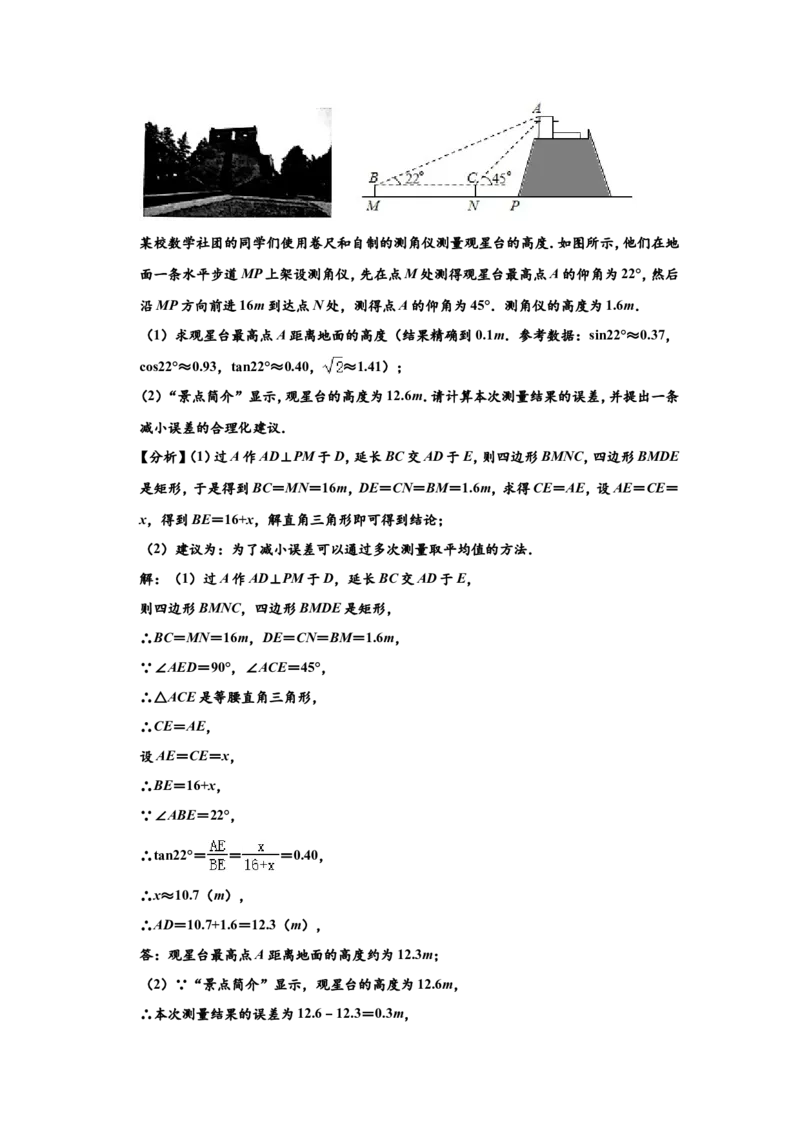
某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地
面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后
沿MP方向前进16m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6m.
(1)求观星台最高点A距离地面的高度(结果精确到0.1m.参考数据:sin22°≈0.37,
cos22°≈0.93,tan22°≈0.40, ≈1.41);
(2)“景点简介”显示,观星台的高度为12.6m.请计算本次测量结果的误差,并提出一条
减小误差的合理化建议.
19.暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.
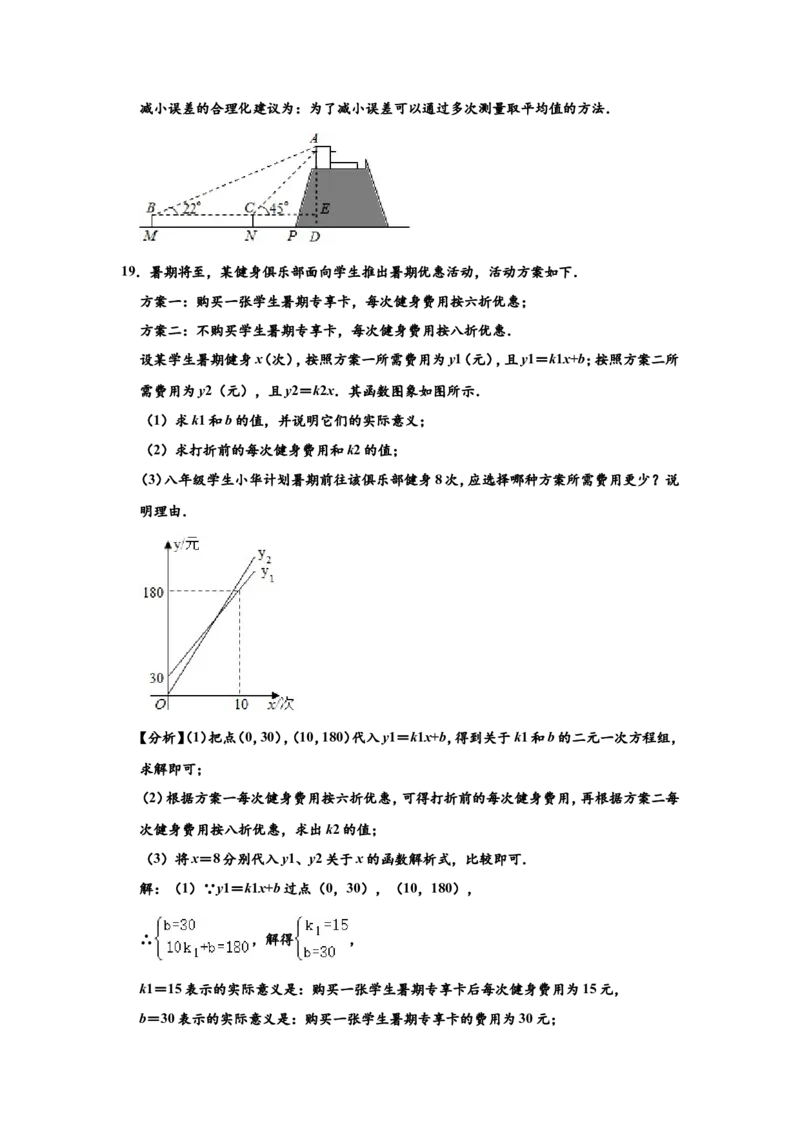
设某学生暑期健身x(次),按照方案一所需费用为y1(元),且y1=k1x+b;按照方案二所
需费用为y2(元),且y2=k2x.其函数图象如图所示.(1)求k1和b的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和k2的值;
(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说
明理由.
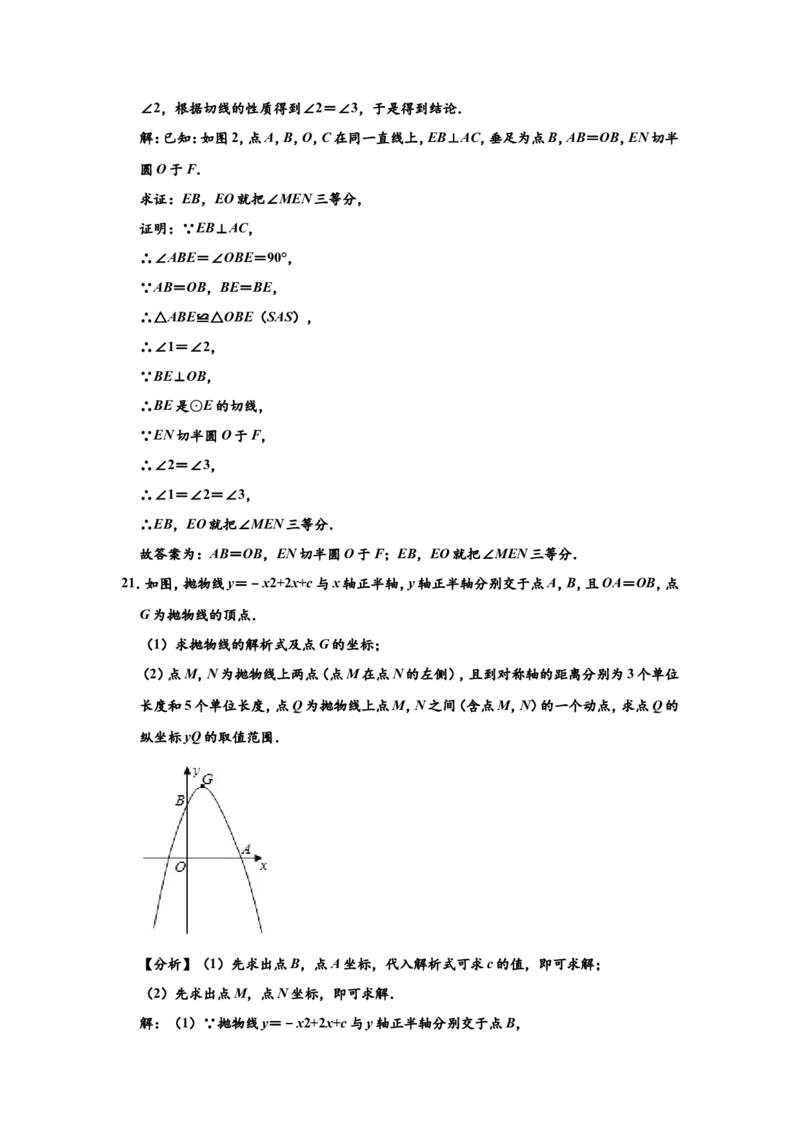
20.我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是
数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种
简易操作工具﹣﹣三分角器.图1是它的示意图,其中AB与半圆O的直径BC在同一直
线上,且AB的长度与半圆的半径相等;DB与AC垂直于点B,DB足够长.
使用方法如图2所示,若要把∠MEN三等分,只需适当放置三分角器,使DB经过∠MEN
的顶点E,点A落在边EM上,半圆O与另一边EN恰好相切,切点为F,则EB,EO就把
∠MEN三等分了.
为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求
证”,请补充完整,并写出“证明”过程.
已知:如图2,点A,B,O,C在同一直线上,EB⊥AC,垂足为点B, .
求证: .
21.如图,抛物线y=﹣x2+2x+c与x轴正半轴,y轴正半轴分别交于点A,B,且OA=OB,点
G为抛物线的顶点.
(1)求抛物线的解析式及点G的坐标;(2)点M,N为抛物线上两点(点M在点N的左侧),且到对称轴的距离分别为3个单位
长度和5个单位长度,点Q为抛物线上点M,N之间(含点M,N)的一个动点,求点Q的
纵坐标yQ的取值范围.
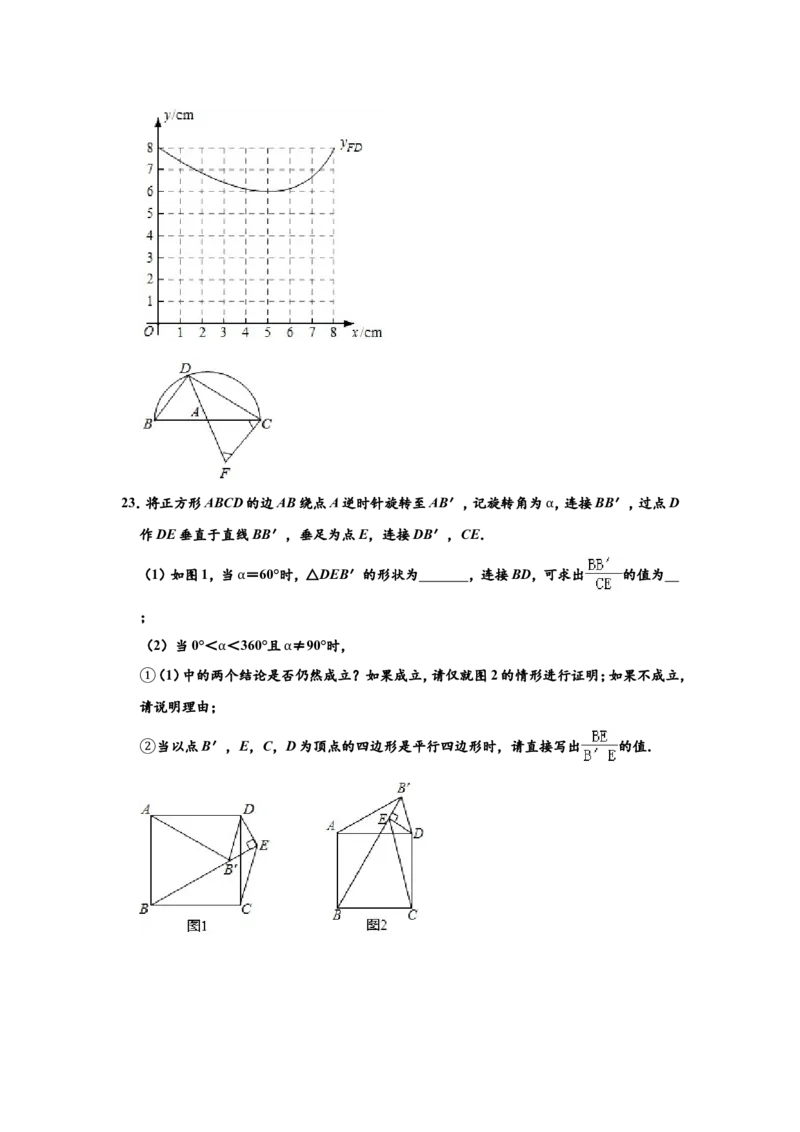
22.小亮在学习中遇到这样一个问题:
如图,点D是 上一动点,线段BC=8cm,点A是线段BC的中点,过点C作CF∥BD,
交DA的延长线于点F.当△DCF为等腰三角形时,求线段BD的长度.
小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验
研究此问题.请将下面的探究过程补充完整:
(1)根据点D在 上的不同位置,画出相应的图形,测量线段BD,CD,FD的长度,得到
下表的几组对应值.
BD/cm 0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
CD/cm 8.0 7.7 7.2 6.6 5.9 a 3.9 2.4 0
FD/cm 8.0 7.4 6.9 6.5 6.1 6.0 6.2 6.7 8.0
操作中发现:
“当点D为 的中点时,BD=5.0cm”.则上表中a的值是 ;
①“线段CF的长度无需测量即可得到”.请简要说明理由.
(②2)将线段BD的长度作为自变量x,CD和FD的长度都是x的函数,分别记为yCD和
yFD,并在平面直角坐标系xOy中画出了函数yFD的图象,如图所示.请在同一坐标系中
画出函数yCD的图象;
(3)继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当△DCF为等腰三
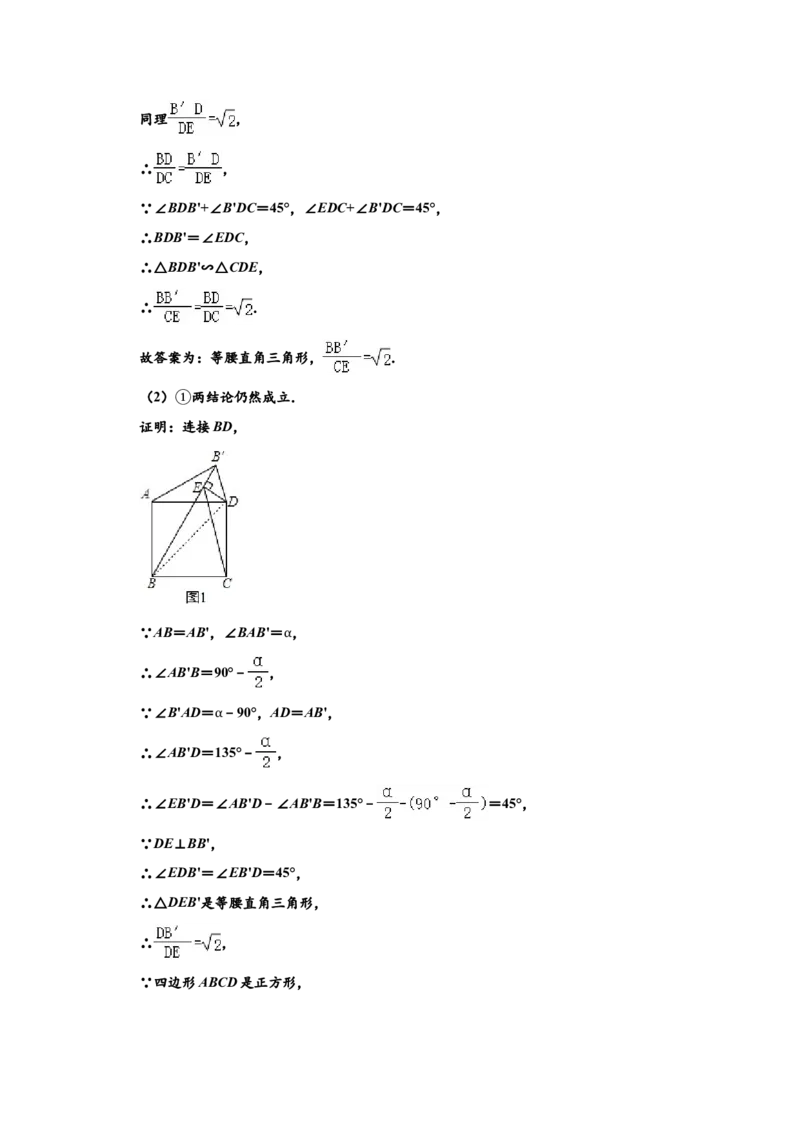
角形时,线段BD长度的近似值(结果保留一位小数).23.将正方形ABCD的边AB绕点A逆时针旋转至AB′,记旋转角为 ,连接BB′,过点D
作DE垂直于直线BB′,垂足为点E,连接DB′,CE. α
(1)如图1,当 =60°时,△DEB′的形状为 ,连接BD,可求出 的值为
α
;
(2)当0°< <360°且 ≠90°时,
(1)中的两α个结论是否α仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,
①请说明理由;
当以点B′,E,C,D为顶点的四边形是平行四边形时,请直接写出 的值.
②参考答案
一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个是正确的.
1.2的相反数是( )
A.﹣2 B.﹣ C. D.2
【分析】利用相反数的概念:只有符号不同的两个数叫做互为相反数,进而得出答案.
解:2的相反数是﹣2.
故选:A.
2.如图摆放的几何体中,主视图与左视图有可能不同的是( )
A. B. C. D.
【分析】分别确定每个几何体的主视图和左视图即可作出判断.
解:A、主视图和左视图是长方形,一定相同,故本选项不合题意题意;
B、主视图和左视图都是等腰三角形,一定相同,故选项不符合题意;
C、主视图和左视图都是圆,一定相同,故选项不符合题意;
D、主视图是长方形,左视图是正方形,故本选项符合题意;
故选:D.
3.要调查下列问题,适合采用全面调查(普查)的是( )
A.中央电视台《开学第一课》的收视率
B.某城市居民6月份人均网上购物的次数
C.即将发射的气象卫星的零部件质量
D.某品牌新能源汽车的最大续航里程
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到
的调查结果比较近似.
解:A、调查中央电视台《开学第一课》的收视率,适合抽查,故本选项不合题意;
B、调查某城市居民6月份人均网上购物的次数,适合抽查,故本选项不合题意;
C、调查即将发射的气象卫星的零部件质量,适合采用全面调查(普查),故本选项符合题
意;
D、调查某品牌新能源汽车的最大续航里程,适合抽查,故本选项不合题意.故选:C.
4.如图,l1∥l2,l3∥l4,若∠1=70°,则∠2的度数为( )
A.100° B.110° C.120° D.130°
【分析】根据平行线的性质即可得到结论.
解:∵l1∥l2,∠1=70°,
∴∠3=∠1=70°,
∵l3∥l4,
∴∠2=180°﹣∠3=180°﹣70°=110°,
故选:B.
5.电子文件的大小常用B,KB,MB,GB等作为单位,其中1GB=210MB,1MB=210KB,
1KB=210B.某视频文件的大小约为1GB,1GB等于( )
A.230B B.830B C.8×1010B D.2×1030B
【分析】列出算式,进行计算即可.
解:由题意得:210×210×210B=210+10+10=230B,
故选:A.
6.若点A(﹣1,y1),B(2,y2),C(3,y3)在反比例函数y=﹣ 的图象上,则y1,y2,y3的大小
关系是( )
A.y1>y2>y3 B.y2>y3>y1 C.y1>y3>y2 D.y3>y2>y1
【分析】根据反比例函数图象上点的坐标特征求出y1、y2、y3的值,比较后即可得出结论.
解:∵点A(﹣1,y1)、B(2,y2)、C(3,y3)在反比例函数y=﹣ 的图象上,∴y1=﹣ =6,y2=﹣ =﹣3,y3=﹣ =﹣2,
又∵﹣3<﹣2<6,
∴y1>y3>y2.
故选:C.
7.定义运算:m☆n=mn2﹣mn﹣1.例如:4☆2=4×22﹣4×2﹣1=7.则方程1☆x=0的根的
情况为( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.无实数根 D.只有一个实数根
【分析】根据新定义运算法则以及即可求出答案.
解:由题意可知:1☆x=x2﹣x﹣1=0,
∴△=1﹣4×1×(﹣1)=5>0,
故选:A.
8.国家统计局统计数据显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务
收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长
率为x,则可列方程为( )
A.500(1+2x)=7500
B.5000×2(1+x)=7500
C.5000(1+x)2=7500
D.5000+5000(1+x)+5000(1+x)2=7500
【分析】根据题意可得等量关系:2017年的快递业务量×(1+增长率)2=2019年的快递业
务量,根据等量关系列出方程即可.
解:设我国2017年至2019年快递业务收入的年平均增长率为x,
由题意得:5000(1+x)2=7500,
故选:C.
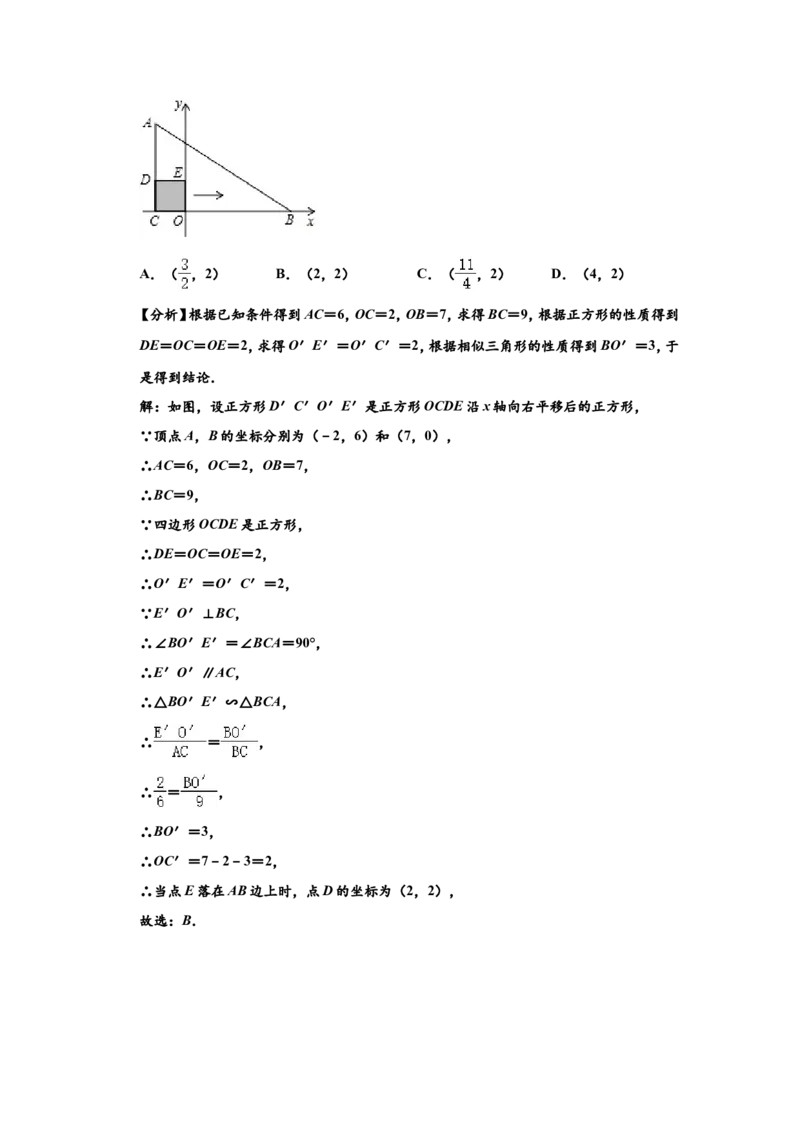
9.如图,在△ABC中,∠ACB=90°,边BC在x轴上,顶点A,B的坐标分别为(﹣2,6)和(7,
0).将正方形OCDE沿x轴向右平移,当点E落在AB边上时,点D的坐标为( )A.( ,2) B.(2,2) C.( ,2) D.(4,2)
【分析】根据已知条件得到AC=6,OC=2,OB=7,求得BC=9,根据正方形的性质得到
DE=OC=OE=2,求得O′E′=O′C′=2,根据相似三角形的性质得到BO′=3,于
是得到结论.
解:如图,设正方形D′C′O′E′是正方形OCDE沿x轴向右平移后的正方形,
∵顶点A,B的坐标分别为(﹣2,6)和(7,0),
∴AC=6,OC=2,OB=7,
∴BC=9,
∵四边形OCDE是正方形,
∴DE=OC=OE=2,
∴O′E′=O′C′=2,
∵E′O′⊥BC,
∴∠BO′E′=∠BCA=90°,
∴E′O′∥AC,
∴△BO′E′∽△BCA,
∴ = ,
∴ = ,
∴BO′=3,
∴OC′=7﹣2﹣3=2,
∴当点E落在AB边上时,点D的坐标为(2,2),
故选:B.10.如图,在△ABC中,AB=BC= ,∠BAC=30°,分别以点A,C为圆心,AC的长为半径
作弧,两弧交于点D,连接DA,DC,则四边形ABCD的面积为( )
A.6 B.9 C.6 D.3
【分析】连接BD交AC于O,根据已知条件得到BD垂直平分AC,求得BD⊥AC,AO=
CO,根据等腰三角形的性质得到∠ACB=∠BAC=30°,根据等边三角形的性质得到
∠DAC=∠DCA=60°,求得AD=CD= AB=3,于是得到结论.
解:连接BD交AC于O,
∵AD=CD,AB=BC,
∴BD垂直平分AC,
∴BD⊥AC,AO=CO,
∵AB=BC,
∴∠ACB=∠BAC=30°,
∵AC=AD=CD,
∴△ACD是等边三角形,
∴∠DAC=∠DCA=60°,
∴∠BAD=∠BCD=90°,∠ADB=∠CDB=30°,
∵AB=BC= ,
∴AD=CD= AB=3,
∴四边形ABCD的面积=2× =3 ,
故选:D.二、填空题(每小题3分,共15分)
11.请写出一个大于1且小于2的无理数 .
【分析】由于所求无理数大于1且小于2,两数平方得大于2小于4,所以可选其中的任意
一个数开平方即可.
解:大于1且小于2的无理数是 ,答案不唯一.
故答案为: .
12.已知关于x的不等式组 其中a,b在数轴上的对应点如图所示,则这个不等式组
的解集为 x > a .
【分析】根据关于x的不等式组的解集表示在数轴上表示方法求出x的取值范围即可.
解:∵b<0<a,
∴关于x的不等式组 的解集为:x>a,
故答案为:x>a.
13.如图所示的转盘,被分成面积相等的四个扇形,分别涂有红、黄、蓝、绿四种颜色.固定指
针,自由转动转盘两次,每次停止后,记下指针所指区域(指针指向区域分界线时,忽略不
计)的颜色,则两次颜色相同的概率是 .
【分析】用树状图或列表法表示所有可能出现的结果,进而求出相应的概率.
解:自由转动转盘两次,指针所指区域所有可能出现的情况如下:共有16种可能出现的结果,其中两次颜色相同的有4种,
∴P(两次颜色相同)= = ,
故答案为: .
14.如图,在边长为2 的正方形ABCD中,点E,F分别是边AB,BC的中点,连接EC,
FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为 1 .
【分析】设DF,CE交于O,根据正方形的性质得到∠B=∠DCF=90°,BC=CD=AB,根
据线段中点的定义得到BE=CF,根据全等三角形的性质得到CE=DF,∠BCE=
∠CDF,求得DF⊥CE,根据勾股定理得到CE=DF= = ,点G,
H分别是EC,FD的中点,根据射影定理即可得到结论.
解:设DF,CE交于O,
∵四边形ABCDA是正方形,
∴∠B=∠DCF=90°,BC=CD=AB,
∵点E,F分别是边AB,BC的中点,
∴BE=CF,
∴△CBE≌△DCF(SAS),
∴CE=DF,∠BCE=∠CDF,
∵∠CDF+∠CFD=90°,
∴∠BCE+∠CFD=90°,
∴∠COF=90°,
∴DF⊥CE,∴CE=DF= = ,
∵点G,H分别是EC,FD的中点,
∴CG=FH= ,
∵∠DCF=90°,CO⊥DF,
∴CF2=OF•DF,
∴OF= = = ,
∴OH= ,OD= ,
∵OC2=OF•OD,
∴OC= = ,
∴OG=CG﹣OC= ﹣ = ,
∴HG= = =1,
故答案为:1.
15.如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交 于点D,点E为半径OB上一
动点.若OB=2,则阴影部分周长的最小值为 .
【分析】利用轴对称的性质,得出当点E移动到点E′时,阴影部分的周长最小,此时的最
小值为弧CD的长与CD′的长度和,分别进行计算即可.
解:如图,作点D关于OB的对称点D′,连接D′C交OB于点E′,连接E′D、OD′,
此时E′C+E′C最小,即:E′C+E′C=CD′,由题意得,∠COD=∠DOB=∠BOD′=30°,
∴∠COD′=90°,
∴CD′= = =2 ,
的长l= = ,
∴阴影部分周长的最小值为2 + = .
故答案为: .
三、解答题(本大题共8个小题,满分75分)
16.先化简,再求值:(1﹣ )÷ ,其中a= +1.
【分析】先根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可.
解:
=
=a﹣1,
把a= +1代入a﹣1= +1﹣1= .
17.为发展乡村经济,某村根据本地特色,创办了山药粉加工厂.该厂需购置一台分装机,计
划从商家推荐试用的甲、乙两台不同品牌的分装机中选择.试用时,设定分装的标准质量
为每袋500g,与之相差大于10g为不合格.为检验分装效果,工厂对这两台机器分装的成
品进行了抽样和分析,过程如下:
[收集数据]从甲、乙两台机器分装的成品中各随机抽取20袋,测得实际质量(单位:g)如
下:甲:501 497 498 502 513 489 506 490 505 486
502 503 498 497 491 500 505 502 504 505
乙:505 499 502 491 487 506 493 505 499 498
502 503 501 490 501 502 511 499 499 501
[整理数据]整理以上数据,得到每袋质量x(g)的频数分布表.
质量 485≤x< 490≤x< 495≤x< 500≤x< 505≤x< 510≤x<
490 495 500 505 510 515
频数
机器
甲 2 2 4 7 4 1
乙 1 3 5 7 3 1
[分析数据]根据以上数据,得到以下统计量.
统计量 平均数 中位数 方差 不合格率
机器
甲 499.7 501.5 42.01 b
乙 499.7 a 31.81 10%
根据以上信息,回答下列问题:
(1)表格中的a= 50 1 ,b= 5% ;
(2)综合上表中的统计量,判断工厂应迭购哪一台分装机,并说明理由.
【分析】(1)根据中位数的计算方法,求出乙机器分装实际质量的中位数;乙机器的不合格
的有1个,调查总数为20,可求出不合格率,从而确定a、b的值;
(2)根据合格率进行判断.
解:(1)将乙的成绩从小到大排列后,处在中间位置的两个数都是501,因此中位数是
501,
b=1÷20=0.05=5%,
故答案为:501,5%;
(2)选择甲机器,理由:甲的不合格率较小,
18.位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之
一.某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地
面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后
沿MP方向前进16m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6m.
(1)求观星台最高点A距离地面的高度(结果精确到0.1m.参考数据:sin22°≈0.37,
cos22°≈0.93,tan22°≈0.40, ≈1.41);
(2)“景点简介”显示,观星台的高度为12.6m.请计算本次测量结果的误差,并提出一条
减小误差的合理化建议.
【分析】(1)过A作AD⊥PM于D,延长BC交AD于E,则四边形BMNC,四边形BMDE
是矩形,于是得到BC=MN=16m,DE=CN=BM=1.6m,求得CE=AE,设AE=CE=
x,得到BE=16+x,解直角三角形即可得到结论;
(2)建议为:为了减小误差可以通过多次测量取平均值的方法.
解:(1)过A作AD⊥PM于D,延长BC交AD于E,
则四边形BMNC,四边形BMDE是矩形,
∴BC=MN=16m,DE=CN=BM=1.6m,
∵∠AED=90°,∠ACE=45°,
∴△ACE是等腰直角三角形,
∴CE=AE,
设AE=CE=x,
∴BE=16+x,
∵∠ABE=22°,
∴tan22°= = =0.40,
∴x≈10.7(m),
∴AD=10.7+1.6=12.3(m),
答:观星台最高点A距离地面的高度约为12.3m;
(2)∵“景点简介”显示,观星台的高度为12.6m,
∴本次测量结果的误差为12.6﹣12.3=0.3m,减小误差的合理化建议为:为了减小误差可以通过多次测量取平均值的方法.
19.暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.
设某学生暑期健身x(次),按照方案一所需费用为y1(元),且y1=k1x+b;按照方案二所
需费用为y2(元),且y2=k2x.其函数图象如图所示.
(1)求k1和b的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和k2的值;
(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说
明理由.
【分析】(1)把点(0,30),(10,180)代入y1=k1x+b,得到关于k1和b的二元一次方程组,
求解即可;
(2)根据方案一每次健身费用按六折优惠,可得打折前的每次健身费用,再根据方案二每
次健身费用按八折优惠,求出k2的值;
(3)将x=8分别代入y1、y2关于x的函数解析式,比较即可.
解:(1)∵y1=k1x+b过点(0,30),(10,180),
∴ ,解得 ,
k1=15表示的实际意义是:购买一张学生暑期专享卡后每次健身费用为15元,
b=30表示的实际意义是:购买一张学生暑期专享卡的费用为30元;(2)由题意可得,打折前的每次健身费用为15÷0.6=25(元),
则k2=25×0.8=20;
(3)选择方案一所需费用更少.理由如下:
由题意可知,y1=15x+30,y2=20x.
当健身8次时,
选择方案一所需费用:y1=15×8+30=150(元),
选择方案二所需费用:y2=20×8=160(元),
∵150<160,
∴选择方案一所需费用更少.
20.我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是
数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种
简易操作工具﹣﹣三分角器.图1是它的示意图,其中AB与半圆O的直径BC在同一直
线上,且AB的长度与半圆的半径相等;DB与AC垂直于点B,DB足够长.
使用方法如图2所示,若要把∠MEN三等分,只需适当放置三分角器,使DB经过∠MEN
的顶点E,点A落在边EM上,半圆O与另一边EN恰好相切,切点为F,则EB,EO就把
∠MEN三等分了.
为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求
证”,请补充完整,并写出“证明”过程.
已知:如图2,点A,B,O,C在同一直线上,EB⊥AC,垂足为点B, AB = OB , EN 切半圆
O 于 F .
求证: EB , EO 就把∠ MEN 三等分 .
【分析】根据垂直的定义得到∠ABE=∠OBE=90°,根据全等三角形的性质得到∠1=∠2,根据切线的性质得到∠2=∠3,于是得到结论.
解:已知:如图2,点A,B,O,C在同一直线上,EB⊥AC,垂足为点B,AB=OB,EN切半
圆O于F.
求证:EB,EO就把∠MEN三等分,
证明:∵EB⊥AC,
∴∠ABE=∠OBE=90°,
∵AB=OB,BE=BE,
∴△ABE≌△OBE(SAS),
∴∠1=∠2,
∵BE⊥OB,
∴BE是 E的切线,
∵EN切⊙半圆O于F,
∴∠2=∠3,
∴∠1=∠2=∠3,
∴EB,EO就把∠MEN三等分.
故答案为:AB=OB,EN切半圆O于F;EB,EO就把∠MEN三等分.
21.如图,抛物线y=﹣x2+2x+c与x轴正半轴,y轴正半轴分别交于点A,B,且OA=OB,点
G为抛物线的顶点.
(1)求抛物线的解析式及点G的坐标;
(2)点M,N为抛物线上两点(点M在点N的左侧),且到对称轴的距离分别为3个单位
长度和5个单位长度,点Q为抛物线上点M,N之间(含点M,N)的一个动点,求点Q的
纵坐标yQ的取值范围.
【分析】(1)先求出点B,点A坐标,代入解析式可求c的值,即可求解;
(2)先求出点M,点N坐标,即可求解.
解:(1)∵抛物线y=﹣x2+2x+c与y轴正半轴分别交于点B,∴点B(0,c),
∵OA=OB=c,
∴点A(c,0),
∴0=﹣c2+2c+c,
∴c=3或0(舍去),
∴抛物线解析式为:y=﹣x2+2x+3,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点G为(1,4);
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴对称轴为直线x=1,
∵点M,N为抛物线上两点(点M在点N的左侧),且到对称轴的距离分别为3个单位长
度和5个单位长度,
∴点M的横坐标为﹣2或4,点N的横坐标为6,
∴点M坐标为(﹣2,﹣5)或(4,﹣5),点N坐标(6,﹣21),
∵点Q为抛物线上点M,N之间(含点M,N)的一个动点,
∴﹣21≤yQ≤4.
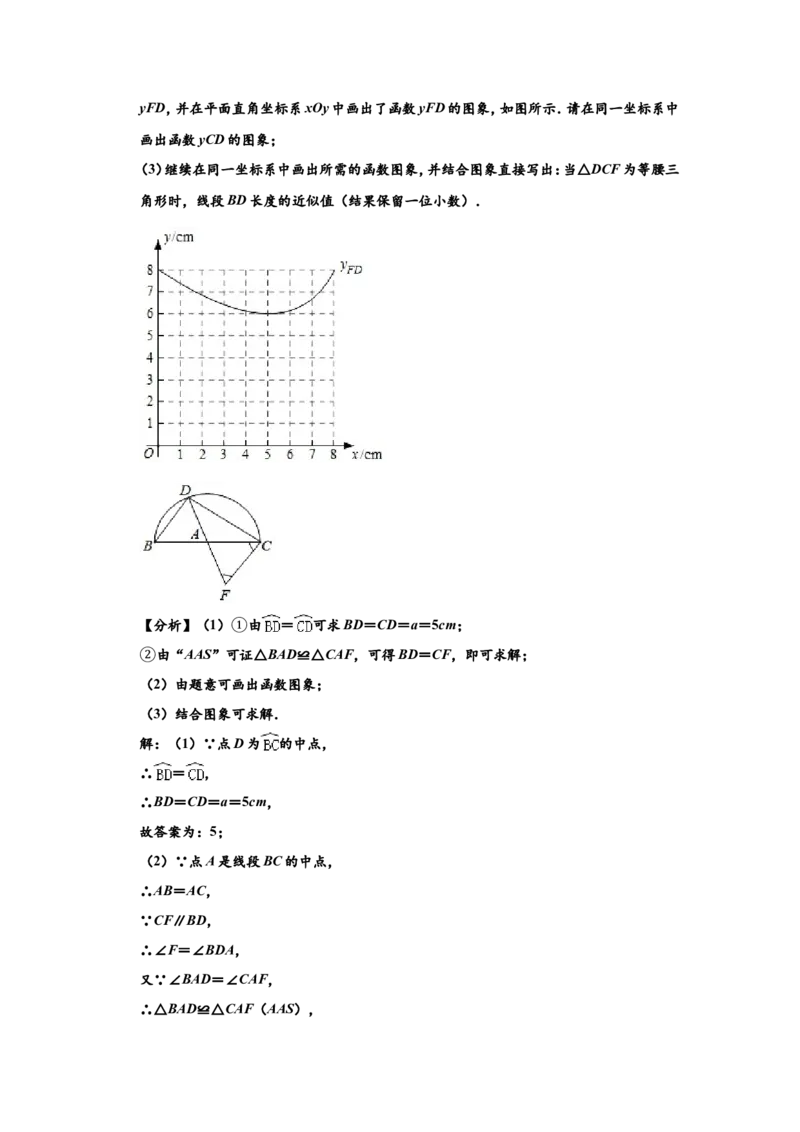
22.小亮在学习中遇到这样一个问题:
如图,点D是 上一动点,线段BC=8cm,点A是线段BC的中点,过点C作CF∥BD,
交DA的延长线于点F.当△DCF为等腰三角形时,求线段BD的长度.
小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验
研究此问题.请将下面的探究过程补充完整:
(1)根据点D在 上的不同位置,画出相应的图形,测量线段BD,CD,FD的长度,得到
下表的几组对应值.
BD/cm 0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
CD/cm 8.0 7.7 7.2 6.6 5.9 a 3.9 2.4 0
FD/cm 8.0 7.4 6.9 6.5 6.1 6.0 6.2 6.7 8.0
操作中发现:
“当点D为 的中点时,BD=5.0cm”.则上表中a的值是 5 ;
①“线段CF的长度无需测量即可得到”.请简要说明理由.
(②2)将线段BD的长度作为自变量x,CD和FD的长度都是x的函数,分别记为yCD和yFD,并在平面直角坐标系xOy中画出了函数yFD的图象,如图所示.请在同一坐标系中
画出函数yCD的图象;
(3)继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当△DCF为等腰三
角形时,线段BD长度的近似值(结果保留一位小数).
【分析】(1) 由 = 可求BD=CD=a=5cm;
由“AAS”可①证△BAD≌△CAF,可得BD=CF,即可求解;
②(2)由题意可画出函数图象;
(3)结合图象可求解.
解:(1)∵点D为 的中点,
∴ = ,
∴BD=CD=a=5cm,
故答案为:5;
(2)∵点A是线段BC的中点,
∴AB=AC,
∵CF∥BD,
∴∠F=∠BDA,
又∵∠BAD=∠CAF,
∴△BAD≌△CAF(AAS),∴BD=CF,
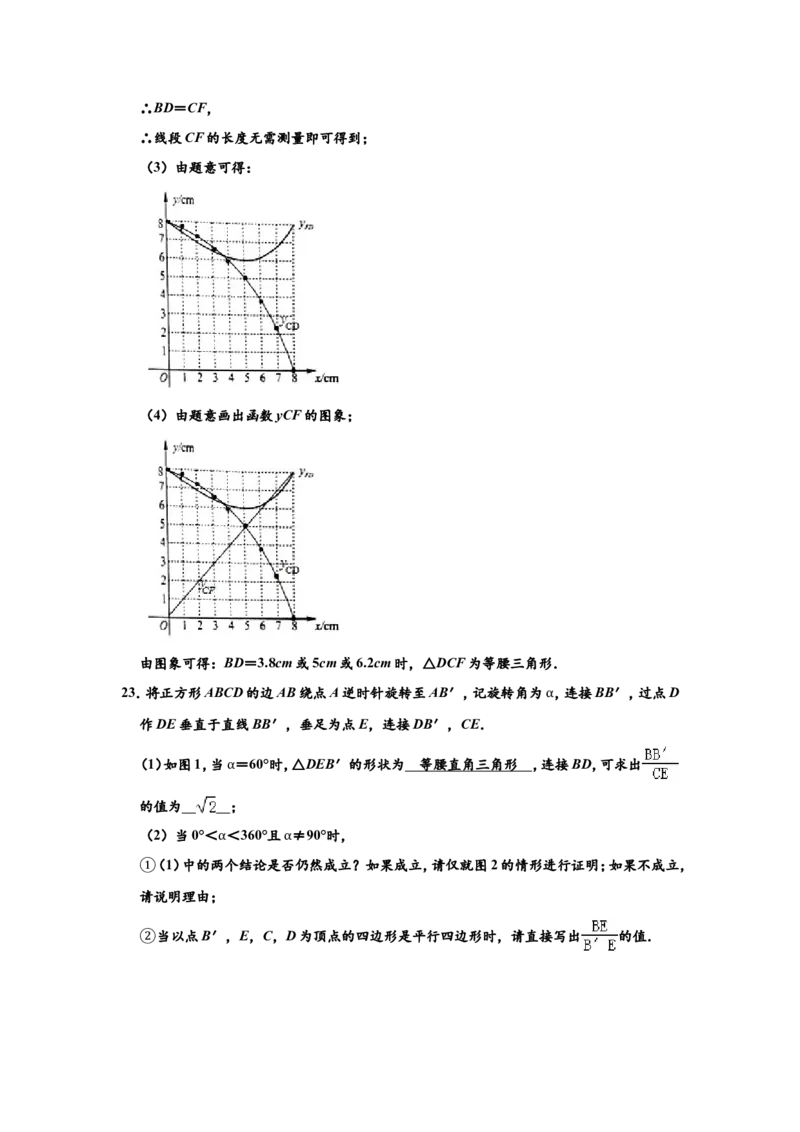
∴线段CF的长度无需测量即可得到;
(3)由题意可得:
(4)由题意画出函数yCF的图象;
由图象可得:BD=3.8cm或5cm或6.2cm时,△DCF为等腰三角形.
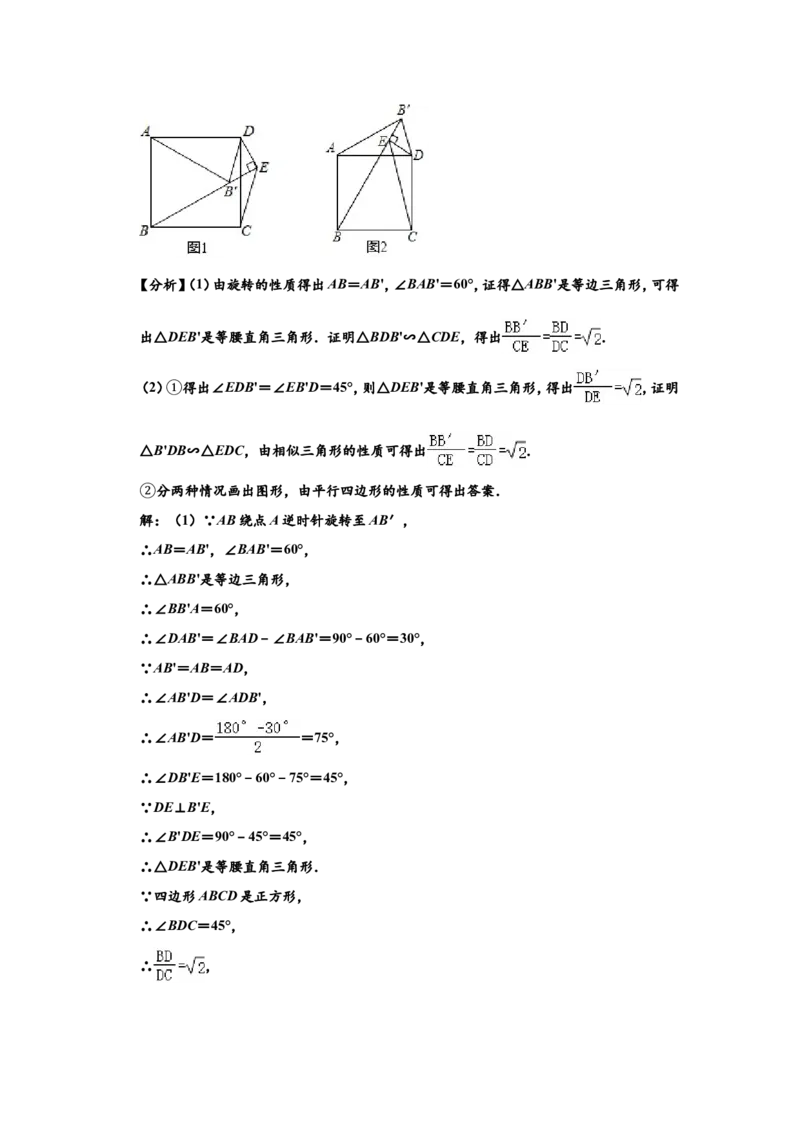
23.将正方形ABCD的边AB绕点A逆时针旋转至AB′,记旋转角为 ,连接BB′,过点D
作DE垂直于直线BB′,垂足为点E,连接DB′,CE. α
(1)如图1,当 =60°时,△DEB′的形状为 等腰直角三角形 ,连接BD,可求出
α
的值为 ;
(2)当0°< <360°且 ≠90°时,
(1)中的两α个结论是否α仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,
①请说明理由;
当以点B′,E,C,D为顶点的四边形是平行四边形时,请直接写出 的值.
②【分析】(1)由旋转的性质得出AB=AB',∠BAB'=60°,证得△ABB'是等边三角形,可得
出△DEB'是等腰直角三角形.证明△BDB'∽△CDE,得出 .
(2) 得出∠EDB'=∠EB'D=45°,则△DEB'是等腰直角三角形,得出 ,证明
①
△B'DB∽△EDC,由相似三角形的性质可得出 .
分两种情况画出图形,由平行四边形的性质可得出答案.
②解:(1)∵AB绕点A逆时针旋转至AB′,
∴AB=AB',∠BAB'=60°,
∴△ABB'是等边三角形,
∴∠BB'A=60°,
∴∠DAB'=∠BAD﹣∠BAB'=90°﹣60°=30°,
∵AB'=AB=AD,
∴∠AB'D=∠ADB',
∴∠AB'D= =75°,
∴∠DB'E=180°﹣60°﹣75°=45°,
∵DE⊥B'E,
∴∠B'DE=90°﹣45°=45°,
∴△DEB'是等腰直角三角形.
∵四边形ABCD是正方形,
∴∠BDC=45°,
∴ ,同理 ,
∴ ,
∵∠BDB'+∠B'DC=45°,∠EDC+∠B'DC=45°,
∴BDB'=∠EDC,
∴△BDB'∽△CDE,
∴ .
故答案为:等腰直角三角形, .
(2) 两结论仍然成立.
证明:①连接BD,
∵AB=AB',∠BAB'= ,
α
∴∠AB'B=90°﹣ ,
∵∠B'AD= ﹣90°,AD=AB',
α
∴∠AB'D=135°﹣ ,
∴∠EB'D=∠AB'D﹣∠AB'B=135°﹣ =45°,
∵DE⊥BB',
∴∠EDB'=∠EB'D=45°,
∴△DEB'是等腰直角三角形,
∴ ,
∵四边形ABCD是正方形,∴ ,∠BDC=45°,
∴ ,
∵∠EDB'=∠BDC,
∴∠EDB'+∠EDB=∠BDC+∠EDB,
即∠B'DB=∠EDC,
∴△B'DB∽△EDC,
∴ .
=3或1.
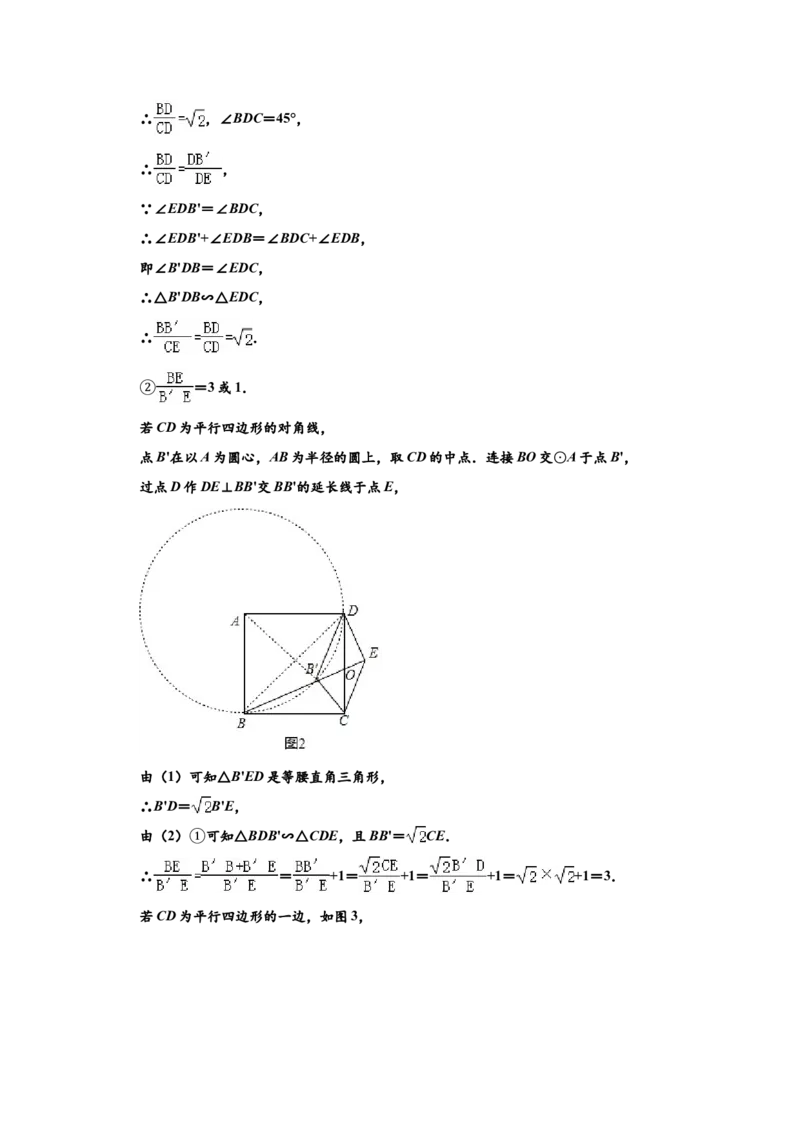
②
若CD为平行四边形的对角线,
点B'在以A为圆心,AB为半径的圆上,取CD的中点.连接BO交 A于点B',
过点D作DE⊥BB'交BB'的延长线于点E, ⊙
由(1)可知△B'ED是等腰直角三角形,
∴B'D= B'E,
由(2) 可知△BDB'∽△CDE,且BB'= CE.
①
∴ = +1= +1= +1= +1=3.
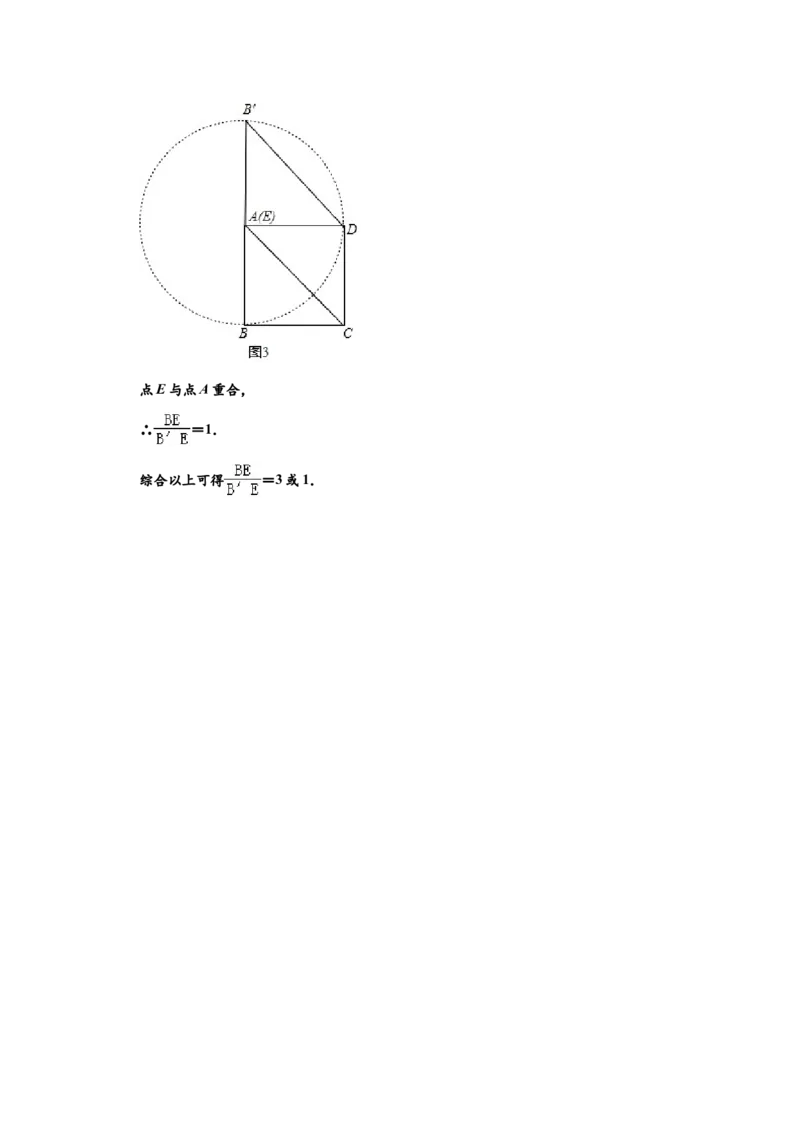
若CD为平行四边形的一边,如图3,点E与点A重合,
∴ =1.
综合以上可得 =3或1.