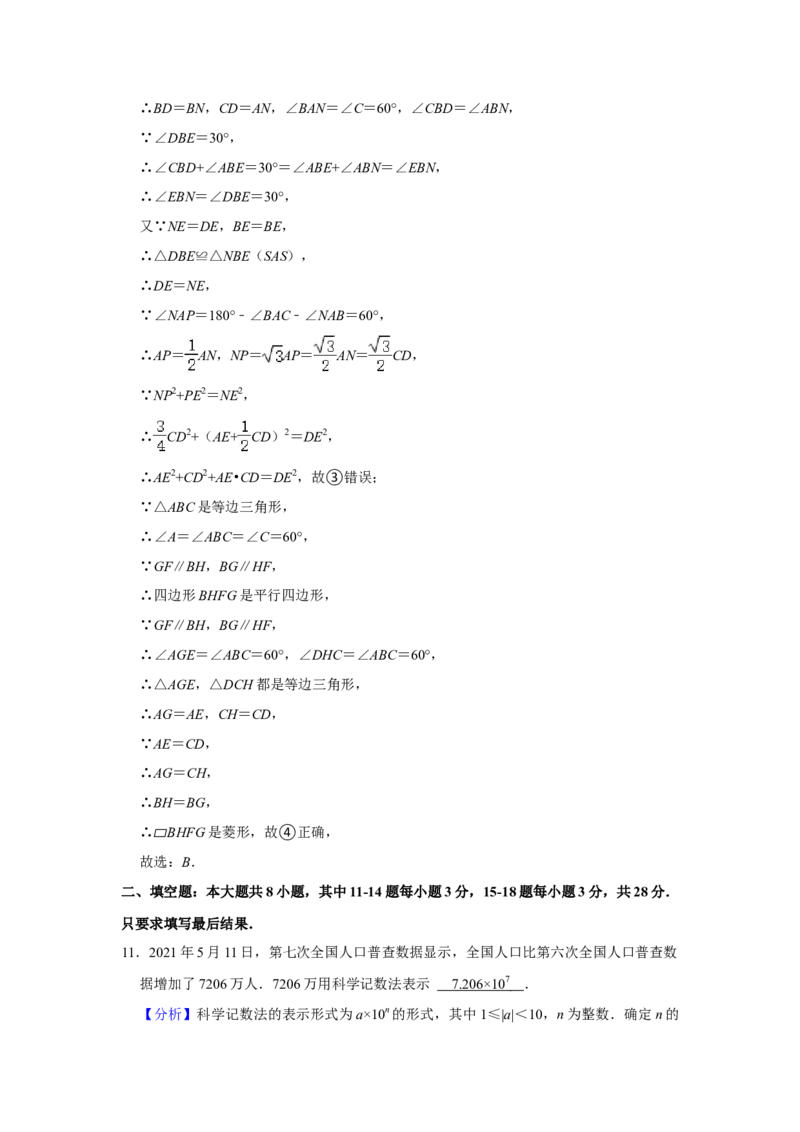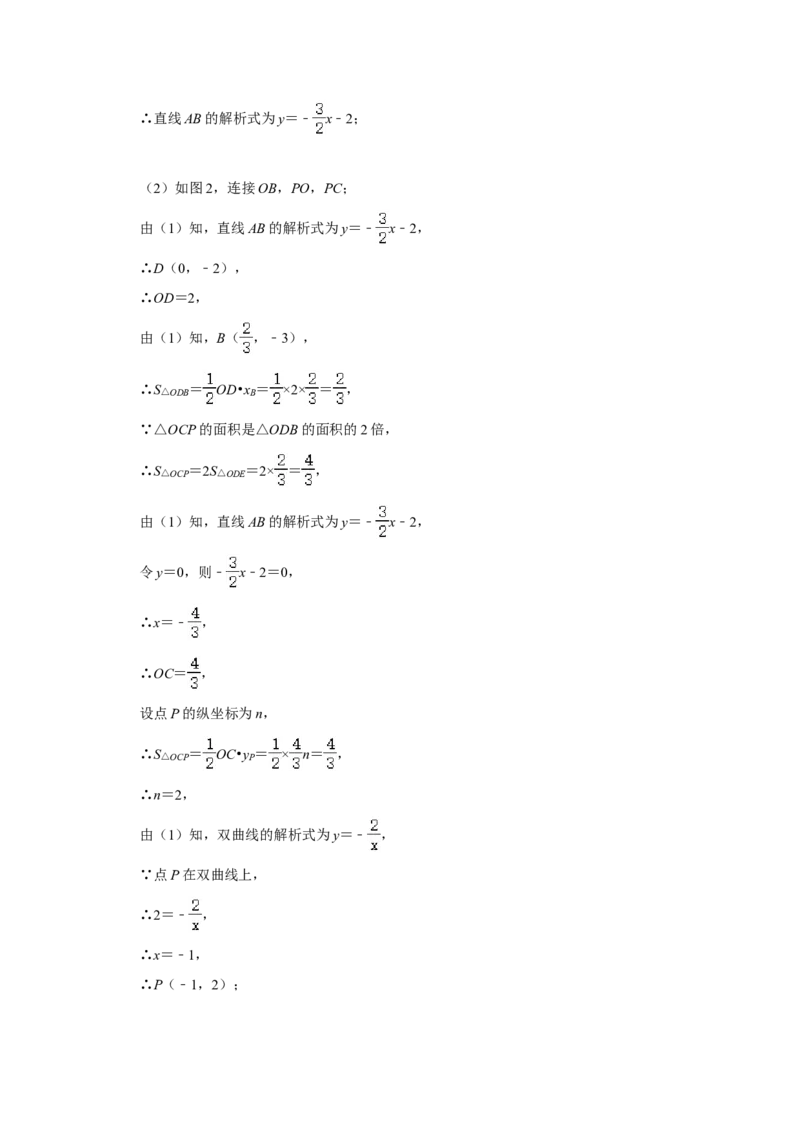文档内容
2021年山东省东营市中考数学试卷
一、选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正
确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.
1.16的算术平方根为( )
A.±4 B.4 C.﹣4 D.8
2.下列运算结果正确的是( )
A.x2+x3=x5 B.(﹣a﹣b)2=a2+2ab+b2
C.(3x3)2=6x6 D.
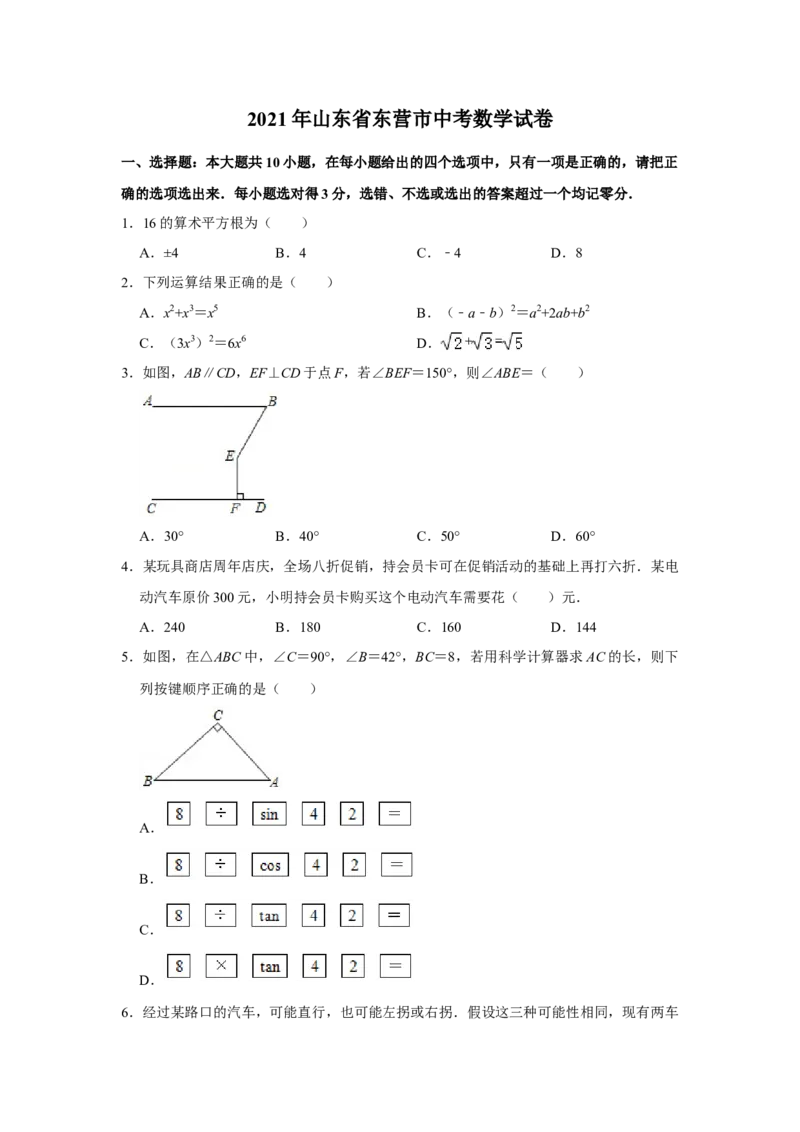
3.如图,AB∥CD,EF⊥CD于点F,若∠BEF=150°,则∠ABE=( )
A.30° B.40° C.50° D.60°
4.某玩具商店周年店庆,全场八折促销,持会员卡可在促销活动的基础上再打六折.某电
动汽车原价300元,小明持会员卡购买这个电动汽车需要花( )元.
A.240 B.180 C.160 D.144
5.如图,在△ABC中,∠C=90°,∠B=42°,BC=8,若用科学计算器求AC的长,则下
列按键顺序正确的是( )
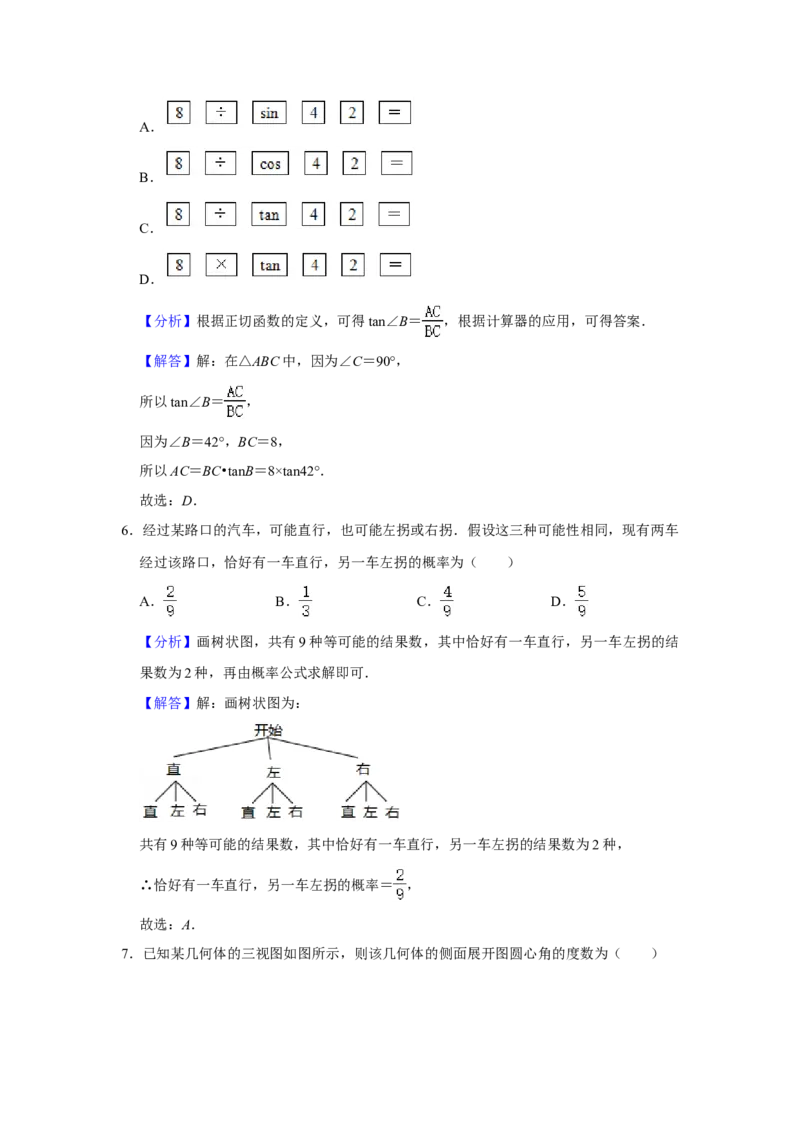
A.
B.
C.
D.
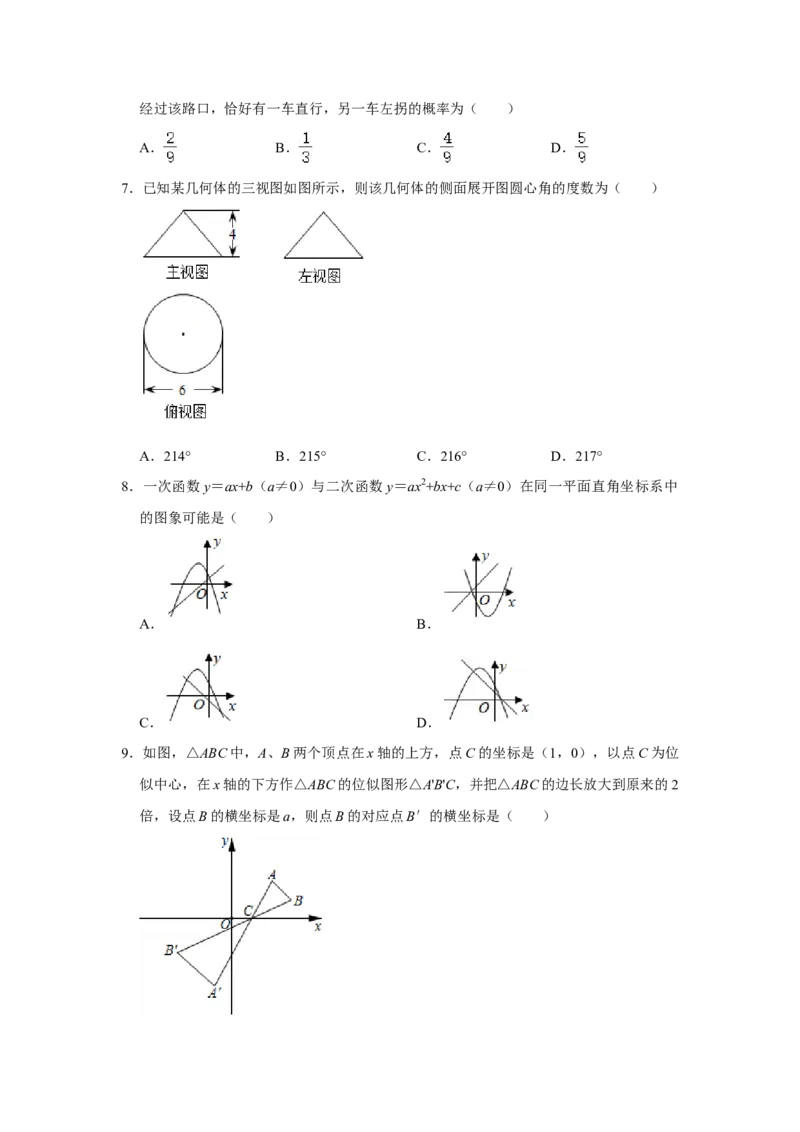
6.经过某路口的汽车,可能直行,也可能左拐或右拐.假设这三种可能性相同,现有两车经过该路口,恰好有一车直行,另一车左拐的概率为( )
A. B. C. D.
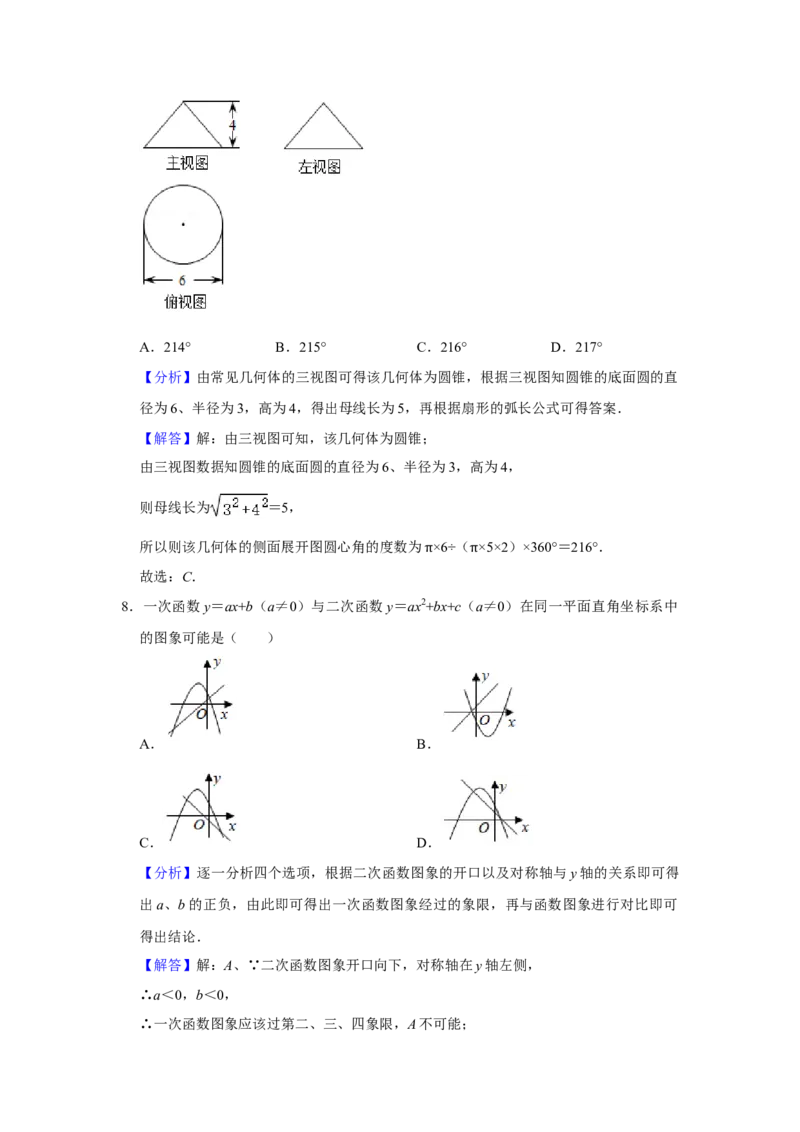
7.已知某几何体的三视图如图所示,则该几何体的侧面展开图圆心角的度数为( )
A.214° B.215° C.216° D.217°
8.一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中
的图象可能是( )
A. B.
C. D.
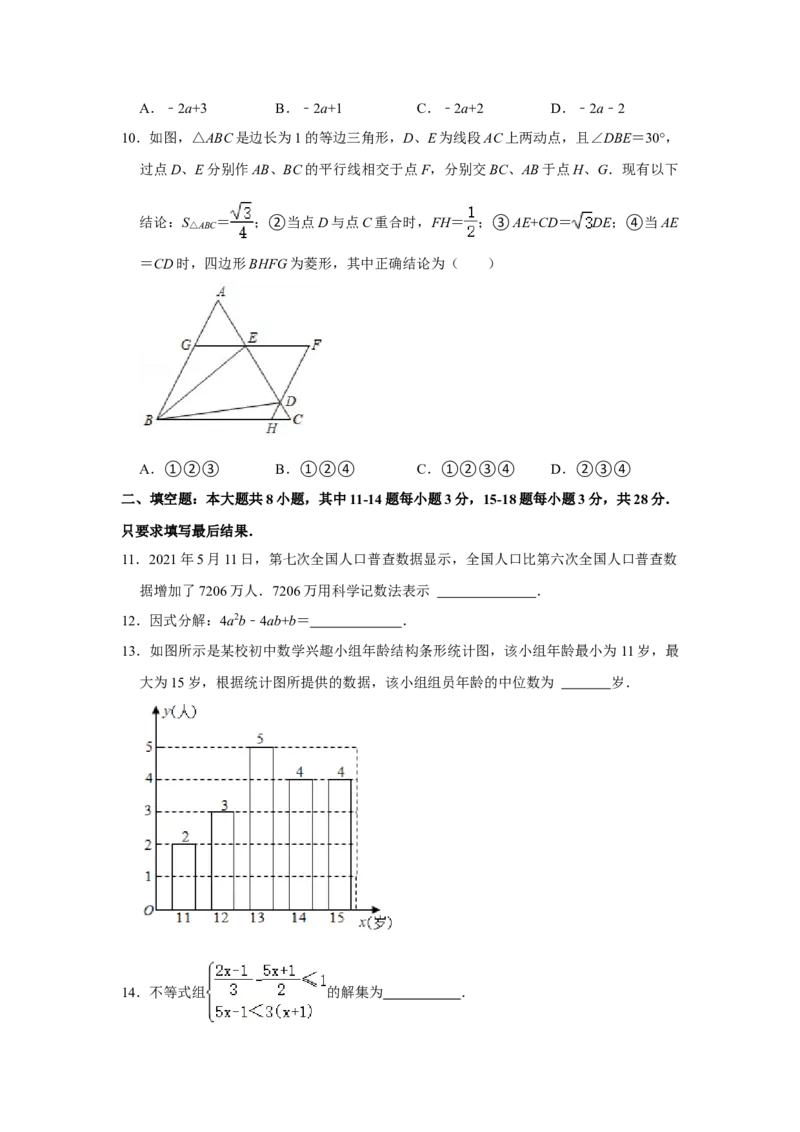
9.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位
似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2
倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )A.﹣2a+3 B.﹣2a+1 C.﹣2a+2 D.﹣2a﹣2
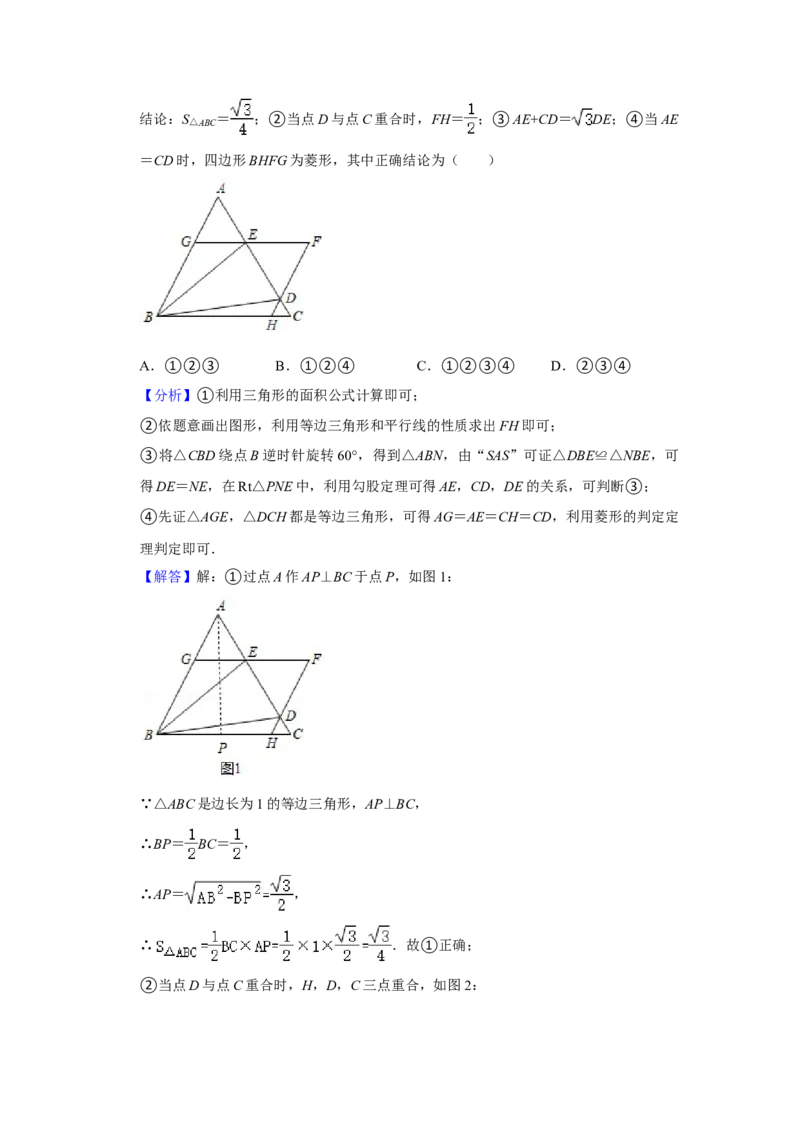
10.如图,△ABC是边长为1的等边三角形,D、E为线段AC上两动点,且∠DBE=30°,
过点D、E分别作AB、BC的平行线相交于点F,分别交BC、AB于点H、G.现有以下
结论:S△ABC = ;②当点D与点C重合时,FH= ;③AE+CD= DE;④当AE
=CD时,四边形BHFG为菱形,其中正确结论为( )
A.①②③ B.①②④ C.①②③④ D.②③④
二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题3分,共28分.
只要求填写最后结果.
11.2021年5月11日,第七次全国人口普查数据显示,全国人口比第六次全国人口普查数
据增加了7206万人.7206万用科学记数法表示 .
12.因式分解:4a2b﹣4ab+b= .
13.如图所示是某校初中数学兴趣小组年龄结构条形统计图,该小组年龄最小为11岁,最
大为15岁,根据统计图所提供的数据,该小组组员年龄的中位数为 岁.
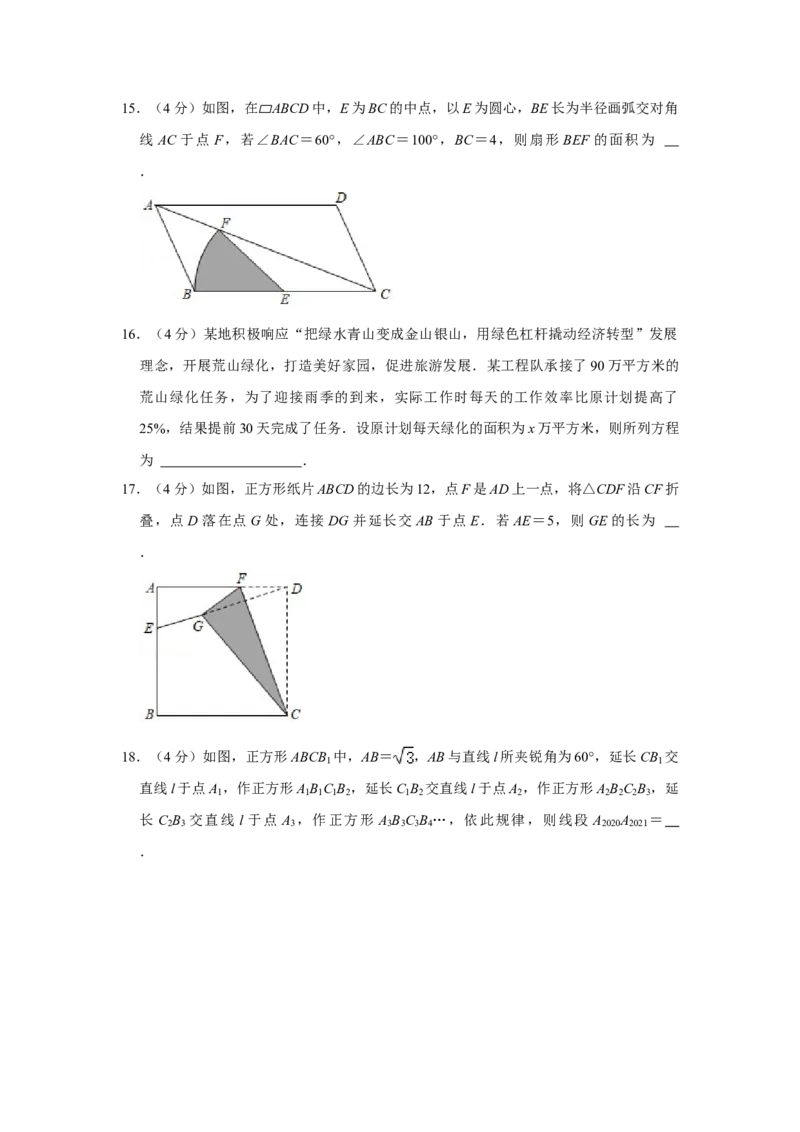
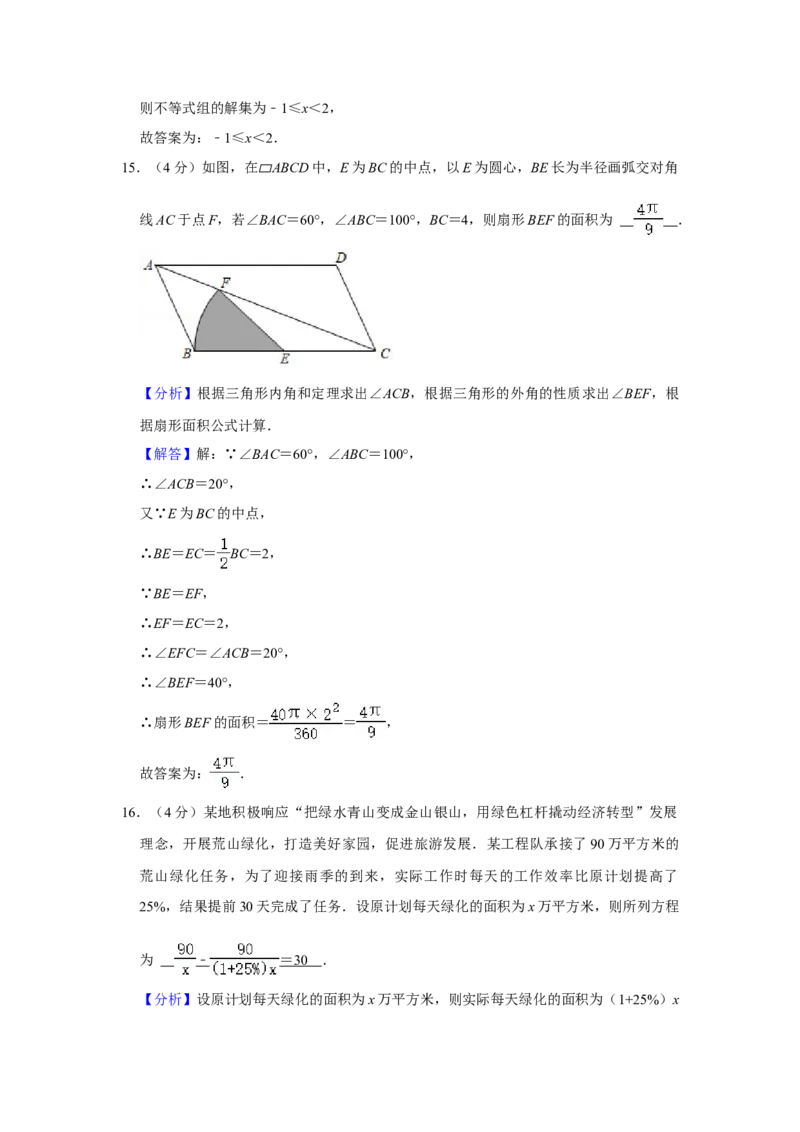
14.不等式组 的解集为 .15.(4分)如图,在 ABCD中,E为BC的中点,以E为圆心,BE长为半径画弧交对角
线 AC 于点 F,若∠▱BAC=60°,∠ABC=100°,BC=4,则扇形 BEF 的面积为
.
16.(4分)某地积极响应“把绿水青山变成金山银山,用绿色杠杆撬动经济转型”发展
理念,开展荒山绿化,打造美好家园,促进旅游发展.某工程队承接了90万平方米的
荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了
25%,结果提前30天完成了任务.设原计划每天绿化的面积为x万平方米,则所列方程
为 .
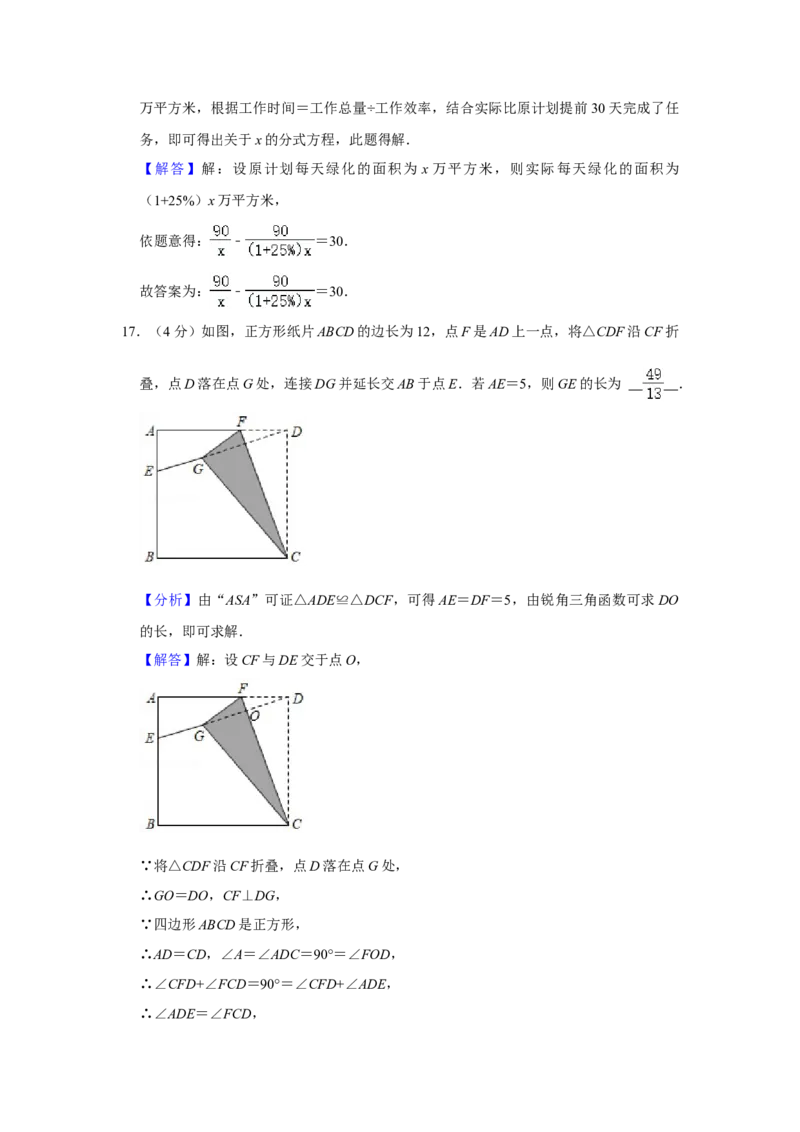
17.(4分)如图,正方形纸片ABCD的边长为12,点F是AD上一点,将△CDF沿CF折
叠,点D落在点G处,连接 DG并延长交 AB于点E.若AE=5,则GE的长为
.
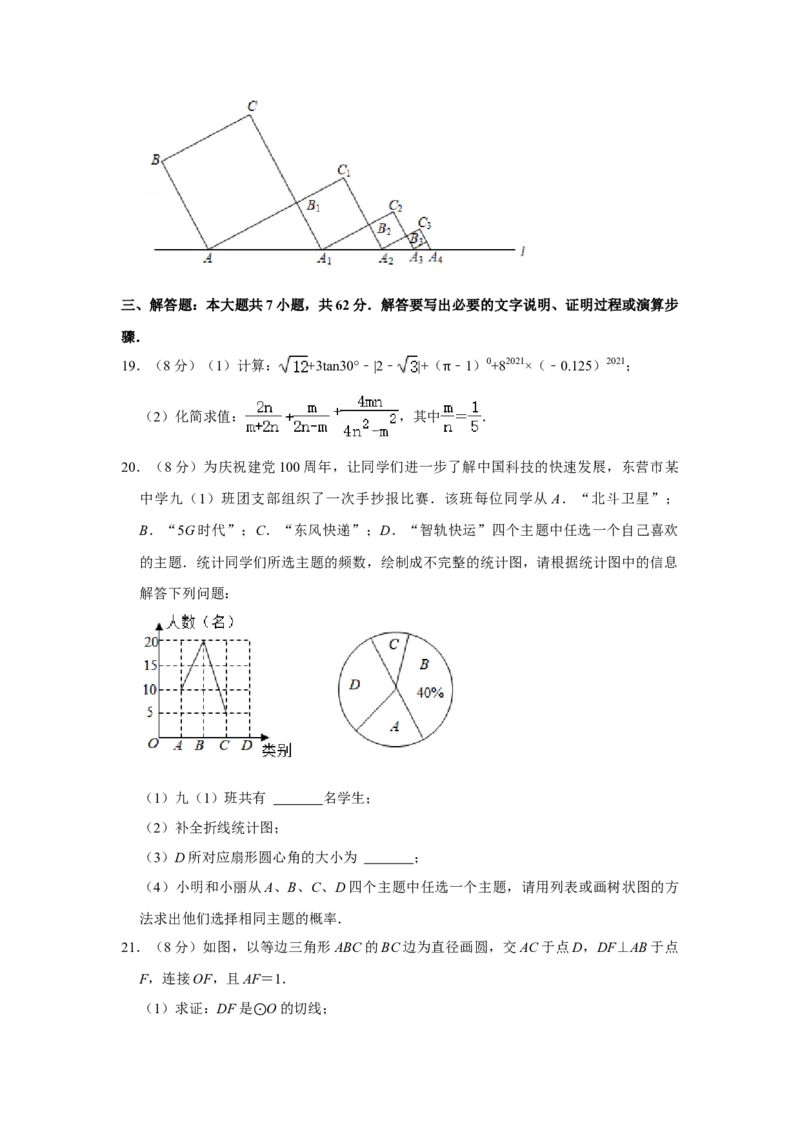
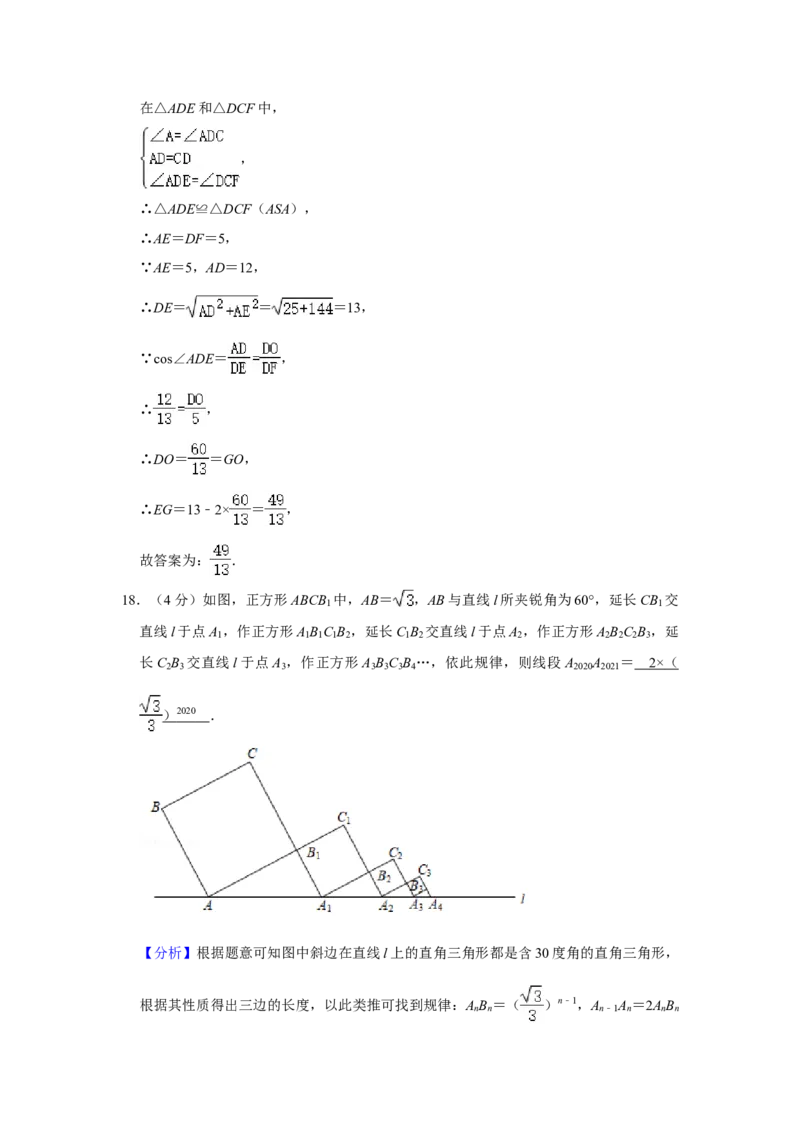
18.(4分)如图,正方形ABCB 中,AB= ,AB与直线l所夹锐角为60°,延长CB 交
1 1
直线l于点A ,作正方形A B C B ,延长C B 交直线l于点A ,作正方形A B C B ,延
1 1 1 1 2 1 2 2 2 2 2 3
长 C B 交直线 l 于点 A ,作正方形 A B C B …,依此规律,则线段 A A =
2 3 3 3 3 3 4 2020 2021
.三、解答题:本大题共7小题,共62分.解答要写出必要的文字说明、证明过程或演算步
骤.
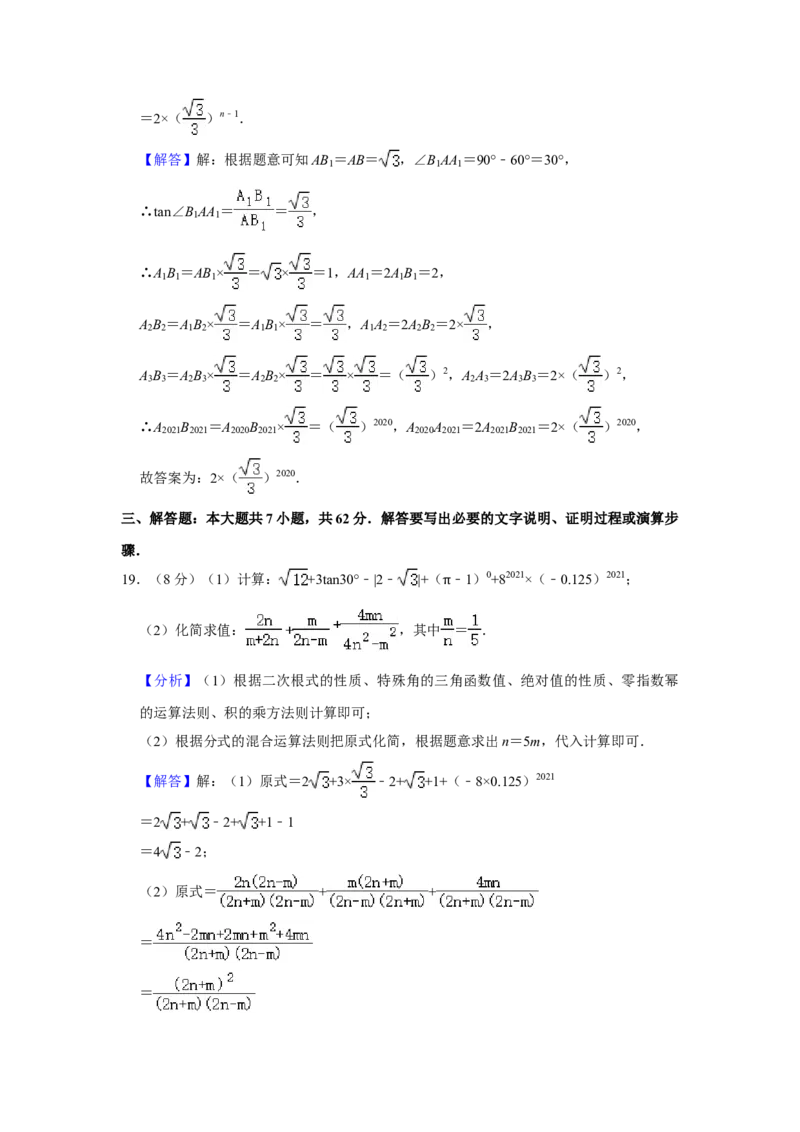
19.(8分)(1)计算: +3tan30°﹣|2﹣ |+( ﹣1)0+82021×(﹣0.125)2021;
π
(2)化简求值: ,其中 = .
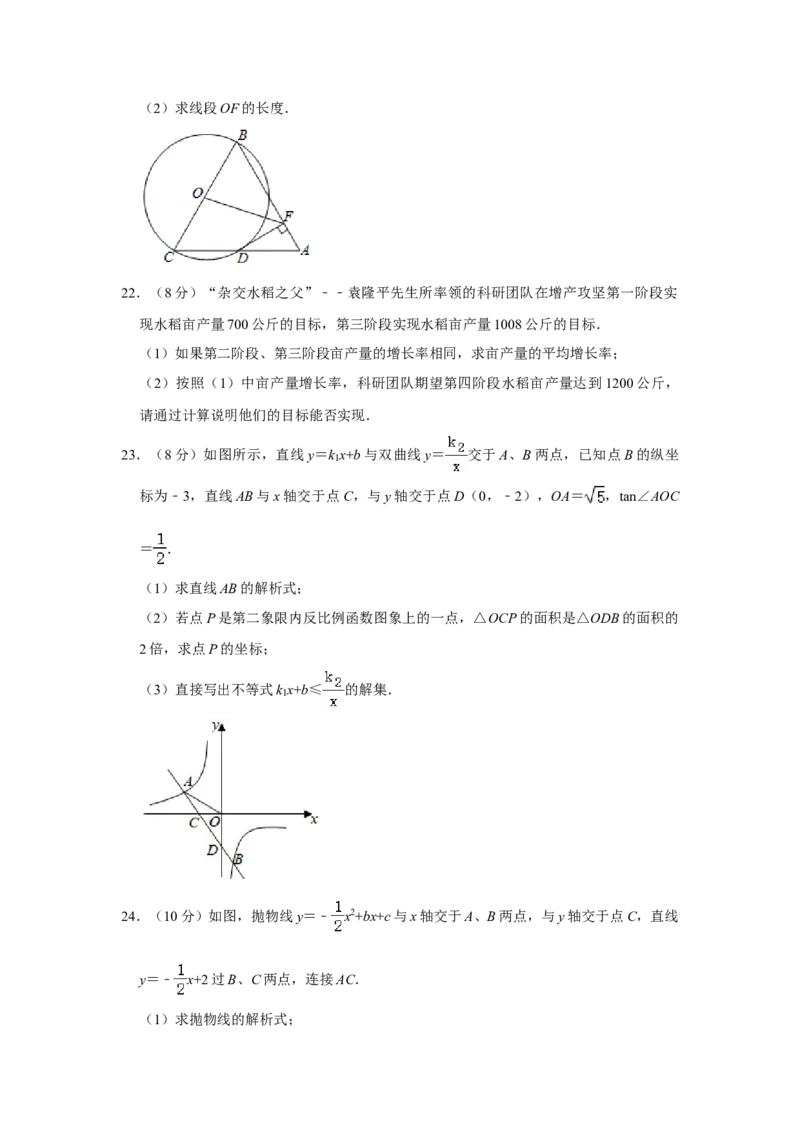
20.(8分)为庆祝建党100周年,让同学们进一步了解中国科技的快速发展,东营市某
中学九(1)班团支部组织了一次手抄报比赛.该班每位同学从 A.“北斗卫星”;
B.“5G时代”;C.“东风快递”;D.“智轨快运”四个主题中任选一个自己喜欢
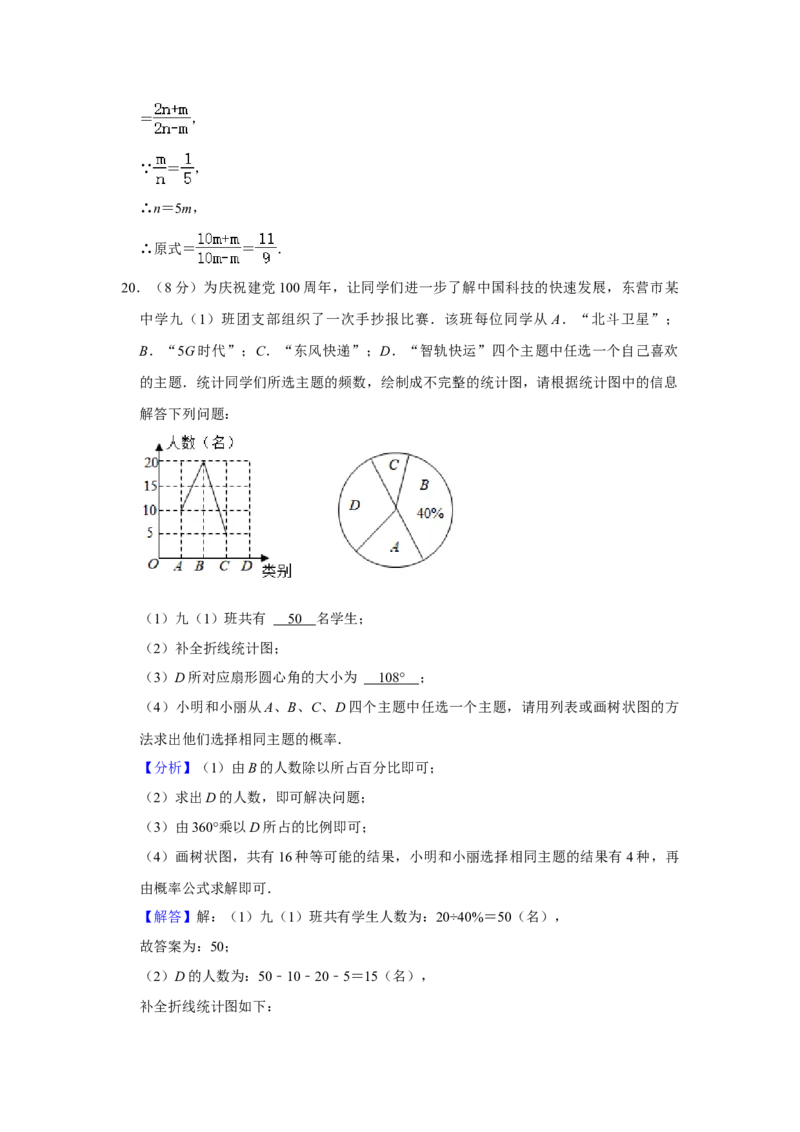
的主题.统计同学们所选主题的频数,绘制成不完整的统计图,请根据统计图中的信息
解答下列问题:
(1)九(1)班共有 名学生;
(2)补全折线统计图;
(3)D所对应扇形圆心角的大小为 ;
(4)小明和小丽从A、B、C、D四个主题中任选一个主题,请用列表或画树状图的方
法求出他们选择相同主题的概率.
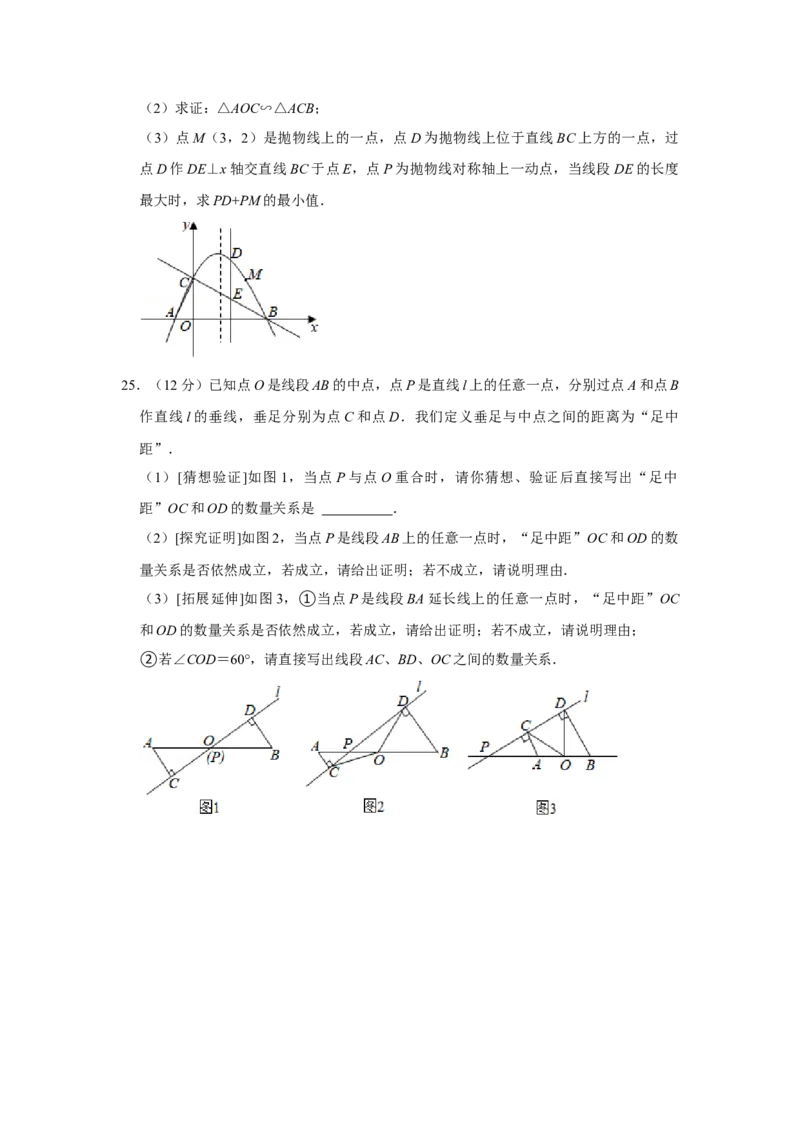
21.(8分)如图,以等边三角形ABC的BC边为直径画圆,交AC于点D,DF⊥AB于点
F,连接OF,且AF=1.
(1)求证:DF是 O的切线;
⊙(2)求线段OF的长度.
22.(8分)“杂交水稻之父”﹣﹣袁隆平先生所率领的科研团队在增产攻坚第一阶段实
现水稻亩产量700公斤的目标,第三阶段实现水稻亩产量1008公斤的目标.
(1)如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率;
(2)按照(1)中亩产量增长率,科研团队期望第四阶段水稻亩产量达到1200公斤,
请通过计算说明他们的目标能否实现.
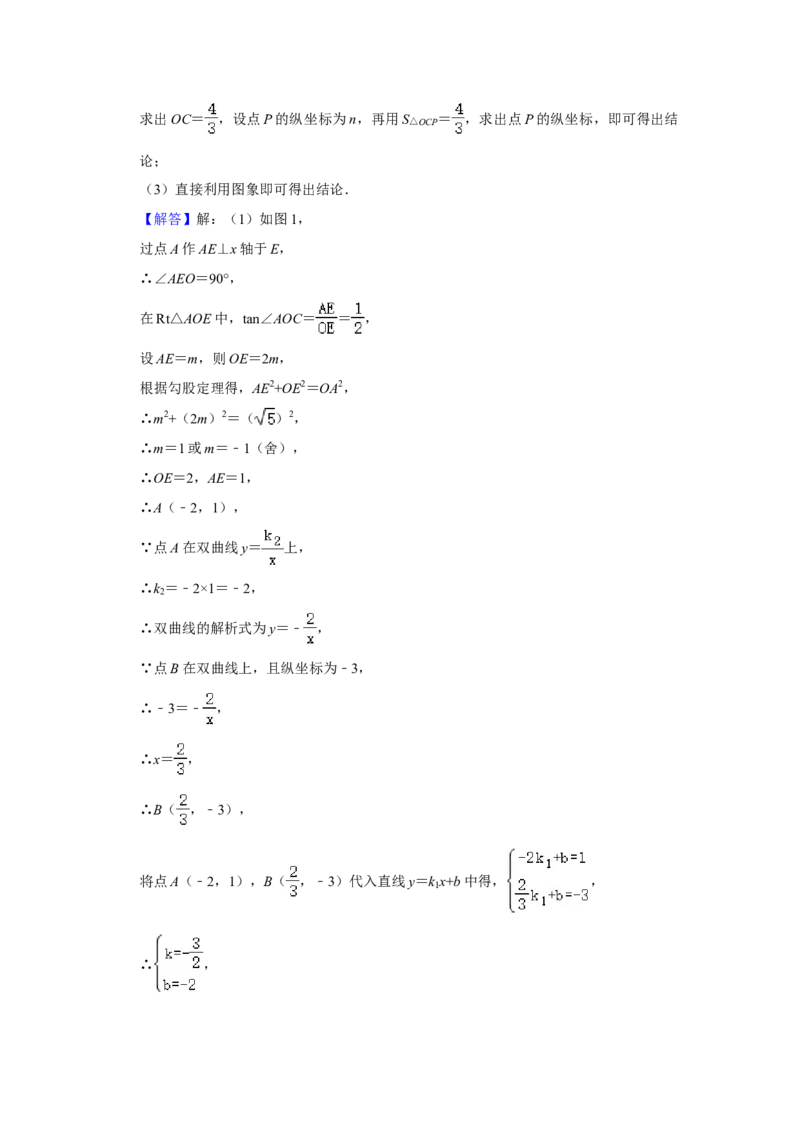
23.(8分)如图所示,直线y=k x+b与双曲线y= 交于A、B两点,已知点B的纵坐
1
标为﹣3,直线AB与x轴交于点C,与y轴交于点D(0,﹣2),OA= ,tan∠AOC
= .
(1)求直线AB的解析式;
(2)若点P是第二象限内反比例函数图象上的一点,△OCP的面积是△ODB的面积的
2倍,求点P的坐标;
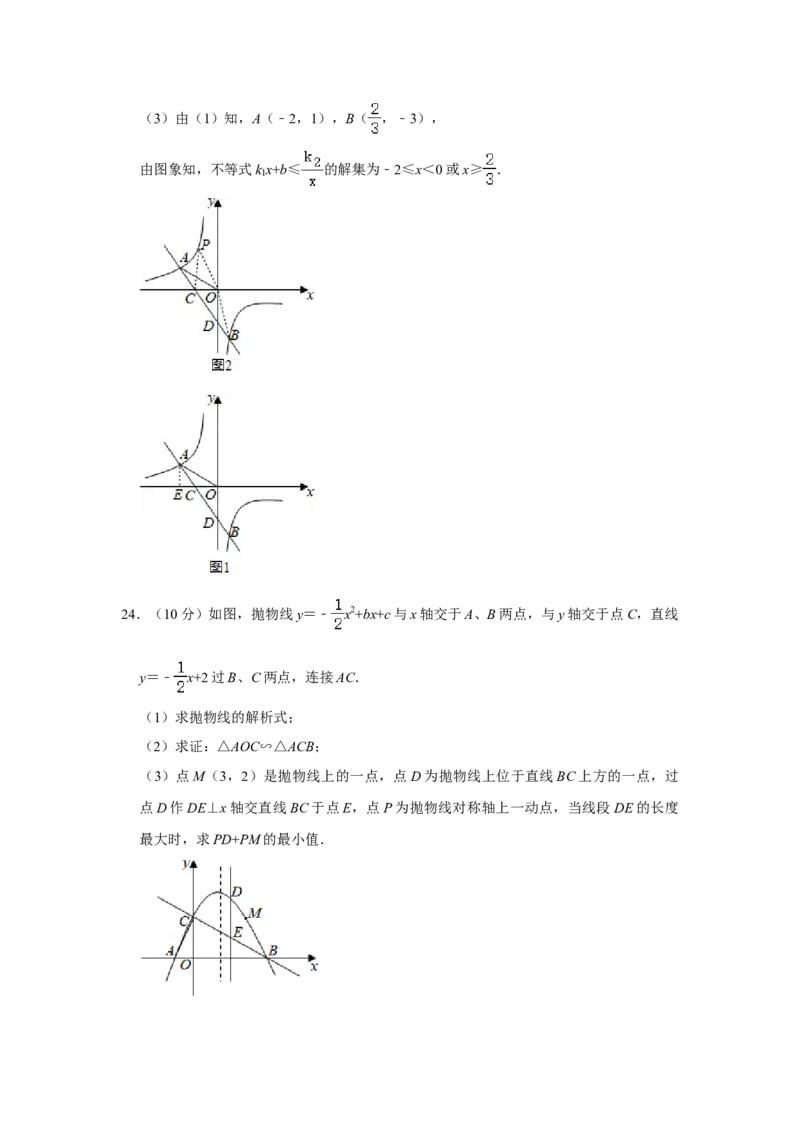
(3)直接写出不等式k x+b≤ 的解集.
1
24.(10分)如图,抛物线y=﹣ x2+bx+c与x轴交于A、B两点,与y轴交于点C,直线
y=﹣ x+2过B、C两点,连接AC.
(1)求抛物线的解析式;(2)求证:△AOC∽△ACB;
(3)点M(3,2)是抛物线上的一点,点D为抛物线上位于直线BC上方的一点,过
点D作DE⊥x轴交直线BC于点E,点P为抛物线对称轴上一动点,当线段DE的长度
最大时,求PD+PM的最小值.
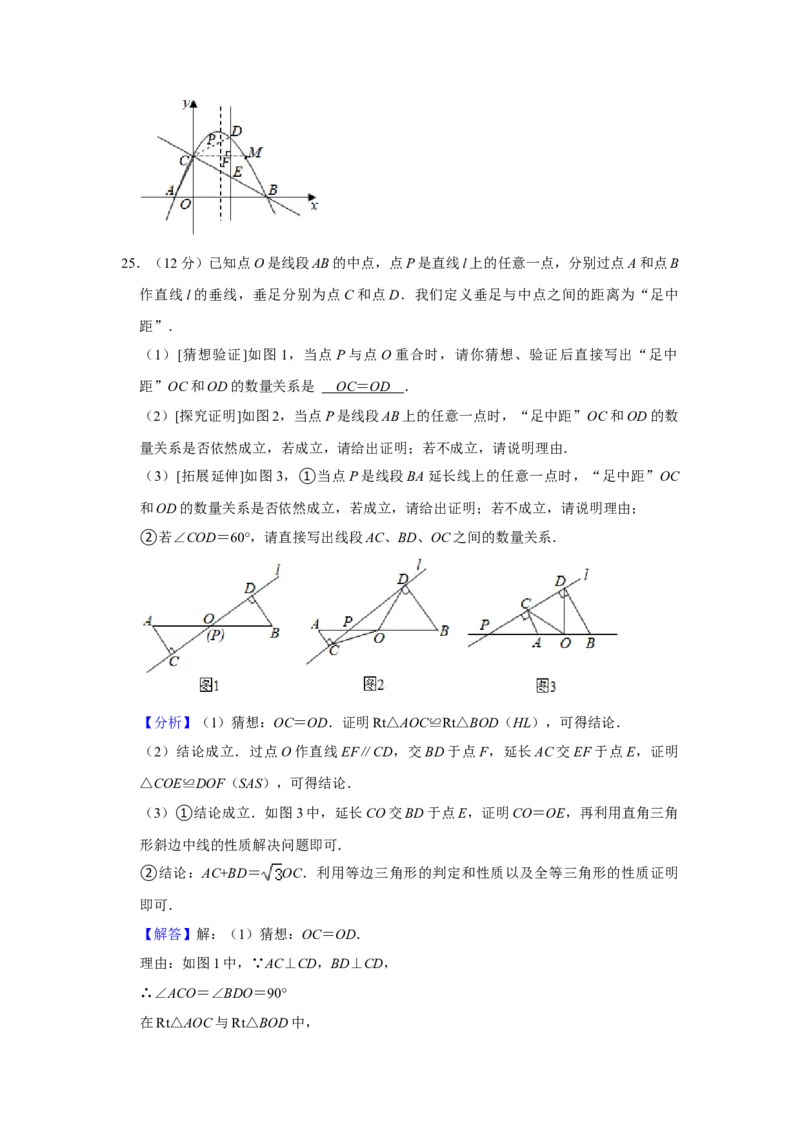
25.(12分)已知点O是线段AB的中点,点P是直线l上的任意一点,分别过点A和点B
作直线l的垂线,垂足分别为点C和点D.我们定义垂足与中点之间的距离为“足中
距”.
(1)[猜想验证]如图1,当点P与点O重合时,请你猜想、验证后直接写出“足中
距”OC和OD的数量关系是 .
(2)[探究证明]如图2,当点P是线段AB上的任意一点时,“足中距”OC和OD的数
量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由.
(3)[拓展延伸]如图3,①当点P是线段BA延长线上的任意一点时,“足中距”OC
和OD的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由;
②若∠COD=60°,请直接写出线段AC、BD、OC之间的数量关系.2021年山东省东营市中考数学试卷
参考答案与试题解析
一、选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正
确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.
1.16的算术平方根为( )
A.±4 B.4 C.﹣4 D.8
【分析】依据算术平方根的性质求解即可.
【解答】解:16的算术平方根为4.
故选:B.
2.下列运算结果正确的是( )
A.x2+x3=x5 B.(﹣a﹣b)2=a2+2ab+b2
C.(3x3)2=6x6 D.
【分析】根据合并同类项法则可判断选项A;根据完全平方公式可判断选项B;根据积
的乘方与幂的乘方运算法则计算可判断选项C;根据二次根式的加法法则计算可判断选
项D.
【解答】解:A、x2与x3不能合并,所以A选项错误;
B、(﹣a﹣b)2=[﹣(a+b)]2=(a+b)2=a2+2ab+b2,所以B选项正确;
C、(3x3)2=9x6,所以C选项错误;
D、 与 不能合并,所以D选项错误.
故选:B.
3.如图,AB∥CD,EF⊥CD于点F,若∠BEF=150°,则∠ABE=( )
A.30° B.40° C.50° D.60°
【分析】过点E作GE∥AB.利用平行线的性质得到∠GEF+∠EFD=180°,由垂直的定
义∠EFD=90°,进而得出∠GEF=90°,根据角的和差得到∠BEG=60°,再根据平行线
的性质求解即可.【解答】解:如图,过点E作GE∥AB,
∵AB∥CD,
∴GE∥CD,
∴∠GEF+∠EFD=180°,
∵EF⊥CD,
∴∠EFD=90°,
∴∠GEF=180°﹣∠EFD=90°,
∵∠BEF=∠BEG+∠GEF=150°,
∴∠BEG=∠BEF﹣∠GEF=60°,
∵GE∥AB,
∴∠ABE=∠BEG=60°,
故选:D.
4.某玩具商店周年店庆,全场八折促销,持会员卡可在促销活动的基础上再打六折.某电
动汽车原价300元,小明持会员卡购买这个电动汽车需要花( )元.
A.240 B.180 C.160 D.144
【分析】打八折是指优惠后的价格是原价的80%,再打六折是指实际花的钱是八折后价
格的60%,根据这些条件列出方程即可.
【解答】解:设小明持会员卡购买这个电动汽车需要花x元,根据题意得:
300×80%×60%=x,
解得x=144
故选:D.
5.如图,在△ABC中,∠C=90°,∠B=42°,BC=8,若用科学计算器求AC的长,则下
列按键顺序正确的是( )A.
B.
C.
D.
【分析】根据正切函数的定义,可得tan∠B= ,根据计算器的应用,可得答案.
【解答】解:在△ABC中,因为∠C=90°,
所以tan∠B= ,
因为∠B=42°,BC=8,
所以AC=BC•tanB=8×tan42°.
故选:D.
6.经过某路口的汽车,可能直行,也可能左拐或右拐.假设这三种可能性相同,现有两车
经过该路口,恰好有一车直行,另一车左拐的概率为( )
A. B. C. D.
【分析】画树状图,共有9种等可能的结果数,其中恰好有一车直行,另一车左拐的结
果数为2种,再由概率公式求解即可.
【解答】解:画树状图为:
共有9种等可能的结果数,其中恰好有一车直行,另一车左拐的结果数为2种,
∴恰好有一车直行,另一车左拐的概率= ,
故选:A.
7.已知某几何体的三视图如图所示,则该几何体的侧面展开图圆心角的度数为( )A.214° B.215° C.216° D.217°
【分析】由常见几何体的三视图可得该几何体为圆锥,根据三视图知圆锥的底面圆的直
径为6、半径为3,高为4,得出母线长为5,再根据扇形的弧长公式可得答案.
【解答】解:由三视图可知,该几何体为圆锥;
由三视图数据知圆锥的底面圆的直径为6、半径为3,高为4,
则母线长为 =5,
所以则该几何体的侧面展开图圆心角的度数为 ×6÷( ×5×2)×360°=216°.
故选:C. π π
8.一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中
的图象可能是( )
A. B.
C. D.
【分析】逐一分析四个选项,根据二次函数图象的开口以及对称轴与y轴的关系即可得
出a、b的正负,由此即可得出一次函数图象经过的象限,再与函数图象进行对比即可
得出结论.
【解答】解:A、∵二次函数图象开口向下,对称轴在y轴左侧,
∴a<0,b<0,
∴一次函数图象应该过第二、三、四象限,A不可能;B、∵二次函数图象开口向上,对称轴在y轴右侧,
∴a>0,b<0,
∴一次函数图象应该过第一、二、四象限,B不可能;
C、∵二次函数图象开口向下,对称轴在y轴左侧,
∴a<0,b<0,
∴一次函数图象应该过第二、三、四象限,C可能;
D、∵二次函数图象开口向下,对称轴在y轴左侧,
∴a<0,b<0,
∴一次函数图象应该过第二、三、四象限,D不可能.
故选:C.
9.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位
似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2
倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )
A.﹣2a+3 B.﹣2a+1 C.﹣2a+2 D.﹣2a﹣2
【分析】设点B′的横坐标为x,根据数轴表示出BC、B′C的横坐标的距离,再根据
位似比列式计算即可.
【解答】解:设点B′的横坐标为x,
则B、C间的横坐标的长度为a﹣1,B′、C间的横坐标的长度为﹣x+1,
∵△ABC放大到原来的2倍得到△A′B′C,
∴2(a﹣1)=﹣x+1,
解得:x=﹣2a+3,
故选:A.
10.如图,△ABC是边长为1的等边三角形,D、E为线段AC上两动点,且∠DBE=30°,
过点D、E分别作AB、BC的平行线相交于点F,分别交BC、AB于点H、G.现有以下结论:S△ABC = ;②当点D与点C重合时,FH= ;③AE+CD= DE;④当AE
=CD时,四边形BHFG为菱形,其中正确结论为( )
A.①②③ B.①②④ C.①②③④ D.②③④
【分析】①利用三角形的面积公式计算即可;
②依题意画出图形,利用等边三角形和平行线的性质求出FH即可;
③将△CBD绕点B逆时针旋转60°,得到△ABN,由“SAS”可证△DBE≌△NBE,可
得DE=NE,在Rt△PNE中,利用勾股定理可得AE,CD,DE的关系,可判断③;
④先证△AGE,△DCH都是等边三角形,可得AG=AE=CH=CD,利用菱形的判定定
理判定即可.
【解答】解:①过点A作AP⊥BC于点P,如图1:
∵△ABC是边长为1的等边三角形,AP⊥BC,
∴BP= BC= ,
∴AP= ,
∴ .故①正确;
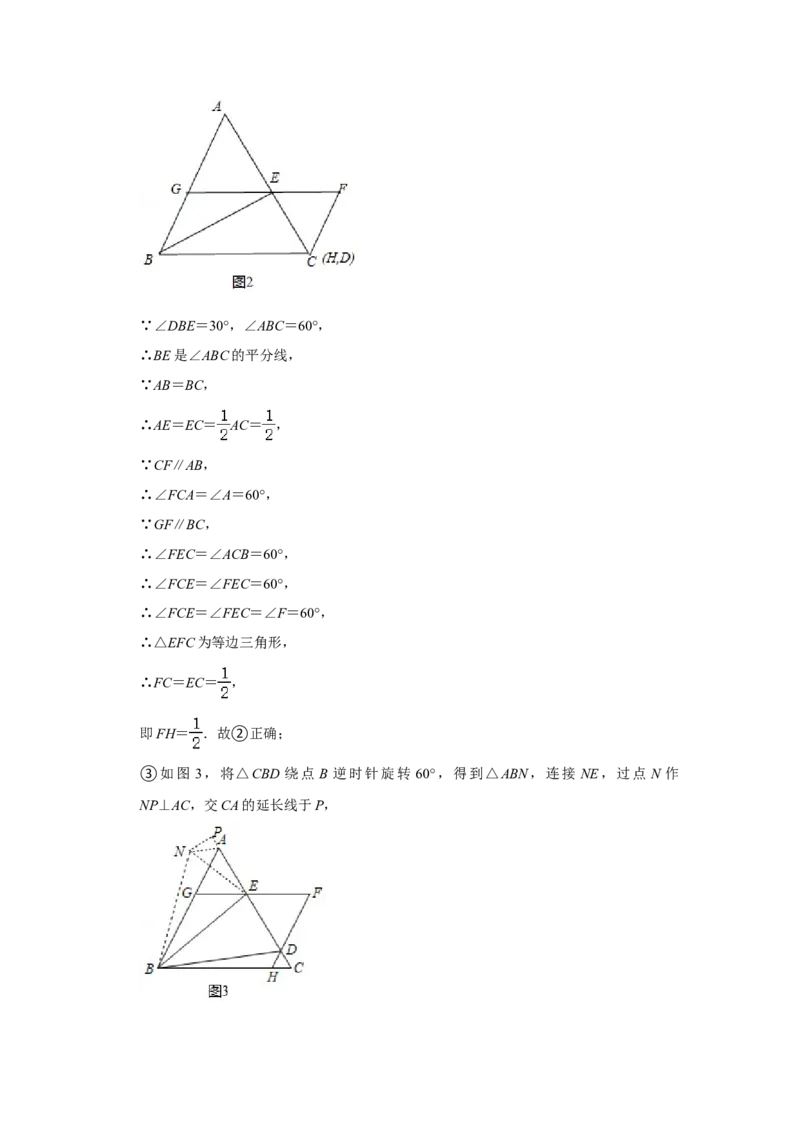
②当点D与点C重合时,H,D,C三点重合,如图2:∵∠DBE=30°,∠ABC=60°,
∴BE是∠ABC的平分线,
∵AB=BC,
∴AE=EC= AC= ,
∵CF∥AB,
∴∠FCA=∠A=60°,
∵GF∥BC,
∴∠FEC=∠ACB=60°,
∴∠FCE=∠FEC=60°,
∴∠FCE=∠FEC=∠F=60°,
∴△EFC为等边三角形,
∴FC=EC= ,
即FH= .故②正确;
③如图 3,将△CBD 绕点 B 逆时针旋转 60°,得到△ABN,连接 NE,过点 N 作
NP⊥AC,交CA的延长线于P,∴BD=BN,CD=AN,∠BAN=∠C=60°,∠CBD=∠ABN,
∵∠DBE=30°,
∴∠CBD+∠ABE=30°=∠ABE+∠ABN=∠EBN,
∴∠EBN=∠DBE=30°,
又∵NE=DE,BE=BE,
∴△DBE≌△NBE(SAS),
∴DE=NE,
∵∠NAP=180°﹣∠BAC﹣∠NAB=60°,
∴AP= AN,NP= AP= AN= CD,
∵NP2+PE2=NE2,
∴ CD2+(AE+ CD)2=DE2,
∴AE2+CD2+AE•CD=DE2,故③错误;
∵△ABC是等边三角形,
∴∠A=∠ABC=∠C=60°,
∵GF∥BH,BG∥HF,
∴四边形BHFG是平行四边形,
∵GF∥BH,BG∥HF,
∴∠AGE=∠ABC=60°,∠DHC=∠ABC=60°,
∴△AGE,△DCH都是等边三角形,
∴AG=AE,CH=CD,
∵AE=CD,
∴AG=CH,
∴BH=BG,
∴ BHFG是菱形,故④正确,
故▱选:B.
二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题3分,共28分.
只要求填写最后结果.
11.2021年5月11日,第七次全国人口普查数据显示,全国人口比第六次全国人口普查数
据增加了7206万人.7206万用科学记数法表示 7.206×1 0 7 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相
同.当原数绝对值≥10时,n是正整数.
【解答】解:7206万=72060000=7.206×107,
故答案为:7.206×107.
12.因式分解:4a2b﹣4ab+b= b ( 2 a ﹣ 1 ) 2 .
【分析】原式提取b,再利用完全平方公式分解即可.
【解答】解:原式=b(4a2﹣4a+1)
=b(2a﹣1)2.
故答案为:b(2a﹣1)2.
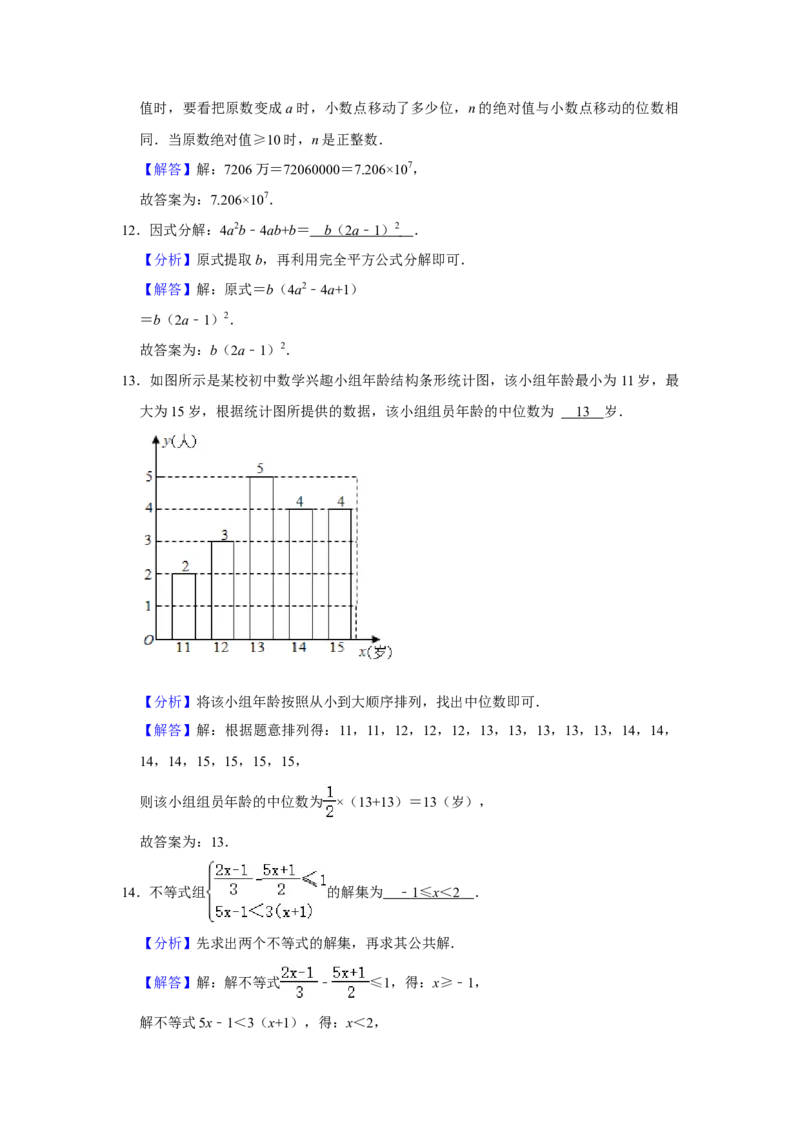
13.如图所示是某校初中数学兴趣小组年龄结构条形统计图,该小组年龄最小为11岁,最
大为15岁,根据统计图所提供的数据,该小组组员年龄的中位数为 1 3 岁.
【分析】将该小组年龄按照从小到大顺序排列,找出中位数即可.
【解答】解:根据题意排列得:11,11,12,12,12,13,13,13,13,13,14,14,
14,14,15,15,15,15,
则该小组组员年龄的中位数为 ×(13+13)=13(岁),
故答案为:13.
14.不等式组 的解集为 ﹣ 1 ≤ x < 2 .
【分析】先求出两个不等式的解集,再求其公共解.
【解答】解:解不等式 ﹣ ≤1,得:x≥﹣1,
解不等式5x﹣1<3(x+1),得:x<2,则不等式组的解集为﹣1≤x<2,
故答案为:﹣1≤x<2.
15.(4分)如图,在 ABCD中,E为BC的中点,以E为圆心,BE长为半径画弧交对角
▱
线AC于点F,若∠BAC=60°,∠ABC=100°,BC=4,则扇形BEF的面积为 .
【分析】根据三角形内角和定理求出∠ACB,根据三角形的外角的性质求出∠BEF,根
据扇形面积公式计算.
【解答】解:∵∠BAC=60°,∠ABC=100°,
∴∠ACB=20°,
又∵E为BC的中点,
∴BE=EC= BC=2,
∵BE=EF,
∴EF=EC=2,
∴∠EFC=∠ACB=20°,
∴∠BEF=40°,
∴扇形BEF的面积= = ,
故答案为: .
16.(4分)某地积极响应“把绿水青山变成金山银山,用绿色杠杆撬动经济转型”发展
理念,开展荒山绿化,打造美好家园,促进旅游发展.某工程队承接了90万平方米的
荒山绿化任务,为了迎接雨季的到来,实际工作时每天的工作效率比原计划提高了
25%,结果提前30天完成了任务.设原计划每天绿化的面积为x万平方米,则所列方程
为 ﹣ = 3 0 .
【分析】设原计划每天绿化的面积为x万平方米,则实际每天绿化的面积为(1+25%)x万平方米,根据工作时间=工作总量÷工作效率,结合实际比原计划提前30天完成了任
务,即可得出关于x的分式方程,此题得解.
【解答】解:设原计划每天绿化的面积为 x 万平方米,则实际每天绿化的面积为
(1+25%)x万平方米,
依题意得: ﹣ =30.
故答案为: ﹣ =30.
17.(4分)如图,正方形纸片ABCD的边长为12,点F是AD上一点,将△CDF沿CF折
叠,点D落在点G处,连接DG并延长交AB于点E.若AE=5,则GE的长为 .
【分析】由“ASA”可证△ADE≌△DCF,可得AE=DF=5,由锐角三角函数可求DO
的长,即可求解.
【解答】解:设CF与DE交于点O,
∵将△CDF沿CF折叠,点D落在点G处,
∴GO=DO,CF⊥DG,
∵四边形ABCD是正方形,
∴AD=CD,∠A=∠ADC=90°=∠FOD,
∴∠CFD+∠FCD=90°=∠CFD+∠ADE,
∴∠ADE=∠FCD,在△ADE和△DCF中,
,
∴△ADE≌△DCF(ASA),
∴AE=DF=5,
∵AE=5,AD=12,
∴DE= = =13,
∵cos∠ADE= ,
∴ ,
∴DO= =GO,
∴EG=13﹣2× = ,
故答案为: .
18.(4分)如图,正方形ABCB 中,AB= ,AB与直线l所夹锐角为60°,延长CB 交
1 1
直线l于点A ,作正方形A B C B ,延长C B 交直线l于点A ,作正方形A B C B ,延
1 1 1 1 2 1 2 2 2 2 2 3
长C B 交直线l于点A ,作正方形A B C B …,依此规律,则线段A A = 2× (
2 3 3 3 3 3 4 2020 2021
) 202 0 .
【分析】根据题意可知图中斜边在直线l上的直角三角形都是含30度角的直角三角形,
根据其性质得出三边的长度,以此类推可找到规律:A n B n =( )n﹣1,A n﹣1 A n =2A n B n=2×( )n﹣1.
【解答】解:根据题意可知AB =AB= ,∠B AA =90°﹣60°=30°,
1 1 1
∴tan∠B AA = = ,
1 1
∴A B =AB × = × =1,AA =2A B =2,
1 1 1 1 1 1
A B =A B × =A B × = ,A A =2A B =2× ,
2 2 1 2 1 1 1 2 2 2
A B =A B × =A B × = × =( )2,A A =2A B =2×( )2,
3 3 2 3 2 2 2 3 3 3
∴A B =A B × =( )2020,A A =2A B =2×( )2020,
2021 2021 2020 2021 2020 2021 2021 2021
故答案为:2×( )2020.
三、解答题:本大题共7小题,共62分.解答要写出必要的文字说明、证明过程或演算步
骤.
19.(8分)(1)计算: +3tan30°﹣|2﹣ |+( ﹣1)0+82021×(﹣0.125)2021;
π
(2)化简求值: ,其中 = .
【分析】(1)根据二次根式的性质、特殊角的三角函数值、绝对值的性质、零指数幂
的运算法则、积的乘方法则计算即可;
(2)根据分式的混合运算法则把原式化简,根据题意求出n=5m,代入计算即可.
【解答】解:(1)原式=2 +3× ﹣2+ +1+(﹣8×0.125)2021
=2 + ﹣2+ +1﹣1
=4 ﹣2;
(2)原式= + +
=
== ,
∵ = ,
∴n=5m,
∴原式= = .
20.(8分)为庆祝建党100周年,让同学们进一步了解中国科技的快速发展,东营市某
中学九(1)班团支部组织了一次手抄报比赛.该班每位同学从 A.“北斗卫星”;
B.“5G时代”;C.“东风快递”;D.“智轨快运”四个主题中任选一个自己喜欢
的主题.统计同学们所选主题的频数,绘制成不完整的统计图,请根据统计图中的信息
解答下列问题:
(1)九(1)班共有 5 0 名学生;
(2)补全折线统计图;
(3)D所对应扇形圆心角的大小为 108 ° ;
(4)小明和小丽从A、B、C、D四个主题中任选一个主题,请用列表或画树状图的方
法求出他们选择相同主题的概率.
【分析】(1)由B的人数除以所占百分比即可;
(2)求出D的人数,即可解决问题;
(3)由360°乘以D所占的比例即可;
(4)画树状图,共有16种等可能的结果,小明和小丽选择相同主题的结果有4种,再
由概率公式求解即可.
【解答】解:(1)九(1)班共有学生人数为:20÷40%=50(名),
故答案为:50;
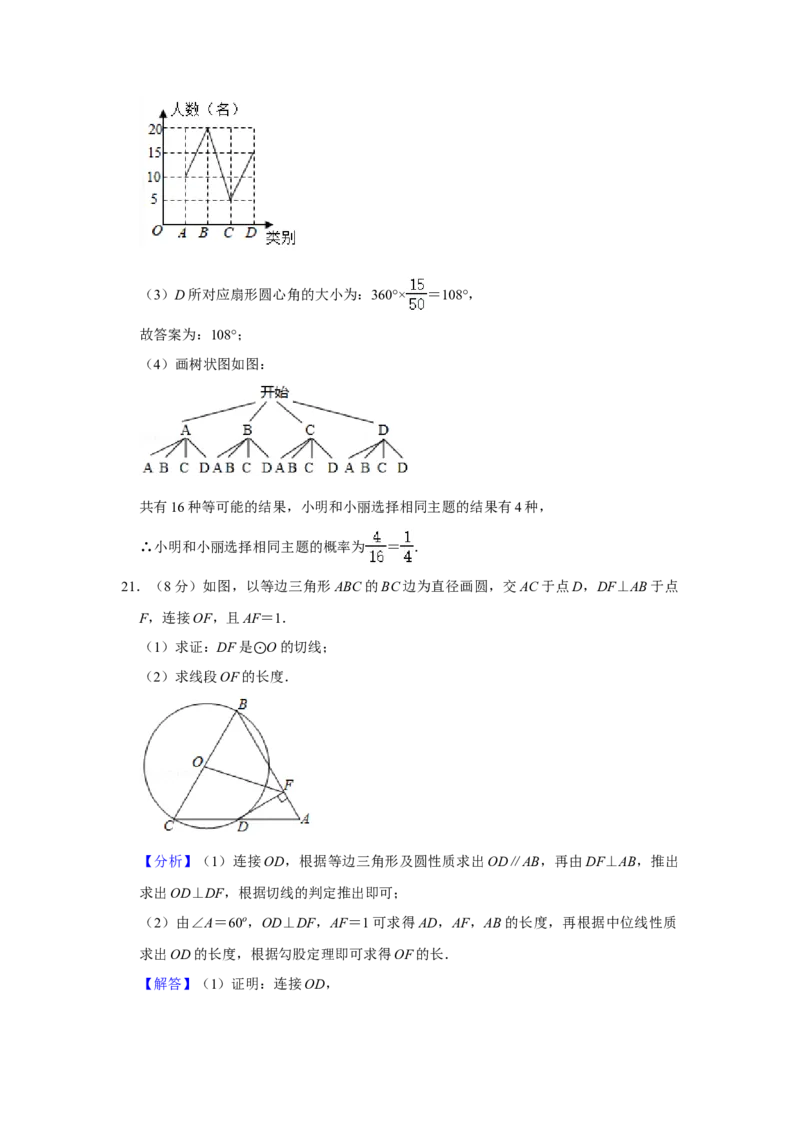
(2)D的人数为:50﹣10﹣20﹣5=15(名),
补全折线统计图如下:(3)D所对应扇形圆心角的大小为:360°× =108°,
故答案为:108°;
(4)画树状图如图:
共有16种等可能的结果,小明和小丽选择相同主题的结果有4种,
∴小明和小丽选择相同主题的概率为 = .
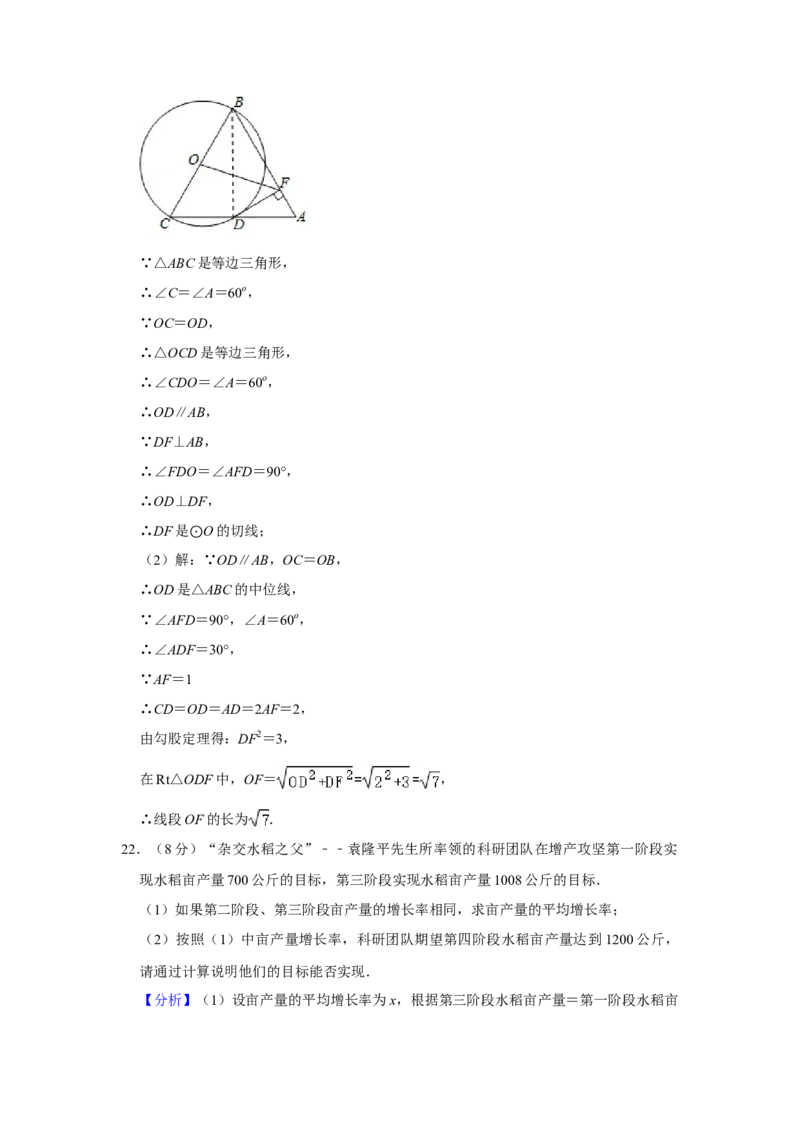
21.(8分)如图,以等边三角形ABC的BC边为直径画圆,交AC于点D,DF⊥AB于点
F,连接OF,且AF=1.
(1)求证:DF是 O的切线;
(2)求线段OF的⊙长度.
【分析】(1)连接OD,根据等边三角形及圆性质求出OD∥AB,再由DF⊥AB,推出
求出OD⊥DF,根据切线的判定推出即可;
(2)由∠A=60o,OD⊥DF,AF=1可求得AD,AF,AB的长度,再根据中位线性质
求出OD的长度,根据勾股定理即可求得OF的长.
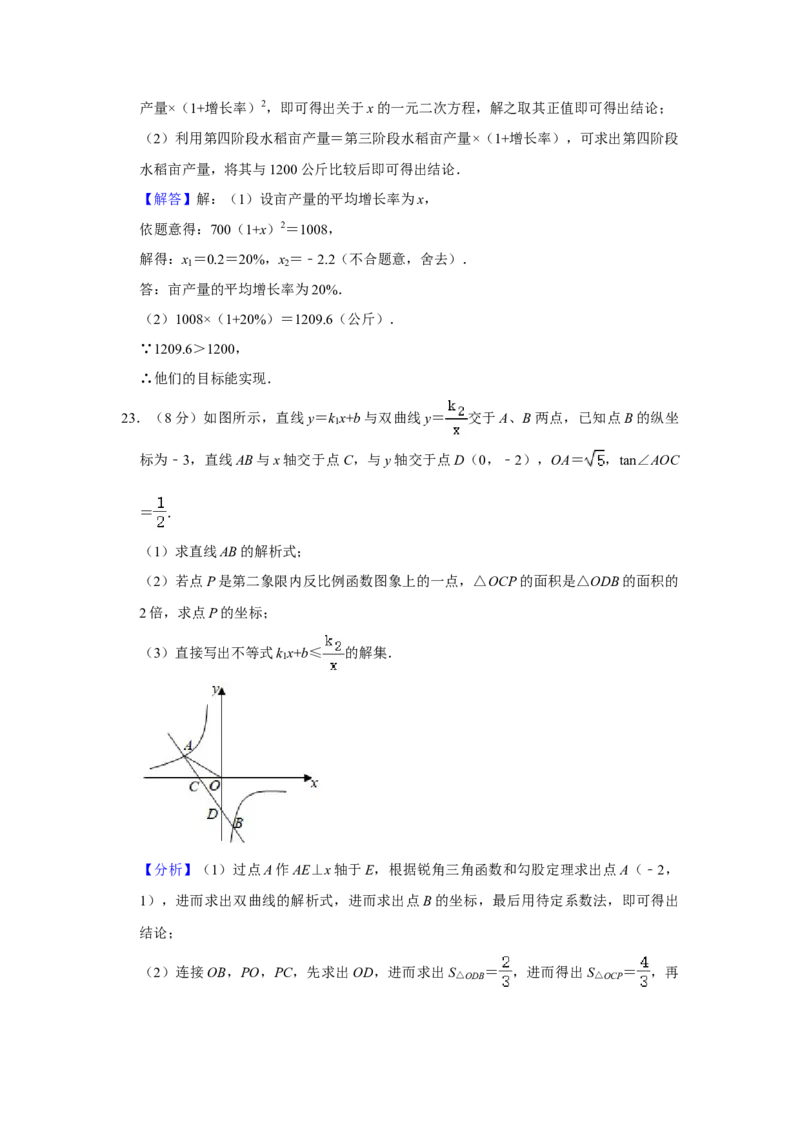
【解答】(1)证明:连接OD,∵△ABC是等边三角形,
∴∠C=∠A=60o,
∵OC=OD,
∴△OCD是等边三角形,
∴∠CDO=∠A=60o,
∴OD∥AB,
∵DF⊥AB,
∴∠FDO=∠AFD=90°,
∴OD⊥DF,
∴DF是 O的切线;
(2)解:⊙∵OD∥AB,OC=OB,
∴OD是△ABC的中位线,
∵∠AFD=90°,∠A=60o,
∴∠ADF=30°,
∵AF=1
∴CD=OD=AD=2AF=2,
由勾股定理得:DF2=3,
在Rt△ODF中,OF= ,
∴线段OF的长为 .
22.(8分)“杂交水稻之父”﹣﹣袁隆平先生所率领的科研团队在增产攻坚第一阶段实
现水稻亩产量700公斤的目标,第三阶段实现水稻亩产量1008公斤的目标.
(1)如果第二阶段、第三阶段亩产量的增长率相同,求亩产量的平均增长率;
(2)按照(1)中亩产量增长率,科研团队期望第四阶段水稻亩产量达到1200公斤,
请通过计算说明他们的目标能否实现.
【分析】(1)设亩产量的平均增长率为x,根据第三阶段水稻亩产量=第一阶段水稻亩产量×(1+增长率)2,即可得出关于x的一元二次方程,解之取其正值即可得出结论;
(2)利用第四阶段水稻亩产量=第三阶段水稻亩产量×(1+增长率),可求出第四阶段
水稻亩产量,将其与1200公斤比较后即可得出结论.
【解答】解:(1)设亩产量的平均增长率为x,
依题意得:700(1+x)2=1008,
解得:x =0.2=20%,x =﹣2.2(不合题意,舍去).
1 2
答:亩产量的平均增长率为20%.
(2)1008×(1+20%)=1209.6(公斤).
∵1209.6>1200,
∴他们的目标能实现.
23.(8分)如图所示,直线y=k x+b与双曲线y= 交于A、B两点,已知点B的纵坐
1
标为﹣3,直线AB与x轴交于点C,与y轴交于点D(0,﹣2),OA= ,tan∠AOC
= .
(1)求直线AB的解析式;
(2)若点P是第二象限内反比例函数图象上的一点,△OCP的面积是△ODB的面积的
2倍,求点P的坐标;
(3)直接写出不等式k x+b≤ 的解集.
1
【分析】(1)过点A作AE⊥x轴于E,根据锐角三角函数和勾股定理求出点A(﹣2,
1),进而求出双曲线的解析式,进而求出点B的坐标,最后用待定系数法,即可得出
结论;
(2)连接OB,PO,PC,先求出OD,进而求出S△ODB = ,进而得出S△OCP = ,再求出OC= ,设点P的纵坐标为n,再用S△OCP = ,求出点P的纵坐标,即可得出结
论;
(3)直接利用图象即可得出结论.
【解答】解:(1)如图1,
过点A作AE⊥x轴于E,
∴∠AEO=90°,
在Rt△AOE中,tan∠AOC= = ,
设AE=m,则OE=2m,
根据勾股定理得,AE2+OE2=OA2,
∴m2+(2m)2=( )2,
∴m=1或m=﹣1(舍),
∴OE=2,AE=1,
∴A(﹣2,1),
∵点A在双曲线y= 上,
∴k =﹣2×1=﹣2,
2
∴双曲线的解析式为y=﹣ ,
∵点B在双曲线上,且纵坐标为﹣3,
∴﹣3=﹣ ,
∴x= ,
∴B( ,﹣3),
将点A(﹣2,1),B( ,﹣3)代入直线y=k x+b中得, ,
1
∴ ,∴直线AB的解析式为y=﹣ x﹣2;
(2)如图2,连接OB,PO,PC;
由(1)知,直线AB的解析式为y=﹣ x﹣2,
∴D(0,﹣2),
∴OD=2,
由(1)知,B( ,﹣3),
∴S△ODB = OD•x
B
= ×2× = ,
∵△OCP的面积是△ODB的面积的2倍,
∴S△OCP =2S△ODE =2× = ,
由(1)知,直线AB的解析式为y=﹣ x﹣2,
令y=0,则﹣ x﹣2=0,
∴x=﹣ ,
∴OC= ,
设点P的纵坐标为n,
∴S△OCP = OC•y
P
= × n= ,
∴n=2,
由(1)知,双曲线的解析式为y=﹣ ,
∵点P在双曲线上,
∴2=﹣ ,
∴x=﹣1,
∴P(﹣1,2);(3)由(1)知,A(﹣2,1),B( ,﹣3),
由图象知,不等式k x+b≤ 的解集为﹣2≤x<0或x≥ .
1
24.(10分)如图,抛物线y=﹣ x2+bx+c与x轴交于A、B两点,与y轴交于点C,直线
y=﹣ x+2过B、C两点,连接AC.
(1)求抛物线的解析式;
(2)求证:△AOC∽△ACB;
(3)点M(3,2)是抛物线上的一点,点D为抛物线上位于直线BC上方的一点,过
点D作DE⊥x轴交直线BC于点E,点P为抛物线对称轴上一动点,当线段DE的长度
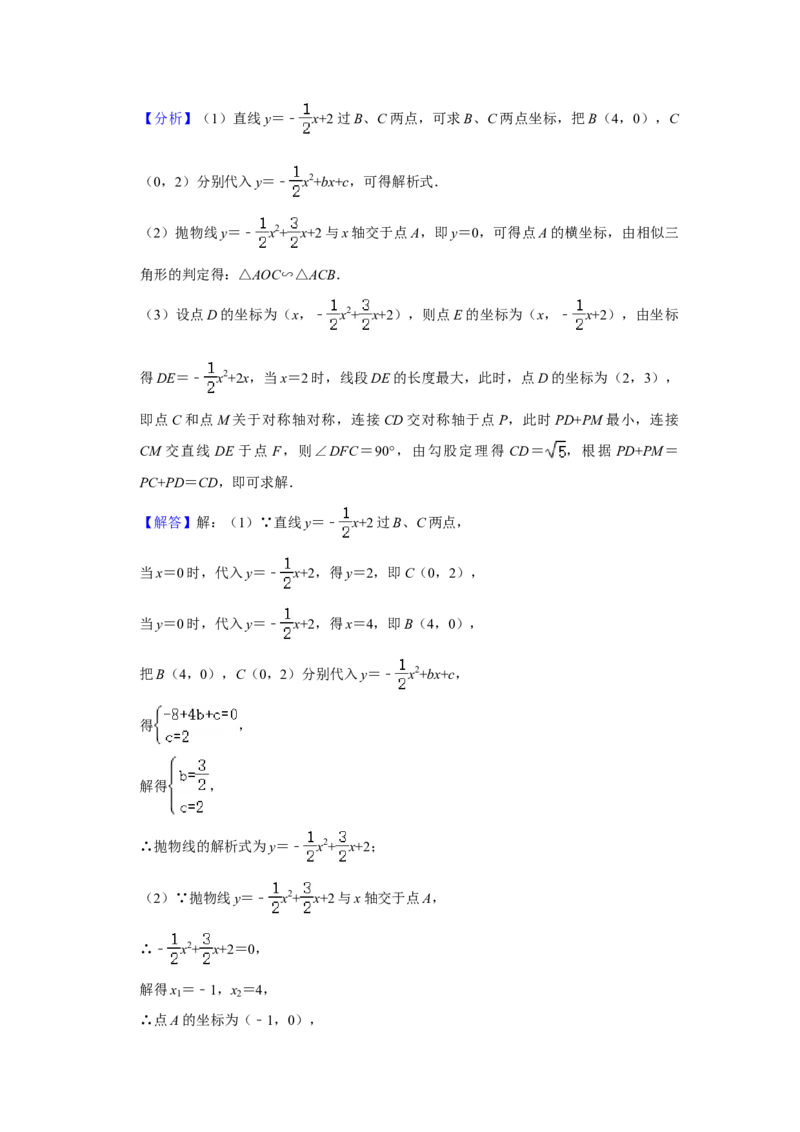
最大时,求PD+PM的最小值.【分析】(1)直线y=﹣ x+2过B、C两点,可求B、C两点坐标,把B(4,0),C
(0,2)分别代入y=﹣ x2+bx+c,可得解析式.
(2)抛物线y=﹣ x2+ x+2与x轴交于点A,即y=0,可得点A的横坐标,由相似三
角形的判定得:△AOC∽△ACB.
(3)设点D的坐标为(x,﹣ x2+ x+2),则点E的坐标为(x,﹣ x+2),由坐标
得DE=﹣ x2+2x,当x=2时,线段DE的长度最大,此时,点D的坐标为(2,3),
即点C和点M关于对称轴对称,连接CD交对称轴于点P,此时PD+PM最小,连接
CM 交直线 DE 于点 F,则∠DFC=90°,由勾股定理得 CD= ,根据 PD+PM=
PC+PD=CD,即可求解.
【解答】解:(1)∵直线y=﹣ x+2过B、C两点,
当x=0时,代入y=﹣ x+2,得y=2,即C(0,2),
当y=0时,代入y=﹣ x+2,得x=4,即B(4,0),
把B(4,0),C(0,2)分别代入y=﹣ x2+bx+c,
得 ,
解得 ,
∴抛物线的解析式为y=﹣ x2+ x+2;
(2)∵抛物线y=﹣ x2+ x+2与x轴交于点A,
∴﹣ x2+ x+2=0,
解得x =﹣1,x =4,
1 2
∴点A的坐标为(﹣1,0),∴AO=1,AB=5,
在Rt△AOC中,AO=1,OC=2,
∴AC= ,
∴ = = ,
∵ = ,
∴ = ,
又∵∠OAC=∠CAB,
∴△AOC∽△ACB;
(3)设点D的坐标为(x,﹣ x2+ x+2),
则点E的坐标为(x,﹣ x+2),
∴DE=﹣ x2+ x+2﹣(﹣ x+2)
=﹣ x2+ x+2+ x﹣2
=﹣ x2+2x,
∵﹣ <0,
∴当x=2时,线段DE的长度最大,
此时,点D的坐标为(2,3),
∵C(0,2),M(3,2),
∴点C和点M关于对称轴对称,
连接CD交对称轴于点P,此时PD+PM最小,
连接CM交直线DE于点F,则∠DFC=90°,点F的坐标为(2,2),
∴CD= = ,
∵PD+PM=PC+PD=CD,
∴PD+PM的最小值为 .25.(12分)已知点O是线段AB的中点,点P是直线l上的任意一点,分别过点A和点B
作直线l的垂线,垂足分别为点C和点D.我们定义垂足与中点之间的距离为“足中
距”.
(1)[猜想验证]如图1,当点P与点O重合时,请你猜想、验证后直接写出“足中
距”OC和OD的数量关系是 OC = OD .
(2)[探究证明]如图2,当点P是线段AB上的任意一点时,“足中距”OC和OD的数
量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由.
(3)[拓展延伸]如图3,①当点P是线段BA延长线上的任意一点时,“足中距”OC
和OD的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由;
②若∠COD=60°,请直接写出线段AC、BD、OC之间的数量关系.
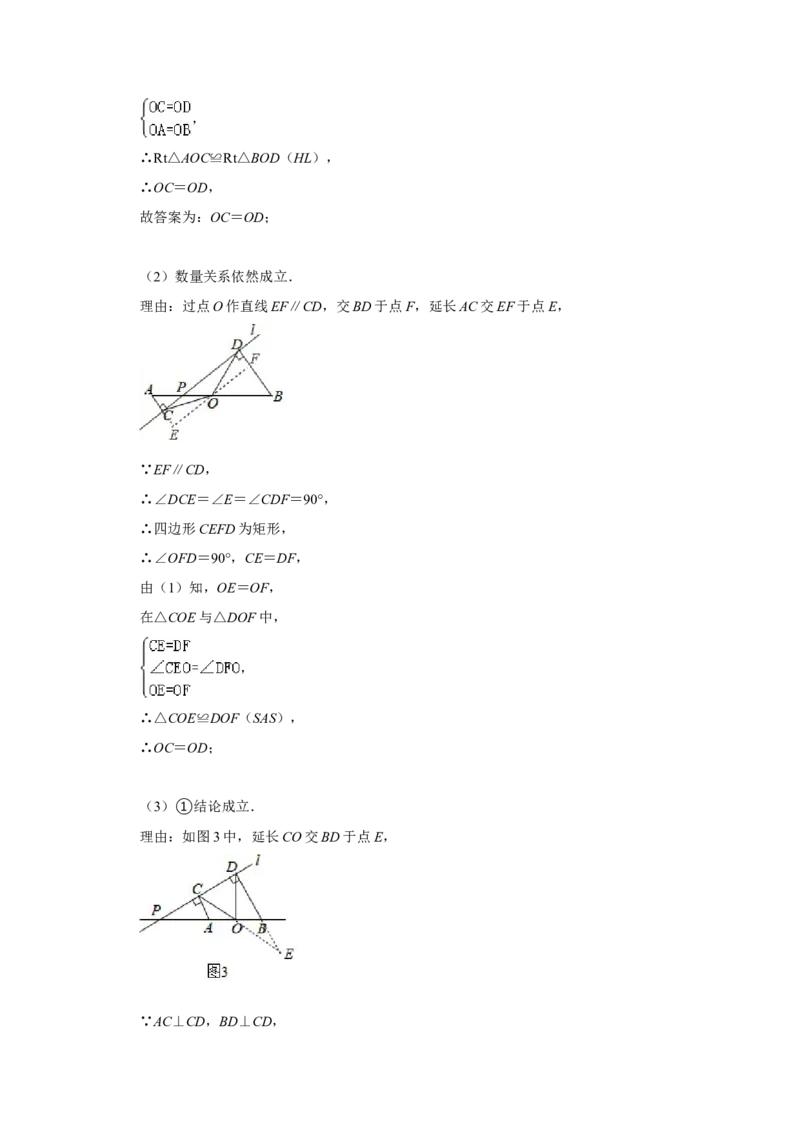
【分析】(1)猜想:OC=OD.证明Rt△AOC≌Rt△BOD(HL),可得结论.
(2)结论成立.过点O作直线EF∥CD,交BD于点F,延长AC交EF于点E,证明
△COE≌DOF(SAS),可得结论.
(3)①结论成立.如图3中,延长CO交BD于点E,证明CO=OE,再利用直角三角
形斜边中线的性质解决问题即可.
②结论:AC+BD= OC.利用等边三角形的判定和性质以及全等三角形的性质证明
即可.
【解答】解:(1)猜想:OC=OD.
理由:如图1中,∵AC⊥CD,BD⊥CD,
∴∠ACO=∠BDO=90°
在Rt△AOC与Rt△BOD中,,
∴Rt△AOC≌Rt△BOD(HL),
∴OC=OD,
故答案为:OC=OD;
(2)数量关系依然成立.
理由:过点O作直线EF∥CD,交BD于点F,延长AC交EF于点E,
∵EF∥CD,
∴∠DCE=∠E=∠CDF=90°,
∴四边形CEFD为矩形,
∴∠OFD=90°,CE=DF,
由(1)知,OE=OF,
在△COE与△DOF中,
,
∴△COE≌DOF(SAS),
∴OC=OD;
(3)①结论成立.
理由:如图3中,延长CO交BD于点E,
∵AC⊥CD,BD⊥CD,∴AC∥BD,
∴∠A=∠B,
∵点O为AB的中点,
∴AO=BO,
又∵∠AOC=∠BOE,
∴△AOC≌△BOE(AAS),
∴CO=CE,
∵∠CDE=90°,
∴OD=OC=OE,
∴OC=OD.
②结论:AC+BD= OC.
理由:如图3中,∵∠COD=60°,OD=OC,
∴△COD是等边三角形,
∴CD=OC,∠OCD=60°,
∵∠CDE=90°,
∴tan60°= ,
∴DE= CD,
∵∴△AOC≌△BOE,
∴AC=BE,
∴AC+BD=BD+BE=DE= CD,
∴AC+BD= OC.