文档内容
浙江省2021年中考(湖州市)
数学试题卷
卷 I
一、选择题(本题有10小题,每小题3分,共30分)
下面每小题给出的四个选项中,只有一个是正确的.请选出各题中一个最符合题意的
选项,并在答题卷上将相应题次中对应字母的方框涂黑,不选、多选、错选均不给分.
1.实数﹣2的绝对值是
A.﹣2 B.2 C. D.
2.化简 的正确结果是
A.4 B.±4 C. D.
3.不等式 的解集是
A. B. C. D.
4.下列事件中,属于不可能事件的是
A.经过红绿灯路口,遇到绿灯
B.射击运动员射击一次,命中靶心
C.班里的两名同学,他们的生日是同一天
D.从一个只装有白球和红球的袋中摸球,摸出黄球
5.将如图所示的长方体牛奶包装盒沿某些棱剪开,且使六个面连在一起,然后铺平,则得
到的图形可能是
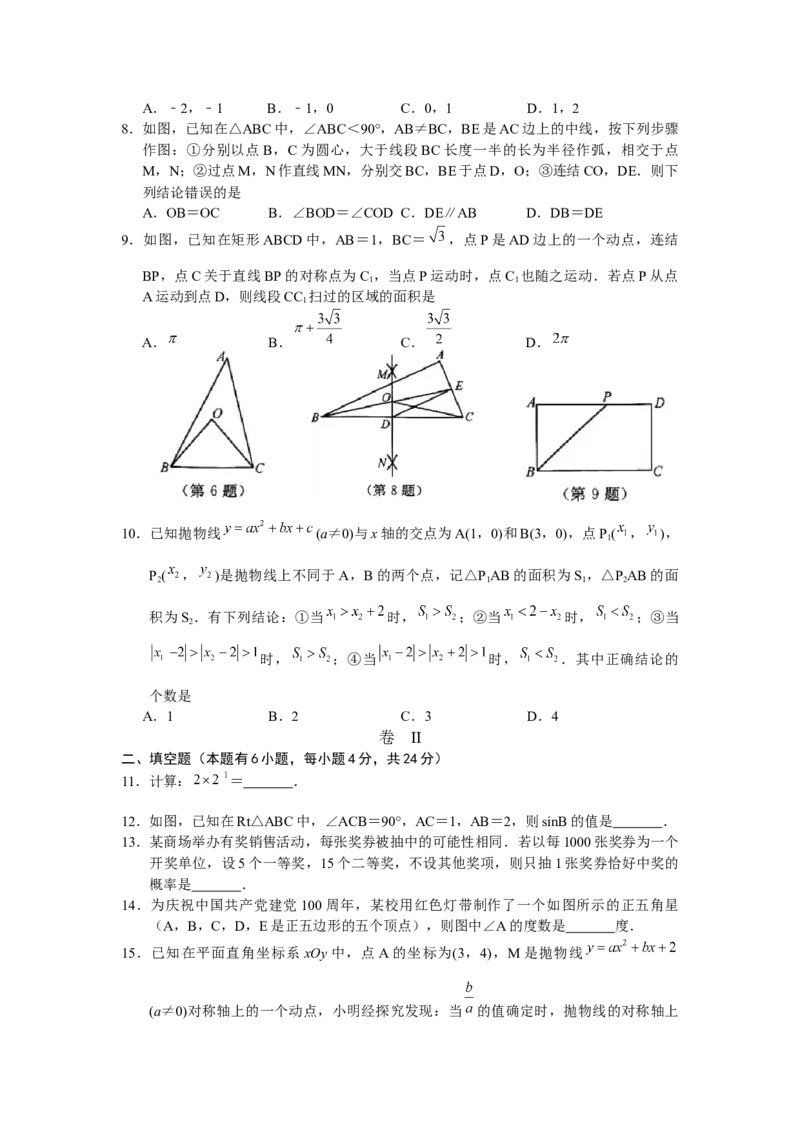
6.如图,已知点O是△ABC的外心,∠A=40°,连结BO,CO,则∠BOC的度数是
A.60° B.70° C.80° D.90°
7.已知a,b是两个连续整数,a< ﹣1<b,则a,b分别是A.﹣2,﹣1 B.﹣1,0 C.0,1 D.1,2
8.如图,已知在△ABC中,∠ABC<90°,AB≠BC,BE是AC边上的中线,按下列步骤
作图:①分别以点B,C为圆心,大于线段BC长度一半的长为半径作弧,相交于点
M,N;②过点M,N作直线MN,分别交BC,BE于点D,O;③连结CO,DE.则下
列结论错误的是
A.OB=OC B.∠BOD=∠COD C.DE∥AB D.DB=DE
9.如图,已知在矩形ABCD中,AB=1,BC= ,点P是AD边上的一个动点,连结
BP,点C关于直线BP的对称点为C ,当点P运动时,点C 也随之运动.若点P从点
1 1
A运动到点D,则线段CC 扫过的区域的面积是
1
A. B. C. D.
10.已知抛物线 (a≠0)与x轴的交点为A(1,0)和B(3,0),点P( , ),
1
P( , )是抛物线上不同于A,B的两个点,记△PAB的面积为S ,△PAB的面
2 1 1 2
积为S .有下列结论:①当 时, ;②当 时, ;③当
2
时, ;④当 时, .其中正确结论的
个数是
A.1 B.2 C.3 D.4
卷 II
二、填空题(本题有6小题,每小题4分,共24分)
11.计算: = .
12.如图,已知在Rt△ABC中,∠ACB=90°,AC=1,AB=2,则sinB的值是 .
13.某商场举办有奖销售活动,每张奖券被抽中的可能性相同.若以每1000张奖券为一个
开奖单位,设5个一等奖,15个二等奖,不设其他奖项,则只抽1张奖券恰好中奖的
概率是 .
14.为庆祝中国共产党建党100周年,某校用红色灯带制作了一个如图所示的正五角星
(A,B,C,D,E是正五边形的五个顶点),则图中∠A的度数是 度.
15.已知在平面直角坐标系 xOy中,点A的坐标为(3,4),M是抛物线
(a≠0)对称轴上的一个动点,小明经探究发现:当 的值确定时,抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定.若抛物线 (a≠0)
的对称轴上存在3个不同的点M,使△AOM为直角三角形,则 的值是 .
16.由沈康身教授所著,数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事
如图,三姐妹为了平分一块边长为1的祖传正方形地毯,先将地毯分割成七块,再拼
成三个小正方形(阴影部分).则图中AB的长应是 .
三、解答题(本题有8小题,共66分)
17.(本小题6分)
计算: .
18.(本小题6分)
解分式方程: .
19.(本小题6分)
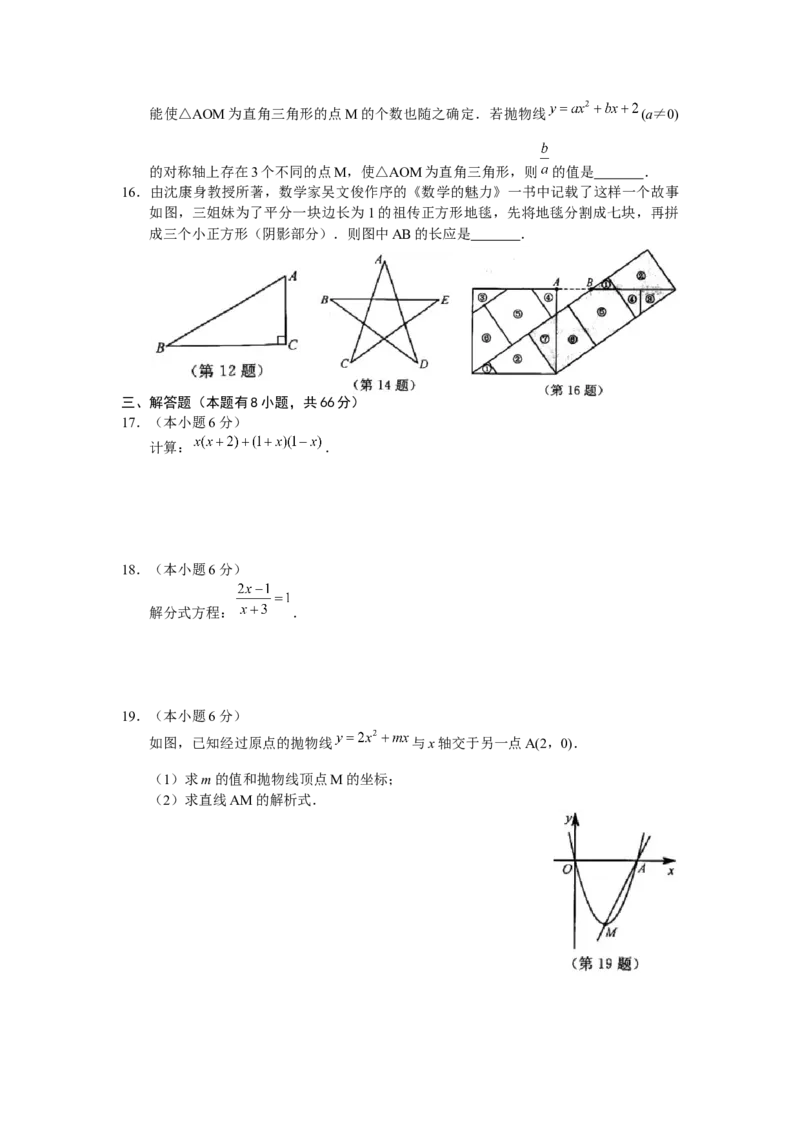
如图,已知经过原点的抛物线 与x轴交于另一点A(2,0).
(1)求m的值和抛物线顶点M的坐标;
(2)求直线AM的解析式.20.(本小题8分)
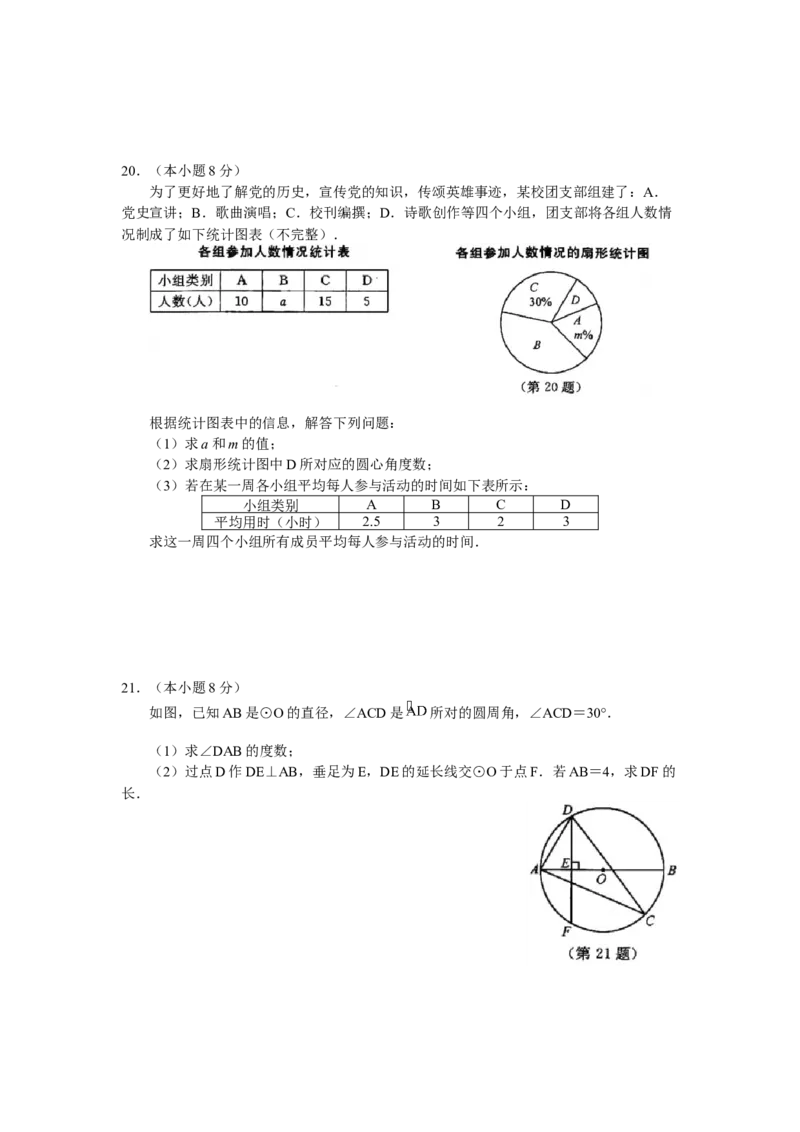
为了更好地了解党的历史,宣传党的知识,传颂英雄事迹,某校团支部组建了:A.
党史宣讲;B.歌曲演唱;C.校刊编撰;D.诗歌创作等四个小组,团支部将各组人数情
况制成了如下统计图表(不完整).
根据统计图表中的信息,解答下列问题:
(1)求a和m的值;
(2)求扇形统计图中D所对应的圆心角度数;
(3)若在某一周各小组平均每人参与活动的时间如下表所示:
小组类别 A B C D
平均用时(小时) 2.5 3 2 3
求这一周四个小组所有成员平均每人参与活动的时间.
21.(本小题8分)
如图,已知AB是⊙O的直径,∠ACD是 所对的圆周角,∠ACD=30°.
(1)求∠DAB的度数;
(2)过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F.若AB=4,求DF的
长.22.(本小题10分)
今年以来,我市接待的游客人数逐月增加,据统计,游玩某景区的游客人数三月份为
4万人,五月份为5.76万人.
(1)求四月和五月这两个月中,该景区游客人数平均每月增长百分之几;
(2)若该景区仅有A,B两个景点,售票处出示的三种购票方式如下表所示:
据预测,六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万.并且当
甲、乙两种门票价格不变时,丙种门票价格每下降1元,将有600人原计划购买甲种门票
的游客和400人原计划购买乙种门票的游客改为购买丙种门票.①若丙种门票价格下降10
元,求景区六月份的门票总收人;②问:将丙种门票价格下降多少元时,景区六月份的门
票总收入有最大值?最大值是多少万元?
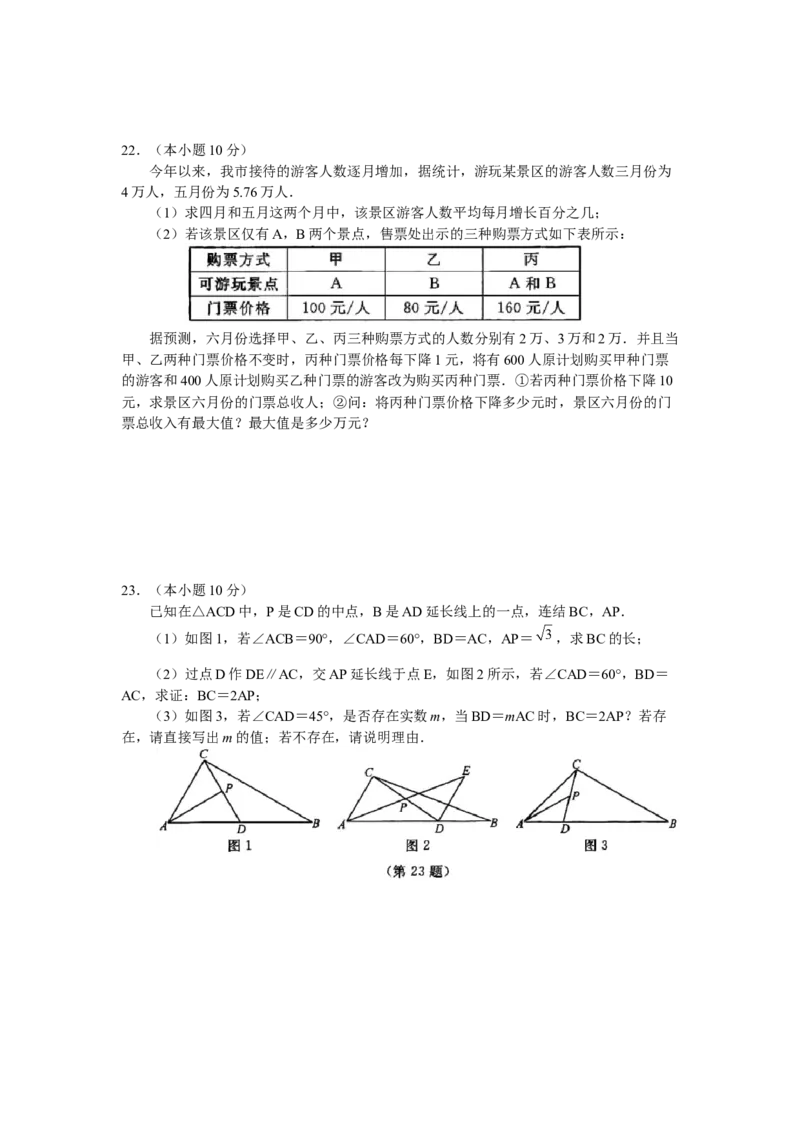
23.(本小题10分)
已知在△ACD中,P是CD的中点,B是AD延长线上的一点,连结BC,AP.
(1)如图1,若∠ACB=90°,∠CAD=60°,BD=AC,AP= ,求BC的长;
(2)过点D作DE∥AC,交AP延长线于点E,如图2所示,若∠CAD=60°,BD=
AC,求证:BC=2AP;
(3)如图3,若∠CAD=45°,是否存在实数m,当BD=mAC时,BC=2AP?若存
在,请直接写出m的值;若不存在,请说明理由.24.(本小题12分)
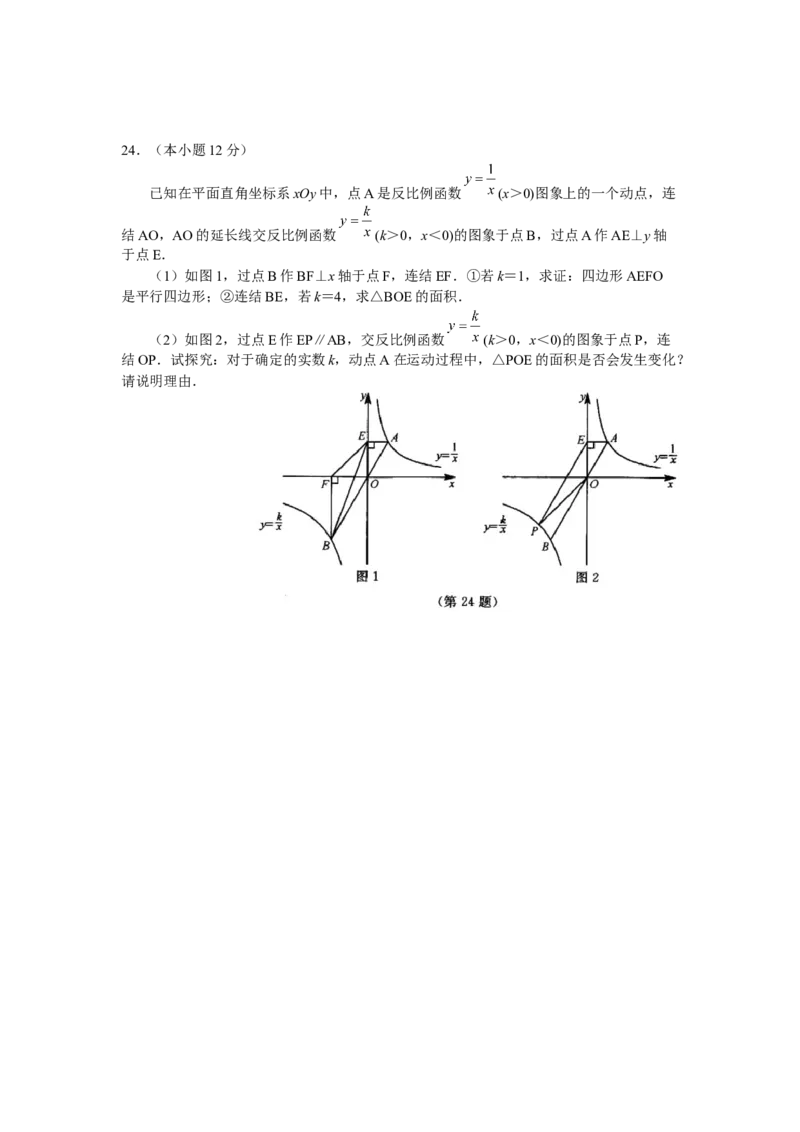
已知在平面直角坐标系xOy中,点A是反比例函数 (x>0)图象上的一个动点,连
结AO,AO的延长线交反比例函数 (k>0,x<0)的图象于点B,过点A作AE⊥y轴
于点E.
(1)如图1,过点B作BF⊥x轴于点F,连结EF.①若k=1,求证:四边形AEFO
是平行四边形;②连结BE,若k=4,求△BOE的面积.
(2)如图2,过点E作EP∥AB,交反比例函数 (k>0,x<0)的图象于点P,连
结OP.试探究:对于确定的实数k,动点A在运动过程中,△POE的面积是否会发生变化?
请说明理由.