2022年陕西省中考数学真题及答案_中考真题_2.数学中考真题2015-2024年_地区卷_陕西数学08-22（陕西省统一试卷）

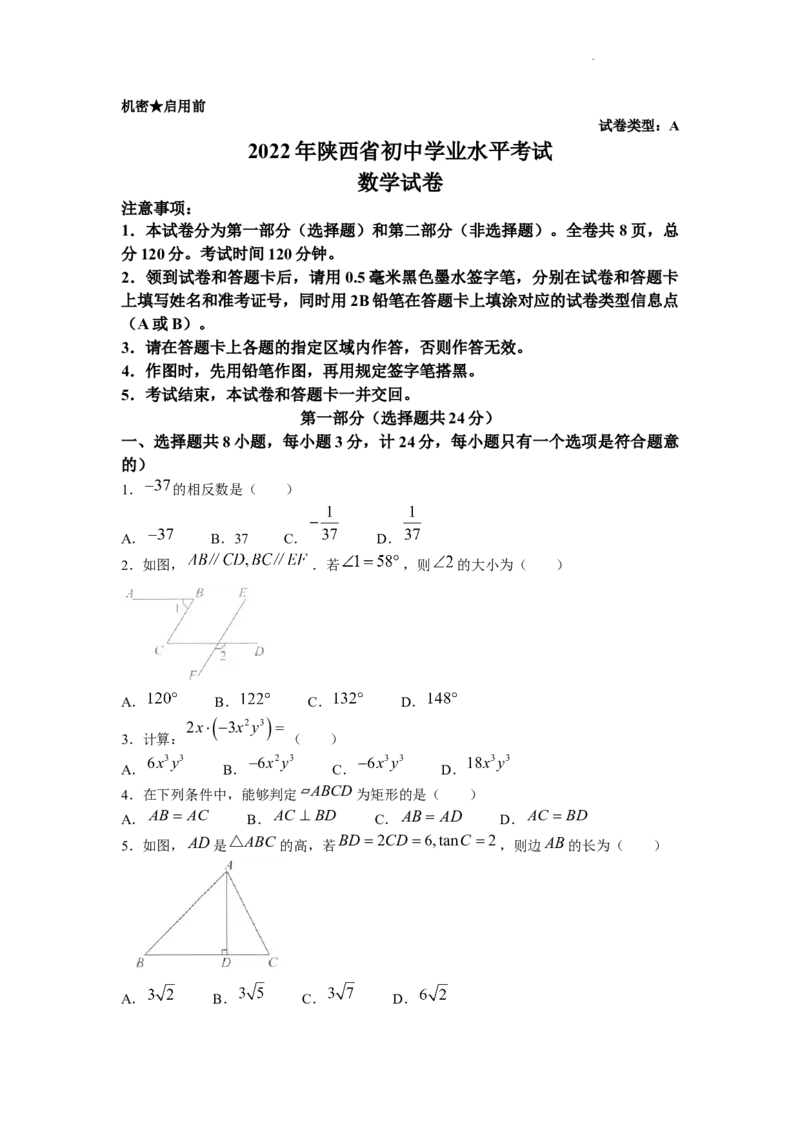
机密★启用前 试卷类型：A 2022 年陕西省初中学业水平考试 数学试卷 注意事项： 1．本试卷分为第一部分（选择题）和第二部分（非选择题）。全卷共 8页，总 分120分。考试时间120分钟。 2．领到试卷和答题卡后，请用0.5毫米黑色墨水签字笔，分别在试卷和答题卡 上填写姓名和准考证号，同时用2B铅笔在答题卡上填涂对应的试卷类型信息点 （A或B）。 3．请在答题卡上各题的指定区域内作答，否则作答无效。 4．作图时，先用铅笔作图，再用规定签字笔搭黑。 5．考试结束，本试卷和答题卡一并交回。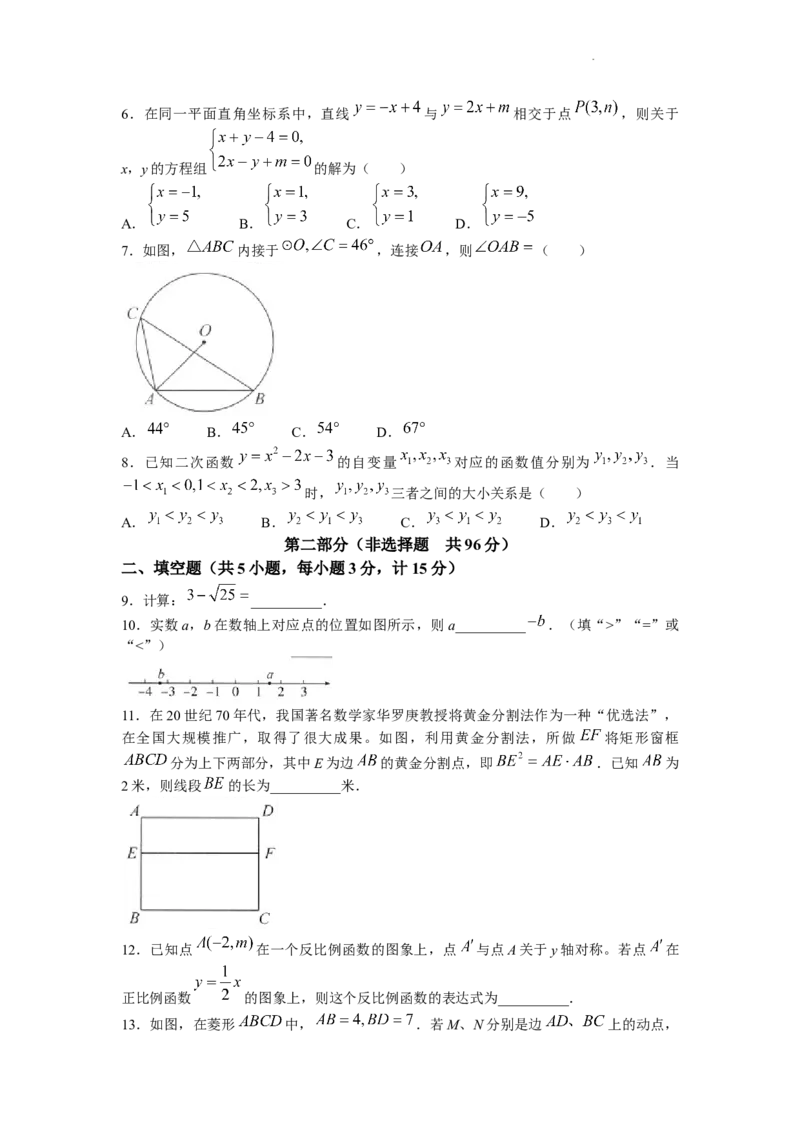 第一部分（选择题共24分） 一、选择题共8小题，每小题3分，计24分，每小题只有一个选项是符合题意 的） 1． 的相反数是（ ） A． B．37 C． D． 2．如图， ．若 ，则 的大小为（ ） A． B． C． D． 2x  3x2y3  3．计算： （ ） 6x3y3 6x2y3 6x3y3 18x3y3 A． B． C． D． 4．在下列条件中，能够判定ABCD为矩形的是（ ） A． AB  AC B．AC  BD C．AB  AD D．AC  BD 5．如图，AD是 △ABC 的高，若 BD 2CD 6,tanC 2 ，则边AB的长为（ ） A． B． C． D． 学科网（北京）股份有限公司6．在同一平面直角坐标系中，直线 与 相交于点 ，则关于 x，y的方程组 的解为（ ） A． B． C． D． 7．如图， 内接于 ，连接 ，则 （ ） A． B． C． D． 8．已知二次函数 的自变量 对应的函数值分别为 ．当 时， 三者之间的大小关系是（ ） A． B． C． D． 第二部分（非选择题 共96分） 二、填空题（共5小题，每小题3分，计15分） 9．计算： __________． 10．实数a，b在数轴上对应点的位置如图所示，则a__________ ．（填“>”“=”或 “<”） 11．在20世纪70年代，我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”， 在全国大规模推广，取得了很大成果。如图，利用黄金分割法，所做 将矩形窗框 分为上下两部分，其中E为边 的黄金分割点，即 ．已知 为 2米，则线段 的长为__________米． 12．已知点 在一个反比例函数的图象上，点 与点A关于y轴对称。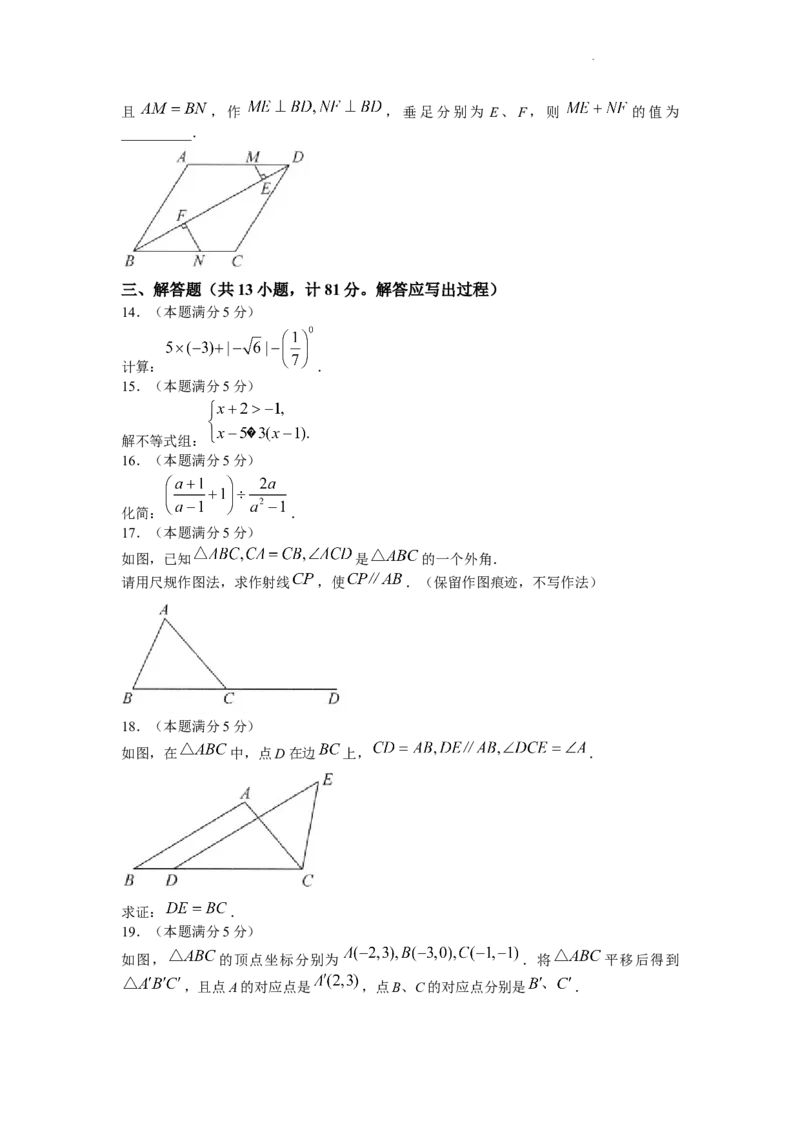若点 在 正比例函数 的图象上，则这个反比例函数的表达式为__________． 13．如图，在菱形 中， ．若M、N分别是边 上的动点， 学科网（北京）股份有限公司且 ，作 ，垂足分别为 E、F，则 的值为 __________． 三、解答题（共13小题，计81分。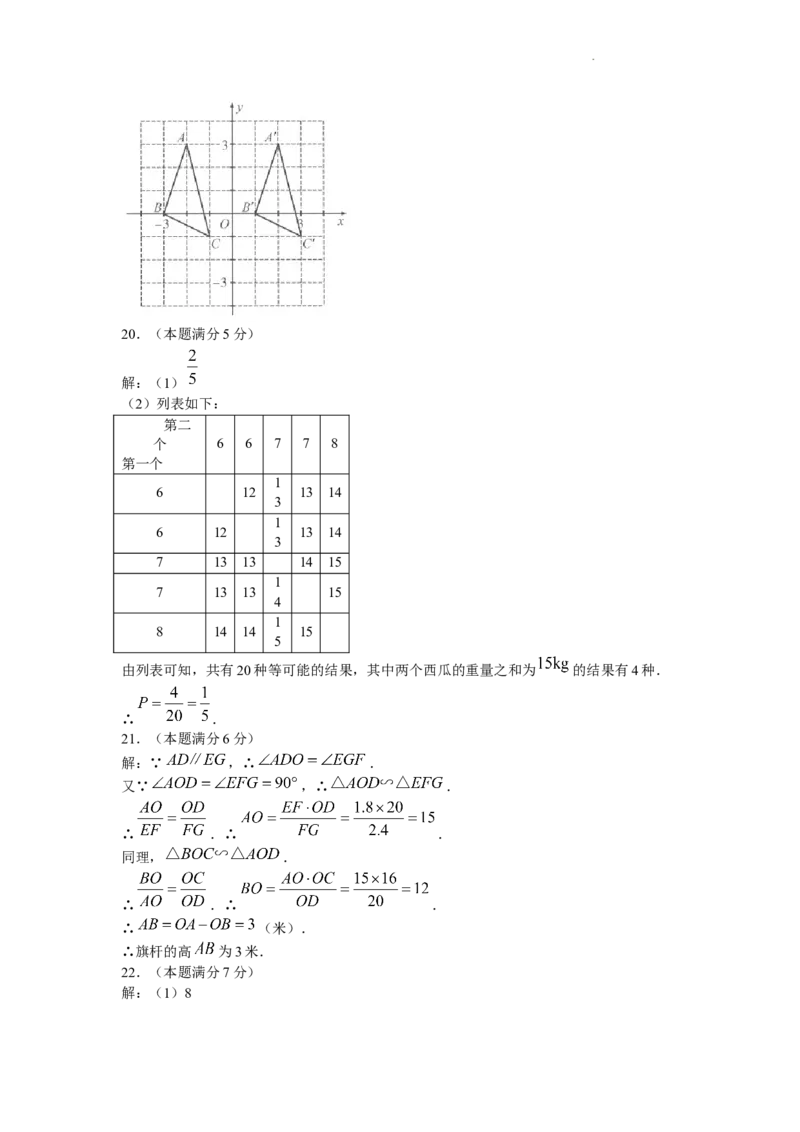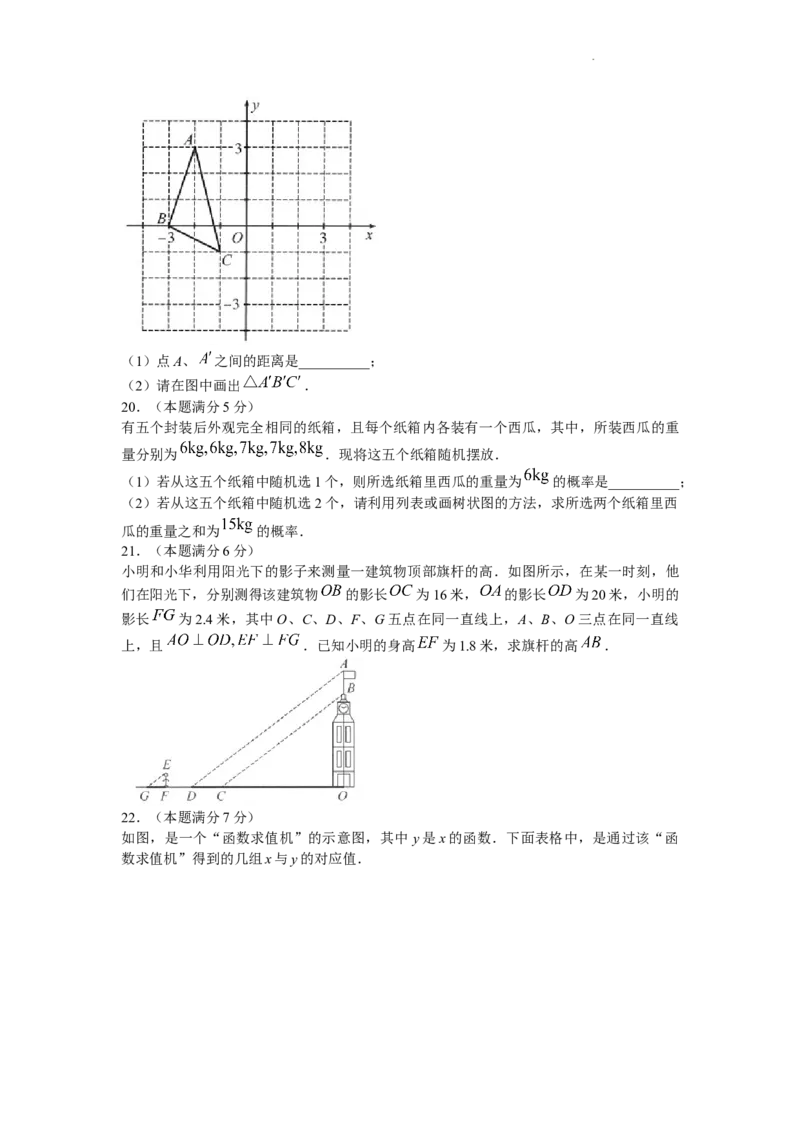解答应写出过程） 14．（本题满分5分） 计算： ． 15．（本题满分5分） 解不等式组： 16．（本题满分5分） 化简： ． 17．（本题满分5分） 如图，已知 是 的一个外角． 请用尺规作图法，求作射线 ，使 ．（保留作图痕迹，不写作法） 18．（本题满分5分） 如图，在 中，点D在边 上， ． 求证： ． 19．（本题满分5分） 如图， 的顶点坐标分别为 ．将 平移后得到 ，且点A的对应点是 ，点B、C的对应点分别是 ． 学科网（北京）股份有限公司（1）点A、 之间的距离是__________； （2）请在图中画出 ． 20．（本题满分5分） 有五个封装后外观完全相同的纸箱，且每个纸箱内各装有一个西瓜，其中，所装西瓜的重 量分别为 ．现将这五个纸箱随机摆放． （1）若从这五个纸箱中随机选1个，则所选纸箱里西瓜的重量为 的概率是__________； （2）若从这五个纸箱中随机选2个，请利用列表或画树状图的方法，求所选两个纸箱里西 瓜的重量之和为 的概率． 21．（本题满分6分） 小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高．如图所示，在某一时刻，他 们在阳光下，分别测得该建筑物 的影长 为16米， 的影长 为20米，小明的 影长 为2.4米，其中O、C、D、F、G五点在同一直线上，A、B、O三点在同一直线 上，且 ．已知小明的身高 为1.8米，求旗杆的高 ． 22．（本题满分7分） 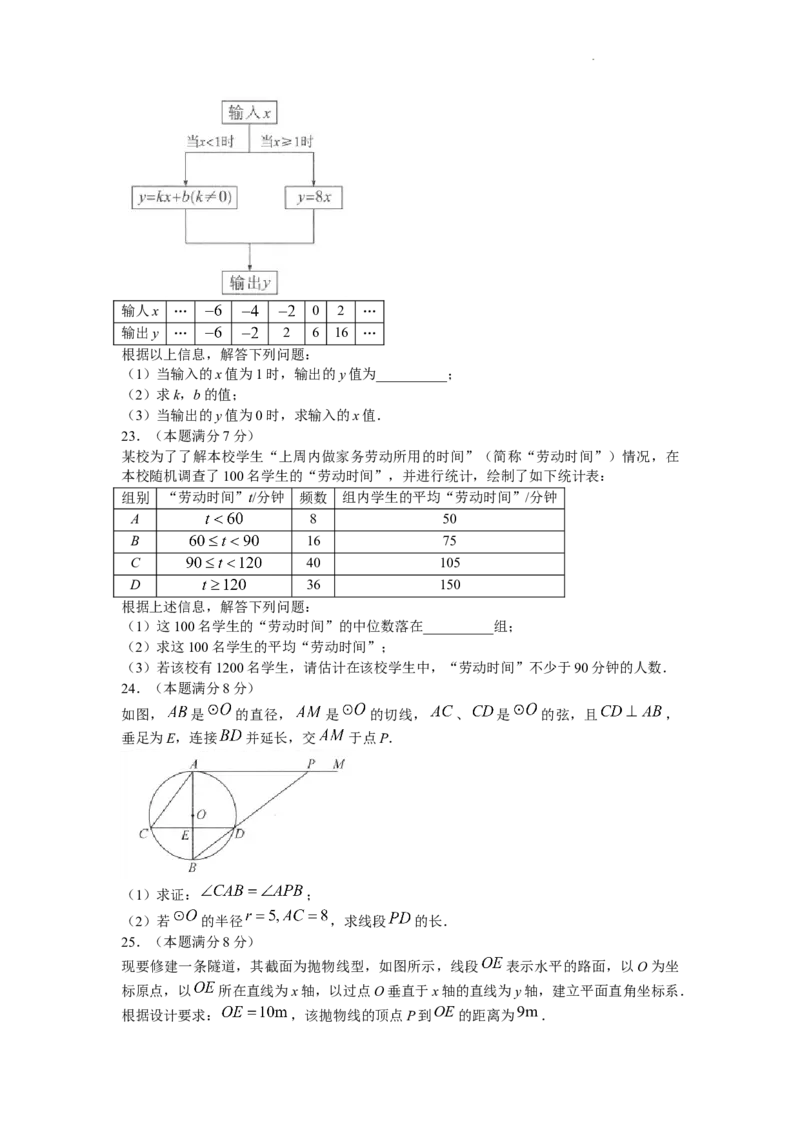如图，是一个“函数求值机”的示意图，其中 y是x的函数．下面表格中，是通过该“函 数求值机”得到的几组x与y的对应值． 学科网（北京）股份有限公司输人x … 0 2 … 输出y … 2 6 16 … 根据以上信息，解答下列问题： （1）当输入的x值为1时，输出的y值为__________； （2）求k，b的值； （3）当输出的y值为0时，求输入的x值． 23．（本题满分7分） 某校为了了解本校学生“上周内做家务劳动所用的时间”（简称“劳动时间”）情况，在 本校随机调查了100名学生的“劳动时间”，并进行统计，绘制了如下统计表： 组别 “劳动时间”t/分钟 频数 组内学生的平均“劳动时间”/分钟 A 8 50 B 16 75 C 40 105 D 36 150 根据上述信息，解答下列问题： （1）这100名学生的“劳动时间”的中位数落在__________组； （2）求这100名学生的平均“劳动时间”； （3）若该校有1200名学生，请估计在该校学生中，“劳动时间”不少于90分钟的人数． 24．（本题满分8分） 如图， 是 的直径， 是 的切线， 、 是 的弦，且 ， 垂足为E，连接 并延长，交 于点P． （1）求证： ； （2）若 的半径 ，求线段 的长． 25．（本题满分8分） 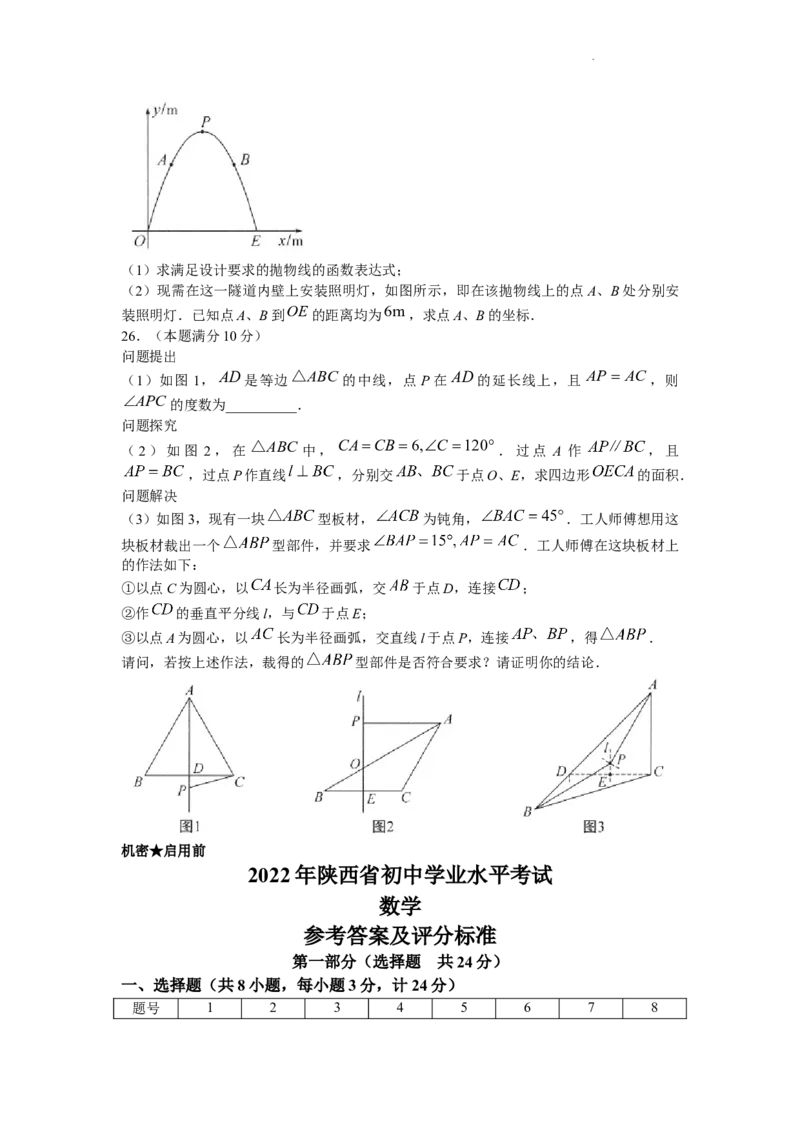现要修建一条隧道，其截面为抛物线型，如图所示，线段 表示水平的路面，以O为坐 标原点，以 所在直线为x轴，以过点O垂直于x轴的直线为y轴，建立平面直角坐标系． 根据设计要求： ，该抛物线的顶点P到 OE 的距离为9m． 学科网（北京）股份有限公司（1）求满足设计要求的抛物线的函数表达式； （2）现需在这一隧道内壁上安装照明灯，如图所示，即在该抛物线上的点A、B处分别安 OE 6m 装照明灯．已知点A、B到 的距离均为 ，求点A、B的坐标． 26．（本题满分10分） 问题提出 （1）如图1， AD是等边 △ABC 的中线，点 P在 AD的延长线上，且 AP  AC ，则 APC的度数为__________． 问题探究 △ABC CACB 6,C 120 （2）如图 2，在 中， ．过点 A 作 ，且 ，过点P作直线 ，分别交 于点O、E，求四边形 的面积． 问题解决 （3）如图3，现有一块 型板材， 为钝角， ．工人师傅想用这 块板材裁出一个 型部件，并要求 ．工人师傅在这块板材上 的作法如下： ①以点C为圆心，以 长为半径画弧，交 于点D，连接 ； ②作 的垂直平分线l，与 于点E； ③以点A为圆心，以 长为半径画弧，交直线l于点P，连接 ，得 ． 请问，若按上述作法，裁得的 型部件是否符合要求？请证明你的结论． 机密★启用前 2022 年陕西省初中学业水平考试 数学 参考答案及评分标准 第一部分（选择题 共24分） 一、选择题（共8小题，每小题3分，计24分） 题号 1 2 3 4 5 6 7 8 学科网（北京）股份有限公司A卷答 B B C D D C A B 案 B卷答 C B A D C B A D 案 第二部分（非选择题 共96分） 二、填空题（共5小题，每小题3分，计15分） 9． 10．< 11． 12． 13． 三、解答题（共13小题，计81分。以下给出了各题的一种解法及评分标准， 其它符合题意的解法请参照相应题的评分标准赋分） 14．（本题满分5分） 解：原式 ． 15．（本题满分5分） 解：由 ，得 ． 由 ，得 ． ∴原不等式组的解集为 ． 16．（本题满分5分） 解：原式 ． 17．（本题满分5分） 解：如图，射线 即为所求作． 18．（本题满分5分） 证明：∵ ，∴ ． 又∵ ，∴ ． ∴ ． 19．（本题满分5分） （1）4 （2）如图， 即为所求作． 学科网（北京）股份有限公司20．（本题满分5分） 解：（1） （2）列表如下： 第二 个 6 6 7 7 8 第一个 1 6 12 13 14 3 1 6 12 13 14 3 7 13 13 14 15 1 7 13 13 15 4 1 8 14 14 15 5 由列表可知，共有20种等可能的结果，其中两个西瓜的重量之和为 的结果有4种． ∴ ． 21．（本题满分6分） 解：∵ ，∴ ． 又∵ ，∴ ． ∴ ．∴ ． 同理， ． ∴ ．∴ ． ∴ （米）． ∴旗杆的高 为3米． 22．（本题满分7分） 解：（1）8 学科网（北京）股份有限公司（2）将 代入 ，得 解之，得 （3）令 ， 由 ，得 ，∴ ．（舍去） 由 ，得 ，∴ ． ∴输出的y值为0时，输入的x值为 ． 23．（本题满分7分） 解：（1）C （2） （分钟）， ∴这100名学生的平均“劳动时间”为112分钟． （3）∵ （人）， ∴估计在该校学生中，“劳动时间”不少于90分钟的有912人． 24．（本题满分8分） （1）证明：∵ 是 的切线，∴ ． ∵ ，∴ ．∴ ． ∵ ，∴ ． （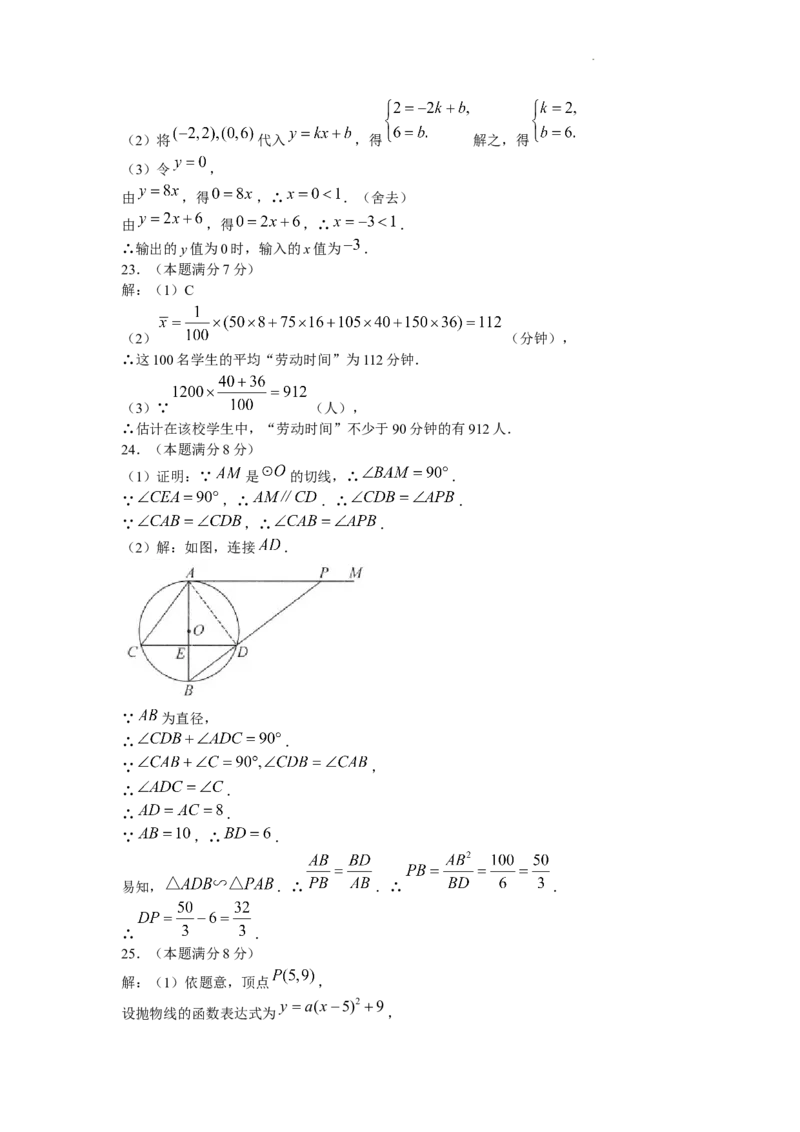2）解：如图，连接 ． ∵ 为直径， ∴ ． ∵ ， ∴ ． ∴ ． ∵ ，∴ ． 易知， ．∴ ．∴ ． ∴ ． 25．（本题满分8分） 解：（1）依题意，顶点 ， y a(x5)2 9 设抛物线的函数表达式为 ， 学科网（北京）股份有限公司9 a  (0,0) 0a(05)2 9 25 将 代入，得 ．解之，得 ． 9 y   (x5)2 9 25 ∴抛物线的函数表达式为 ． 9  (x5)2 96 y 6 25 （2）令 ，得 ． 5 3 5 3 x  5,x  5 1 3 2 3 解之，得 ．  5 3   5 3  A5 ,6,B5 ,6 3 3     ∴ ． 26．（本题满分10分） 解：（1） 75 （2）如图1，连接BP． 图1 ∵ ，∴四边形 是菱形． ∴ ．∵ ，∴ ． ∵ ，∴ ． ∴ ． ∵ ，∴ ． ∴ ．∴ ． （3）符合要求． 由作法，知 ． ∵ ，∴ ． 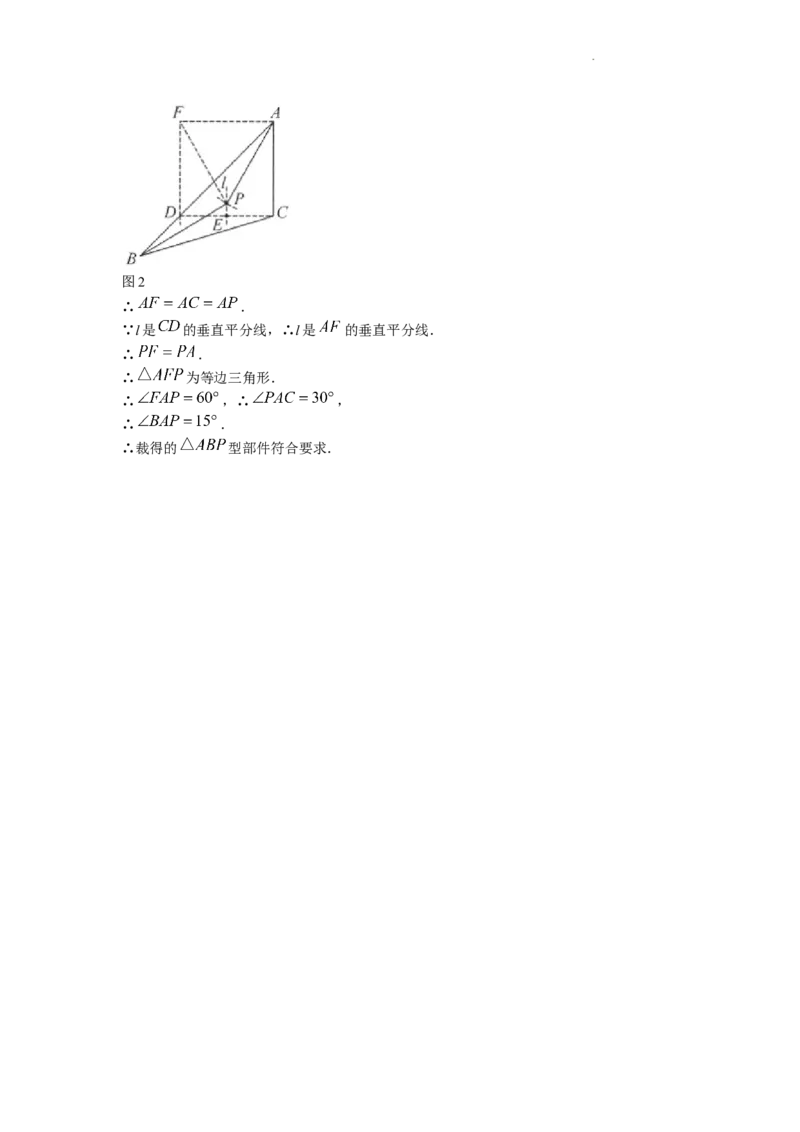如图2，以 为边，作正方形 ，连接 ． 学科网（北京）股份有限公司图2 ∴ ． ∵l是 的垂直平分线，∴l是 的垂直平分线． ∴ ． ∴ 为等边三角形． ∴ ，∴ ， ∴ ． ∴裁得的 型部件符合要求． 学科网（北京）股份有限公司