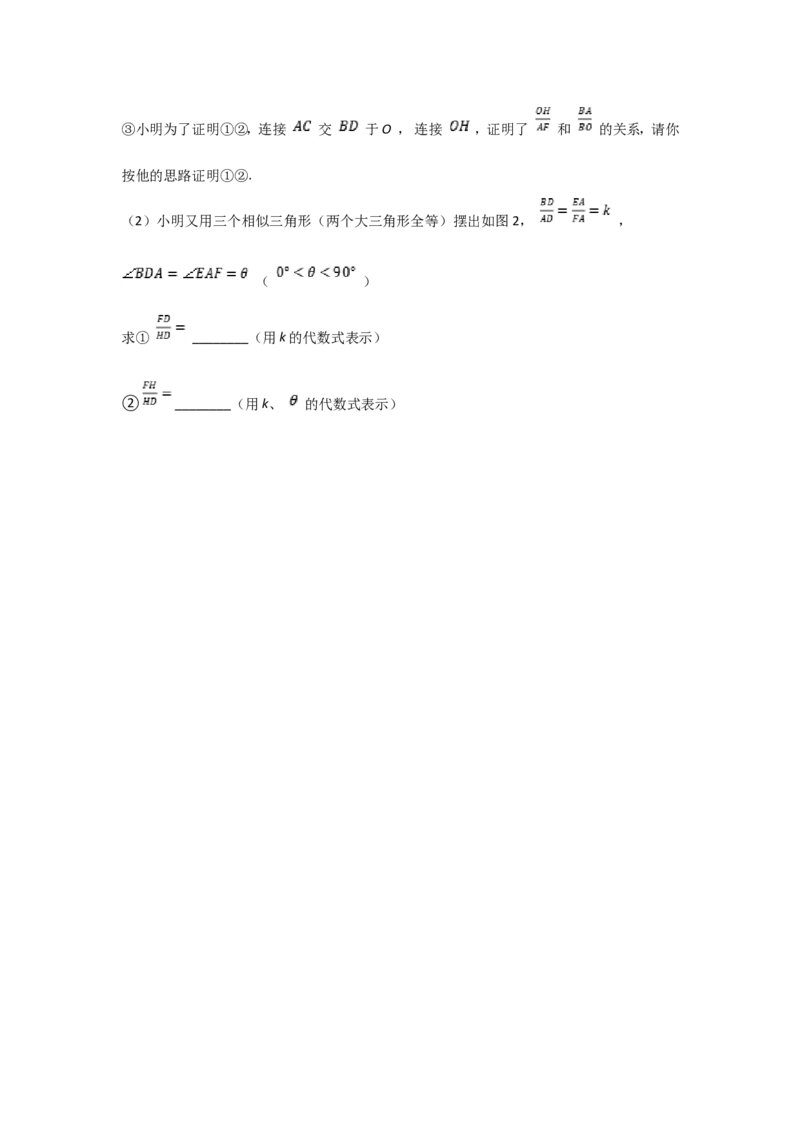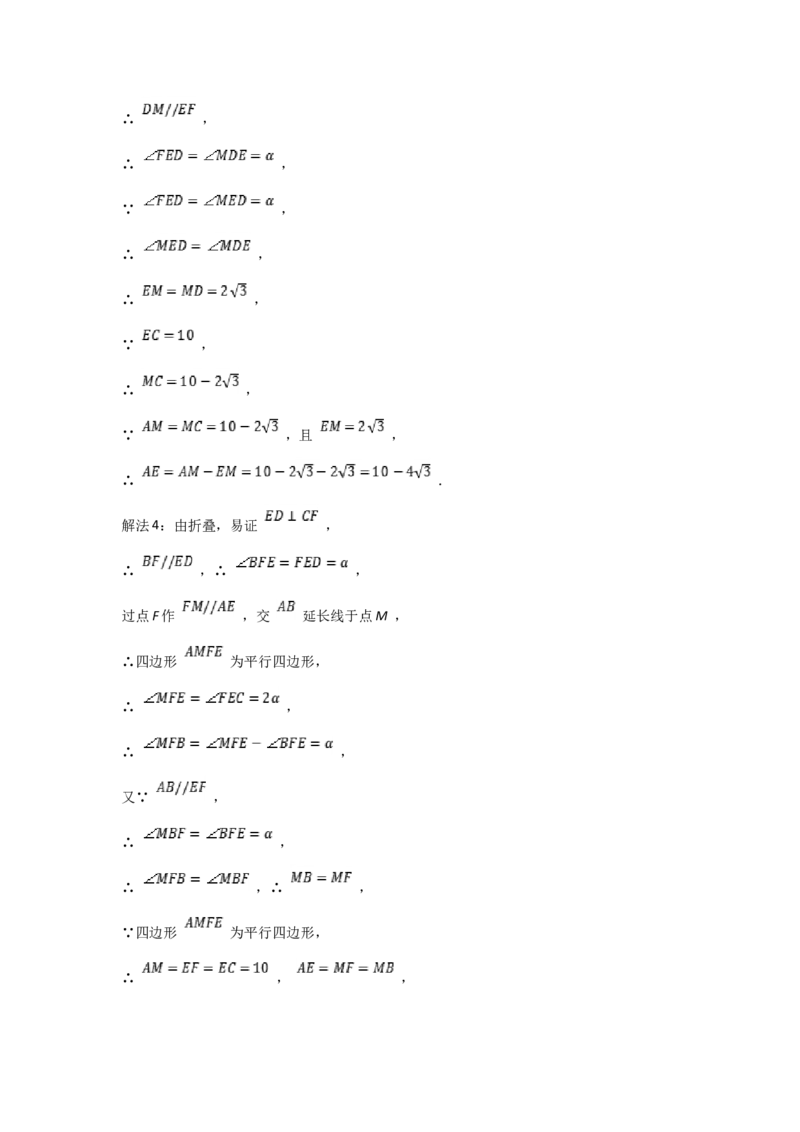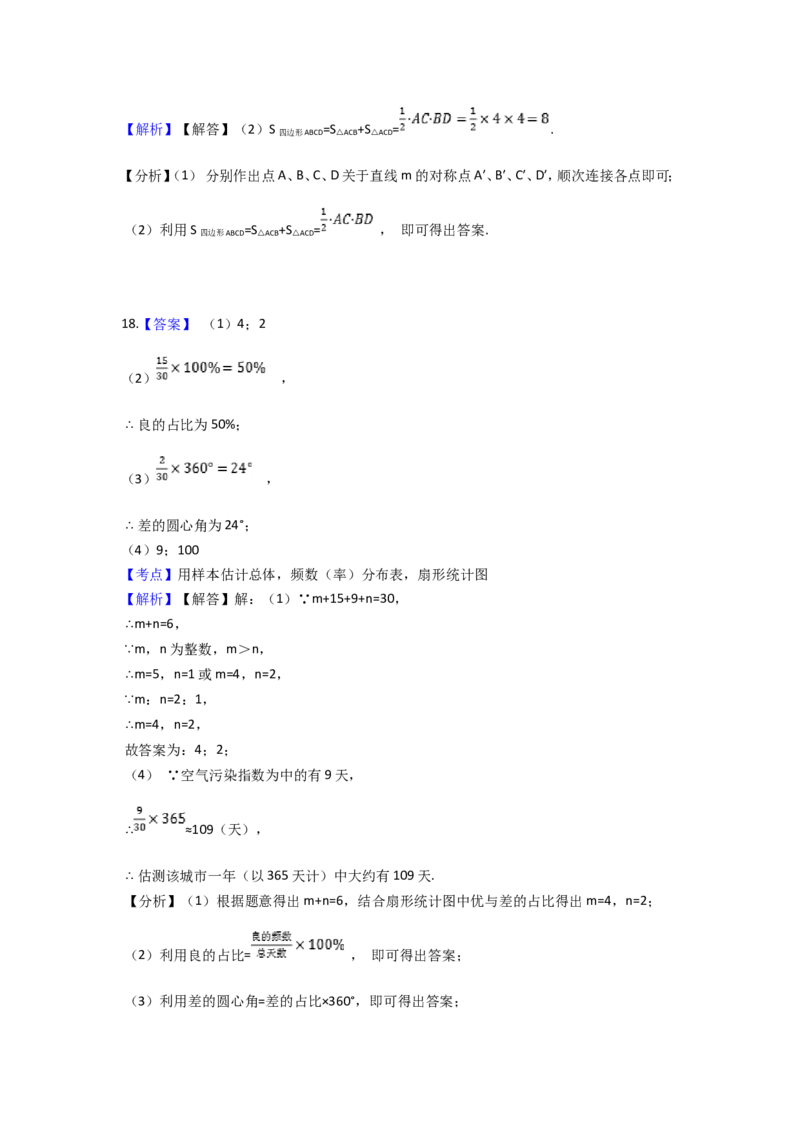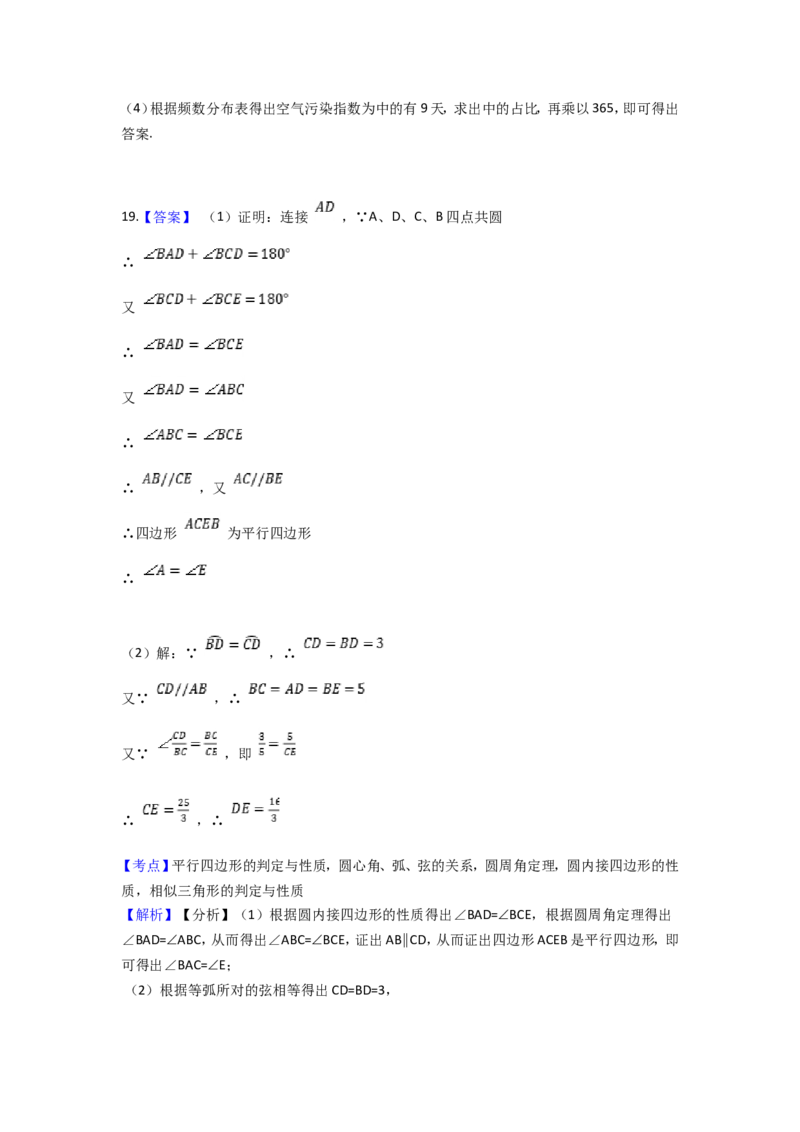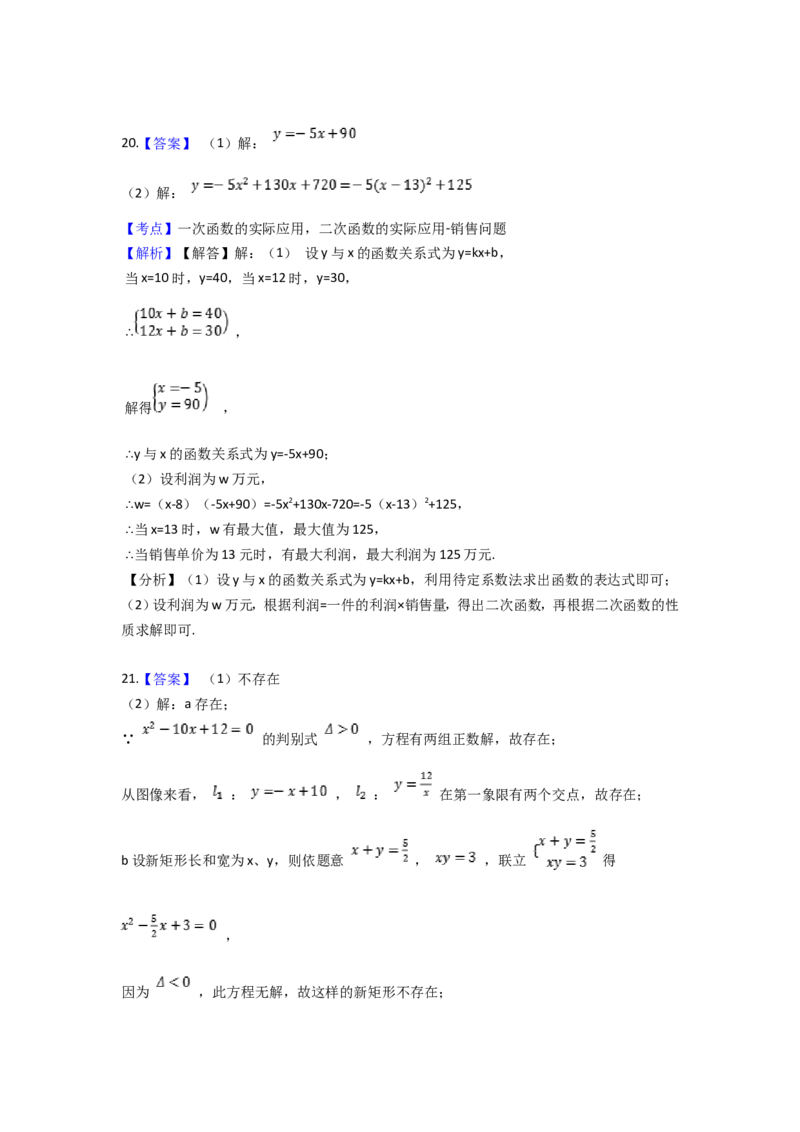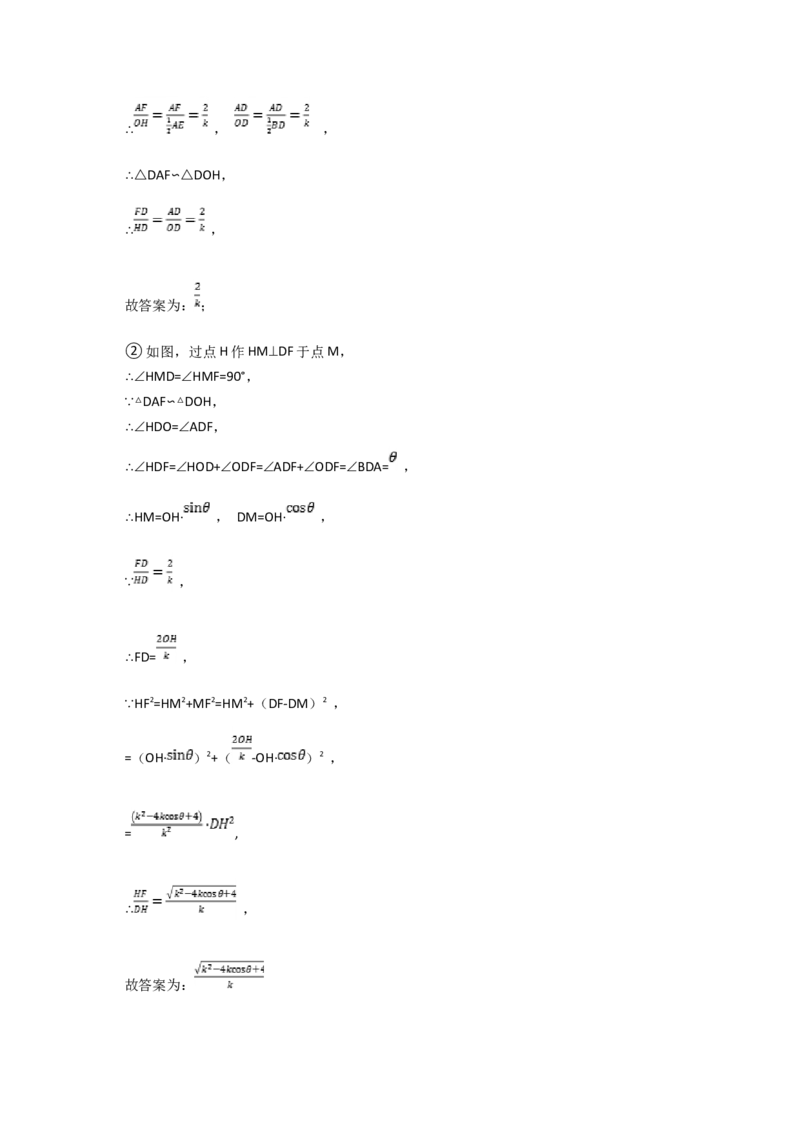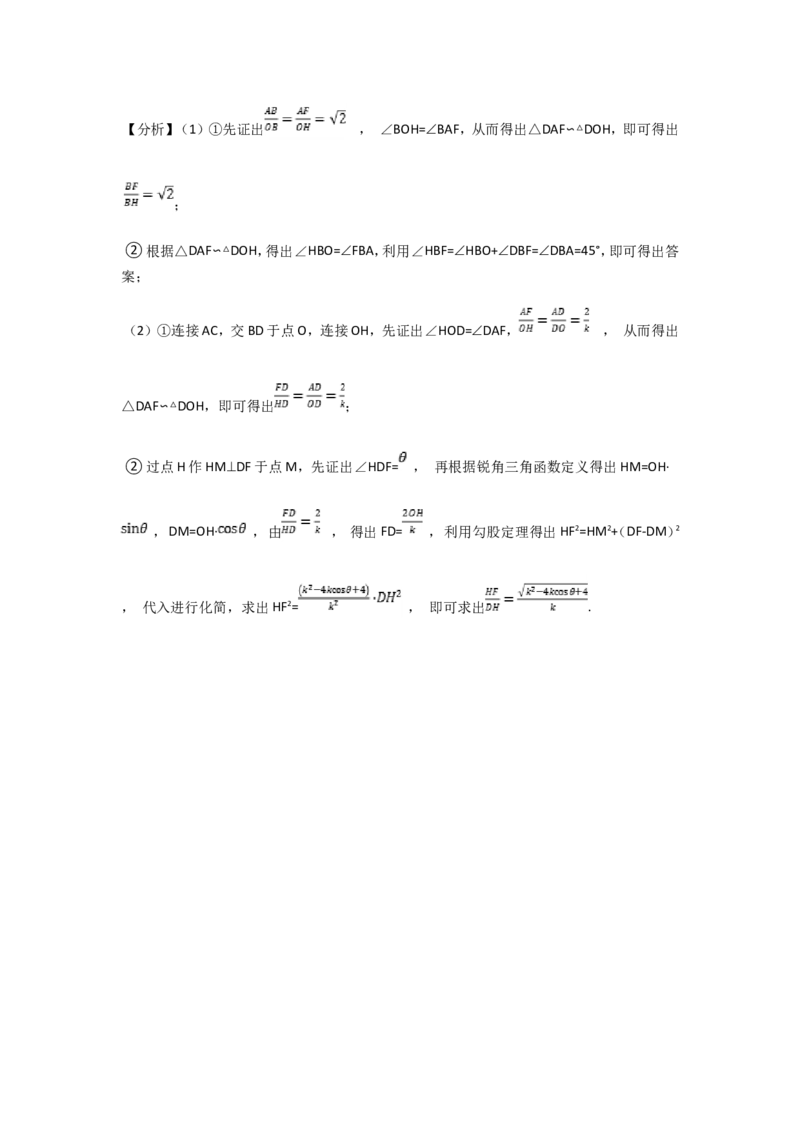文档内容
广东省深圳市2021年中考数学真题试卷
一、选择题(每题3分,共30分)(共10题;共30分)
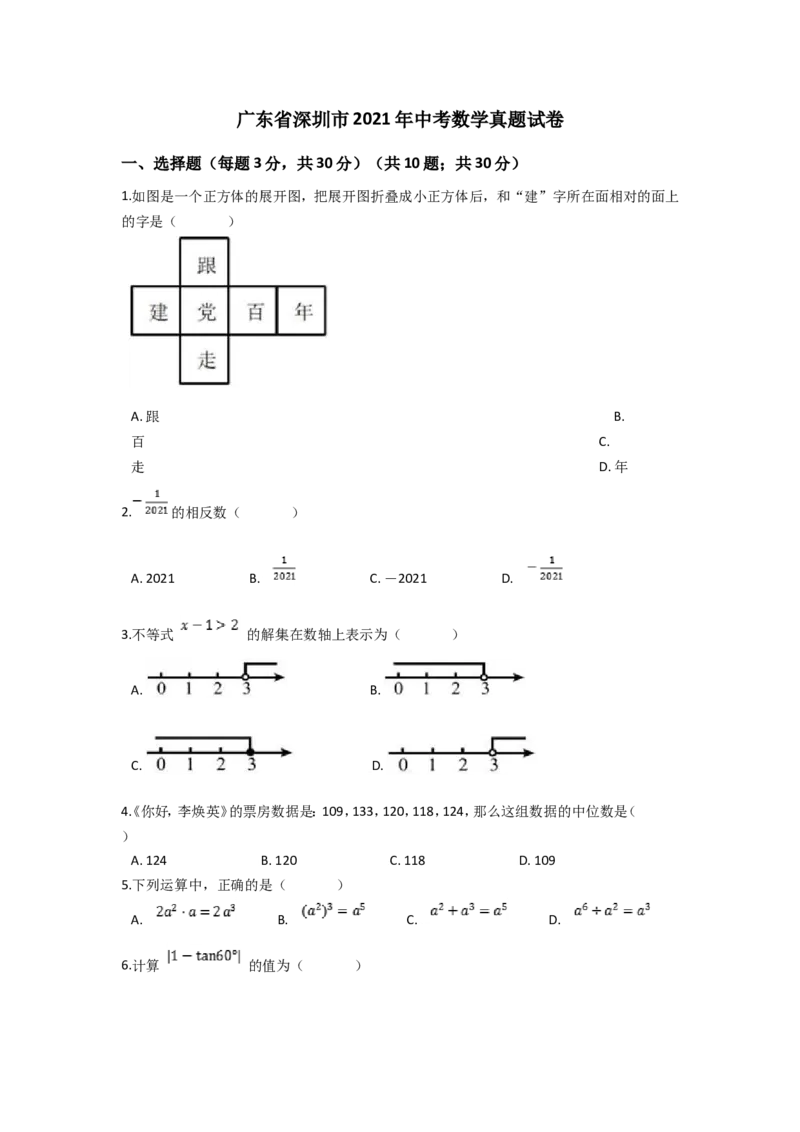
1.如图是一个正方体的展开图,把展开图折叠成小正方体后,和“建”字所在面相对的面上
的字是( )
A. 跟 B.
百 C.
走 D. 年
2. 的相反数( )
A. 2021 B. C. -2021 D.
3.不等式 的解集在数轴上表示为( )
A. B.
C. D.
4《. 你好,李焕英》的票房数据是:109,133,120,118,124,那么这组数据的中位数是(
)
A. 124 B. 120 C. 118 D. 109
5.下列运算中,正确的是( )
A. B. C. D.
6.计算 的值为( )A. B. 0 C. D.
7.《九章算术》中有问题:1亩好田是300元,7亩坏田是500元,一人买了好田坏田一共是
100亩,花费了10000元,问他买了多少亩好田和坏田?设好田买了x亩,坏田买了y亩,根
据题意列方程组得( )
A. B.
C. D.
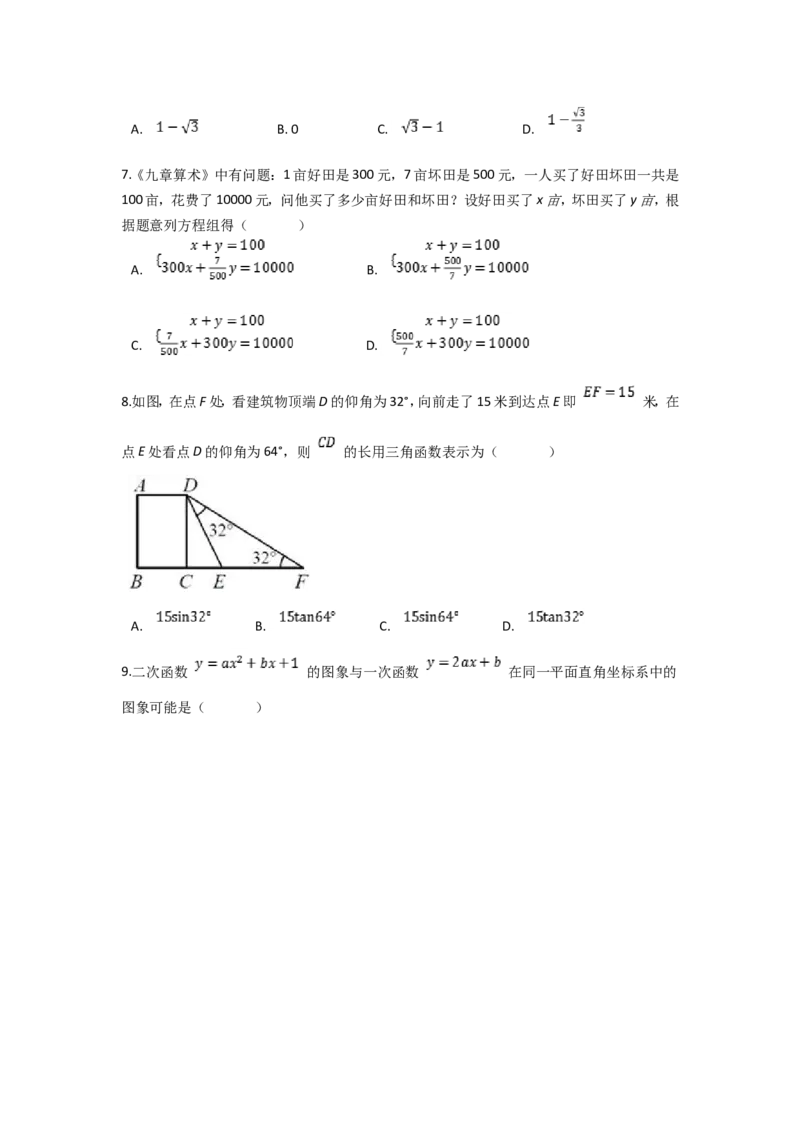
8.如图,在点F处,看建筑物顶端D的仰角为32°,向前走了15米到达点E即 米,在
点E处看点D的仰角为64°,则 的长用三角函数表示为( )
A. B. C. D.
9.二次函数 的图象与一次函数 在同一平面直角坐标系中的
图象可能是( )A. B.
C. D.
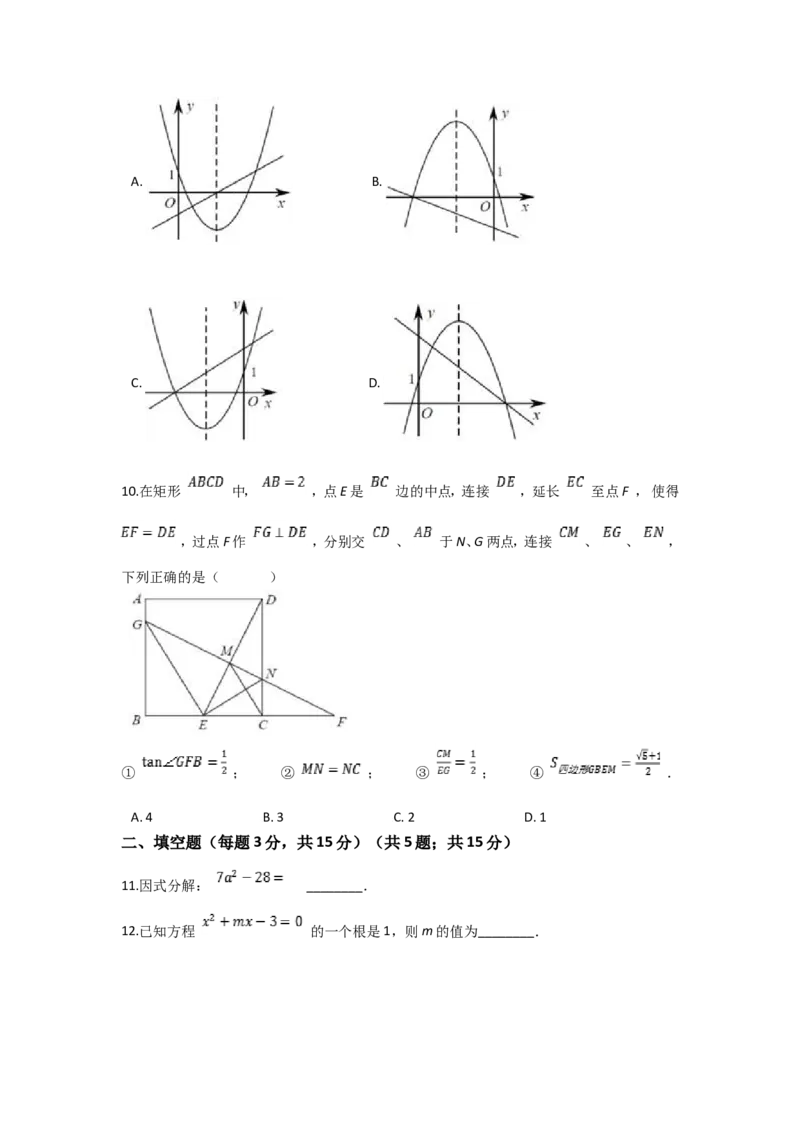
10.在矩形 中, ,点E是 边的中点,连接 ,延长 至点F , 使得
,过点F作 ,分别交 、 于N、G两点,连接 、 、 ,
下列正确的是( )
① ; ② ; ③ ; ④ .
A. 4 B. 3 C. 2 D. 1
二、填空题(每题3分,共15分)(共5题;共15分)
11.因式分解: ________.
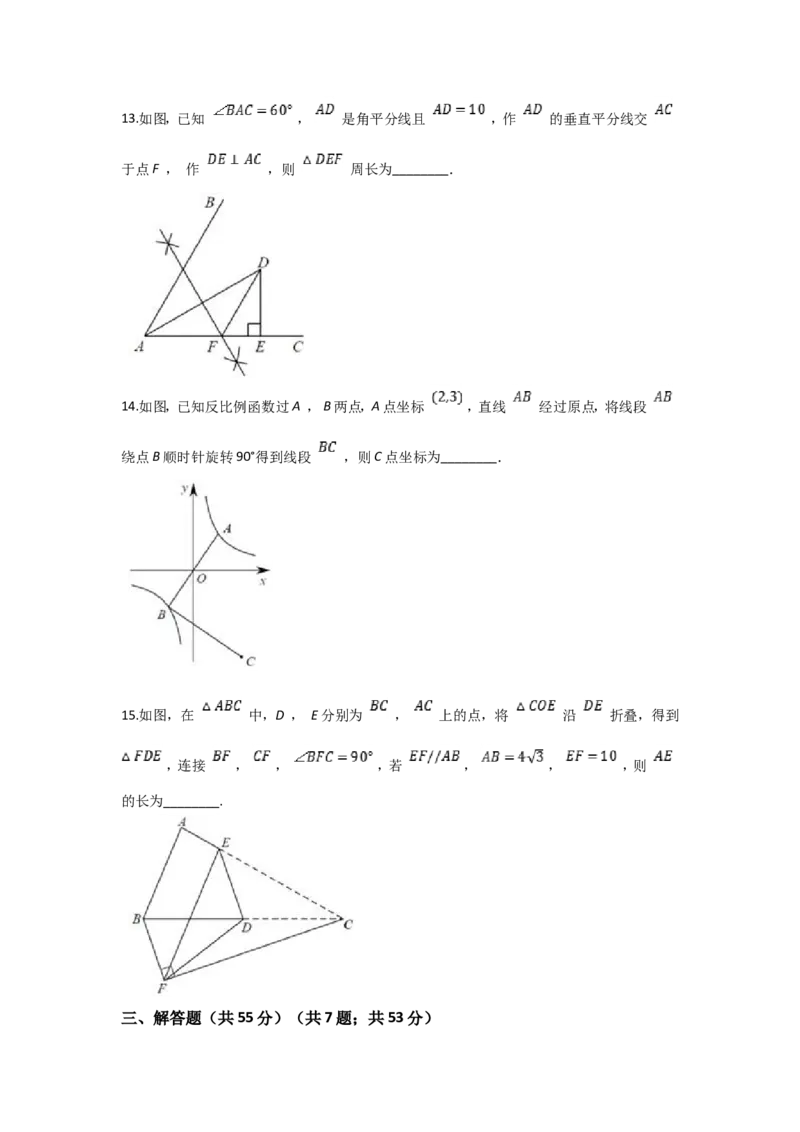
12.已知方程 的一个根是1,则m的值为________.13.如图,已知 , 是角平分线且 ,作 的垂直平分线交
于点F , 作 ,则 周长为________.
14.如图,已知反比例函数过A , B两点,A点坐标 ,直线 经过原点,将线段
绕点B顺时针旋转90°得到线段 ,则C点坐标为________.
15.如图,在 中,D , E分别为 , 上的点,将 沿 折叠,得到
,连接 , , ,若 , , ,则
的长为________.
三、解答题(共55分)(共7题;共53分)16.先化简再求值: ,其中 .
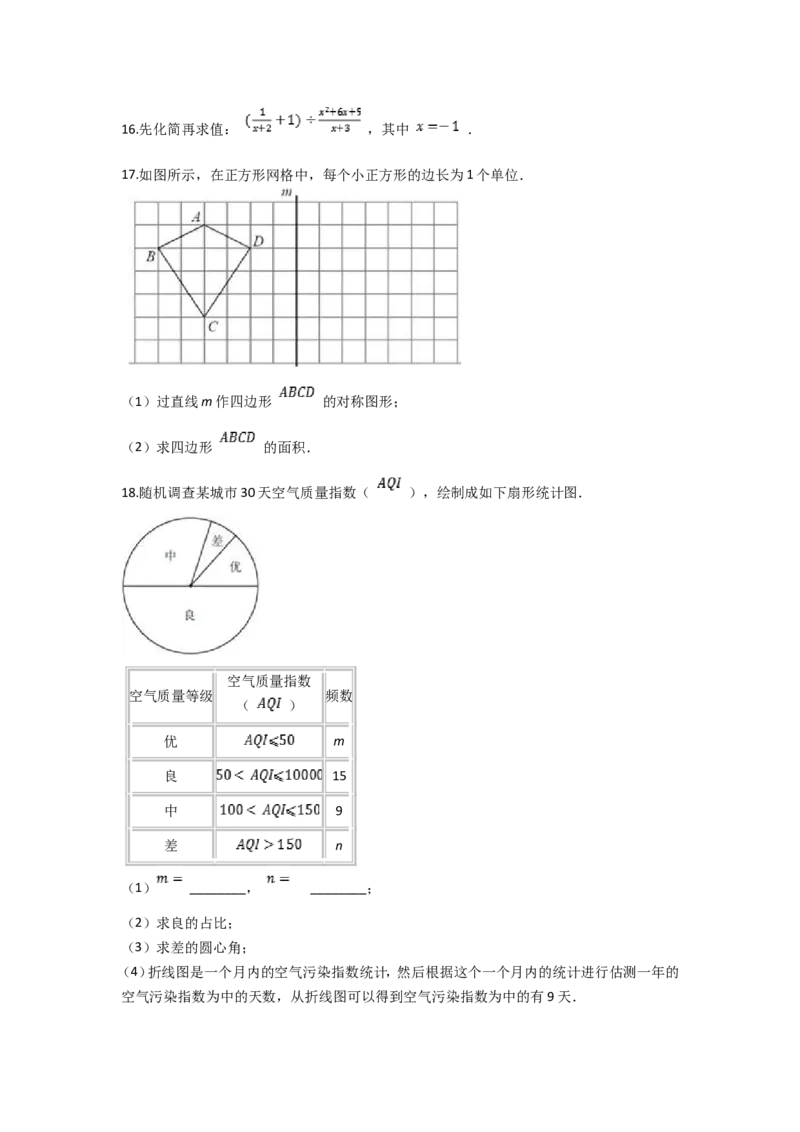
17.如图所示,在正方形网格中,每个小正方形的边长为1个单位.
(1)过直线m作四边形 的对称图形;
(2)求四边形 的面积.
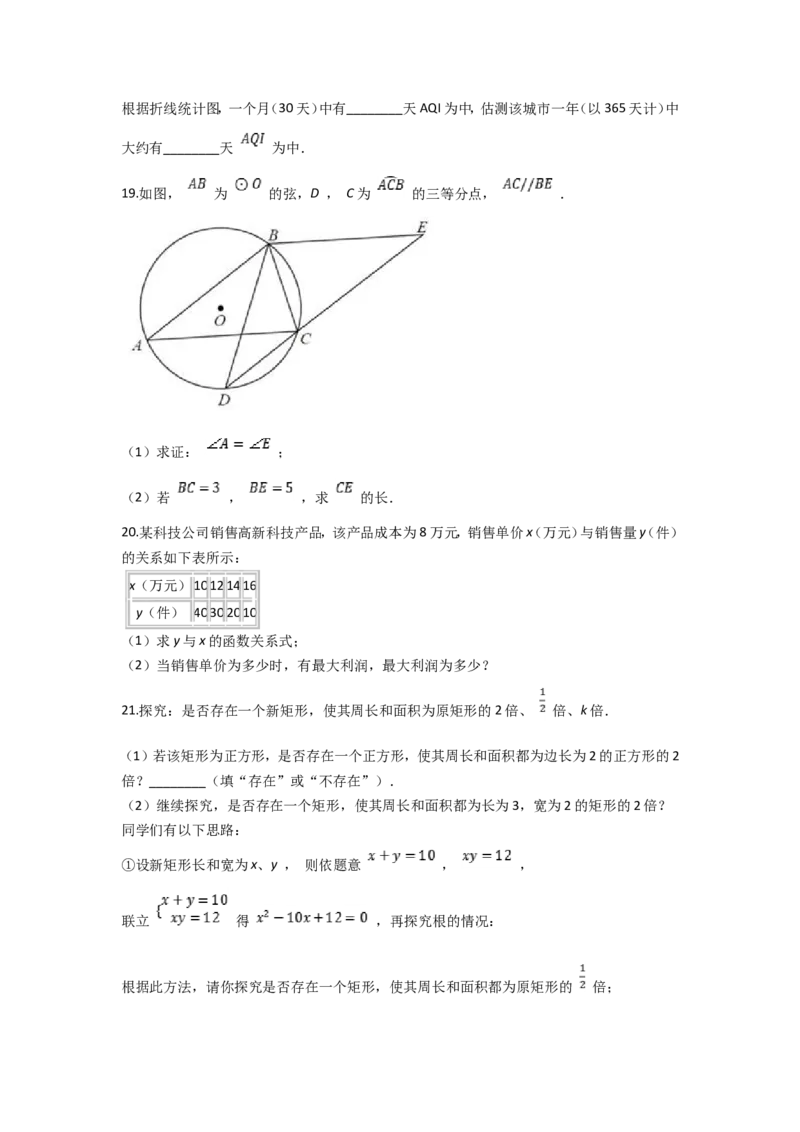
18.随机调查某城市30天空气质量指数( ),绘制成如下扇形统计图 .
空气质量指数
空气质量等级 频数
( )
优 m
良 15
中 9
差 n
(1) ________, ________;
(2)求良的占比;
(3)求差的圆心角;
(4)折线图是一个月内的空气污染指数统计,然后根据这个一个月内的统计进行估测一年的
空气污染指数为中的天数,从折线图可以得到空气污染指数为中的有9天.根据折线统计图,一个月(30天)中有________天AQI为中,估测该城市一年(以365天计)中
大约有________天 为中.
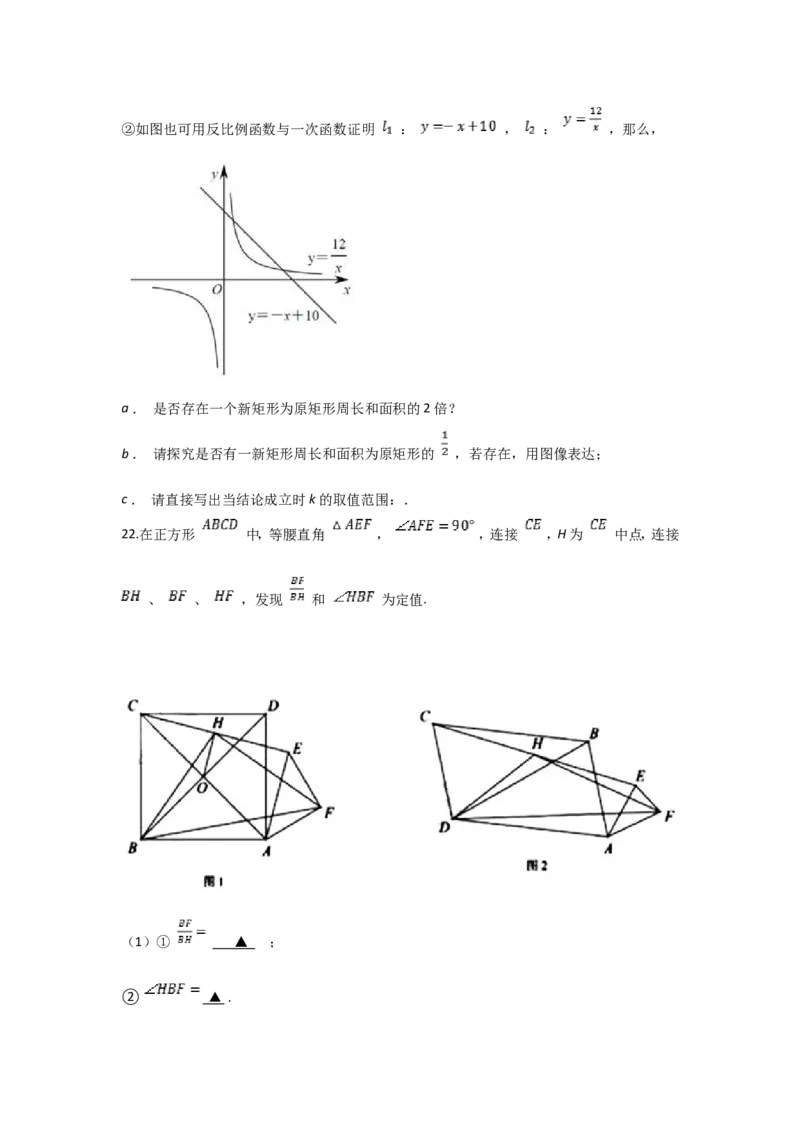
19.如图, 为 的弦,D , C为 的三等分点, .
(1)求证: ;
(2)若 , ,求 的长.
20.某科技公司销售高新科技产品,该产品成本为8万元,销售单价x(万元)与销售量y(件)
的关系如下表所示:
x(万元)10121416
y(件) 40302010
(1)求y与x的函数关系式;
(2)当销售单价为多少时,有最大利润,最大利润为多少 ?
21.探究:是否存在一个新矩形,使其周长和面积为原矩形的2倍、 倍、k倍.
(1)若该矩形为正方形,是否存在一个正方形,使其周长和面积都为边长为2的正方形的2
倍?________(填“存在”或“不存在”) .
(2)继续探究,是否存在一个矩形,使其周长和面积都为长为3,宽为2的矩形的2倍?
同学们有以下思路:
①设新矩形长和宽为x、y , 则依题意 , ,
联立 得 ,再探究根的情况:
根据此方法,请你探究是否存在一个矩形,使其周长和面积都为原矩形的 倍;②如图也可用反比例函数与一次函数证明 : , : ,那么,
a . 是否存在一个新矩形为原矩形周长和面积的2倍?
b . 请探究是否有一新矩形周长和面积为原矩形的 ,若存在,用图像表达;
c . 请直接写出当结论成立时k的取值范围:.
22.在正方形 中,等腰直角 , ,连接 ,H为 中点,连接
、 、 ,发现 和 为定值.
(1)① ▲ ;
② ▲ .③小明为了证明①②,连接 交 于O , 连接 ,证明了 和 的关系,请你
按他的思路证明①②.
(2)小明又用三个相似三角形(两个大三角形全等)摆出如图2, ,
( )
求① ________(用k的代数式表示)
② ________(用k、 的代数式表示)答案解析部分
一、选择题(每题3分,共30分)
1.【答案】 B
【考点】几何体的展开图
【解析】【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方
形,“建”与“百”是相对面,“党”与“年”是相对面,“跟”与“走”是相对面 ,
故答案为:B.
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点进行解答,
即可得出答案.
2.【答案】 B
【考点】相反数及有理数的相反数
【解析】【解答】解:- 的相反数是 .
故答案为:B.
【分析】根据相反数的定义:只有符号不同的两个数是互为相反数,即可得出答案.
3.【答案】 D
【考点】解一元一次不等式,在数轴上表示不等式的解集
【解析】【解答】解:x-1>2,
∴x>3,
在数轴上表示为 :
故答案为:D.
【分析】先求出不等式的解集,再在数轴上表示出来,即可得出答案.
4.【答案】 B
【考点】中位数
【解析】【解答】解:从小到大排列:109,118,120,124,133,
∴ 这组数据的中位数是120.
故答案为:B.
【分析】中位数是将数据按照从小到大或从大到小的顺序排列,如果数据个数是奇数,则处
于最中间位置的数就是这组数据的中位数,如果数据的个数是偶数,则中间两个数据的平均
数是这组数据的中位数,据此即可得出答案.5.【答案】 A
【考点】同底数幂的除法,单项式乘单项式,合并同类项法则及应用,幂的乘 方
【解析】【解答】解:A、2a2·a=2a3 , 故A正确;
B、(a2)3=a6 , 故B错误;
C、a2和a3不是同类项,不能合并,故C错误;
D、a6÷a2=a4 , 故D错误.
故答案为:A.
【 分析】根据单项式乘以单项式的法则、幂的乘方法则、合并同类项法则、同底数幂的除法法
则,逐项进行判断,即可得出答案.
6.【答案】 C
【考点】特殊角的三角函数值,实数的绝对值
【解析】【解答】解: .
故答案为:C.
【分析】把 代入,再根据绝对值的意义进行计算,即可得出答案.
7.【答案】 B
【考点】二元一次方程组的其他应用
【解析】【解答】解: 设一亩好田为x元,一亩坏田为y元,
根据题意得: .
故答案为:B.
【分析】设一亩好田为x元,一亩坏田为y元,根据题意找出等量关系,列出方程组即可.
8.【答案】 C
【考点】三角形的外角性质,等腰三角形的判定,锐角三角函数的定义
【解析】【解答】解:∵∠F=32°,∠DEC=64°,
∴∠EDF=∠DEC-∠F=64°-32°=32°=∠F,
∴DE=EF=15,
在Rt△DCE中, ,
∴CD= .
故答案为:C.【 分析】根据三角形的外角性质求出∠EDF=32°=∠F,得出DE=EF=15,再根据锐角三角函数的
定义得出 , 即可得出答案.
9.【答案】 A
【考点】二次函数与一次函数的综合应用
【解析】【解答】解:∵二次函数y=ax2+bx+1的对称轴为直线x=- , 一次函数y=2ax+b与x轴
的交点坐标为(- , 0),
∴抛物线的对称轴与直线的交点为(- , 0),
故A符合题意.
故答案为:A.
【 分析】求出抛物线的对称轴为直线x=- , 直线与x轴的交点坐标为(- , 0),得出抛物
线的对称轴与直线的交点为(- , 0),逐项进行判断,即可得出答案.
10.【答案】 B
【考点】三角形全等的判定,等腰三角形的判定与性质,相似三角形的判定与性质,锐角三角
函数的定义
【解析】【解答】
故答案为:① ,①正确;
②∵ , ,
∴ ,
∵ , , ,∴ ( ),∴ ,∴ ,
∵ , , ,
∴ ( ),∴ ,故②正确;
③∵ , ,∴ ,
∵在 和 中: , ,
∴ ( ),∴ ,
∵ ,∴ ,
又∵ ,
∴ ,∴ ,∴ ,
∵ , ,
∴ ,故③错误;
④由上述可知: , ,∴ ,
∵ ,∴ ,
∴ ,故④正确.
故选B.
【分析】①先证出∠GFB=∠EDC,得出 , 即可判断①正确;
②先证出△DEC≌△FEM,得出EM=EC,从而得出DM=FC,进而证出△DMN≌△FCN,得出
MN=NC,即可判断②正确;
③先证出MC∥GE,得出 , 再求出EF,CF的长,得出 , 即可判断③错误;
④先求出BF的长,根据 , 求出GB的长,利用
, 即可判断④正确.
二、填空题(每题3分,共15分)
11.【答案】 7(a+2)(a-2)
【考点】提公因式法与公式法的综合运用
【解析】【解答】解:7a2-28=7(a2-4)=7(a+2)(a-2).
【分析】先提公因式7,再根据平方差公式分解因式,即可得出答案.
12.【答案】 2
【考点】二元一次方程的解
【解析】【解答】将 代入得: ,解得
【 分析】根据一元二次方程根的定义把x=1代入方程,得出关于m的 一元一次方程,解方程
求出m的值 ,即可得出答案.
13.【答案】
【考点】线段垂直平分线的性质,含30°角的直角三角形,角平分线的定义
【解析】【解答】 (垂直平分线上的点到线段两端点距离相等)
∴
∵ , 是角平分线
∴
∵
∴ ,
∴
【 分析】根据线段垂直平分线的性质得出DF=AF,根据角平分线的定义得出∠DAE=30°,从而
求出DE和AE的长,再利用△DEF的周长=DE+DF+EF=AE+DE,即可得出答案.
14.【答案】 (4,-7)【考点】坐标与图形性质,待定系数法求一次函数解析式,待定系数法求反比例函数解析式,
三角形全等的判定(AAS)
【解析】【解答】设 : ,反比例:
将点A代入可得:
;
联立可得:
过点B作y轴的平行线l
过点A , 点C作l的垂线,分别交于D , E两点
则
利用“一线三垂直”易证
,
∴ .
【 分析】利用待定系数法求出反比例函数和正比例函数的解析式,求出点B的坐标,过点B作
y轴的平行线l,过点A、点C作l的垂线,垂足分别为D,E两点,求出点D的坐标,再证出
△ABD≌△BEC,得出BE和CE的长,即可求出点C的坐标.
15.【答案】
【考点】等腰三角形的判定与性质,平行四边形的判定与性质,轴对称的性质
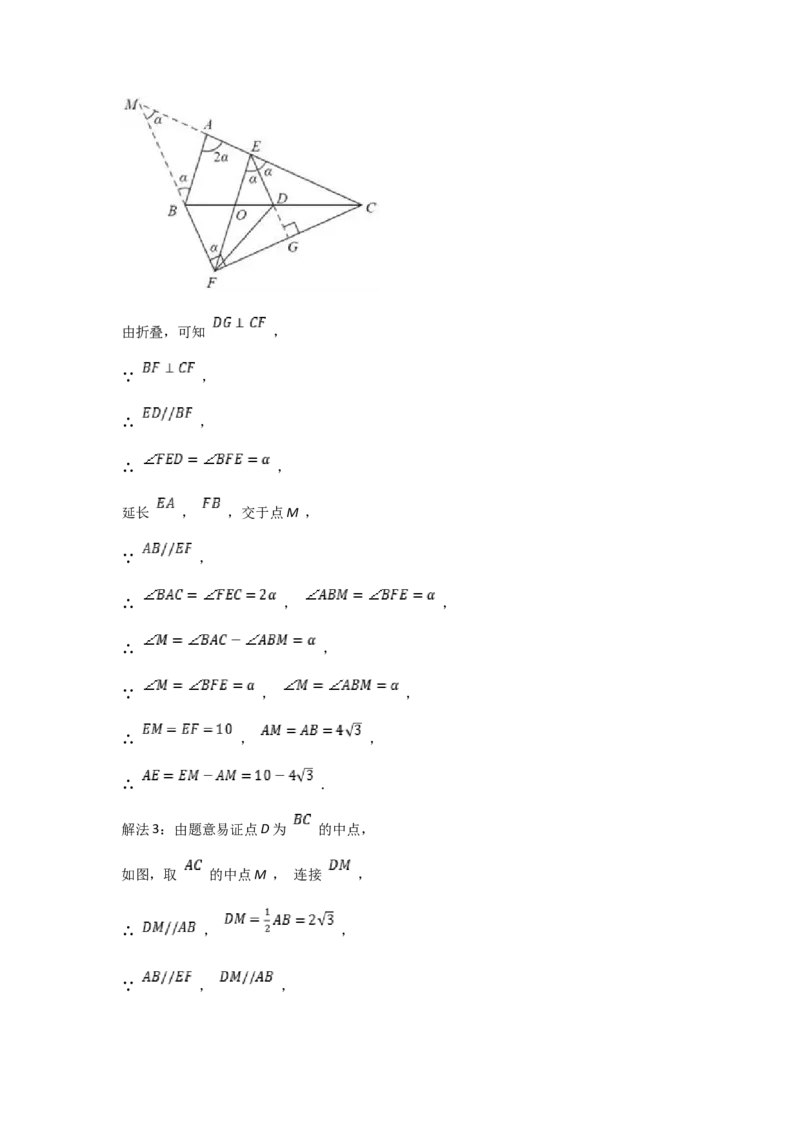
【解析】【解答】解法1:如图,延长 ,交 于点G ,由折叠,可知 ,
∵ ,∴ ,
延长 , ,交于点M ,
∵ ,且 ,
∴四边形 为平行四边形,
∴ ,
又易证 ,
∴ ,
∵ ,
∴ .
解法2:如图,延长 ,交 于点G ,由折叠,可知 ,
∵ ,
∴ ,
∴ ,
延长 , ,交于点M ,
∵ ,
∴ , ,
∴ ,
∵ , ,
∴ , ,
∴ .
解法3:由题意易证点D为 的中点,
如图,取 的中点M , 连接 ,
∴ , ,
∵ , ,∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∵ ,且 ,
∴ .
解法4:由折叠,易证 ,
∴ ,∴ ,
过点F作 ,交 延长线于点M ,
∴四边形 为平行四边形,
∴ ,
∴ ,
又∵ ,
∴ ,
∴ ,∴ ,
∵四边形 为平行四边形,
∴ , ,∴ ,
∴ .
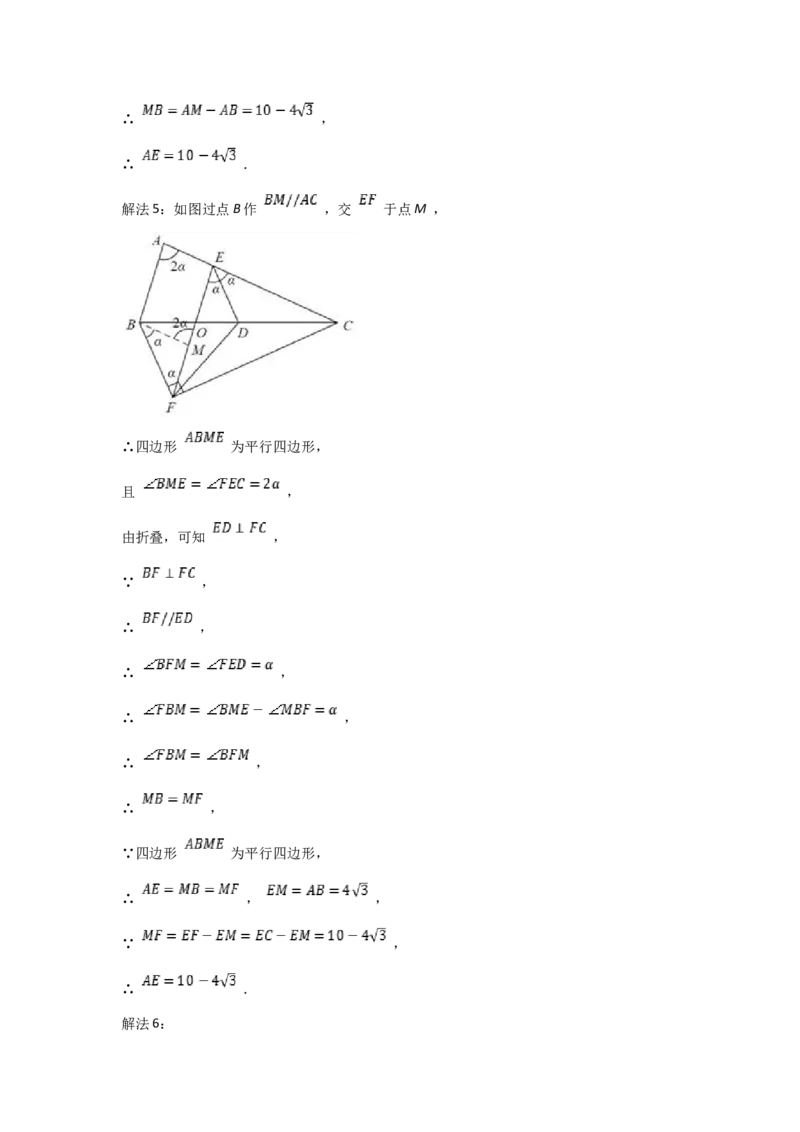
解法5:如图过点B作 ,交 于点M ,
∴四边形 为平行四边形,
且 ,
由折叠,可知 ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ ,
∵四边形 为平行四边形,
∴ , ,
∵ ,
∴ .
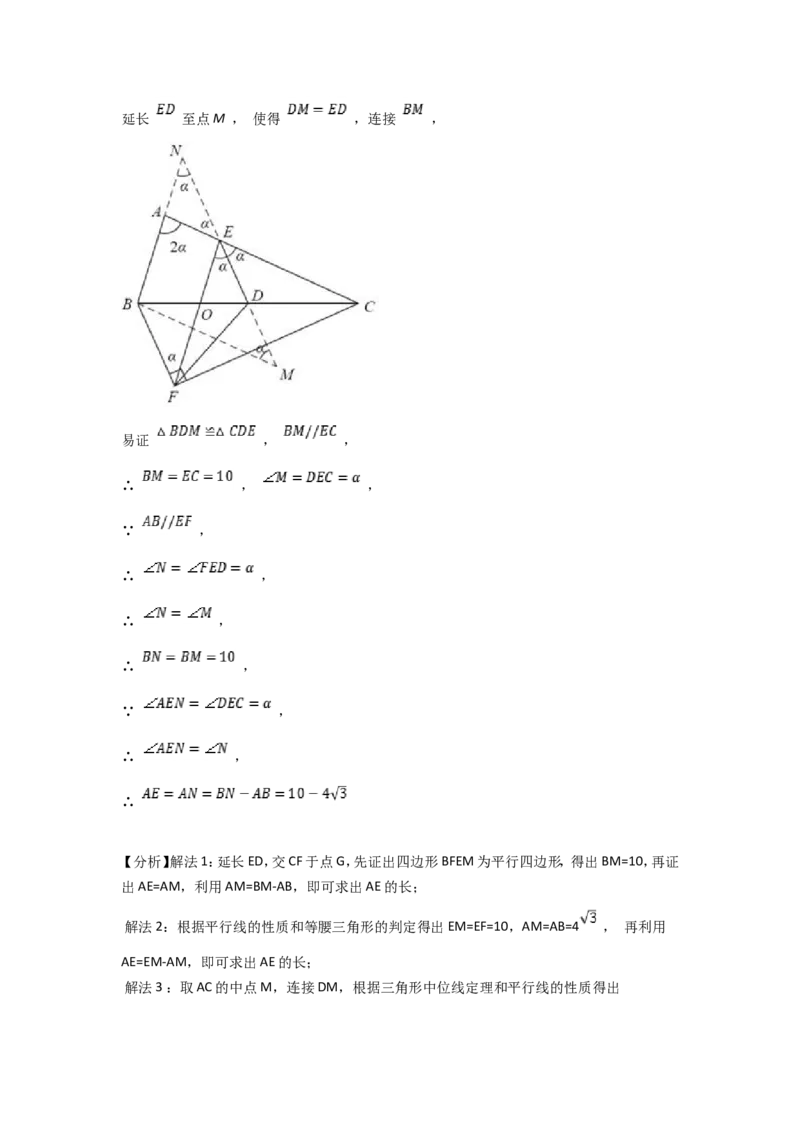
解法6:延长 至点M , 使得 ,连接 ,
易证 , ,
∴ , ,
∵ ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴
【 分析】解法1:延长ED,交CF于点G,先证出四边形BFEM为平行四边形,得出BM=10,再证
出AE=AM,利用AM=BM-AB,即可求出AE的长;
解法2:根据平行线的性质和等腰三角形的判定得出EM=EF=10,AM=AB=4 , 再利用
AE=EM-AM,即可求出AE的长;
解法3 :取AC的中点M,连接DM,根据三角形中位线定理和平行线的性质得出∠MED=∠MDE,得出EM=MD=2 , 从而求出AM的长,利用AE=AM-EM,即可求出AE的
长;
解法4:先证出四边形AMFE为平行四边形,得出AM=EF=EC=10,AE=MF=MB,利用MB=AM-
AB , 即可求出AE的长;
解法5:过点B作BM∥AC,交EF于点M,先证出四边形ABME为平行四边形,得出
AE=MB=MF,EM=AB=4 , 利用MF=EF-EM=EC-EM, 即可求出AE的长;
解法6:延长ED至点M,使得DM=ED ,连接BM,根据等角对等边证出BN=BM=10,AE=AN ,
利用AN=BN-AB,即可求出AE的长.
三、解答题(共55分)
16.【答案】 解:原式
当 时,原式
【考点】分式的混合运算,利用分式运算化简求值
【解析】【分析】先根据分式的混合运算顺序和运算法则化简原式,再把x的值代入进行计算,
即可得出答案.
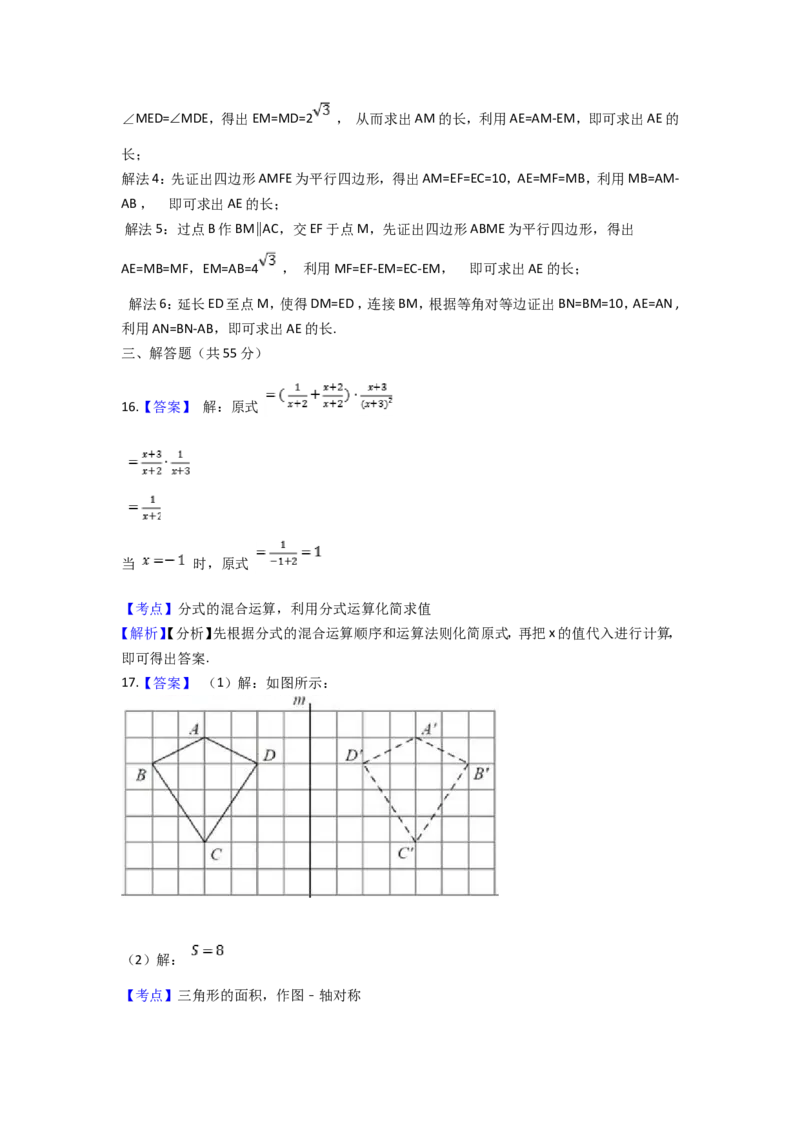
17.【答案】 (1)解:如图所示 :
(2)解:
【考点】三角形的面积,作图﹣轴对称【解析】【解答】(2)S =S +S = .
四边形ABCD △ACB △ACD
【 分析】(1) 分别作出点A、B、C、D关于直线m的对称点A′、B′、C′、D′,顺次连接各点即可;
(2)利用S =S +S = , 即可得出答案.
四边形ABCD △ACB △ACD
18.【答案】 (1)4;2
(2) ,
∴ 良的占比为50%;
(3) ,
∴ 差的圆心角为24°;
(4)9;100
【考点】用样本估计总体,频数(率)分布表,扇形统计 图
【解析】【解答】解:(1)∵m+15+9+n=30,
∴m+n=6,
∵m,n为整数,m>n,
∴m=5,n=1或m=4,n=2,
∵m:n=2:1,
∴m=4,n=2,
故答案为:4;2;
(4) ∵空气污染指数为中的有9天,
∴ ≈109(天),
∴ 估测该城市一年(以365天计)中大约有109天.
【分析】(1)根据题意得出m+n=6,结合扇形统计图中优与差的占比得出m=4,n=2;
(2)利用良的占比= , 即可得出答案;
(3)利用差的圆心角=差的占比×360°,即可得出答案;( 4)根据频数分布表得出空气污染指数为中的有9天,求出中的占比,再乘以365,即可得出
答案.
19.【答案】 (1)证明:连接 ,∵A、D、C、B四点共圆
∴
又
∴
又
∴
∴ ,又
∴四边形 为平行四边形
∴
(2)解:∵ ,∴
又∵ ,∴
又∵ ,即
∴ ,∴
【考点】平行四边形的判定与性质,圆心角、弧、弦的关系,圆周角定理,圆内接四边形的性
质,相似三角形的判定与性质
【解析】【分析】(1)根据圆内接四边形的性质得出∠BAD=∠BCE,根据圆周角定理得出
∠BAD=∠ABC,从而得出∠ABC=∠BCE,证出AB∥CD,从而证出四边形ACEB是平行四边形,即
可得出∠BAC=∠E;
(2)根据等弧所对的弦相等得出CD=BD=3,20.【答案】 (1)解:
(2)解:
【考点】一次函数的实际应用,二次函数的实际应用-销售问题
【解析】【解答】解:(1) 设y与x的函数关系式为y=kx+b,
当x=10时,y=40,当x=12时,y=30,
∴ ,
解得 ,
∴y与x的函数关系式为y=-5x+90;
(2)设利润为w万元,
∴w=(x-8)(-5x+90)=-5x2+130x-720=-5(x-13)2+125,
∴当x=13时,w有最大值,最大值为125,
∴当销售单价为13元时,有最大利润,最大利润为125万元.
【分析】(1)设y与x的函数关系式为y=kx+b,利用待定系数法求出函数的表达式即可;
( 2)设利润为w万元,根据利润=一件的利润×销售量,得出二次函数,再根据二次函数的性
质求解即可.
21.【答案】 (1)不存在
(2)解:a存在;
∵ 的判别式 ,方程有两组正数解,故存在;
从图像来看, : , : 在第一象限有两个交点,故存在;
b设新矩形长和宽为x、y,则依题意 , ,联立 得
,
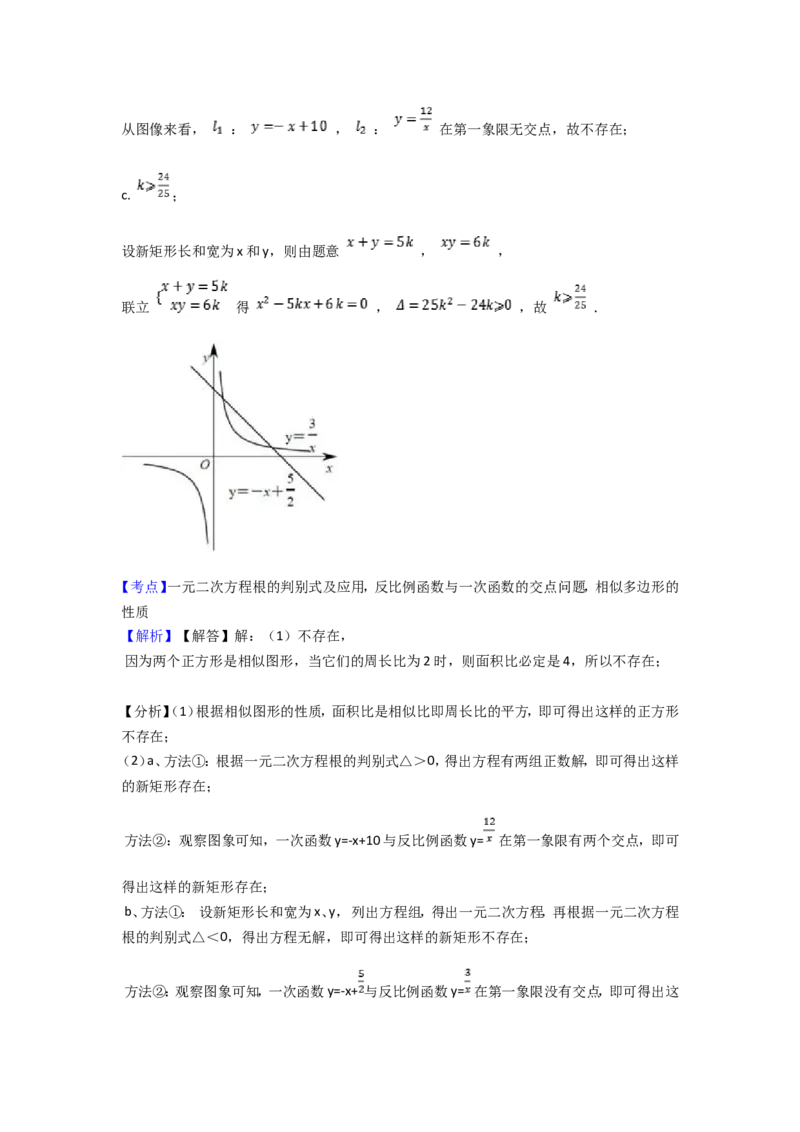
因为 ,此方程无解,故这样的新矩形不存在;从图像来看, : , : 在第一象限无交点,故不存在;
c. ;
设新矩形长和宽为x和y,则由题意 , ,
联立 得 , ,故 .
【考点】一元二次方程根的判别式及应用,反比例函数与一次函数的交点问题,相似多边形的
性质
【解析】【解答】解:(1)不存在,
因为两个正方形是相似图形,当它们的周长比为2时,则面积比必定是4,所以不存在;
【 分析】(1)根据相似图形的性质,面积比是相似比即周长比的平方,即可得出这样的正方形
不存在;
(2)a、方法①:根据一元二次方程根的判别式△>0,得出方程有两组正数解,即可得出这样
的新矩形存在;
方法②:观察图象可知,一次函数y=-x+10与反比例函数y= 在第一象限有两个交点,即可
得出这样的新矩形存在;
b、方法①: 设新矩形长和宽为x、y, 列出方程组,得出一元二次方程,再根据一元二次方程
根的判别式△<0,得出方程无解,即可得出这样的新矩形不存在;
方法②:观察图象可知,一次函数y=-x+ 与反比例函数y= 在第一象限没有交点,即可得出这样的新矩形不存在;
c、方法①: 设新矩形长和宽为x、y, 列出方程组,得出一元二次方程,再根据一元二次方程
根的判别式△≥0,求出k的取值范围,即可得出答案.
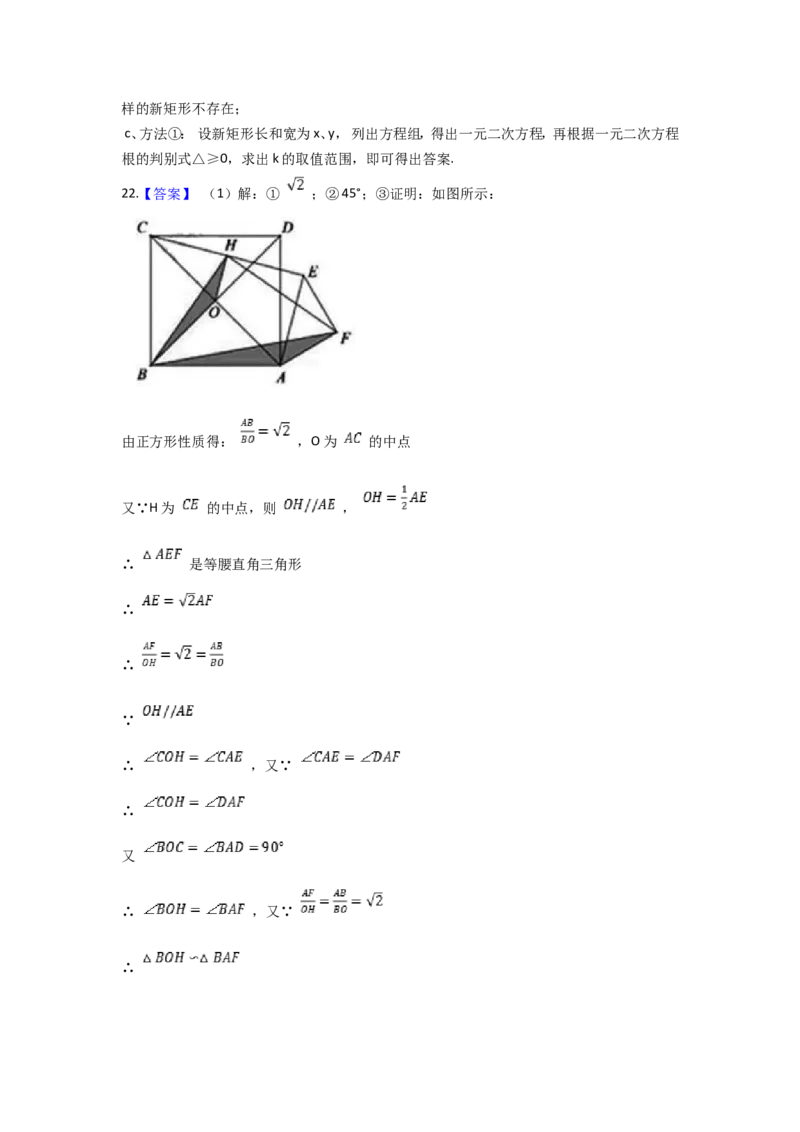
22.【答案】 (1)解:① ;②45°;③证明:如图所示 :
由正方形性质得: ,O为 的中点
又∵H为 的中点,则 ,
∴ 是等腰直角三角形
∴
∴
∵
∴ ,又∵
∴
又
∴ ,又∵
∴∴ ,
∴
(2) ;
【考点】勾股定理,平行四边形的判定与性质,相似三角形的判定与性质,锐角三角函数的定
义
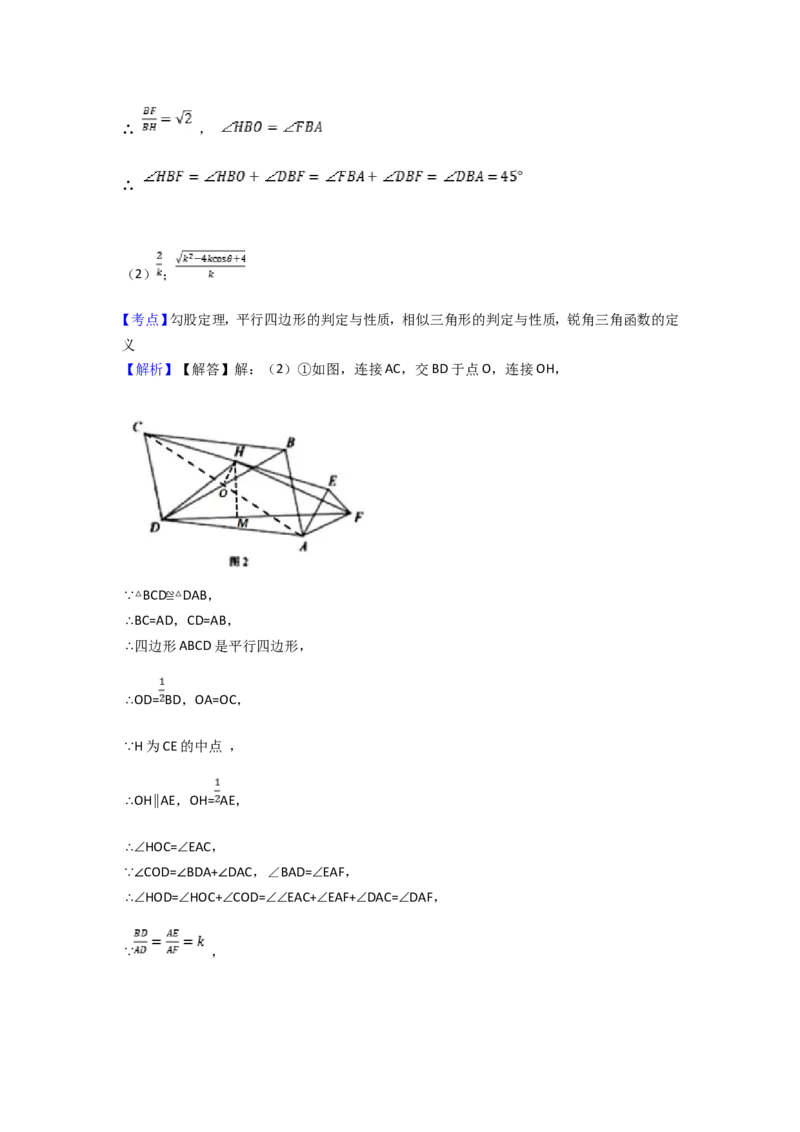
【解析】【解答】解:(2)①如图,连接AC,交BD于点O,连接OH,
∵△BCD≌△DAB,
∴BC=AD,CD=AB,
∴四边形ABCD是平行四边形,
∴OD= BD,OA=OC,
∵H为CE的中点 ,
∴OH∥AE,OH= AE,
∴∠HOC=∠EAC,
∵∠COD=∠BDA+∠DAC,∠BAD=∠EAF,
∴∠HOD=∠HOC+∠COD=∠∠EAC+∠EAF+∠DAC=∠DAF,
∵ ,∴ , ,
∴△DAF∽△DOH,
∴ ,
故答案为: ;
②如图,过点H作HM⊥DF于点M,
∴∠HMD=∠HMF=90°,
∵△DAF∽△DOH,
∴∠HDO=∠ADF,
∴∠HDF=∠HOD+∠ODF=∠ADF+∠ODF=∠BDA= ,
∴HM=OH· , DM=OH· ,
∵ ,
∴FD= ,
∵HF2=HM2+MF2=HM2+(DF-DM)2 ,
=(OH· )2+( -OH· )2 ,
= ,
∴ ,
故答案为:【分析】(1)①先证出 , ∠BOH=∠BAF,从而得出△DAF∽△DOH,即可得出
;
②根据△DAF∽△DOH,得出∠HBO=∠FBA,利用∠HBF=∠HBO+∠DBF=∠DBA=45°,即可得出答
案;
(2)①连接AC,交BD于点O,连接OH,先证出∠HOD=∠DAF, , 从而得出
△DAF∽△DOH,即可得出 ;
②过点H作HM⊥DF于点M,先证出∠HDF= , 再根据锐角三角函数定义得出HM=OH·
, DM=OH· , 由 , 得出FD= , 利用勾股定理得出HF2=HM2+(DF-DM)2
, 代入进行化简,求出HF2= , 即可求出 .