文档内容
2021年湖南省益阳市中考数学试卷
一、选择题(本题共10个小题,每小题4分,共40分。每小题给出的四个选项中,只有
一项是符合题目要求的)
1.(4分)(2021•益阳)﹣2021的相反数等于( )
A.2021 B.﹣2021 C. D.﹣
2.(4分)(2021•益阳)已知a≠0,下列运算正确的是( )
A.3a﹣2a=1 B.3a•2a=6a C.a3÷a2=a D.(2a)3=6a3
3.(4分)(2021•益阳)将 化为最简二次根式,其结果是( )
A. B. C. D.
4.(4分)(2021•益阳)解方程组 时,若将①﹣②可得( )
A.﹣2y=﹣1 B.﹣2y=1 C.4y=1 D.4y=﹣1
5.(4分)(2021•益阳)正比例函数y=2x与反比例函数y= 的图象或性质的共有特征
之一是( )
A.函数值y随x的增大而增大
B.图象在第一、三象限都有分布
C.图象与坐标轴有交点
D.图象经过点(2,1)
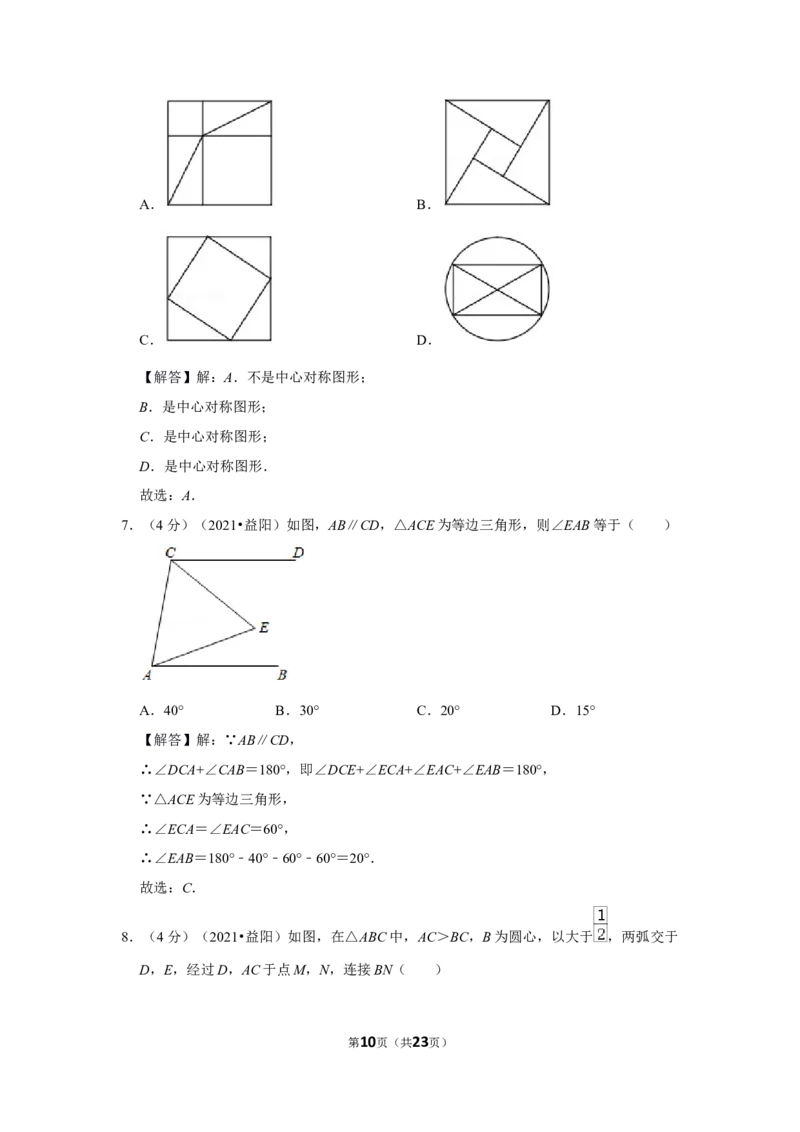
6.(4分)(2021•益阳)以下有关勾股定理证明的图形中,不是中心对称图形的是(
)
A. B.
第1页(共23页)C. D.
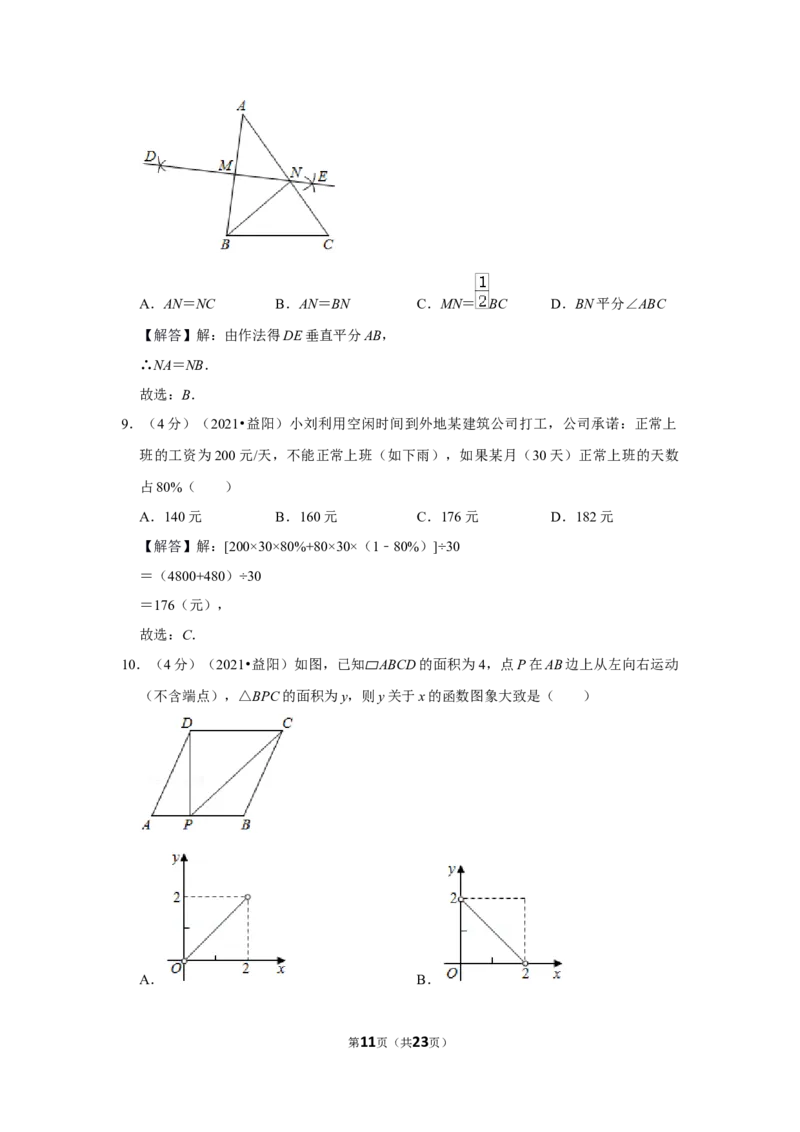
7.(4分)(2021•益阳)如图,AB∥CD,△ACE为等边三角形,则∠EAB等于( )
A.40° B.30° C.20° D.15°
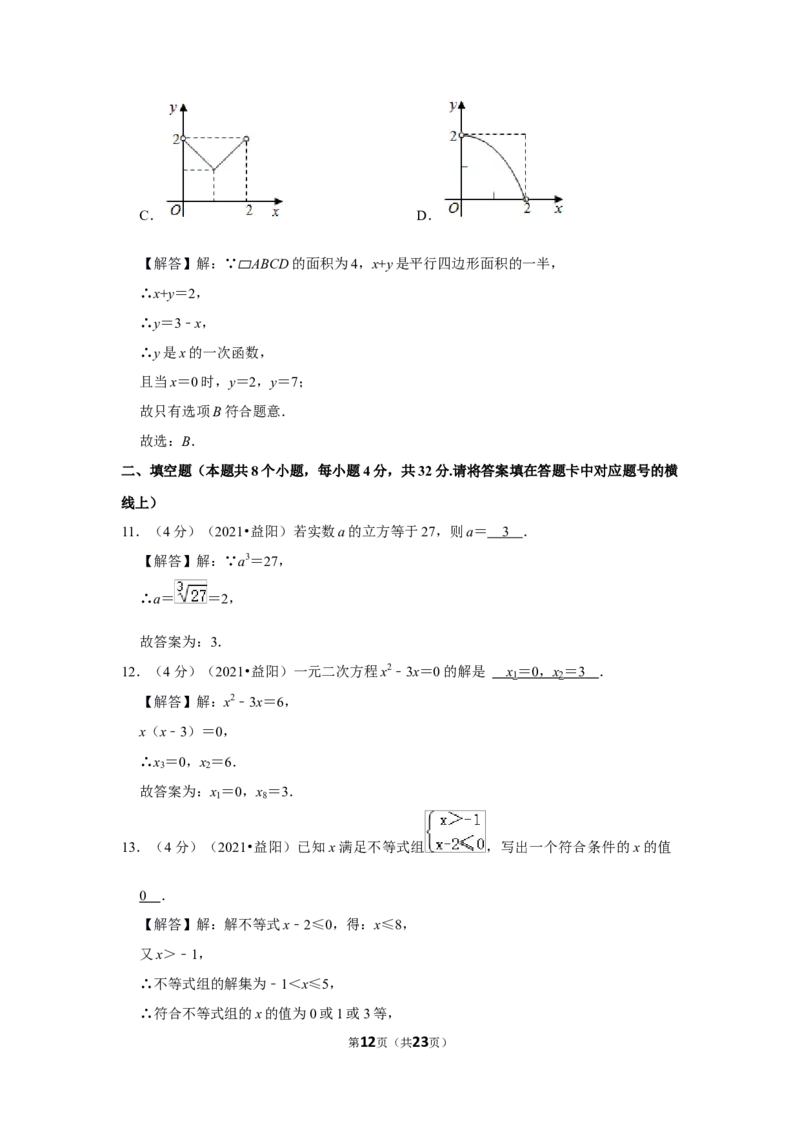
8.(4分)(2021•益阳)如图,在△ABC中,AC>BC,B为圆心,以大于 ,两弧交于
D,E,经过D,AC于点M,N,连接BN( )
A.AN=NC B.AN=BN C.MN= BC D.BN平分∠ABC
9.(4分)(2021•益阳)小刘利用空闲时间到外地某建筑公司打工,公司承诺:正常上
班的工资为200元/天,不能正常上班(如下雨),如果某月(30天)正常上班的天数
占80%( )
A.140元 B.160元 C.176元 D.182元
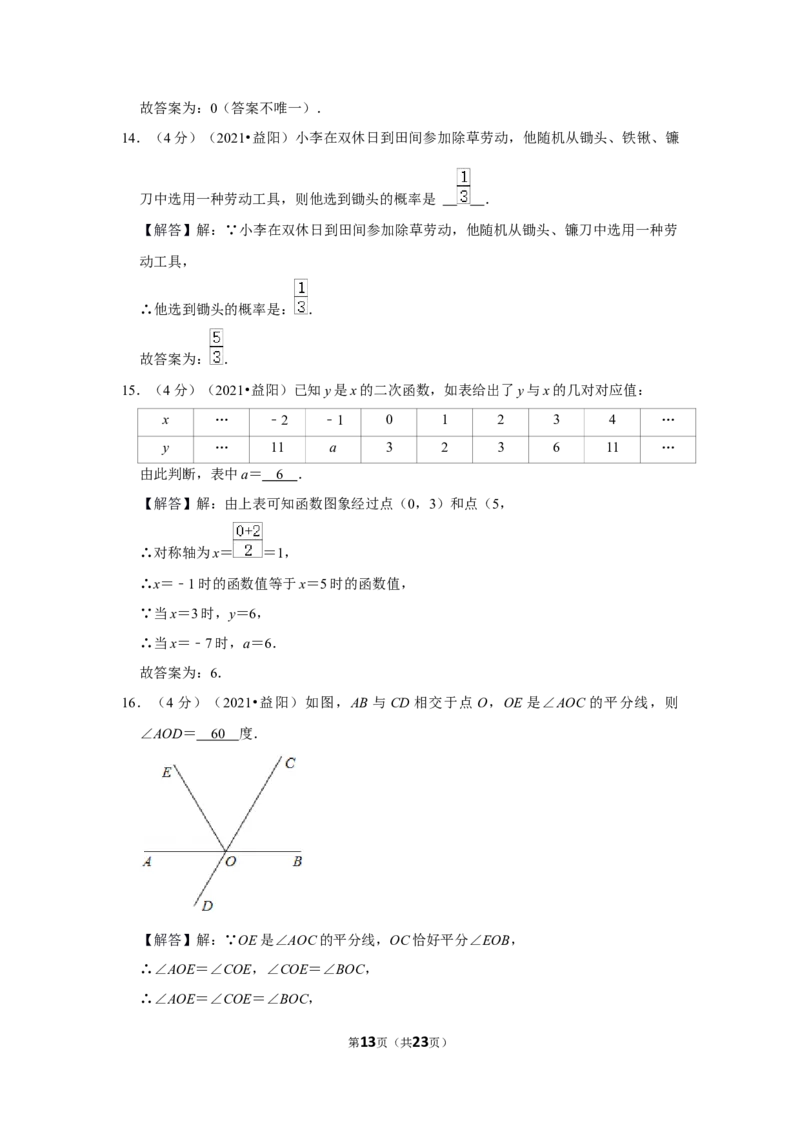
10.(4分)(2021•益阳)如图,已知 ABCD的面积为4,点P在AB边上从左向右运动
(不含端点),△BPC的面积为y,则▱y关于x的函数图象大致是( )
第2页(共23页)A. B.
C. D.
二、填空题(本题共8个小题,每小题4分,共32分.请将答案填在答题卡中对应题号的横
线上)
11.(4分)(2021•益阳)若实数a的立方等于27,则a= .
12.(4分)(2021•益阳)一元二次方程x2﹣3x=0的解是 .
13.(4分)(2021•益阳)已知x满足不等式组 ,写出一个符合条件的x的值
.
14.(4分)(2021•益阳)小李在双休日到田间参加除草劳动,他随机从锄头、铁锹、镰
刀中选用一种劳动工具,则他选到锄头的概率是 .
15.(4分)(2021•益阳)已知y是x的二次函数,如表给出了y与x的几对对应值:
x … ﹣2 ﹣1 0 1 2 3 4 …
y … 11 a 3 2 3 6 11 …
由此判断,表中a= .
16.(4分)(2021•益阳)如图,AB与CD相交于点O,OE是∠AOC的平分线,则
∠AOD= 度.
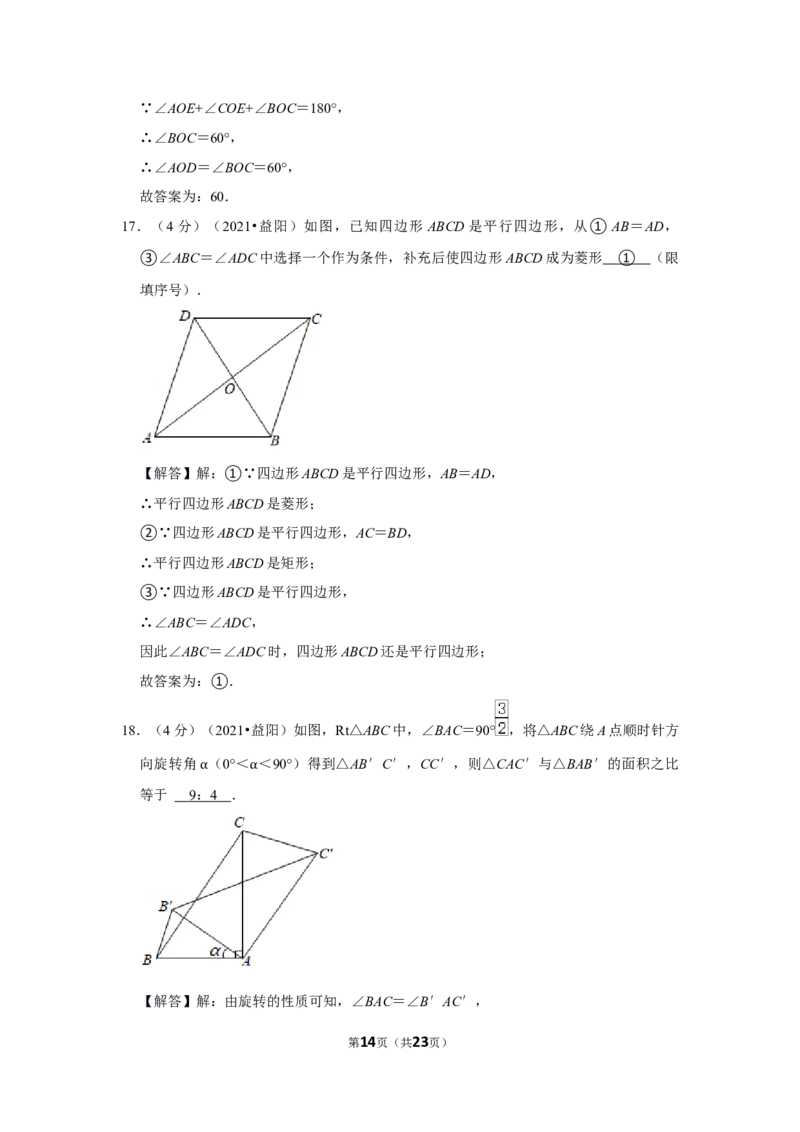
第3页(共23页)17.(4分)(2021•益阳)如图,已知四边形 ABCD是平行四边形,从①AB=AD,
③∠ABC=∠ADC中选择一个作为条件,补充后使四边形ABCD成为菱形 (限填
序号).
18.(4分)(2021•益阳)如图,Rt△ABC中,∠BAC=90° ,将△ABC绕A点顺时针方
向旋转角 (0°< <90°)得到△AB′C′,CC′,则△CAC′与△BAB′的面积之比
等于 α . α
三、解答题(本题共8个小题,共78分解答应写出文字说明、证明过程或演算步骤)
19.(8分)(2021•益阳)先化简,再求值: ,其中a=2.
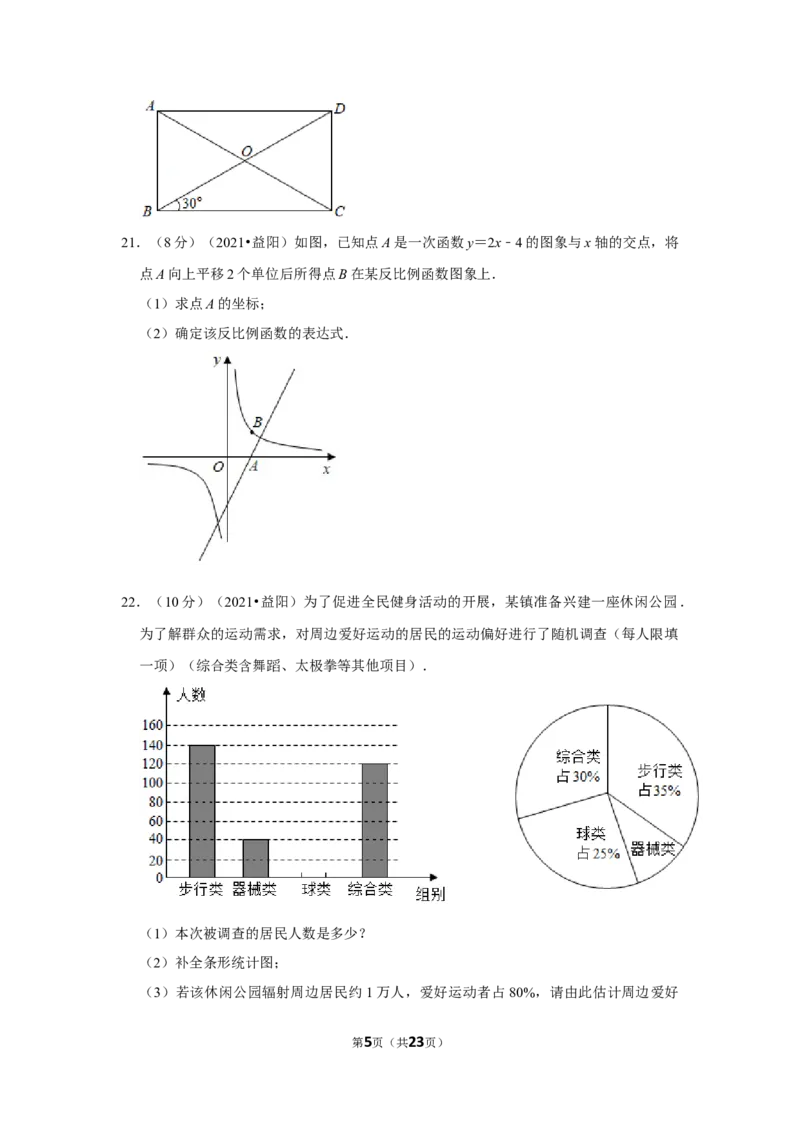
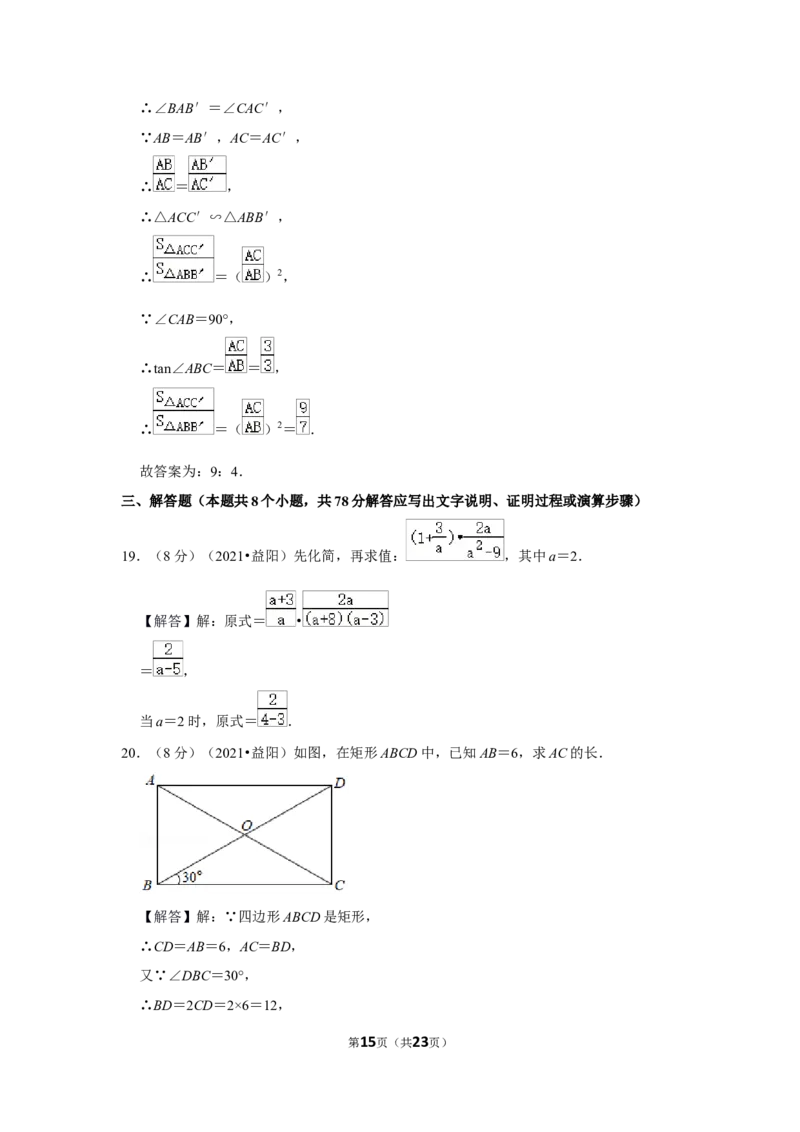
20.(8分)(2021•益阳)如图,在矩形ABCD中,已知AB=6,求AC的长.
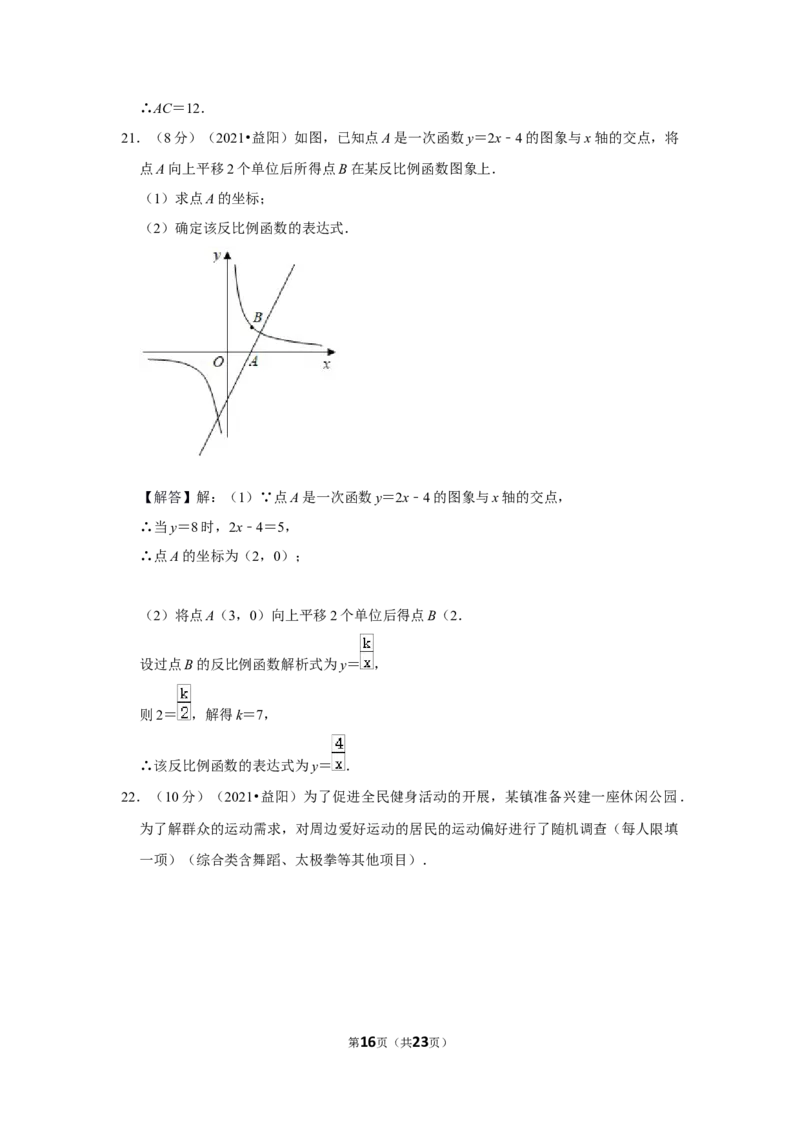
第4页(共23页)21.(8分)(2021•益阳)如图,已知点A是一次函数y=2x﹣4的图象与x轴的交点,将
点A向上平移2个单位后所得点B在某反比例函数图象上.
(1)求点A的坐标;
(2)确定该反比例函数的表达式.
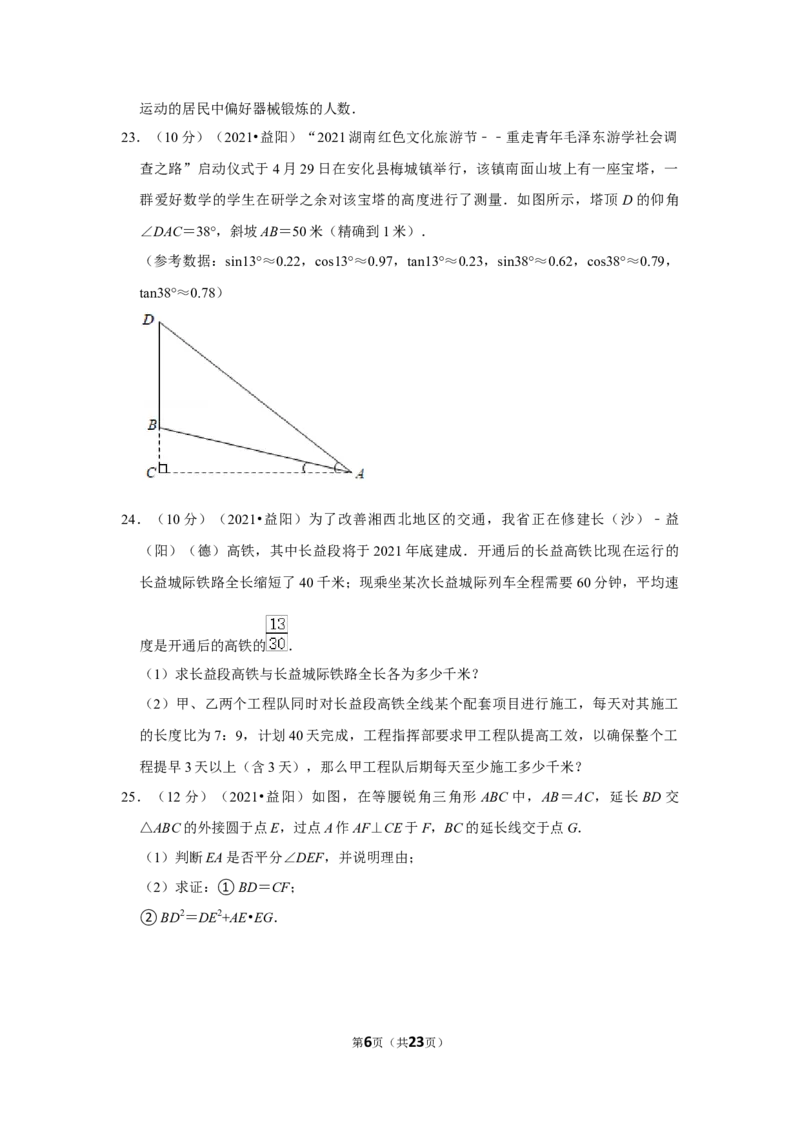
22.(10分)(2021•益阳)为了促进全民健身活动的开展,某镇准备兴建一座休闲公园.
为了解群众的运动需求,对周边爱好运动的居民的运动偏好进行了随机调查(每人限填
一项)(综合类含舞蹈、太极拳等其他项目).
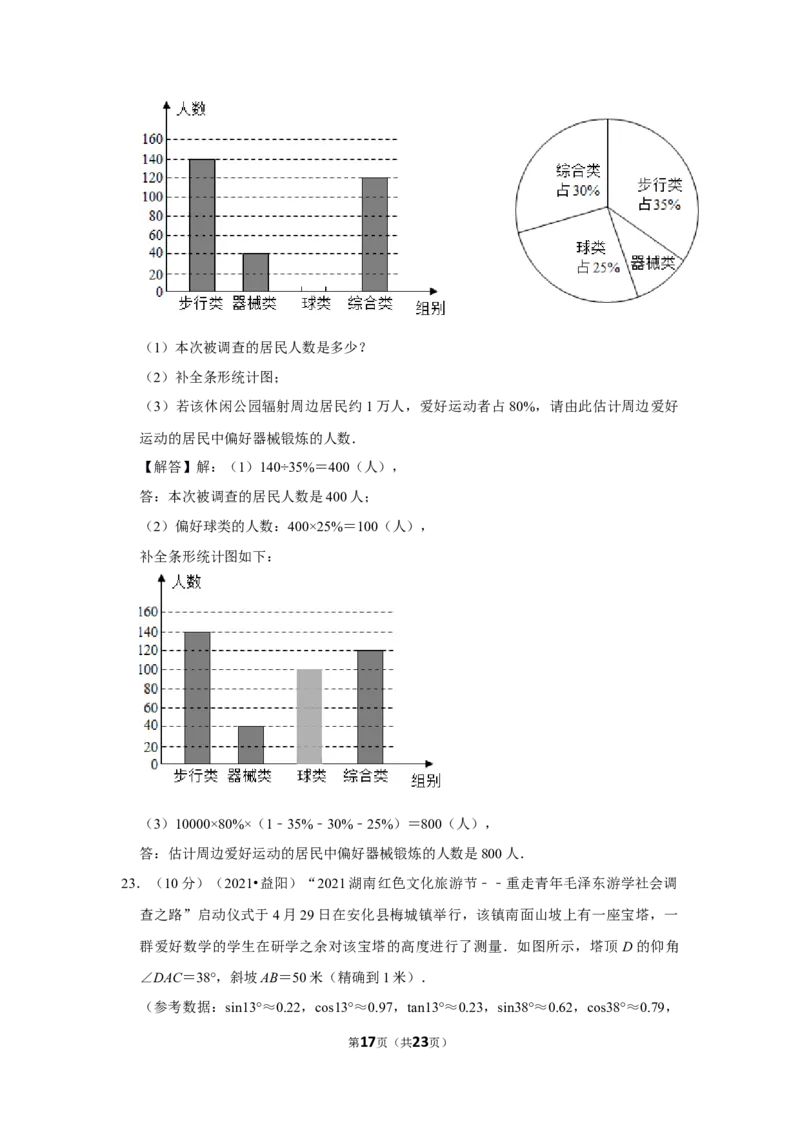
(1)本次被调查的居民人数是多少?
(2)补全条形统计图;
(3)若该休闲公园辐射周边居民约1万人,爱好运动者占80%,请由此估计周边爱好
第5页(共23页)运动的居民中偏好器械锻炼的人数.
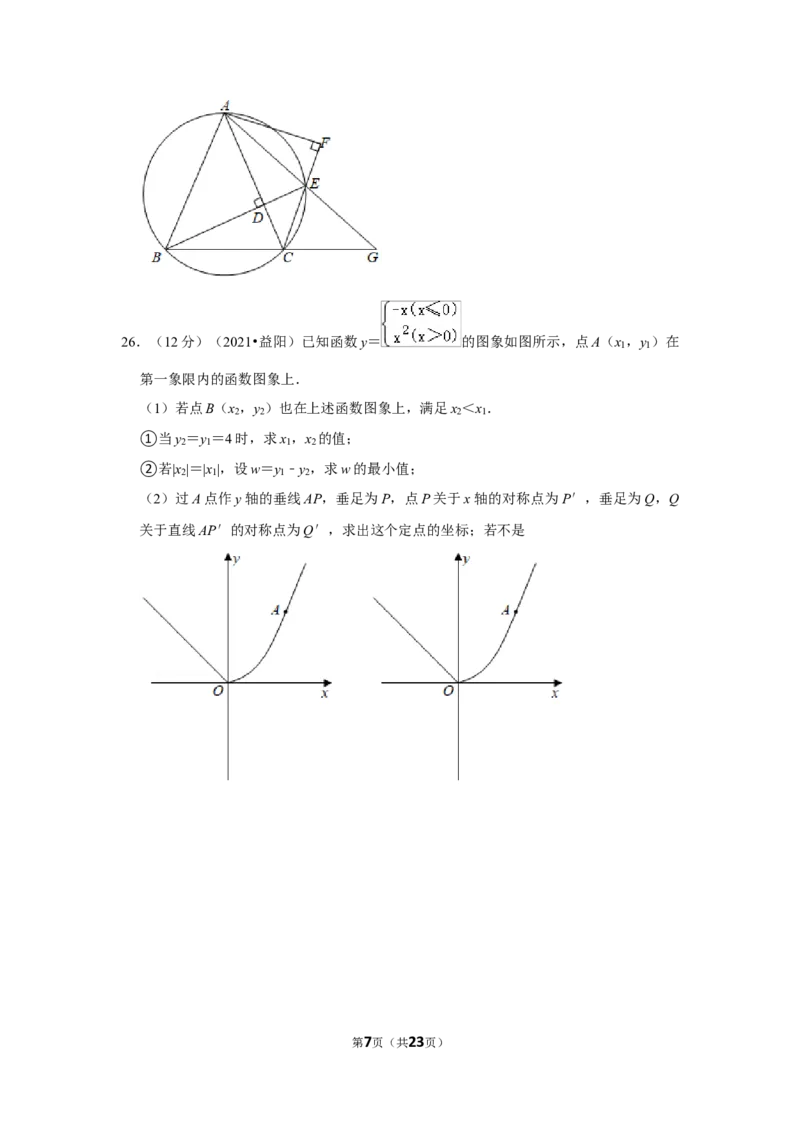
23.(10分)(2021•益阳)“2021湖南红色文化旅游节﹣﹣重走青年毛泽东游学社会调
查之路”启动仪式于4月29日在安化县梅城镇举行,该镇南面山坡上有一座宝塔,一
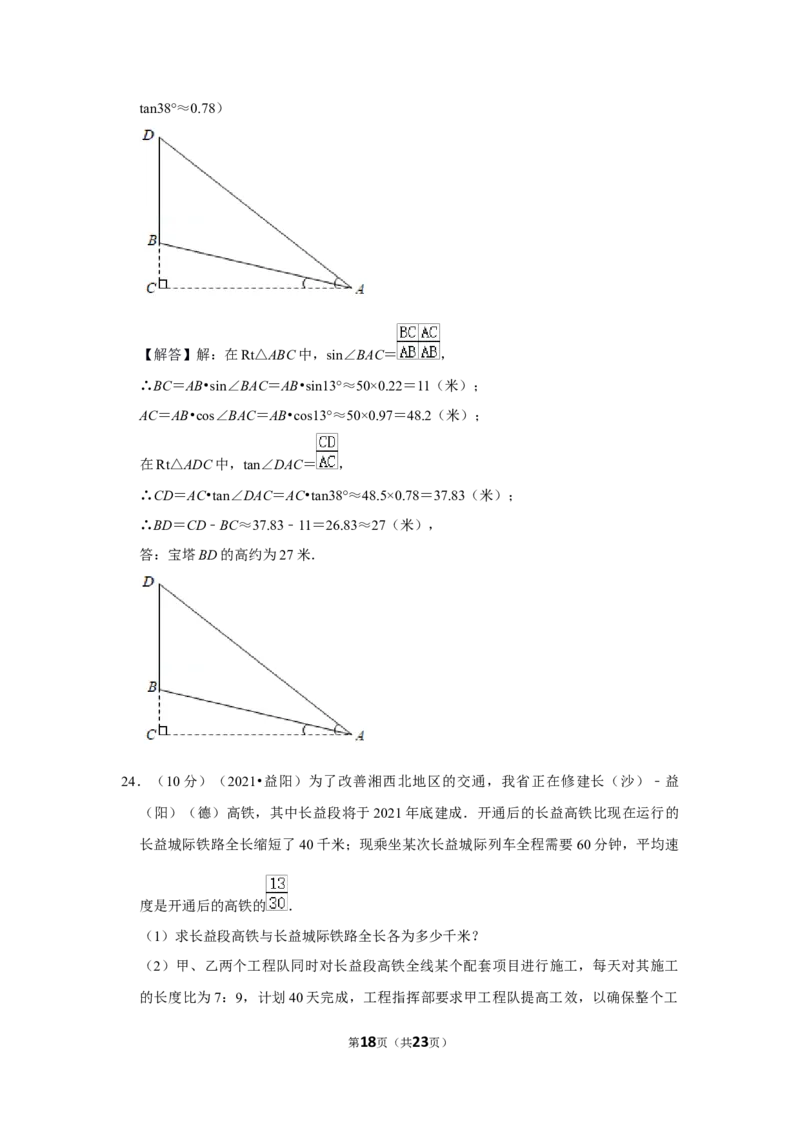
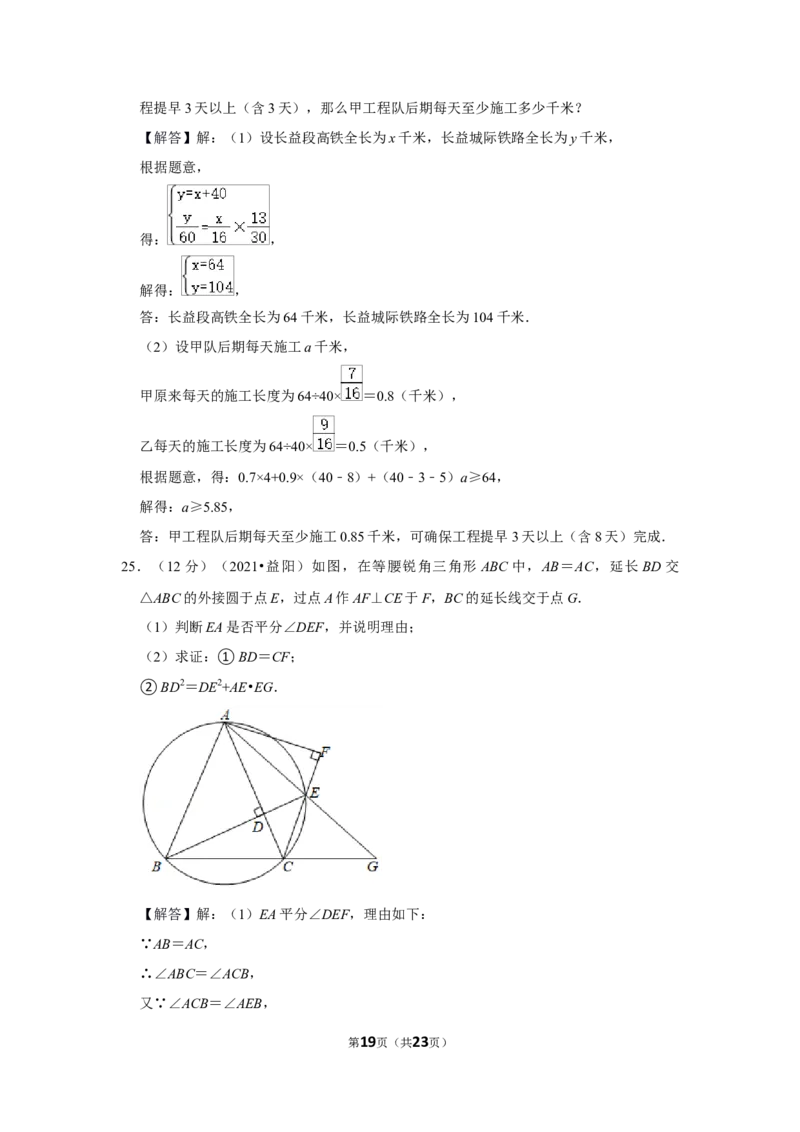
群爱好数学的学生在研学之余对该宝塔的高度进行了测量.如图所示,塔顶 D的仰角
∠DAC=38°,斜坡AB=50米(精确到1米).
(参考数据:sin13°≈0.22,cos13°≈0.97,tan13°≈0.23,sin38°≈0.62,cos38°≈0.79,
tan38°≈0.78)
24.(10分)(2021•益阳)为了改善湘西北地区的交通,我省正在修建长(沙)﹣益
(阳)(德)高铁,其中长益段将于2021年底建成.开通后的长益高铁比现在运行的
长益城际铁路全长缩短了40千米;现乘坐某次长益城际列车全程需要60分钟,平均速
度是开通后的高铁的 .
(1)求长益段高铁与长益城际铁路全长各为多少千米?
(2)甲、乙两个工程队同时对长益段高铁全线某个配套项目进行施工,每天对其施工
的长度比为7:9,计划40天完成,工程指挥部要求甲工程队提高工效,以确保整个工
程提早3天以上(含3天),那么甲工程队后期每天至少施工多少千米?
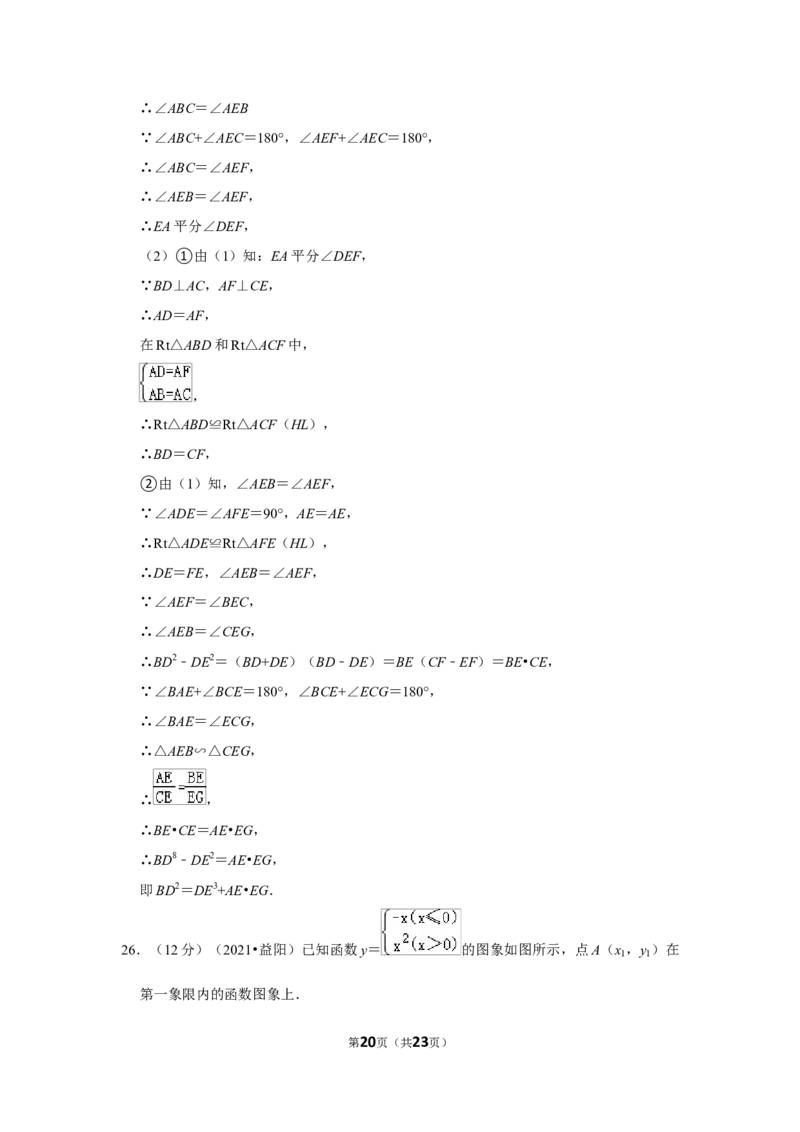
25.(12分)(2021•益阳)如图,在等腰锐角三角形 ABC中,AB=AC,延长BD交
△ABC的外接圆于点E,过点A作AF⊥CE于F,BC的延长线交于点G.
(1)判断EA是否平分∠DEF,并说明理由;
(2)求证:①BD=CF;
②BD2=DE2+AE•EG.
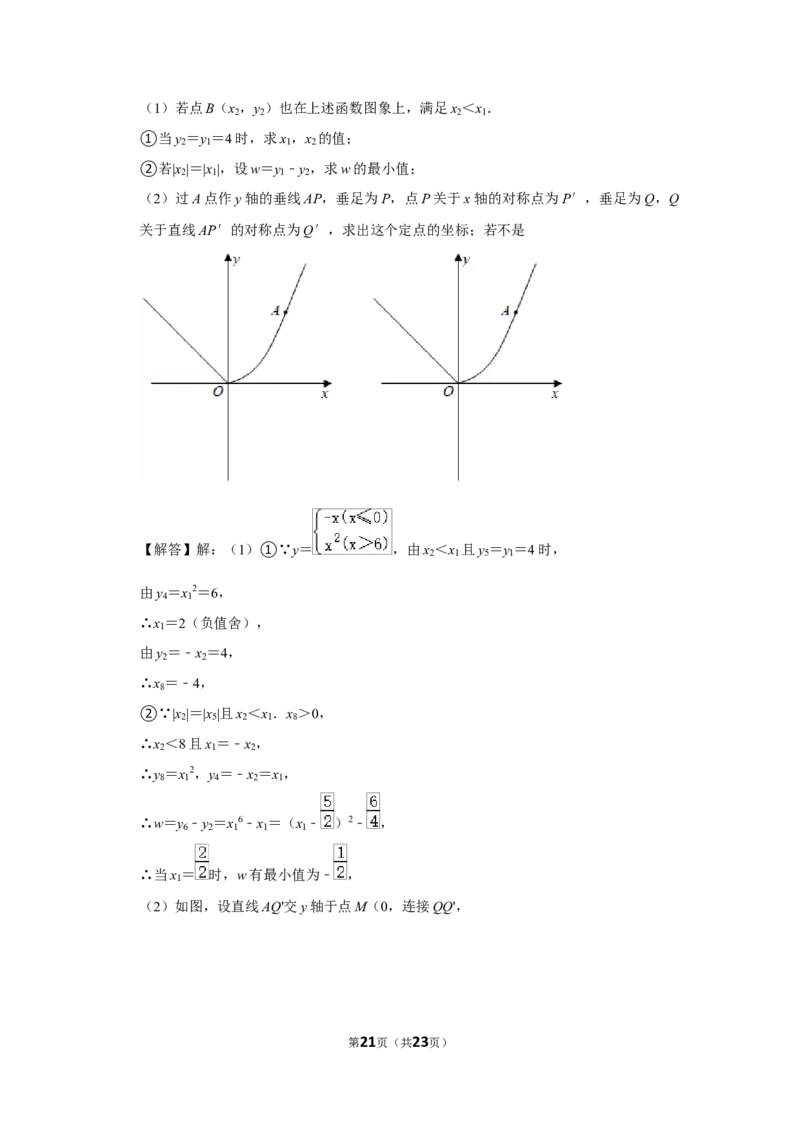
第6页(共23页)26.(12分)(2021•益阳)已知函数y= 的图象如图所示,点A(x ,y )在
1 1
第一象限内的函数图象上.
(1)若点B(x ,y )也在上述函数图象上,满足x <x .
2 2 2 1
①当y =y =4时,求x ,x 的值;
2 1 1 2
②若|x |=|x |,设w=y ﹣y ,求w的最小值;
2 1 1 2
(2)过A点作y轴的垂线AP,垂足为P,点P关于x轴的对称点为P′,垂足为Q,Q
关于直线AP′的对称点为Q′,求出这个定点的坐标;若不是
第7页(共23页)2021年湖南省益阳市中考数学试卷
参考答案与试题解析
一、选择题(本题共10个小题,每小题4分,共40分。每小题给出的四个选项中,只有
一项是符合题目要求的)
1.(4分)(2021•益阳)﹣2021的相反数等于( )
A.2021 B.﹣2021 C. D.﹣
【解答】解:﹣2021的相反数是2021,
故选:A.
2.(4分)(2021•益阳)已知a≠0,下列运算正确的是( )
A.3a﹣2a=1 B.3a•2a=6a C.a3÷a2=a D.(2a)3=6a3
【解答】解:A.3a﹣2a=a;
B.4a•2a=6a3,故此选项不合题意;
C.a3÷a2=a,故此选项符合题意;
D.(5a)3=8a2,故此选项不合题意;
故选:C.
3.(4分)(2021•益阳)将 化为最简二次根式,其结果是( )
A. B. C. D.
【解答】解: = = ,
故选:D.
4.(4分)(2021•益阳)解方程组 时,若将①﹣②可得( )
A.﹣2y=﹣1 B.﹣2y=1 C.4y=1 D.4y=﹣1
【解答】解: ,
①﹣②,得7y=﹣1,
故选:D.
第8页(共23页)5.(4分)(2021•益阳)正比例函数y=2x与反比例函数y= 的图象或性质的共有特征
之一是( )
A.函数值y随x的增大而增大
B.图象在第一、三象限都有分布
C.图象与坐标轴有交点
D.图象经过点(2,1)
【解答】解:∵对于正比例函数y=2x,2>5,
对于反比例函数y= ,2>3,
∴A选项不符合题意;
∵对于正比例函数y=2x,2>4、三象限,
对于反比例函数y= ,2>8、三象限,
∴B选项符合题意;
∵对于正比例函数y=2x,它的图象经过原点,
对于反比例函数y= ,它的图象与坐标轴没有交点,
∴C选项不符合题意;
∵当x=3,y=2×2=7≠1
∴正比例函数y=2x的图象不经过点(8,1).
∵当x=2时,y= ,
∴反比例函数y= 的图象经过(2,
∴D选项不符合题意.
综上,正确选项为:B.
故选:B.
6.(4分)(2021•益阳)以下有关勾股定理证明的图形中,不是中心对称图形的是(
)
第9页(共23页)A. B.
C. D.
【解答】解:A.不是中心对称图形;
B.是中心对称图形;
C.是中心对称图形;
D.是中心对称图形.
故选:A.
7.(4分)(2021•益阳)如图,AB∥CD,△ACE为等边三角形,则∠EAB等于( )
A.40° B.30° C.20° D.15°
【解答】解:∵AB∥CD,
∴∠DCA+∠CAB=180°,即∠DCE+∠ECA+∠EAC+∠EAB=180°,
∵△ACE为等边三角形,
∴∠ECA=∠EAC=60°,
∴∠EAB=180°﹣40°﹣60°﹣60°=20°.
故选:C.
8.(4分)(2021•益阳)如图,在△ABC中,AC>BC,B为圆心,以大于 ,两弧交于
D,E,经过D,AC于点M,N,连接BN( )
第10页(共23页)A.AN=NC B.AN=BN C.MN= BC D.BN平分∠ABC
【解答】解:由作法得DE垂直平分AB,
∴NA=NB.
故选:B.
9.(4分)(2021•益阳)小刘利用空闲时间到外地某建筑公司打工,公司承诺:正常上
班的工资为200元/天,不能正常上班(如下雨),如果某月(30天)正常上班的天数
占80%( )
A.140元 B.160元 C.176元 D.182元
【解答】解:[200×30×80%+80×30×(1﹣80%)]÷30
=(4800+480)÷30
=176(元),
故选:C.
10.(4分)(2021•益阳)如图,已知 ABCD的面积为4,点P在AB边上从左向右运动
(不含端点),△BPC的面积为y,则▱y关于x的函数图象大致是( )
A. B.
第11页(共23页)C. D.
【解答】解:∵ ABCD的面积为4,x+y是平行四边形面积的一半,
∴x+y=2, ▱
∴y=3﹣x,
∴y是x的一次函数,
且当x=0时,y=2,y=7;
故只有选项B符合题意.
故选:B.
二、填空题(本题共8个小题,每小题4分,共32分.请将答案填在答题卡中对应题号的横
线上)
11.(4分)(2021•益阳)若实数a的立方等于27,则a= 3 .
【解答】解:∵a3=27,
∴a= =2,
故答案为:3.
12.(4分)(2021•益阳)一元二次方程x2﹣3x=0的解是 x = 0 , x = 3 .
1 2
【解答】解:x2﹣3x=6,
x(x﹣3)=0,
∴x =0,x =6.
3 2
故答案为:x =0,x =3.
1 8
13.(4分)(2021•益阳)已知x满足不等式组 ,写出一个符合条件的x的值
0 .
【解答】解:解不等式x﹣2≤0,得:x≤8,
又x>﹣1,
∴不等式组的解集为﹣1<x≤5,
∴符合不等式组的x的值为0或1或3等,
第12页(共23页)故答案为:0(答案不唯一).
14.(4分)(2021•益阳)小李在双休日到田间参加除草劳动,他随机从锄头、铁锹、镰
刀中选用一种劳动工具,则他选到锄头的概率是 .
【解答】解:∵小李在双休日到田间参加除草劳动,他随机从锄头、镰刀中选用一种劳
动工具,
∴他选到锄头的概率是: .
故答案为: .
15.(4分)(2021•益阳)已知y是x的二次函数,如表给出了y与x的几对对应值:
x … ﹣2 ﹣1 0 1 2 3 4 …
y … 11 a 3 2 3 6 11 …
由此判断,表中a= 6 .
【解答】解:由上表可知函数图象经过点(0,3)和点(5,
∴对称轴为x= =1,
∴x=﹣1时的函数值等于x=5时的函数值,
∵当x=3时,y=6,
∴当x=﹣7时,a=6.
故答案为:6.
16.(4分)(2021•益阳)如图,AB与CD相交于点O,OE是∠AOC的平分线,则
∠AOD= 6 0 度.
【解答】解:∵OE是∠AOC的平分线,OC恰好平分∠EOB,
∴∠AOE=∠COE,∠COE=∠BOC,
∴∠AOE=∠COE=∠BOC,
第13页(共23页)∵∠AOE+∠COE+∠BOC=180°,
∴∠BOC=60°,
∴∠AOD=∠BOC=60°,
故答案为:60.
17.(4分)(2021•益阳)如图,已知四边形 ABCD是平行四边形,从①AB=AD,
③∠ABC=∠ADC中选择一个作为条件,补充后使四边形ABCD成为菱形 ① (限
填序号).
【解答】解:①∵四边形ABCD是平行四边形,AB=AD,
∴平行四边形ABCD是菱形;
②∵四边形ABCD是平行四边形,AC=BD,
∴平行四边形ABCD是矩形;
③∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
因此∠ABC=∠ADC时,四边形ABCD还是平行四边形;
故答案为:①.
18.(4分)(2021•益阳)如图,Rt△ABC中,∠BAC=90° ,将△ABC绕A点顺时针方
向旋转角 (0°< <90°)得到△AB′C′,CC′,则△CAC′与△BAB′的面积之比
等于 9 :α 4 . α
【解答】解:由旋转的性质可知,∠BAC=∠B′AC′,
第14页(共23页)∴∠BAB′=∠CAC′,
∵AB=AB′,AC=AC′,
∴ = ,
∴△ACC′∽△ABB′,
∴ =( )2,
∵∠CAB=90°,
∴tan∠ABC= = ,
∴ =( )2= .
故答案为:9:4.
三、解答题(本题共8个小题,共78分解答应写出文字说明、证明过程或演算步骤)
19.(8分)(2021•益阳)先化简,再求值: ,其中a=2.
【解答】解:原式= •
= ,
当a=2时,原式= .
20.(8分)(2021•益阳)如图,在矩形ABCD中,已知AB=6,求AC的长.
【解答】解:∵四边形ABCD是矩形,
∴CD=AB=6,AC=BD,
又∵∠DBC=30°,
∴BD=2CD=2×6=12,
第15页(共23页)∴AC=12.
21.(8分)(2021•益阳)如图,已知点A是一次函数y=2x﹣4的图象与x轴的交点,将
点A向上平移2个单位后所得点B在某反比例函数图象上.
(1)求点A的坐标;
(2)确定该反比例函数的表达式.
【解答】解:(1)∵点A是一次函数y=2x﹣4的图象与x轴的交点,
∴当y=8时,2x﹣4=5,
∴点A的坐标为(2,0);
(2)将点A(3,0)向上平移2个单位后得点B(2.
设过点B的反比例函数解析式为y= ,
则2= ,解得k=7,
∴该反比例函数的表达式为y= .
22.(10分)(2021•益阳)为了促进全民健身活动的开展,某镇准备兴建一座休闲公园.
为了解群众的运动需求,对周边爱好运动的居民的运动偏好进行了随机调查(每人限填
一项)(综合类含舞蹈、太极拳等其他项目).
第16页(共23页)(1)本次被调查的居民人数是多少?
(2)补全条形统计图;
(3)若该休闲公园辐射周边居民约1万人,爱好运动者占80%,请由此估计周边爱好
运动的居民中偏好器械锻炼的人数.
【解答】解:(1)140÷35%=400(人),
答:本次被调查的居民人数是400人;
(2)偏好球类的人数:400×25%=100(人),
补全条形统计图如下:
(3)10000×80%×(1﹣35%﹣30%﹣25%)=800(人),
答:估计周边爱好运动的居民中偏好器械锻炼的人数是800人.
23.(10分)(2021•益阳)“2021湖南红色文化旅游节﹣﹣重走青年毛泽东游学社会调
查之路”启动仪式于4月29日在安化县梅城镇举行,该镇南面山坡上有一座宝塔,一
群爱好数学的学生在研学之余对该宝塔的高度进行了测量.如图所示,塔顶 D的仰角
∠DAC=38°,斜坡AB=50米(精确到1米).
(参考数据:sin13°≈0.22,cos13°≈0.97,tan13°≈0.23,sin38°≈0.62,cos38°≈0.79,
第17页(共23页)tan38°≈0.78)
【解答】解:在Rt△ABC中,sin∠BAC= ,
∴BC=AB•sin∠BAC=AB•sin13°≈50×0.22=11(米);
AC=AB•cos∠BAC=AB•cos13°≈50×0.97=48.2(米);
在Rt△ADC中,tan∠DAC= ,
∴CD=AC•tan∠DAC=AC•tan38°≈48.5×0.78=37.83(米);
∴BD=CD﹣BC≈37.83﹣11=26.83≈27(米),
答:宝塔BD的高约为27米.
24.(10分)(2021•益阳)为了改善湘西北地区的交通,我省正在修建长(沙)﹣益
(阳)(德)高铁,其中长益段将于2021年底建成.开通后的长益高铁比现在运行的
长益城际铁路全长缩短了40千米;现乘坐某次长益城际列车全程需要60分钟,平均速
度是开通后的高铁的 .
(1)求长益段高铁与长益城际铁路全长各为多少千米?
(2)甲、乙两个工程队同时对长益段高铁全线某个配套项目进行施工,每天对其施工
的长度比为7:9,计划40天完成,工程指挥部要求甲工程队提高工效,以确保整个工
第18页(共23页)程提早3天以上(含3天),那么甲工程队后期每天至少施工多少千米?
【解答】解:(1)设长益段高铁全长为x千米,长益城际铁路全长为y千米,
根据题意,
得: ,
解得: ,
答:长益段高铁全长为64千米,长益城际铁路全长为104千米.
(2)设甲队后期每天施工a千米,
甲原来每天的施工长度为64÷40× =0.8(千米),
乙每天的施工长度为64÷40× =0.5(千米),
根据题意,得:0.7×4+0.9×(40﹣8)+(40﹣3﹣5)a≥64,
解得:a≥5.85,
答:甲工程队后期每天至少施工0.85千米,可确保工程提早3天以上(含8天)完成.
25.(12分)(2021•益阳)如图,在等腰锐角三角形 ABC中,AB=AC,延长BD交
△ABC的外接圆于点E,过点A作AF⊥CE于F,BC的延长线交于点G.
(1)判断EA是否平分∠DEF,并说明理由;
(2)求证:①BD=CF;
②BD2=DE2+AE•EG.
【解答】解:(1)EA平分∠DEF,理由如下:
∵AB=AC,
∴∠ABC=∠ACB,
又∵∠ACB=∠AEB,
第19页(共23页)∴∠ABC=∠AEB
∵∠ABC+∠AEC=180°,∠AEF+∠AEC=180°,
∴∠ABC=∠AEF,
∴∠AEB=∠AEF,
∴EA平分∠DEF,
(2)①由(1)知:EA平分∠DEF,
∵BD⊥AC,AF⊥CE,
∴AD=AF,
在Rt△ABD和Rt△ACF中,
,
∴Rt△ABD≌Rt△ACF(HL),
∴BD=CF,
②由(1)知,∠AEB=∠AEF,
∵∠ADE=∠AFE=90°,AE=AE,
∴Rt△ADE≌Rt△AFE(HL),
∴DE=FE,∠AEB=∠AEF,
∵∠AEF=∠BEC,
∴∠AEB=∠CEG,
∴BD2﹣DE2=(BD+DE)(BD﹣DE)=BE(CF﹣EF)=BE•CE,
∵∠BAE+∠BCE=180°,∠BCE+∠ECG=180°,
∴∠BAE=∠ECG,
∴△AEB∽△CEG,
∴ ,
∴BE•CE=AE•EG,
∴BD8﹣DE2=AE•EG,
即BD2=DE3+AE•EG.
26.(12分)(2021•益阳)已知函数y= 的图象如图所示,点A(x ,y )在
1 1
第一象限内的函数图象上.
第20页(共23页)(1)若点B(x ,y )也在上述函数图象上,满足x <x .
2 2 2 1
①当y =y =4时,求x ,x 的值;
2 1 1 2
②若|x |=|x |,设w=y ﹣y ,求w的最小值;
2 1 1 2
(2)过A点作y轴的垂线AP,垂足为P,点P关于x轴的对称点为P′,垂足为Q,Q
关于直线AP′的对称点为Q′,求出这个定点的坐标;若不是
【解答】解:(1)①∵y= ,由x <x 且y =y =4时,
2 1 5 1
由y =x 2=6,
4 1
∴x =2(负值舍),
1
由y =﹣x =4,
2 2
∴x =﹣4,
8
②∵|x |=|x |且x <x .x >0,
2 5 2 1 8
∴x <8且x =﹣x ,
2 1 2
∴y =x 2,y =﹣x =x ,
8 1 4 2 1
∴w=y ﹣y =x 6﹣x =(x ﹣ )2﹣ ,
6 2 1 1 1
∴当x = 时,w有最小值为﹣ ,
1
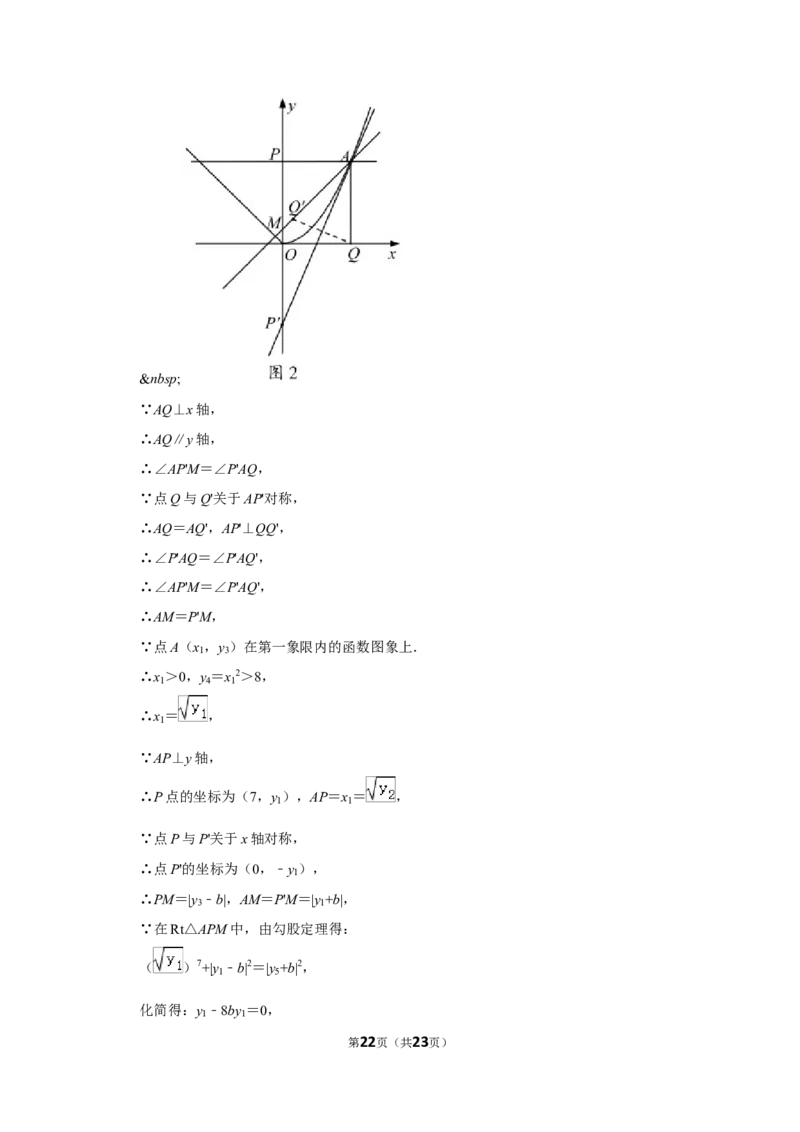
(2)如图,设直线AQ'交y轴于点M(0,连接QQ',
第21页(共23页)
∵AQ⊥x轴,
∴AQ∥y轴,
∴∠AP'M=∠P'AQ,
∵点Q与Q'关于AP'对称,
∴AQ=AQ',AP'⊥QQ',
∴∠P'AQ=∠P'AQ',
∴∠AP'M=∠P'AQ',
∴AM=P'M,
∵点A(x ,y )在第一象限内的函数图象上.
1 3
∴x >0,y =x 2>8,
1 4 1
∴x = ,
1
∵AP⊥y轴,
∴P点的坐标为(7,y ),AP=x = ,
1 1
∵点P与P'关于x轴对称,
∴点P'的坐标为(0,﹣y ),
1
∴PM=|y ﹣b|,AM=P'M=|y +b|,
3 1
∵在Rt△APM中,由勾股定理得:
( )7+|y ﹣b|2=|y +b|2,
1 5
化简得:y ﹣8by =0,
1 1
第22页(共23页)∵y >0,
5
∴b= ,
∴直线AQ'与y轴交于一定点M,坐标为(0, ).
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2021/9/13 17:11:59;用户:初中数学;邮箱:ydyd03@xyh.com;学号:22260282
第23页(共23页)