文档内容
2022年湖南省益阳市中考数学试卷
一、选择题(本题共10个小题,每小题4分,共40分。每小题给出的四个选项中,只有一项是符合题目
要求的)
1.四个实数﹣ ,1,2, 中,比0小的数是( )
A.﹣ B.1 C.2 D.
2.下列各式中,运算结果等于a2的是( )
A.a3﹣a B.a+a C.a•a D.a6÷a3
3.若x=2是下列四个选项中的某个不等式组的一个解,则这个不等式组是( )
A. B. C. D.
4.若x=﹣1是方程x2+x+m=0的一个根,则此方程的另一个根是( )
A.﹣1 B.0 C.1 D.2
5.已知一个函数的因变量y与自变量x的几组对应值如表,则这个函数的表达式可以是( )
x … ﹣1 0 1 2 …
y … ﹣2 0 2 4 …
A.y=2x B.y=x﹣1 C.y= D.y=x2
6.在某市组织的物理实验操作考试中,考试所用实验室共有 24个测试位,分成6组,同组4个测试位各
有一道相同试题,各组的试题不同,分别标记为A,B,C,D,E,F,考生从中随机抽取一道试题,则
某个考生抽到试题A的概率为( )
A. B. C. D.
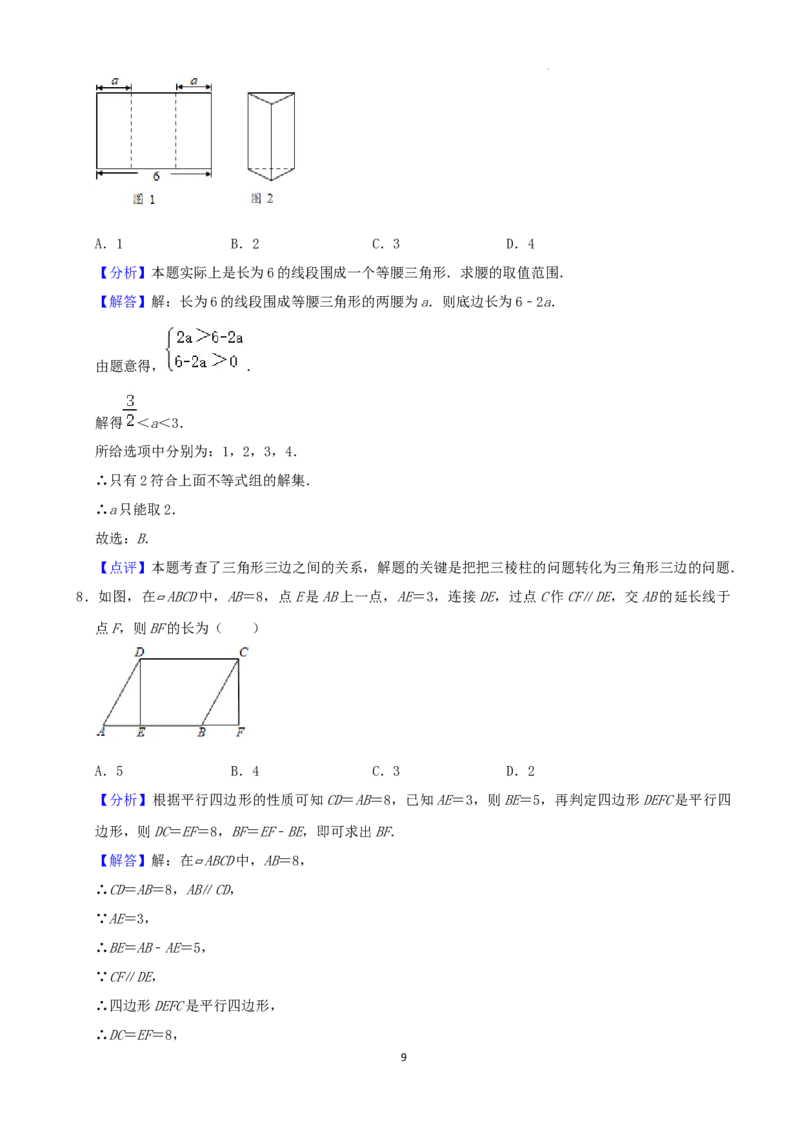
7.如图1所示,将长为6的矩形纸片沿虚线折成3个矩形,其中左右两侧矩形的宽相等,若要将其围成如
图2所示的三棱柱形物体,则图中a的值可以是( )
A.1 B.2 C.3 D.4
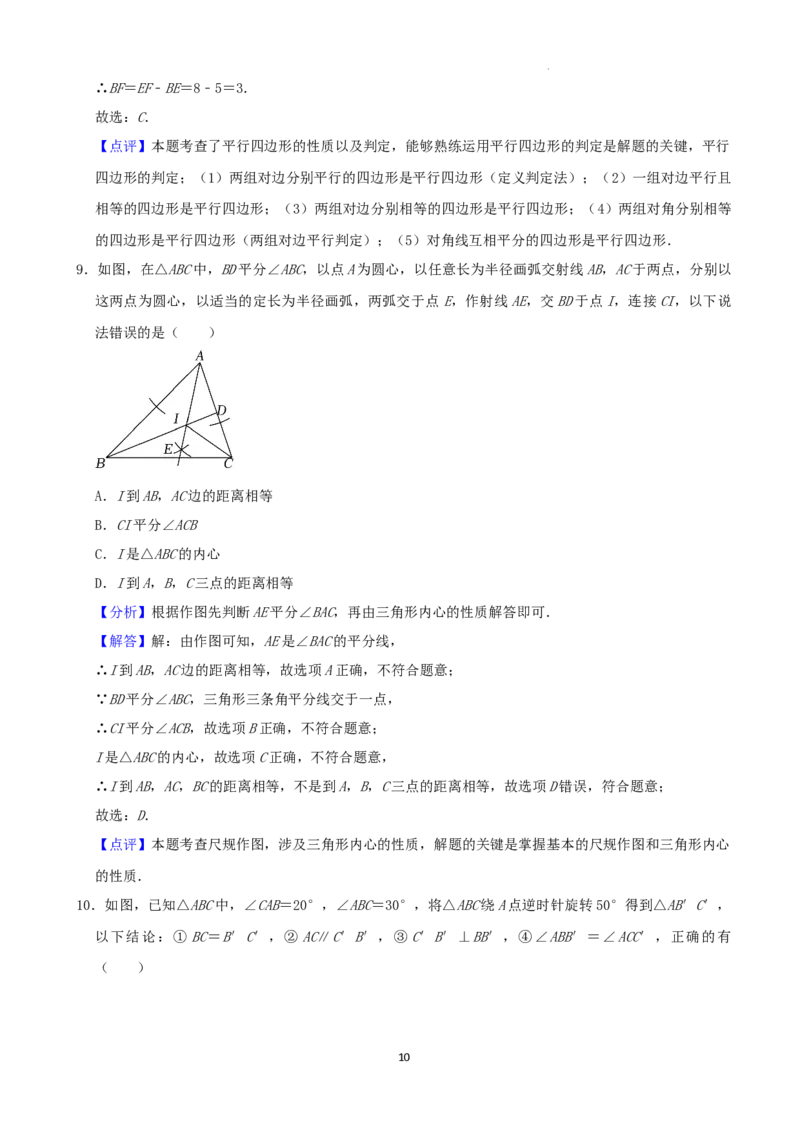
8.如图,在 ABCD中,AB=8,点E是AB上一点,AE=3,连接DE,过点C作CF∥DE,交AB的延长线于
▱
1
学科网(北京)股份有限公司点F,则BF的长为( )
A.5 B.4 C.3 D.2
9.如图,在△ABC中,BD平分∠ABC,以点A为圆心,以任意长为半径画弧交射线AB,AC于两点,分别以
这两点为圆心,以适当的定长为半径画弧,两弧交于点E,作射线AE,交BD于点I,连接CI,以下说
法错误的是( )
A.I到AB,AC边的距离相等
B.CI平分∠ACB
C.I是△ABC的内心
D.I到A,B,C三点的距离相等
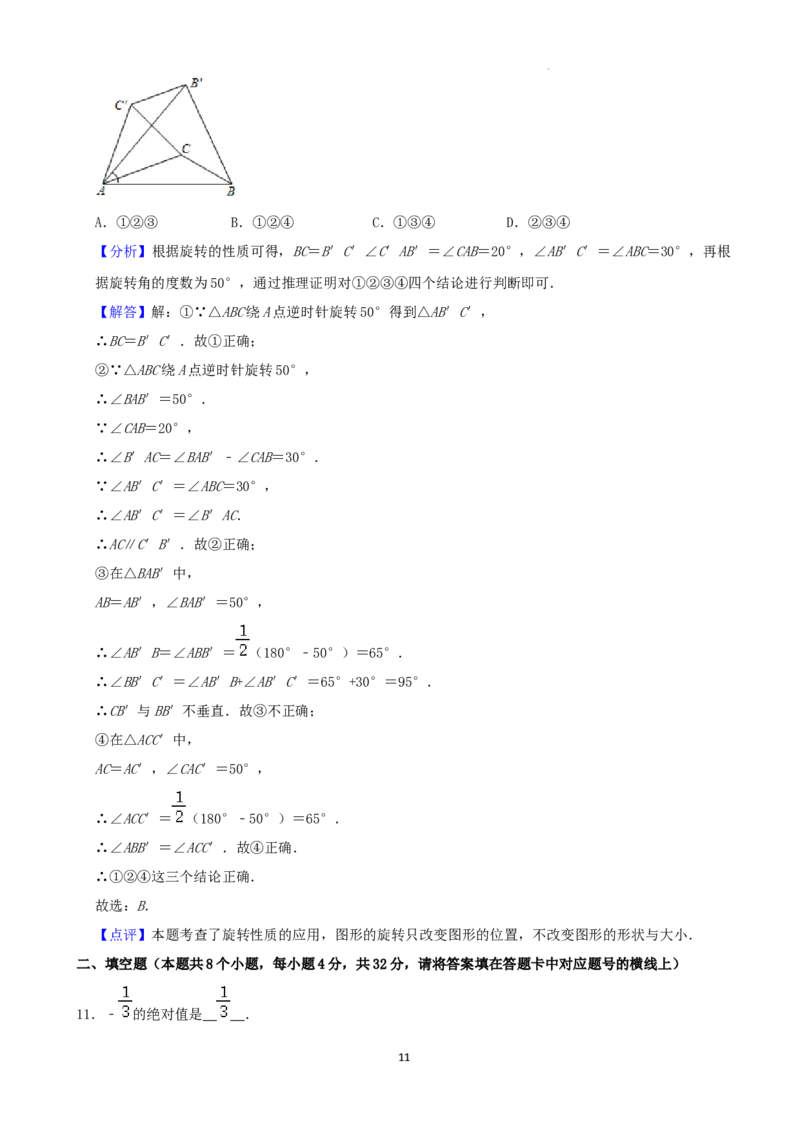
10.如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB′C′,
以下结论:①BC=B′C′,②AC∥C′B′,③C′B′⊥BB′,④∠ABB′=∠ACC′,正确的有
( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题(本题共8个小题,每小题4分,共32分,请将答案填在答题卡中对应题号的横线上)
11.﹣ 的绝对值是 .
12.计算: ﹣ = .
13.已知m,n同时满足2m+n=3与2m﹣n=1,则4m2﹣n2的值是 .
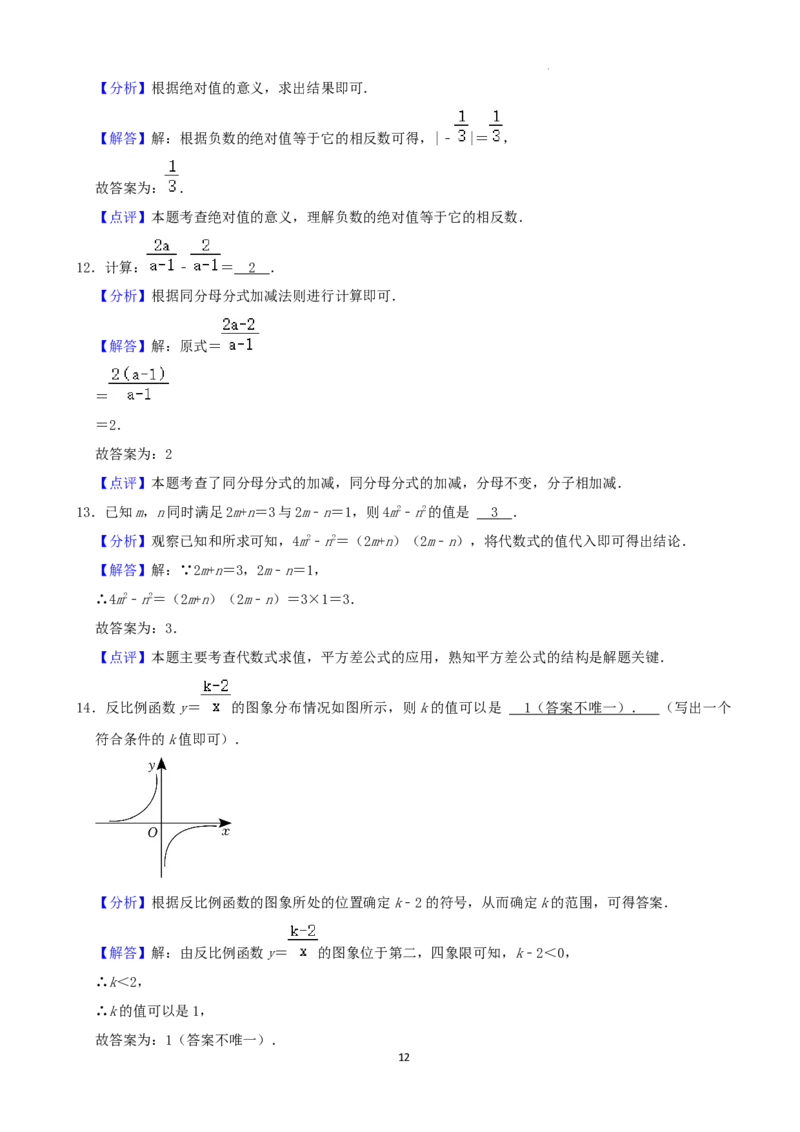
14.反比例函数y= 的图象分布情况如图所示,则k的值可以是 (写出一个符合条件的k值
2
学科网(北京)股份有限公司即可).
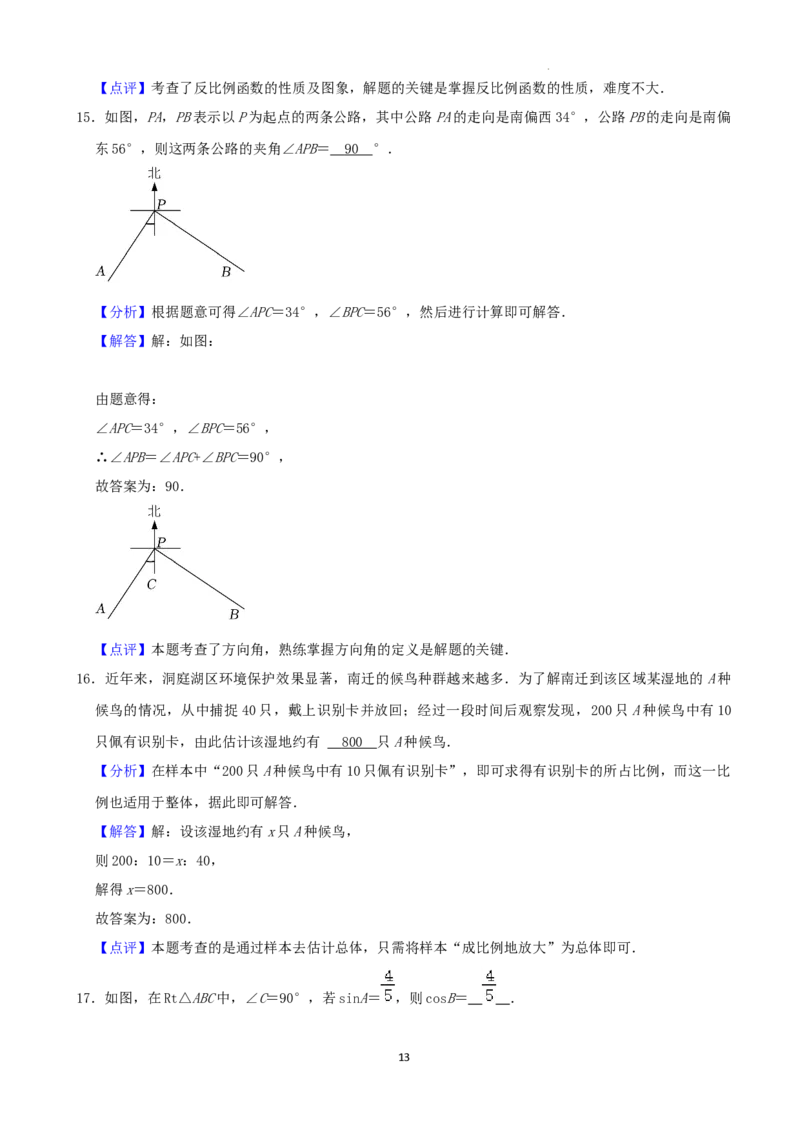
15.如图,PA,PB表示以P为起点的两条公路,其中公路PA的走向是南偏西34°,公路PB的走向是南偏
东56°,则这两条公路的夹角∠APB= °.
16.近年来,洞庭湖区环境保护效果显著,南迁的候鸟种群越来越多.为了解南迁到该区域某湿地的A种
候鸟的情况,从中捕捉40只,戴上识别卡并放回;经过一段时间后观察发现,200只A种候鸟中有10
只佩有识别卡,由此估计该湿地约有 只A种候鸟.
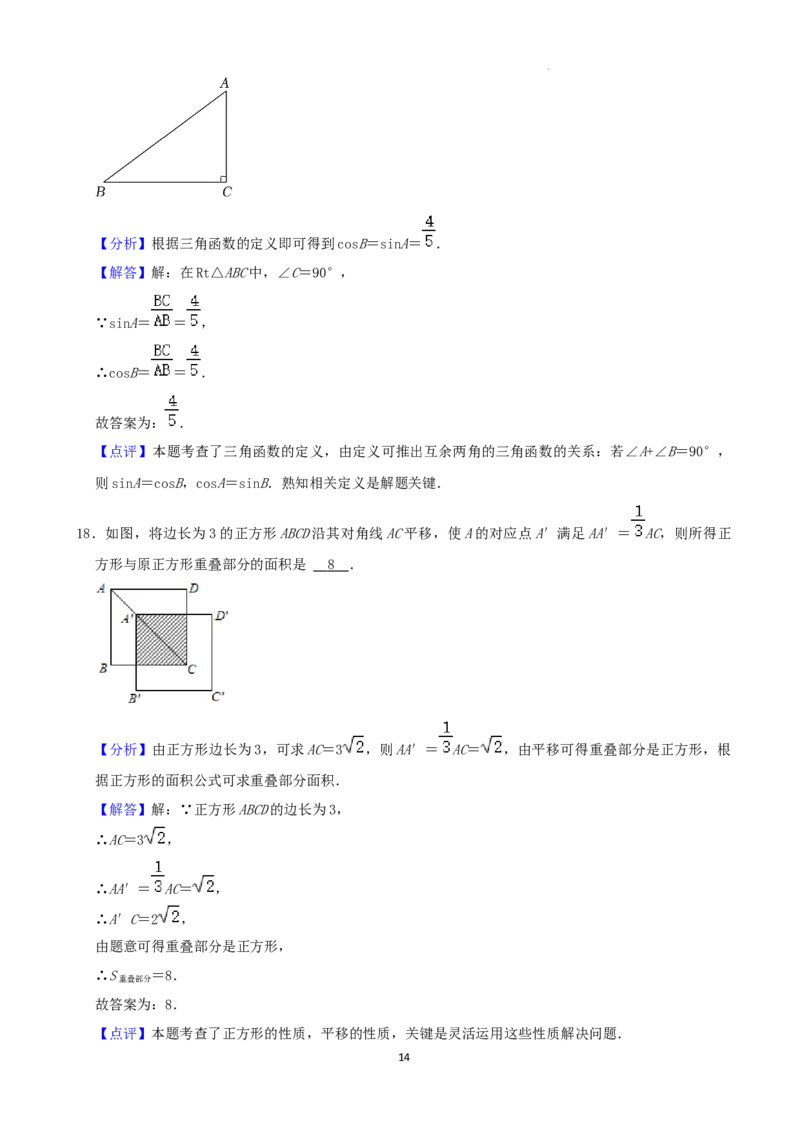
17.如图,在Rt△ABC中,∠C=90°,若sinA= ,则cosB= .
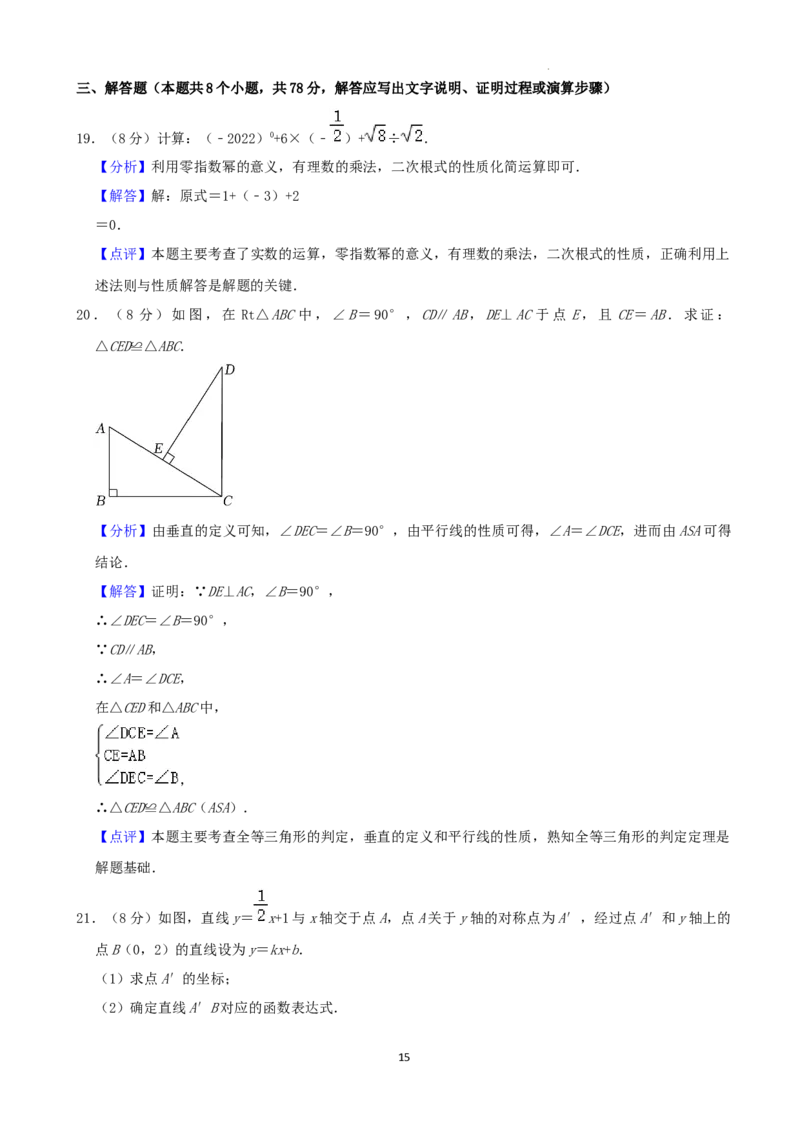
18.如图,将边长为3的正方形ABCD沿其对角线AC平移,使A的对应点A′满足AA′= AC,则所得正
方形与原正方形重叠部分的面积是 .
三、解答题(本题共8个小题,共78分,解答应写出文字说明、证明过程或演算步骤)
19.(8分)计算:(﹣2022)0+6×(﹣ )+ ÷ .
20.(8 分)如图,在 Rt△ABC中,∠B=90°,CD∥AB,DE⊥AC于点 E,且 CE=AB.求证:
3
学科网(北京)股份有限公司△CED≌△ABC.
21.(8分)如图,直线y= x+1与x轴交于点A,点A关于y轴的对称点为A′,经过点A′和y轴上的
点B(0,2)的直线设为y=kx+b.
(1)求点A′的坐标;
(2)确定直线A′B对应的函数表达式.
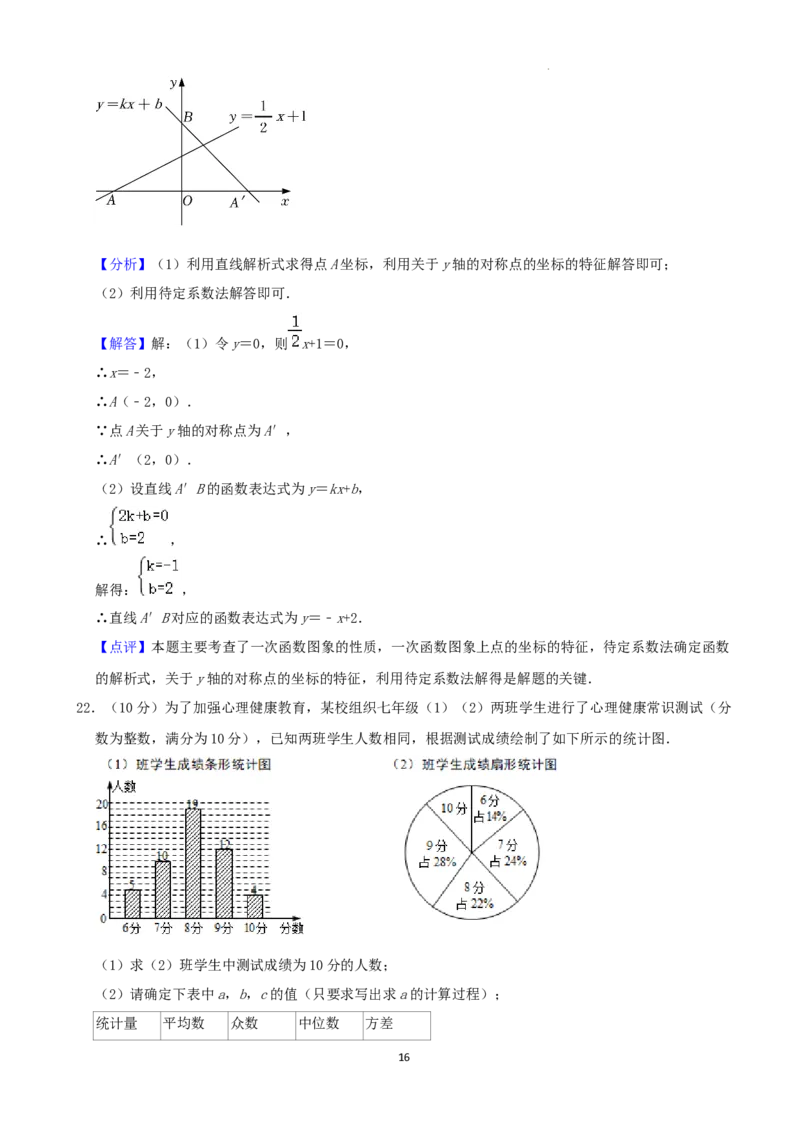
22.(10分)为了加强心理健康教育,某校组织七年级(1)(2)两班学生进行了心理健康常识测试(分
数为整数,满分为10分),已知两班学生人数相同,根据测试成绩绘制了如下所示的统计图.
(1)求(2)班学生中测试成绩为10分的人数;
(2)请确定下表中a,b,c的值(只要求写出求a的计算过程);
统计量 平均数 众数 中位数 方差
(1)班 8 8 c 1.16
(2)班 a b 8 1.56
(3)从上表中选择合适的统计量,说明哪个班的成绩更均匀.
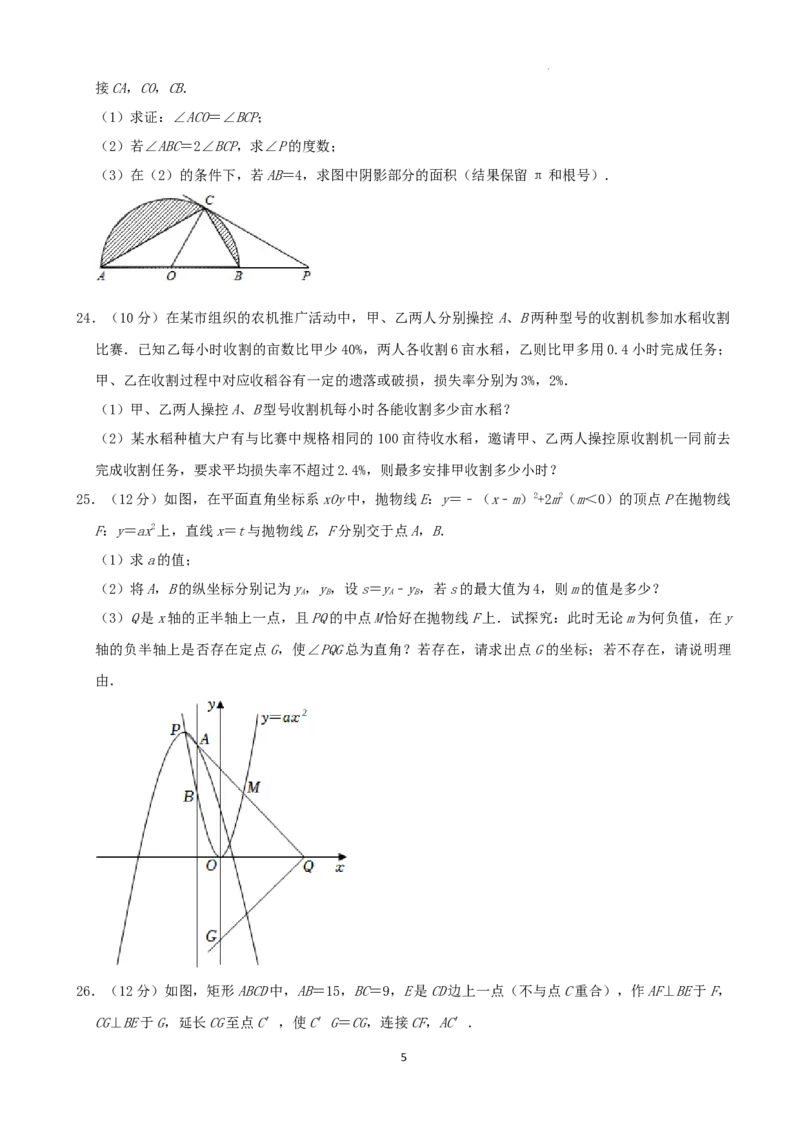
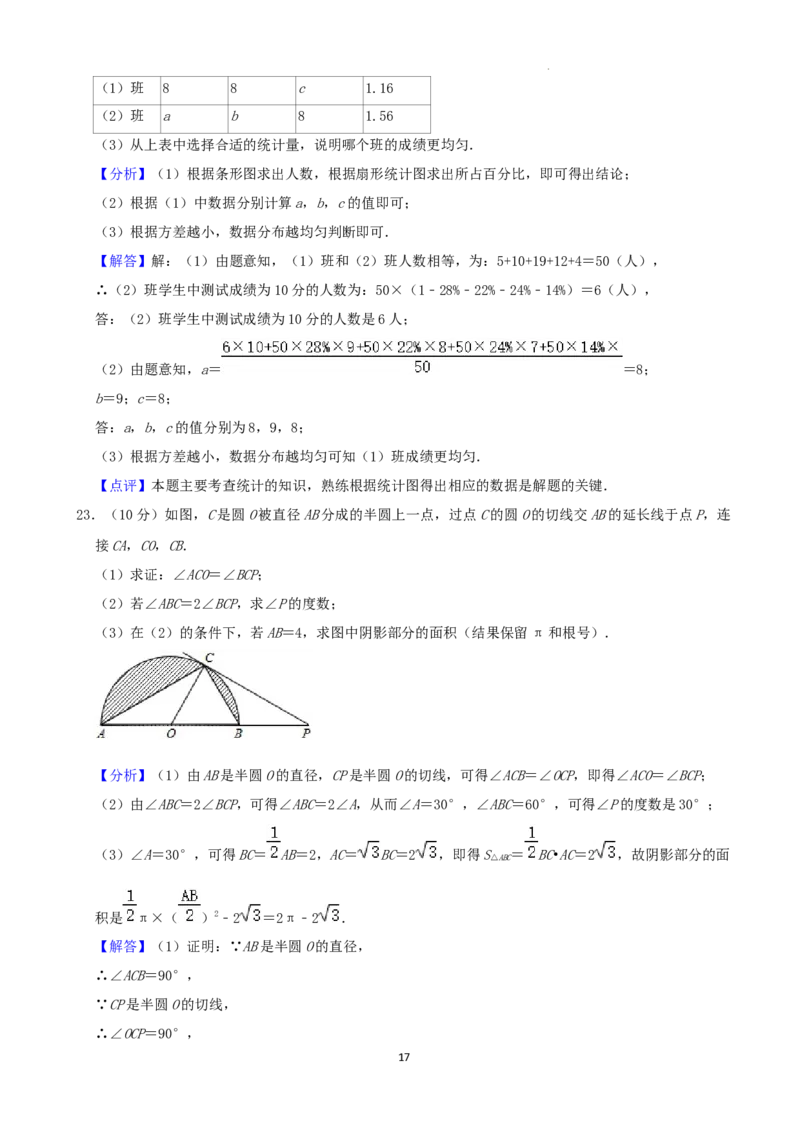
23.(10分)如图,C是圆O被直径AB分成的半圆上一点,过点C的圆O的切线交AB的延长线于点P,连
4
学科网(北京)股份有限公司接CA,CO,CB.
(1)求证:∠ACO=∠BCP;
(2)若∠ABC=2∠BCP,求∠P的度数;
(3)在(2)的条件下,若AB=4,求图中阴影部分的面积(结果保留π和根号).
24.(10分)在某市组织的农机推广活动中,甲、乙两人分别操控A、B两种型号的收割机参加水稻收割
比赛.已知乙每小时收割的亩数比甲少40%,两人各收割6亩水稻,乙则比甲多用0.4小时完成任务;
甲、乙在收割过程中对应收稻谷有一定的遗落或破损,损失率分别为3%,2%.
(1)甲、乙两人操控A、B型号收割机每小时各能收割多少亩水稻?
(2)某水稻种植大户有与比赛中规格相同的100亩待收水稻,邀请甲、乙两人操控原收割机一同前去
完成收割任务,要求平均损失率不超过2.4%,则最多安排甲收割多少小时?
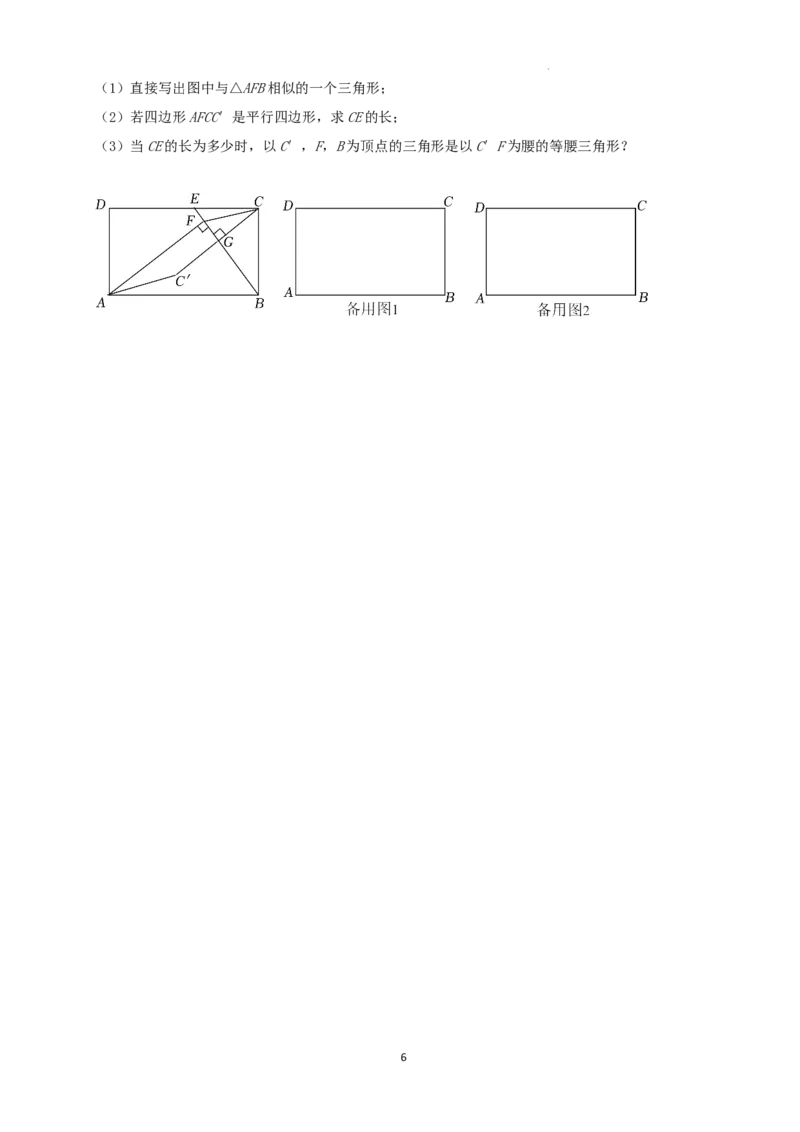
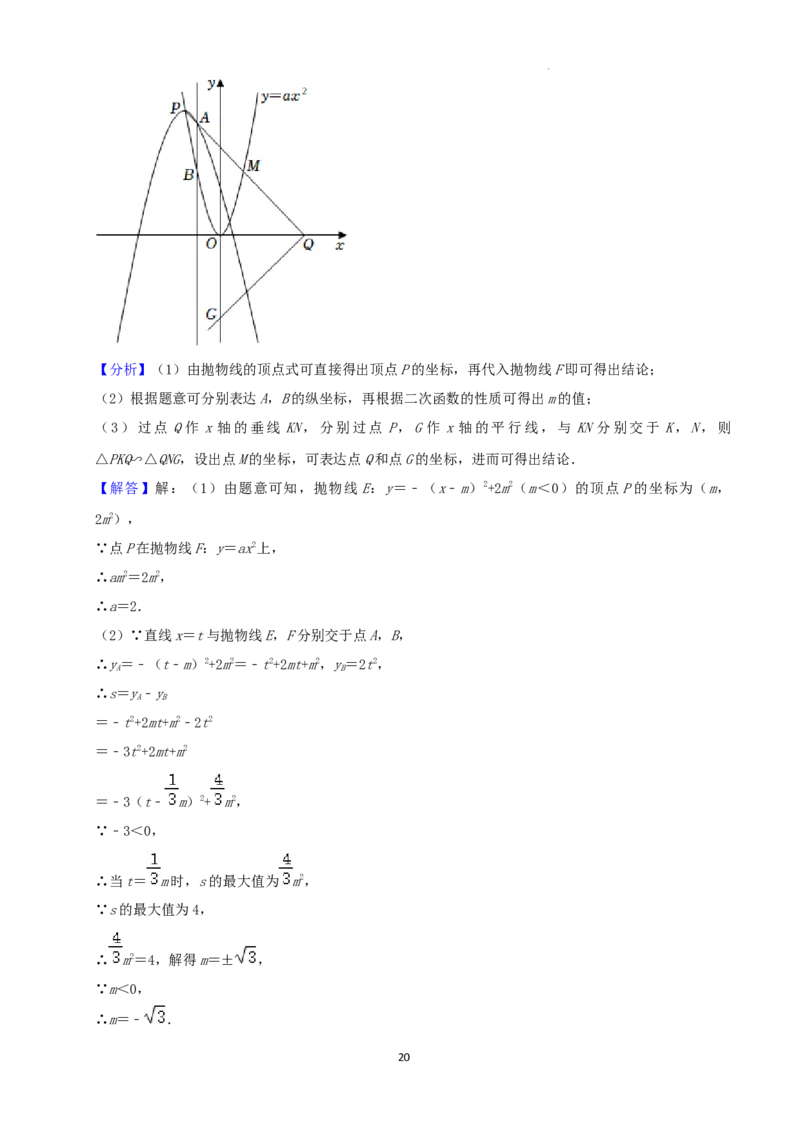
25.(12分)如图,在平面直角坐标系xOy中,抛物线E:y=﹣(x﹣m)2+2m2(m<0)的顶点P在抛物线
F:y=ax2上,直线x=t与抛物线E,F分别交于点A,B.
(1)求a的值;
(2)将A,B的纵坐标分别记为y,y,设s=y﹣y,若s的最大值为4,则m的值是多少?
A B A B
(3)Q是x轴的正半轴上一点,且PQ的中点M恰好在抛物线F上.试探究:此时无论m为何负值,在y
轴的负半轴上是否存在定点G,使∠PQG总为直角?若存在,请求出点G的坐标;若不存在,请说明理
由.
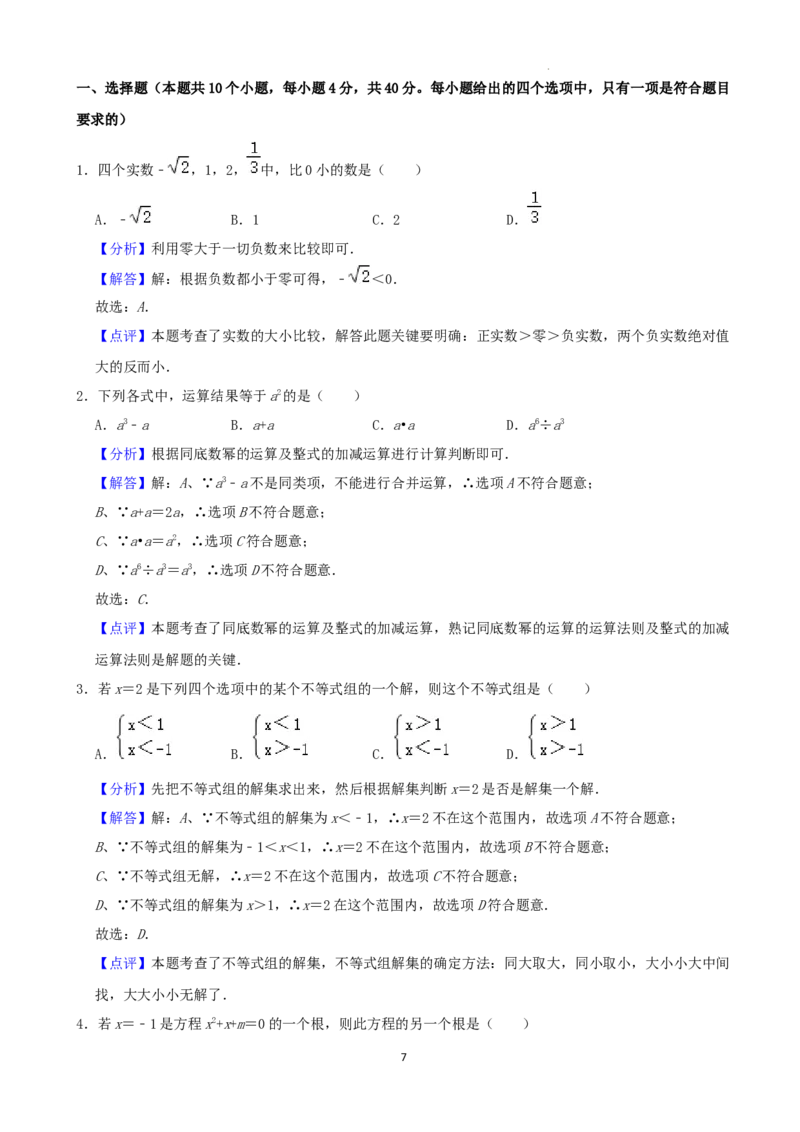
26.(12分)如图,矩形ABCD中,AB=15,BC=9,E是CD边上一点(不与点C重合),作AF⊥BE于F,
CG⊥BE于G,延长CG至点C′,使C′G=CG,连接CF,AC′.
5
学科网(北京)股份有限公司(1)直接写出图中与△AFB相似的一个三角形;
(2)若四边形AFCC′是平行四边形,求CE的长;
(3)当CE的长为多少时,以C′,F,B为顶点的三角形是以C′F为腰的等腰三角形?
6
学科网(北京)股份有限公司一、选择题(本题共10个小题,每小题4分,共40分。每小题给出的四个选项中,只有一项是符合题目
要求的)
1.四个实数﹣ ,1,2, 中,比0小的数是( )
A.﹣ B.1 C.2 D.
【分析】利用零大于一切负数来比较即可.
【解答】解:根据负数都小于零可得,﹣ <0.
故选:A.
【点评】本题考查了实数的大小比较,解答此题关键要明确:正实数>零>负实数,两个负实数绝对值
大的反而小.
2.下列各式中,运算结果等于a2的是( )
A.a3﹣a B.a+a C.a•a D.a6÷a3
【分析】根据同底数幂的运算及整式的加减运算进行计算判断即可.
【解答】解:A、∵a3﹣a不是同类项,不能进行合并运算,∴选项A不符合题意;
B、∵a+a=2a,∴选项B不符合题意;
C、∵a•a=a2,∴选项C符合题意;
D、∵a6÷a3=a3,∴选项D不符合题意.
故选:C.
【点评】本题考查了同底数幂的运算及整式的加减运算,熟记同底数幂的运算的运算法则及整式的加减
运算法则是解题的关键.
3.若x=2是下列四个选项中的某个不等式组的一个解,则这个不等式组是( )
A. B. C. D.
【分析】先把不等式组的解集求出来,然后根据解集判断x=2是否是解集一个解.
【解答】解:A、∵不等式组的解集为x<﹣1,∴x=2不在这个范围内,故选项A不符合题意;
B、∵不等式组的解集为﹣1<x<1,∴x=2不在这个范围内,故选项B不符合题意;
C、∵不等式组无解,∴x=2不在这个范围内,故选项C不符合题意;
D、∵不等式组的解集为x>1,∴x=2在这个范围内,故选项D符合题意.
故选:D.
【点评】本题考查了不等式组的解集,不等式组解集的确定方法:同大取大,同小取小,大小小大中间
找,大大小小无解了.
4.若x=﹣1是方程x2+x+m=0的一个根,则此方程的另一个根是( )
7
学科网(北京)股份有限公司A.﹣1 B.0 C.1 D.2
【分析】根据根与系数的关系即可求出答案.
【解答】解:设x2+x+m=0另一个根是α,
∴﹣1+α=﹣1,
∴α=0,
故选:B.
【点评】本题考查一元二次方程根与系数的关系,解题的关键是熟练运用一元二次方程根与系数的关系,
本题属于基础题型.
5.已知一个函数的因变量y与自变量x的几组对应值如表,则这个函数的表达式可以是( )
x … ﹣1 0 1 2 …
y … ﹣2 0 2 4 …
A.y=2x B.y=x﹣1 C.y= D.y=x2
【分析】观察表中x,y的对应值可以看出,y的值恰好是x值的2倍.从而求出y与x的函数表达式.
【解答】解:根据表中数据可以看出:y的值是x值的2倍.
∴y=2x.
故选:A.
【点评】本题考查了列正比例函数表达式,解题的关键是根据所给的数据找出自变量与因变量之间的关
系.
6.在某市组织的物理实验操作考试中,考试所用实验室共有 24个测试位,分成6组,同组4个测试位各
有一道相同试题,各组的试题不同,分别标记为A,B,C,D,E,F,考生从中随机抽取一道试题,则
某个考生抽到试题A的概率为( )
A. B. C. D.
【分析】根据抽到试题A的概率=试题A出现的结果数÷所有可能出现的结果数即可得出答案.
【解答】解:总共有24道题,试题A共有4道,
P(抽到试题A)= = ,
故选:C.
【点评】本题考查了概率公式,掌握到试题A的概率=试题A出现的结果数÷所有可能出现的结果数是
解题的关键.
7.如图1所示,将长为6的矩形纸片沿虚线折成3个矩形,其中左右两侧矩形的宽相等,若要将其围成如
图2所示的三棱柱形物体,则图中a的值可以是( )
8
学科网(北京)股份有限公司A.1 B.2 C.3 D.4
【分析】本题实际上是长为6的线段围成一个等腰三角形.求腰的取值范围.
【解答】解:长为6的线段围成等腰三角形的两腰为a.则底边长为6﹣2a.
由题意得, .
解得 <a<3.
所给选项中分别为:1,2,3,4.
∴只有2符合上面不等式组的解集.
∴a只能取2.
故选:B.
【点评】本题考查了三角形三边之间的关系,解题的关键是把把三棱柱的问题转化为三角形三边的问题.
8.如图,在 ABCD中,AB=8,点E是AB上一点,AE=3,连接DE,过点C作CF∥DE,交AB的延长线于
▱
点F,则BF的长为( )
A.5 B.4 C.3 D.2
【分析】根据平行四边形的性质可知CD=AB=8,已知AE=3,则BE=5,再判定四边形DEFC是平行四
边形,则DC=EF=8,BF=EF﹣BE,即可求出BF.
【解答】解:在 ABCD中,AB=8,
▱
∴CD=AB=8,AB∥CD,
∵AE=3,
∴BE=AB﹣AE=5,
∵CF∥DE,
∴四边形DEFC是平行四边形,
∴DC=EF=8,
9
学科网(北京)股份有限公司∴BF=EF﹣BE=8﹣5=3.
故选:C.
【点评】本题考查了平行四边形的性质以及判定,能够熟练运用平行四边形的判定是解题的关键,平行
四边形的判定;(1)两组对边分别平行的四边形是平行四边形(定义判定法);(2)一组对边平行且
相等的四边形是平行四边形;(3)两组对边分别相等的四边形是平行四边形;(4)两组对角分别相等
的四边形是平行四边形(两组对边平行判定);(5)对角线互相平分的四边形是平行四边形.
9.如图,在△ABC中,BD平分∠ABC,以点A为圆心,以任意长为半径画弧交射线AB,AC于两点,分别以
这两点为圆心,以适当的定长为半径画弧,两弧交于点E,作射线AE,交BD于点I,连接CI,以下说
法错误的是( )
A.I到AB,AC边的距离相等
B.CI平分∠ACB
C.I是△ABC的内心
D.I到A,B,C三点的距离相等
【分析】根据作图先判断AE平分∠BAC,再由三角形内心的性质解答即可.
【解答】解:由作图可知,AE是∠BAC的平分线,
∴I到AB,AC边的距离相等,故选项A正确,不符合题意;
∵BD平分∠ABC,三角形三条角平分线交于一点,
∴CI平分∠ACB,故选项B正确,不符合题意;
I是△ABC的内心,故选项C正确,不符合题意,
∴I到AB,AC,BC的距离相等,不是到A,B,C三点的距离相等,故选项D错误,符合题意;
故选:D.
【点评】本题考查尺规作图,涉及三角形内心的性质,解题的关键是掌握基本的尺规作图和三角形内心
的性质.
10.如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB′C′,
以下结论:①BC=B′C′,②AC∥C′B′,③C′B′⊥BB′,④∠ABB′=∠ACC′,正确的有
( )
10
学科网(北京)股份有限公司A.①②③ B.①②④ C.①③④ D.②③④
【分析】根据旋转的性质可得,BC=B′C′∠C′AB′=∠CAB=20°,∠AB′C′=∠ABC=30°,再根
据旋转角的度数为50°,通过推理证明对①②③④四个结论进行判断即可.
【解答】解:①∵△ABC绕A点逆时针旋转50°得到△AB′C′,
∴BC=B′C′.故①正确;
②∵△ABC绕A点逆时针旋转50°,
∴∠BAB′=50°.
∵∠CAB=20°,
∴∠B′AC=∠BAB′﹣∠CAB=30°.
∵∠AB′C′=∠ABC=30°,
∴∠AB′C′=∠B′AC.
∴AC∥C′B′.故②正确;
③在△BAB′中,
AB=AB′,∠BAB′=50°,
∴∠AB′B=∠ABB′= (180°﹣50°)=65°.
∴∠BB′C′=∠AB′B+∠AB′C′=65°+30°=95°.
∴CB′与BB′不垂直.故③不正确;
④在△ACC′中,
AC=AC′,∠CAC′=50°,
∴∠ACC′= (180°﹣50°)=65°.
∴∠ABB′=∠ACC′.故④正确.
∴①②④这三个结论正确.
故选:B.
【点评】本题考查了旋转性质的应用,图形的旋转只改变图形的位置,不改变图形的形状与大小.
二、填空题(本题共8个小题,每小题4分,共32分,请将答案填在答题卡中对应题号的横线上)
11.﹣ 的绝对值是 .
11
学科网(北京)股份有限公司【分析】根据绝对值的意义,求出结果即可.
【解答】解:根据负数的绝对值等于它的相反数可得,|﹣ |= ,
故答案为: .
【点评】本题考查绝对值的意义,理解负数的绝对值等于它的相反数.
12.计算: ﹣ = 2 .
【分析】根据同分母分式加减法则进行计算即可.
【解答】解:原式=
=
=2.
故答案为:2
【点评】本题考查了同分母分式的加减,同分母分式的加减,分母不变,分子相加减.
13.已知m,n同时满足2m+n=3与2m﹣n=1,则4m2﹣n2的值是 3 .
【分析】观察已知和所求可知,4m2﹣n2=(2m+n)(2m﹣n),将代数式的值代入即可得出结论.
【解答】解:∵2m+n=3,2m﹣n=1,
∴4m2﹣n2=(2m+n)(2m﹣n)=3×1=3.
故答案为:3.
【点评】本题主要考查代数式求值,平方差公式的应用,熟知平方差公式的结构是解题关键.
14.反比例函数y= 的图象分布情况如图所示,则k的值可以是 1 (答案不唯一). (写出一个
符合条件的k值即可).
【分析】根据反比例函数的图象所处的位置确定k﹣2的符号,从而确定k的范围,可得答案.
【解答】解:由反比例函数y= 的图象位于第二,四象限可知,k﹣2<0,
∴k<2,
∴k的值可以是1,
故答案为:1(答案不唯一).
12
学科网(北京)股份有限公司【点评】考查了反比例函数的性质及图象,解题的关键是掌握反比例函数的性质,难度不大.
15.如图,PA,PB表示以P为起点的两条公路,其中公路PA的走向是南偏西34°,公路PB的走向是南偏
东56°,则这两条公路的夹角∠APB= 9 0 °.
【分析】根据题意可得∠APC=34°,∠BPC=56°,然后进行计算即可解答.
【解答】解:如图:
由题意得:
∠APC=34°,∠BPC=56°,
∴∠APB=∠APC+∠BPC=90°,
故答案为:90.
【点评】本题考查了方向角,熟练掌握方向角的定义是解题的关键.
16.近年来,洞庭湖区环境保护效果显著,南迁的候鸟种群越来越多.为了解南迁到该区域某湿地的A种
候鸟的情况,从中捕捉40只,戴上识别卡并放回;经过一段时间后观察发现,200只A种候鸟中有10
只佩有识别卡,由此估计该湿地约有 80 0 只A种候鸟.
【分析】在样本中“200只A种候鸟中有10只佩有识别卡”,即可求得有识别卡的所占比例,而这一比
例也适用于整体,据此即可解答.
【解答】解:设该湿地约有x只A种候鸟,
则200:10=x:40,
解得x=800.
故答案为:800.
【点评】本题考查的是通过样本去估计总体,只需将样本“成比例地放大”为总体即可.
17.如图,在Rt△ABC中,∠C=90°,若sinA= ,则cosB= .
13
学科网(北京)股份有限公司【分析】根据三角函数的定义即可得到cosB=sinA= .
【解答】解:在Rt△ABC中,∠C=90°,
∵sinA= = ,
∴cosB= = .
故答案为: .
【点评】本题考查了三角函数的定义,由定义可推出互余两角的三角函数的关系:若∠A+∠B=90°,
则sinA=cosB,cosA=sinB.熟知相关定义是解题关键.
18.如图,将边长为3的正方形ABCD沿其对角线AC平移,使A的对应点A′满足AA′= AC,则所得正
方形与原正方形重叠部分的面积是 8 .
【分析】由正方形边长为3,可求AC=3 ,则AA′= AC= ,由平移可得重叠部分是正方形,根
据正方形的面积公式可求重叠部分面积.
【解答】解:∵正方形ABCD的边长为3,
∴AC=3 ,
∴AA′= AC= ,
∴A′C=2 ,
由题意可得重叠部分是正方形,
∴S =8.
重叠部分
故答案为:8.
【点评】本题考查了正方形的性质,平移的性质,关键是灵活运用这些性质解决问题.
14
学科网(北京)股份有限公司三、解答题(本题共8个小题,共78分,解答应写出文字说明、证明过程或演算步骤)
19.(8分)计算:(﹣2022)0+6×(﹣ )+ ÷ .
【分析】利用零指数幂的意义,有理数的乘法,二次根式的性质化简运算即可.
【解答】解:原式=1+(﹣3)+2
=0.
【点评】本题主要考查了实数的运算,零指数幂的意义,有理数的乘法,二次根式的性质,正确利用上
述法则与性质解答是解题的关键.
20.(8 分)如图,在 Rt△ABC中,∠B=90°,CD∥AB,DE⊥AC于点 E,且 CE=AB.求证:
△CED≌△ABC.
【分析】由垂直的定义可知,∠DEC=∠B=90°,由平行线的性质可得,∠A=∠DCE,进而由ASA可得
结论.
【解答】证明:∵DE⊥AC,∠B=90°,
∴∠DEC=∠B=90°,
∵CD∥AB,
∴∠A=∠DCE,
在△CED和△ABC中,
,
∴△CED≌△ABC(ASA).
【点评】本题主要考查全等三角形的判定,垂直的定义和平行线的性质,熟知全等三角形的判定定理是
解题基础.
21.(8分)如图,直线y= x+1与x轴交于点A,点A关于y轴的对称点为A′,经过点A′和y轴上的
点B(0,2)的直线设为y=kx+b.
(1)求点A′的坐标;
(2)确定直线A′B对应的函数表达式.
15
学科网(北京)股份有限公司【分析】(1)利用直线解析式求得点A坐标,利用关于y轴的对称点的坐标的特征解答即可;
(2)利用待定系数法解答即可.
【解答】解:(1)令y=0,则 x+1=0,
∴x=﹣2,
∴A(﹣2,0).
∵点A关于y轴的对称点为A′,
∴A′(2,0).
(2)设直线A′B的函数表达式为y=kx+b,
∴ ,
解得: ,
∴直线A′B对应的函数表达式为y=﹣x+2.
【点评】本题主要考查了一次函数图象的性质,一次函数图象上点的坐标的特征,待定系数法确定函数
的解析式,关于y轴的对称点的坐标的特征,利用待定系数法解得是解题的关键.
22.(10分)为了加强心理健康教育,某校组织七年级(1)(2)两班学生进行了心理健康常识测试(分
数为整数,满分为10分),已知两班学生人数相同,根据测试成绩绘制了如下所示的统计图.
(1)求(2)班学生中测试成绩为10分的人数;
(2)请确定下表中a,b,c的值(只要求写出求a的计算过程);
统计量 平均数 众数 中位数 方差
16
学科网(北京)股份有限公司(1)班 8 8 c 1.16
(2)班 a b 8 1.56
(3)从上表中选择合适的统计量,说明哪个班的成绩更均匀.
【分析】(1)根据条形图求出人数,根据扇形统计图求出所占百分比,即可得出结论;
(2)根据(1)中数据分别计算a,b,c的值即可;
(3)根据方差越小,数据分布越均匀判断即可.
【解答】解:(1)由题意知,(1)班和(2)班人数相等,为:5+10+19+12+4=50(人),
∴(2)班学生中测试成绩为10分的人数为:50×(1﹣28%﹣22%﹣24%﹣14%)=6(人),
答:(2)班学生中测试成绩为10分的人数是6人;
(2)由题意知,a= =8;
b=9;c=8;
答:a,b,c的值分别为8,9,8;
(3)根据方差越小,数据分布越均匀可知(1)班成绩更均匀.
【点评】本题主要考查统计的知识,熟练根据统计图得出相应的数据是解题的关键.
23.(10分)如图,C是圆O被直径AB分成的半圆上一点,过点C的圆O的切线交AB的延长线于点P,连
接CA,CO,CB.
(1)求证:∠ACO=∠BCP;
(2)若∠ABC=2∠BCP,求∠P的度数;
(3)在(2)的条件下,若AB=4,求图中阴影部分的面积(结果保留π和根号).
【分析】(1)由AB是半圆O的直径,CP是半圆O的切线,可得∠ACB=∠OCP,即得∠ACO=∠BCP;
(2)由∠ABC=2∠BCP,可得∠ABC=2∠A,从而∠A=30°,∠ABC=60°,可得∠P的度数是30°;
(3)∠A=30°,可得BC= AB=2,AC= BC=2 ,即得S = BC•AC=2 ,故阴影部分的面
△ABC
积是 π×( )2﹣2 =2π﹣2 .
【解答】(1)证明:∵AB是半圆O的直径,
∴∠ACB=90°,
∵CP是半圆O的切线,
∴∠OCP=90°,
17
学科网(北京)股份有限公司∴∠ACB=∠OCP,
∴∠ACO=∠BCP;
(2)解:由(1)知∠ACO=∠BCP,
∵∠ABC=2∠BCP,
∴∠ABC=2∠ACO,
∵OA=OC,
∴∠ACO=∠A,
∴∠ABC=2∠A,
∵∠ABC+∠A=90°,
∴∠A=30°,∠ABC=60°,
∴∠ACO=∠BCP=30°,
∴∠P=∠ABC﹣∠BCP=60°﹣30°=30°,
答:∠P的度数是30°;
(3)解:由(2)知∠A=30°,
∵∠ACB=90°,
∴BC= AB=2,AC= BC=2 ,
∴S = BC•AC= ×2×2 =2 ,
△ABC
∴阴影部分的面积是 π×( )2﹣2 =2π﹣2 ,
答:阴影部分的面积是2π﹣2 .
【点评】本题考查圆的综合应用,涉及圆的切线性质,直角三角形性质及应用等知识,题目难度不大.
24.(10分)在某市组织的农机推广活动中,甲、乙两人分别操控A、B两种型号的收割机参加水稻收割
比赛.已知乙每小时收割的亩数比甲少40%,两人各收割6亩水稻,乙则比甲多用0.4小时完成任务;
甲、乙在收割过程中对应收稻谷有一定的遗落或破损,损失率分别为3%,2%.
(1)甲、乙两人操控A、B型号收割机每小时各能收割多少亩水稻?
(2)某水稻种植大户有与比赛中规格相同的100亩待收水稻,邀请甲、乙两人操控原收割机一同前去
完成收割任务,要求平均损失率不超过2.4%,则最多安排甲收割多少小时?
【分析】(1)设甲操控A型号收割机每小时收割x亩水稻,则乙操控B型号收割机每小时收割(1﹣
40%)x亩水稻,利用工作时间=工作总量÷工作效率,结合乙比甲多用0.4小时完成任务,即可得出关
于x的分式方程,解之经检验后即可求出甲操控A型号收割机每小时收割水稻的亩数,再将其代入(1
﹣40)x中即可求出乙操控B型号收割机每小时收割水稻的亩数;
18
学科网(北京)股份有限公司(2)设安排甲收割y小时,则安排乙收割 小时,根据要求平均损失率不超过2.4%,即可得出
关于y的一元一次不等式,解之取其中的最大值即可得出结论.
【解答】解:(1)设甲操控A型号收割机每小时收割x亩水稻,则乙操控B型号收割机每小时收割(1
﹣40%)x亩水稻,
依题意得: ﹣ =0.4,
解得:x=10,
经检验,x=10是原方程的解,且符合题意,
∴(1﹣40%)x=(1﹣40%)×10=6.
答:甲操控A型号收割机每小时收割10亩水稻,乙操控B型号收割机每小时收割6亩水稻.
(2)设安排甲收割y小时,则安排乙收割 小时,
依题意得:3%×10y+2%×6× ≤2.4%×100,
解得:y≤4.
答:最多安排甲收割4小时.
【点评】本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系
正确列出分式方程;(2)根据各数量之间的关系,正确列出一元一次不等式.
25.(12分)如图,在平面直角坐标系xOy中,抛物线E:y=﹣(x﹣m)2+2m2(m<0)的顶点P在抛物线
F:y=ax2上,直线x=t与抛物线E,F分别交于点A,B.
(1)求a的值;
(2)将A,B的纵坐标分别记为y,y,设s=y﹣y,若s的最大值为4,则m的值是多少?
A B A B
(3)Q是x轴的正半轴上一点,且PQ的中点M恰好在抛物线F上.试探究:此时无论m为何负值,在y
轴的负半轴上是否存在定点G,使∠PQG总为直角?若存在,请求出点G的坐标;若不存在,请说明理
由.
19
学科网(北京)股份有限公司【分析】(1)由抛物线的顶点式可直接得出顶点P的坐标,再代入抛物线F即可得出结论;
(2)根据题意可分别表达A,B的纵坐标,再根据二次函数的性质可得出m的值;
(3)过点 Q作 x轴的垂线 KN,分别过点 P,G作 x轴的平行线,与 KN分别交于 K,N,则
△PKQ∽△QNG,设出点M的坐标,可表达点Q和点G的坐标,进而可得出结论.
【解答】解:(1)由题意可知,抛物线E:y=﹣(x﹣m)2+2m2(m<0)的顶点P的坐标为(m,
2m2),
∵点P在抛物线F:y=ax2上,
∴am2=2m2,
∴a=2.
(2)∵直线x=t与抛物线E,F分别交于点A,B,
∴y=﹣(t﹣m)2+2m2=﹣t2+2mt+m2,y=2t2,
A B
∴s=y﹣y
A B
=﹣t2+2mt+m2﹣2t2
=﹣3t2+2mt+m2
=﹣3(t﹣ m)2+ m2,
∵﹣3<0,
∴当t= m时,s的最大值为 m2,
∵s的最大值为4,
∴ m2=4,解得m=± ,
∵m<0,
∴m=﹣ .
20
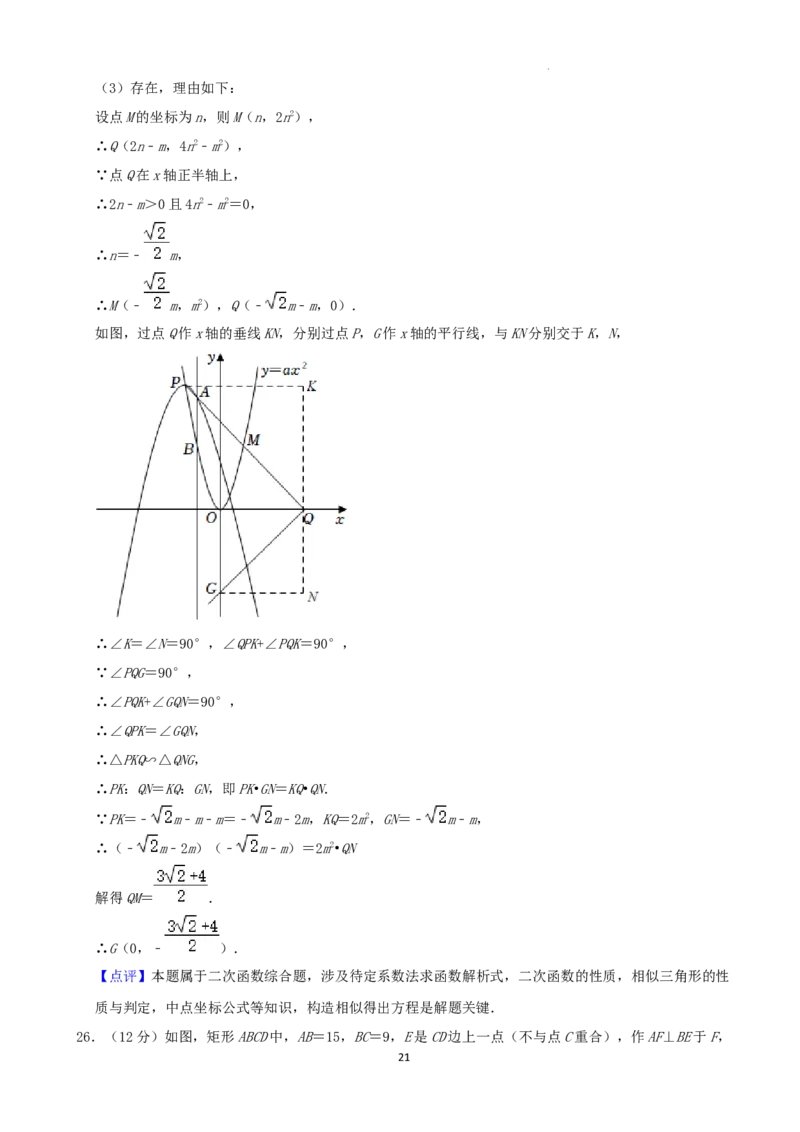
学科网(北京)股份有限公司(3)存在,理由如下:
设点M的坐标为n,则M(n,2n2),
∴Q(2n﹣m,4n2﹣m2),
∵点Q在x轴正半轴上,
∴2n﹣m>0且4n2﹣m2=0,
∴n=﹣ m,
∴M(﹣ m,m2),Q(﹣ m﹣m,0).
如图,过点Q作x轴的垂线KN,分别过点P,G作x轴的平行线,与KN分别交于K,N,
∴∠K=∠N=90°,∠QPK+∠PQK=90°,
∵∠PQG=90°,
∴∠PQK+∠GQN=90°,
∴∠QPK=∠GQN,
∴△PKQ∽△QNG,
∴PK:QN=KQ:GN,即PK•GN=KQ•QN.
∵PK=﹣ m﹣m﹣m=﹣ m﹣2m,KQ=2m2,GN=﹣ m﹣m,
∴(﹣ m﹣2m)(﹣ m﹣m)=2m2•QN
解得QM= .
∴G(0,﹣ ).
【点评】本题属于二次函数综合题,涉及待定系数法求函数解析式,二次函数的性质,相似三角形的性
质与判定,中点坐标公式等知识,构造相似得出方程是解题关键.
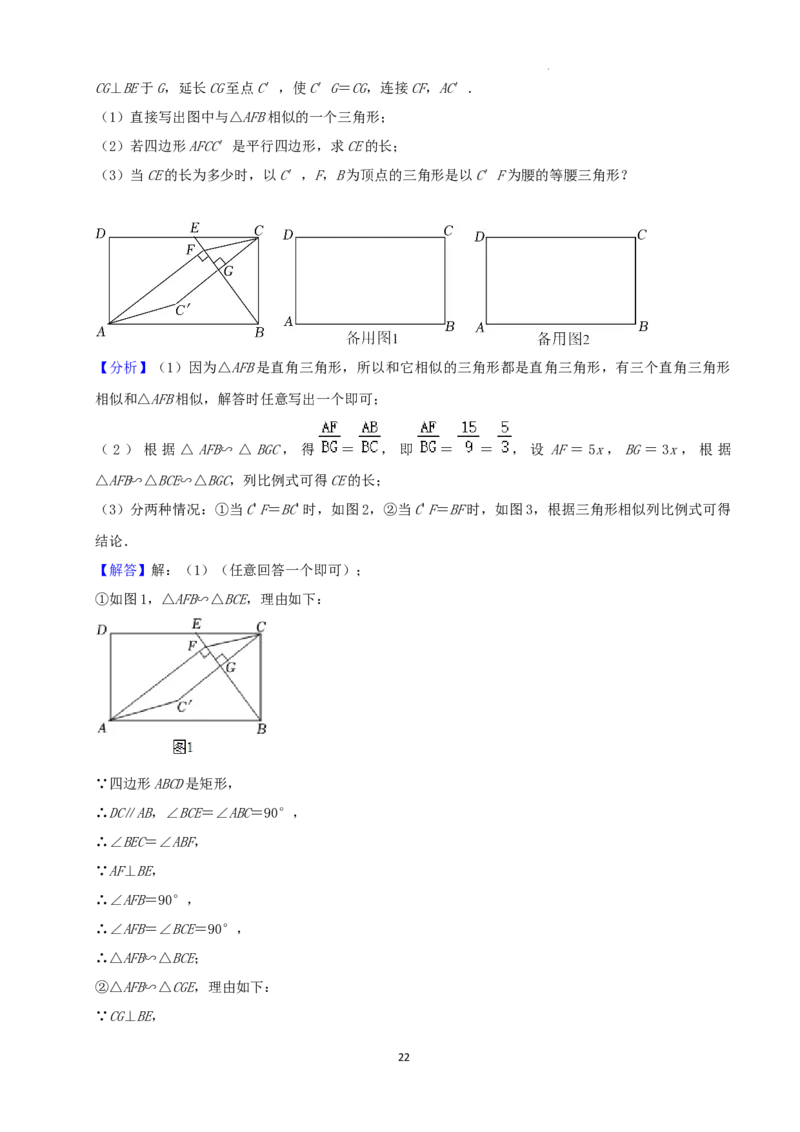
26.(12分)如图,矩形ABCD中,AB=15,BC=9,E是CD边上一点(不与点C重合),作AF⊥BE于F,
21
学科网(北京)股份有限公司CG⊥BE于G,延长CG至点C′,使C′G=CG,连接CF,AC′.
(1)直接写出图中与△AFB相似的一个三角形;
(2)若四边形AFCC′是平行四边形,求CE的长;
(3)当CE的长为多少时,以C′,F,B为顶点的三角形是以C′F为腰的等腰三角形?
【分析】(1)因为△AFB是直角三角形,所以和它相似的三角形都是直角三角形,有三个直角三角形
相似和△AFB相似,解答时任意写出一个即可;
( 2 ) 根 据 △AFB∽ △BGC, 得 = , 即 = = , 设 AF= 5x,BG= 3x, 根 据
△AFB∽△BCE∽△BGC,列比例式可得CE的长;
(3)分两种情况:①当C'F=BC'时,如图2,②当C'F=BF时,如图3,根据三角形相似列比例式可得
结论.
【解答】解:(1)(任意回答一个即可);
①如图1,△AFB∽△BCE,理由如下:
∵四边形ABCD是矩形,
∴DC∥AB,∠BCE=∠ABC=90°,
∴∠BEC=∠ABF,
∵AF⊥BE,
∴∠AFB=90°,
∴∠AFB=∠BCE=90°,
∴△AFB∽△BCE;
②△AFB∽△CGE,理由如下:
∵CG⊥BE,
22
学科网(北京)股份有限公司∴∠CGE=90°,
∴∠CGE=∠AFB,
∵∠CEG=∠ABF,
∴△AFB∽△CGE;
③△AFB∽△BGC,理由如下:
∵∠ABF+∠CBG=∠CBG+∠BCG=90°,
∴∠ABF=∠BCG,
∵∠AFB=∠CGB=90°,
∴△AFB∽△BGC;
(2)∵四边形AFCC'是平行四边形,
∴AF=CC',
由(1)知:△AFB∽△BGC,
∴ = ,即 = = ,
设AF=5x,BG=3x,
∴CC'=AF=5x,
∵CG=C'G,
∴CG=C'G=2.5x,
∵△AFB∽△BCE∽△BGC,
∴ = ,即 = ,
∴CE=7.5;
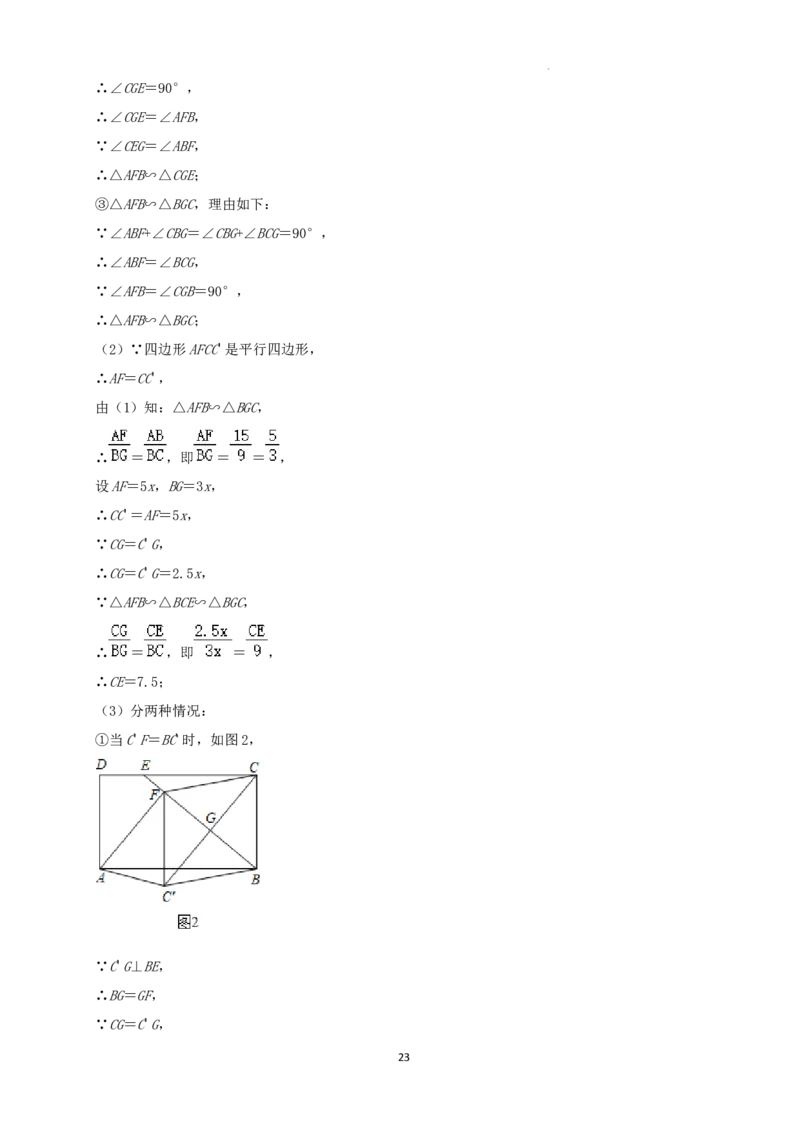
(3)分两种情况:
①当C'F=BC'时,如图2,
∵C'G⊥BE,
∴BG=GF,
∵CG=C'G,
23
学科网(北京)股份有限公司∴四边形BCFC'是菱形,
∴CF=CB=9,
由(2)知:AF=5x,BG=3x,
∴BF=6x,
∵△AFB∽△BCE,
∴ = ,即 = ,
∴ = ,
∴CE= ;
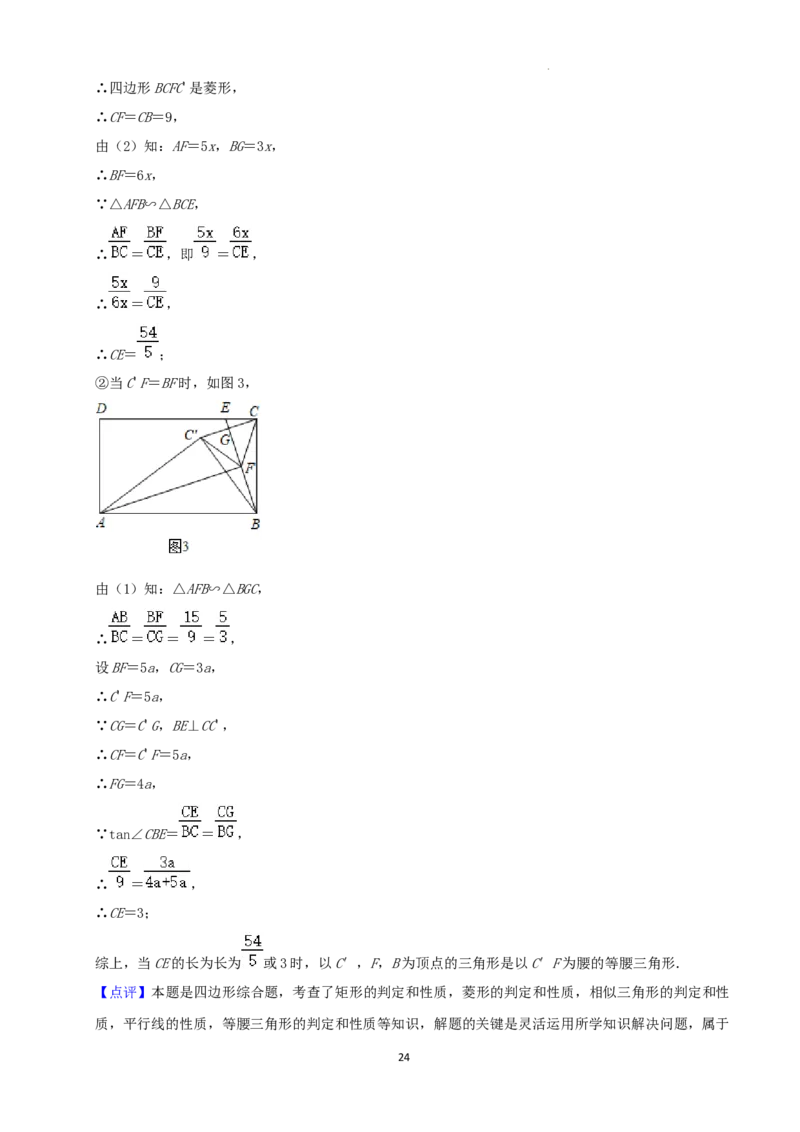
②当C'F=BF时,如图3,
由(1)知:△AFB∽△BGC,
∴ = = = ,
设BF=5a,CG=3a,
∴C'F=5a,
∵CG=C'G,BE⊥CC',
∴CF=C'F=5a,
∴FG=4a,
∵tan∠CBE= = ,
∴ = ,
∴CE=3;
综上,当CE的长为长为 或3时,以C′,F,B为顶点的三角形是以C′F为腰的等腰三角形.
【点评】本题是四边形综合题,考查了矩形的判定和性质,菱形的判定和性质,相似三角形的判定和性
质,平行线的性质,等腰三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于
24
学科网(北京)股份有限公司中考压轴题.
25
学科网(北京)股份有限公司26
学科网(北京)股份有限公司