文档内容
2019年内蒙古赤峰市中考数学试卷
一、选择题(每小题给出的选项中只有一个符合题意,请将符合题意的选项序号,在答题卡的
对应位置上按要求涂黑.每小题3分,共42分)
1.(3分)在﹣4、﹣ 、0、4这四个数中,最小的数是( )
A.4 B.0 C.﹣ D.﹣4
2.(3分)2013﹣2018年我国与“一带一路”沿线国家货物贸易总额超过 60000亿元,将
60000用科学记数法表示为( )
A.6×104 B.0.6×105 C.6×106 D.60×103
3.(3分)下列运算正确的是( )
A. + = B.x3•x2=x5 C.(x3)2=x5 D.x6÷x2=x3
4.(3分)不透明袋子中有除颜色外完全相同的4个黑球和2个白球,从袋子中随机摸出3个
球,下列事件是必然事件的是( )
A.3个都是黑球 B.2个黑球1个白球
C.2个白球1个黑球 D.至少有1个黑球
5.(3分)如图是一个几何体的三视图,则这个几何体是( )
A.三棱锥 B.圆锥 C.三棱柱 D.圆柱
6.(3分)不等式组 的解集在数轴上表示正确的是( )
A. B.
C. D.
7.(3分)如图是九年级某考生做的水滴入一个玻璃容器的示意图(滴水速度保持不变),能
正确反映容器中水的高度(h)与时间(t)之间对应关系的大致图象是( )
1A. B.
C. D.
8.(3分)如图,菱形ABCD周长为20,对角线AC、BD相交于点O,E是CD的中点,则OE的长是
( )
A.2.5 B.3 C.4 D.5
9.(3分)某品牌手机三月份销售400万部,四月份、五月份销售量连续增长,五月份销售量
达到900万部,求月平均增长率.设月平均增长率为x,根据题意列方程为( )
A.400(1+x2)=900 B.400(1+2x)=900
C.900(1﹣x)2=400 D.400(1+x)2=900
10.(3分)如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,点D是⊙O上一点,∠ADC=30°,则
∠BOC的度数为( )
A.30° B.40° C.50° D.60°
11.(3分)如图,点P是反比例函数y=(k≠0)的图象上任意一点,过点P作PM⊥x轴,垂足
为M.若△POM的面积等于2,则k的值等于( )
2A.﹣4 B.4 C.﹣2 D.2
12.(3分)如图,D、E分别是△ABC边AB,AC上的点,∠ADE=∠ACB,若AD=2,AB=6,AC=4,
则AE的长是( )
A.1 B.2 C.3 D.4
13.(3分)如图,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=
15°,则∠ACB的度数为( )
A.65° B.70° C.75° D.85°
14.(3分)如图,小聪用一张面积为1的正方形纸片,按如下方式操作:
①将正方形纸片四角向内折叠,使四个顶点重合,展开后沿折痕剪开,把四个等腰直角三
角形扔掉;
②在余下纸片上依次重复以上操作,当完成第2019次操作时,余下纸片的面积为( )
A.22019 B. C. D.
二、填空题(请把答案填写在答题卡相应的横线上.每小题3分,共12分)
315.(3分)因式分解:x3﹣2x2y+xy2= .
16.(3分)如图是甲、乙两名射击运动员10次射击成绩的统计表和折线统计图.
平均数 中位数 众数
甲 8 8 8
乙 8 8 8
你认为甲、乙两名运动员, 的射击成绩更稳定.(填甲或乙)
17.(3分)如图,一根竖直的木杆在离地面3.1m处折断,木杆顶端落在地面上,且与地面成
38°角,则木杆折断之前高度约为 m.
(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)
18.(3分)二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b>0;②a﹣b+c=0;
③一元二次方程ax2+bx+c+1=0(a≠0)有两个不相等的实数根;④当x<﹣1或x>3时,y
>0.上述结论中正确的是 .(填上所有正确结论的序号)
三、解答题(在答题卡上解答,答在本试卷上无效,解答时要写出必要的文字说明、证明过程
或演算步骤.共8题,满分96分)
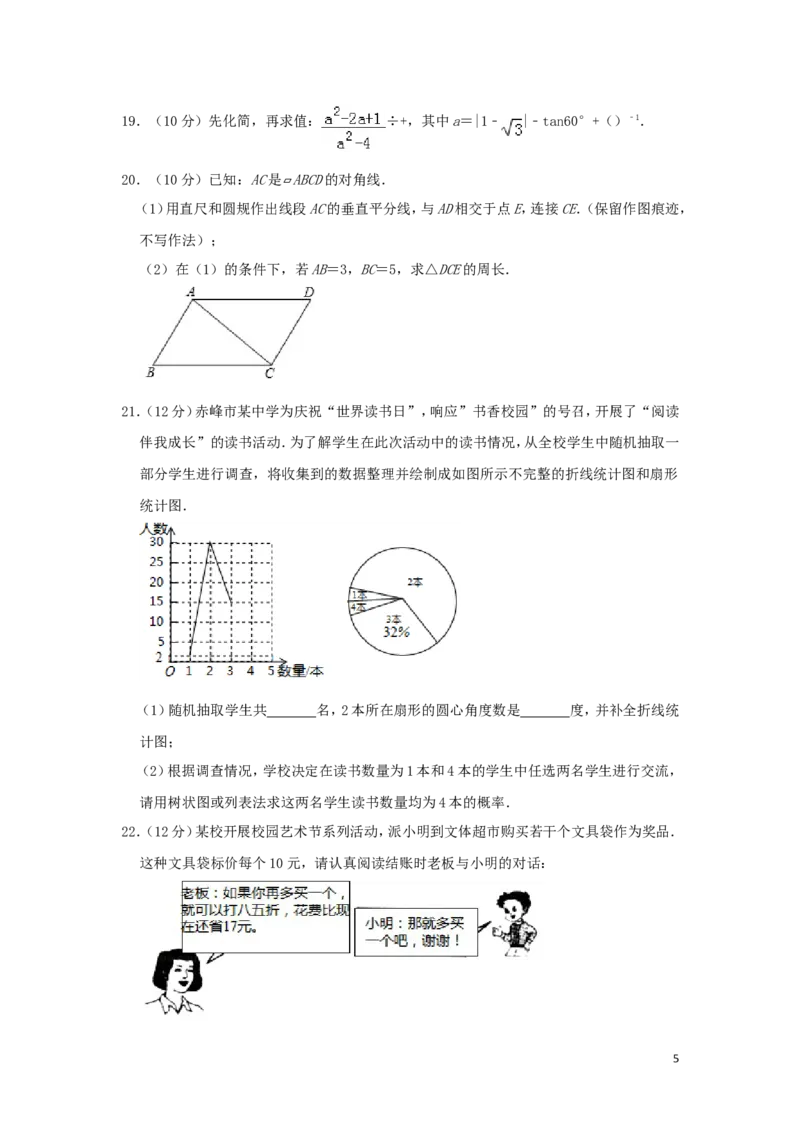
419.(10分)先化简,再求值: ÷+,其中a=|1﹣ |﹣tan60°+()﹣1.
20.(10分)已知:AC是 ABCD的对角线.
▱
(1)用直尺和圆规作出线段AC的垂直平分线,与AD相交于点E,连接CE.(保留作图痕迹,
不写作法);
(2)在(1)的条件下,若AB=3,BC=5,求△DCE的周长.
21.(12分)赤峰市某中学为庆祝“世界读书日”,响应”书香校园”的号召,开展了“阅读
伴我成长”的读书活动.为了解学生在此次活动中的读书情况,从全校学生中随机抽取一
部分学生进行调查,将收集到的数据整理并绘制成如图所示不完整的折线统计图和扇形
统计图.
(1)随机抽取学生共 名,2本所在扇形的圆心角度数是 度,并补全折线统
计图;
(2)根据调查情况,学校决定在读书数量为1本和4本的学生中任选两名学生进行交流,
请用树状图或列表法求这两名学生读书数量均为4本的概率.
22.(12分)某校开展校园艺术节系列活动,派小明到文体超市购买若干个文具袋作为奖品.
这种文具袋标价每个10元,请认真阅读结账时老板与小明的对话:
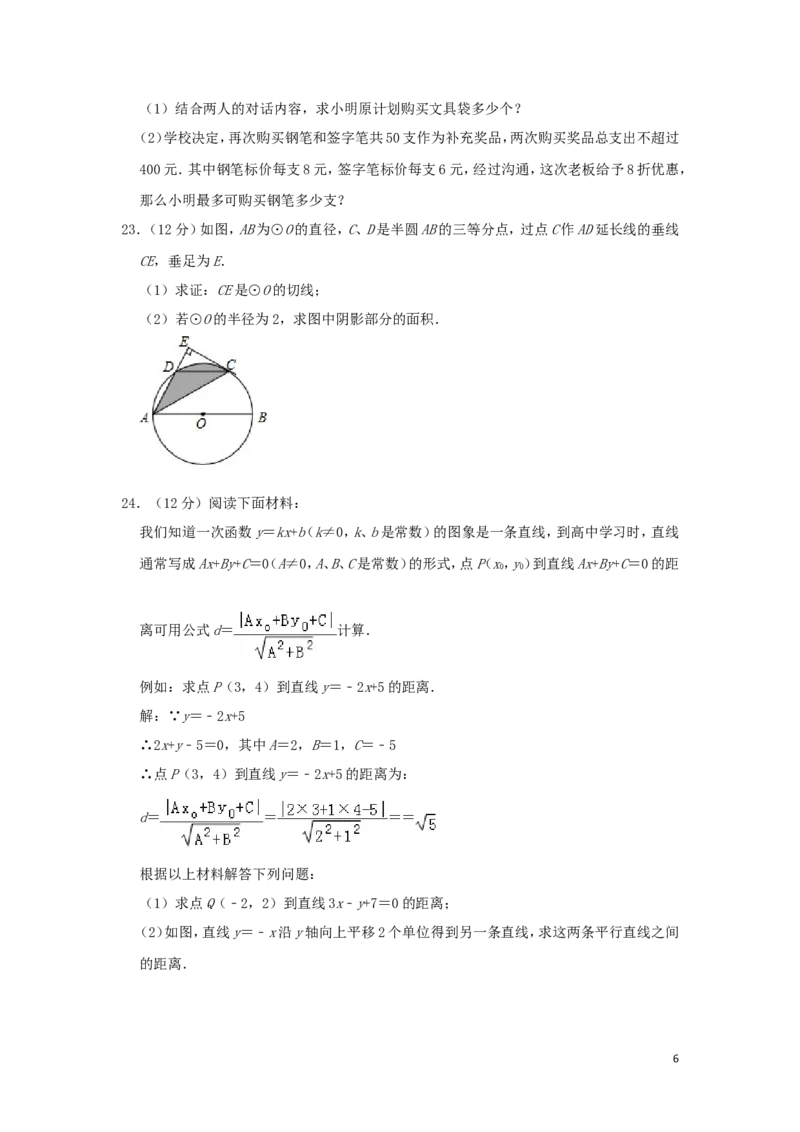
5(1)结合两人的对话内容,求小明原计划购买文具袋多少个?
(2)学校决定,再次购买钢笔和签字笔共50支作为补充奖品,两次购买奖品总支出不超过
400元.其中钢笔标价每支8元,签字笔标价每支6元,经过沟通,这次老板给予8折优惠,
那么小明最多可购买钢笔多少支?
23.(12分)如图,AB为⊙O的直径,C、D是半圆AB的三等分点,过点C作AD延长线的垂线
CE,垂足为E.
(1)求证:CE是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
24.(12分)阅读下面材料:
我们知道一次函数y=kx+b(k≠0,k、b是常数)的图象是一条直线,到高中学习时,直线
通常写成Ax+By+C=0(A≠0,A、B、C是常数)的形式,点P(x,y)到直线Ax+By+C=0的距
0 0
离可用公式d= 计算.
例如:求点P(3,4)到直线y=﹣2x+5的距离.
解:∵y=﹣2x+5
∴2x+y﹣5=0,其中A=2,B=1,C=﹣5
∴点P(3,4)到直线y=﹣2x+5的距离为:
d= = ==
根据以上材料解答下列问题:
(1)求点Q(﹣2,2)到直线3x﹣y+7=0的距离;
(2)如图,直线y=﹣x沿y轴向上平移2个单位得到另一条直线,求这两条平行直线之间
的距离.
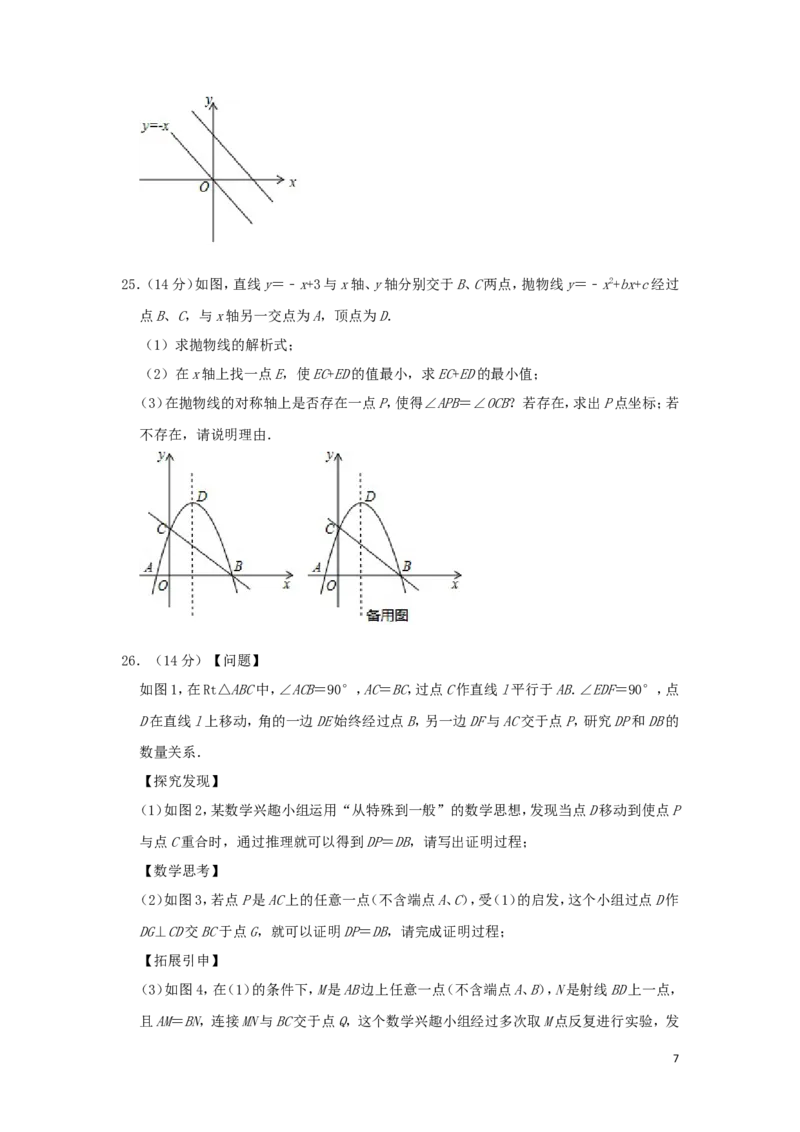
625.(14分)如图,直线y=﹣x+3与x轴、y轴分别交于B、C两点,抛物线y=﹣x2+bx+c经过
点B、C,与x轴另一交点为A,顶点为D.
(1)求抛物线的解析式;
(2)在x轴上找一点E,使EC+ED的值最小,求EC+ED的最小值;
(3)在抛物线的对称轴上是否存在一点P,使得∠APB=∠OCB?若存在,求出P点坐标;若
不存在,请说明理由.
26.(14分)【问题】
如图1,在Rt△ABC中,∠ACB=90°,AC=BC,过点C作直线l平行于AB.∠EDF=90°,点
D在直线l上移动,角的一边DE始终经过点B,另一边DF与AC交于点P,研究DP和DB的
数量关系.
【探究发现】
(1)如图2,某数学兴趣小组运用“从特殊到一般”的数学思想,发现当点D移动到使点P
与点C重合时,通过推理就可以得到DP=DB,请写出证明过程;
【数学思考】
(2)如图3,若点P是AC上的任意一点(不含端点A、C),受(1)的启发,这个小组过点D作
DG⊥CD交BC于点G,就可以证明DP=DB,请完成证明过程;
【拓展引申】
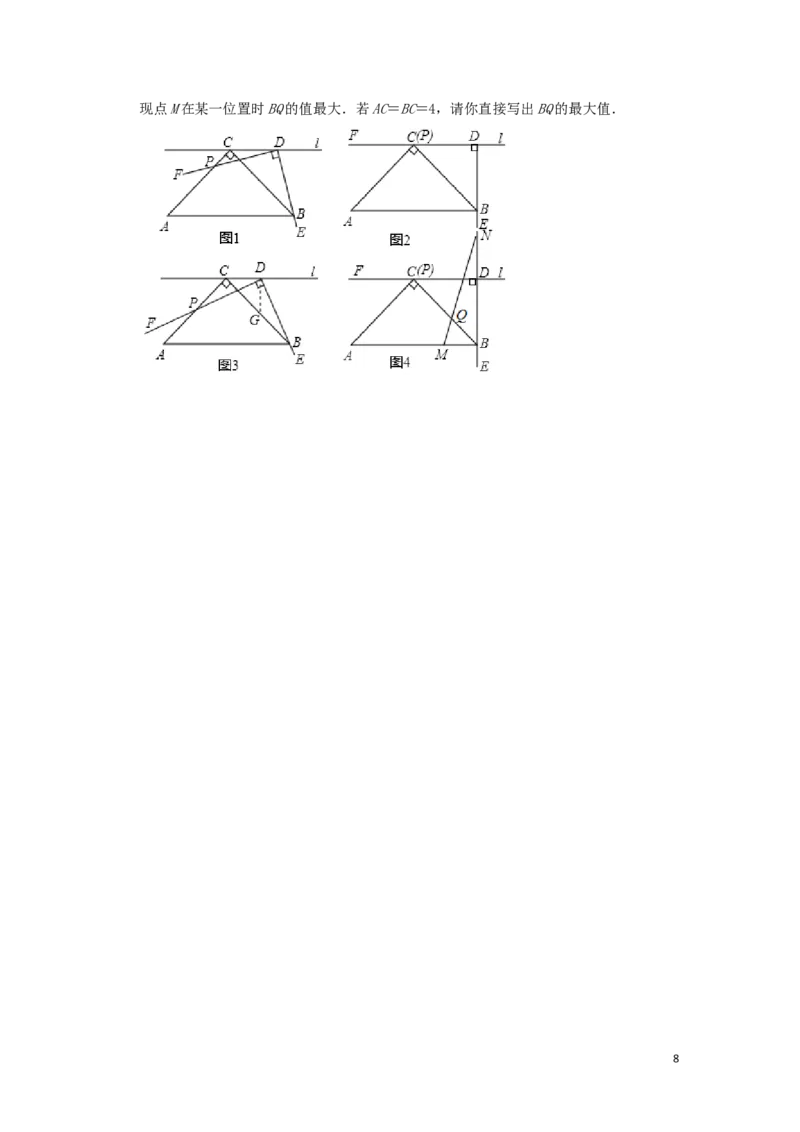
(3)如图4,在(1)的条件下,M是AB边上任意一点(不含端点A、B),N是射线BD上一点,
且AM=BN,连接MN与BC交于点Q,这个数学兴趣小组经过多次取M点反复进行实验,发
7现点M在某一位置时BQ的值最大.若AC=BC=4,请你直接写出BQ的最大值.
82019年内蒙古赤峰市中考数学试卷
参考答案与试题解析
一、选择题(每小题给出的选项中只有一个符合题意,请将符合题意的选项序号,在答题卡的
对应位置上按要求涂黑.每小题3分,共42分)
1.【解答】解:﹣4<﹣ <0<4,
∴在﹣4、﹣ 、0、4这四个数中,最小的数是﹣4.
故选:D.
2.【解答】解:60000=6×104,
故选:A.
3.【解答】解:A、 + 无法计算,故此选项错误;
B、x3•x2=x5,正确;
C、(x3)2=x6,故此选项错误;
D、x6÷x2=x4,故此选项错误;
故选:B.
4.【解答】解:A袋子中装有4个黑球和2个白球,摸出的三个球中可能为两个白球一个黑球,
所以A不是必然事件;
B.C.袋子中有4个黑球,有可能摸到的全部是黑球,B、C有可能不发生,所以B、C不是必
然事件;
D.白球只有两个,如果摸到三个球不可能都是白梂,因此至少有一个是黑球,D正确.
故选:D.
5.【解答】解:由于主视图和左视图为三角形可得此几何体为锥体,由俯视图为圆形可得为圆
锥.
故选:B.
6.【解答】解:
解不等式①得:x≥1,
解不等式②得:x>3,
∴不等式组的解集为x>3,
在数轴上表示为:
,
9故选:C.
7.【解答】解:由于容器的形状是下宽上窄,所以水的深度上升是先慢后快.
表现出的函数图形为先缓,后陡.
故选:D.
8.【解答】解:∵四边形ABCD为菱形,
∴CD=BC==5,且O为BD的中点,
∵E为CD的中点,
∴OE为△BCD的中位线,
∴OE=CB=2.5,
故选:A.
9.【解答】解:设月平均增长率为x,
根据题意得:400(1+x)2=900.
故选:D.
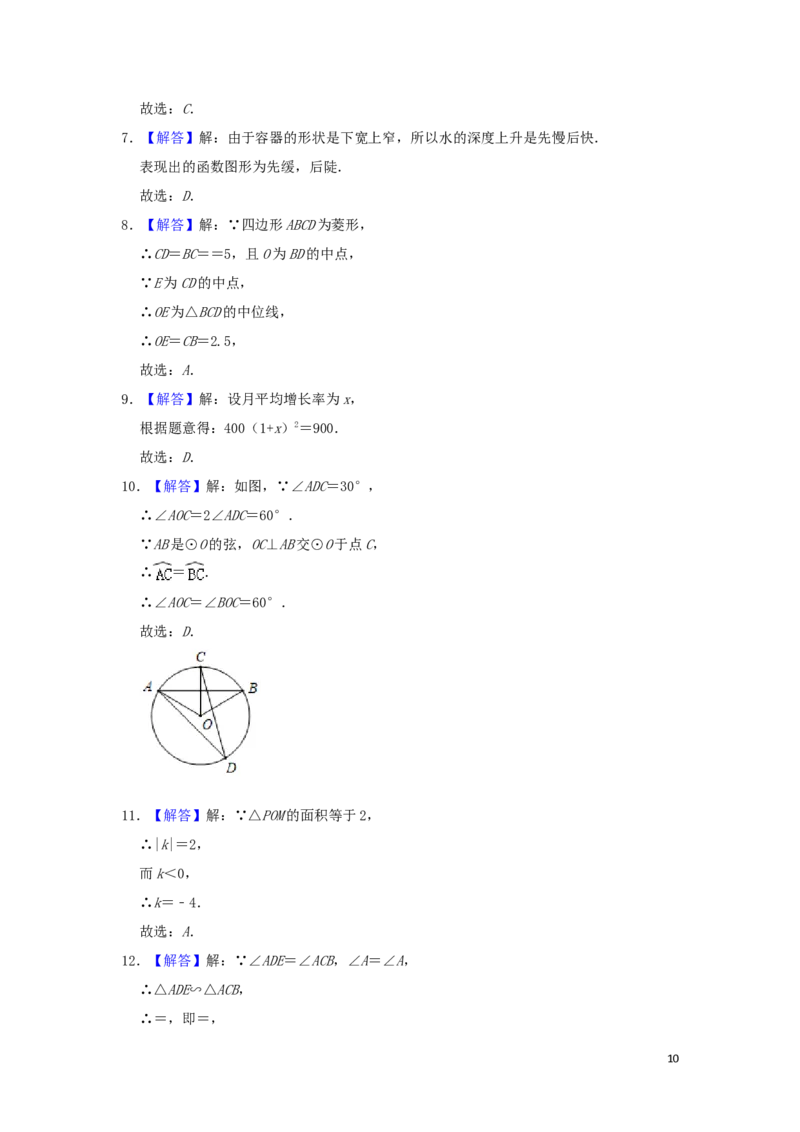
10.【解答】解:如图,∵∠ADC=30°,
∴∠AOC=2∠ADC=60°.
∵AB是⊙O的弦,OC⊥AB交⊙O于点C,
∴ = .
∴∠AOC=∠BOC=60°.
故选:D.
11.【解答】解:∵△POM的面积等于2,
∴|k|=2,
而k<0,
∴k=﹣4.
故选:A.
12.【解答】解:∵∠ADE=∠ACB,∠A=∠A,
∴△ADE∽△ACB,
∴=,即=,
10解得,AE=3,
故选:C.
13.【解答】解:∵DE⊥AB,∠A=35°
∴∠AFE=∠CFD=55°,
∴∠ACB=∠D+∠CFD=15°+55°=70°.
故选:B.
14.【解答】解:正方形纸片四角向内折叠,使四个顶点重合,展开后沿折痕剪开,
第一次:余下面积,
第二次:余下面积 ,
第三次:余下面积 ,
当完成第2019次操作时,余下纸片的面积为 ,
故选:C.
二、填空题(请把答案填写在答题卡相应的横线上.每小题3分,共12分)
15.【解答】解:原式=x(x2﹣2xy+y2)=x(x﹣y)2,
故答案为:x(x﹣y)2
16.【解答】解:由统计表可知,
甲和乙的平均数、中位数和众数都相等,
由折线统计图可知,乙的波动小,成绩比较稳定,
故答案为:乙.
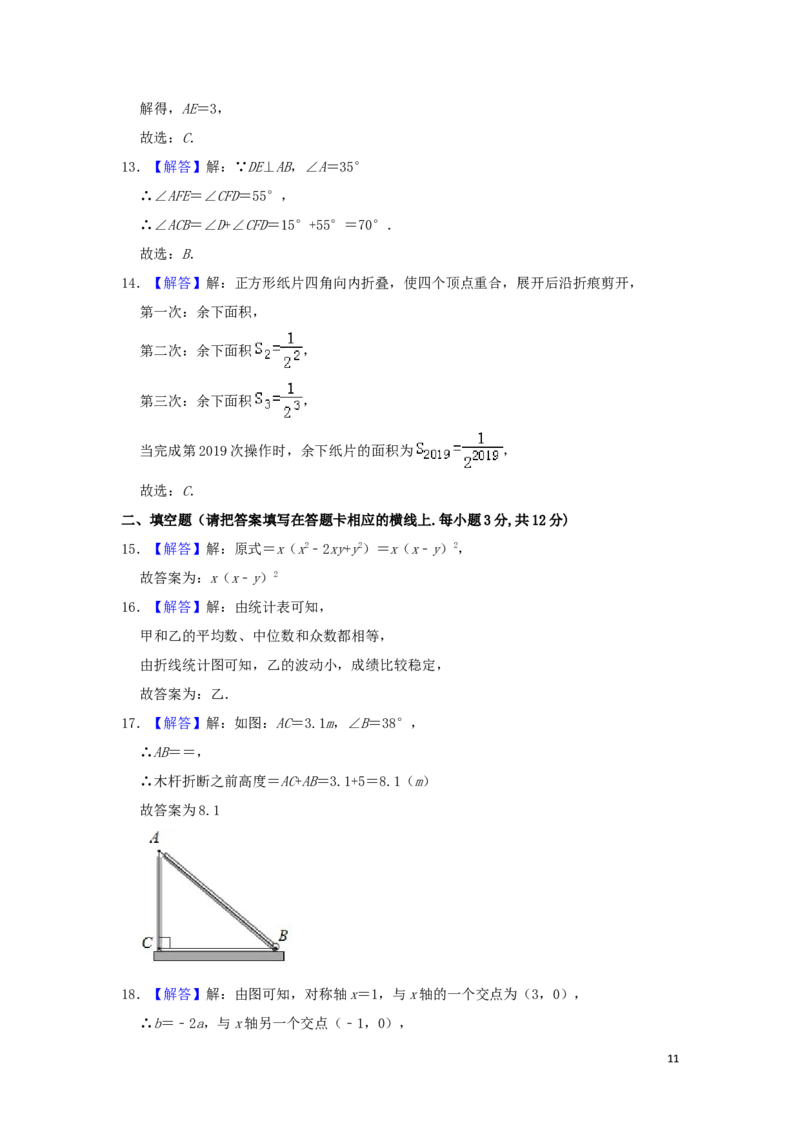
17.【解答】解:如图:AC=3.1m,∠B=38°,
∴AB==,
∴木杆折断之前高度=AC+AB=3.1+5=8.1(m)
故答案为8.1
18.【解答】解:由图可知,对称轴x=1,与x轴的一个交点为(3,0),
∴b=﹣2a,与x轴另一个交点(﹣1,0),
11①∵a>0,
∴b<0;
∴①错误;
②当x=﹣1时,y=0,
∴a﹣b+c=0;
②正确;
③一元二次方程ax2+bx+c+1=0可以看作函数y=ax2+bx+c与y=﹣1的交点,
由图象可知函数y=ax2+bx+c与y=﹣1有两个不同的交点,
∴一元二次方程ax2+bx+c+1=0(a≠0)有两个不相等的实数根;
∴③正确;
④由图象可知,y>0时,x<﹣1或x>3
∴④正确;
故答案为②③④.
三、解答题(在答题卡上解答,答在本试卷上无效,解答时要写出必要的文字说明、证明过程
或演算步骤.共8题,满分96分)
19.【解答】解: ÷+
=
=
=,
当a=|1﹣ |﹣tan60°+()﹣1= ﹣1﹣ +2=1时,原式=.
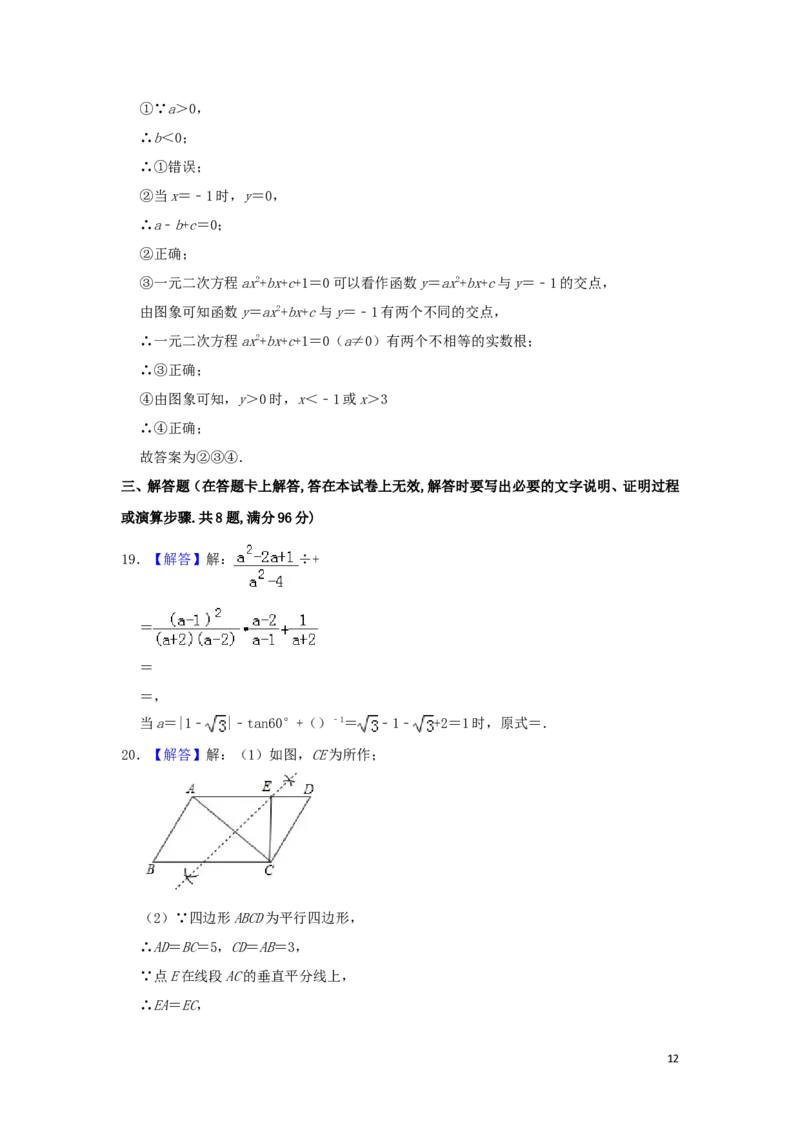
20.【解答】解:(1)如图,CE为所作;
(2)∵四边形ABCD为平行四边形,
∴AD=BC=5,CD=AB=3,
∵点E在线段AC的垂直平分线上,
∴EA=EC,
12∴△DCE的周长=CE+DE+CD=EA+DE+CD=AD+CD=5+3=8.
21.【解答】解:(1)16÷32%=50,
所以随机抽取学生共50名,
2本所在扇形的圆心角度数=360°×=216°;
4本的人数为50﹣2﹣16﹣30=2(人),
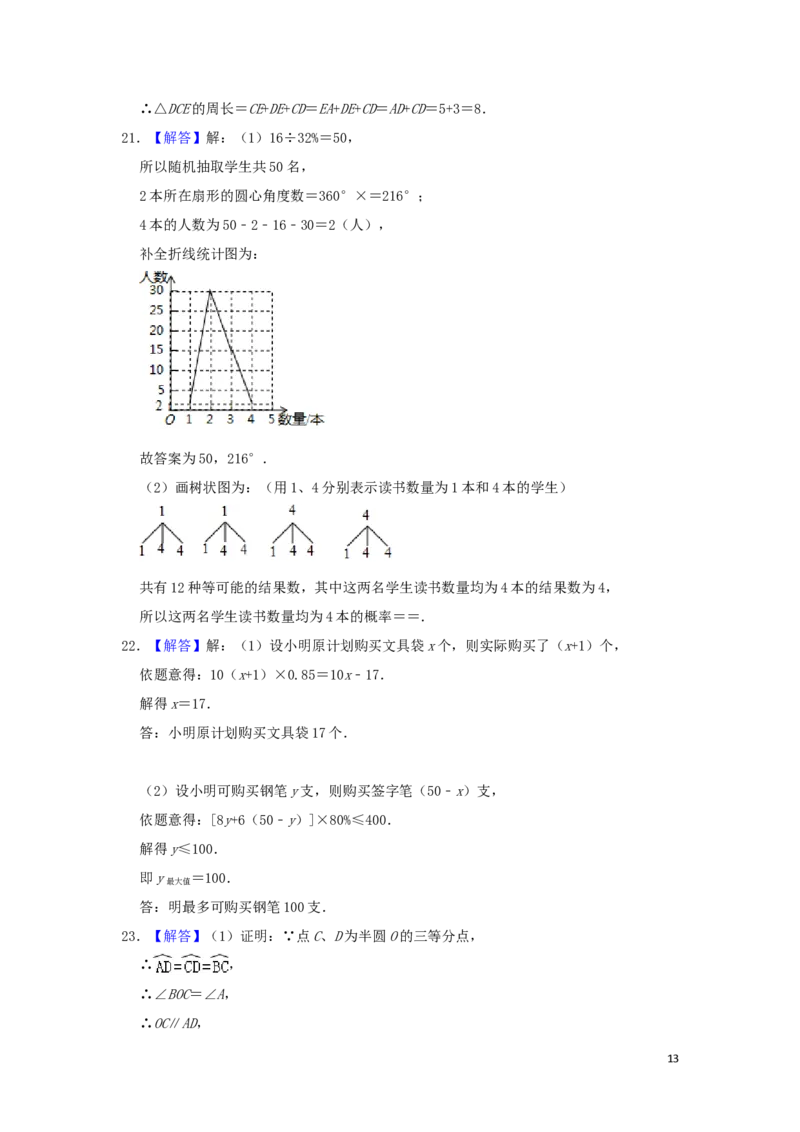
补全折线统计图为:
故答案为50,216°.
(2)画树状图为:(用1、4分别表示读书数量为1本和4本的学生)
共有12种等可能的结果数,其中这两名学生读书数量均为4本的结果数为4,
所以这两名学生读书数量均为4本的概率==.
22.【解答】解:(1)设小明原计划购买文具袋x个,则实际购买了(x+1)个,
依题意得:10(x+1)×0.85=10x﹣17.
解得x=17.
答:小明原计划购买文具袋17个.
(2)设小明可购买钢笔y支,则购买签字笔(50﹣x)支,
依题意得:[8y+6(50﹣y)]×80%≤400.
解得y≤100.
即y =100.
最大值
答:明最多可购买钢笔100支.
23.【解答】(1)证明:∵点C、D为半圆O的三等分点,
∴ ,
∴∠BOC=∠A,
∴OC∥AD,
13∵CE⊥AD,
∴CE⊥OC,
∴CE为⊙O的切线;
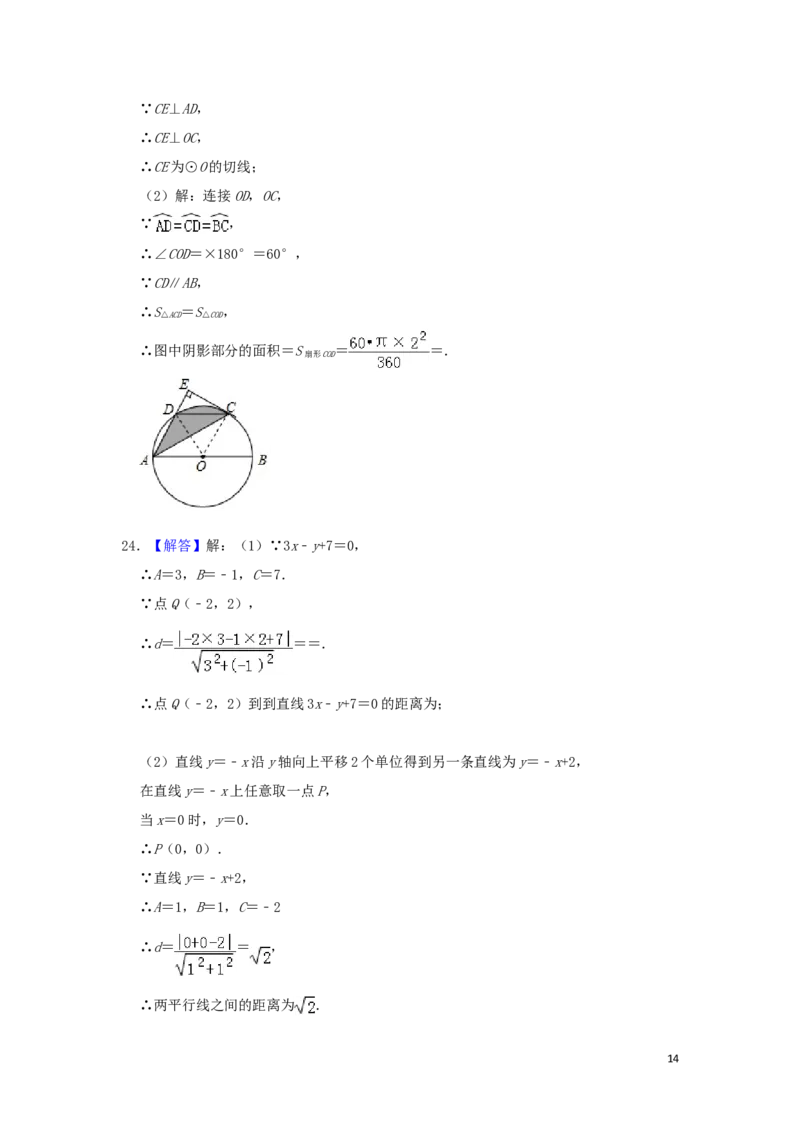
(2)解:连接OD,OC,
∵ ,
∴∠COD=×180°=60°,
∵CD∥AB,
∴S =S ,
△ACD △COD
∴图中阴影部分的面积=S = =.
扇形COD
24.【解答】解:(1)∵3x﹣y+7=0,
∴A=3,B=﹣1,C=7.
∵点Q(﹣2,2),
∴d= ==.
∴点Q(﹣2,2)到到直线3x﹣y+7=0的距离为;
(2)直线y=﹣x沿y轴向上平移2个单位得到另一条直线为y=﹣x+2,
在直线y=﹣x上任意取一点P,
当x=0时,y=0.
∴P(0,0).
∵直线y=﹣x+2,
∴A=1,B=1,C=﹣2
∴d= = ,
∴两平行线之间的距离为 .
1425.【解答】解:(1)直线y=﹣x+3与x轴、y轴分别交于B、C两点,则点B、C的坐标分别为
(3,0)、(0,3),
将点B、C的坐标代入二次函数表达式得:,解得:,
故函数的表达式为:y=﹣x2+2x+3,
令y=0,则x=﹣1或3,故点A(﹣1,0);
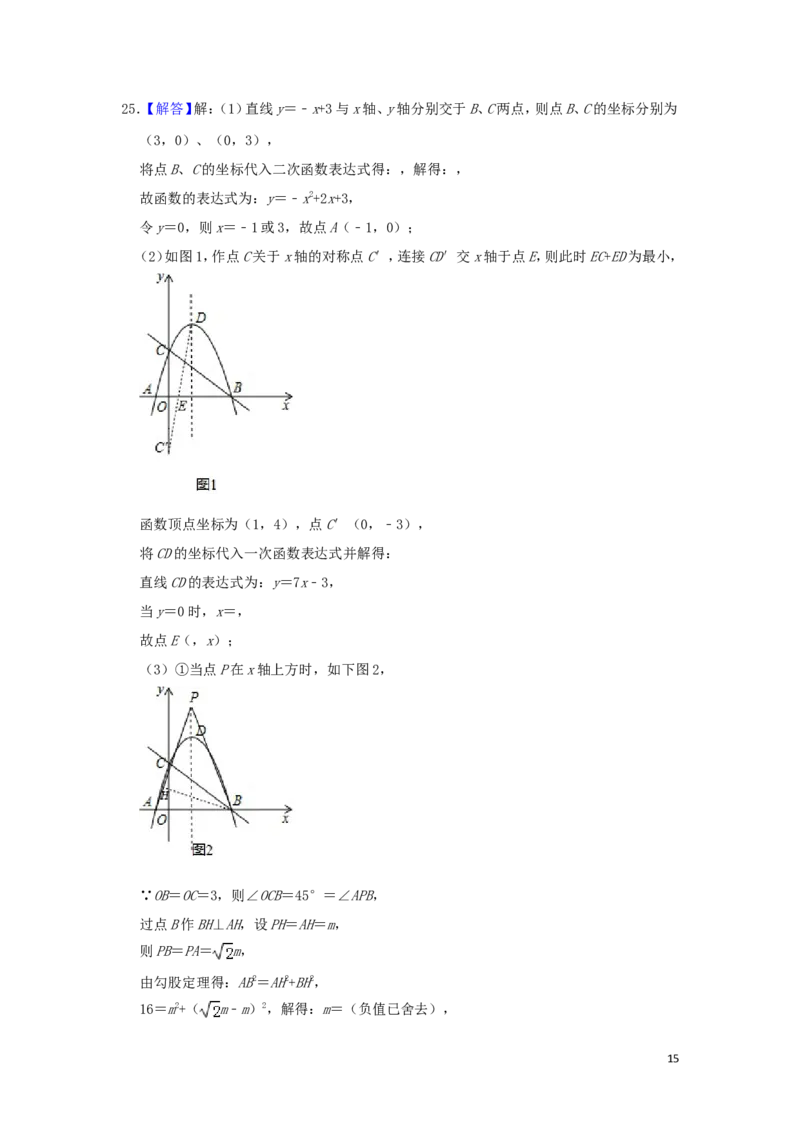
(2)如图1,作点C关于x轴的对称点C′,连接CD′交x轴于点E,则此时EC+ED为最小,
函数顶点坐标为(1,4),点C′(0,﹣3),
将CD的坐标代入一次函数表达式并解得:
直线CD的表达式为:y=7x﹣3,
当y=0时,x=,
故点E(,x);
(3)①当点P在x轴上方时,如下图2,
∵OB=OC=3,则∠OCB=45°=∠APB,
过点B作BH⊥AH,设PH=AH=m,
则PB=PA= m,
由勾股定理得:AB2=AH2+BH2,
16=m2+( m﹣m)2,解得:m=(负值已舍去),
15则PB= m=1+ ,
则y= = ;
P
②当点P在x轴下方时,
则y=﹣( );
P
故点P的坐标为(1, )或(1, ).
26.【解答】证明:【探究发现】
(1)∵∠ACB=90°,AC=BC
∴∠CAB=∠CBA=45°
∵CD∥AB
∴∠CBA=∠DCB=45°,且BD⊥CD
∴∠DCB=∠DBC=45°
∴DB=DC
即DB=DP
【数学思考】
(2)∵DG⊥CD,∠DCB=45°
∴∠DCG=∠DGC=45°
∴DC=DG,∠DCP=∠DGB=135°,
∵∠BDP=∠CDG=90°
∴∠CDP=∠BDG,且DC=DG,∠DCP=∠DGB=135°,
∴△CDP≌△GDB(ASA)
∴BD=DP
【拓展引申】
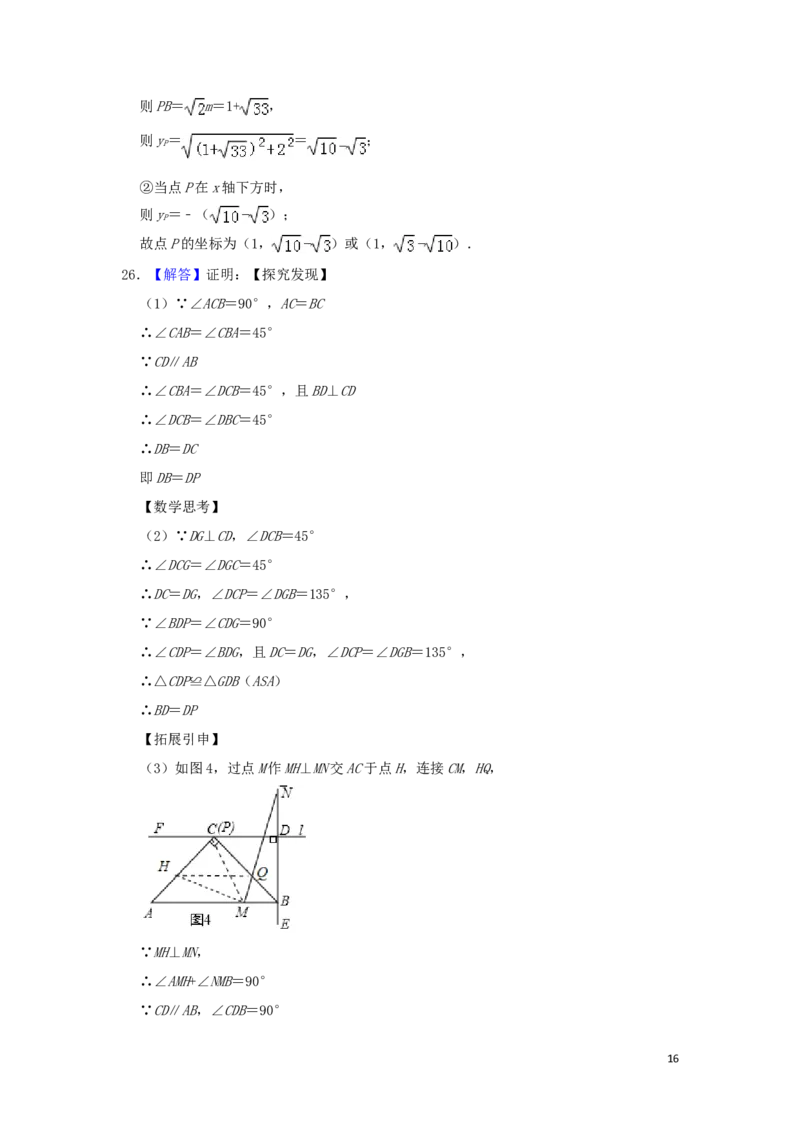
(3)如图4,过点M作MH⊥MN交AC于点H,连接CM,HQ,
∵MH⊥MN,
∴∠AMH+∠NMB=90°
∵CD∥AB,∠CDB=90°
16∴∠DBM=90°
∴∠NMB+∠MNB=90°
∴∠HMA=∠MNB,且AM=BN,∠CAB=∠CBN=45°
∴△AMH≌△BNQ(ASA)
∴AH=BQ
∵∠ACB=90°,AC=BC=4,
∴AB=4 ,AC﹣AH=BC﹣BQ
∴CH=CQ
∴∠CHQ=∠CQH=45°=∠CAB
∴HQ∥AB
∴∠HQM=∠QMB
∵∠ACB=∠HMQ=90°
∴点H,点M,点Q,点C四点共圆,
∴∠HCM=∠HQM
∴∠HCM=∠QMB,且∠A=∠CBA=45°
∴△ACM∽△BMQ
∴
∴
∴BQ=
∴AM=2 时,BQ有最大值为2.
1718