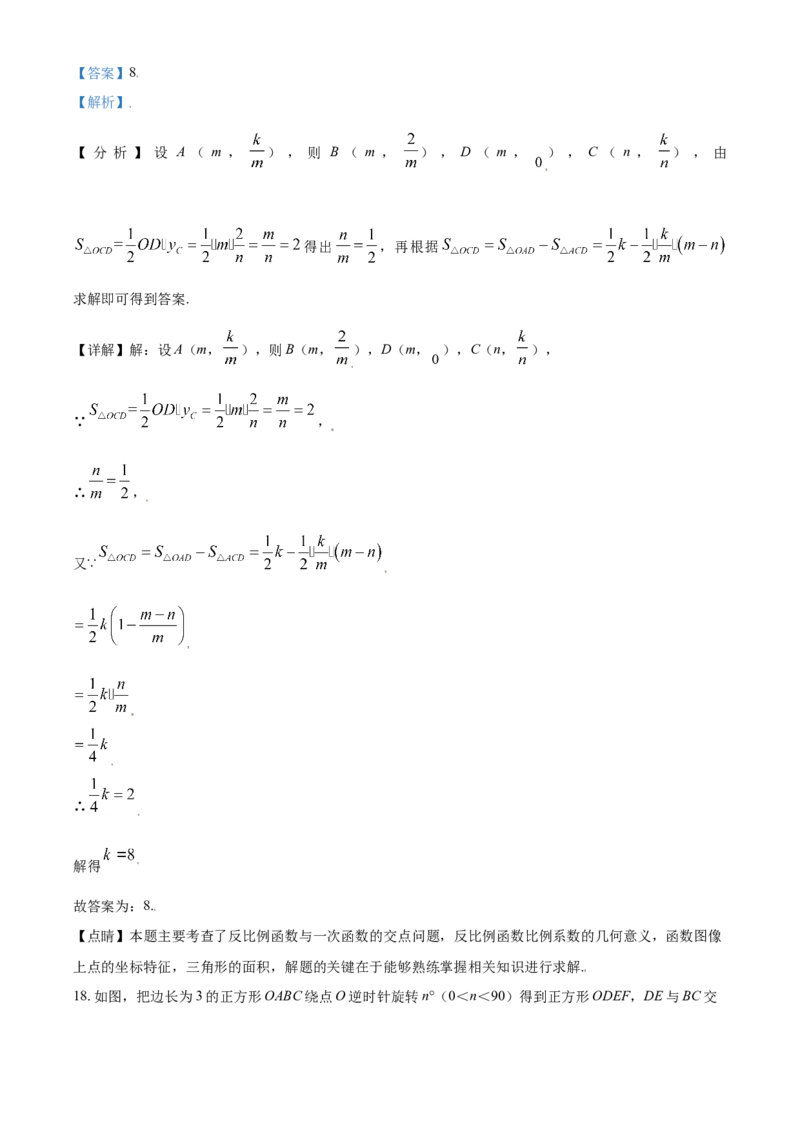文档内容
2021 年四川省巴中市中考数学试卷
一、选择题
1. 下列各式的值最小的是( )
A. 20 B. |﹣2| C. 2﹣1 D. ﹣(﹣2)
【答案】C
【解析】
【分析】直接利用零指数幂的性质以及负整数指数幂的性质、绝对值的性质、相反数分别化简得出答案.
【详解】解:20=1,|-2|=2,2-1= ,-(-2)=2,
∵ <1<2,
∴最小的是2-1.
故选:C.
【点睛】此题主要考查了零指数幂的性质以及负整数指数幂的性质、绝对值的性质、相反数,正确化简各
数是解题关键.
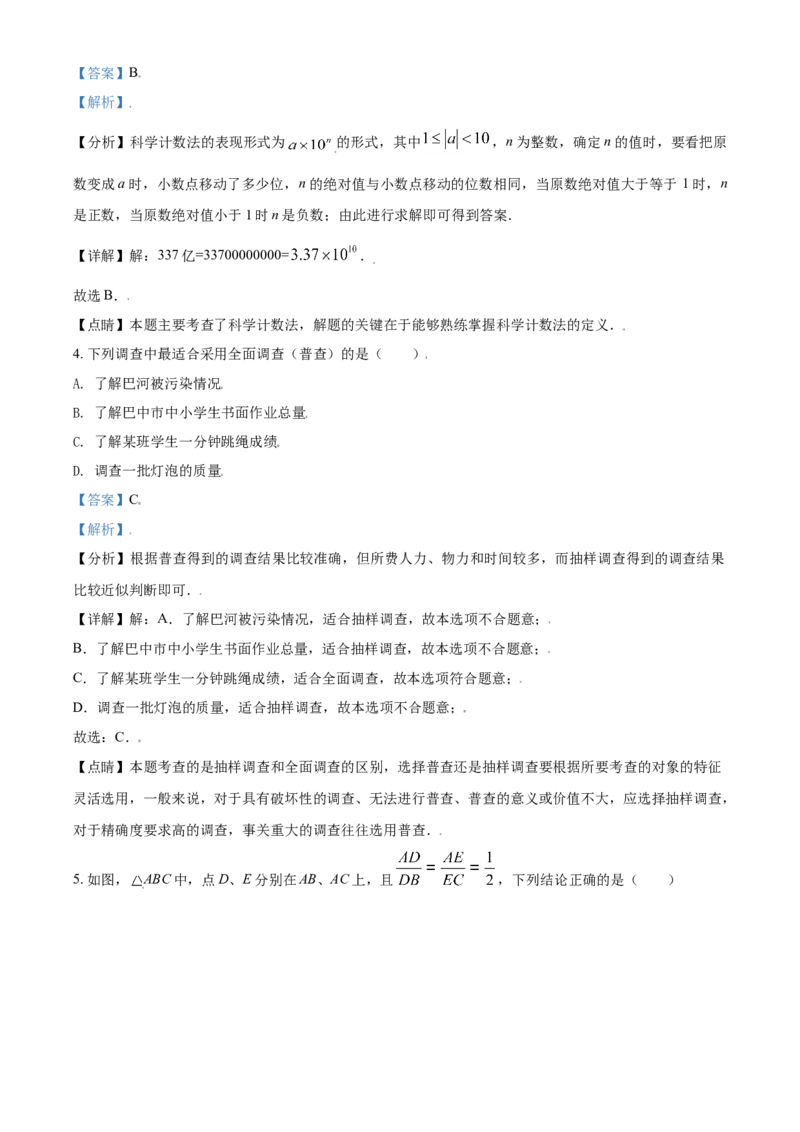
2. 某立体图形的表面展开图如图所示,这个立体图形是( )
A. B. C. D.
【答案】A
【解析】
【分析】利用立体图形及其表面展开图的特点解题.
【详解】解:四个三角形和一个四边形,是四棱锥的组成,所以该立体图形的名称为四棱锥.
故选:A.
【点睛】本题考查了几何体的展开图,熟练掌握常见立体图形的平面展开图的特征,是解决此类问题的关
键.
3. 据中央电视台新闻联播报道:今年4月我国国际收支口径的国际货物和服务贸易顺差337亿美元.用科
学记数法表示337亿正确的是( )
A. 337×108 B. 3.37×1010 C. 3.37×1011 D. 0.337×1011【答案】B
【解析】
【分析】科学计数法的表现形式为 的形式,其中 ,n为整数,确定n的值时,要看把原
数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,当原数绝对值大于等于 1时,n
是正数,当原数绝对值小于1时n是负数;由此进行求解即可得到答案.
【详解】解:337亿=33700000000= .
故选B.
【点睛】本题主要考查了科学计数法,解题的关键在于能够熟练掌握科学计数法的定义.
4. 下列调查中最适合采用全面调查(普查)的是( )
A. 了解巴河被污染情况
B. 了解巴中市中小学生书面作业总量
C. 了解某班学生一分钟跳绳成绩
D. 调查一批灯泡的质量
【答案】C
【解析】
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果
比较近似判断即可.
【详解】解:A.了解巴河被污染情况,适合抽样调查,故本选项不合题意;
B.了解巴中市中小学生书面作业总量,适合抽样调查,故本选项不合题意;
C.了解某班学生一分钟跳绳成绩,适合全面调查,故本选项符合题意;
D.调查一批灯泡的质量,适合抽样调查,故本选项不合题意;
故选:C.
【点睛】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征
灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,
对于精确度要求高的调查,事关重大的调查往往选用普查.
5. 如图, ABC中,点D、E分别在AB、AC上,且 ,下列结论正确的是( )A. DE:BC=1:2
的
B. ADE与 ABC 面积比为1:3
C. ADE与 ABC的周长比为1:2
.
D DE BC
【答案】D
【解析】
【分析】根据相似三角形的判定与性质进行逐一判断即可.
【详解】解:∵ ,
∴AD:AB=AE:AC=1:3,
∵∠A=∠A,
∴△ADE∽△ABC,
∴DE:BC=1:3,故A错误;
∵△ADE∽△ABC,
∴△ADE与 ABC的面积比为1:9,周长的比为1:3,故B和C错误;
∵△ADE∽△△ABC,
∴∠ADE=∠B,
∴DE∥BC.故D正确.
故选:D.
【点睛】本题考查了相似三角形的判定与性质,解决本题的关键是掌握相似三角形的判定与性质.
6. 关于x的分式方程 3=0有解,则实数m应满足的条件是( )
A. m=﹣2 B. m≠﹣2 C. m=2 D. m≠2
【答案】B
【解析】【分析】解分式方程得: 即 ,由题意可知 ,即可得到 .
【详解】解:
方程两边同时乘以 得: ,
∴ ,
∵分式方程有解,
∴ ,
∴ ,
∴ ,
∴ ,
故选B.
【点睛】本题主要考查了分式方程的解,熟练掌握分式方程的解法,理解分式方程有意义的条件是解题的
关键.
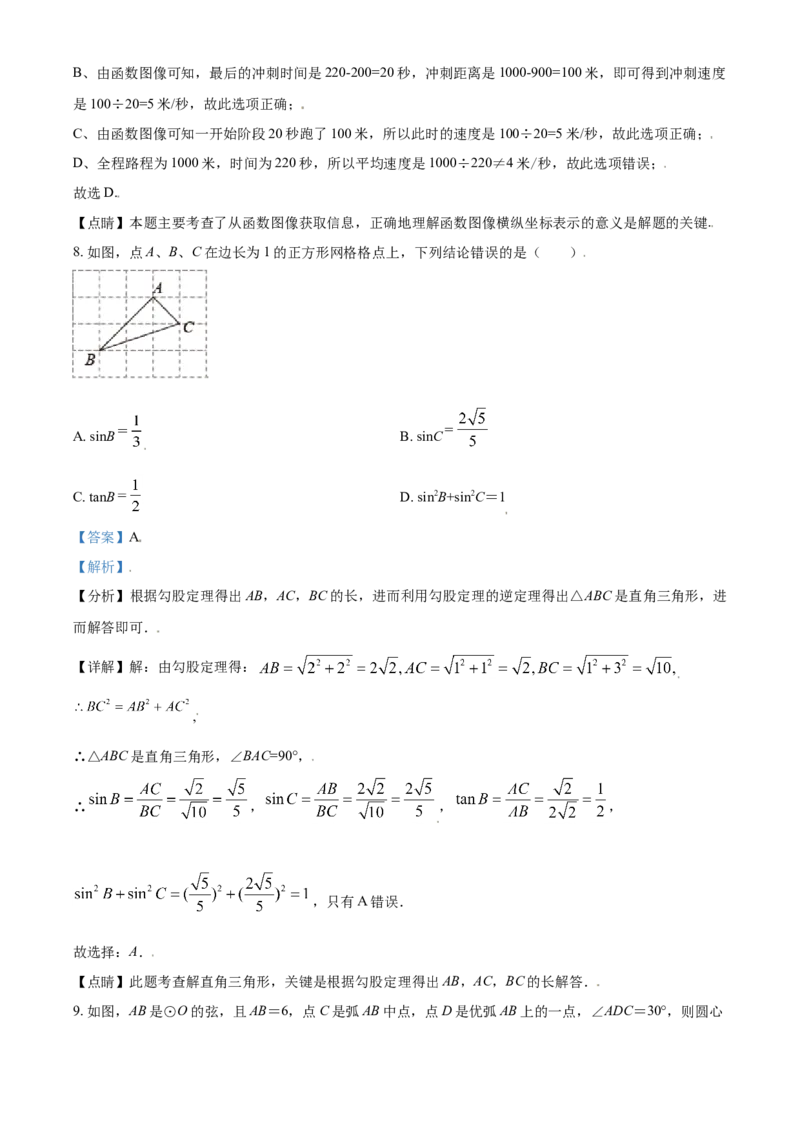
7. 小风在1000米中长跑训练时,已跑路程x(米)与所用时间t(秒)之间的函数图象如图所示,下列说
法错误的是( )
A. 小风的成绩是220秒
B. 小风最后冲刺阶段的速度是5米/秒
C. 小风第一阶段与最后冲刺阶段速度相等
D. 小风的平均速度是4米/秒
【答案】D
【解析】
【分析】根据函数图像上的数据,求出相应阶段的速度即可得到正确的结论.
【详解】解:A、由函数图像可知,小风到底终点的时间是220秒,故此选项正确;B、由函数图像可知,最后的冲刺时间是220-200=20秒,冲刺距离是1000-900=100米,即可得到冲刺速度
是100÷20=5米/秒,故此选项正确;
C、由函数图像可知一开始阶段20秒跑了100米,所以此时的速度是100÷20=5米/秒,故此选项正确;
D、全程路程为1000米,时间为220秒,所以平均速度是1000÷220≠4米/秒,故此选项错误;
故选D.
【点睛】本题主要考查了从函数图像获取信息,正确地理解函数图像横纵坐标表示的意义是解题的关键.
8. 如图,点A、B、C在边长为1的正方形网格格点上,下列结论错误的是( )
A. sinB B. sinC
C. tanB D. sin2B+sin2C=1
【答案】A
【解析】
【分析】根据勾股定理得出AB,AC,BC的长,进而利用勾股定理的逆定理得出△ABC是直角三角形,进
而解答即可.
【详解】解:由勾股定理得:
,
∴△ABC是直角三角形,∠BAC=90°,
∴ , , ,
,只有A错误.
故选择:A.
【点睛】此题考查解直角三角形,关键是根据勾股定理得出AB,AC,BC的长解答.
9. 如图,AB是⊙O的弦,且AB=6,点C是弧AB中点,点D是优弧AB上的一点,∠ADC=30°,则圆心O到弦AB的距离等于( )
A. B. C. D.
【答案】C
【解析】
【分析】连接OA,AC,OC,OC交AB于E,先根据垂径定理求出AE=3,然后证明三角形OAC是等边三
角形,从而可以得到∠OAE=30°,再利用三线合一定理求解即可.
【详解】解:如图所示,连接OA,AC,OC,OC交AB于E,
∵C是弧AB的中点,AB=6,
∴OC⊥AB,AE=BE=3,
∵∠ADC=30°,
∴∠AOC=2∠ADC=60°,
又∵OA=OC,
∴△OAC是等边三角形,
∵OC⊥AB,
∴ , ,
∴
∴
∴圆心O到弦AB的距离为 ,
故选C.【点睛】本题主要考查了圆周角与圆心角的关系,等边三角形的性质与判定,勾股定理,垂径定理,解题
的关键在于能够熟练掌握相关知识进行求解.
10. 两千多年前,古希腊数学家欧多克索斯发现了黄金分割,即:如图,点P是线段AB上一点(AP>
BP),若满足 ,则称点P是AB的黄金分割点.黄金分割在日常生活中处处可见,例如:主持
人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好.若舞台长20米,主持人从舞台一侧进
入,设他至少走x米时恰好站在舞台的黄金分割点上,则x满足的方程是( )
A. (20﹣x)2=20x B. x2=20(20﹣x)
C. x(20﹣x)=202 D. 以上都不对
【答案】A
【解析】
【分析】点P是AB的黄金分割点,且PB<PA,PB=x,则PA=20−x,则 ,即可求解.
【详解】解:由题意知,点P是AB的黄金分割点,
且PB<PA,PB=x,则PA=20−x,
∴ ,
∴(20−x)2=20x,
故选:A.
【点睛】本题考查了黄金分割,理解黄金分割的概念,找出黄金分割中成比例的对应线段是解决问题的关
键.
11. 如图,矩形AOBC的顶点A、B在坐标轴上,点C的坐标是(﹣10,8),点D在AC上,将 BCD沿BD
翻折,点C恰好落在OA边上点E处,则tan∠DBE等于( )A. B. C. D.
【答案】D
【解析】
【分析】先根据四边形ABCD是矩形,C(-10,8),得出BC=AO=10,AC=OB=8,∠A=∠O=∠C=90°,
再由折叠的性质得到CD=DE,BC=BE=10,∠DEB=∠C=90°,利用勾股定理先求出OE的长,即可得到
AE,再利用勾股定理求出DE,利用 求解即可.
【详解】解:∵四边形ABCD是矩形,C(-10,8),
∴BC=AO=10,AC=OB=8,∠A=∠O=∠C=90°,
由折叠的性质可知:CD=DE,BC=BE=10,∠DEB=∠C=90°,
在直角三角形BEO中: ,
∴ ,
设 ,则
在直角三角形ADE中: ,
∴ ,
解得 ,
∴ ,
∵∠DEB=90°,
∴ ,
故选D.【点睛】本题主要考查了矩形的性质,折叠的性质,勾股定理,三角函数,解题的关键在于能够熟练掌握
相关知识进行求解.
12. 已知二次函数y=ax2+bx+c的自变量x与函数y的部分对应值见表格,则下列结论:①c=2;②b2﹣
4ac>0;③方程ax2+bx=0的两根为x=﹣2,x=0;④7a+c<0.其中正确的有( )
1 2
x … ﹣3 ﹣2 ﹣1 1 2 …
y … 1.875 3 m 1.875 0 …
A. ①④ B. ②③ C. ③④ D. ②④
【答案】B
【解析】
【分析】由表格可以得到二次函数图象经过点点(-3,1.875)和点(1,1.875),这两点关于对称轴对称,
由此得到对称轴直线,设出二次函数顶点式,代入两点,求解出二次函数解析式,得到 a,b,c的值,依
次代入到①②③④中进行判断即可解决.
【详解】解:由表格可以得到,二次函数图象经过点 和点 ,
点 与点 是关于二次函数对称轴对称的,
二次函数的对称轴为直线 ,
设二次函数解析式为 ,
代入点 , 得,
,解得 ,
二次函数的解析式为: ,
,
,
①是错误的,
,
②是正确的,
方程 为 ,
即为 ,
, ,
③是正确的,
,
④是错误的,
②③是正确的,
故选:B.
【点睛】本题考查了二次函数系数特征和二次函数解析式求法,利用待定系数法求解函数解析式是通法,
由表格提炼出对称轴 的信息,是解题的突破口,此题,也可以通过二次函数系数特征来解决.
二、填空题
13. 函数y 中自变量x的取值范围是___________.
【答案】x≤2且x≠−3
【解析】
【分析】根据被开方数大于等于0,分母不等于0列式计算即可得解.【详解】解:由题意得,2−x≥0且x+3≠0,
解得x≤2且x≠−3.
故答案为:x≤2且x≠−3.
【点睛】本题考查了函数自变量的范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可
取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,
被开方数非负.
14. 关于x的方程2x2+mx﹣4=0的一根为x=1,则另一根为________.
【答案】x=-2
2
【解析】
【分析】设方程的另一根为x,根据根与系数的关系可得x=-2,解答出即可.
2 2
【详解】解:设方程的另一根为x,
2
∵关于x的方程2x2+mx-4=0的一根为x=1,
则1×x= =-2,
2
解得x=-2.
2
故答案为:x=-2.
2
【点睛】本题主要考查了一元二次方程根与系数的关系:x,x 是一元二次方程ax2+bx+c=0(a≠0)的两根
1 2
时,x+x= ,x•x= .
1 2 1 2
15. 为优选品种,某农业科技小组对甲、乙两种杂交水稻进行种植对比试验研究,近五年来这两种杂交水
稻的亩产量的平均数 (单位:千克)及方差s2见表格.明年准备从中选出一种品质更优的杂交水稻进行
种植,则应选的品种是_______.
甲 乙
880 880
s2 2160 2500
【答案】甲
【解析】
【分析】由表格可知两者的平均数相同,比较方差的大小即可.
【详解】解:由表格可知甲、乙两种水稻的平均数相同,但是甲的方差小于乙的方差∴甲更稳定,
∴应该选甲,
故答案为:甲.
【点睛】本题主要考查了利用方差作决策,解题的关键在于能够熟练掌握方差的定义.
16. y与x之间的函数关系可记为y=f(x).例如:函数y=x2可记为f(x)=x2.若对于自变量取值范围
内的任意一个x,都有f(﹣x)=f(x),则f(x)是偶函数;若对于自变量取值范围内的任意一个x,都
有f(﹣x)=﹣f(x),则f(x)是奇函数.例如:f(x)=x2是偶函数,f(x) 是奇函数.若f(x)
=ax2+(a﹣5)x+1是偶函数,则实数a=__________.
【答案】5
【解析】
【分析】由f(x)=ax2+(a-5)x+1是偶函数,得a(-x)2+(a-5)•(-x)+1=ax2+(a-5)x+1,解得a=5.
【详解】解:∵f(x)=ax2+(a-5)x+1是偶函数,
∴对于自变量取值范围内的任意一个x,都有f(-x)=f(x),即a(-x)2+(a-5)•(-x)+1=ax2+(a-5)
x+1,
∴(10-2a)x=0,可知10-2a=0,
∴a=5,
故答案为:5.
【点睛】本题考查新定义:偶函数与奇函数,解题的关键是理解偶函数定义,列出a(-x)2+(a-5)•(-
x)+1=ax2+(a-5)x+1.
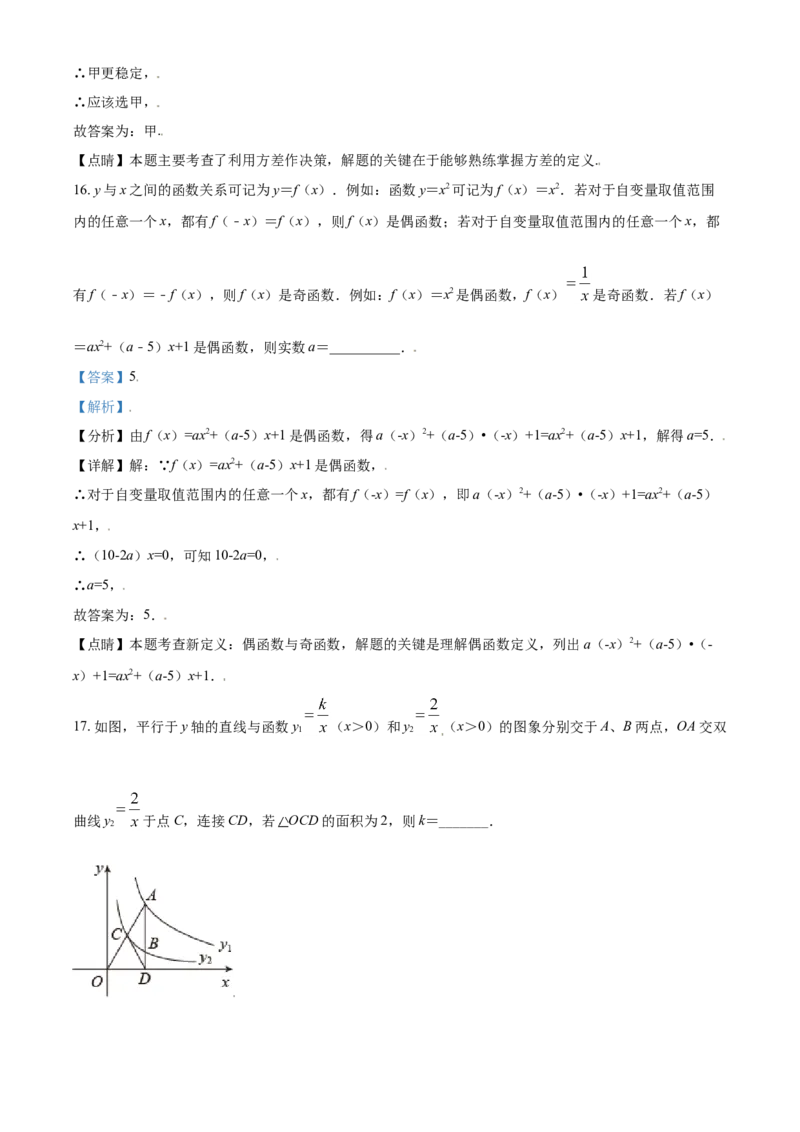
17. 如图,平行于y轴的直线与函数y (x>0)和y (x>0)的图象分别交于A、B两点,OA交双
1 2
曲线y 于点C,连接CD,若 OCD的面积为2,则k=_______.
2【答案】8
【解析】
【 分 析 】 设 A ( m , ) , 则 B ( m , ) , D ( m , ) , C ( n , ) , 由
得出 ,再根据
求解即可得到答案.
【详解】解:设A(m, ),则B(m, ),D(m, ),C(n, ),
∵ ,
∴ ,
又∵
∴
解得
故答案为:8.
【点睛】本题主要考查了反比例函数与一次函数的交点问题,反比例函数比例系数的几何意义,函数图像
上点的坐标特征,三角形的面积,解题的关键在于能够熟练掌握相关知识进行求解.
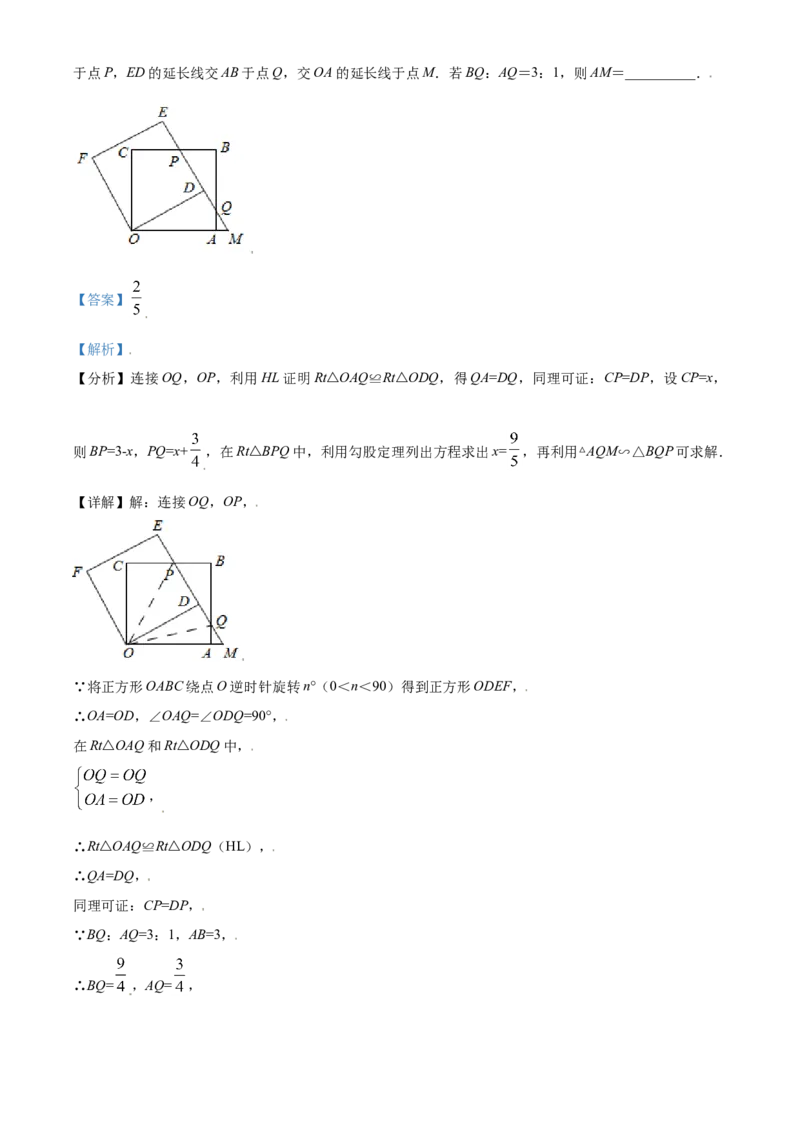
18. 如图,把边长为3的正方形OABC绕点O逆时针旋转n°(0<n<90)得到正方形ODEF,DE与BC交于点P,ED的延长线交AB于点Q,交OA的延长线于点M.若BQ:AQ=3:1,则AM=__________.
【答案】
【解析】
【分析】连接OQ,OP,利用HL证明Rt△OAQ≌Rt△ODQ,得QA=DQ,同理可证:CP=DP,设CP=x,
则BP=3-x,PQ=x+ ,在Rt△BPQ中,利用勾股定理列出方程求出x= ,再利用△AQM∽△BQP可求解.
【详解】解:连接OQ,OP,
∵将正方形OABC绕点O逆时针旋转n°(0<n<90)得到正方形ODEF,
∴OA=OD,∠OAQ=∠ODQ=90°,
在Rt△OAQ和Rt△ODQ中,
,
∴Rt△OAQ≌Rt△ODQ(HL),
∴QA=DQ,
同理可证:CP=DP,
∵BQ:AQ=3:1,AB=3,
∴BQ= ,AQ= ,设CP=x,则BP=3-x,PQ=x+ ,
在Rt△BPQ中,由勾股定理得:
(3-x)2+( )2=(x+ )2,
解得x= ,
∴BP= ,
∵∠AQM=∠BQP,∠BAM=∠B,
∴△AQM∽△BQP,
∴ ,
∴ ,
∴AM= .
故答案为: .
【点睛】本题主要考查了旋转的性质,全等三角形的判定与性质,勾股定理,相似三角形的判定与性质等
知识,利用全等证明QA=DQ,CP=DP是解题的关键.
三、解答题
19. (1)计算:2sin60°+| 2|﹣( )﹣1 ;
(2)解不等式组 ,并把解集在数轴上表示出来;(3)先化简,再求值: (1 ),请从﹣4,﹣3,0,1中选一个合适的数作为a的值
代入求值.
【答案】(1) (2)−3<x≤−1;数轴见解析(3) ;当a=1时,原式=5
【解析】
【分析】(1)根据特殊角的三角函数值、去绝对值的方法、负整数指数幂、二次根式的除法可以解答本
题;
(2)先求出每个不等式的解集,然后取其公共部分,即可得到不等式组的解集,然后再在数轴上表示出
来即可;
(3)根据分式的除法和加法可以化简题目中的式子,然后从−4,−3,0,1中选一个使得原分式有意义的
值代入化简后的式子即可解答本题.
【详解】解:(1)2sin60°+| 2|﹣( )-1
=
;
(2) ,
解不等式①,得
x>−3,
解不等式②,得
x≤−1,
∴原不等式组的解集是−3<x≤−1,
解集在数轴上表示如下:
;(3) (1 )
=
=
= ,
∵a(a+3)≠0,a+4≠0,
∴a≠−4,−3,0,
∴a=1,
当a=1时,原式= =5.
【点睛】本题考查特殊角的三角函数值、去绝对值的方法、负整数指数幂、二次根式的除法、解一元一次
不等式组、分式的化简求值,解答本题的关键是明确它们各自的计算方法,认真计算,注意要检查.
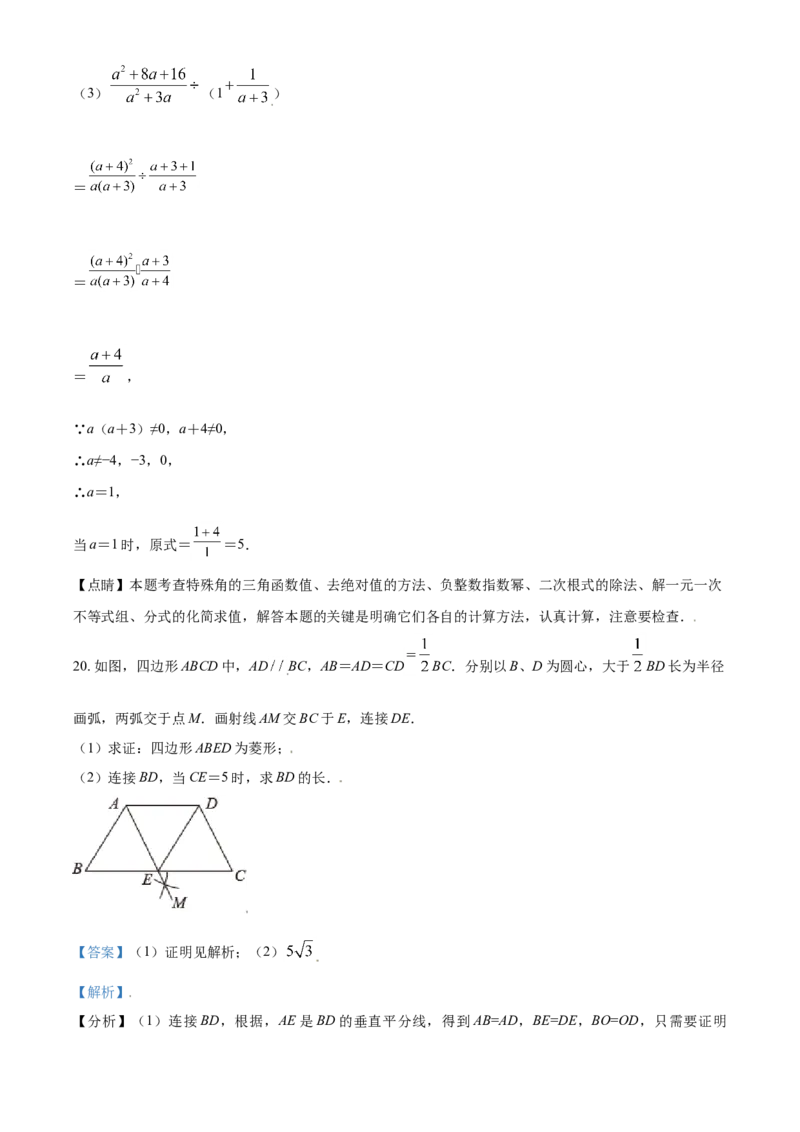
20. 如图,四边形ABCD中,AD BC,AB=AD=CD BC.分别以B、D为圆心,大于 BD长为半径
画弧,两弧交于点M.画射线AM交BC于E,连接DE.
(1)求证:四边形ABED为菱形;
(2)连接BD,当CE=5时,求BD的长.
【答案】(1)证明见解析;(2)
【解析】
【分析】(1)连接BD,根据,AE是BD的垂直平分线,得到AB=AD,BE=DE,BO=OD,只需要证明△OAD≌△OEB,即可得到答案;
(2)根据(1)可以证明三角形DEC是等边三角形,从而可以证明∠BDC=90°,再利用三角函数求解即可
得到答案.
【详解】解:(1)如图所示,连接BD,
由题意可知,AE是BD的垂直平分线,
∴AB=AD,BE=DE,BO=OD,
∵AD∥BC,
∴∠OAD=∠OEB,∠ODA=∠OBE,
在△OAD和△OEB中,
,
∴△OAD≌△OEB(AAS),
∴AD=BE,
∴AD=AB=BE=ED,
∴四边形ABCD是菱形;
(2)由(1)得AD=AB=BE=ED,
∴∠DBE=∠EDB,
∵ ,
∴ ,
∴ ,
∴三角形DEC是等边三角形,
∴∠C=∠DEC=∠CDE=60°,
∵∠BDE+∠EBD=∠DEC,
∴∠BDE=30°,
∴∠BDC=90°
∴【点睛】本题主要考查了菱形的判定,平行线的性质,全等三角形的性质与判定,特殊角的三角函数,等
边三角形的性质与判定,解题的关键在于能够熟练掌握相关知识进行求解.
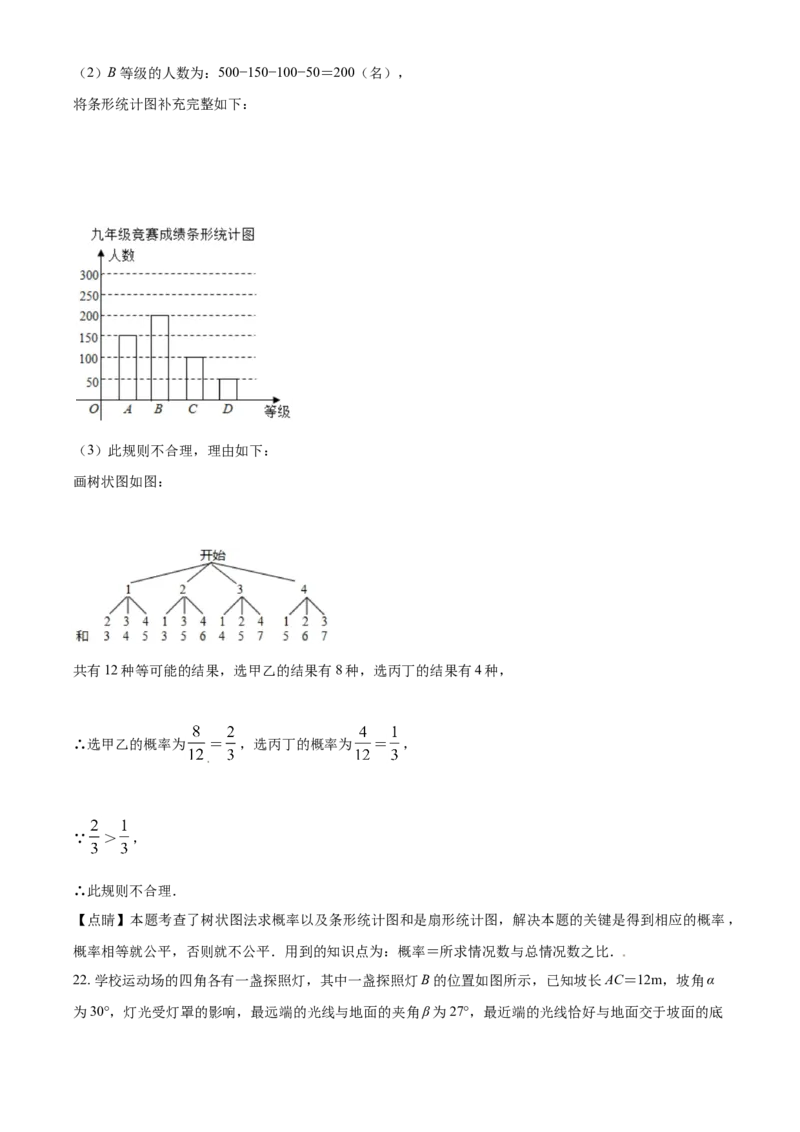
21. 为迎接建党100周年、巴中市组织了多形式的党史学习教育活动,某校开展了以“听党话、跟党走”为
主题的知识竞赛,成绩以A、B、C、D四个等级呈现.现将九年级学生成绩统计如图所示.
的
(1)该校九年级共有 名学生,“D”等级所占圆心角 度数为 ;
(2)请将条形统计图补充完整;
(3)学校从获得满分的四位同学甲、乙、丙、丁中选2名同学参加全市现场党史知识竞赛,选取规则如下:
在一个不透明的口袋中,装有4个大小质地均相同的小球,分别标有数字1、2、3、4.从中摸出两个小球,
若两个数字之和为奇数,则选甲乙;若两个数字之和为偶数,则选丙丁,请用树状图或列表法说明此规则
是否合理.
【答案】(1)500,36°(2)见解析(3)不合理;理由见解析
【解析】
【分析】(1)由A等级的学生除以所占的比例求出该校九年级共有的学生,即可解决问题;
(2)求出B等级的人数,将条形统计图补充完整即可;
(3)画树状图,共有12种等可能的结果,选甲乙的结果有8种,选丙丁的结果有4种,再由概率公式求
出选甲乙的概率和选丙丁的概率,即可得出结论.
【详解】解:(1)该校九年级共有学生:150÷30%=500(名),
则D等级所占圆心角的度数为:360°× =36°,
故答案为:500,36°;(2)B等级的人数为:500−150−100−50=200(名),
将条形统计图补充完整如下:
(3)此规则不合理,理由如下:
画树状图如图:
共有12种等可能的结果,选甲乙的结果有8种,选丙丁的结果有4种,
∴选甲乙的概率为 = ,选丙丁的概率为 = ,
∵ > ,
∴此规则不合理.
【点睛】本题考查了树状图法求概率以及条形统计图和是扇形统计图,解决本题的关键是得到相应的概率,
概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.
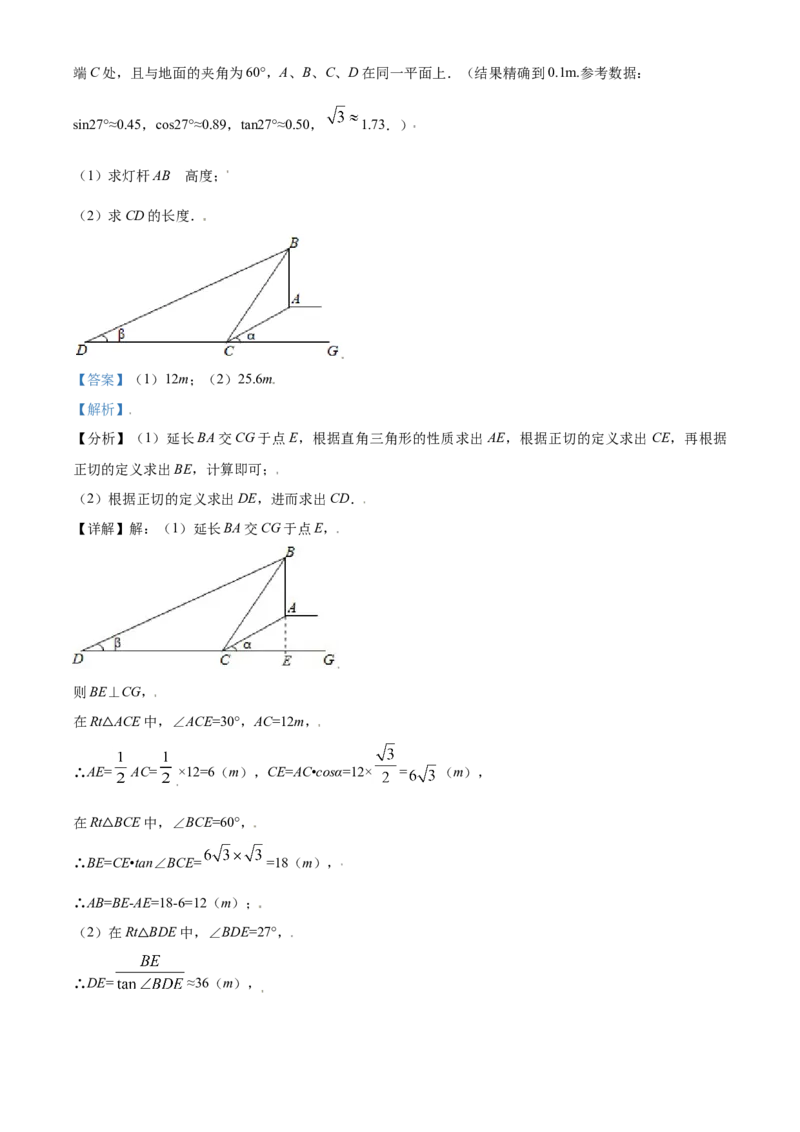
22. 学校运动场的四角各有一盏探照灯,其中一盏探照灯B的位置如图所示,已知坡长AC=12m,坡角α
为30°,灯光受灯罩的影响,最远端的光线与地面的夹角β为27°,最近端的光线恰好与地面交于坡面的底端C处,且与地面的夹角为60°,A、B、C、D在同一平面上.(结果精确到0.1m.参考数据:
sin27°≈0.45,cos27°≈0.89,tan27°≈0.50, 1.73.)
的
(1)求灯杆AB 高度;
(2)求CD的长度.
【答案】(1)12m;(2)25.6m
【解析】
【分析】(1)延长BA交CG于点E,根据直角三角形的性质求出 AE,根据正切的定义求出CE,再根据
正切的定义求出BE,计算即可;
(2)根据正切的定义求出DE,进而求出CD.
【详解】解:(1)延长BA交CG于点E,
则BE⊥CG,
在Rt ACE中,∠ACE=30°,AC=12m,
△
∴AE= AC= ×12=6(m),CE=AC•cosα=12× = (m),
在Rt BCE中,∠BCE=60°,
△
∴BE=CE•tan∠BCE= =18(m),
∴AB=BE-AE=18-6=12(m);
(2)在Rt BDE中,∠BDE=27°,
△
∴DE= ≈36(m),∴CD=DE-CE= ≈25.6(m).
【点睛】本题考查的是解直角三角形的应用—坡度坡角问题,掌握正切的定义是解题的关键.
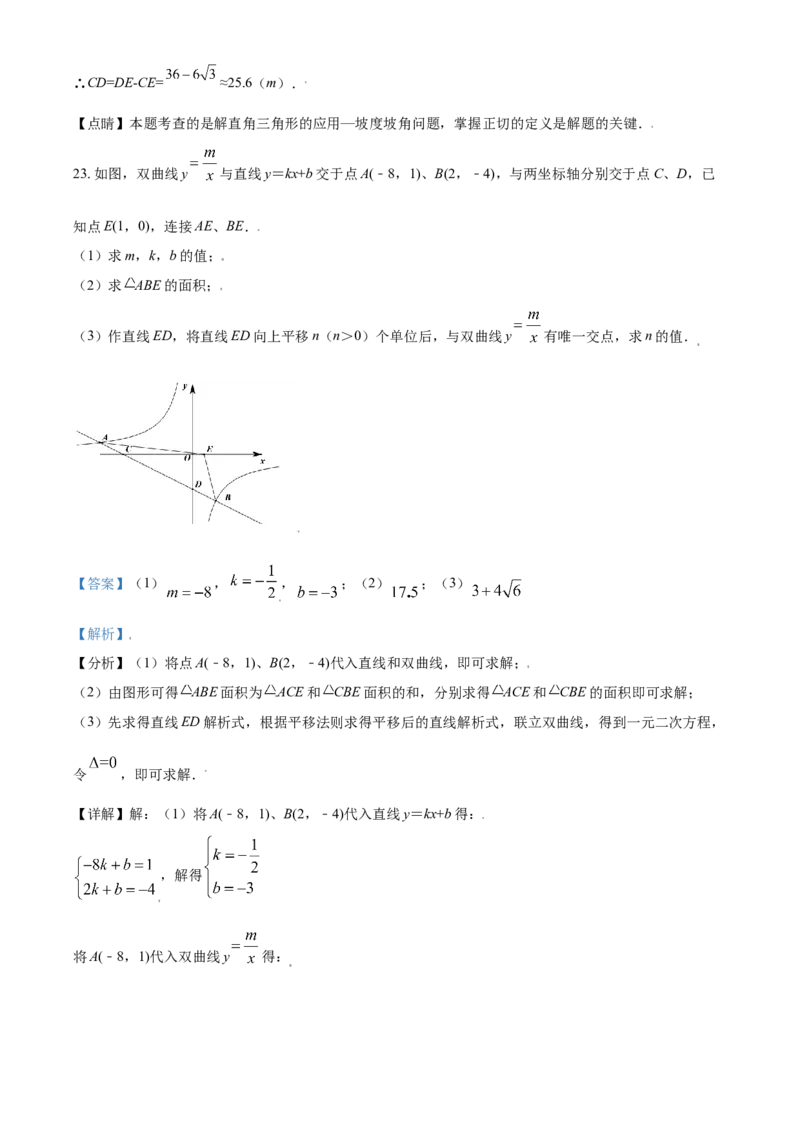
23. 如图,双曲线y 与直线y=kx+b交于点A(﹣8,1)、B(2,﹣4),与两坐标轴分别交于点C、D,已
知点E(1,0),连接AE、BE.
(1)求m,k,b的值;
(2)求 ABE的面积;
(3)作直线ED,将直线ED向上平移n(n>0)个单位后,与双曲线y 有唯一交点,求n的值.
【答案】(1) , , ;(2) ;(3)
【解析】
【分析】(1)将点A(﹣8,1)、B(2,﹣4)代入直线和双曲线,即可求解;
(2)由图形可得 ABE面积为 ACE和 CBE面积的和,分别求得 ACE和 CBE的面积即可求解;
(3)先求得直线ED解析式,根据平移法则求得平移后的直线解析式,联立双曲线,得到一元二次方程,
令 ,即可求解.
【详解】解:(1)将A(﹣8,1)、B(2,﹣4)代入直线y=kx+b得:
,解得
将A(﹣8,1)代入双曲线y 得:,解得
(2)将 代入直线 得, ,即
将 代入直线 得, ,即
∵E(1,0)
∴
,
由图像可得
(3)设直线 解析式为 ,将E(1,0)、 代入,得:
,解得
∴直线 解析式为
直线ED向上平移n(n>0)个单位,则 ,联立双曲线得:
,化简得
∵与双曲线y 有唯一交点
∴
解得
又∵n>0
∴【点睛】此题考查了一次函数与反比例函数的综合应用、涉及了一元二次方程根与系数的关系,熟练掌握
相关基本性质是解题的关键.
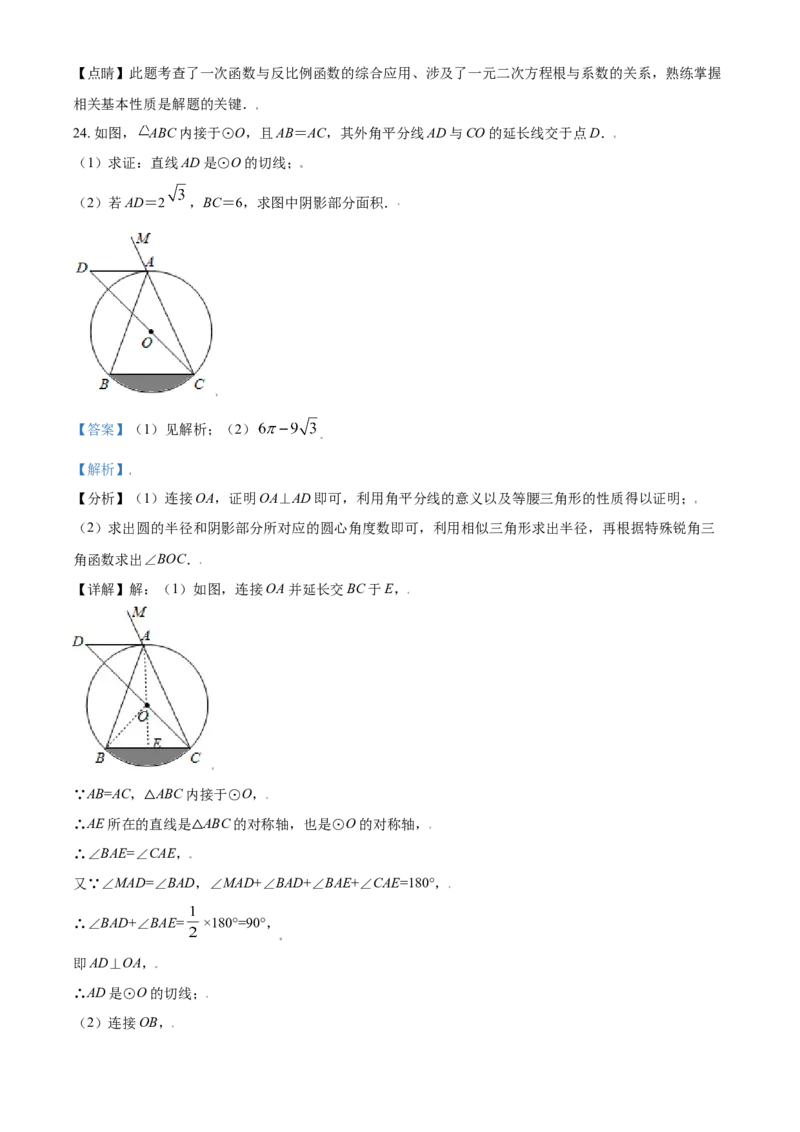
24. 如图, ABC内接于⊙O,且AB=AC,其外角平分线AD与CO的延长线交于点D.
(1)求证:直线AD是⊙O的切线;
(2)若AD=2 ,BC=6,求图中阴影部分面积.
【答案】(1)见解析;(2)
【解析】
【分析】(1)连接OA,证明OA⊥AD即可,利用角平分线的意义以及等腰三角形的性质得以证明;
(2)求出圆的半径和阴影部分所对应的圆心角度数即可,利用相似三角形求出半径,再根据特殊锐角三
角函数求出∠BOC.
【详解】解:(1)如图,连接OA并延长交BC于E,
∵AB=AC, ABC内接于⊙O,
∴AE所在的△直线是 ABC的对称轴,也是⊙O的对称轴,
∴∠BAE=∠CAE,△
又∵∠MAD=∠BAD,∠MAD+∠BAD+∠BAE+∠CAE=180°,
∴∠BAD+∠BAE= ×180°=90°,
即AD⊥OA,
∴AD是⊙O的切线;
(2)连接OB,∵∠OAD=∠OEC=90°,∠AOD=∠EOC,
∴△AOD∽ EOC,
△
∴ ,
由(1)可知 是 的对称轴,
垂直平分 ,
,
设半径为 ,在 中,由勾股定理得,
,
,
解得 (取正值),
经检验 是原方程的解,
即 ,
又 ,
是等边三角形,
, ,
.
【点睛】本题考查了切线的判定和性质、角平分线的性质,圆周角定理,三角形外接圆与外心,扇形面积
的计算,灵活运用切线的判定方法是解题的关键.
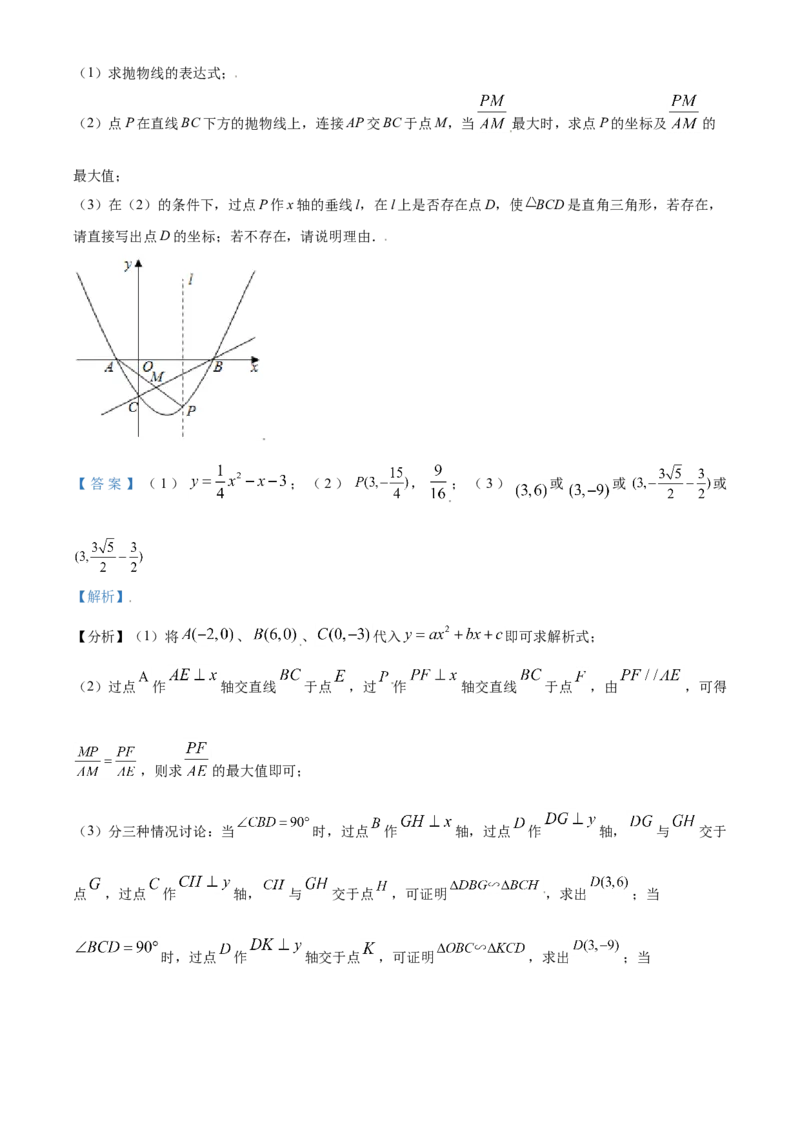
25. 已知抛物线y=ax2+bx+c与x轴交于A(﹣2,0)、B(6,0)两点,与y轴交于点C(0,﹣3).(1)求抛物线的表达式;
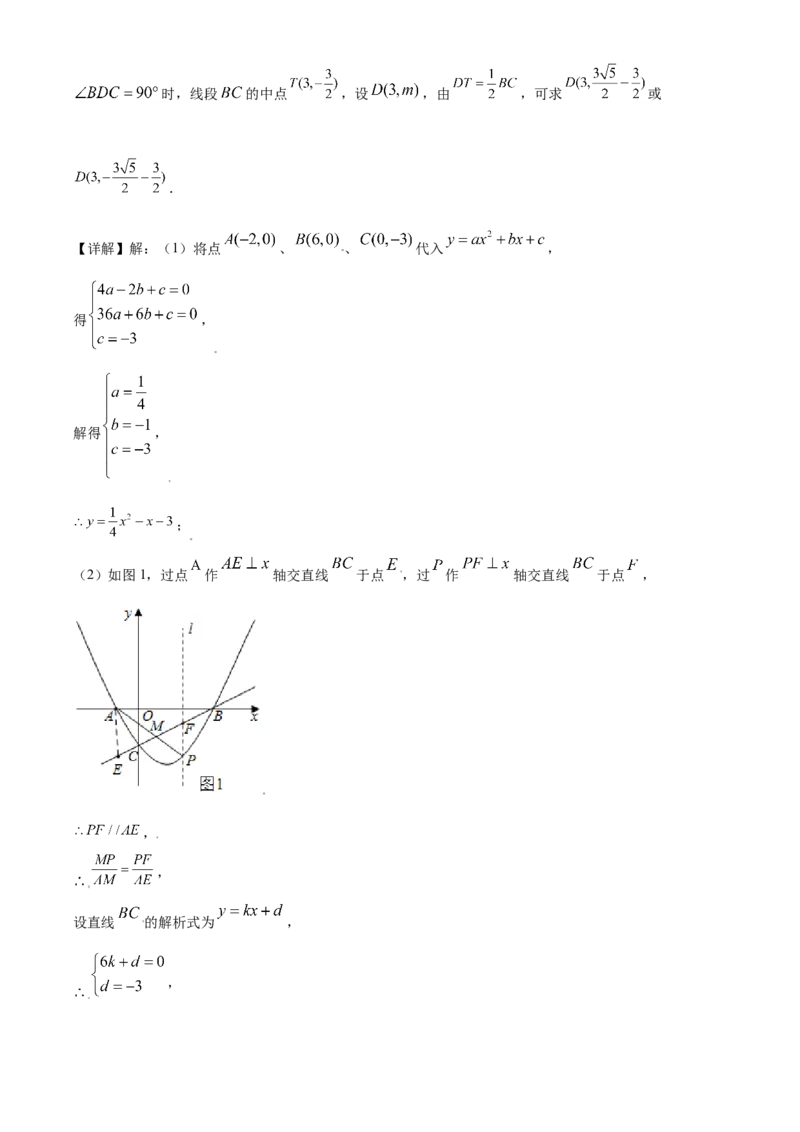
(2)点P在直线BC下方的抛物线上,连接AP交BC于点M,当 最大时,求点P的坐标及 的
最大值;
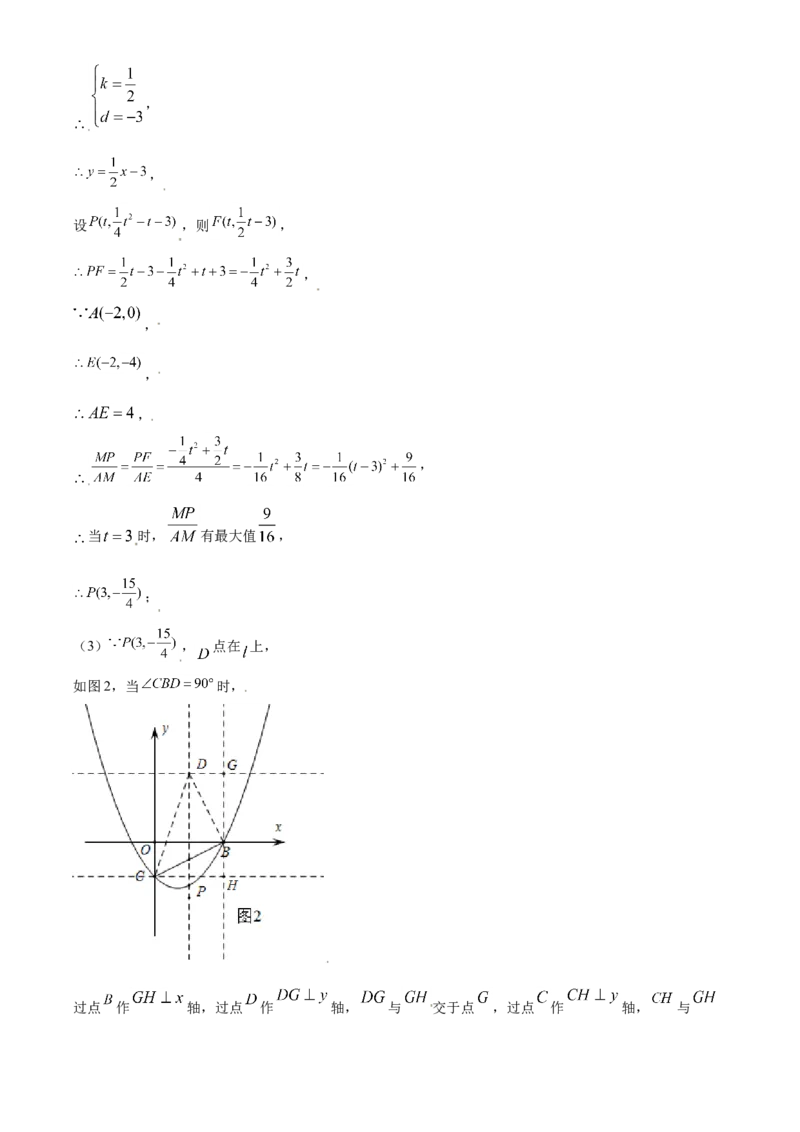
(3)在(2)的条件下,过点P作x轴的垂线l,在l上是否存在点D,使 BCD是直角三角形,若存在,
请直接写出点D的坐标;若不存在,请说明理由.
【答案】(1) ;(2) , ;(3) 或 或 或
【解析】
【分析】(1)将 、 、 代入 即可求解析式;
(2)过点 作 轴交直线 于点 ,过 作 轴交直线 于点 ,由 ,可得
,则求 的最大值即可;
(3)分三种情况讨论:当 时,过点 作 轴,过点 作 轴, 与 交于
点 ,过点 作 轴, 与 交于点 ,可证明 ,求出 ;当
时,过点 作 轴交于点 ,可证明 ,求出 ;当时,线段 的中点 ,设 ,由 ,可求 或
.
【详解】解:(1)将点 、 、 代入 ,
得 ,
解得 ,
;
(2)如图1,过点 作 轴交直线 于点 ,过 作 轴交直线 于点 ,
,
,
设直线 的解析式为 ,
,,
,
设 ,则 ,
,
,
,
,
,
当 时, 有最大值 ,
;
(3) , 点在 上,
如图2,当 时,
过点 作 轴,过点 作 轴, 与 交于点 ,过点 作 轴, 与交于点 ,
, ,
,
,
,即 ,
,
;
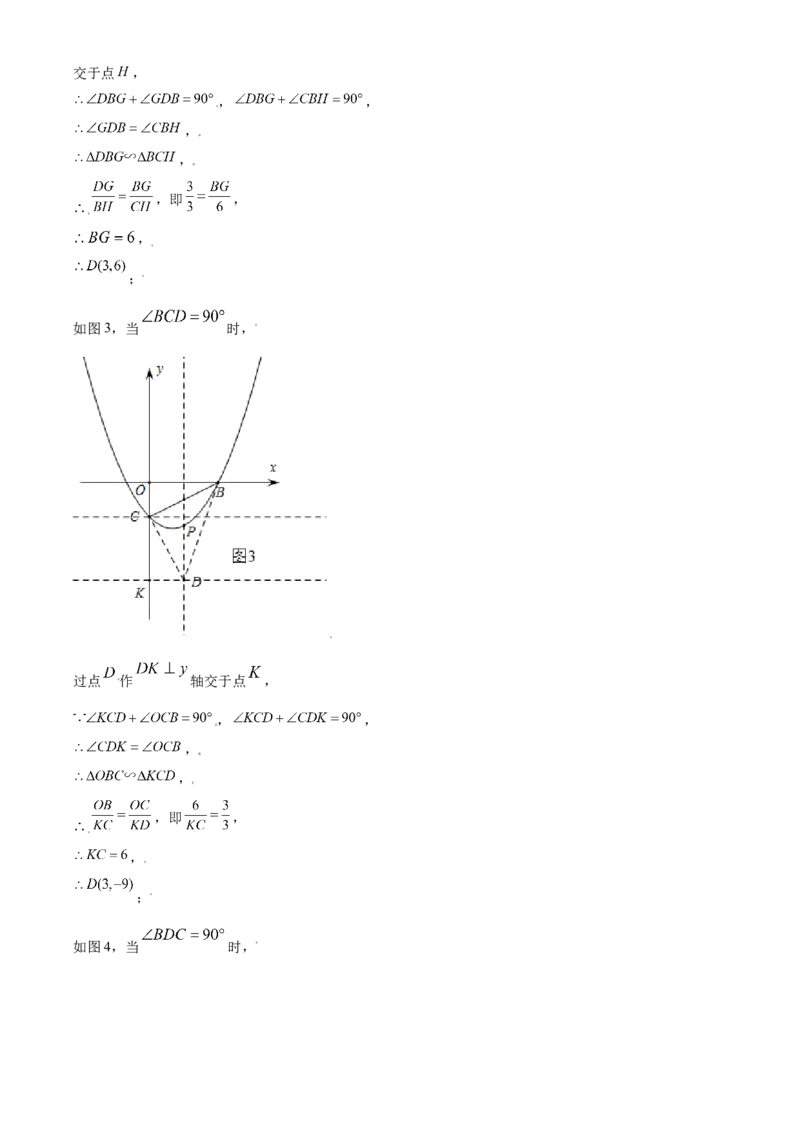
如图3,当 时,
过点 作 轴交于点 ,
, ,
,
,
,即 ,
,
;
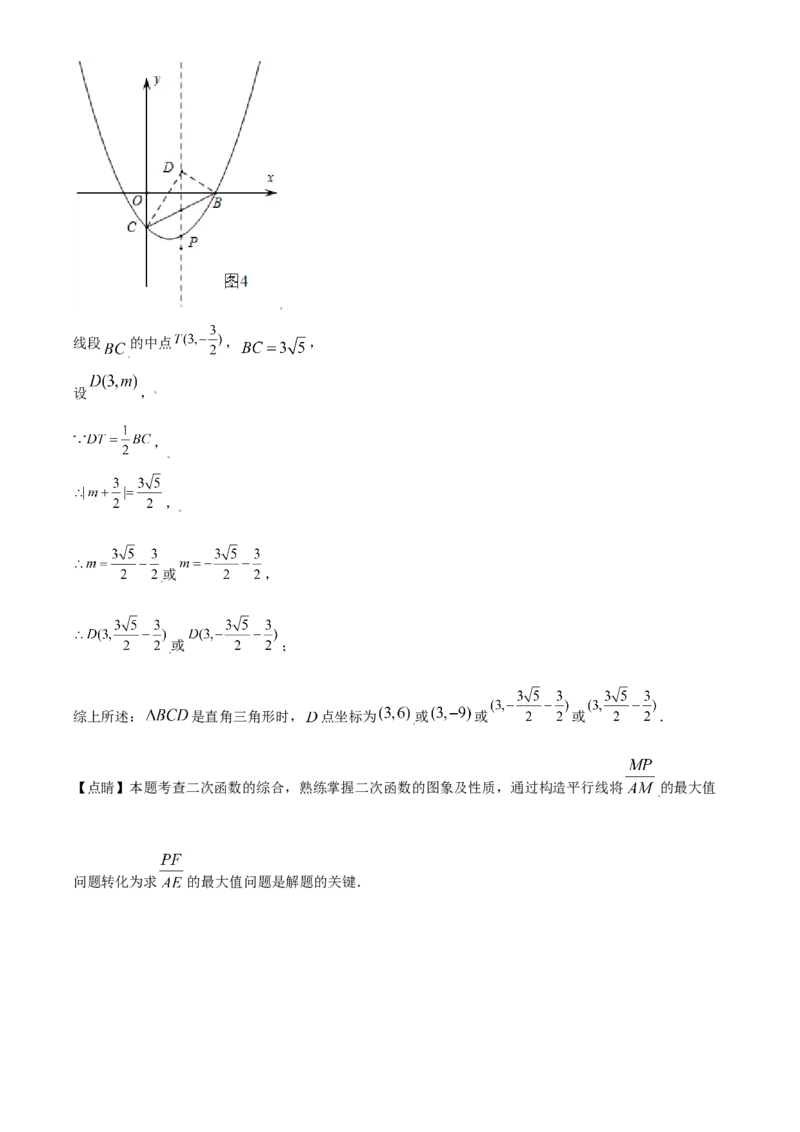
如图4,当 时,线段 的中点 , ,
设 ,
,
,
或 ,
或 ;
综上所述: 是直角三角形时, 点坐标为 或 或 或 .
【点睛】本题考查二次函数的综合,熟练掌握二次函数的图象及性质,通过构造平行线将 的最大值
问题转化为求 的最大值问题是解题的关键.