文档内容
2023 年高考考前押题密卷(全国甲卷)
数学(理科)·全解全析
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如
需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写
在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回
第Ⅰ卷
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要
求的.
1.已知全集 ,集合 , 则集合 等于
( )
A. B. C. D.
【答案】B
【详解】由题意知 , ,
所以 , ,故选:B.
2.(改编)复数 与下列复数相等的是( )
A. B. C. D.
【答案】A
【详解】由题设, ,故B、C、D错误;
1
学科网(北京)股份有限公司而 ,故A正确. 故选:A
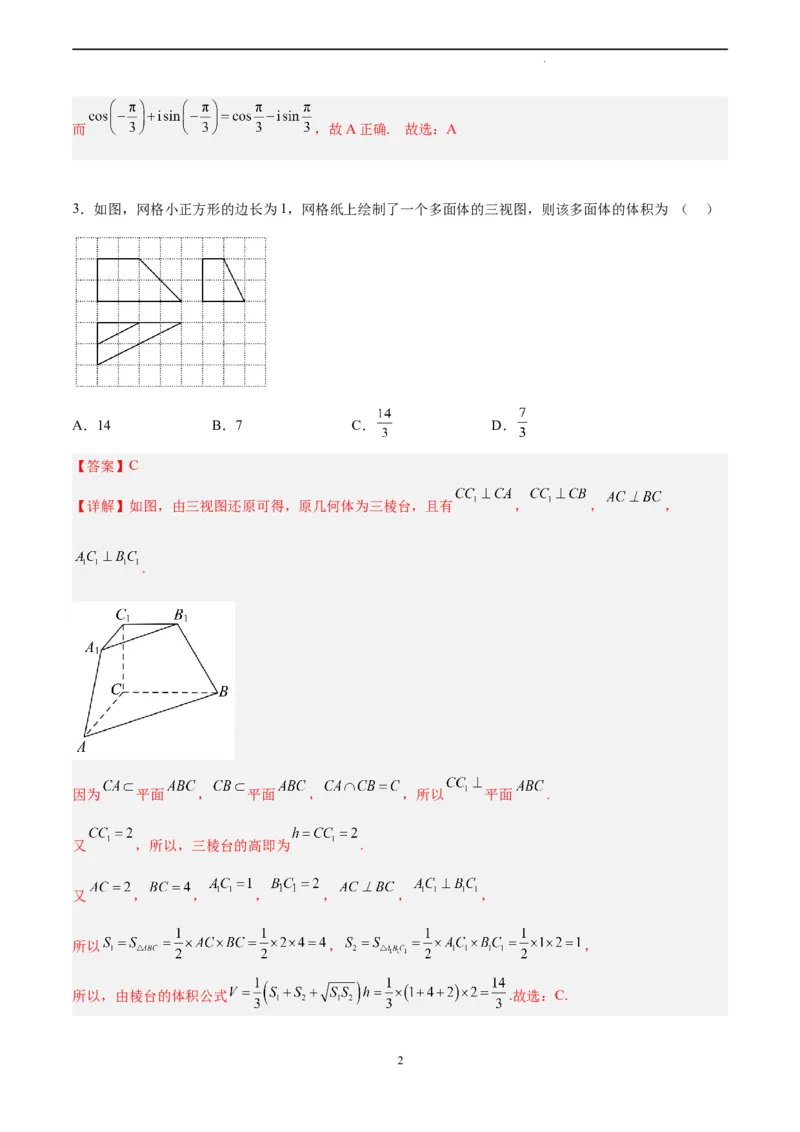
3.如图,网格小正方形的边长为1,网格纸上绘制了一个多面体的三视图,则该多面体的体积为 ( )
A.14 B.7 C. D.
【答案】C
【详解】如图,由三视图还原可得,原几何体为三棱台,且有 , , ,
.
因为 平面 , 平面 , ,所以 平面 .
又 ,所以,三棱台的高即为 .
又 , , , , , ,
所以 , ,
所以,由棱台的体积公式 .故选:C.
2
学科网(北京)股份有限公司4.某公司对2022年的营收额进行了统计,并绘制扇形统计图如图所示,在华中地区的三省中,湖北省的
营收额最多,河南省的营收额最少,湖南省的营收额约2156万元.则下列说法错误的是( )
A.该公司在湖南省的营收额在华中地区的营收额的占比约为35.6%
B.该公司在华东地区的营收额比西南地区、东北地区及湖北省的营收额之和还多
C.该公司在华南地区的营收额比河南省营收额的三倍还多
D.该公司2022年营收总额约为30800万元
【答案】A
【详解】选项A,由右图华中地区的扇形图及湖北省的营收额最多,河南省的营收额最少,可知湖北省的
营收额约为 ,河南省的营收额约为 ,则湖南省的营收额约为 ,
因为华中地区的总营收额为 ,所以该公司湖南省的营收额在华中地区的营收额的占比约为
,所以A错误.
选项B,由左图2022年的营收额的扇形图知,华东地区的营收额约为 ,西南地区的营收额约为
,东北地区营收额约为 ,
由选项A中得出湖北省的营收额约为 ,所以西南地区、东北地区及湖北省的营收额之和为
,
因为 ,所以该公司华东地区的营收额比西南地区、东北地区及湖北省的营收额之和还多,所
以B正确.选项C,由左图2022年的营收额的扇形图知,华南地区的营收额约为 ,
由选项A中得出河南省的营收额约为 ,
因为 , ,所以该公司在华南地区的营收额比河南省营收额的三倍还多,
所以C正确.选项D,由已知湖南省的营收额约2156万元,由选项A中得出湖南省的营收额约为 ,
所以该公司2022年营收总额约 万元,所以D正确. 故选:A.
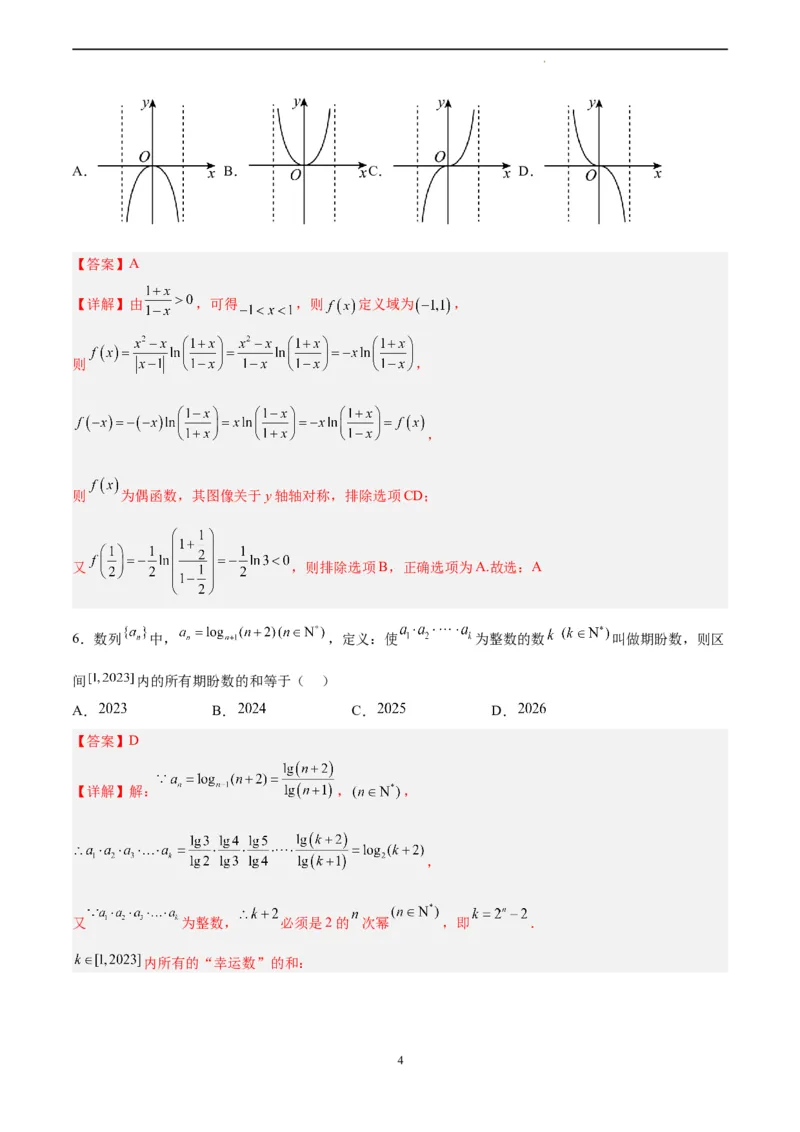
5.函数 的图象大致为( )
3
学科网(北京)股份有限公司A. B. C. D.
【答案】A
【详解】由 ,可得 ,则 定义域为 ,
则 ,
,
则 为偶函数,其图像关于y轴轴对称,排除选项CD;
又 ,则排除选项B,正确选项为A.故选:A
6.数列 中, ,定义:使 为整数的数 叫做期盼数,则区
间 内的所有期盼数的和等于( )
A. B. C. D.
【答案】D
【详解】解: , ,
,
又 为整数, 必须是2的 次幂 ,即 .
内所有的“幸运数”的和:
4
学科网(北京)股份有限公司,故选:D.
7.已知 ,函数 在区间 上单调递减,则 的取值范围是( )
A. B. C. D.
【答案】D
【详解】由 ,得 ,
即函数的单调递减区间为 ,
令 ,则函数 其中一个的单调递减区间为: 函数 在区间 内单调递减,
则满足 ,得 ,所以 的取值范围是 .故选:D.
8.(改编)在平面直角坐标系 y中,圆 的方程为 ,若直线 上存在一点 ,使
过点 所作的圆的两条切线相互垂直,则实数 的值不可能是( )
A. B. C. D.
【答案】B
【详解】由 ,得 ,则圆心 ,半径 ,
因为过点 所作的圆的两条切线相互垂直,所以 , 及两切点构成正方形,且对角线 ,
在直线 上,则圆心到直线的距离 ,解得 或
根据选项,满足条件的为B.故选:B.
5
学科网(北京)股份有限公司9.在二项式 的展开式中,二项式的系数和为256,把展开式中所有的项重新排成一列,有理
项都互不相邻的概率为( )
A. B. C. D.
【答案】C
【详解】在二项式 展开式中,二项式系数的和为 ,所以 .
则 即 ,通项公式为 ,
故展开式共有9项,当 时,展开式为有理项,
把展开式中所有的项重新排成一列,有理项都互不相邻,
即把其它的6个无理项先任意排,再把这三个有理项插入其中的7个空中,方法共有 种,
故有理项都互不相邻的概率为 , 故选:C
10.如图, 为正方体,下列错误的是( )
A. 平面 B.平面 平面 .
C. 与 共面 D.异面直线 与 所成的角为90度
【答案】C
【详解】对于A,由正方体的性质知: , 平面 , 平面 ,
6
学科网(北京)股份有限公司所以 平面 ,故A正确;
对于B,由正方体的性质知: 平面 ,
平面 , 平面 ,所以 ,
又因为 , 平面 ,所以 平面 ,
平面 ,则平面 平面 ,故B正确;
对于C, 平面 ,因为 平面 , 平面 ,
平面 ,由异面直线的判定定理知 与 是异面直线,故C不正确;
对于D,以 为坐标原点,建立如下图所示的空间直角坐标系,设正方体的边长为2,
, , , , , ,
所以异面直线 与 所成的角为90度,故D正确.故选:C.
11.若存在 ,使得关于 的不等式 成立,则实数 的最小值为( )
A.2 B. C. D.
【答案】D
【详解】由 两边取对数可得 ①,
7
学科网(北京)股份有限公司令 则 ,因为 ,所以 ,则①可转化得 ,
因为 , 因为存在 ,使得关于 的不等式 成立,
所以存在 , 成立,故求 的最小值即可,令
,
令 ,
令 , ,
所以 在 上单调递减,所以 , ,所以 在 上单调递减,
所以 在 上单调递减, ,
,所以实数 的最小值为 故选:D
12.如图拋物线 的顶点为 ,焦点为 ,准线为 ,焦准距为4;抛物线 的顶点为 ,焦点也为 ,
准线为 ,焦准距为6. 和 交于 、 两点,分别过 、 作直线与两准线垂直,垂足分别为M、
N、S、T,过 的直线与封闭曲线 交于 、 两点,则下列说法错误的是( )
A. B.四边形 的面积为100 C. D. 的取值范围为
8
学科网(北京)股份有限公司【答案】B
【详解】设直线 与直线 分别交于 ,由题可知 ,
所以 , ,故A正确;
如图以 为原点建立平面直角坐标系,则 , ,所以抛物线 的方程为 ,
连接 ,由抛物线的定义可知 ,
又 ,所以 ,代入 ,可得 ,
所以 ,又 ,故四边形 的面积为 ,故B错误;
连接 ,因为 ,所以 ,
所以 ,故 ,故C正确;
根据抛物线的对称性不妨设点 在封闭曲线 的上部分,设 在直线 上的射影分别为 ,
当点 在抛物线 ,点 在抛物线 上时, ,
当 与 重合时, 最小,最小值为 ,
当 与 重合,点 在抛物线 上时,因为 ,直线 ,
与抛物线 的方程为 联立,可得 ,设 ,
9
学科网(北京)股份有限公司则 , ,所以 ;
当点 在抛物线 ,点 在抛物线 上时,设 ,
与抛物线 的方程为 联立,可得 ,设 ,
则 , ,当 ,
即 时取等号,故此时 ;
当点 在抛物线 ,点 在抛物线 上时,根据抛物线的对称性可知, ;
综上, ,故D正确. 故选:B.
第Ⅱ卷
二、填空题:本题共4小题,每小题5分,共20分.微信搜索“高中试卷君”公众号 领取押题卷联考卷
13.已知向量 , 满足 , , , 的夹角为150°,则 与 的夹角为______.
【答案】
【详解】因为 , 与 的夹角为 ,所以 ,
所以 ,
得 ,又 ,所以 ,
又因为 ,所以 . 故答案为: .
14.已知曲线 在 处的切线为m,则过点 且与切线m垂直的直线方程为
__________.
10
学科网(北京)股份有限公司【答案】 .
【分析】求得 ,得到切线的斜率,进而求得所求直线的斜率,结合点斜式方程,即可求
解.
【详解】由函数 ,可得 ,
则 ,即切线m的斜率为 ,
所以所求直线的斜率为1,其方程为 ,即 .故答案为: .
15.在等比数列 中, 是函数 的极值点,则 =__________.
【答案】
【分析】由题,利用导数及韦达定理可得 ,后利用等比中项性质可得答案.
【详解】 ,由题 是方程 的两个不等实根,
则由韦达定理 ,所以
又 是 的等比中项且 与 同号,则 .故答案为: .
16.已知双曲线 的上焦点为 ,过焦点 作 的一条渐近线的垂线,垂足为 ,
并与另一条渐近线交于点 ,若 ,则 的离心率为 。
【答案】 或
【详解】当 时,直线 与另一条渐近线平行,所以 .
当 时,如图1,过 作另一条渐近线的垂线,垂足为 ,则 ,
11
学科网(北京)股份有限公司由 ,得 ,则 ,所以 ,
则 , ,所以 ,
则 , .
当 时,如图2,过 作另一条渐近线的垂线,垂足为 ,则 ,
由 ,得 ,则 ,则 ,
所以 ,则 , ,
所以 ,则 , .
综上, 的离心率为 或 .
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考
生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.已知条件:① ;② ;③ .从三
个条件中任选一个,补充在下面的问题中,并解答.
12
学科网(北京)股份有限公司问题:在 中,角 , , 所对的边分别为 , , ,满足:___________.
(1)求角 的大小;(2)若 , 与 的平分线交于点 ,求 周长的最大值.
注:如果选择多个条件分别作答,按第一个解答计分
【答案】(1)条件选择见解析, ;(2) .
【详解】(1)选择条件①, ,
在 中,由余弦定理得 ,(2分)
整理得 ,则 ,又 ,所以 .(5分)
选择条件②, ,于是 ,
在 中,由正弦定理得, ,(2分)
因为 ,则 ,即 ,(3分)
因为 ,因此 ,即 ,又 ,所以 .(5分)
选择条件③, ,
在 中,因为 ,即 ,(2分)
则 ,又 ,即有 ,则 ,所以 .(5分)
(2)由(1)知, ,有 ,(6分)
而 与 的平分线交于点 ,即有 ,于是 ,(7分)
13
学科网(北京)股份有限公司设 ,则 ,且 ,(8分)
在 中,由正弦定理得, ,
所以 , ,(9分)
所以 的周长为
,(10分)
由 ,得 ,则当 ,即 时, 的周长取得最大值 ,
所以 周长的最大值为 .(12分)
18.区块链技术被认为是继蒸汽机、电力、互联网之后,下一代颠覆性的核心技术.区块链作为构造信任
的机器,将可能彻底改变整个人类社会价值传递的方式,2018年至2022年五年期间,中国的区块链企业
数量逐年增长,居世界前列.现收集我国近5年区块链企业总数量相关数据,如表:
年份 2018 2019 2020 2021 2022
编号x 1 2 3 4 5
企业总数量y(单位:千个) 2.156 3.727 8.305 24.279 36.224
(1)根据表中数据判断, 与 (其中e=2.71828…为自然对数的底数),哪一个回归方程类
型适宜预测未来几年我国区块链企业总数量?(给出结果即可,不必说明理由)
(2)根据(1)的结果,求 关于 的回归方程;(结果精确到小数点后第三位)
14
学科网(北京)股份有限公司附:线性回归方程 中, ,
参考数据: , , ,
(3)为了促进公司间的合作与发展,区块链联合总部决定进行一次信息化技术比赛,邀请甲、乙、丙三家区
块链公司参赛,比赛规则如下:①每场比赛有两个公司参加,并决出胜负;②每场比赛获胜的公司与未参
加此场比赛的公司进行下一场的比赛;③在比赛中,若有一个公司首先获胜两场,则本次比赛结束,该公
司就获得此次信息化比赛的“优胜公司”.已知在每场比赛中,甲胜乙的概率为 ,甲胜丙的概率为 ,
乙胜丙的概率为 ,请通过计算说明,哪两个公司进行首场比赛时,甲公司获得“优胜公司”的概率最大?
【答案】(1) 适宜 (2) (3)甲公司获得“优胜公司”的概率最大
【详解】(1)根据表中数据可知增加的速度逐渐变快,
所以回归方程 适宜预测未来几年我国区块链企业总数量;(2分)
(2)对 两边取自然对数,得 ,令 ,得 ,(3分)
由于 , , ,(4分)
则 , ,(6分)
∴ 关于 的回归直线方程为 ,则 关于 的回归方程为 ;(7分)
(3)对于首场比赛的选择有以下三种情况:A:甲与乙先赛;B:甲与丙先赛;C:丙与乙先赛,
由于在每场比赛中,甲胜乙的概率为 ,甲胜丙的概率为 ,乙胜丙的概率为 ,(8分)
则甲公司获胜的概率分别是 ,(9分)
15
学科网(北京)股份有限公司,(10分)
,(11分)
由于 ,∴甲与丙两公司进行首场比赛时,甲公司获得“优胜公司”的概率最大.(12分)
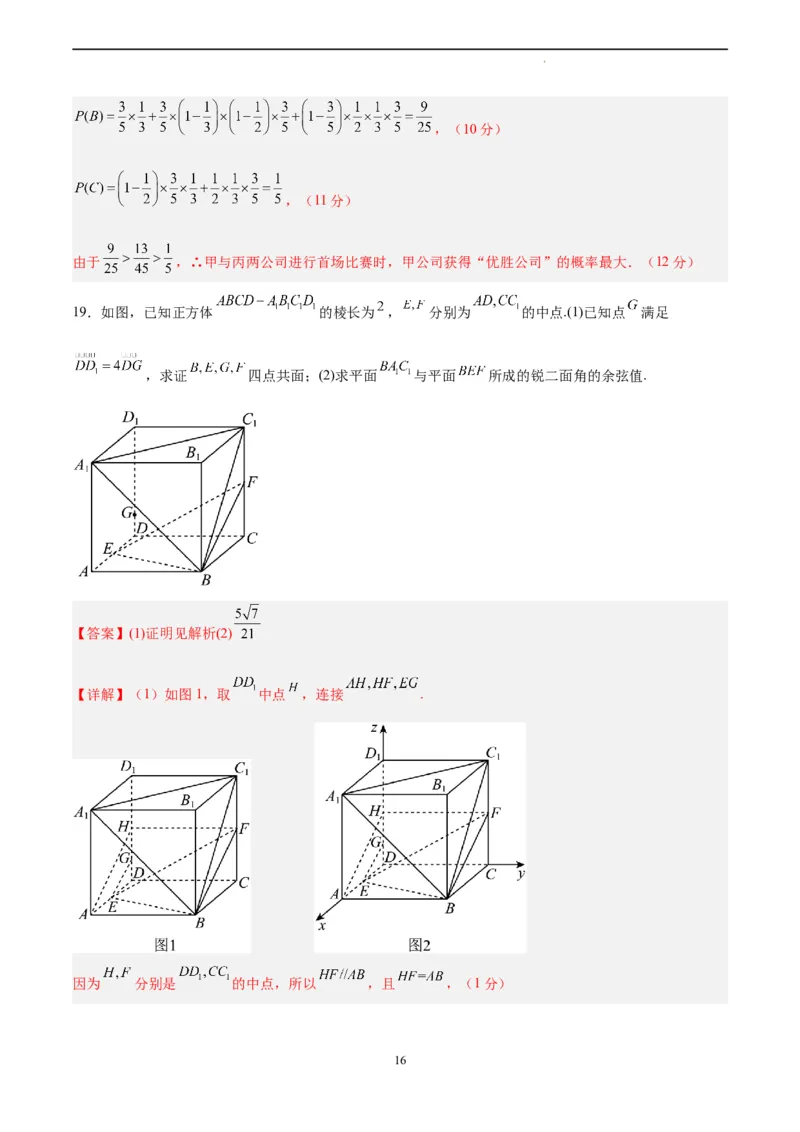
19.如图,已知正方体 的棱长为 , 分别为 的中点.(1)已知点 满足
,求证 四点共面;(2)求平面 与平面 所成的锐二面角的余弦值.
【答案】(1)证明见解析(2)
【详解】(1)如图1,取 中点 ,连接 .
因为 分别是 的中点,所以 ,且 ,(1分)
16
学科网(北京)股份有限公司所以 是平行四边形,所以 .因为 ,所以 .(3分)
又 ,所以 ,所以 是 的中点.(5分)
又因为 是 的中点,所以 ,所以 ,所以 四点共面.(6分)
(2)如图2,以点 为坐标原点,分别以 为 轴,建立空间直角坐标系,
则 , , , , , , ,
所以 , , , .(7分)
设平面 的一个法向量为 ,
由 可得, ,取 ,则 是平面 的一个法向量.(9分)
设平面 的一个法向量为 ,
由 可得, ,取 ,则 是平面 的一个法向量.(11分)
所以, ,
所以平面 与平面 所成锐二面角的余弦值为 .(12分)
20.已知椭圆 的长轴长为4,A,B是其左、右顶点,M是椭圆上异于A,B的动点,
且 .(1)求椭圆C的方程;(2)若P为直线 上一点,PA,PB分别与椭圆交于C,D两点.
①证明:直线CD过椭圆右焦点 ;②椭圆的左焦点为 ,求 的内切圆的最大面积.
【答案】(1) (2)①证明见解析;②
17
学科网(北京)股份有限公司【详解】(1)由已知得: , , ,设 ,
因为M在椭圆上,所以 ① (2分)
因为 ,将①式代入,得 ,所以 ,
所以椭圆 的方程为 .(4分)
(2)①设 ,则 , ,所以 , ,
联立方程 ,得 , 则 .(5分)
联立方程 ,得 , ,则 ,(6分)
椭圆的右焦点为 , , ,(7分)
因为 ,说明C,D, 三点共线,即直线CD恒过 点.(8分)
②因为直线CD恒过 点,所以 的周长为 ,
设 内切圆的半径为 ,所以 的面积 ,
18
学科网(北京)股份有限公司所以 ,即 ,(9分)
若内切圆的面积最大,即r最大,也就是 最大,
因为 三点不共线,所以直线CD的斜率不为0,设直线CD的方程为 ,
代入 得: ,可得 , ,
又因为
令 ,(*)式化为: , (11分)
因为函数 在 上单调递增,所以当 ,即 时,(*)式取最大值3,
所以 ,故 ,所以得到 内切圆面积的最大值为 ,当 时取得.(12分)
21.已知函数 ,设m,n为两个不相等的正数,且 .(1)求实数a的取
值范围;(2)证明: . 微信搜索“高中试卷君”公众号 领取押题卷联考卷
【答案】(1) (2)证明见解析
【详解】(1)由题意, 有两个不相等正根,
所以 有两个不相等正根,即 有两个不相等正根,(1分)
19
学科网(北京)股份有限公司记函数 ,则 ,
令 ,得 ,令 ,得 ,令 ,得 ,
所以函数 的单调递增区间为 ,单调递减区间为 ,(3分)
令 得 ,且 ,x无限趋近于0时,函数值无限趋向于0,
作出函数 的图象,如图
(4分)
要使 有两个不相等正根,则函数 与函数 有两个交点,
由图知 ,故实数a的取值范围 .(5分)
(2)函数 定义域为 ,
当 时, , 在 上单调递增,不符合题意;
当 时,若 时, , 在 上单调递减,若 时, , 在
上单调递增,(7分)
由题意,不妨设 ,先证明 .要证 ,即证 ;
因为 ,且 在 上单调递增,故只需证明 ,(8分)
令 ,
则 ,所以 在 上单调递增,(9分)
20
学科网(北京)股份有限公司所以当 时, ,则有 ,
因为 ,所以 ,则 ,故 ;
再证 ,即证 .因为 ,且 在 上单调递增,(10分)
只需证明 ,即证 ,
因为 ,所以 ,
所以只需证明 ,令 ,(11分)
则 .令 ,
当 时, ,所以 在 上单调递增,
当 时, ,于是 ,
从而可得 在 上单调递减,故 ,
所以 成立,故 .综上, .(12分)
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
[选修4-4:坐标系与参数方程]
22.杭州2022年第19届亚运会(The 19th Asian Games Hangzhou 2022),简称“杭州2022年亚运会”,
将在中国浙江杭州举行,原定于2022年9月10日至25日举办;2022年7月19日亚洲奥林匹克理事会宣
布将于2023年9月23日至10月8日举办,赛事名称和标识保持不变。某高中体育爱好者为纪念在我国举
办的第三次亚运会,借四叶草具有幸福幸运的象征意义,准备设计一枚四叶草徽章捐献给亚运会。如图,
在极坐标系Ox中,方程 表示的图形为“四叶草”对应的曲线C.(1)设直线l:
21
学科网(北京)股份有限公司与C交于异于O的两点A、B,求线段AB的长;
(2)设P和Q是C上的两点,且 ,求 的最大值.
【答案】(1)9 (2)
【详解】(1)设A、B两点的极坐标分别为 、 ,(2分)
则 ,
,因此, ;(5分)
(2)根据对称性,不妨设 、 ,
.(8分)
∵ ,则 ,
所以当 时,即 , 时, .(10分)
[选修4-5:不等式选讲] 微信搜索“高中试卷君”公众号 领取押题卷联考卷
23.已知函数 .(1)求不等式 的解集;(2)若 的最小值为m,正数a,b,c
22
学科网(北京)股份有限公司满足 ,求证 .
【答案】(1) (2)答案见详解
【详解】(1)当 时, ,
解 ,即 ,解得 ;
当 时, ,
解 ,即 ,解得 ,无解;
当 时, ,
解 ,即 ,解得 .(4分)
综上所述,不等式 的解集为 . (5分)
(2)由(1)可知, .
当 时, ;
当 时, ;
当 时, ,(7分)
所以函数 的最小值为2,所以 ,所以 .(8分)
由柯西不等式可得, ,(9分)
当且仅当 时,等号成立.所以 ,所以 。(10分)
23
学科网(北京)股份有限公司24
学科网(北京)股份有限公司