文档内容
2021年甘肃省白银市中考数学试卷
参考答案与试题解析
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项。
1.【分析】根据倒数的定义进行答题.
【解答】解:设3的倒数是a,则3a=1,
解得,a= .
故选:D.
【点评】主要考查倒数的概念及性质.倒数的定义:若两个数的乘积是1,我们就称这两个
数互为倒数.
2.【分析】根据轴对称图形的概念判断求解.
【解答】解:A.不是轴对称图形,故此选项不合题意;
B.是轴对称图形,故此选项符合题意;
C.不是轴对称图形,故此选项不合题意;
D.不是轴对称图形,故此选项不合题意;
故选:B.
【点评】本题考查了轴对称图形,轴对称图形的判断方法:把某个图形沿某条直线折叠,如
果图形的两部分能够重合,那么这个图形是轴对称图形.
3.【分析】根据二次根式的加减法对A、B进行判断;根据二次根式的乘法法则对C进行判断;
根据二次根式的除法法则对D进行判断.
【解答】解:A、原式=2 ,所以A选项的计算错误;
B、原式=3 ,所以B选项的计算错误;
C、原式= = ,所以C选项的计算正确;
D、原式= = =2,所以D选项的计算错误.
故选:C.
【点评】本题考查了二次根式的混合运算,解题的关键是掌握二次根式的乘法和除法法则.
4.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,
要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原
数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:将50亿用科学记数法表示为5×109.
故选:B.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中
1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
5.【分析】根据“上加下减”的原则求解即可.
【解答】解:将直线y=5x向下平移2个单位长度,所得的函数解析式为y=5x﹣2.
故选:A.
【点评】本题考查的是一次函数的图象与几何变换,熟知函数图象变换的法则是解答此题
的关键.
6.【分析】根据角的和差得到∠ABF=70°,再根据两直线平行,同位角相等即可得解.
【解答】解:∵∠ABC=90°,∠CBF=20°,
∴∠ABF=∠ABC﹣∠CBF=70°,
∵DE∥BF,
∴∠ADE=∠ABF=70°,
故选:A.
【点评】此题考查了平行线的性质,熟记平行线的性质定理是解题的关键.
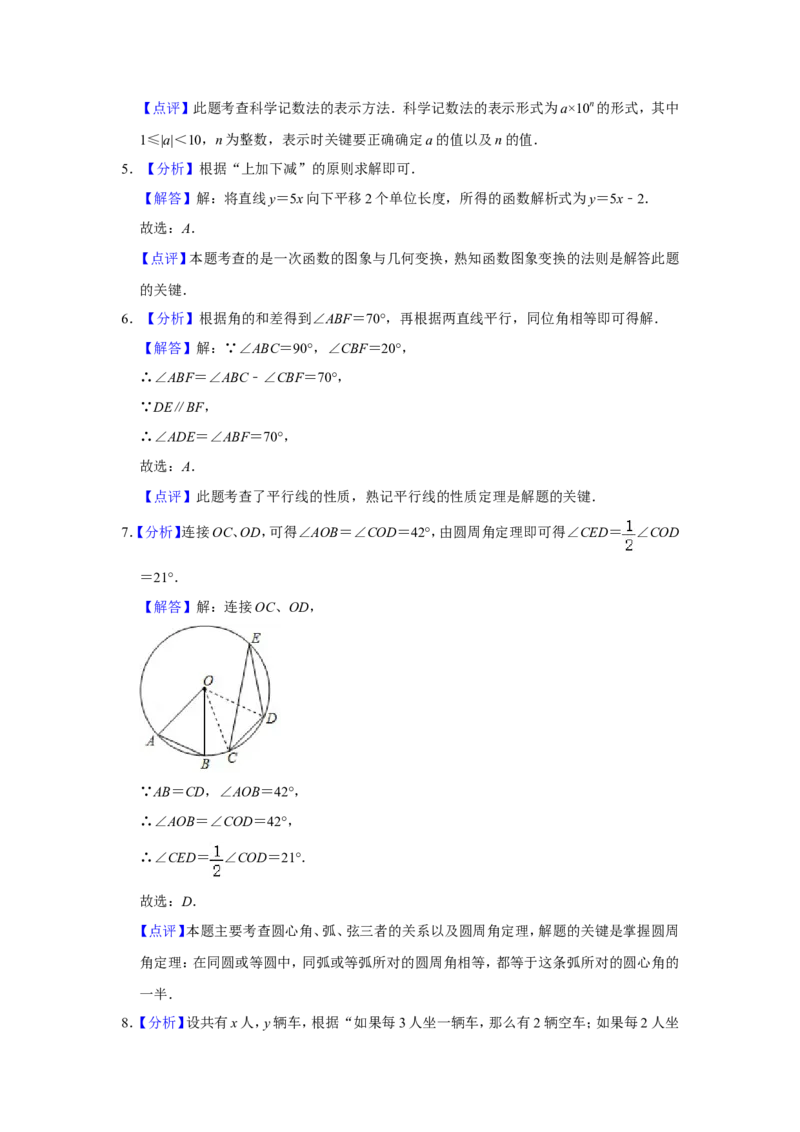
7.【分析】连接OC、OD,可得∠AOB=∠COD=42°,由圆周角定理即可得∠CED= ∠COD
=21°.
【解答】解:连接OC、OD,
∵AB=CD,∠AOB=42°,
∴∠AOB=∠COD=42°,
∴∠CED= ∠COD=21°.
故选:D.
【点评】本题主要考查圆心角、弧、弦三者的关系以及圆周角定理,解题的关键是掌握圆周
角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的
一半.
8.【分析】设共有x人,y辆车,根据“如果每3人坐一辆车,那么有2辆空车;如果每2人坐一辆车,那么有9人需要步行”,即可得出关于x,y的二元一次方程组,此题得解.
【解答】解:设共有x人,y辆车,
依题意得: .
故选:C.
【点评】本题考查了由实际问题抽象出二元一次方程组以及数学常识,找准等量关系,正
确列出二元一次方程组是解题的关键.
9.【分析】根据(m,n)是“相随数对”得出9m+4n=0,再将原式化成9m+4n﹣2,最后整体代
入求值即可.
【解答】解:∵(m,n)是“相随数对”,
∴ + = ,
∴ = ,
即9m+4n=0,
∴3m+2[3m+(2n﹣1)]
=3m+2[3m+2n﹣1]
=3m+6m+4n﹣2
=9m+4n﹣2
=0﹣2
=﹣2,
故选:A.
【点评】本题考查代数式求值,理解“相随数对”的意义是正确计算的关键.
10.【分析】先根据AB=BC结合图2得出AB= ,进而利用勾股定理得,AD²+BD²=13,
再由运动结合△ADM的面积的变化,得出点M和点B重合时,△ADM的面积最大,其值
为3,即 AD•BD=3,进而建立二元二次方程组求解,即可得出结论.
【解答】解:由图2知,AB+BC=2 ,
∵AB=BC,
∴AB= ,
∵AB=BC,BD⊥AC,
∴AC=2AD,∠ADB=90°,在Rt△ABD中,AD²+BD²=AB²=13①,
设点M到AC的距离为h,
∴S△ADM = AD•h,
∵动点M从A点出发,沿折线AB→BC方向运动,
∴当点M运动到点B时,△ADM的面积最大,即h=BD,
由图2知,△ADM的面积最大为3,
∴ AD•BD=3,
∴AD•BD=6②,
①+2×②得,AD²+BD²+2AD•BD=13+2×6=25,
∴(AD+BD)²=25,
∴AD+BD=5(负值舍去),
∴BD=5﹣AD③,
将③代入②得,AD(5﹣AD)=6,
∴AD=3或AD=2,
∵AD>BD,
∴AD=3,
∴AC=2AD=6,
故选:B.
【点评】此题主要考查了等腰三角形的性质,三角形的面积公式,判断出AB= 和点M
和点B重合时,△ADM的面积为3是解本题的关键.
二、填空题:本大题共8小题,每小题3分,共24分。
11.【分析】提取公因式进行因式分解.
【解答】解:4m﹣2m2=2m(2﹣m),
故答案为:2m(2﹣m).
【点评】本题考查提公因式法进行因式分解,掌握提取公因式的技巧准确计算是解题关键.
12.【分析】根据解一元一次不等式基本步骤:移项、合并同类项、系数化为1可得.
【解答】解:移项,得: x>1+ ,
合并同类项,得: x> ,系数化为1,得:x> ,
故答案为:x> .
【点评】本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关
键,尤其需要注意不等式两边都乘以或除以同一个负数,不等号方向要改变.
13.【分析】根据根的判别式Δ=0,即可得出关于k的一元一次方程,解之即可得出k值.
【解答】解:∵关于x的方程x2﹣2x+k=0有两个相等的实数根,
∴Δ=(﹣2)2﹣4×1×k=0,
解得:k=1.
故答案为:1.
【点评】本题考查了根的判别式,牢记“当Δ=0时,方程有两个相等的实数根”是解题的
关键.
14.【分析】根据众数的定义就可解决问题.
【解答】解:36.6℃出现的次数最多有4次,所以众数是36.6℃.
故答案为:36.6.
【点评】本题主要考查了众数的定义,正确理解众数的意义是解决本题的关键.
15.【分析】先利用直角三角形斜边上的中线等于斜边的一半,求出AD长,再根据矩形的性
质得出AD∥BC,∠B=90°,然后解直角三角形ABE即可.
【解答】解:∵∠AED=90°,F是AD边的中点,EF=4cm,
∴AD=2EF=8cm,
∵∠EAD=30°,
∴AE=AD•cos30°=8× =4 cm,
又∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠BEA=∠EAD=30°,
在Rt△ABE中,
BE=AE•cos∠BEA=4 ×cos30°=4 × =6(cm),
故答案为:6.
【点评】本题考查了矩形的性质直角三角形斜边上的中线以及解直角三角形,关键是利用直角三角形斜边上的中线求出AD的长.
16.【分析】反比例函数y= 的图象在一、三象限,在每个象限内,y随x的增大而减小,
判断出y的值的大小关系.
【解答】解:∵k=a2+1>0,
∴反比例函数y= 的图象在一、三象限,且在每个象限内y随x的增大而减小,
∵点A(﹣3,y ),B(﹣4,y )同在第三象限,且﹣3>﹣4,
1 2
∴y <y ,
1 2
故答案为:<.
【点评】本题考查反比例函数的图象和性质,掌握反比例函数的增减性是解决问题的关键,
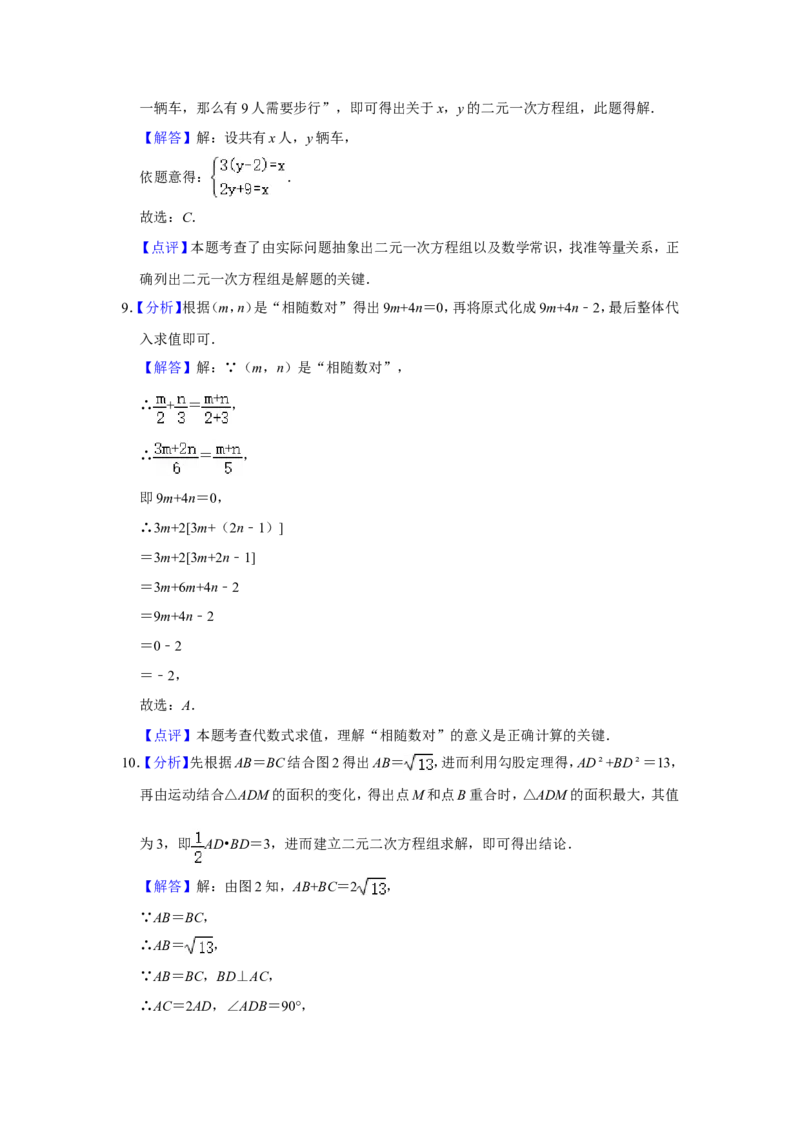
17.【分析】连接AC,根据圆周角定理得出AC为圆的直径,解直角三角形求出AB,根据扇形
面积公式求出即可.
【解答】解:连接AC,
∵从一块直径为4dm的圆形铁皮上剪出一个圆心角为90°的扇形,即∠ABC=90°,
∴AC为直径,即AC=4dm,AB=BC(扇形的半径相等),
∵AB2+BC2=22,
∴AB=BC=2 dm,
∴阴影部分的面积是 =2 (dm2).
π
故答案为:2 .
【点评】本题π考查了圆周角定理和扇形的面积计算,能熟记扇形的面积公式是解此题的关
键.
18.【分析】根据已知的式子可以得到每个式子的第一项中a的次数是式子的序号;第二项的
符号:第奇数项是正号,第偶数项是负号;第二项中b的次数是序号的2倍减1,据此即可
写出.
【解答】解:观察代数式,得到第n个式子是:an+(﹣1)n+1•2b2n﹣1.故答案为:an+(﹣1)n+1•2b2n﹣1.
【点评】本题考查了探索规律,根据所排列的代数式,总结出规律是解题的关键.
三、解答题:本大题共5小题,共26分。解答时,应写出必要的文字说明、证明过程或演算步
骤。
19.【分析】根据零指数幂,负整数指数幂,特殊角的三角函数值计算即可.
【解答】解:原式=1+2﹣2×
=3﹣ .
【点评】本题考查了零指数幂,负整数指数幂,特殊角的三角函数值,牢记 a﹣p=
(a≠0)是解题的关键.
20.【分析】首先将分式的分子与分母进行分解因式进而化简,再将x的值代入求出答案.
【解答】解:原式=( ﹣ )• = • =﹣ ,
当x=4时,原式=﹣ =﹣ .
【点评】此题主要考查了分式的化简求值,正确分解因式是解题关键.
21.【分析】(1)①根据要求作出图形即可.
②根据要求作出图形即可.
(2)证明△DFB≌△DCB可得结论.
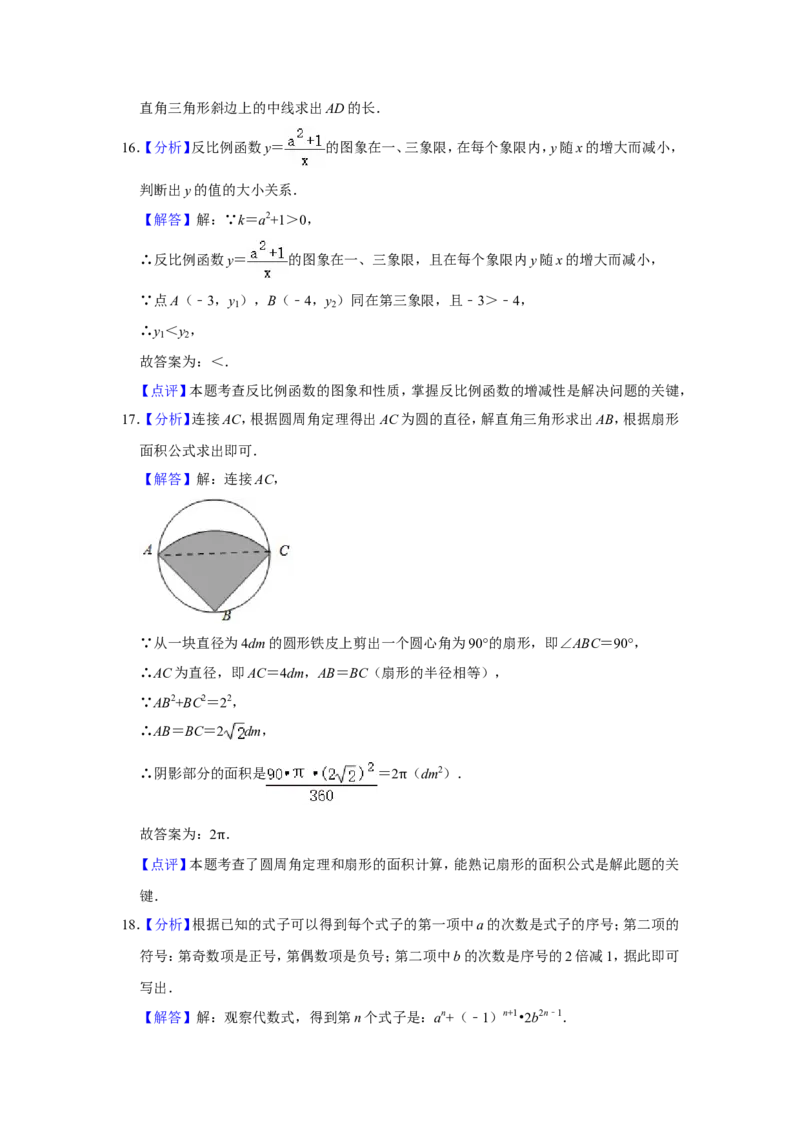
【解答】解:(1)①如图,直线DE,线段AD,线段CD即为所求.
②如图,点F,线段CD,BD,BF即为所求作.
(2)结论:BF=BC.
理由:∵DE垂直平分线段AC,
∴DA=DC,
∴∠DAC=∠DCA,
∵AD=DF,∴DF=DC, = ,
∴∠DBC=∠DBF,
∵∠DFB+∠DAC=180°.∠DCB+∠DCA=180°,
∴∠DFB=∠DCB,
在△DFB和△DCB中,
,
∴△DFB≌△DCB(AAS),
∴BF=BC.
【点评】本题考查作图﹣复杂作图,线段的垂直平分线的性质,全等三角形的判定和性质,
圆周角定理等知识,解题的关键是熟练掌握五种基本作图,正确寻找全等三角形解决问题.
22.【分析】设设CD=xcm,在Rt△ACD中,可得出AD= ,在Rt△BCD中,BD=
,再由AD+BD=AB,列式计算即可得出答案.
【解答】解:设CD=xm,
在Rt△ACD中,AD= ,
在Rt△BCD中,BD= ,
∵AD+BD=AB,
∴ ,
解得,x≈33.4.
答:宝塔的高度约为33.4m.
【点评】本题主要考查了解直角三角形的应用,熟练掌握解直角三角形的方法进行计算是
解决本题的关键.
23.【分析】(1)设白球有x个,根据多次摸球试验后发现,摸到红球的频率稳定在0.75左右
可估计摸到红球的概率为0.75,据此利用概率公式列出关于x的方程,解之即可;
(2)画树状图列出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即
可.
【解答】解:(1)∵通过多次摸球试验后发现,摸到红球的频率稳定在0.75左右,∴估计摸到红球的概率为0.75,
设白球有x个,
根据题意,得: =0.75,
解得x=1,
经检验x=1是分式方程的解,
∴估计箱子里白色小球的个数为1;
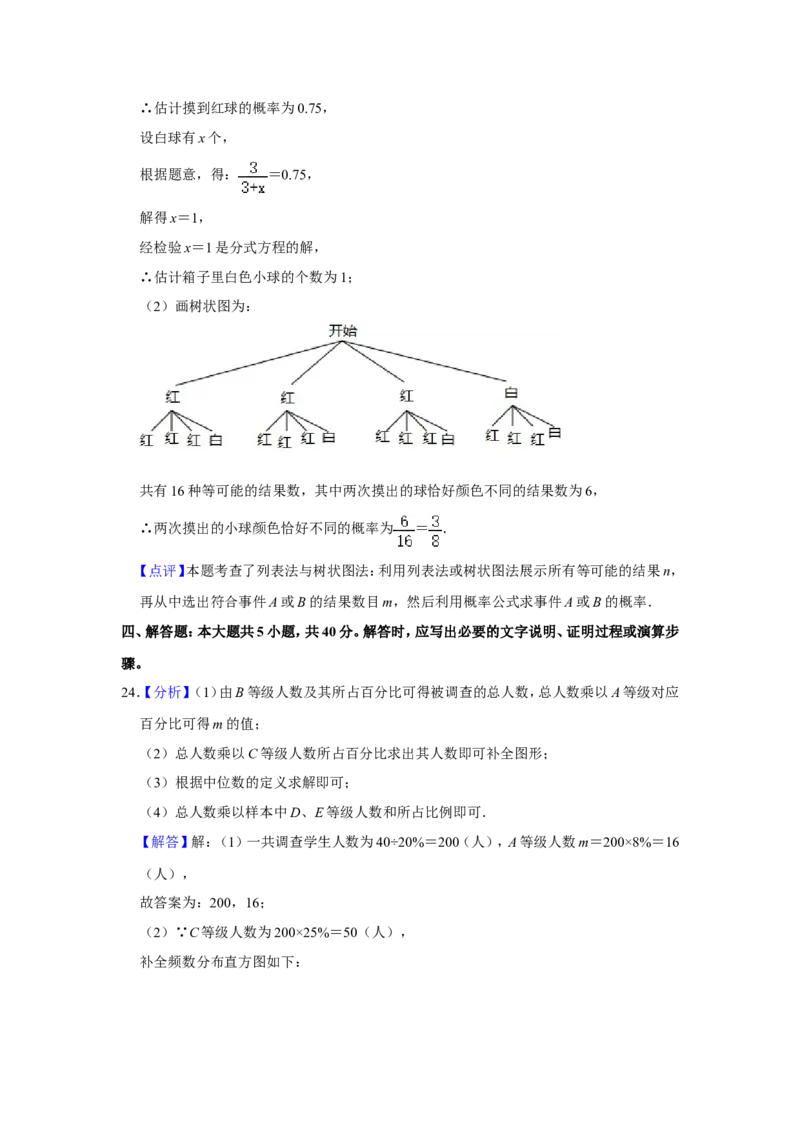
(2)画树状图为:
共有16种等可能的结果数,其中两次摸出的球恰好颜色不同的结果数为6,
∴两次摸出的小球颜色恰好不同的概率为 = .
【点评】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,
再从中选出符合事件A或B的结果数目m,然后利用概率公式求事件A或B的概率.
四、解答题:本大题共5小题,共40分。解答时,应写出必要的文字说明、证明过程或演算步
骤。
24.【分析】(1)由B等级人数及其所占百分比可得被调查的总人数,总人数乘以A等级对应
百分比可得m的值;
(2)总人数乘以C等级人数所占百分比求出其人数即可补全图形;
(3)根据中位数的定义求解即可;
(4)总人数乘以样本中D、E等级人数和所占比例即可.
【解答】解:(1)一共调查学生人数为40÷20%=200(人),A等级人数m=200×8%=16
(人),
故答案为:200,16;
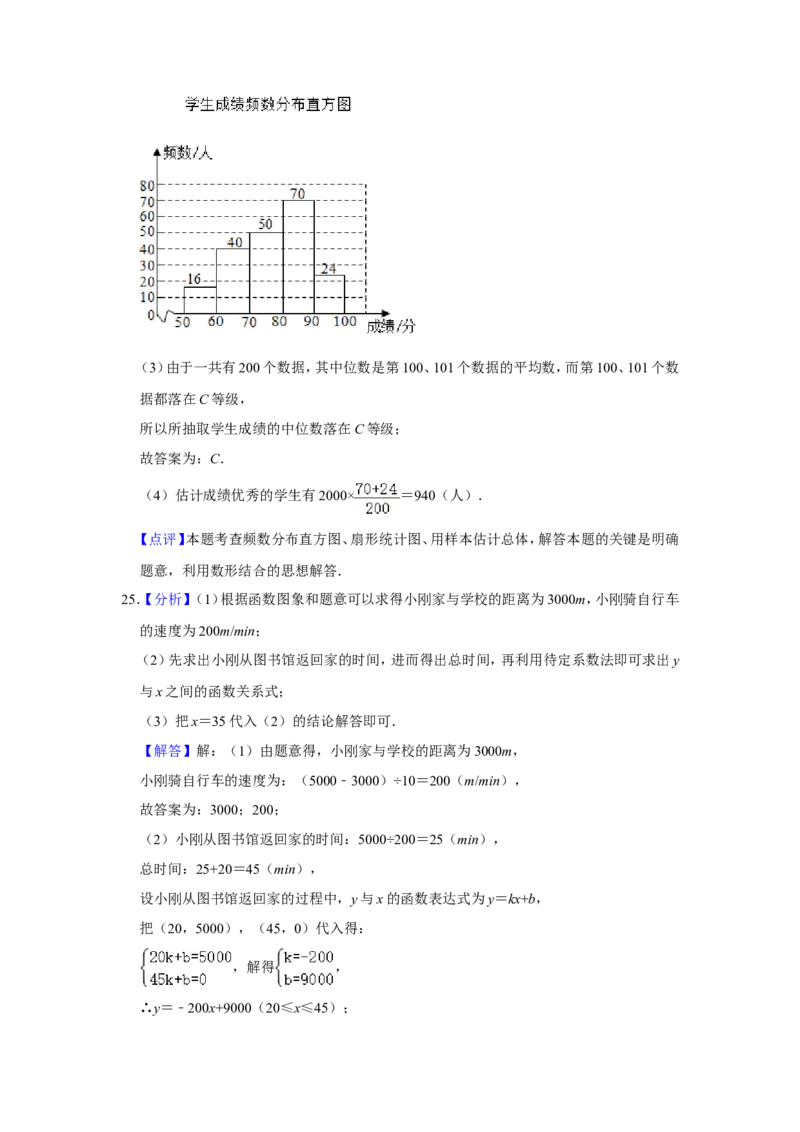
(2)∵C等级人数为200×25%=50(人),
补全频数分布直方图如下:(3)由于一共有200个数据,其中位数是第100、101个数据的平均数,而第100、101个数
据都落在C等级,
所以所抽取学生成绩的中位数落在C等级;
故答案为:C.
(4)估计成绩优秀的学生有2000× =940(人).
【点评】本题考查频数分布直方图、扇形统计图、用样本估计总体,解答本题的关键是明确
题意,利用数形结合的思想解答.
25.【分析】(1)根据函数图象和题意可以求得小刚家与学校的距离为3000m,小刚骑自行车
的速度为200m/min;
(2)先求出小刚从图书馆返回家的时间,进而得出总时间,再利用待定系数法即可求出y
与x之间的函数关系式;
(3)把x=35代入(2)的结论解答即可.
【解答】解:(1)由题意得,小刚家与学校的距离为3000m,
小刚骑自行车的速度为:(5000﹣3000)÷10=200(m/min),
故答案为:3000;200;
(2)小刚从图书馆返回家的时间:5000÷200=25(min),
总时间:25+20=45(min),
设小刚从图书馆返回家的过程中,y与x的函数表达式为y=kx+b,
把(20,5000),(45,0)代入得:
,解得 ,
∴y=﹣200x+9000(20≤x≤45);(3)小刚出发35分钟时,即当x=35时,
y=﹣200×35+9000=2000.
答:此时他离家2000m.
【点评】本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条
件,利用该数形结合的思想和分类讨论的数学思想解答.
26.【分析】(1)由等腰三角形的性质与已知条件得出,∠OCA=∠DCB,由圆周角定理可得
∠ACB=90°,进而得到∠OCD=90°,即可得出结论;
(2)根据平行线分线段成比例定理得到 = = ,设BD=2x,则OB=OC=3x,OD=
OB+BD=5x,在Rt△OCD中,根据勾股定理求出x=1,即 O的半径为3,由平行线的性
质得到∠OCB=∠EOC,在Rt△OCE中,可求得tan∠EO⊙C=2,即tan∠OCB=2.
【解答】(1)证明:∵OA=OC,
∴∠OAC=∠OCA,
∵∠DCB=∠OAC,
∴∠OCA=∠DCB,
∵AB是 O的直径,
∴∠ACB⊙=90°,
∴∠OCA+∠OCB=90°,
∴∠DCB+∠OCB=90°,
即∠OCD=90°,
∴OC⊥DC,
∵OC是 O的半径,
∴CD是⊙O的切线;
(2)解:⊙∵OE∥BC,
∴ = ,
∵CD=4,CE=6,
∴ = = ,
设BD=2x,则OB=OC=3x,OD=OB+BD=5x,
∵OC⊥DC,
∴△OCD是直角三角形,在Rt△OCD中,OC2+CD2=OD2,
∴(3x)2+42=(5x)2,
解得,x=1,
∴OC=3x=3,即 O的半径为3,
∵BC∥OE, ⊙
∴∠OCB=∠EOC,
在Rt△OCE中,tan∠EOC= = =2,
∴tan∠OCB=tan∠EOC=2.
【点评】本题考查了圆周角定理、勾股定理、平行线的性质、等腰三角形的性质、切线的判
定、三角函数、平行线分线段成比例定理等知识;熟练掌握切线的判定与平行线分线段成
比例定理是解题的关键.
27.【分析】(1)根据矩形的性质得∠DAB=∠B=90°,由等角的余角相等可得∠ADE=
∠BAF,利用AAS可得△ADE≌△BAF(AAS),由全等三角形的性质得AD=AB,即可得四
边形ABCD是正方形;
(2)利用AAS可得△ADE≌△BAF(AAS),由全等三角形的性质得AE=BF,由已知BH=
AE可得BH=BF,根据线段垂直平分线的性质可得即可得AH=AF,△AHF是等腰三角形;
类比迁移:延长CB到点H,使BH=AE=6,连接AH,利用SAS可得△DAE≌△ABH
(SAS),由全等三角形的性质得AH=DE,∠AHB=∠DEA=60°,由已知DE=AF可得AH
=AF,可得△AHF是等边三角形,则AH=HF=HB+BF=AE+BF=6+2=8,等量代换可得
DE=AH=8.
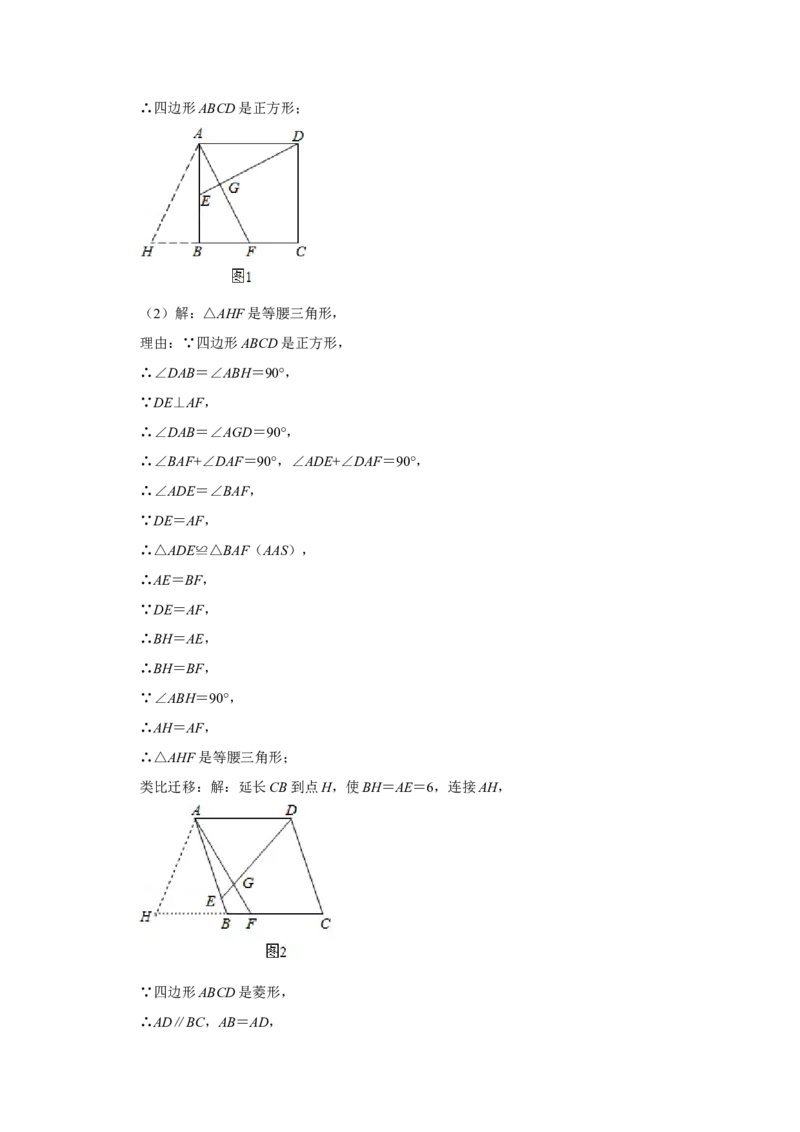
【解答】(1)证明:∵四边形ABCD是矩形,
∴∠DAB=∠B=90°,
∵DE⊥AF,
∴∠DAB=∠AGD=90°,
∴∠BAF+∠DAF=90°,∠ADE+∠DAF=90°,
∴∠ADE=∠BAF,
∵DE=AF,
∴△ADE≌△BAF(AAS),
∴AD=AB,
∵四边形ABCD是矩形,∴四边形ABCD是正方形;
(2)解:△AHF是等腰三角形,
理由:∵四边形ABCD是正方形,
∴∠DAB=∠ABH=90°,
∵DE⊥AF,
∴∠DAB=∠AGD=90°,
∴∠BAF+∠DAF=90°,∠ADE+∠DAF=90°,
∴∠ADE=∠BAF,
∵DE=AF,
∴△ADE≌△BAF(AAS),
∴AE=BF,
∵DE=AF,
∴BH=AE,
∴BH=BF,
∵∠ABH=90°,
∴AH=AF,
∴△AHF是等腰三角形;
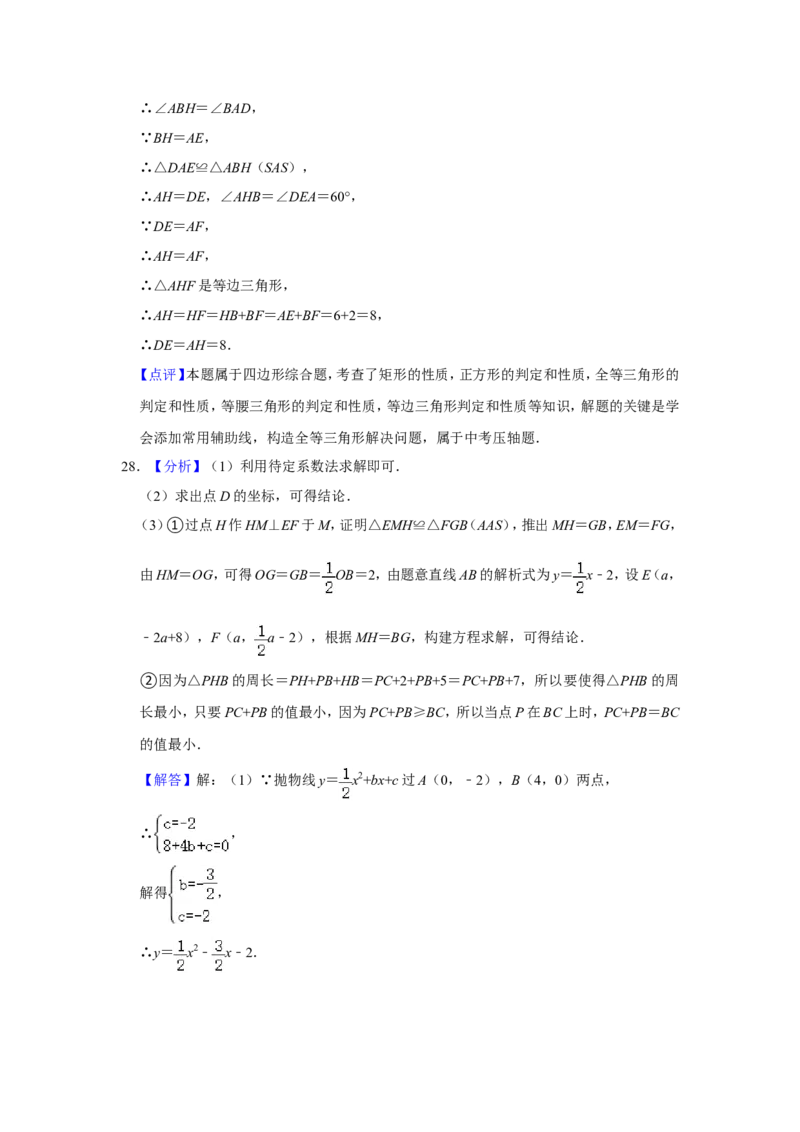
类比迁移:解:延长CB到点H,使BH=AE=6,连接AH,
∵四边形ABCD是菱形,
∴AD∥BC,AB=AD,∴∠ABH=∠BAD,
∵BH=AE,
∴△DAE≌△ABH(SAS),
∴AH=DE,∠AHB=∠DEA=60°,
∵DE=AF,
∴AH=AF,
∴△AHF是等边三角形,
∴AH=HF=HB+BF=AE+BF=6+2=8,
∴DE=AH=8.
【点评】本题属于四边形综合题,考查了矩形的性质,正方形的判定和性质,全等三角形的
判定和性质,等腰三角形的判定和性质,等边三角形判定和性质等知识,解题的关键是学
会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.
28.【分析】(1)利用待定系数法求解即可.
(2)求出点D的坐标,可得结论.
(3)①过点H作HM⊥EF于M,证明△EMH≌△FGB(AAS),推出MH=GB,EM=FG,
由HM=OG,可得OG=GB= OB=2,由题意直线AB的解析式为y= x﹣2,设E(a,
﹣2a+8),F(a, a﹣2),根据MH=BG,构建方程求解,可得结论.
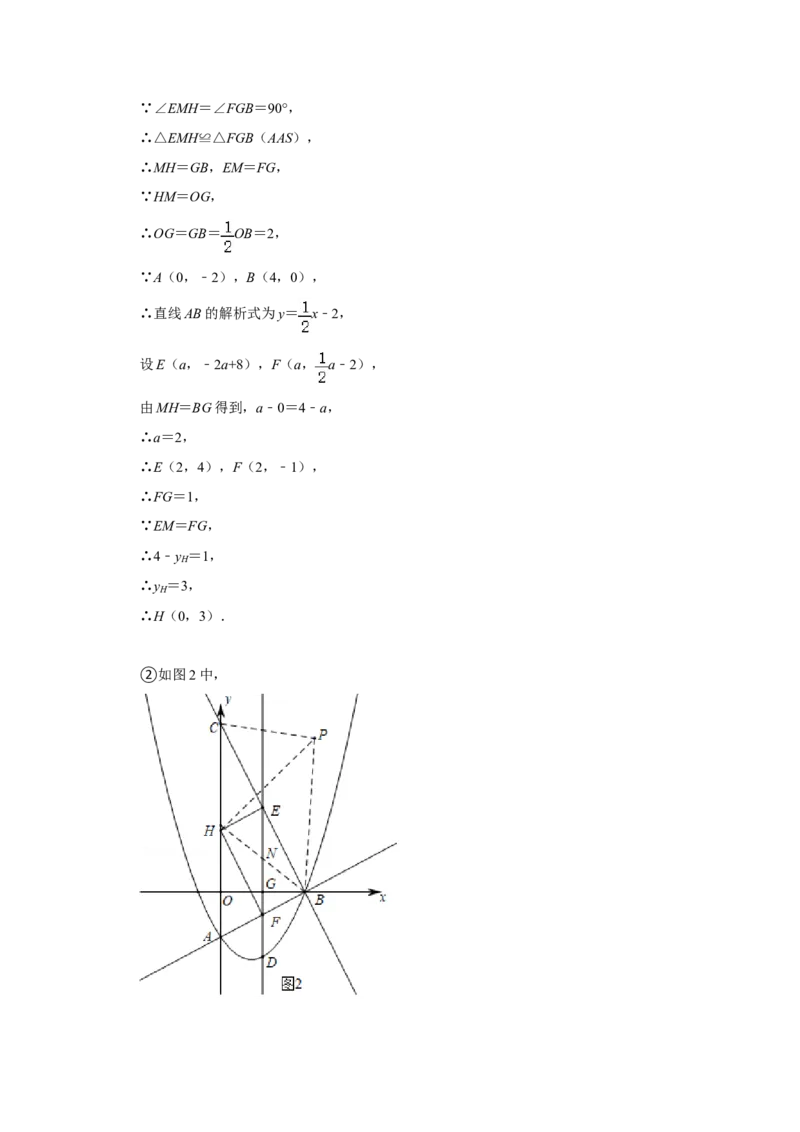
②因为△PHB的周长=PH+PB+HB=PC+2+PB+5=PC+PB+7,所以要使得△PHB的周
长最小,只要PC+PB的值最小,因为PC+PB≥BC,所以当点P在BC上时,PC+PB=BC
的值最小.
【解答】解:(1)∵抛物线y= x2+bx+c过A(0,﹣2),B(4,0)两点,
∴ ,
解得 ,
∴y= x2﹣ x﹣2.(2)∵B(4,0),A(0,﹣2),
∴OB=4,OA=2,
∵GF⊥x轴,OA⊥x轴,
在Rt△BOA和Rt△BGF中,tan∠ABO= = ,
即 = ,
∴GB=1,
∴OG=OB﹣GB=4﹣1=3,
当x=3时,y = ×9﹣ ×3﹣2=﹣2,
D
∴D(3,﹣2),即GD=2,
∴FD=GD﹣GF=2﹣ = ,
∴S△BDF = •DF•BG= × ×1= .
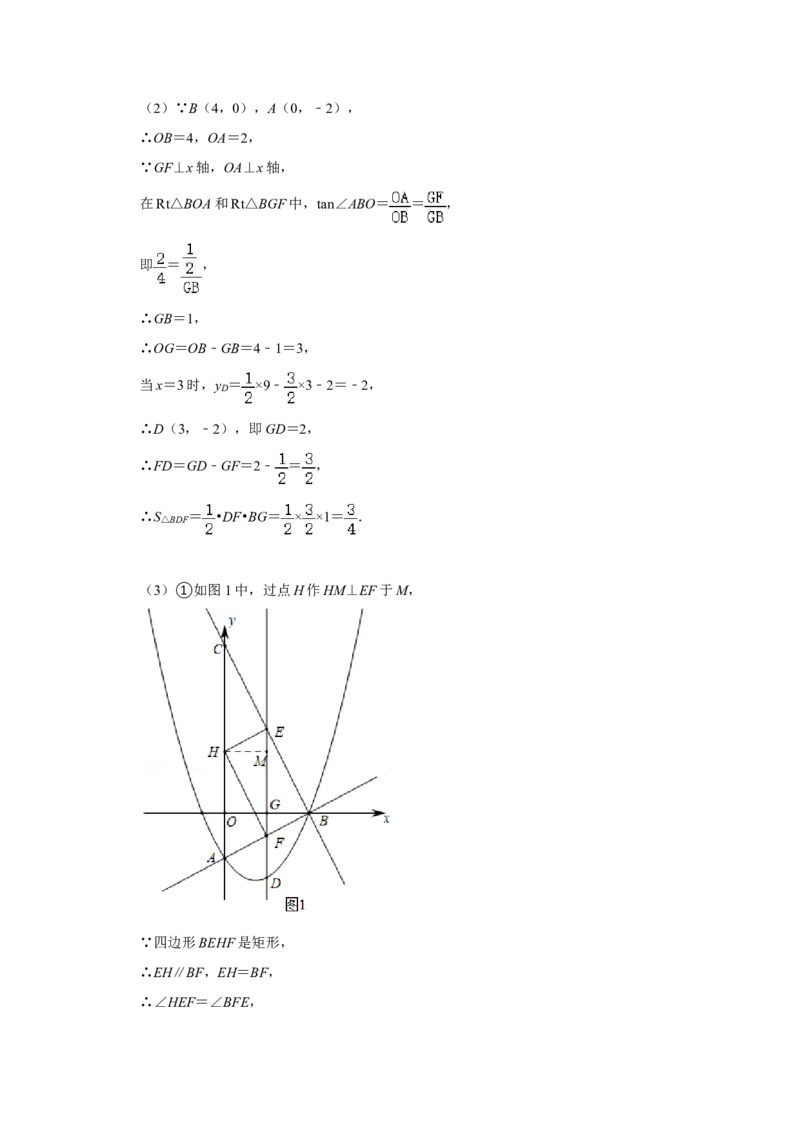
(3)①如图1中,过点H作HM⊥EF于M,
∵四边形BEHF是矩形,
∴EH∥BF,EH=BF,
∴∠HEF=∠BFE,∵∠EMH=∠FGB=90°,
∴△EMH≌△FGB(AAS),
∴MH=GB,EM=FG,
∵HM=OG,
∴OG=GB= OB=2,
∵A(0,﹣2),B(4,0),
∴直线AB的解析式为y= x﹣2,
设E(a,﹣2a+8),F(a, a﹣2),
由MH=BG得到,a﹣0=4﹣a,
∴a=2,
∴E(2,4),F(2,﹣1),
∴FG=1,
∵EM=FG,
∴4﹣y =1,
H
∴y =3,
H
∴H(0,3).
②如图2中,BH= = =5,
∵PH=PC+2,
∴△PHB的周长=PH+PB+HB=PC+2+PB+5=PC+PB+7,
要使得△PHB的周长最小,只要PC+PB的值最小,
∵PC+PB≥BC,
∴当点P在BC上时,PC+PB=BC的值最小,
∵BC= = =4 ,
∴△PHB的周长的最小值为4 +7.
【点评】本题属于二次函数综合题,考查了二次函数的性质,一次函数的性质,全等三角形
的判定和性质,矩形的判定和性质,两点之间线段最短等知识,解题的关键是学会寻找全
等三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2022/1/24 19:15:56;用户:我不叫王海宁;邮箱:orFmNtygTZdeoRRXtaD47YJRzPg0@weixin.jyeoo.com;学号:39962365