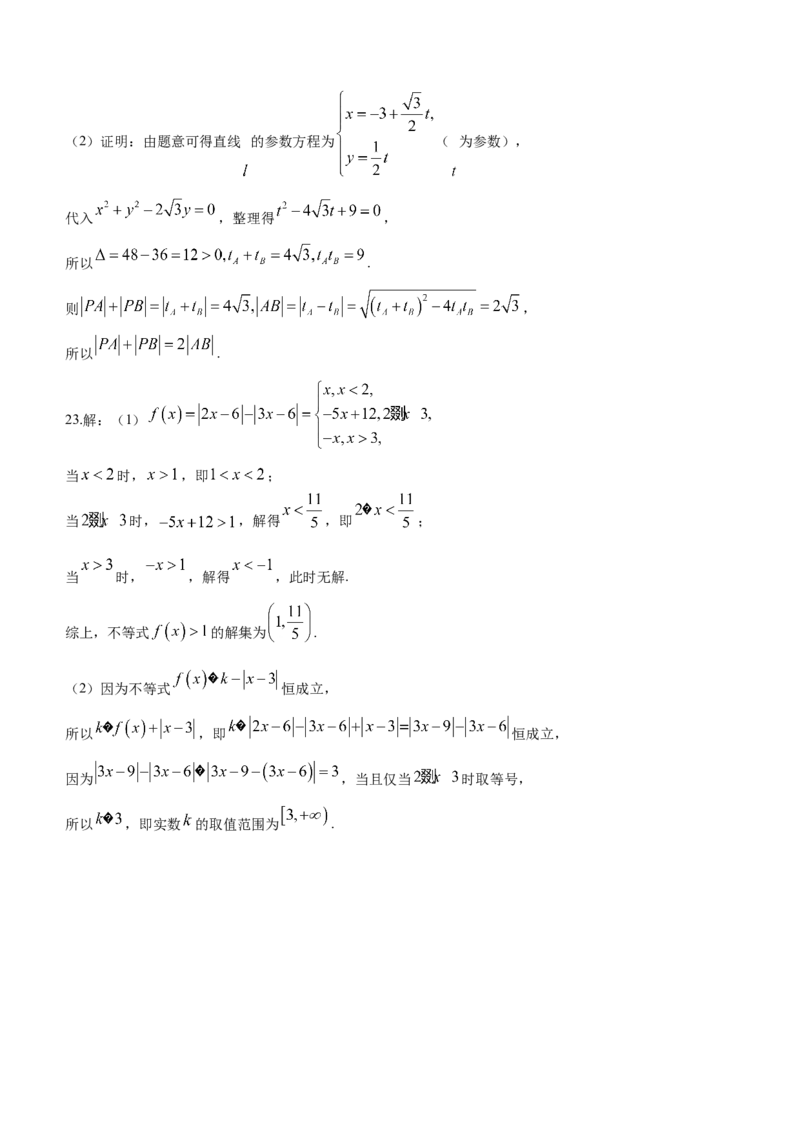文档内容
商洛市 2024 届高三尖子生学情诊断考试(第二次)
数学试卷(文科)
考生注意:
1.本试卷分选择题和非选择题两部分.满分150分,考试时间120分钟.
2.答题前,考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚.
3.考生作答时,请将答案答在答题卡上.选择题每小题选出答案后,用2B铅笔把答题卡上对应题
目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内
作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效.
4.本卷命题范围:高考范围.
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符
合题目要求的.
1.已知集合 ,则 ( )
A. B. C. D.
2.法国数学家棣莫弗(1667-1754年)发现了棣莫弗定理:设两个复数 ,
,则 .设 ,则
的虚部为( )
A. B. C.1 D.0
3.一组数据: ,则这组数据的方差为( )
A.5.2 B.26 C.5 D.4.2
4.设向量 的夹角的余弦值为 ,则 ( )
A.-1 B.1 C.-5 D.5
5.执行如图所示的程序框图,输出 的值为( )
学科网(北京)股份有限公司A.70 B.112 C.168 D.240
6.设 是等差数列 的前 项和,且 ,则 ( )
A.34 B.30 C.26 D.22
7.已知偶函数 在 上单调递增,若 ,则( )
A. B. C. D.
8.已知 ,则 ( )
A. B. C. D.
9.在平面直角坐标系 中,抛物线 的焦点为 是 上的一点,点 是 轴上的一点,且
,则 的面积为( )
A. B. C. D.
10.数学家斐波那契在研究兔子繁殖问题时,发现有这样一个数列 ,其中从第3项起,每
一项都等于它前面两项之和,即 ,这样的数列称为“斐波那契数列”.若
,则 ( )
A.175 B.176 C.177 D.178
11.已知三棱锥 的顶点都在球 的球面上,且 平面 ,若 ,
学科网(北京)股份有限公司,则球 的体积为( )
A. B. C. D.
12.已知函数 ,若对任意的 ,当 时,都有
,则实数 的取值范围为( )
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分.
13.已知 ,设函数 ,则 的单调递减区间是__________.
14.已知函数 ,若曲线 在点 处的切线与直线 平行,
则 __________.
15.已知双曲线 的离心率为 ,其中一条渐近线与圆 交于
两点,则 __________.
16.魔方,又叫鲁比克方块,最早是由匈牙利布达佩斯建筑学院厄尔诺•鲁比克教授于1974年发明的机械益智
玩具.魔方拥有竞速、盲拧、单拧等多种玩法,风靡程度经久未衰,每年都会举办大小赛事,是最受欢迎的智力
游戏之一.一个三阶魔方,由27个棱长为1的正方体组成,如图是把魔方的中间一层转动了 ,则该魔方的
表面积增加了__________.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试
题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(本小题满分12分)
学科网(北京)股份有限公司随着科学技术飞速发展,科技创新型人才需求量增大,在2015年,国家开始大力推行科技特长生招生扶持政
策,教育部也出台了《关于“十三五”期间全面深入推进教育信息化工作的指导意见(征求意见稿)》为选
拔和培养科技创新型人才做好准备.某调研机构调查了 两个参加国内学科竞赛的中学,从 两个中学
的参赛学员中随机抽取了60人统计其参赛获奖情况,并将结果整理如下:
未获得区前三名及以上名次 获得区前三名及以上名次
中学 11 6
中学 34 9
(1)试判断是否有 的把握认为获得区前三名及以上名次与所在的学校有关?
(2)用分层抽样的方法,从样本中获得区前三名及以上名次的学生中抽取5人,再从这5人中任选3人进行
深度调研,求所选的3人中恰有2人来自 中学的概率.
附: ,其中 .
0.10 0.05 0.025 0.010
2.706 3.841 5.024 6.635
18.(本小题满分12分)
在 中,内角 的对边分别为 ,且 .
(1)证明: 是钝角三角形;
(2) 平分 ,且交 于点 ,若 ,求 的周长.
19.(本小题满分12分)
如图,在多面体 中,平面 平面 ,四边形 是矩形,四边形 是边长
为2的菱形, 是侧棱 上的一点,且 .
学科网(北京)股份有限公司(1)证明: ;
(2)若 为棱 的中点,求点 到平面 的距离.
20.(本小题满分12分)
设 分别是椭圆 的左、右焦点, ,椭圆的离心率为 .
(1)求椭圆 的方程;
(2)作直线 与椭圆 交于不同的两点 ,其中点 的坐标为 ,若点 是线段 垂直平
分线上一点,且满足 ,求实数 的值.
21.(本小题满分12分)
已知函数 的导函数为 .
(1)证明:函数 有且只有一个极值点;
(2)若 恒成立,求实数 的取值范围.
(二)选考题:共10分.请考生在第22,23两题中任选一题作答.如果多做,则按所做的第一题
计分.
22.(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系 中,曲线 的参数方程为 ( 为参数),以原点 为极点, 轴
的正半轴为极轴建立极坐标系.
(1)求曲线 的普通方程和极坐标方程;
(2)在平面直角坐标系 中,过点 且倾斜角为 的直线 与曲线 交于 两点,证明:
.
学科网(北京)股份有限公司23.(本小题满分10分)选修4-5:不等式选讲
已知函数 .
(1)求不等式 的解集;
(2)若不等式 恒成立,求实数 的取值范围.
商洛市 2024 届高三尖子生学情诊断考试(第二次)•数学试卷(文科)
参考答案、提示及评分细则
1.A 因为 ,所以
.故选A.
学科网(北京)股份有限公司2.B ,所以
,所以 的虚部为 .故选B.
3.A 依题意这组数据的平均数为 ,所以方差为
.2.故选A.
4.B 设 与 的夹角为 ,因为 与 的夹角的余弦值为 ,即 ,又 ,所以
,所以 .故选B.
5.C 第一次执行,由 ,则 ,又由 ,则进入循环;第一次循环,由
,则 ,又由 ,则进入循环;第二次循环,由 ,则
,又由 ,则进入循环;第三次循环,由 ,则
,又由 ,则进入循环;第四次循环,由 ,则
,又由 ,则进入循环;第五次循环,由 ,则
,又由 ,则进入循环;第六次循环,由 112,则
,又由 ,不成立,退出循环,则输出 .故选C.
6.B 设等差数列 的公差为 ,由 ,所以 解
学科网(北京)股份有限公司得 ,所以 .故选B.
7.A 因为偶函数 在 上单调递增,所以 在 上单调递减. ,
所以只需比较 的大小即可.因为 ,所以 .又因为 ,所以 ,故
.而 在 上单调递减,所以 ,即 .故选A.
8.C 由 ,可得 ,即 ,所以
.故选C.
9.D 由题意知 ,设 ,所以 ,又 ,
所以 ,所以 ,所以 ,解得 ,所以
的面积 .故选D.
10.B 由从第三项起,每个数等于它前面两个数的和, ,由 ,得
,所以 ,将这 个式子左、右两边分别相加可得
,所以 .所以
所以 .故选B.
11.D 在 中, ,由余弦定理得 ,
学科网(北京)股份有限公司设 外接圆的圆心为 ,则 平面 ,且 ,而 平面 ,因此
,取 的中点 ,连接 ,则四边形 为矩形,则 ,球 的半径
,体积 .故选D.
12.C 不等式 等价于 ,令
,根据题意对任意的 ,当 时, ,所
以函数 在 上单调递减,所以 在 上恒
成立,即 在 上恒成立.令 ,则 ,所以当 时,
, 单调递增;当 时, 单调递减.所以 ,所以
.故选C.
13. (开区间,半开半闭区间也正确) 依题意 ,令 ,解得
,所以 的单调递减区间是 .
14.6 由题意知 ,所以 ,解得 .
学科网(北京)股份有限公司15. 圆 的圆心 ,半径 ,由双曲线 的离心率为
,得 ,解得 ,于是双曲线的渐近线方程为 ,即 .当渐
近线为 时,点 到此直线的距离 ,即直线 与已知圆相离,不
符合要求;当渐近线为 时,点 到此直线的距离 ,则直线 与已
知圆相交,弦长 .
16. 如图,转动 后,此时魔方相对原来魔方多出了16个小三角形的面积,俯视图如图,由
图形的对称性可知, 为等腰直角三角形,设直角边 ,则斜边 ,故
,可得 .由几何关系得 ,故转动后的
表面积 ,故表面积增加了
.
学科网(北京)股份有限公司17.解:(1)补全 列联表如下:
未获得区前三名及以上名次 获得区前三名及以上名次 总计
中学 11 6 17
中学 34 9 43
总计 45 15 60
所以 ,
故没有 的把握认为获得区前三名及以上名次与所在的学校有关.
(2)由题知,用分层抽样抽取的5人中,来自 中学的有2人,记为 ,来自 中学的有3人,记为
,
从这5人中任选3人进行深度调研,所有的结果有 ,
共10种,
其中恰有2人来自 中学的结果有 ,共6种,
故所求概率 .
18.(1)证明:在 中, ,
由正弦定理,得 ,即 ,
由余弦定理,得 ,
学科网(北京)股份有限公司因为 ,所以 ,
所以 是钝角三角形.
(2)解:因为 ,
且 ,
所以 ,
由余弦定理,得 ,
解得 (负值舍去),
所以 的周长为 .
19.(1)证明:连接 ,则 ,
因为平面 平面 ,平面 平面 平面 ,所以
平面 ,
又 平面 ,所以 ,
又 平面 ,
所以 平面 ,
又 平面 ,所以 .
(2)解:因为平面 平面 ,平面 平面 平面
,所以 平面 ,
学科网(北京)股份有限公司因为 平面 ,所以平面 平面 .
过 在平面 内作 ,交棱 的延长线于点 ,
因为平面 平面 ,所以 平面 ,
因为 ,所以 ,
因为 平面 ,且 平面 ,所以 平面 ,
所以点 到平面 的距离等于 .
因为 ,所以 ,
所以 ,
所以 .
由 平面 ,得 ,所以 ,
因为 ,设点 到平面 的距离为 ,
所以 ,即 ,
所以 ,即点 到平面 的距离为 .
20.解:(1)设椭圆 的半焦距为 .
因为 ,所以 ,解得 ,
因为椭圆的离心率为 ,所以 ,即 ,解得 ,
则 ,
故椭圆 的方程为 .
学科网(北京)股份有限公司(2)由 ,根据题意可知直线 的斜率存在,
可设直线 的斜率为 ,则直线 的方程为 .
把 代入椭圆 的方程,消去 整理得 .
设 ,则 ,则 ,
所以线段 的中点坐标为 .
①当 时, ,线段 的垂直平分线为 轴,于是 .
由 ,解得 ;
②当 时,线段 的垂直平分线的方程为 .
由点 是线段 的垂直平分线上一点,令 ,得 .
因为 ,
所以 ,
解得 ,
所以 .
综上所述,实数 的值为 .
21.(1)证明:由题意知 的定义域为 ,且 ,
令 ,则 ,
学科网(北京)股份有限公司所以 (即 )在 上单调递增,
又
所以 在 上有唯一零点 ,
当 时, ,当 时, ,
所以 在 上单调递减,在 上单调递增,
所以函数 有且只有一个极值点 .
(2)解: 恒成立,
即 恒成立,
即 恒成立,即 恒成立.
令 ,则 ,所以 ,
令 ,则 ,
令 ,得 ,令 ,得 ,
所以 在 上单调递增,在 上单调递减,
所以 ,所以 ,解得 ,
即实数 的取值范围为 .
22.(1)解:由 得到 ,
即 ,所以曲线 的普通方程为 .
又因为 ,则 ,
整理得 ,即曲线 的极坐标方程为 ,
学科网(北京)股份有限公司(2)证明:由题意可得直线 的参数方程为 ( 为参数),
代入 ,整理得 ,
所以 .
则 ,
所以 .
23.解:(1)
当 时, ,即 ;
当 时, ,解得 ,即 ;
当 时, ,解得 ,此时无解.
综上,不等式 的解集为 .
(2)因为不等式 恒成立,
所以 ,即 恒成立,
因为 ,当且仅当 时取等号,
所以 ,即实数 的取值范围为 .
学科网(北京)股份有限公司