文档内容
2021年贵州省铜仁市中考数学试卷
一、选择题:(本大题共10个小题,每小题4分,共40分)本题每小题均有A、B、C、
D四个备选答案,其中只有一个是正确的,请你将正确答案的序号填涂在相应的答题卡上.
1.2021年2月25日,全国脱贫攻坚总结表彰大会在京举行,习近平总书记在大会上庄严
宣告:“我国脱贫攻坚战取得了全面胜利.这是中国人民的伟大光荣,是中国共产党的
伟大光荣,是中华民族的伟大光荣!”现行标准下9899万农村贫困人口全部脱贫,创造
了又一个彪炳史册的人间奇迹.98990000用科学记数法表示为( )
A.9.899×106 B.98.99×107 C.9.899×108 D.9.899×107
2.如图,是一个底面为等边三角形的正三棱柱,它的主视图是( )
A. B. C. D.
3.有6位同学一次数学测验分数分别是:125,130,130,132,140,145,则这组数据的
中位数是( )
A.130 B.132 C.131 D.140
4.下列等式正确的是( )
A.|﹣3|+tan45°=﹣2 B.(xy)5÷( )5=x10
C.(a﹣b)2=a2+2ab+b2 D.x3y﹣xy3=xy(x+y)(x﹣y)
5.直线AB、BC、CD、EG如图所示,∠1=∠2=80°,∠3=40°,则下列结论错误的是(
)
A.AB∥CD B.∠EBF=40° C.∠FCG+∠3=∠2 D.EF>BE
6.用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的镶嵌.工人师傅不能用下列哪种形状、大小完全相同的一
种地砖在平整的地面上镶嵌( )
A.等边三角形 B.正方形 C.正五边形 D.正六边形
7.不等式组 的解集在以下数轴表示中正确的是( )
A. B.
C. D.
8.已知直线y=kx+2过一、二、三象限,则直线y=kx+2与抛物线y=x2﹣2x+3的交点个
数为( )
A.0个 B.1个 C.2个 D.1个或2个
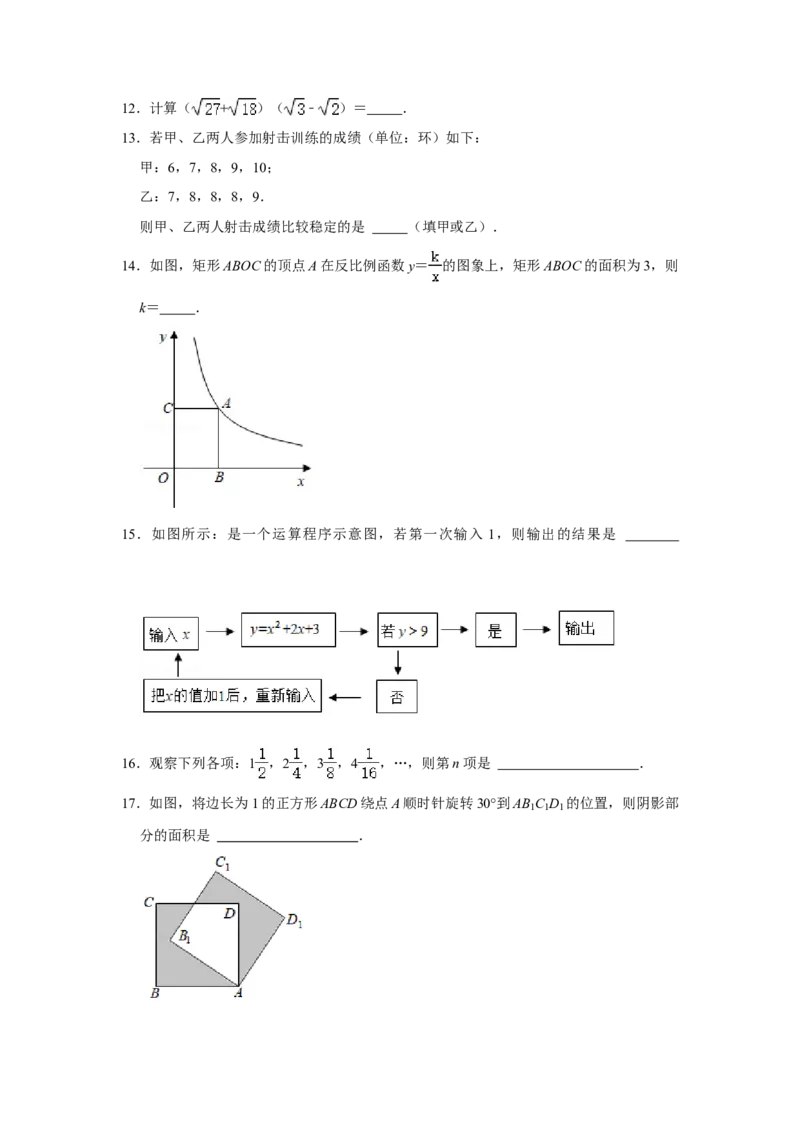
9.如图,在Rt△ABC中,∠C=90°,AB=10,BC=8,按下列步骤作图:
步骤1:以点A为圆心,小于AC的长为半径作弧分别交AC、AB于点D、E.
步骤2:分别以点D、E为圆心,大于 DE的长为半径作弧,两弧交于点M.
步骤3:作射线AM交BC于点F.
则AF的长为( )
A.6 B.3 C.4 D.6
10.已知抛物线y=a(x﹣h)2+k与x轴有两个交点A(﹣1,0),B(3,0),抛物线y=
a(x﹣h﹣m)2+k与x轴的一个交点是(4,0),则m的值是( )
A.5 B.﹣1 C.5或1 D.﹣5或﹣1
二、填空题:(本大题共8个小题,每小题4分,共32分)
11.要使分式 有意义,则x的取值范围是 .12.计算( + )( ﹣ )= .
13.若甲、乙两人参加射击训练的成绩(单位:环)如下:
甲:6,7,8,9,10;
乙:7,8,8,8,9.
则甲、乙两人射击成绩比较稳定的是 (填甲或乙).
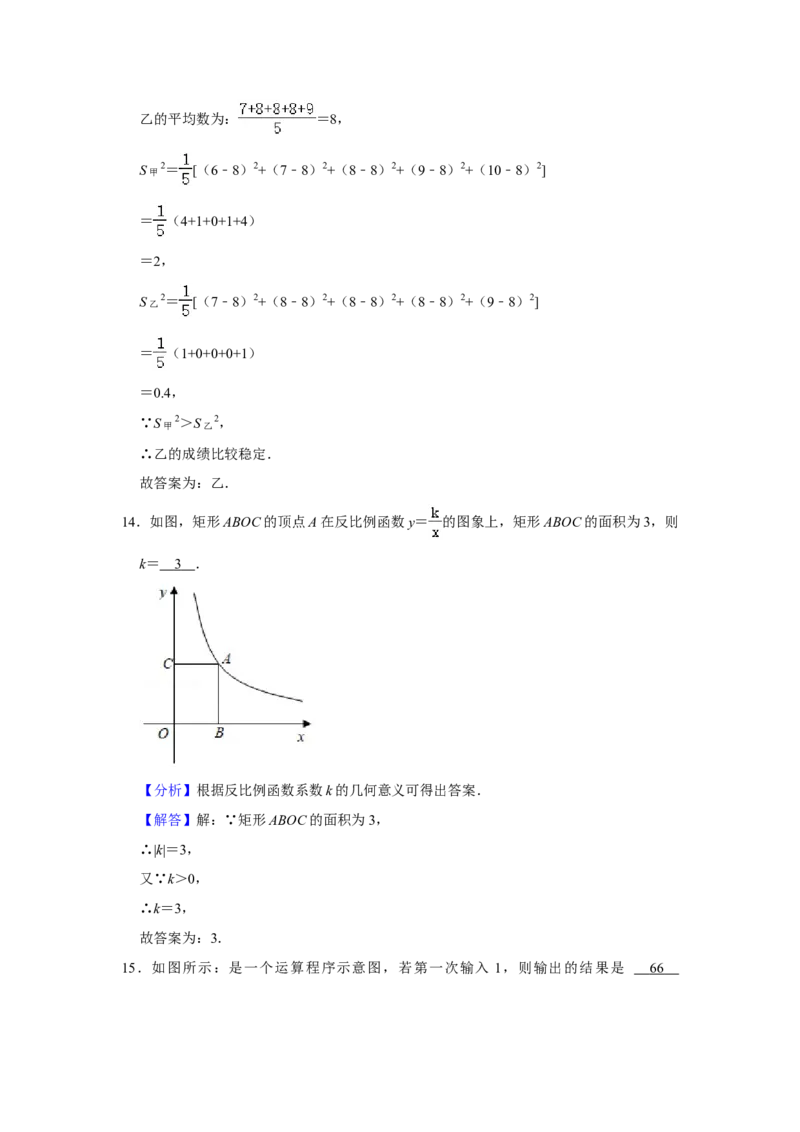
14.如图,矩形ABOC的顶点A在反比例函数y= 的图象上,矩形ABOC的面积为3,则
k= .
15.如图所示:是一个运算程序示意图,若第一次输入 1,则输出的结果是
16.观察下列各项:1 ,2 ,3 ,4 ,…,则第n项是 .
17.如图,将边长为1的正方形ABCD绕点A顺时针旋转30°到AB C D 的位置,则阴影部
1 1 1
分的面积是 .18.如图,E、F分别是正方形ABCD的边AB、BC上的动点,满足AE=BF,连接CE、
DF,相交于点 G,连接 AG,若正方形的边长为 2.则线段 AG 的最小值为
.
三、解答题:(本大题共4个小题,每小题10分,共40分,要有解题的主要过程)
19.(10分)某品牌汽车销售店销售某种品牌的汽车,每辆汽车的进价 16(万元).当每
辆售价为22(万元)时,每月可销售4辆汽车.根据市场行情,现在决定进行降价销售.
通过市场调查得到了每辆降价的费用y (万元)与月销售量x(辆)(x≥4)满足某种
1
函数关系的五组对应数据如下表:
x 4 5 6 7 8
y 0 0.5 1 1.5 2
1
(1)请你根据所给材料和初中所学的函数知识写出 y 与 x 的关系式 y =
1 1
;
(2)每辆原售价为22万元,不考虑其它成本,降价后每月销售利润y=(每辆原售价
﹣y ﹣进价)x,请你根据上述条件,求出月销售量x(x≥4)为多少时,销售利润最大?
1
最大利润是多少?
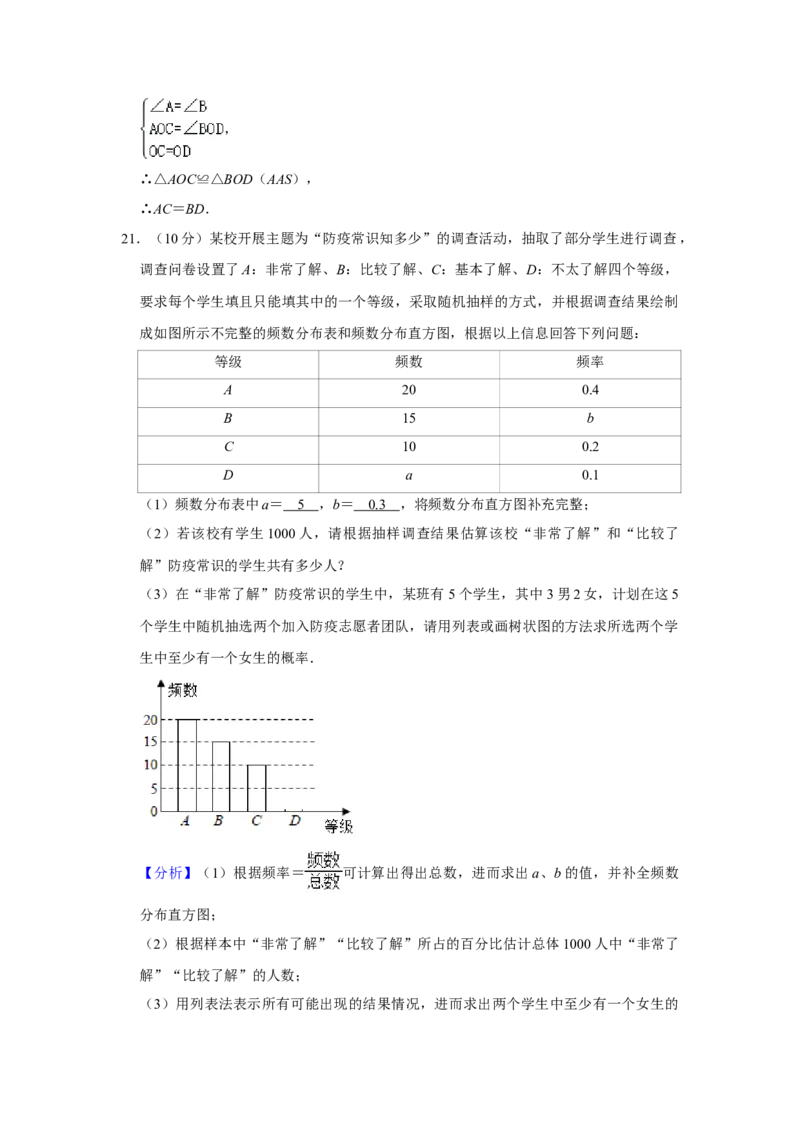
20.(10分)如图,AB交CD于点O,在△AOC与△BOD中,有下列三个条件:①OC
=OD,②AC=BD,③∠A=∠B.请你在上述三个条件中选择两个为条件,另一个能
作为这两个条件推出来的结论,并证明你的结论(只要求写出一种正确的选法).
(1)你选的条件为 、 ,结论为 ;
(2)证明你的结论.
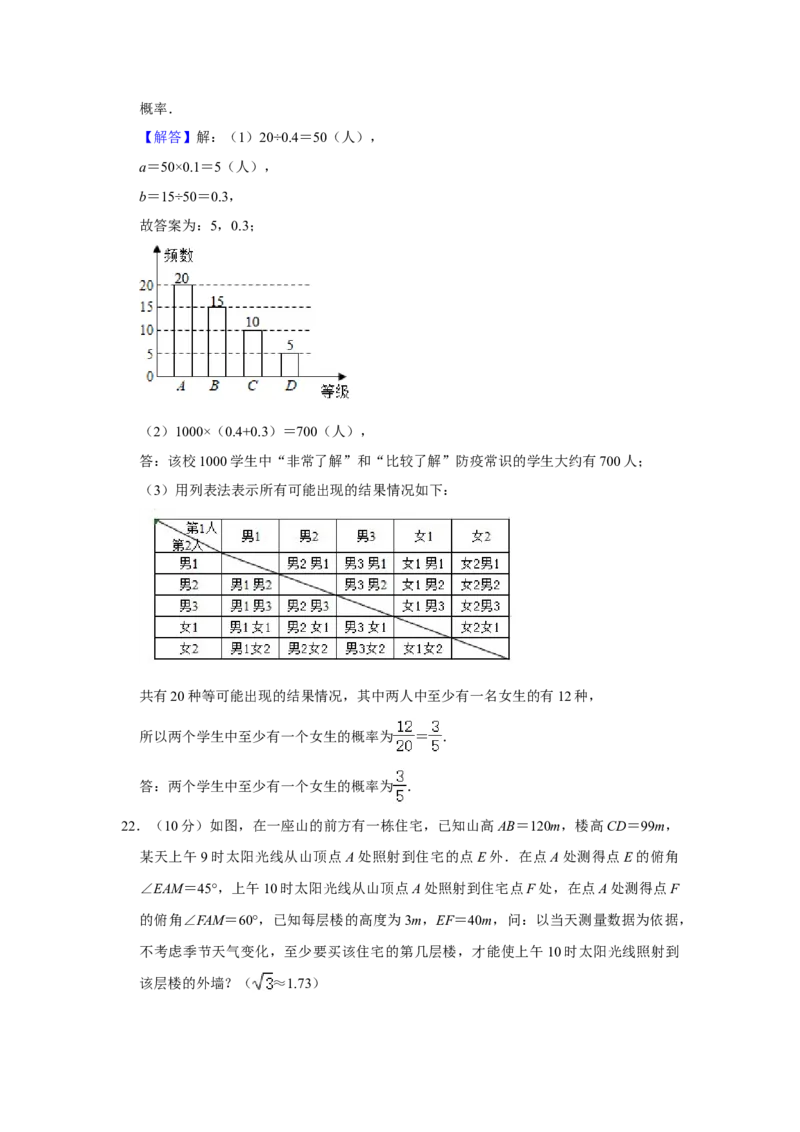
21.(10分)某校开展主题为“防疫常识知多少”的调查活动,抽取了部分学生进行调查,
调查问卷设置了A:非常了解、B:比较了解、C:基本了解、D:不太了解四个等级,要求每个学生填且只能填其中的一个等级,采取随机抽样的方式,并根据调查结果绘制
成如图所示不完整的频数分布表和频数分布直方图,根据以上信息回答下列问题:
等级 频数 频率
A 20 0.4
B 15 b
C 10 0.2
D a 0.1
(1)频数分布表中a= ,b= ,将频数分布直方图补充完整;
(2)若该校有学生1000人,请根据抽样调查结果估算该校“非常了解”和“比较了
解”防疫常识的学生共有多少人?
(3)在“非常了解”防疫常识的学生中,某班有 5个学生,其中3男2女,计划在这5
个学生中随机抽选两个加入防疫志愿者团队,请用列表或画树状图的方法求所选两个学
生中至少有一个女生的概率.
22.(10分)如图,在一座山的前方有一栋住宅,已知山高AB=120m,楼高CD=99m,
某天上午9时太阳光线从山顶点A处照射到住宅的点E外.在点A处测得点E的俯角
∠EAM=45°,上午10时太阳光线从山顶点A处照射到住宅点F处,在点A处测得点F
的俯角∠FAM=60°,已知每层楼的高度为3m,EF=40m,问:以当天测量数据为依据,
不考虑季节天气变化,至少要买该住宅的第几层楼,才能使上午10时太阳光线照射到
该层楼的外墙?( ≈1.73)四、(本大题满分12分)
23.(12分)某快递公司为了提高工作效率,计划购买A、B两种型号的机器人来搬运货
物,已知每台A型机器人比每台B型机器人每天多搬运20吨,并且3台A型机器人和2
台B型机器人每天共搬运货物460吨.
(1)求每台A型机器人和每台B型机器人每天分别搬运货物多少吨?
(2)每台A型机器人售价3万元,每台B型机器人售价2万元,该公司计划采购A、B
两种型号的机器人共20台,必须满足每天搬运的货物不低于1800吨,请根据以上要求,
求出A、B两种机器人分别采购多少台时,所需费用最低?最低费用是多少?
五、(本大题满分12分)
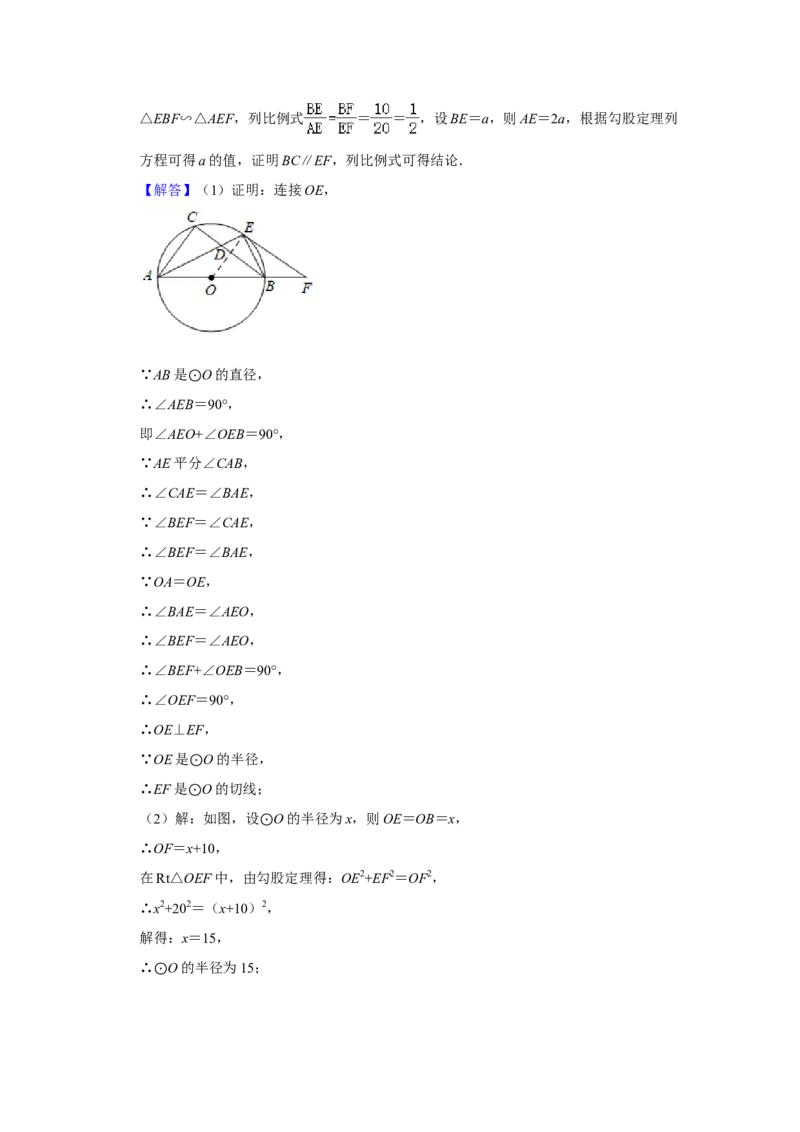
24.(12分)如图,已知△ABC内接于 O,AB是 O的直径,∠CAB的平分线交BC于
点D,交 O于点E,连接EB,作∠B⊙EF=∠CAE⊙,交AB的延长线于点F.
(1)求证⊙:EF是 O的切线;
(2)若BF=10,⊙EF=20,求 O的半径和AD的长.
⊙
六、(本大题满分14分)
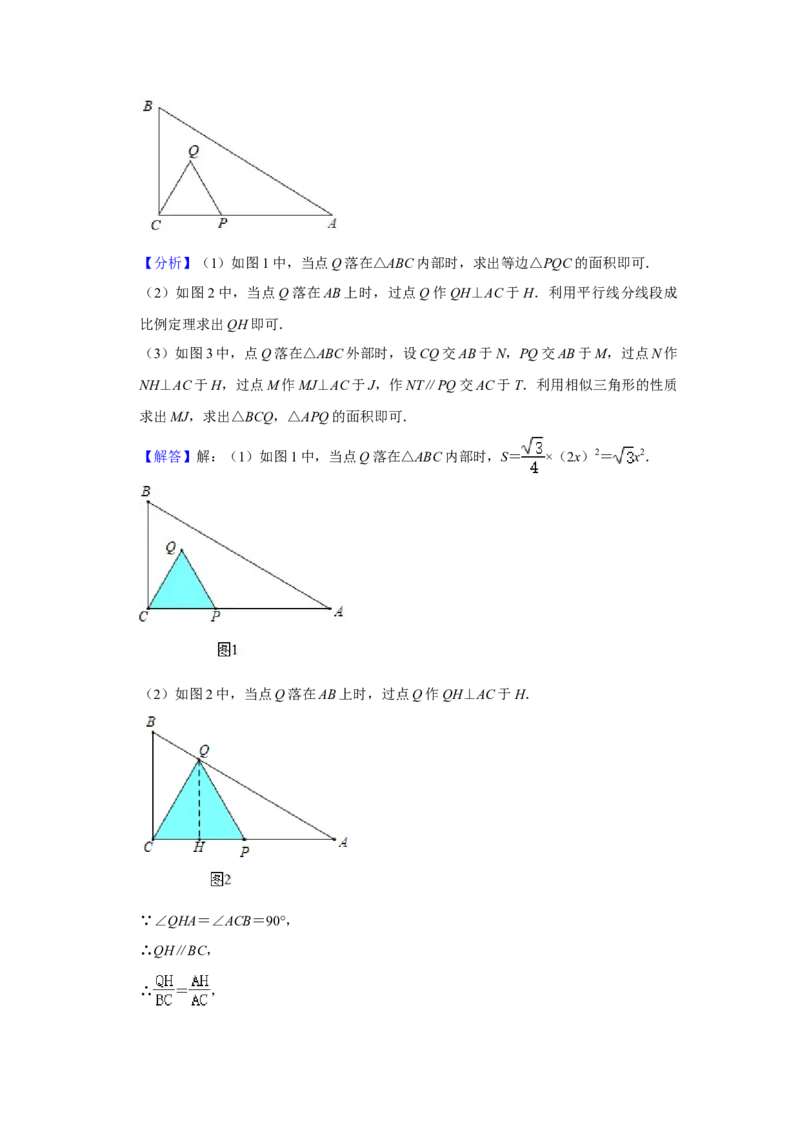
25.(14分)如图,在△ABC中,∠ACB=90°,BC=6 cm,AC=12cm.点P是CA边
上的一动点,点P从点C出发以每秒2cm的速度沿CA方向匀速运动,以CP为边作等
边△CPQ(点B、点Q在AC同侧),设点P运动的时间为x秒,△ABC与△CPQ重叠
部分的面积为S.
(1)当点Q落在△ABC内部时,求此时△ABC与△CPQ重叠部分的面积S(用含x的
代数式表示,不要求写x的取值范围);
(2)当点Q落在AB上时,求此时△ABC与△CPQ重叠部分的面积S的值;
(3)当点Q落在△ABC外部时,求此时△ABC与△CPQ重叠部分的面积S(用含x的
代数式表示).2021年贵州省铜仁市中考数学试卷
参考答案与试题解析
一、选择题:(本大题共10个小题,每小题4分,共40分)本题每小题均有A、B、C、
D四个备选答案,其中只有一个是正确的,请你将正确答案的序号填涂在相应的答题卡上.
1.2021年2月25日,全国脱贫攻坚总结表彰大会在京举行,习近平总书记在大会上庄严
宣告:“我国脱贫攻坚战取得了全面胜利.这是中国人民的伟大光荣,是中国共产党的
伟大光荣,是中华民族的伟大光荣!”现行标准下9899万农村贫困人口全部脱贫,创造
了又一个彪炳史册的人间奇迹.98990000用科学记数法表示为( )
A.9.899×106 B.98.99×107 C.9.899×108 D.9.899×107
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的
值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相
同.当原数绝对值≥10时,n是正整数.
【解答】解:98990000=9.899×107.
故选:D.
2.如图,是一个底面为等边三角形的正三棱柱,它的主视图是( )
A. B. C. D.
【分析】找到从正面看所得到的图形即可.
【解答】解:如图所示的正三棱柱,其主视图是矩形,矩形中间有一条纵向的虚线.
故选:A.
3.有6位同学一次数学测验分数分别是:125,130,130,132,140,145,则这组数据的
中位数是( )
A.130 B.132 C.131 D.140
【分析】根据中位数的意义求解即可.
【解答】解:这组数据从小到大排列处在中间位置的两个数的平均数为 =131,
故选:C.
4.下列等式正确的是( )
A.|﹣3|+tan45°=﹣2 B.(xy)5÷( )5=x10
C.(a﹣b)2=a2+2ab+b2 D.x3y﹣xy3=xy(x+y)(x﹣y)
【分析】利用分式的乘除法、提公因式法与公式法分解因式、特殊角的三角函数求解即
可.
【解答】解:A.|﹣3|+tan45°=3+1=4,故A不符合题意;
B.(xy)5÷( )5=x5y5÷ =x5y5• =y10,故B不符合题意;
C.(a﹣b)2=a2﹣2ab+b2,故C不符合题意;
D.x3y﹣xy3=xy(x2﹣y2)=xy(x+y)(x﹣y),故D符合题意;
故选:D.
5.直线AB、BC、CD、EG如图所示,∠1=∠2=80°,∠3=40°,则下列结论错误的是(
)
A.AB∥CD B.∠EBF=40° C.∠FCG+∠3=∠2 D.EF>BE
【分析】根据平行线的判定、对顶角相等及三角形的外角定理求解判断即可得解.
【解答】解:∵∠1=∠2=80°,
∴AB∥CD,
故A正确,不符合题意;
∵∠3=40°,
∴∠EFB=∠3=40°,
∵∠1=∠EBF+∠EFB,
∴∠EBF=40°=∠EFB,
∴EF=BE,
故B正确,不符合题意;故D错误,符合题意;∵∠2是△FCG的外角,
∴∠FCG+∠3=∠2,
故C正确,不符合题意;
故选:D.
6.用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地
铺成一片,这就是平面图形的镶嵌.工人师傅不能用下列哪种形状、大小完全相同的一
种地砖在平整的地面上镶嵌( )
A.等边三角形 B.正方形 C.正五边形 D.正六边形
【分析】正多边形镶嵌有三个条件限制:①边长相等;②顶点公共;③在一个顶点处
各正多边形的内角之和为360°.判断一种或几种图形是否能够镶嵌,只要看一看拼在同
一顶点处的几个角能否构成周角,若能构成360°,则说明能够进行平面镶嵌,反之则不
能.
【解答】解:A选项,等边三角形的内角为60°,360°÷60°=6(个),所以6个等边三
角形可以在一个顶点处实现内角之和等于360°,不符合题意;
B选项,正方形的内角为90°,360°÷90°=4(个),所以4个正方形可以在一个顶点处
实现内角之和等于360°,不符合题意;
C选项,正五边形的内角为108°,360÷108°=3 ,所以正五边形不能在一个顶点处实
现内角之和等于360°,符合题意;
D选项,正六边形的内角为120°,360°÷120°=3(个),所以3个正六边形可以在一个
顶点处实现内角之和等于360°,不符合题意;
故选:C.
7.不等式组 的解集在以下数轴表示中正确的是( )
A. B.
C. D.
【分析】解两个一元一次不等式,再在数轴上画出两个不等式的解集.
【解答】解: ,解不等式①,得:x<3,
解不等式②,得:x≥1,
如图,在数轴上表示不等式①、②的解集,可知所求不等式组的解集是:1≤x<3.
故选:B.
8.已知直线y=kx+2过一、二、三象限,则直线y=kx+2与抛物线y=x2﹣2x+3的交点个
数为( )
A.0个 B.1个 C.2个 D.1个或2个
【分析】先判断k的正负性,再建立方程组,利用判别式即可判断交点个数.
【解答】解:∵直线y=kx+2过一、二、三象限.
∴k>0.
联立直线y=kx+2与抛物线y=x2﹣2x+3组成方程组得:
.
∴x2﹣2x+3=kx+2.
∴x2﹣(2+k)x+1=0.
∴Δ=(﹣2﹣k)2﹣4=k2+4k
∵k>0.
∴Δ>0.
∴直线y=kx+2与抛物线y=x2﹣2x+3的交点个数为2个.
故选:C.
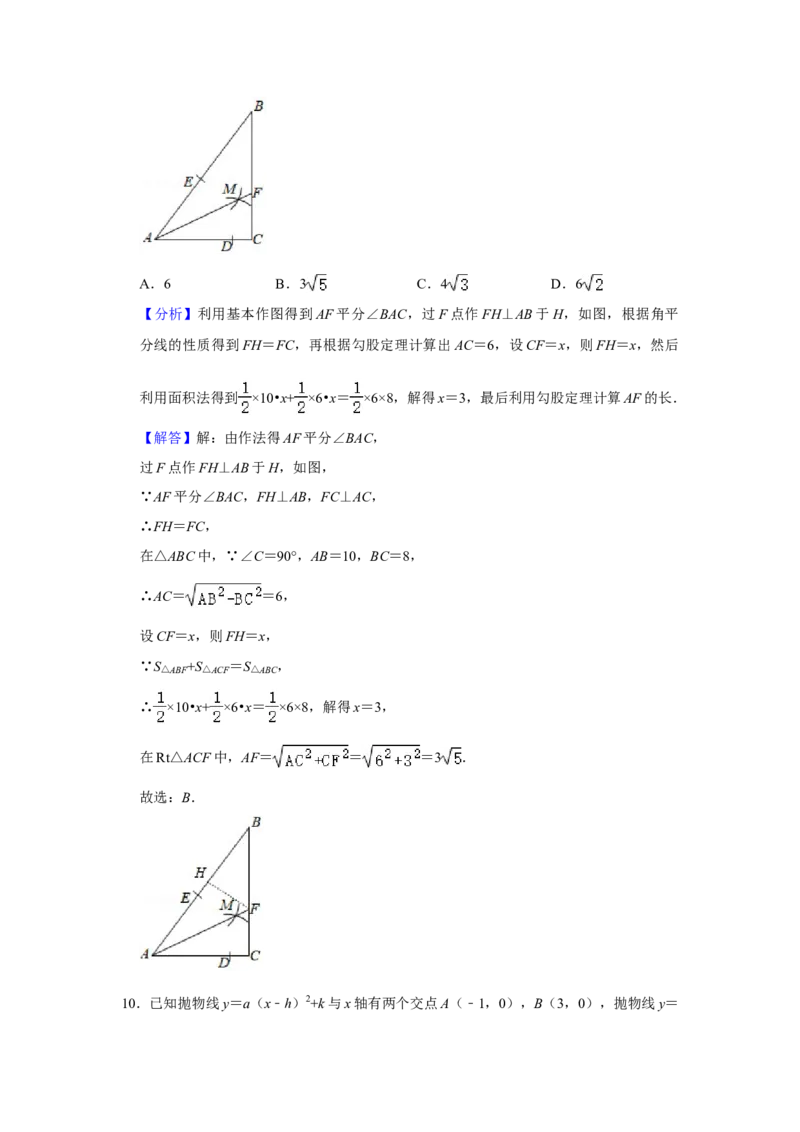
9.如图,在Rt△ABC中,∠C=90°,AB=10,BC=8,按下列步骤作图:
步骤1:以点A为圆心,小于AC的长为半径作弧分别交AC、AB于点D、E.
步骤2:分别以点D、E为圆心,大于 DE的长为半径作弧,两弧交于点M.
步骤3:作射线AM交BC于点F.
则AF的长为( )A.6 B.3 C.4 D.6
【分析】利用基本作图得到AF平分∠BAC,过F点作FH⊥AB于H,如图,根据角平
分线的性质得到FH=FC,再根据勾股定理计算出AC=6,设CF=x,则FH=x,然后
利用面积法得到 ×10•x+ ×6•x= ×6×8,解得x=3,最后利用勾股定理计算AF的长.
【解答】解:由作法得AF平分∠BAC,
过F点作FH⊥AB于H,如图,
∵AF平分∠BAC,FH⊥AB,FC⊥AC,
∴FH=FC,
在△ABC中,∵∠C=90°,AB=10,BC=8,
∴AC= =6,
设CF=x,则FH=x,
∵S△ABF +S△ACF =S△ABC ,
∴ ×10•x+ ×6•x= ×6×8,解得x=3,
在Rt△ACF中,AF= = =3 .
故选:B.
10.已知抛物线y=a(x﹣h)2+k与x轴有两个交点A(﹣1,0),B(3,0),抛物线y=a(x﹣h﹣m)2+k与x轴的一个交点是(4,0),则m的值是( )
A.5 B.﹣1 C.5或1 D.﹣5或﹣1
【分析】先利用二次函数的性质得到两抛物线的对称轴,然后利用A点或B点向右平移
得到点(4,0)得到m的值.
【解答】解:∵抛物线y=a(x﹣h)2+k的对称轴为直线x=h,抛物线y=a(x﹣h﹣
m)2+k的对称轴为直线x=h+m,
∴当点A(﹣1,0)平移后的对应点为(4,0),则m=4﹣(﹣1)=5;
当点B(3,0)平移后的对应点为(4,0),则m=4﹣3=1,
即m的值为5或1.
故选:C.
二、填空题:(本大题共8个小题,每小题4分,共32分)
11.要使分式 有意义,则x的取值范围是 x ≠﹣ 1 .
【分析】直接利用分式有意义的条件分析得出答案.
【解答】解:要使分式 有意义,则x+1≠0,
解得:x≠﹣1.
故答案为:x≠﹣1.
12.计算( + )( ﹣ )= 3 .
【分析】先把二次根式化为最简二次根式,然后利用平方差公式计算.
【解答】解:原式=(3 +3 )( ﹣ )
=3( + )( ﹣ )
=3×(3﹣2)
=3.
故答案为3.
13.若甲、乙两人参加射击训练的成绩(单位:环)如下:
甲:6,7,8,9,10;
乙:7,8,8,8,9.
则甲、乙两人射击成绩比较稳定的是 乙 (填甲或乙).
【分析】根据方差的定义,方差越小数据越稳定即可求解.
【解答】解:甲的平均数为: =8,乙的平均数为: =8,
S甲 2= [(6﹣8)2+(7﹣8)2+(8﹣8)2+(9﹣8)2+(10﹣8)2]
= (4+1+0+1+4)
=2,
S乙 2= [(7﹣8)2+(8﹣8)2+(8﹣8)2+(8﹣8)2+(9﹣8)2]
= (1+0+0+0+1)
=0.4,
∵S甲 2>S乙 2,
∴乙的成绩比较稳定.
故答案为:乙.
14.如图,矩形ABOC的顶点A在反比例函数y= 的图象上,矩形ABOC的面积为3,则
k= 3 .
【分析】根据反比例函数系数k的几何意义可得出答案.
【解答】解:∵矩形ABOC的面积为3,
∴|k|=3,
又∵k>0,
∴k=3,
故答案为:3.
15.如图所示:是一个运算程序示意图,若第一次输入 1,则输出的结果是 66【分析】第一次输入x的值为1,计算出y=6,选择否的程序;第二次输入x的值为7,
计算出y=66,选择是的程序,输出即可.
【解答】解:当x=1时,y=1+2+3=6,
∵6<9,
∴选择否的程序,
∴6+1=7,
当x=7时,y=49+14+3=66,
∵66>9,
∴选择是的程序,
故答案为:66.
16.观察下列各项:1 ,2 ,3 ,4 ,…,则第n项是 n .
【分析】根据题目中数字的特点,可以发现数字的整数部分是连续的整数,从1开始,
而分数部分的分母是2的n次方,n从1开始,分子都是1,然后即可写出第n项对应的
数字.
【解答】解:∵一列数为1 ,2 ,3 ,4 ,…,、
∴这列数可以写成:1 ,2 ,3 ,4 ,…,
∴第n项是n ,
故答案为:n .
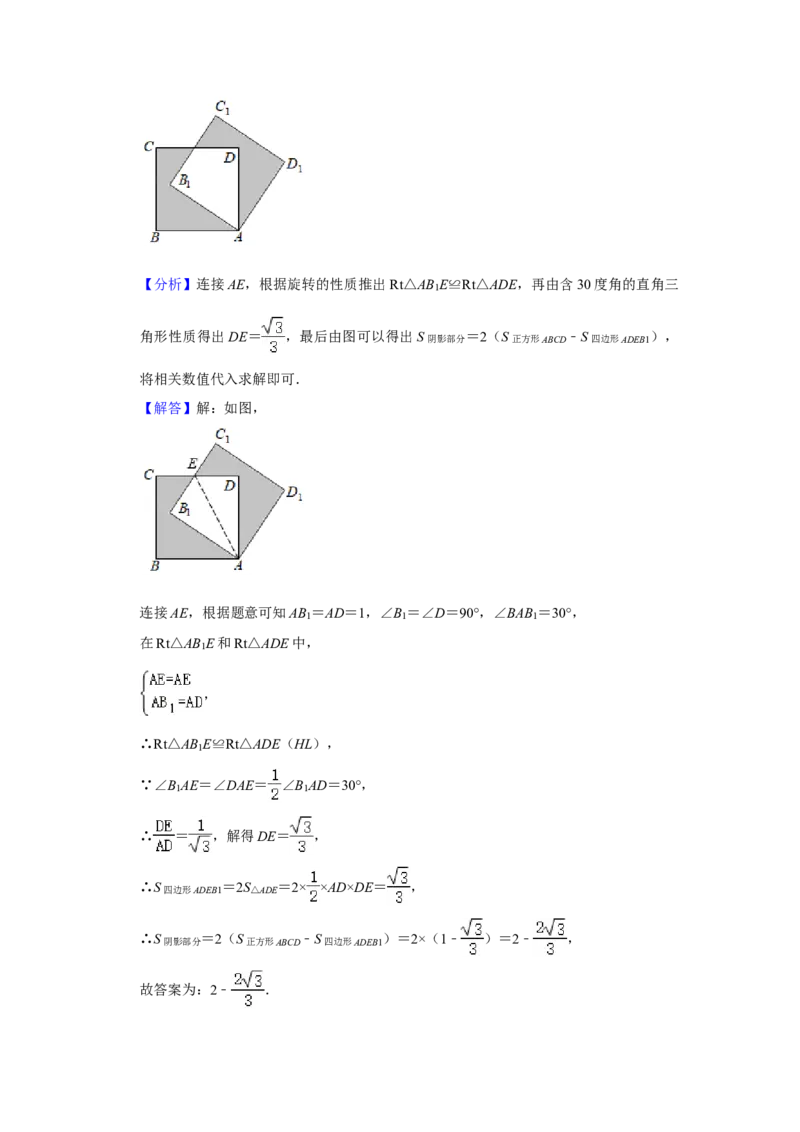
17.如图,将边长为1的正方形ABCD绕点A顺时针旋转30°到AB C D 的位置,则阴影部
1 1 1
分的面积是 2 ﹣ .【分析】连接AE,根据旋转的性质推出Rt△AB E≌Rt△ADE,再由含30度角的直角三
1
角形性质得出DE= ,最后由图可以得出S阴影部分 =2(S正方形ABCD ﹣S四边形ADEB1 ),
将相关数值代入求解即可.
【解答】解:如图,
连接AE,根据题意可知AB =AD=1,∠B =∠D=90°,∠BAB =30°,
1 1 1
在Rt△AB E和Rt△ADE中,
1
,
∴Rt△AB E≌Rt△ADE(HL),
1
∵∠B AE=∠DAE= ∠B AD=30°,
1 1
∴ = ,解得DE= ,
∴S四边形ADEB1 =2S△ADE =2× ×AD×DE= ,
∴S阴影部分 =2(S正方形ABCD ﹣S四边形ADEB1 )=2×(1﹣ )=2﹣ ,
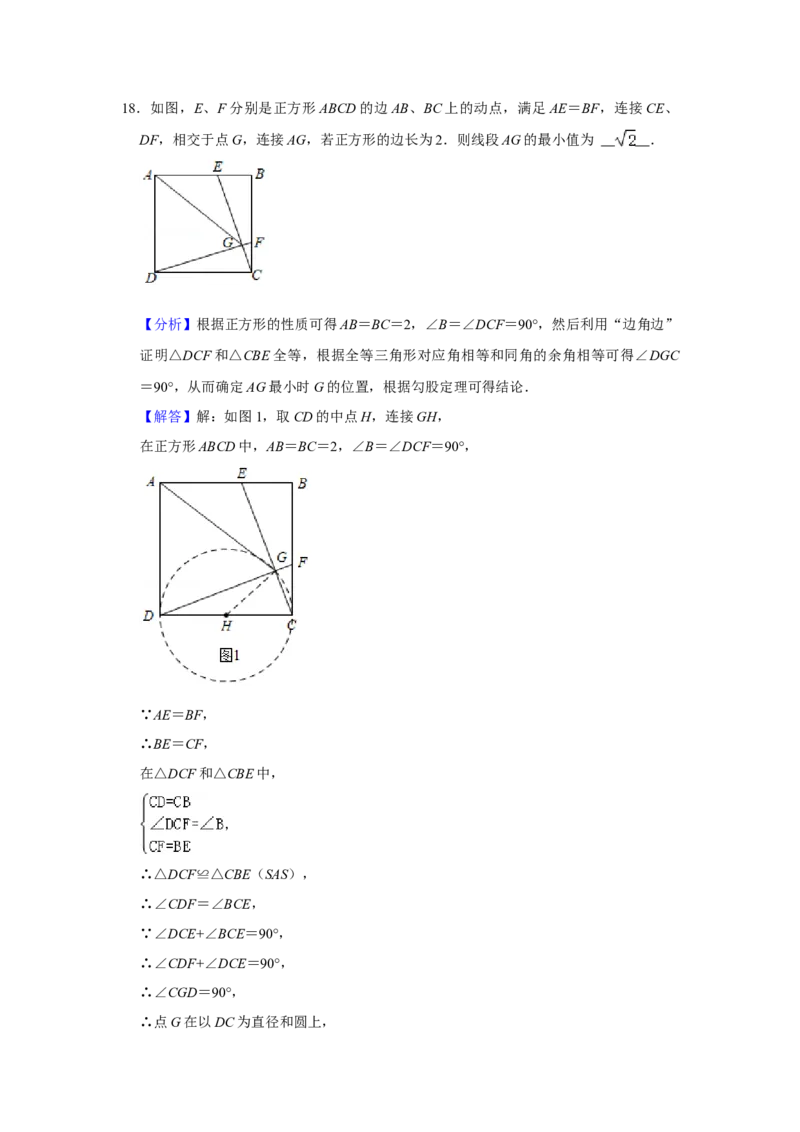
故答案为:2﹣ .18.如图,E、F分别是正方形ABCD的边AB、BC上的动点,满足AE=BF,连接CE、
DF,相交于点G,连接AG,若正方形的边长为2.则线段AG的最小值为 .
【分析】根据正方形的性质可得AB=BC=2,∠B=∠DCF=90°,然后利用“边角边”
证明△DCF和△CBE全等,根据全等三角形对应角相等和同角的余角相等可得∠DGC
=90°,从而确定AG最小时G的位置,根据勾股定理可得结论.
【解答】解:如图1,取CD的中点H,连接GH,
在正方形ABCD中,AB=BC=2,∠B=∠DCF=90°,
∵AE=BF,
∴BE=CF,
在△DCF和△CBE中,
,
∴△DCF≌△CBE(SAS),
∴∠CDF=∠BCE,
∵∠DCE+∠BCE=90°,
∴∠CDF+∠DCE=90°,
∴∠CGD=90°,
∴点G在以DC为直径和圆上,如图2,连接AC,BD交于点O,取DC的中点H,
由勾股定理得:AC= =2 ,
∵E、F分别是正方形ABCD的边AB、BC上的动点,
∴点G在以H为圆心,CH为半径的 圆上运动,当点G与O重合时,AG最小,
此时AG=AO= AC= ,
即AG的最小值= .
故答案为: ;
三、解答题:(本大题共4个小题,每小题10分,共40分,要有解题的主要过程)
19.(10分)某品牌汽车销售店销售某种品牌的汽车,每辆汽车的进价 16(万元).当每
辆售价为22(万元)时,每月可销售4辆汽车.根据市场行情,现在决定进行降价销售.
通过市场调查得到了每辆降价的费用y (万元)与月销售量x(辆)(x≥4)满足某种
1
函数关系的五组对应数据如下表:
x 4 5 6 7 8
y 0 0.5 1 1.5 2
1
(1)请你根据所给材料和初中所学的函数知识写出 y 与x的关系式 y = x ﹣ 2
1 1
( x ≥ 4 ). ;
(2)每辆原售价为22万元,不考虑其它成本,降价后每月销售利润y=(每辆原售价
﹣y ﹣进价)x,请你根据上述条件,求出月销售量x(x≥4)为多少时,销售利润最大?
1
最大利润是多少?
【分析】(1)由表格数据判断y 与x成一次函数关系;
1
(2)根据公式:每月销售利润y=(每辆原售价﹣y ﹣进价)x,求出利润y与x间的关
1系,利用二次函数的性质求出利润最大值和月销售量.
【解答】解:(1)由题意可知:y 与x成一次函数关系,
1
设y =kx+b(k≠0),
1
∵x=4时,y =0,x=6时,y =1,
1 1
∴ ,
解得: ,
∴y = x﹣2(x≥4).
1
故答案为:y = x﹣2(x≥4).
1
(2)由(1)得:y = x﹣2(x≥4),
1
∴y=[22﹣( x﹣2)﹣16]x= x2+8x= (x﹣8)2+32,
∴x=8时,y =32,
max
答:月销售量为8时,最大销售利润为32万元.
20.(10分)如图,AB交CD于点O,在△AOC与△BOD中,有下列三个条件:①OC
=OD,②AC=BD,③∠A=∠B.请你在上述三个条件中选择两个为条件,另一个能
作为这两个条件推出来的结论,并证明你的结论(只要求写出一种正确的选法).
(1)你选的条件为 ① 、 ③ ,结论为 ② ;
(2)证明你的结论.
【分析】(1)根据全等三角形的判定即可选出条件、结论;
(2)由选择的条件证明△AOC≌△BOD,即可得证.
【解答】(1)解:由AAS,选的条件是:①,③,结论是②,
故答案为:①,③,②(答案不唯一);
(2)证明:在△AOC和△BOD中,,
∴△AOC≌△BOD(AAS),
∴AC=BD.
21.(10分)某校开展主题为“防疫常识知多少”的调查活动,抽取了部分学生进行调查,
调查问卷设置了A:非常了解、B:比较了解、C:基本了解、D:不太了解四个等级,
要求每个学生填且只能填其中的一个等级,采取随机抽样的方式,并根据调查结果绘制
成如图所示不完整的频数分布表和频数分布直方图,根据以上信息回答下列问题:
等级 频数 频率
A 20 0.4
B 15 b
C 10 0.2
D a 0.1
(1)频数分布表中a= 5 ,b= 0. 3 ,将频数分布直方图补充完整;
(2)若该校有学生1000人,请根据抽样调查结果估算该校“非常了解”和“比较了
解”防疫常识的学生共有多少人?
(3)在“非常了解”防疫常识的学生中,某班有 5个学生,其中3男2女,计划在这5
个学生中随机抽选两个加入防疫志愿者团队,请用列表或画树状图的方法求所选两个学
生中至少有一个女生的概率.
【分析】(1)根据频率= 可计算出得出总数,进而求出a、b的值,并补全频数
分布直方图;
(2)根据样本中“非常了解”“比较了解”所占的百分比估计总体1000人中“非常了
解”“比较了解”的人数;
(3)用列表法表示所有可能出现的结果情况,进而求出两个学生中至少有一个女生的概率.
【解答】解:(1)20÷0.4=50(人),
a=50×0.1=5(人),
b=15÷50=0.3,
故答案为:5,0.3;
(2)1000×(0.4+0.3)=700(人),
答:该校1000学生中“非常了解”和“比较了解”防疫常识的学生大约有700人;
(3)用列表法表示所有可能出现的结果情况如下:
共有20种等可能出现的结果情况,其中两人中至少有一名女生的有12种,
所以两个学生中至少有一个女生的概率为 = .
答:两个学生中至少有一个女生的概率为 .
22.(10分)如图,在一座山的前方有一栋住宅,已知山高AB=120m,楼高CD=99m,
某天上午9时太阳光线从山顶点A处照射到住宅的点E外.在点A处测得点E的俯角
∠EAM=45°,上午10时太阳光线从山顶点A处照射到住宅点F处,在点A处测得点F
的俯角∠FAM=60°,已知每层楼的高度为3m,EF=40m,问:以当天测量数据为依据,
不考虑季节天气变化,至少要买该住宅的第几层楼,才能使上午10时太阳光线照射到
该层楼的外墙?( ≈1.73)【分析】利用锐角三角函数关系表示出ME、MF,根据EF=MF﹣ME=40m可得AM=
54.6m,求出DF,根据每层楼的高度为3m即可得出答案.
【解答】解:根据题意可知:
四边形ABDM是矩形,
∴AB=MD=120m,
在Rt△AME中,ME=AMtan45°=AM,
在Rt△AMF中,MF=AMtan60°= AM,
∵EF=MF﹣ME=40m,
∴ AM﹣AM=40,
∴AM≈54.6(m),
∴MF≈54.6×1.73≈94.46(m),
∴DF=120﹣94.46=25.54(m),
25.54÷3≈8.5,
∴至少要买该住宅的第9层楼,才能使上午10时太阳光线照射到该层楼的外墙.
答:至少要买该住宅的第9层楼,才能使上午10时太阳光线照射到该层楼的外墙.
四、(本大题满分12分)
23.(12分)某快递公司为了提高工作效率,计划购买A、B两种型号的机器人来搬运货
物,已知每台A型机器人比每台B型机器人每天多搬运20吨,并且3台A型机器人和2
台B型机器人每天共搬运货物460吨.
(1)求每台A型机器人和每台B型机器人每天分别搬运货物多少吨?
(2)每台A型机器人售价3万元,每台B型机器人售价2万元,该公司计划采购A、B
两种型号的机器人共20台,必须满足每天搬运的货物不低于1800吨,请根据以上要求,
求出A、B两种机器人分别采购多少台时,所需费用最低?最低费用是多少?
【分析】(1)题目中的等量关系是:①每台A型机器人比每台B型机器人每天多搬运20吨,②3台A型机器人和2台B型机器人每天共搬运货物460吨.
(2)题目中的不等关系是:每天搬运的 不低于1800吨,等量关系是:总费用=A型机
器费用+B型机器费用,极值问题来利用函数的递增情况解决.
【解答】(1)解:设每台A型机器人每天分别搬运货物x吨,每台B型机器人每天分
别搬运货物y吨.
解得
(2)设:A种机器人采购m台,B种机器人采购(20﹣m)台,总费用为w.
100m+80(20﹣m)≥1800.
解得:m≥10.
w=3m+2(20﹣m)
=m+40.
∵1>0,
∴w随着m的减少而减少.
∴当m=10 w有最小值,w小 =10+40=50.
∴A、B两种机器人分别采购10台,20台时,所需费用最低,最低费用是50万.
五、(本大题满分12分)
24.(12分)如图,已知△ABC内接于 O,AB是 O的直径,∠CAB的平分线交BC于
点D,交 O于点E,连接EB,作∠B⊙EF=∠CAE⊙,交AB的延长线于点F.
(1)求证⊙:EF是 O的切线;
(2)若BF=10,⊙EF=20,求 O的半径和AD的长.
⊙
【分析】(1)连接OE,根据圆周角定理得∠AEB=90°,根据角平分线的定义和同圆的
半径相等,等边对等角及等量代换可得∠OEF=90°,根据切线的判定定理可得结论;
(2)如图,设 O的半径为x,则OE=OB=x,根据勾股定理列方程可得x的值,证明
⊙△EBF∽△AEF,列比例式 = = ,设BE=a,则AE=2a,根据勾股定理列
方程可得a的值,证明BC∥EF,列比例式可得结论.
【解答】(1)证明:连接OE,
∵AB是 O的直径,
∴∠AEB⊙=90°,
即∠AEO+∠OEB=90°,
∵AE平分∠CAB,
∴∠CAE=∠BAE,
∵∠BEF=∠CAE,
∴∠BEF=∠BAE,
∵OA=OE,
∴∠BAE=∠AEO,
∴∠BEF=∠AEO,
∴∠BEF+∠OEB=90°,
∴∠OEF=90°,
∴OE⊥EF,
∵OE是 O的半径,
∴EF是⊙O的切线;
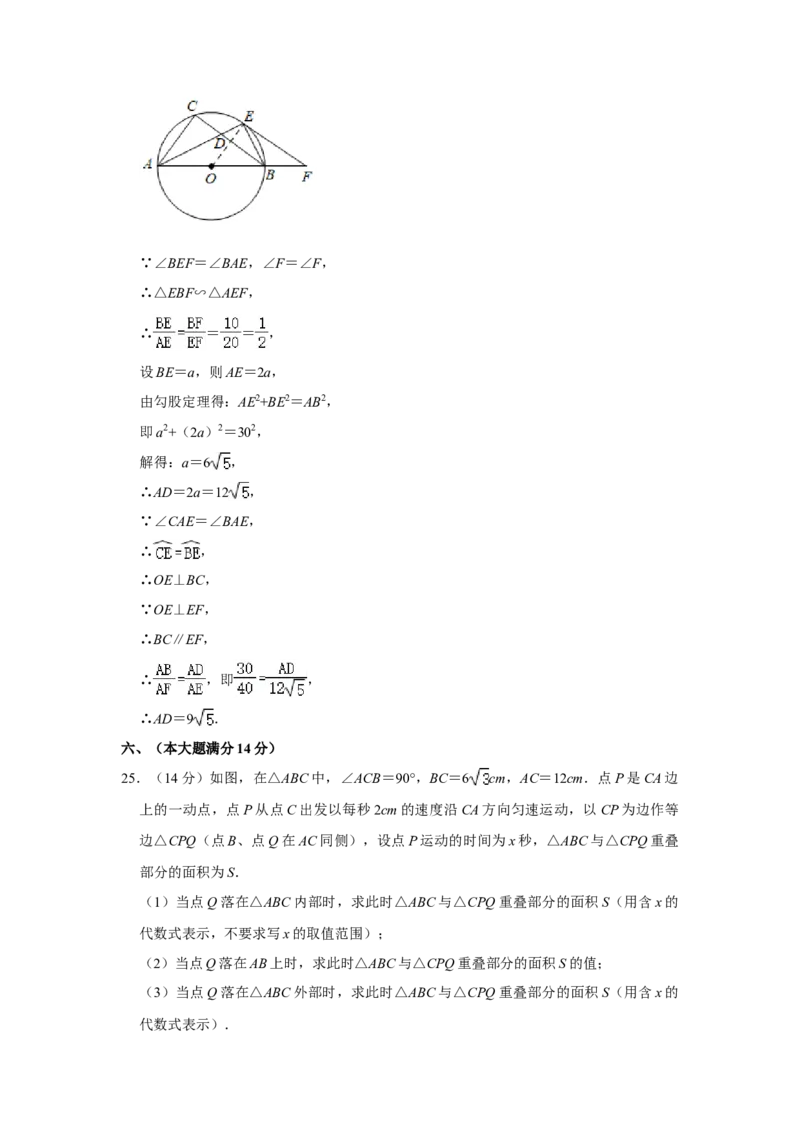
(2)解⊙:如图,设 O的半径为x,则OE=OB=x,
∴OF=x+10, ⊙
在Rt△OEF中,由勾股定理得:OE2+EF2=OF2,
∴x2+202=(x+10)2,
解得:x=15,
∴ O的半径为15;
⊙∵∠BEF=∠BAE,∠F=∠F,
∴△EBF∽△AEF,
∴ = = ,
设BE=a,则AE=2a,
由勾股定理得:AE2+BE2=AB2,
即a2+(2a)2=302,
解得:a=6 ,
∴AD=2a=12 ,
∵∠CAE=∠BAE,
∴ ,
∴OE⊥BC,
∵OE⊥EF,
∴BC∥EF,
∴ ,即 ,
∴AD=9 .
六、(本大题满分14分)
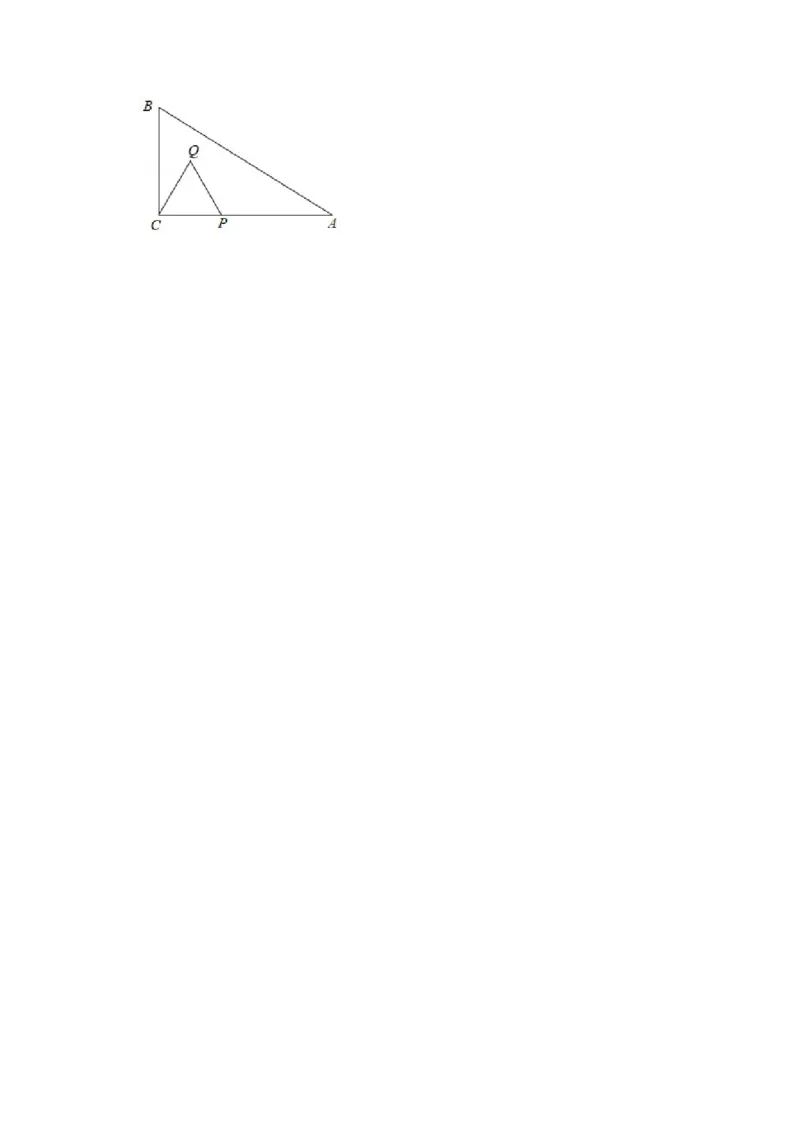
25.(14分)如图,在△ABC中,∠ACB=90°,BC=6 cm,AC=12cm.点P是CA边
上的一动点,点P从点C出发以每秒2cm的速度沿CA方向匀速运动,以CP为边作等
边△CPQ(点B、点Q在AC同侧),设点P运动的时间为x秒,△ABC与△CPQ重叠
部分的面积为S.
(1)当点Q落在△ABC内部时,求此时△ABC与△CPQ重叠部分的面积S(用含x的
代数式表示,不要求写x的取值范围);
(2)当点Q落在AB上时,求此时△ABC与△CPQ重叠部分的面积S的值;
(3)当点Q落在△ABC外部时,求此时△ABC与△CPQ重叠部分的面积S(用含x的
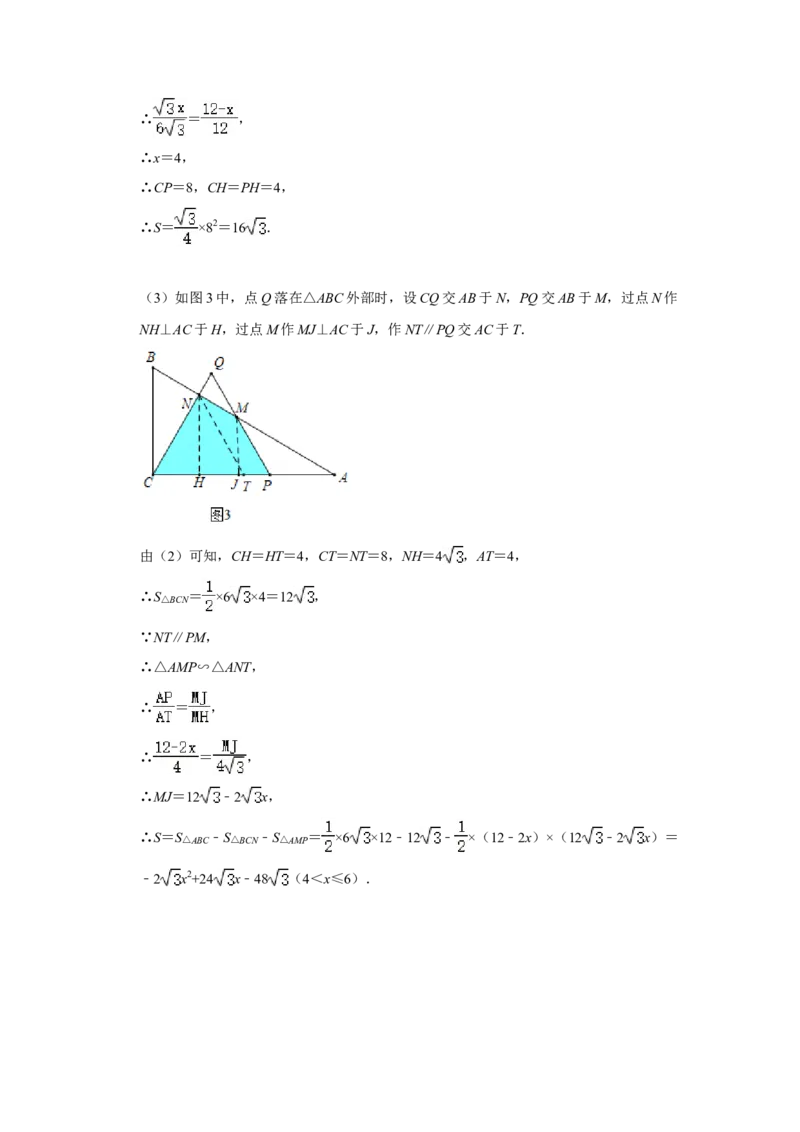
代数式表示).【分析】(1)如图1中,当点Q落在△ABC内部时,求出等边△PQC的面积即可.
(2)如图2中,当点Q落在AB上时,过点Q作QH⊥AC于H.利用平行线分线段成
比例定理求出QH即可.
(3)如图3中,点Q落在△ABC外部时,设CQ交AB于N,PQ交AB于M,过点N作
NH⊥AC于H,过点M作MJ⊥AC于J,作NT∥PQ交AC于T.利用相似三角形的性质
求出MJ,求出△BCQ,△APQ的面积即可.
【解答】解:(1)如图1中,当点Q落在△ABC内部时,S= ×(2x)2= x2.
(2)如图2中,当点Q落在AB上时,过点Q作QH⊥AC于H.
∵∠QHA=∠ACB=90°,
∴QH∥BC,
∴ = ,∴ = ,
∴x=4,
∴CP=8,CH=PH=4,
∴S= ×82=16 .
(3)如图3中,点Q落在△ABC外部时,设CQ交AB于N,PQ交AB于M,过点N作
NH⊥AC于H,过点M作MJ⊥AC于J,作NT∥PQ交AC于T.
由(2)可知,CH=HT=4,CT=NT=8,NH=4 ,AT=4,
∴S△BCN = ×6 ×4=12 ,
∵NT∥PM,
∴△AMP∽△ANT,
∴ = ,
∴ = ,
∴MJ=12 ﹣2 x,
∴S=S△ABC ﹣S△BCN ﹣S△AMP = ×6 ×12﹣12 ﹣ ×(12﹣2x)×(12 ﹣2 x)=
﹣2 x2+24 x﹣48 (4<x≤6).