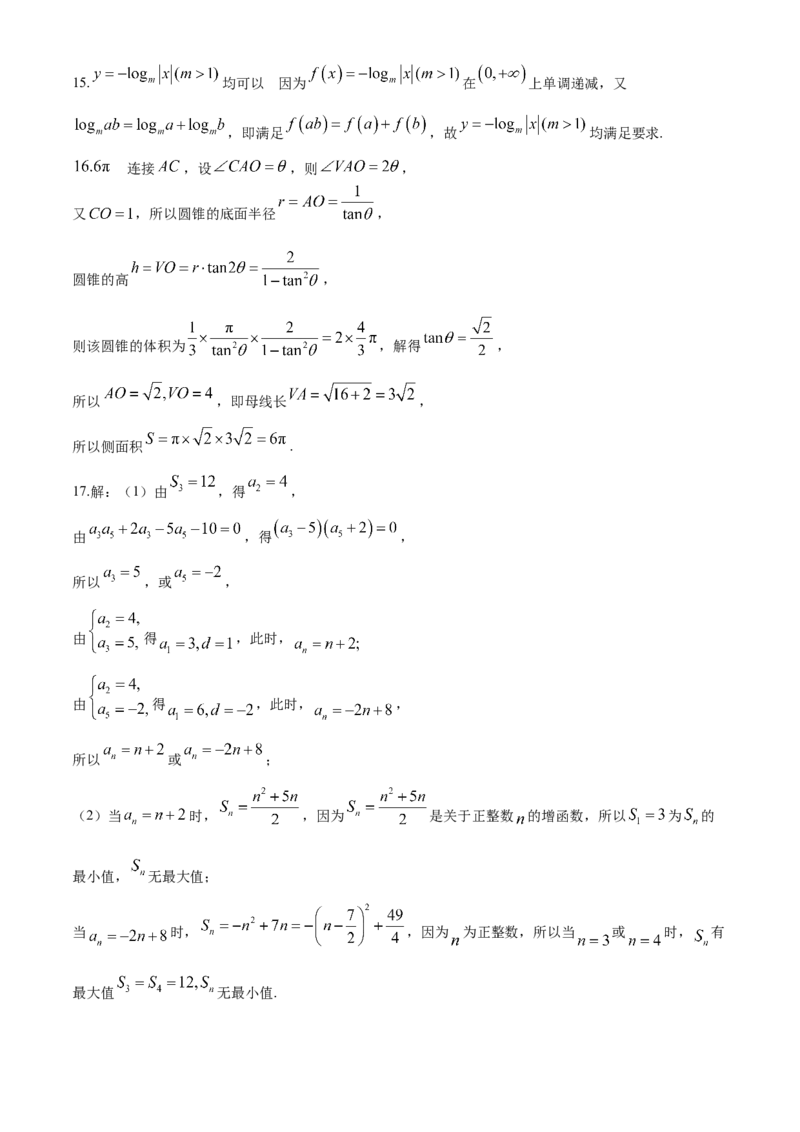文档内容
2024 年陕西省高三教学质量检测试题(二)
文科数学试题
全卷满分150分 考试时间120分钟.
注意事项:
1.答题前,先将自己的姓名,准考证号填写在试卷和答题卡上,并将条形码粘贴在答题卡上
的指定位置.
2.请按题号顺序在答题卡上各题目的答题区域内作答,写在试卷,草稿纸和答题卡上的非答
题区域均无效.
3.选择题用2B铅笔在答题卡上把所选答案的标号涂黑:非选择题用黑色签字笔在答题卡上作
答;字体工整,笔迹清楚.
4.考试结束后,请将试卷和答题卡一并上交.
5.本卷主要考查内容:高考范围.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.已知集合 ,则 ( )
A. B. C. D.
2.复数 的模为( )
A.1 B. C.3 D.
3.命题“ ”的否定为( )
A. B.
C. D.
4.函数 在 上的值域为( )
A. B. C. D.
5.已知双曲线 的焦距为4,则该双曲线的离心率为( )
学科网(北京)股份有限公司A.2 B. C. D.
6.已知变量 满足约束条件 则 的最小值为( )
A.-3 B.-1 C. D.-2
7.在 上随机取一个数 ,满足 的概率为( )
A. B. C. D.
8.商后母戊鼎(也称司母戊鼎)是迄今世界上出土最大、最重的青铜礼器,享有“镇国之宝”的美誉,某礼
品公司计划制作一批该鼎的工艺品,已知工艺品四足均为圆柱形,圆柱的高为 ,半径为 ,中间
容器部分可近似看作一个无盖的长方体容器,该长方体壁厚 ,外面部分的长、宽、高的尺寸分别为
, , .两耳的总体积与其中一足的体积近似相等.则该工艺品所耗费原材料的体积约为(
)
A. B.
C. D.
9.已知函数 ,过原点作曲线 的切线 ,则切点 的坐标为( )
A. B. C. D.
10.已知 均为锐角,且 ,则 ( )
A. B. C. D.
学科网(北京)股份有限公司11.在 中,内角 所对的边分别为 ,向量 .已知
,且 ,则 的值为( )
A.16 B.18 C.20 D.24
12.已知点 是圆 上的动点,以 为圆心的圆经过点 ,且与圆 相交于 两点.
则点 到直线 的距离为( )
A. B. C. D.不是定值
二、填空题:本大题共4小题,每小题5分,共20分.
13.已知 ,若 ,则 __________.
14.已知抛物线 上的点 到焦点的距离比到 轴的距离大2,则 __________.
15.偶函数 的定义域为 ,函数 在 上递减,且对于任意 均有
,写出符合要求的一个函数 为__________.
16.如图,已知球 与圆锥 的侧面和底面均相切,且球的体积为圆锥体积的一半.若球的半径为1,则该
圆锥的侧面积为__________.
三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤、第17~21题为必考题,每
个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分、
17.(本小题满分12分)
已知 为数列 的前 项和,且 ,( 为常数).若
.求:
(1)数列 的通项公式;
学科网(北京)股份有限公司(2) 的最值.
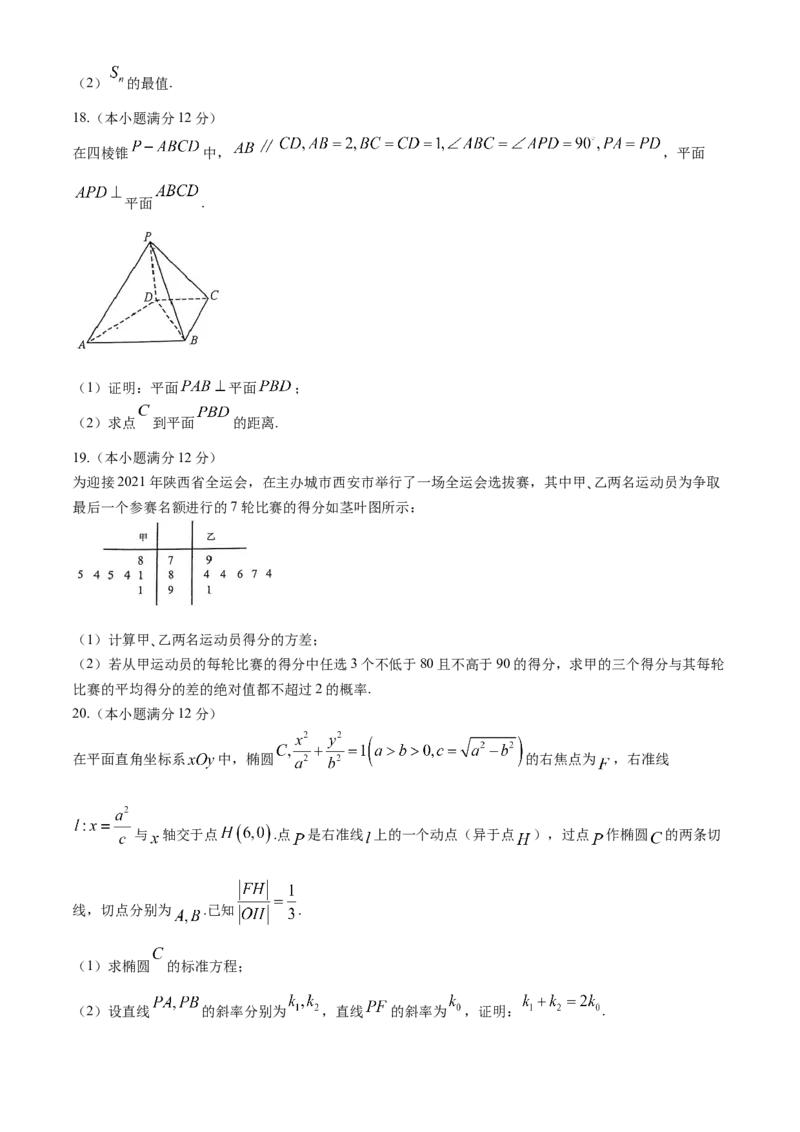
18.(本小题满分12分)
在四棱锥 中, ,平面
平面 .
(1)证明:平面 平面 ;
(2)求点 到平面 的距离.
19.(本小题满分12分)
为迎接2021年陕西省全运会,在主办城市西安市举行了一场全运会选拔赛,其中甲、乙两名运动员为争取
最后一个参赛名额进行的7轮比赛的得分如茎叶图所示:
(1)计算甲、乙两名运动员得分的方差;
(2)若从甲运动员的每轮比赛的得分中任选3个不低于80且不高于90的得分,求甲的三个得分与其每轮
比赛的平均得分的差的绝对值都不超过2的概率.
20.(本小题满分12分)
在平面直角坐标系 中,椭圆 的右焦点为 ,右准线
与 轴交于点 .点 是右准线 上的一个动点(异于点 ),过点 作椭圆 的两条切
线,切点分别为 .已知 .
(1)求椭圆 的标准方程;
(2)设直线 的斜率分别为 ,直线 的斜率为 ,证明: .
学科网(北京)股份有限公司21.(本小题满分12分)
已知函数 .
(1)讨论函数 在区间 上的单调性;
(2)当 时,证明: .
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题
计分.
22.(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系 中,已知椭圆 的直角坐标方程为 .以坐标原点为极点, 轴的非负半
轴为极轴建立极坐标系,直线 的极坐标方程为 .
(1)求椭圆 的一个参数方程和直线 的直角坐标方程;
(2)若 是椭圆 上的任意一点,求点 到直线 的距离的最大值.
23.(本小题满分10分)选修4-5:不等式选讲
已知函数 .
(1)求不等式 的解集;
(2)若 ,证明: .
学科网(北京)股份有限公司2024 年陕西省高三教学质量检测试题(二)
文数参考答案
1.A 由 ,有 ,故选A.
2.B 由 ,可得 ,故选B.
3.B .
4.A 由 ,可得 ,则 .
5.C 由题意可知, ,则 ,所以 .
学科网(北京)股份有限公司6.D 线性区域的端点坐标为 ,可知当 时, 的最小值为 .
7.B 由 ,解得 ,所求概率为 .
8.A 四足及两耳的体积为 ,容器部分的体积为
,则总体积为 .
9.B ,设切点为 ,则切线方程为 ,
因为过原点,所以 ,解得 ,则 .
10.C 易知 ,所以 ,即
.
11.D 因为 ,所以 ,由正弦定理可知, ,由余弦定
理,可得 ,则 .
12.A 设 ,则圆 ,
整理得 ,又圆 ,
两圆方程相减,可得直线 的方程为 ,
点 到直线 的距离 .
13. 由题意可知, ,解得 .
14. ,即 .
学科网(北京)股份有限公司15. 均可以 因为 在 上单调递减,又
,即满足 ,故 均满足要求.
连接 ,设 ,则 ,
又 ,所以圆锥的底面半径 ,
圆锥的高 ,
则该圆锥的体积为 ,解得 ,
所以 ,即母线长 ,
所以侧面积 .
17.解:(1)由 ,得 ,
由 ,得 ,
所以 ,或 ,
由 得 ,此时,
由 得 ,此时, ,
所以 或 ;
(2)当 时, ,因为 是关于正整数 的增函数,所以 为 的
最小值, 无最大值;
当 时, ,因为 为正整数,所以当 或 时, 有
最大值 无最小值.
学科网(北京)股份有限公司18.(1)证明:取 中点为 ,
则 且 ,
又平面 平面 ,故 平面 ,
又 平面 ,而 平面 ,故平面 平面
(2)解:取 的中点 ,连 ,
由 为 的中点,可得 ,
又由平面 平面 ,可得 平面 ,
在直角梯形 中, ,可得 ,
在Rt 中,可得 ,
在Rt 中,由 ,可得 ,
设点 到平面 的距离为 ,
有 ,可得 ,
故点 到平面 的距离为 .
19.解:(1)易算出甲运动员得分平均分为84,乙运动员得分平均分为85,
故 ;
.
(2)由茎叶图可知,甲运动员七轮比赛的得分情况为: .所以甲每轮比赛的平均得
学科网(北京)股份有限公司分为 ,显然甲运动员每轮比赛得分中不低于80且不高于90的得
分共有5个,分别为 ,其中81分与平均得分的绝对值大于2,
所求概率 .
20.(1)解:由题意可知, ,且 ,解得 ,
所以 ,即椭圆 的标准方程为 ;
(2)证明:设 ,所作切线斜率为 ,则切线方程为 ,
椭圆 的方程联立, 消去 ,
整理得 ,
则 ,整理得 ,
所以 ,又因为 ,所以 .
21.解:(1)函数 的定义域为 ,
,
令 ,可得 ,
①当 时,可得 ,此时函数 在区间 上单调递增;
②当 时,可得 ,此时函数 在区间 上单调递减,在区间 上单调递
增;
(2)当 时,不等式 可化为 ,
学科网(北京)股份有限公司不等式两边同除以 后整理为 ,
令 ,有 ,
令 可得函数 的增区间为 ,减区间为 ,
可得 ,
故不等式 成立.
22.解:(1)椭圆 的参数方程为 ( 为参数)
直线 的极坐标方程可化为 ,
可化为 ,
将 代入可得直线 的直角坐标方程为 ;
(2)设点 的坐标为 ,
点 到直线 的距离为 ,
故 的最大值为 .
23.解:(1)不等式 可化为 .
①当 时,不等式可化为 ,解得 ,有 ;
②当 时,不等式可化为 ,解得 ,有 ;
③当 时,不等式可化为 ,解得 ,无解,
由上知不等式 的解集为 ;
学科网(北京)股份有限公司(2)由
当 时, ;
当 时, ;
当 时, ,
可得函数 的最大值为2.
,当且仅当 时取等号,
故有 .
学科网(北京)股份有限公司