陕西省咸阳市2024届高三下学期高考模拟检测(二)数学（理科）试题+(1)_2024年3月_013月合集_2024届陕西省咸阳市高三下学期高考模拟检测(二)

咸阳市 2024 年高考模拟检测（二） 数学（理科）试题 注意事项： 1．本试题共 4页，满分 150分，时间 120分钟 2．答卷前，考生务必将答题卡上密封线内的各项目填写清楚 3．回答选择题时，选出每小题答案后，用 2B铅笔把答题卡上对应题目的答案标号涂黑，如需 改动，用橡皮擦干净后，再选涂其它答案标号，回答非选择题时，将答案写在答题卡上，写在 本试卷上无效。 4．考试结束后，监考员将答题卡按顺序收回，装袋整理；试题不回收。 第Ⅰ卷（选择题 共 60分） 一、选择题：本大题共 12小题，每小题 5分，共 60分．在每小题给出的四个选项中，只有一 项是符题目要求的。 1．若复数z满足(1i)z 34i，则复数z的共轭复数的虚部为（ ） 1 7 7 7 A． B． C． i D． 2 2 2 2 2．已知集合A  x x1 0  ,B   x y log  x2 16  ，则AI  ð B  （ ）  5x  2 R A．1,4 B．1,4 C．1,5 D．4,5 r uuur 3．已知在边长为1的菱形ABCD中，角A为60，若点E为线段CD的中点，财AEEB （ ） 3 3 3 3 A． B． C． D． 2 4 4 2 4．已知角的始边为x轴的非负半轴，顶点为坐标原点，若它的终边经过点P1,2，则sin2cos2 （ ） 1 9 7 1 A． B． C． D． 5 5 5 5 5．已知等差数列a 的前n项和为S ，若S 2,S 12，则S （ ） n n 4 8 20 A．30 B．58 C．60 D．90 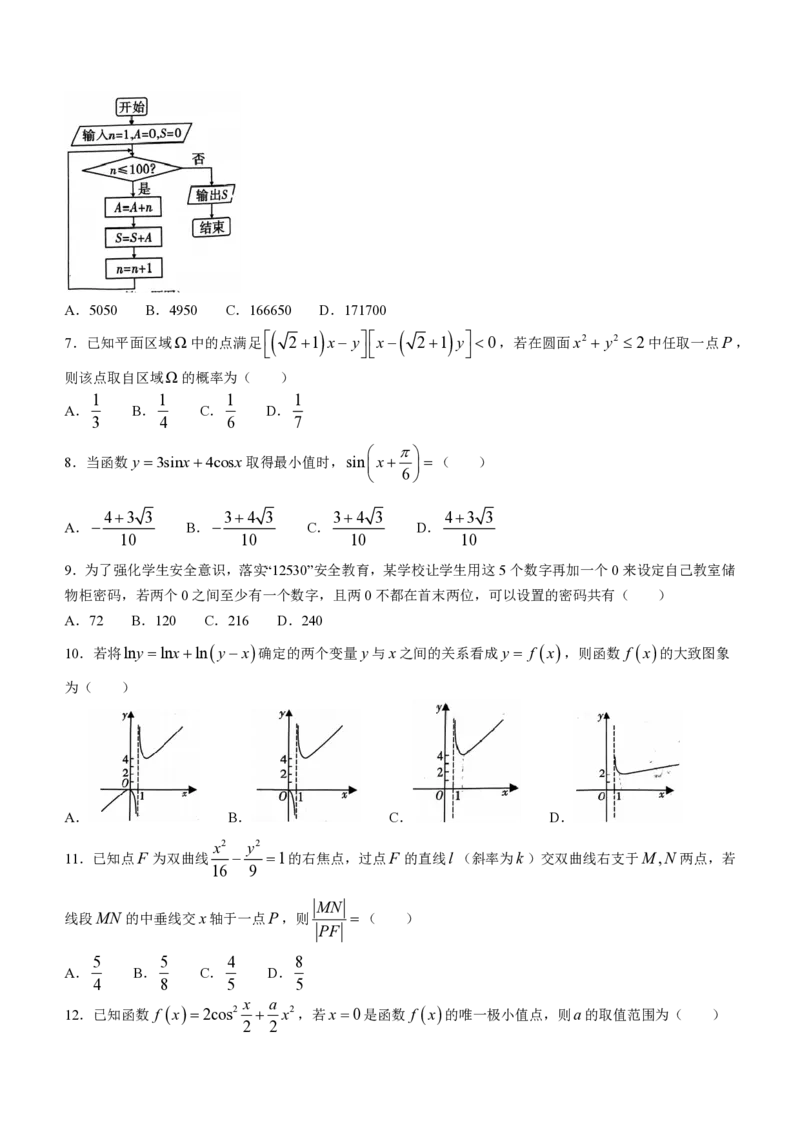6．执行下侧的程序框图，则输出的结果是（ ） 学科网（北京）股份有限公司A．5050 B．4950 C．166650 D．171700 7．已知平面区域Ω中的点满足 2 1  x yx  2 1  y0，若在圆面x2  y2 2中任取一点P，    则该点取自区域Ω的概率为（ ） 1 1 1 1 A． B． C． D． 3 4 6 7   8．当函数 y 3sinx4cosx取得最小值时，sin  x  （ ）  6 43 3 34 3 34 3 43 3 A． B． C． D． 10 10 10 10 9．为了强化学生安全意识，落实“12530”安全教育，某学校让学生用这5个数字再加一个0来设定自己教室储 物柜密码，若两个0之间至少有一个数字，且两0不都在首末两位，可以设置的密码共有（ ） A．72 B．120 C．216 D．240 10．若将lny lnxlnyx确定的两个变量 y与x之间的关系看成 y  f x，则函数 f x的大致图象 为（ ） A． B． C． D． x2 y2 11．已知点F 为双曲线  1的右焦点，过点F 的直线l （斜率为k）交双曲线右支于M,N 两点，若 16 9 MN 线段MN 的中垂线交x轴于一点P，则 （ ） PF 5 5 4 8 A． B． C． D． 4 8 5 5 x a 12．已知函数 f x2cos2  x2，若x 0是函数 f x的唯一极小值点，则a的取值范围为（ ） 2 2 学科网（北京）股份有限公司A．1, B．0,1 C．1, D．,1 第Ⅱ卷（非选择题 共 90分） 二、填空题：本大题共 4小题，每小题 5 分，共 20分。 4 9 13．已知总体的各个个体的值由小到大依次为2,4,4,6,a,b,12,14,18,20，且总体的平均值为10，则  的 a b 最小值为________。 14．P为抛物线 y2 4x上任意一点，点A2,4，设点P到 y轴的距离为d ，则 PA d 的最小值为________。 15．已知a,b,c分别为△ABC 三个内角A,B,C 所对的边，若a bcosC 3csinB，设点D为边AC的中 点，且BD  AC 4，则S ________。 △ABC 16．已知三棱锥D ABC 中，AB 4,AC 3,BC 5，三角形DBC为正三角形，若二面角DBC A 为120，则该三棱锥的外接球的体积为________。 三、解答题：共 70分。解答应写出文字说明、证明过程或演算步骤。第 17~21题为必考题，每 个试题考生都必须作答。第 22，23题为选考题，考生根据要求作答。 （一）必考题：共 60分。 17．（本小题满分12分） nn1 已知正项数列a 满足a2 a2 L a2   nN* 。 n 1 2 n 2 （1）若b a a ，请判断并证明数列b 的单调性； n n1 n n 2  1  （2）若c   ，求数列c 的前n项和S 。 n a a n n   n1 n 18．（本小题满分12分） 陕西省从2022年秋季启动新高考，新高考“312”模式中“3”为全国统一高考科目的语文、数学、外语， “1”为首选科目，要求从物理、历史2门科目中确定1门，“2”为再选科目，要求从思想政治、地理、化学、生 物学4门科目中确定2门，共计产生12种组合。某班有学生50名，在选科时，首选科目选历史和物理的统计 数据如下表所示： 历史 物理 合计 男生 2 23 25 女生 8 17 25 合计 10 40 50 n(ad bc)2 附：2  ，其中n abcd 。 abcdacbd 学科网（北京）股份有限公司 0.100 0.050 0.010 0.005 0.001  2.706 3.841 6.635 7.879 10.828 a （1）根据表中的数据，判断是否有99%的把握认为学生选择历史与性别有关； （2）从选择历史的10名学生中任意抽取3名同学参加学校“铭记历史，强国有我”演讲比赛，设X 为抽取的 三名学生中女生的人数，求X 的分布列，并求数学期望和方差。 19．（本小题满分12分） 在几何体中，底面ABC是边长为2的正三角形。AE 平面ABC，若 AE∥CD∥BF,AE 5,CD 4,BF 3。 （1）求证：平面DEF 平面AEFB；  （2）是否在线段AE上存在一点P，使得二面角PDF E的大小为 。若存在，求出AP的长度，若不 3 存在，请说明理由。 20．（本小题满分12分） 已知两圆C :(x1)2  y2 25,C :(x1)2  y2 1，动圆C在圆C 的内部，且与圆C 相内切，与圆C 相 1 2 1 1 2 外切。 （1）求点C的轨迹方程； （2）设点M 1,0,N1,0，过点M 的直线交C于P,Q两点，求△PQN 的内切圆面积的最大值。 21．（本小题满分12分） 已知函数 f xaex1xlna。 （1）讨论 f x的单调性； （2）若 f xlnxx1，求a的取值范围。 （二）选考题：共 10分，考生从 22，23 题中任选一题作答，如果多做，则按所做的第一题计 分。 22．（本小题满分10分）【选修4-4：坐标系与参数方程】 x tcos, 在平面直角坐标系xOy中，直线l 的参数方程为， （t为参数），以坐标原点O为极原点，x y 1tsin 轴正半轴为极轴，建立极坐标系。曲线C的极坐标方程为2 2cos3。 （1）求曲线C的直角坐标方程和直线l 的一般方程； （2）设直线l 与曲线C交于A,B两点，求△ABC 面积的最大值。 23．（本小题满分10分）【选修4-5：不等式选讲】 已知函数 f x 2x1 3x3 。 学科网（北京）股份有限公司（1）解不等式 f x5； （2）设函数gx 3x2 12xm，若函数 f x与gx的图象无公共点，求参数m的取值范围。 咸阳市 2024 年高考模拟检测（二） 数学（理科）试题参考答案及评分标准 一、选择题：本大题共 12小题，每小题 5分，共 60分．在每小题给出的四个选项中，只有一 项是符合题目要求的 1．D 2．B 3．C 4．C 5．D 6．D 7．B 8．A 9．C 10．C 11．D 12．A 二、填空题：本大题共 4小题，每小题 5 分，共 20分。 5 1625 13 13． 14． 17 1 15．2 3 16．  4 162 三、解答题：共 70分。解答应写出文字说明、证明过程或演算步骤。第 17~21题为必考题，每 个试题考生都必须作答，第 22，23题为选考题，考生根据要求作答。 （一）必考题：共 60分。 nn1 17．解：（1）因为a2 a2 L a2   nN* ，① 1 2 n 2 当n 1时，a2 1； 1 nn1 当n2时，a2 a2 L a2  ，② 1 2 n1 2 nn1 nn1 ①-②得：a2   nn2， n 2 2 又n 1时，a2 1a2， n 1 又a 0，所以a  n， n n 则b a a  n1 n ， n n1 n      又b b  n2  n1  n1  n n1 n 1 1   n2  n1 n1 n n  n2  0,    n2  n1 n1 n 学科网（北京）股份有限公司所以，数列b 是单调递减数列。（9分） n 2  1  1 1 1 （2）由（1）知c      ， n a a nn1 n n1   n1 n  1 1 1 1 1 1 1  则S c c c L c   1          L     n 1 2 3 n  2 2 3 3 4 n n1 1 n 1  .（12分） n1 n1 18．解：（1）将表中的数据带入，得到 n(ad bc)2 50(217823)2 2   4.56.635， abcdacbd 25251040 所以没有99%的把握认为学生选择历史与性别有关。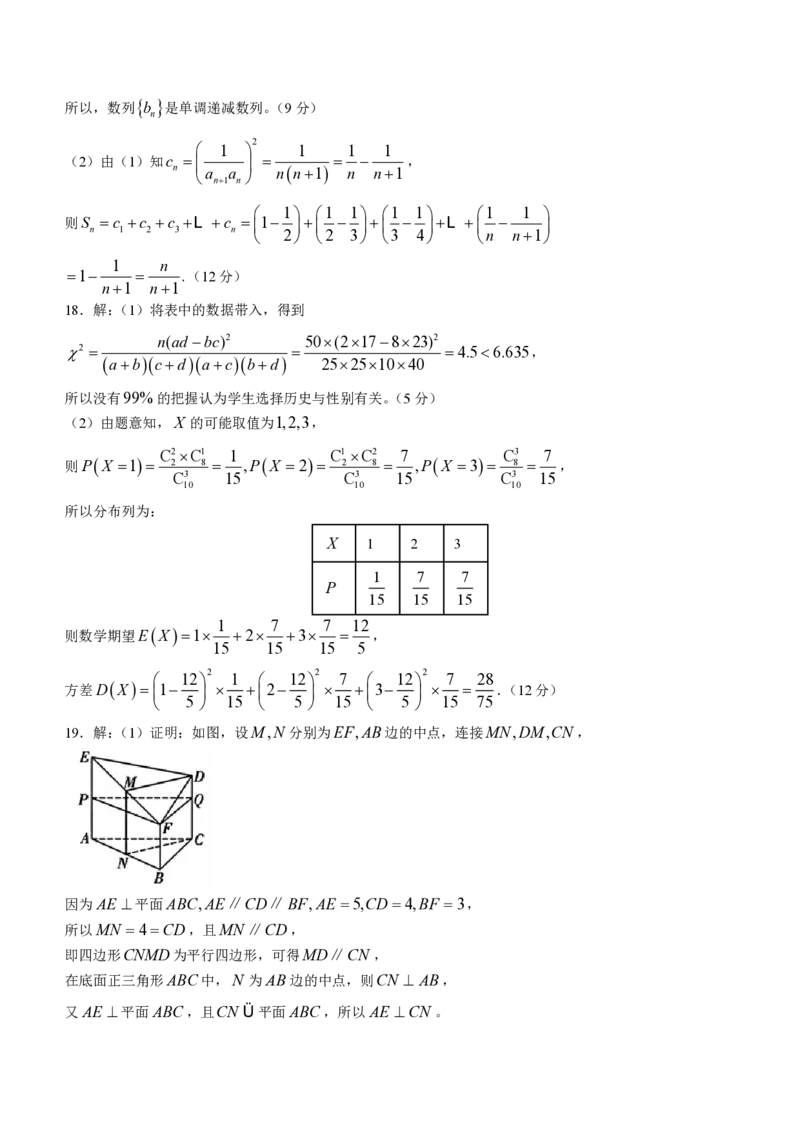（5分） （2）由题意知，X 的可能取值为1,2,3， C2C1 1 C1 C2 7 C3 7 则PX 1 2 8  ,PX 2 2 8  ,PX 3 8  ， C3 15 C3 15 C3 15 10 10 10 所以分布列为： X 1 2 3 1 7 7 P 15 15 15 1 7 7 12 则数学期望EX1 2 3  ， 15 15 15 5 2 2 2  12 1  12 7  12 7 28 方差DX  1     2     3    ．（12分）  5  15  5  15  5  15 75 19．解：（1）证明：如图，设M,N 分别为EF,AB边的中点，连接MN,DM,CN ， 因为AE 平面ABC,AE∥CD∥BF,AE 5,CD 4,BF 3， 所以MN 4CD，且MN∥CD， 即四边形CNMD为平行四边形，可得MD∥CN ， 在底面正三角形ABC中，N 为AB边的中点，则CN  AB， 又AE 平面ABC，且CN Ü平面ABC，所以AE CN 。 学科网（北京）股份有限公司由于AEI AB  A，且AE、ABÜ平面ABFE，所以CN 平面ABFE。 因为MD∥CN,CN 平面ABFE，则MD 平面ABFE， 又MDÜ平面DEF ，则平面DEF 平面AEFB。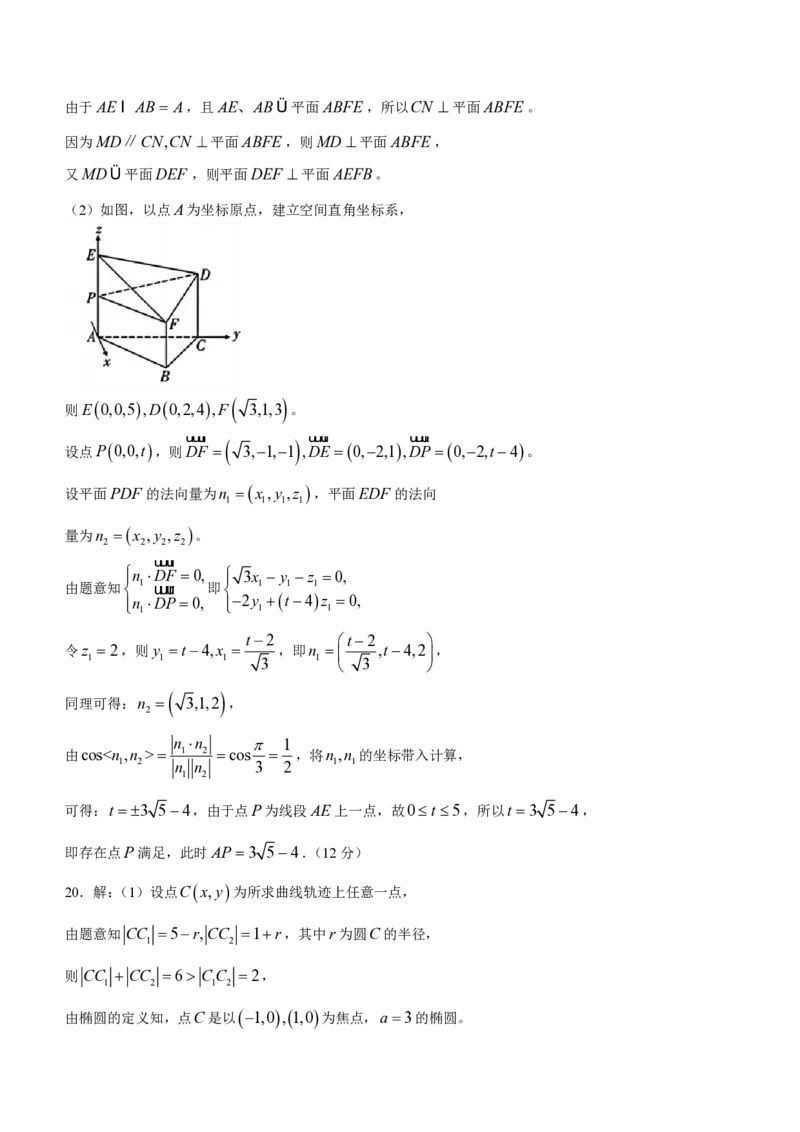 （2）如图，以点A为坐标原点，建立空间直角坐标系，   则E0,0,5,D0,2,4,F 3,1,3 。 uuur uuur uuur 设点P0,0,t，则DF   3,1,1  ,DE 0,2,1,DP 0,2,t4。 设平面PDF 的法向量为n x ,y ,z ，平面EDF 的法向 1 1 1 1 量为n x ,y ,z 。 2 2 2 2 uuur  n DF 0,  3x  y z 0, 由题意知 1 uuur 即 1 1 1  n 1 DP 0,  2y 1 t4z 1 0, t2 t2  令z 2，则 y t4,x  ，即n  ,t4,2 ，   1 1 1 3 1  3    同理可得：n  3,1,2 ， 2 n n  1 由cos 1 2 cos  ，将n ,n 的坐标带入计算， 1 2 n n 3 2 1 1 1 2 可得：t  3 54，由于点P为线段AE上一点，故0t 5，所以t 3 54， 即存在点P满足，此时AP 3 54．（12分） 20．解：（1）设点Cx,y为所求曲线轨迹上任意一点， 由题意知 CC 5r,CC 1r，其中r为圆C的半径， 1 2 则 CC  CC 6 CC 2， 1 2 1 2 由椭圆的定义知，点C是以1,0,1,0为焦点，a 3的椭圆。 学科网（北京）股份有限公司x2 y2 所以点C的轨迹方程为  1． 9 8 （2）由题意知，直线PQ的斜率不为0，故设直线PQ的方程为x my1， x2 y2   1, 联立 9 8 消去x得  8m2 9  y2 16my640，  x my1, Δ(16m)2 464  8m2 9  2304  m2 1  0, 16m 64 设点Px ,y ,Qx ,y ，则 y  y  ,y y   ， 1 1 2 2 1 2 8m2 9 1 2 8m2 9 1 48 m2 1 S  MN y  y  y  y 2 4y y  ， △PNQ 2 1 2 1 2 1 2 8m2 9 又△PNQ的周长l 为4312， 2S 8 m2 1 8 所以△PNQ的内切圆半径r    ， l 8m2 9 1 8 m2 1 m2 1 令t  m2 1，则t 1， 1 1 设函数 f t8t ，则 ft8 ，在1,上 ft0，函数 f t单调递增，即 f t9， t t2 8 64 则r  ，此时△PNQ的内切圆面积的最大值S r2  。（12分） 9 max 81 21．解：（1）因为 f xaex1xlna，定义域为R，所以 fxaex11， 因为a 0，令 fxaex110，解得x 1lna， 当x1lna时， fx0，则 f x在,1lna上单调递减； 当x 1lna时 fx0，则 f x在1lna,上单调递增； 综上： f x在,1lna上单调递减， f x在1lna,上单调递增。 （2）因为 f xaex1xlna，所以 f xlnxx1等价于 elnax1lna x1lnx x elnx lnx， 令gxex  x，上述不等式等价于glna x1 glnx， 学科网（北京）股份有限公司显然gx为单调增函数，所求不等式等价于lna x1lnx，即lna 1lnxx， 1 1x 令hx1lnxx，则hx 1 ， x x 在0,1上hx0,hx单调递增；在1,上hx0,hx单调递减， h(x) h10， max lna 0，即a 1,a的取值范围是1,。 （二）选考题：共 10分，考生从 22，23 题中任选一题作答，如果多做，则按所做的第一题计 分。 22．（本小题满分10分）【选修4-4：坐标系与参数方程】 解：（1）Q曲线C的极坐标方程为2 2cos3， 曲线C的直角坐标方程为x2  y2 2x30，即(x1)2  y2 4。（2分） x tcos, 又Q直线l 的参数方程为 （t为参数）， y 1tsin 直线l 的一般方程为sinxcosycos0。 x tcos, （2）将直线l 的参数方程 （t为参数）带入(x1)2  y2 4中， y 1tsin 得到(tcos1)2 (tsin1)2 4，   化简可以得到：t2 2 2sin    t20，  4    则t t  2 2sin    ,tt  20， 1 2  4  1 2   AB  t  t  t t  t t 2 4tt  8sin2  8   1 2 1 2 1 2 1 2  4      4 1cos 2 8  124sin22 3sin2,      2  圆心C到直线l 的距离d  43sin2  1sin2， 1 3sin21sin2 则S   AB d  3sin2 1sin2 2， △ABC 2 2 当且仅当3sin21sin2，即sin21时取等号。 学科网（北京）股份有限公司所以△ABC 的面积的最大值为2。（10分） 23．（本小题满分10分）【选修4-5：不等式选讲】  1 25x,x   ,  2   1 解：（1） f x 2x1 3x3  4x,  x1, 2  5x2,x 1,    1  1 x   ,   x1, x 1, 若 f x5，即 2 或 2 或  25x 5  4x 5 5x25, 3 7 解之得：x  或x  。 5 5 3 7  则原不等式的解集为 x x 或x  。（5分） 5 5 （2）函数gx 3x2 12xm，若函数 f x与gx的图象无公共点，即 f x gx在1,上无解， 可得：3x2 7xm20在1,上无解， 即m  3x2 7x2  ,x1,， min 2  7 73 73 因为函数 y 3x2 7x23  x   ，当x1,,y   ，  6 12 min 12 73  73 所以m ，即m的取值范围为 , 。（10分） 12  12 学科网（北京）股份有限公司