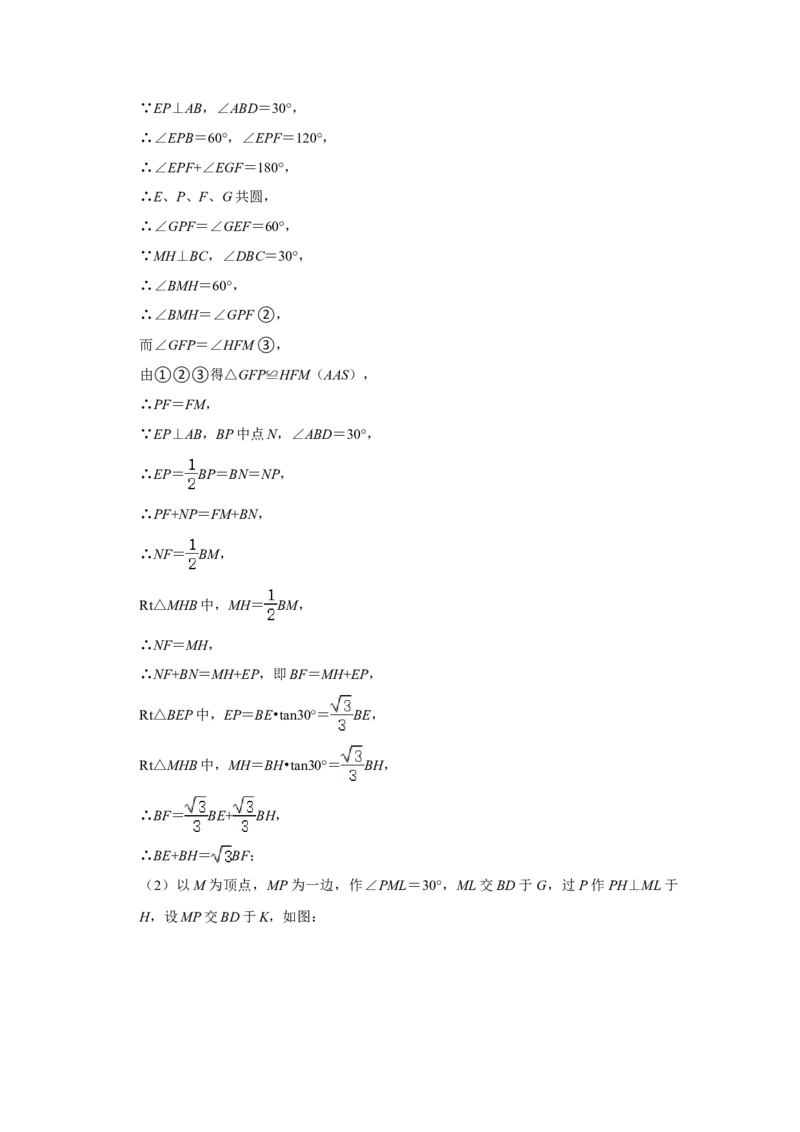文档内容
2021年重庆市中考数学试卷(B 卷)
一、选择题:(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了
代号为A,B,C,D的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答
案所对应的方框涂黑
1.3的相反数是( )
A.3 B. C.﹣3 D.﹣
2.不等式x>5的解集在数轴上表示正确的是( )
A. B.
C. D.
3.计算x4÷x结果正确的是( )
A.x4 B.x3 C.x2 D.x
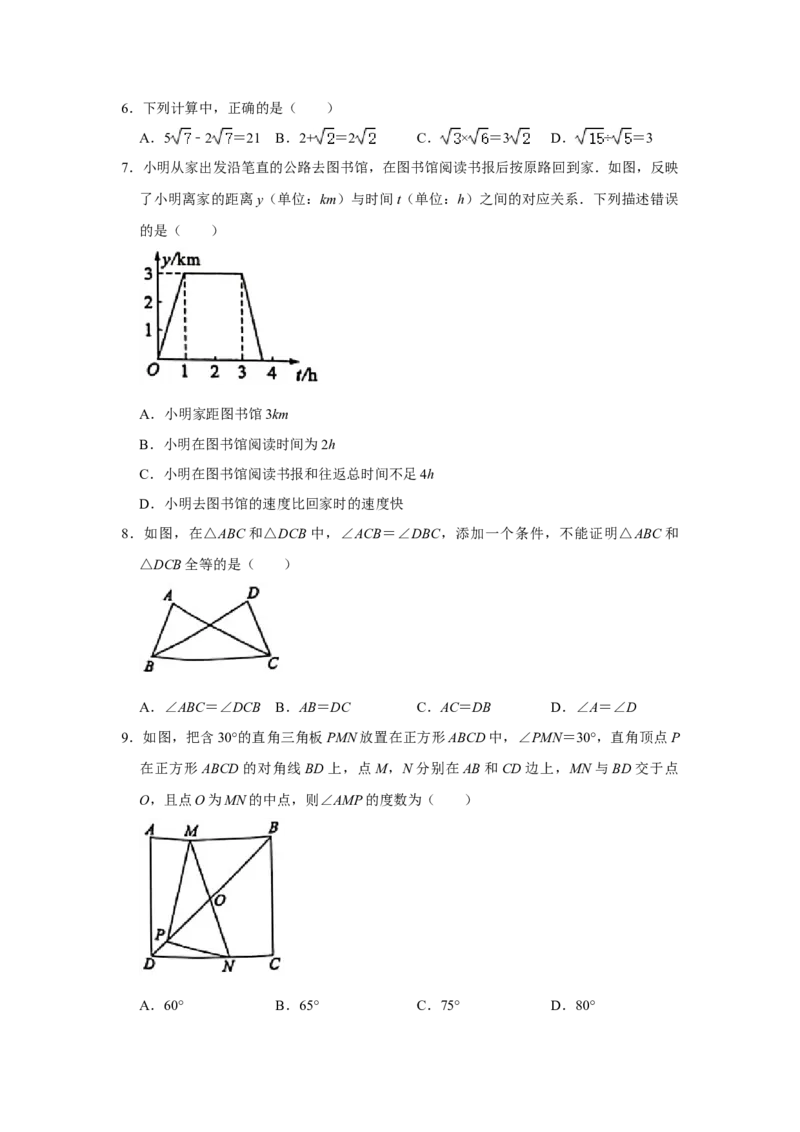
4.如图,在平面直角坐标系中,将△OAB以原点O为位似中心放大后得到△OCD,若B
(0,1),D(0,3),则△OAB与△OCD的相似比是( )
A.2:1 B.1:2 C.3:1 D.1:3
5.如图,AB是 O的直径,AC,BC是 O的弦,若∠A=20°,则∠B的度数为( )
⊙ ⊙
A.70° B.90° C.40° D.60°6.下列计算中,正确的是( )
A.5 ﹣2 =21 B.2+ =2 C. × =3 D. ÷ =3
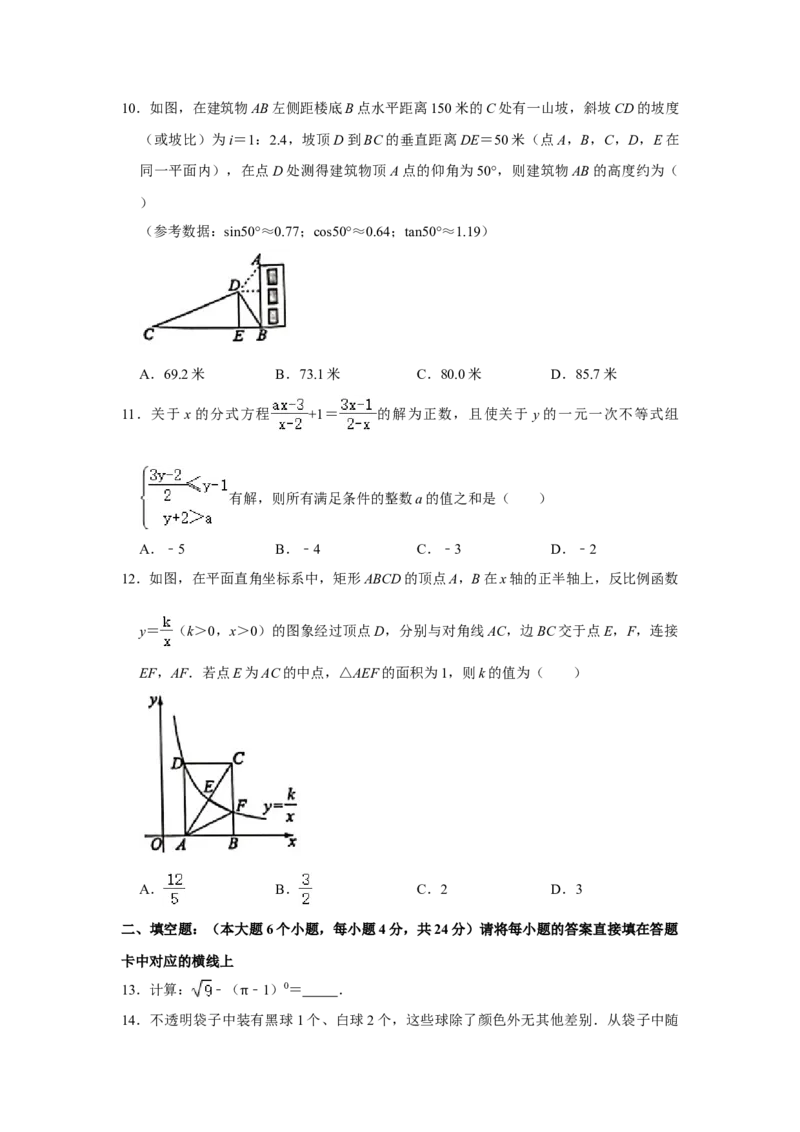
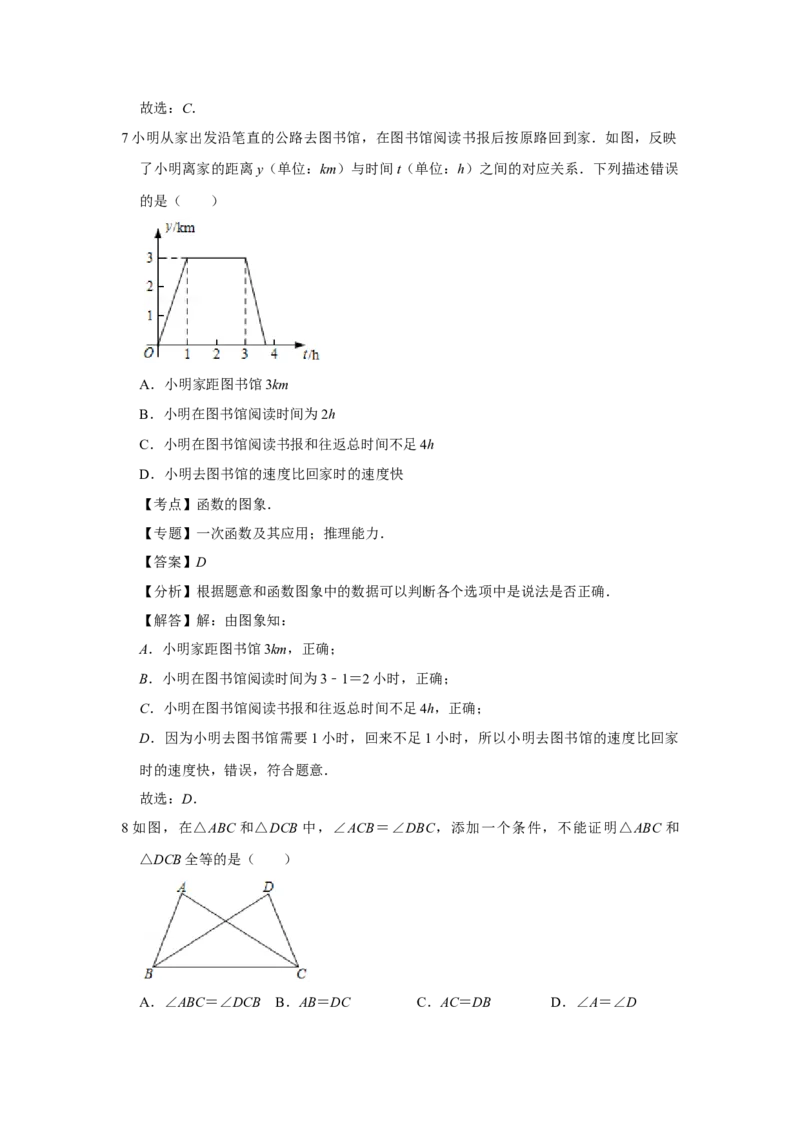
7.小明从家出发沿笔直的公路去图书馆,在图书馆阅读书报后按原路回到家.如图,反映
了小明离家的距离y(单位:km)与时间t(单位:h)之间的对应关系.下列描述错误
的是( )
A.小明家距图书馆3km
B.小明在图书馆阅读时间为2h
C.小明在图书馆阅读书报和往返总时间不足4h
D.小明去图书馆的速度比回家时的速度快
8.如图,在△ABC和△DCB中,∠ACB=∠DBC,添加一个条件,不能证明△ABC和
△DCB全等的是( )
A.∠ABC=∠DCB B.AB=DC C.AC=DB D.∠A=∠D
9.如图,把含30°的直角三角板PMN放置在正方形ABCD中,∠PMN=30°,直角顶点P
在正方形ABCD的对角线BD上,点M,N分别在AB和CD边上,MN与BD交于点
O,且点O为MN的中点,则∠AMP的度数为( )
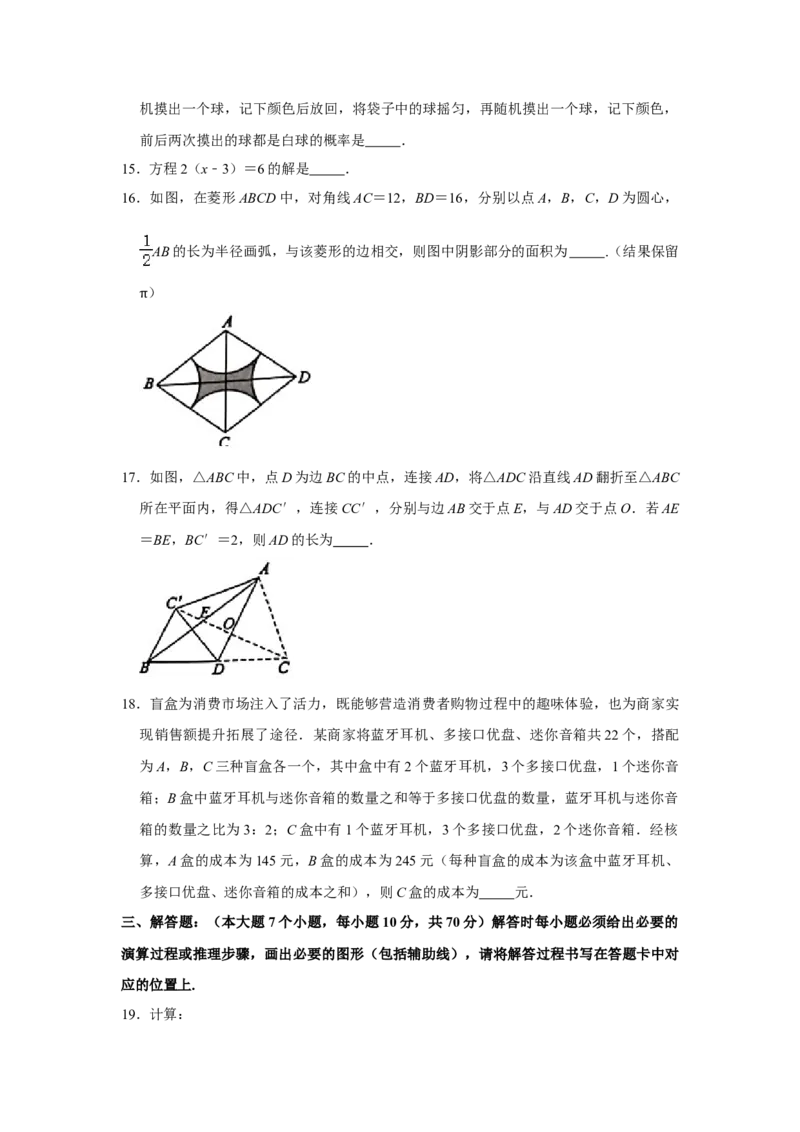
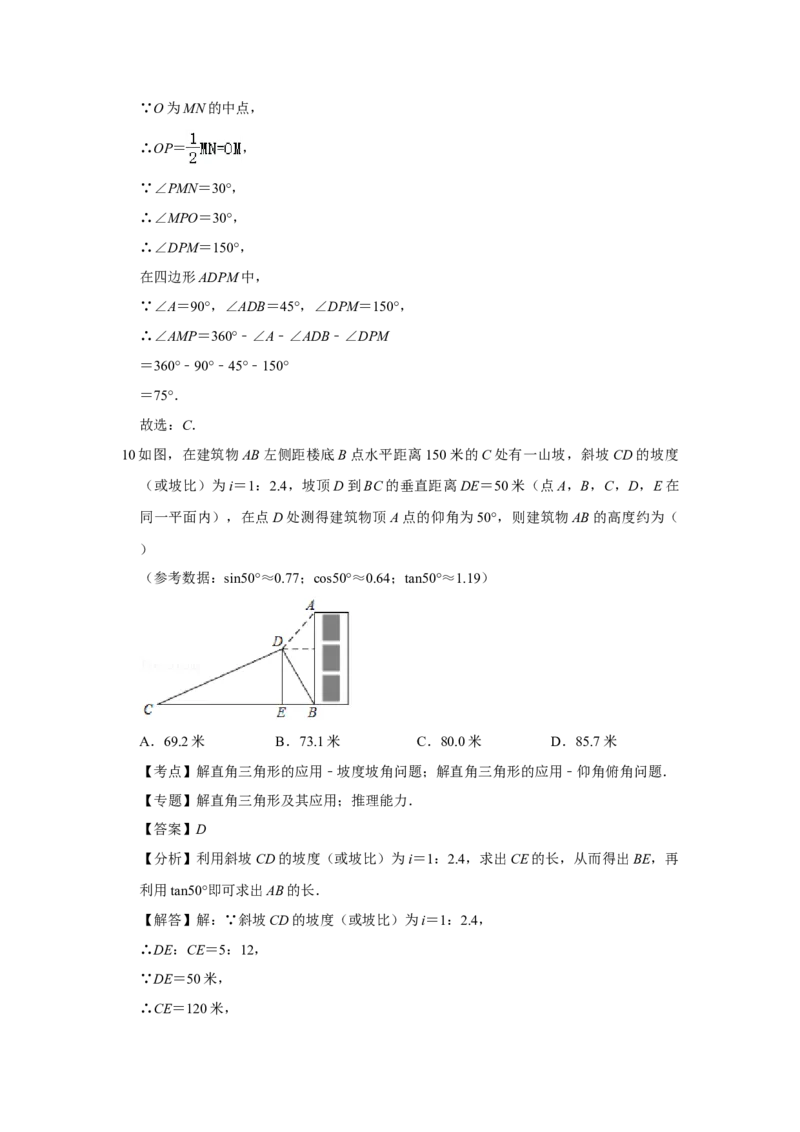
A.60° B.65° C.75° D.80°10.如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度
(或坡比)为i=1:2.4,坡顶D到BC的垂直距离DE=50米(点A,B,C,D,E在
同一平面内),在点D处测得建筑物顶A点的仰角为50°,则建筑物AB的高度约为(
)
(参考数据:sin50°≈0.77;cos50°≈0.64;tan50°≈1.19)
A.69.2米 B.73.1米 C.80.0米 D.85.7米
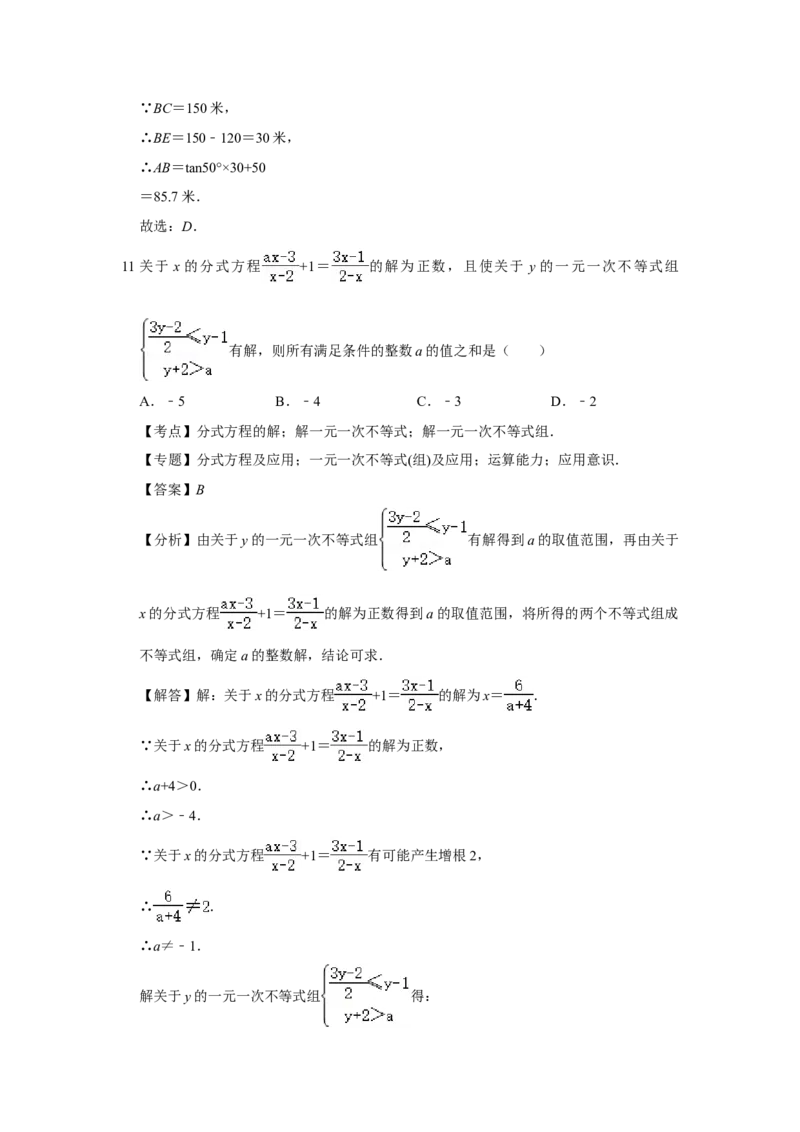
11.关于 x的分式方程 +1= 的解为正数,且使关于 y的一元一次不等式组
有解,则所有满足条件的整数a的值之和是( )
A.﹣5 B.﹣4 C.﹣3 D.﹣2
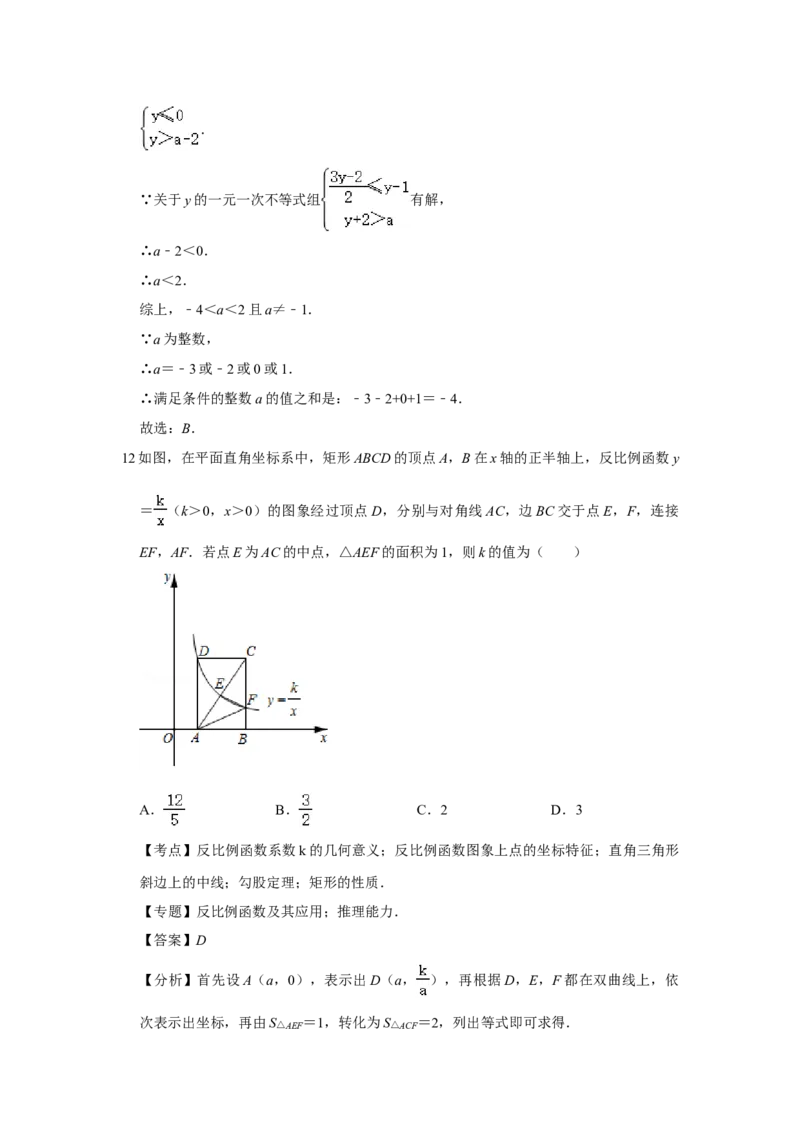
12.如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数
y= (k>0,x>0)的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接
EF,AF.若点E为AC的中点,△AEF的面积为1,则k的值为( )
A. B. C.2 D.3
二、填空题:(本大题6个小题,每小题4分,共24分)请将每小题的答案直接填在答题
卡中对应的横线上
13.计算: ﹣( ﹣1)0= .
14.不透明袋子中装π有黑球1个、白球2个,这些球除了颜色外无其他差别.从袋子中随机摸出一个球,记下颜色后放回,将袋子中的球摇匀,再随机摸出一个球,记下颜色,
前后两次摸出的球都是白球的概率是 .
15.方程2(x﹣3)=6的解是 .
16.如图,在菱形ABCD中,对角线AC=12,BD=16,分别以点A,B,C,D为圆心,
AB的长为半径画弧,与该菱形的边相交,则图中阴影部分的面积为 .(结果保留
)
π
17.如图,△ABC中,点D为边BC的中点,连接AD,将△ADC沿直线AD翻折至△ABC
所在平面内,得△ADC′,连接CC′,分别与边AB交于点E,与AD交于点O.若AE
=BE,BC′=2,则AD的长为 .
18.盲盒为消费市场注入了活力,既能够营造消费者购物过程中的趣味体验,也为商家实
现销售额提升拓展了途径.某商家将蓝牙耳机、多接口优盘、迷你音箱共22个,搭配
为A,B,C三种盲盒各一个,其中盒中有2个蓝牙耳机,3个多接口优盘,1个迷你音
箱;B盒中蓝牙耳机与迷你音箱的数量之和等于多接口优盘的数量,蓝牙耳机与迷你音
箱的数量之比为3:2;C盒中有1个蓝牙耳机,3个多接口优盘,2个迷你音箱.经核
算,A盒的成本为145元,B盒的成本为245元(每种盲盒的成本为该盒中蓝牙耳机、
多接口优盘、迷你音箱的成本之和),则C盒的成本为 元.
三、解答题:(本大题7个小题,每小题10分,共70分)解答时每小题必须给出必要的
演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对
应的位置上.
19.计算:(1)a(2a+3b)+(a﹣b)2;
(2) ÷(x+ ).
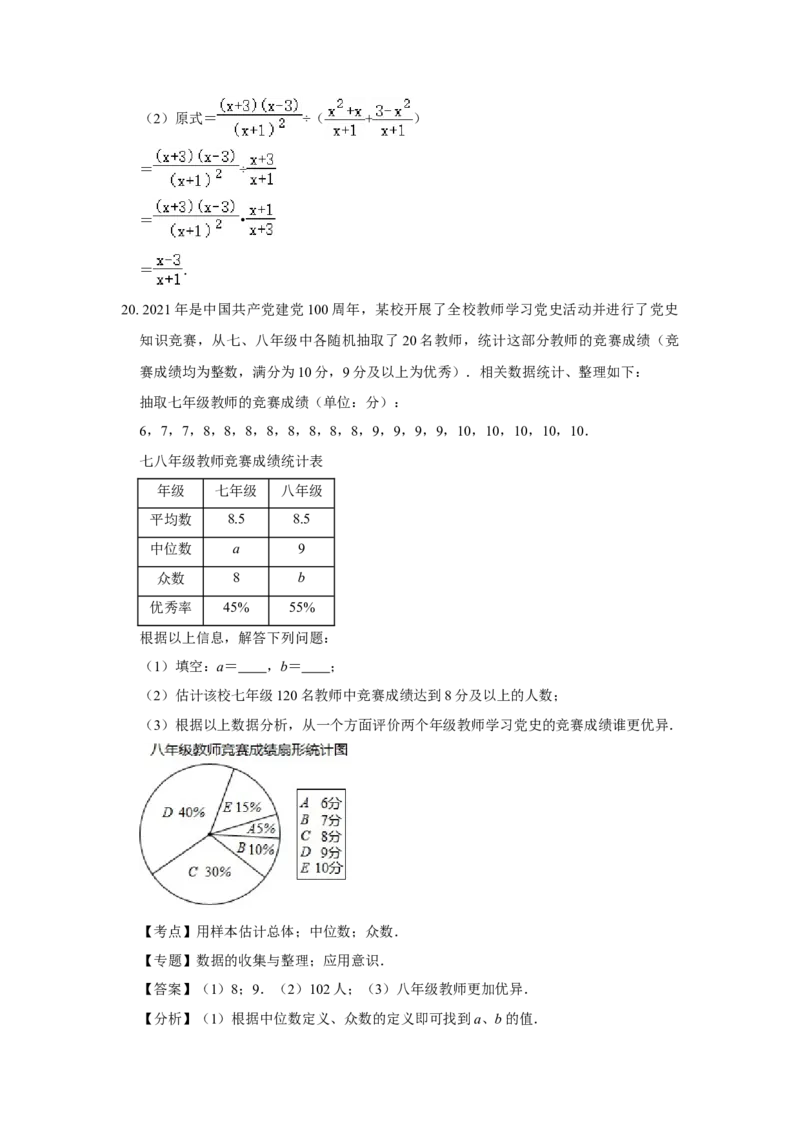
20.2021年是中国共产党建党100周年,某校开展了全校教师学习党史活动并进行了党史
知识竞赛,从七、八年级中各随机抽取了20名教师,统计这部分教师的竞赛成绩(竞
赛成绩均为整数,满分为10分,9分及以上为优秀).相关数据统计、整理如下:
抽取七年级教师的竞赛成绩(单位:分):
6,7,7,8,8,8,8,8,8,8,8,9,9,9,9,10,10,10,10,10
七八年级教师竞赛成绩统计表
年级 七年级 八年级
平均数 8.5 8.5
中位数 a 9
众数 8 b
优秀率 45% 55%
根据以上信息,解答下列问题:
(1)填空:a= ,b= ;
(2)估计该校七年级120名教师中竞赛成绩达到8分及以上的人数;
(3)根据以上数据分析,从一个方面评价两个年级教师学习党史的竞赛成绩谁更优异.
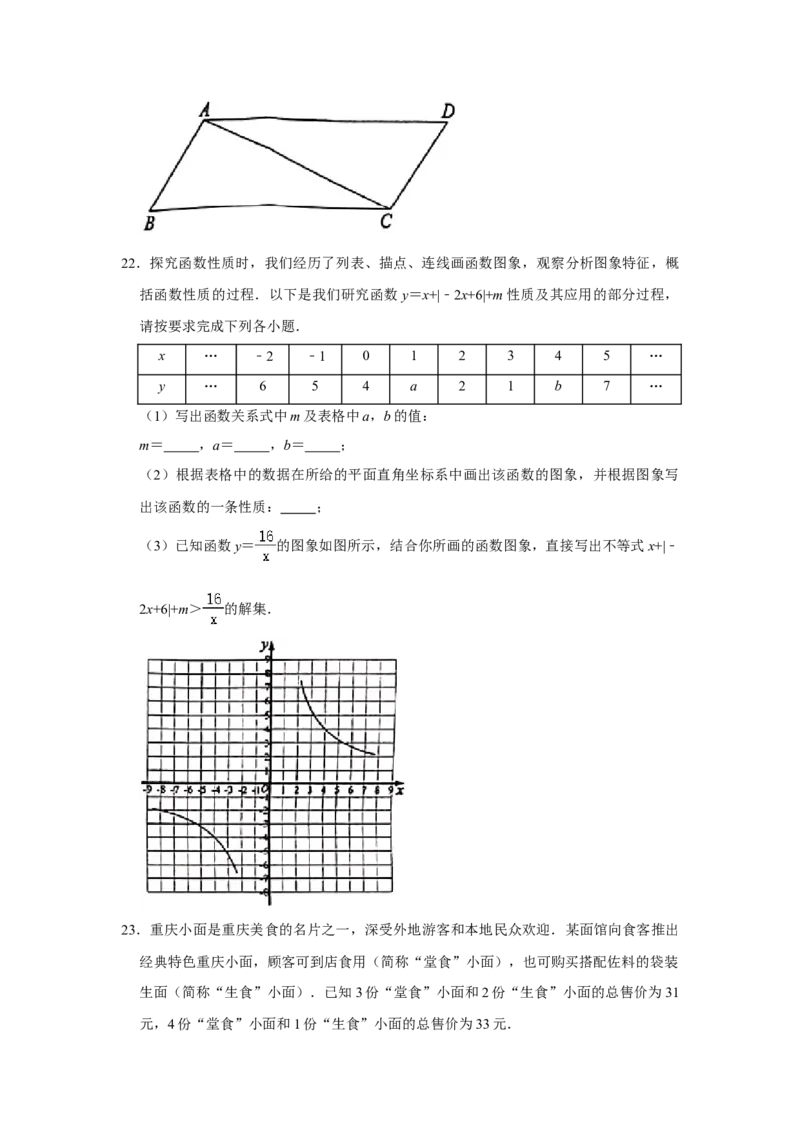
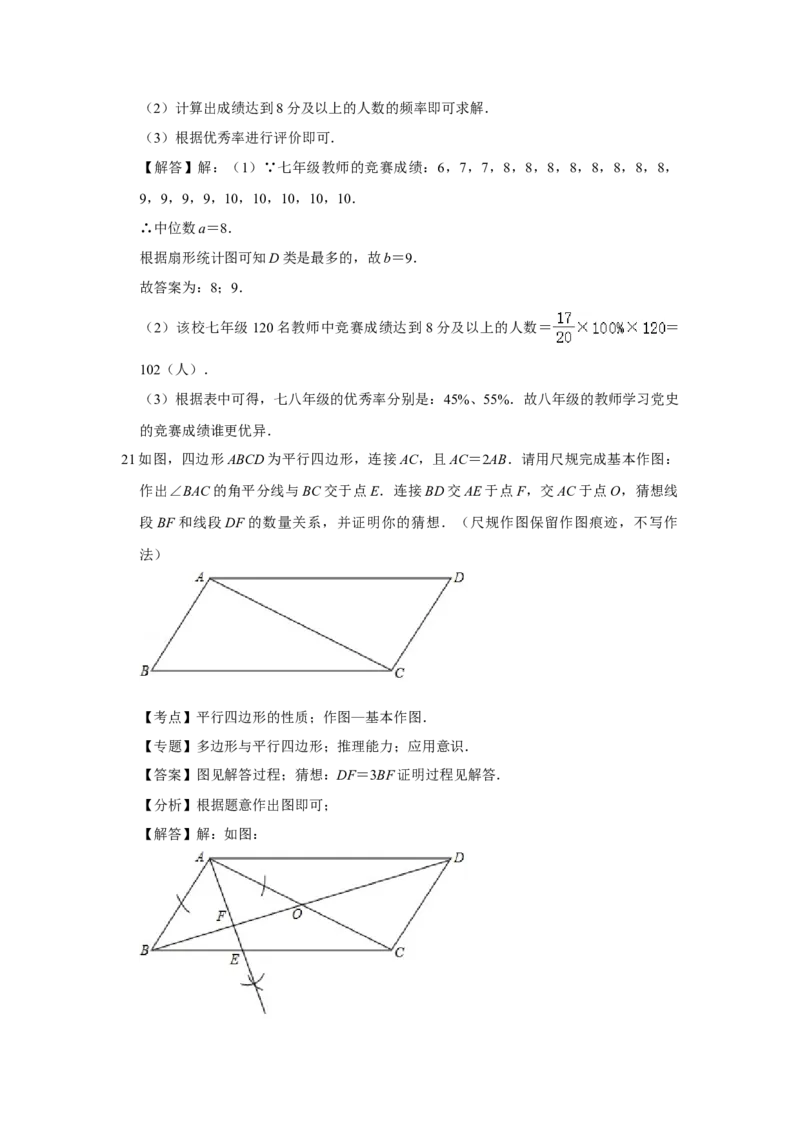
21.如图,四边形ABCD为平行四边形,连接AC,且AC=2AB.请用尺规完成基本作图:
作出∠BAC的角平分线与BC交于点E.连接BD交AE于点F,交AC于点O,猜想线
段BF和线段DF的数量关系,并证明你的猜想.(尺规作图保留作图痕迹,不写作
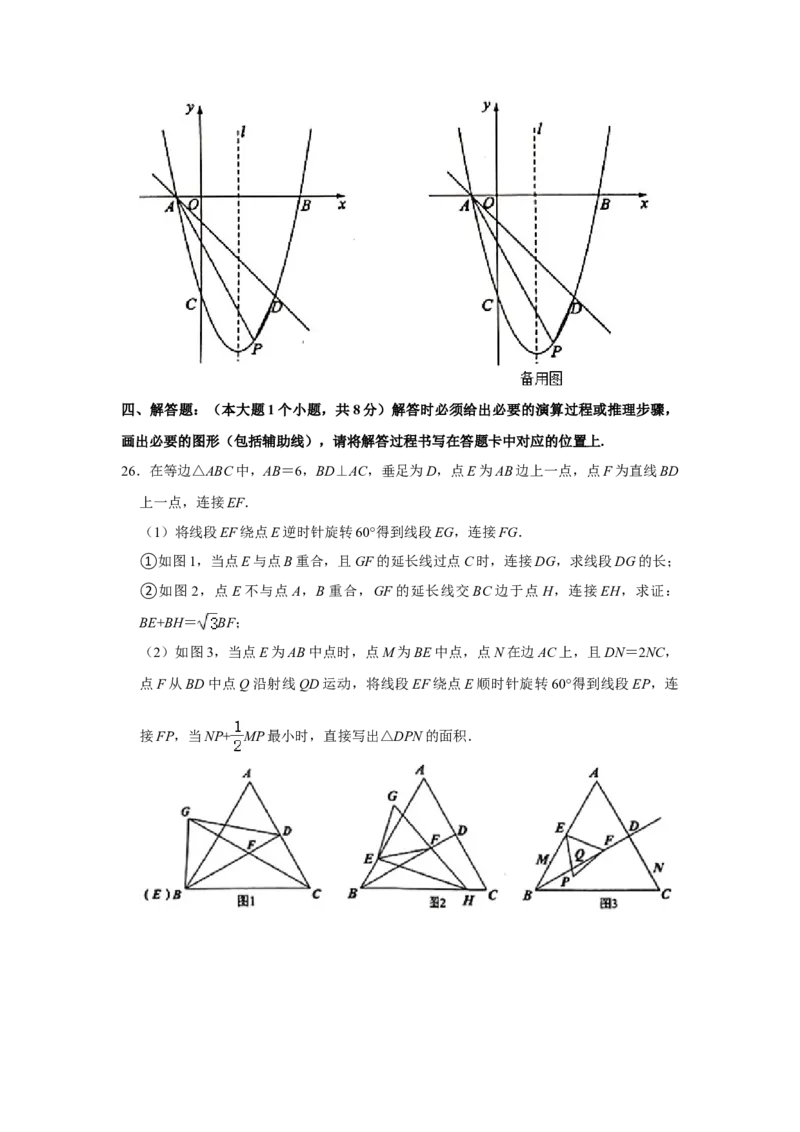
法)22.探究函数性质时,我们经历了列表、描点、连线画函数图象,观察分析图象特征,概
括函数性质的过程.以下是我们研究函数y=x+|﹣2x+6|+m性质及其应用的部分过程,
请按要求完成下列各小题.
x … ﹣2 ﹣1 0 1 2 3 4 5 …
y … 6 5 4 a 2 1 b 7 …
(1)写出函数关系式中m及表格中a,b的值:
m= ,a= ,b= ;
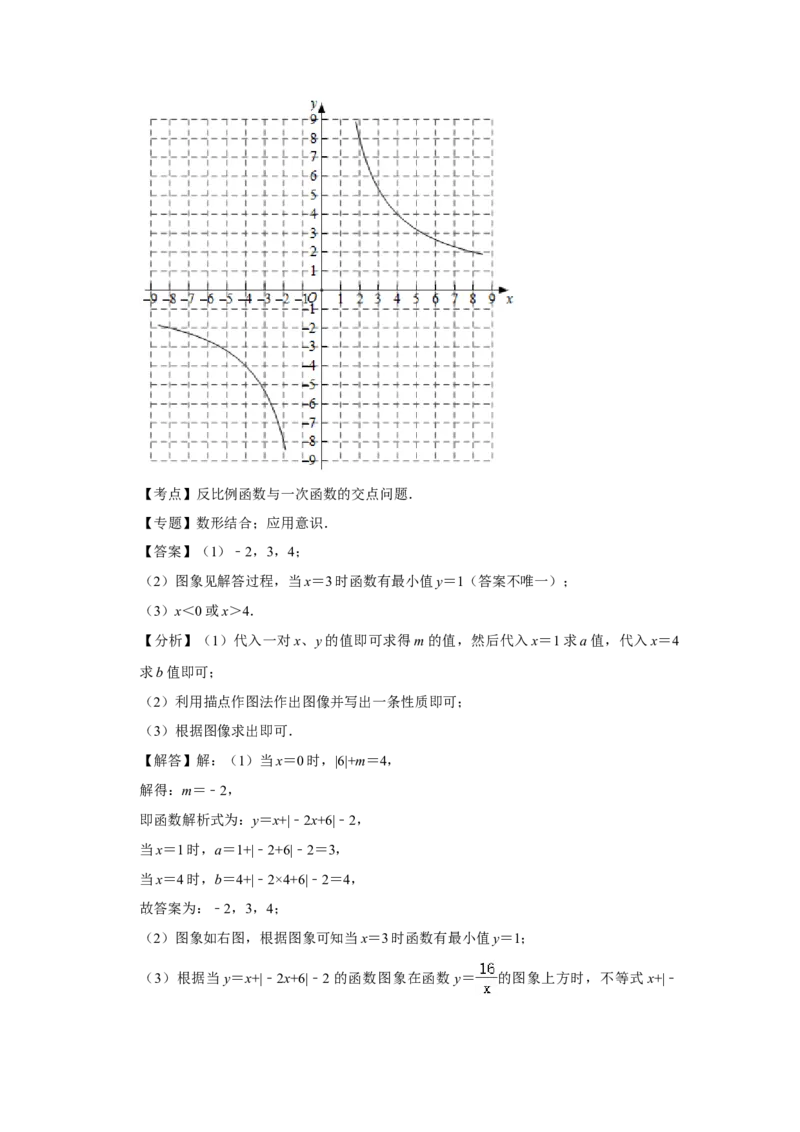
(2)根据表格中的数据在所给的平面直角坐标系中画出该函数的图象,并根据图象写
出该函数的一条性质: ;
(3)已知函数y= 的图象如图所示,结合你所画的函数图象,直接写出不等式x+|﹣
2x+6|+m> 的解集.
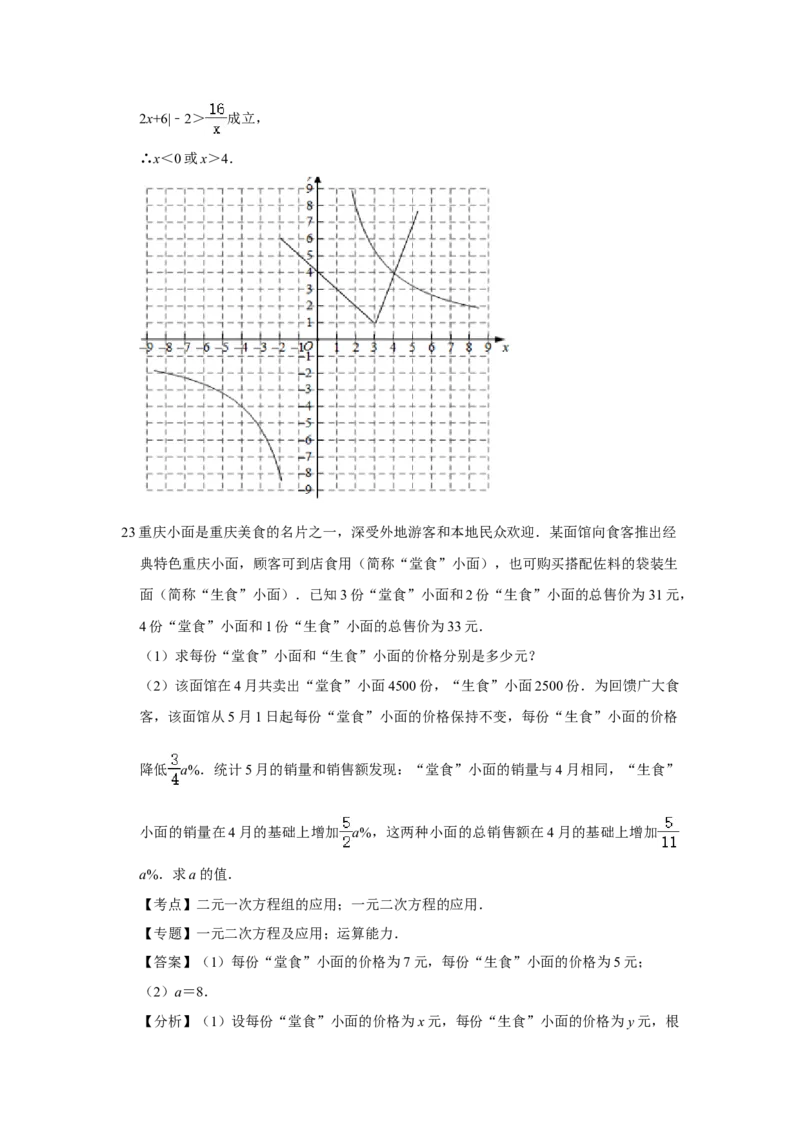
23.重庆小面是重庆美食的名片之一,深受外地游客和本地民众欢迎.某面馆向食客推出
经典特色重庆小面,顾客可到店食用(简称“堂食”小面),也可购买搭配佐料的袋装
生面(简称“生食”小面).已知3份“堂食”小面和2份“生食”小面的总售价为31
元,4份“堂食”小面和1份“生食”小面的总售价为33元.(1)求每份“堂食”小面和“生食”小面的价格分别是多少元?
(2)该面馆在4月共卖出“堂食”小面4500份,“生食”小面2500份.为回馈广大食
客,该面馆从5月1日起每份“堂食”小面的价格保持不变,每份“生食”小面的价格
降低 a%.统计5月的销量和销售额发现:“堂食”小面的销量与4月相同,“生食”
小面的销量在4月的基础上增加 a%,这两种小面的总销售额在4月的基础上增加
a%.求a的值.
24.对于任意一个四位数m,若干位上的数字与个位上的数字之和是百位上的数字与十位
上的数字之和的2倍,则称这个四位数m为“共生数”.例如:m=3507,因为3+7=
2×(5+0),所以3507是“共生数”;m=4135,因为4+5≠2×(1+3),所以4135不
是“共生数”.
(1)判断5313,6437是否为“共生数”?并说明理由;
(2)对于“共生数”n,当十位上的数字是千位上的数字的2倍,百位上的数字与个位
上的数字之和能被9整除时,记F(n)= .求满足F(n)各数位上的数字之和是偶
数的所有n.
25.如图,在平面直角坐标系中,抛物线 y=ax2+bx﹣4(a≠0)与x轴交于点A(﹣1,
0),B(4,0),与y轴交于点C.
(1)求该抛物线的解析式;
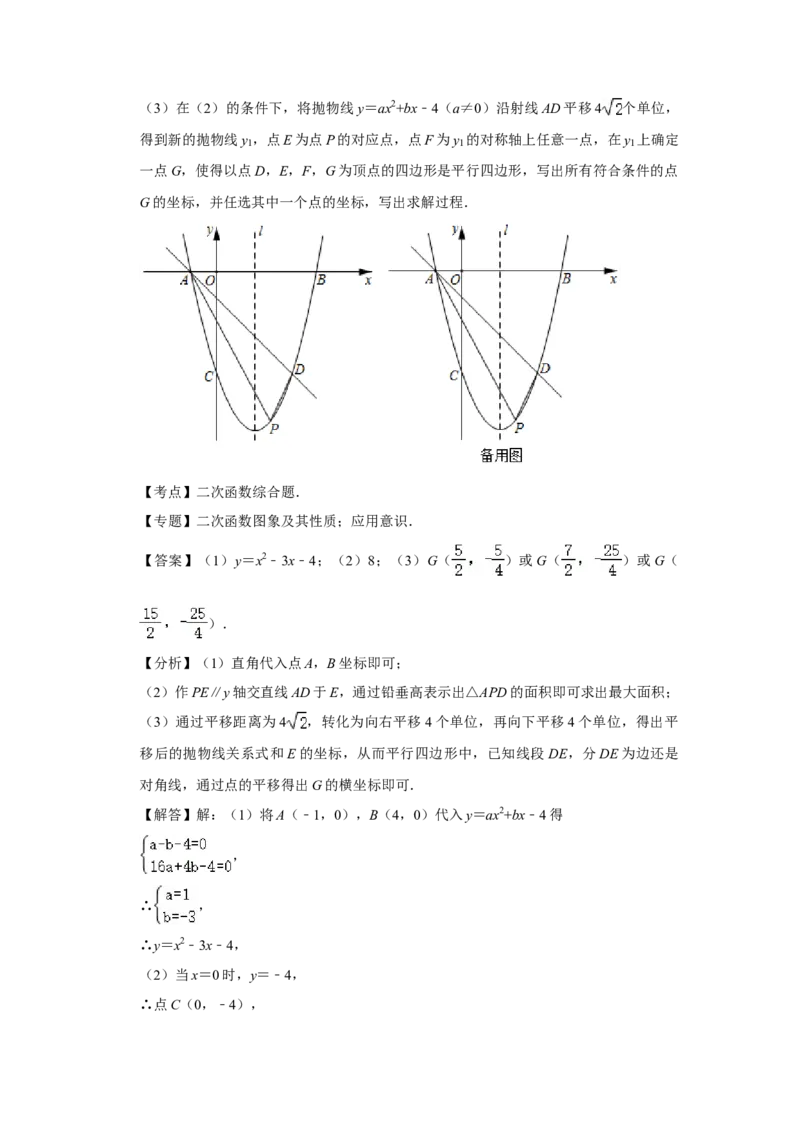
(2)直线l为该抛物线的对称轴,点D与点C关于直线l对称,点P为直线AD下方抛
物线上一动点,连接PA,PD,求△PAD面积的最大值.
(3)在(2)的条件下,将抛物线y=ax2+bx﹣4(a≠0)沿射线AD平移4 个单位,
得到新的抛物线y ,点E为点P的对应点,点F为y 的对称轴上任意一点,在y 上确定
1 1 1
一点G,使得以点D,E,F,G为顶点的四边形是平行四边形,写出所有符合条件的点
G的坐标,并任选其中一个点的坐标,写出求解过程.四、解答题:(本大题1个小题,共8分)解答时必须给出必要的演算过程或推理步骤,
画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
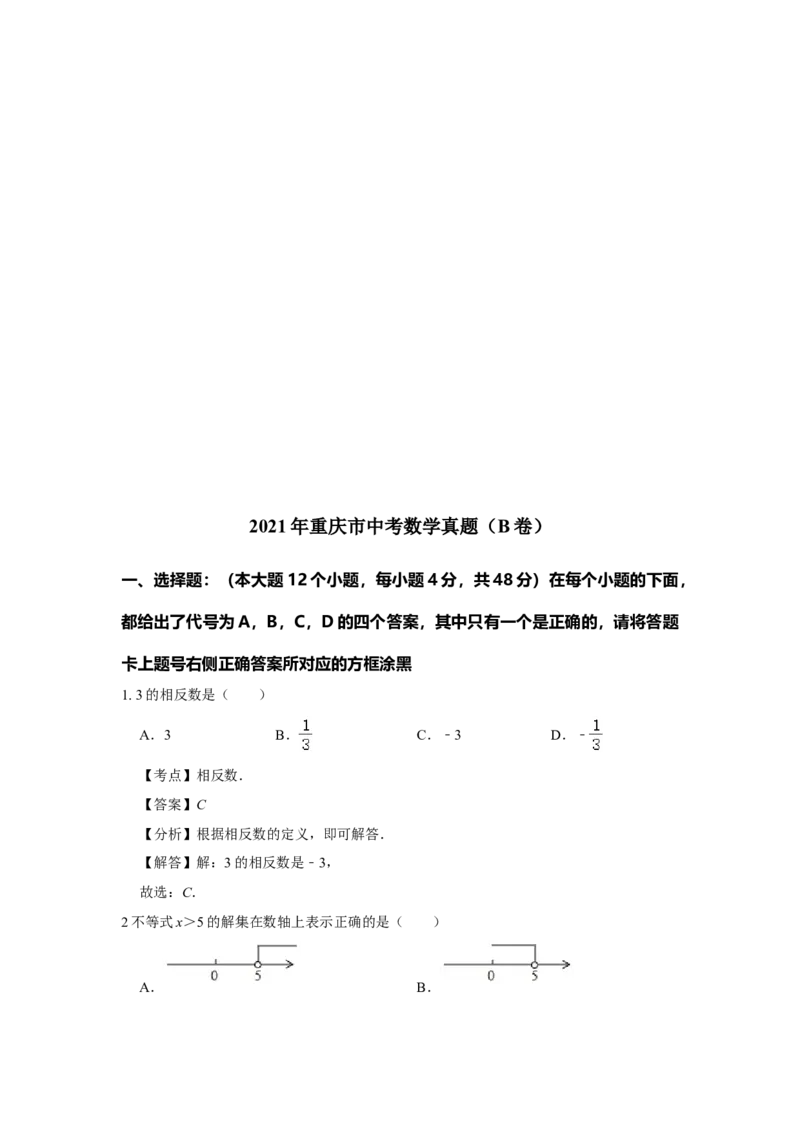
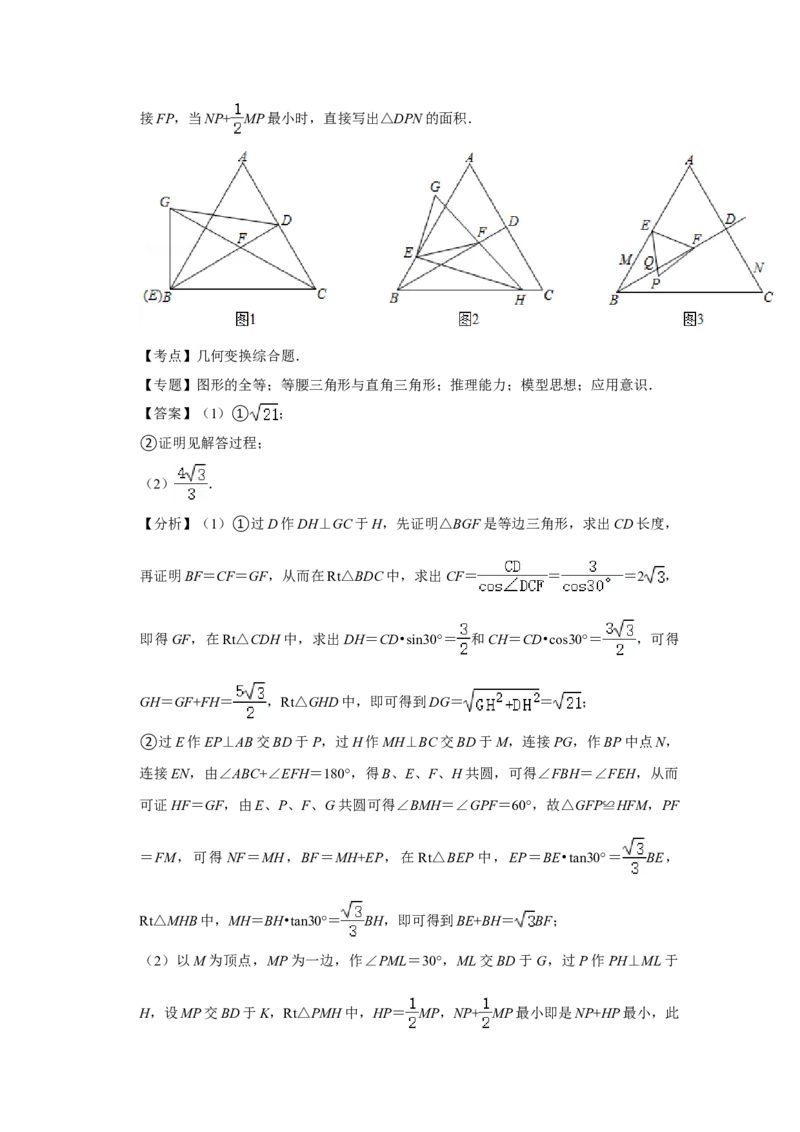
26.在等边△ABC中,AB=6,BD⊥AC,垂足为D,点E为AB边上一点,点F为直线BD
上一点,连接EF.
(1)将线段EF绕点E逆时针旋转60°得到线段EG,连接FG.
①如图1,当点E与点B重合,且GF的延长线过点C时,连接DG,求线段DG的长;
②如图2,点E不与点A,B重合,GF的延长线交BC边于点H,连接EH,求证:
BE+BH= BF;
(2)如图3,当点E为AB中点时,点M为BE中点,点N在边AC上,且DN=2NC,
点F从BD中点Q沿射线QD运动,将线段EF绕点E顺时针旋转60°得到线段EP,连
接FP,当NP+ MP最小时,直接写出△DPN的面积.2021年重庆市中考数学真题(B卷)
一、选择题:(本大题12个小题,每小题4分,共48分)在每个小题的下面,
都给出了代号为A,B,C,D的四个答案,其中只有一个是正确的,请将答题
卡上题号右侧正确答案所对应的方框涂黑
1. 3的相反数是( )
A.3 B. C.﹣3 D.﹣
【考点】相反数.
【答案】C
【分析】根据相反数的定义,即可解答.
【解答】解:3的相反数是﹣3,
故选:C.
2不等式x>5的解集在数轴上表示正确的是( )
A. B.C. D.
【考点】在数轴上表示不等式的解集.
【专题】数与式;数感.
【答案】A
【分析】明确x>5在数轴上表示5的右边的部分即可.
【解答】解:不等式x>5的解集在数轴上表示为:5右边的部分,不包括5,
故选:A.
3计算x4÷x结果正确的是( )
A.x4 B.x3 C.x2 D.x
【考点】同底数幂的除法.
【专题】整式;运算能力.
【答案】B
【分析】根据同底数幂的除法法则计算即可.
【解答】解:原式=x4﹣1=x3,
故选:B.
4如图,在平面直角坐标系中,将△OAB以原点O为位似中心放大后得到△OCD,若B
(0,1),D(0,3),则△OAB与△OCD的相似比是( )
A.2:1 B.1:2 C.3:1 D.1:3
【考点】坐标与图形性质;位似变换.
【专题】图形的相似;应用意识.
【答案】D
【分析】根据信息,找到OB与OD的比值即可.
【解答】解:∵B(0,1),D(0,3),∴OB=1,OD=3,
∵△OAB以原点O为位似中心放大后得到△OCD,
∴△OAB与△OCD的相似比是OB:OD=1:3,
故选:D.
5如图,AB是 O的直径,AC,BC是 O的弦,若∠A=20°,则∠B的度数为( )
⊙ ⊙
A.70° B.90° C.40° D.60°
【考点】圆周角定理.
【专题】圆的有关概念及性质;应用意识.
【答案】A
【分析】根据直径所对的圆周角为90°,即可求解.
【解答】解:∵AB是 O的直径,
∴∠C=90°, ⊙
∵∠A=20°,
∴∠B=90°﹣∠A=70°,
故选:A.
6下列计算中,正确的是( )
A.5 ﹣2 =21 B.2+ =2 C. × =3 D. ÷ =3
【考点】二次根式的混合运算.
【专题】二次根式;运算能力.
【答案】C
【分析】根据合并同类二次根式法则、同类二次根式的定义、二次根式的乘法和除法法
则逐一判断即可.
【解答】解:A.5 ﹣2 =3 ,此选项计算错误;
B.2与 不是同类二次根式,不能合并,此选项计算错误;
C. × = × × =3 ,此选项计算正确;
D. ÷ = = ,此选项计算错误;故选:C.
7小明从家出发沿笔直的公路去图书馆,在图书馆阅读书报后按原路回到家.如图,反映
了小明离家的距离y(单位:km)与时间t(单位:h)之间的对应关系.下列描述错误
的是( )
A.小明家距图书馆3km
B.小明在图书馆阅读时间为2h
C.小明在图书馆阅读书报和往返总时间不足4h
D.小明去图书馆的速度比回家时的速度快
【考点】函数的图象.
【专题】一次函数及其应用;推理能力.
【答案】D
【分析】根据题意和函数图象中的数据可以判断各个选项中是说法是否正确.
【解答】解:由图象知:
A.小明家距图书馆3km,正确;
B.小明在图书馆阅读时间为3﹣1=2小时,正确;
C.小明在图书馆阅读书报和往返总时间不足4h,正确;
D.因为小明去图书馆需要1小时,回来不足1小时,所以小明去图书馆的速度比回家
时的速度快,错误,符合题意.
故选:D.
8如图,在△ABC和△DCB 中,∠ACB=∠DBC,添加一个条件,不能证明△ABC和
△DCB全等的是( )
A.∠ABC=∠DCB B.AB=DC C.AC=DB D.∠A=∠D【考点】全等三角形的判定.
【专题】三角形;图形的全等;应用意识.
【答案】B
【分析】根据证明三角形全等的条件AAS,SAS,ASA,SSS逐一验证选项即可.
【解答】解:在△ABC和△DCB中,
∵∠ACB=∠DBC,BC=BC,
A:当∠ABC=∠DCB时,△ABC≌△DCB(ASA),
故A能证明;
B:当AB=DC时,不能证明两三角形全等,
故B不能证明;
C:当AC=DB时,△ABC≌△DCB(SAS),
故C能证明;
D:当∠A=∠D时,△ABC≌△DCB(AAS),
故D能证明;
故选:B.
9如图,把含30°的直角三角板PMN放置在正方形ABCD中,∠PMN=30°,直角顶点P在
正方形ABCD的对角线BD上,点M,N分别在AB和CD边上,MN与BD交于点O,
且点O为MN的中点,则∠AMP的度数为( )
A.60° B.65° C.75° D.80°
【考点】直角三角形斜边上的中线;正方形的性质.
【专题】矩形 菱形 正方形;推理能力.
【答案】C
【分析】根据直角三角形斜边上的中线等于斜边的一半可知:OM=OP,从而得出
∠DPM=150°,利用四边形内角和定理即可求得.
【解答】解:在Rt△PMN中,∠MPN=90°,∵O为MN的中点,
∴OP= ,
∵∠PMN=30°,
∴∠MPO=30°,
∴∠DPM=150°,
在四边形ADPM中,
∵∠A=90°,∠ADB=45°,∠DPM=150°,
∴∠AMP=360°﹣∠A﹣∠ADB﹣∠DPM
=360°﹣90°﹣45°﹣150°
=75°.
故选:C.
10如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度
(或坡比)为i=1:2.4,坡顶D到BC的垂直距离DE=50米(点A,B,C,D,E在
同一平面内),在点D处测得建筑物顶A点的仰角为50°,则建筑物AB的高度约为(
)
(参考数据:sin50°≈0.77;cos50°≈0.64;tan50°≈1.19)
A.69.2米 B.73.1米 C.80.0米 D.85.7米
【考点】解直角三角形的应用﹣坡度坡角问题;解直角三角形的应用﹣仰角俯角问题.
【专题】解直角三角形及其应用;推理能力.
【答案】D
【分析】利用斜坡CD的坡度(或坡比)为i=1:2.4,求出CE的长,从而得出BE,再
利用tan50°即可求出AB的长.
【解答】解:∵斜坡CD的坡度(或坡比)为i=1:2.4,
∴DE:CE=5:12,
∵DE=50米,
∴CE=120米,∵BC=150米,
∴BE=150﹣120=30米,
∴AB=tan50°×30+50
=85.7米.
故选:D.
11 关于 x 的分式方程 +1= 的解为正数,且使关于 y 的一元一次不等式组
有解,则所有满足条件的整数a的值之和是( )
A.﹣5 B.﹣4 C.﹣3 D.﹣2
【考点】分式方程的解;解一元一次不等式;解一元一次不等式组.
【专题】分式方程及应用;一元一次不等式(组)及应用;运算能力;应用意识.
【答案】B
【分析】由关于y的一元一次不等式组 有解得到a的取值范围,再由关于
x的分式方程 +1= 的解为正数得到a的取值范围,将所得的两个不等式组成
不等式组,确定a的整数解,结论可求.
【解答】解:关于x的分式方程 +1= 的解为x= .
∵关于x的分式方程 +1= 的解为正数,
∴a+4>0.
∴a>﹣4.
∵关于x的分式方程 +1= 有可能产生增根2,
∴ .
∴a≠﹣1.
解关于y的一元一次不等式组 得:.
∵关于y的一元一次不等式组 有解,
∴a﹣2<0.
∴a<2.
综上,﹣4<a<2且a≠﹣1.
∵a为整数,
∴a=﹣3或﹣2或0或1.
∴满足条件的整数a的值之和是:﹣3﹣2+0+1=﹣4.
故选:B.
12如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数y
= (k>0,x>0)的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接
EF,AF.若点E为AC的中点,△AEF的面积为1,则k的值为( )
A. B. C.2 D.3
【考点】反比例函数系数k的几何意义;反比例函数图象上点的坐标特征;直角三角形
斜边上的中线;勾股定理;矩形的性质.
【专题】反比例函数及其应用;推理能力.
【答案】D
【分析】首先设A(a,0),表示出D(a, ),再根据D,E,F都在双曲线上,依
次表示出坐标,再由S△AEF =1,转化为S△ACF =2,列出等式即可求得.【解答】解:设A(a,0),
∵矩形ABCD,
∴D(a, ),
∵矩形ABCD,E为AC的中点,
则E也为BD的中点,
∵点B在x轴上,
∴E的纵坐标为 ,
∴ ,
∵E为AC的中点,
∴点C(3a, ),
∴点F(3a, ),
∵△AEF的面积为1,AE=EC,
∴S△ACF =2,
∴ ,
解得:k=3.
故选:D.
二、填空题:(本大题6个小题,每小题4分,共24分)请将每小题的答案
直接填在答题卡中对应的横线上
13计算: ﹣( ﹣1)0= .
【考点】实数的π运算;零指数幂.
【专题】实数;运算能力.
【答案】2.
【分析】利用算术平方根,零指数幂的意义进行运算.
【解答】解:原式=3﹣1=2.
故答案为:2.
14不透明袋子中装有黑球1个、白球2个,这些球除了颜色外无其他差别.从袋子中随机摸出一个球,记下颜色后放回,将袋子中的球摇匀,再随机摸出一个球,记下颜色,前
后两次摸出的球都是白球的概率是 .
【考点】列表法与树状图法.
【专题】概率及其应用;数据分析观念.
【答案】 .
【分析】列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解
即可.
【解答】解:列表如下
黑 白 白
黑 (黑,黑) (白,黑) (白,黑)
白 (黑,白) (白,白) (白,白)
白 (黑,白) (白,白) (白,白)
由表可知,共有9种等可能结果,其中前后两次摸出的球都是白球的有4种结果,
所以前后两次摸出的球都是白球的概率为 ,
故答案为: .
15方程2(x﹣3)=6的解是 .
【考点】解一元一次方程.
【专题】一次方程(组)及应用;运算能力.
【答案】x=6.
【分析】按照去括号,移项,合并同类项的步骤解方程即可.
【解答】解:方程两边同除以2得:
x﹣3=3.
移项,合并同类项得:
x=6.
故答案为:x=6.
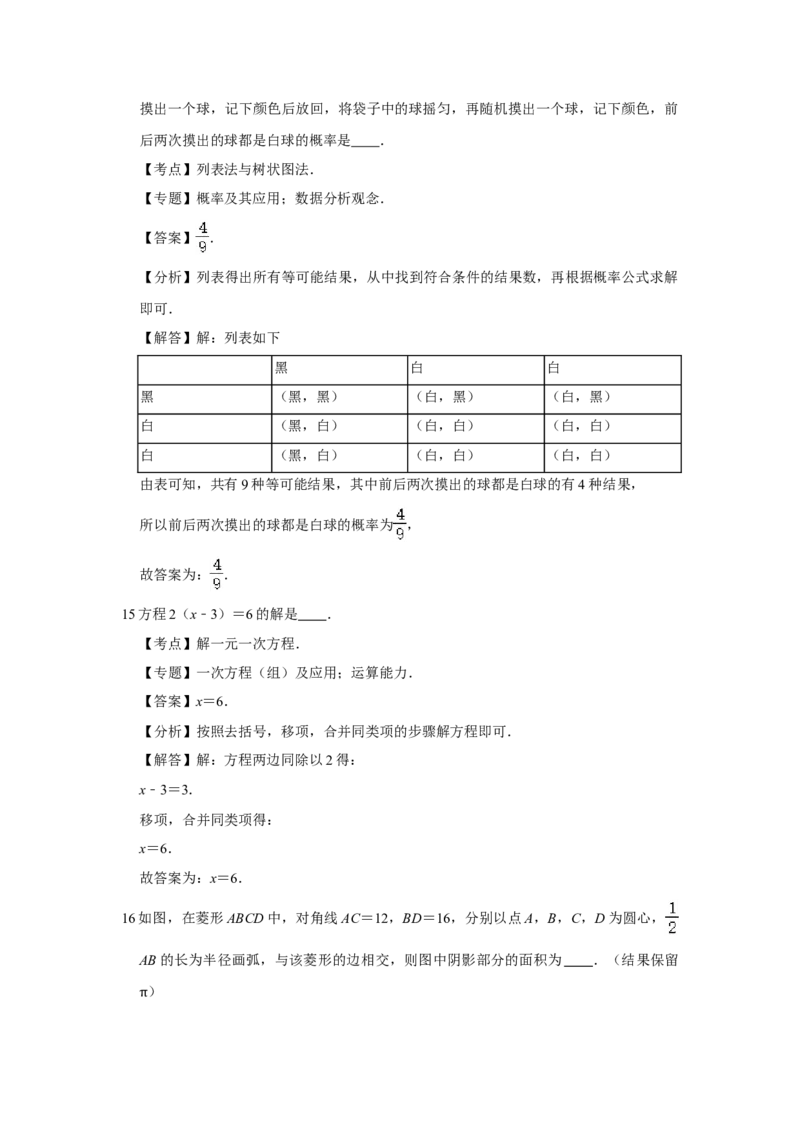
16如图,在菱形ABCD中,对角线AC=12,BD=16,分别以点A,B,C,D为圆心,
AB的长为半径画弧,与该菱形的边相交,则图中阴影部分的面积为 .(结果保留
)
π【考点】菱形的性质;扇形面积的计算.
【专题】矩形 菱形 正方形;与圆有关的计算;运算能力;应用意识.
【答案】96﹣100 .
【分析】先求出菱π形面积,再计算四个扇形的面积即可求解.
【解答】解:在菱形ABCD中,有:AC=12,BD=16.
∴ .
∵∠ABC+∠BCD+∠CDA+∠DAB=360°.
∴四个扇形的面积,是一个以 AB的长为半径的圆.
∴图中阴影部分的面积= ×12×16﹣ ×102=96﹣100 .
π π
故答案为:96﹣100 .
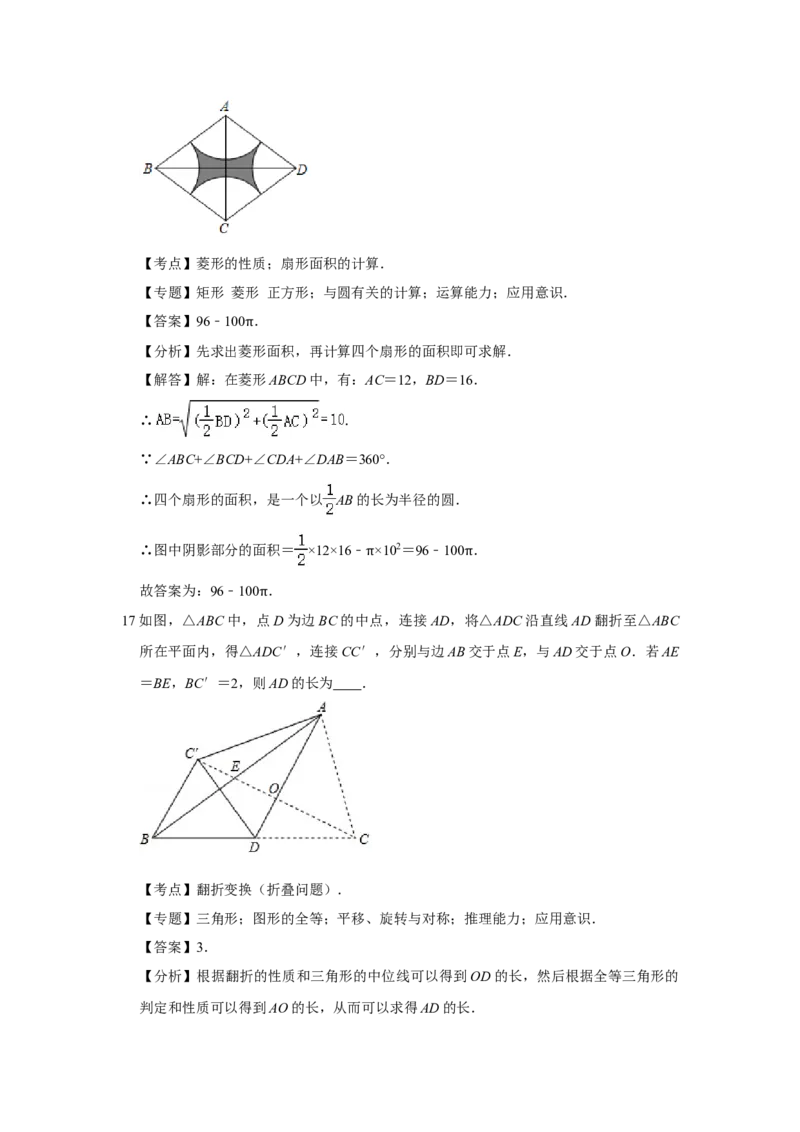
17如图,△ABC中,点π D为边BC的中点,连接AD,将△ADC沿直线AD翻折至△ABC
所在平面内,得△ADC′,连接CC′,分别与边AB交于点E,与AD交于点O.若AE
=BE,BC′=2,则AD的长为 .
【考点】翻折变换(折叠问题).
【专题】三角形;图形的全等;平移、旋转与对称;推理能力;应用意识.
【答案】3.
【分析】根据翻折的性质和三角形的中位线可以得到OD的长,然后根据全等三角形的
判定和性质可以得到AO的长,从而可以求得AD的长.【解答】解:由题意可得,
△DCAQ≌△DC′A,OC=OC′,∠COD=∠C′OD=90°,
∴点O为CC′的中点,
∵点D为BC的中点,
∴OD是△BCC′的中位线,
∴OD= BC′,OD∥BC′,
∴∠COD=∠EC′B=90°,
∵AE=BE,BC′=2,
∴OD=1,
在△EC′B和△EOA中,
,
∴△EC′B≌△EOA(AAS),
∴BC′=AO,
∴AO=2,
∴AD=AO+OD=2+1=3,
故答案为:3.
18盲盒为消费市场注入了活力,既能够营造消费者购物过程中的趣味体验,也为商家实现
销售额提升拓展了途径.某商家将蓝牙耳机、多接口优盘、迷你音箱共22个,搭配为
A,B,C三种盲盒各一个,其中A盒中有2个蓝牙耳机,3个多接口优盘,1个迷你音
箱;B盒中蓝牙耳机与迷你音箱的数量之和等于多接口优盘的数量,蓝牙耳机与迷你音
箱的数量之比为3:2;C盒中有1个蓝牙耳机,3个多接口优盘,2个迷你音箱.经核
算,A盒的成本为145元,B盒的成本为245元(每种盲盒的成本为该盒中蓝牙耳机、
多接口优盘、迷你音箱的成本之和),则C盒的成本为 元.
【考点】三元一次方程组的应用.
【专题】一次方程(组)及应用;应用意识.
【答案】155.
【分析】根据题意确定B盲盒各种物品的数量,设出三种物品的价格列出代数式,解代
数式即可.
【解答】解:∵蓝牙耳机、多接口优盘、迷你音箱共22个,A盒中有2个蓝牙耳机,3个多接口优盘,1个迷你音箱;C盒中有1个蓝牙耳机,3个多接口优盘,2个迷你音箱;
∴B盒中蓝牙耳机、多接口优盘、迷你音箱共22﹣2﹣3﹣1﹣1﹣3﹣2=10(个),
∵B盒中蓝牙耳机与迷你音箱的数量之和等于多接口优盘的数量,蓝牙耳机与迷你音箱
的数量之比为3:2,
∴B盒中有多接口优盘10× =5(个),蓝牙耳机有5× =3(个),迷你音箱有10
﹣5﹣3=2(个),
设蓝牙耳机、多接口优盘、迷你音箱的成本价分别为a元,b元,c元,
由题知: ,
∵①×2﹣②得:a+b=45,
②×2﹣①×3得:b+c=55,
∴C盒的成本为:a+3b+2c=(a+b)+(2b+2c)=45+55×2=155(元),
故答案为:155.
三、解答题:(本大题7个小题,每小题10分,共70分)解答时每小题必须
给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答
过程书写在答题卡中对应的位置上.
19计算:
(1)a(2a+3b)+(a﹣b)2;
(2) ÷(x+ ).
【考点】单项式乘多项式;完全平方公式;分式的混合运算.
【专题】整式;分式;运算能力.
【答案】(1)3a2+ab+b2;(2) .
【分析】(1)先利用单项式乘多项式法则、完全平方公式计算,再合并同类项即可;
(2)先将被除式分子、分母因式分解,同时计算括号内分式的加法,再将除法转化为
乘法,继而约分即可.
【解答】解:(1)原式=2a2+3ab+a2﹣2ab+b2
=3a2+ab+b2;(2)原式= ÷( + )
= ÷
= •
= .
20. 2021年是中国共产党建党100周年,某校开展了全校教师学习党史活动并进行了党史
知识竞赛,从七、八年级中各随机抽取了20名教师,统计这部分教师的竞赛成绩(竞
赛成绩均为整数,满分为10分,9分及以上为优秀).相关数据统计、整理如下:
抽取七年级教师的竞赛成绩(单位:分):
6,7,7,8,8,8,8,8,8,8,8,9,9,9,9,10,10,10,10,10.
七八年级教师竞赛成绩统计表
年级 七年级 八年级
平均数 8.5 8.5
中位数 a 9
众数 8 b
优秀率 45% 55%
根据以上信息,解答下列问题:
(1)填空:a= ,b= ;
(2)估计该校七年级120名教师中竞赛成绩达到8分及以上的人数;
(3)根据以上数据分析,从一个方面评价两个年级教师学习党史的竞赛成绩谁更优异.
【考点】用样本估计总体;中位数;众数.
【专题】数据的收集与整理;应用意识.
【答案】(1)8;9.(2)102人;(3)八年级教师更加优异.
【分析】(1)根据中位数定义、众数的定义即可找到a、b的值.(2)计算出成绩达到8分及以上的人数的频率即可求解.
(3)根据优秀率进行评价即可.
【解答】解:(1)∵七年级教师的竞赛成绩:6,7,7,8,8,8,8,8,8,8,8,
9,9,9,9,10,10,10,10,10.
∴中位数a=8.
根据扇形统计图可知D类是最多的,故b=9.
故答案为:8;9.
(2)该校七年级120名教师中竞赛成绩达到8分及以上的人数= =
102(人).
(3)根据表中可得,七八年级的优秀率分别是:45%、55%.故八年级的教师学习党史
的竞赛成绩谁更优异.
21如图,四边形ABCD为平行四边形,连接AC,且AC=2AB.请用尺规完成基本作图:
作出∠BAC的角平分线与BC交于点E.连接BD交AE于点F,交AC于点O,猜想线
段BF和线段DF的数量关系,并证明你的猜想.(尺规作图保留作图痕迹,不写作
法)
【考点】平行四边形的性质;作图—基本作图.
【专题】多边形与平行四边形;推理能力;应用意识.
【答案】图见解答过程;猜想:DF=3BF证明过程见解答.
【分析】根据题意作出图即可;
【解答】解:如图:猜想:DF=3BF.
证明:∵四边形ABCD为平行四边形.
∴OA=OC,OD=OB.
∵AC=2AB.
∴AO=AB.
∵∠BAC的角平分线与BC交于点E.
∴BF=FO.
∴DF=3BF.
22探究函数性质时,我们经历了列表、描点、连线画函数图象,观察分析图象特征,概括
函数性质的过程.以下是我们研究函数y=x+|﹣2x+6|+m性质及其应用的部分过程,请
按要求完成下列各小题.
x … ﹣2 ﹣1 0 1 2 3 4 5 …
y … 6 5 4 a 2 1 b 7 …
(1)写出函数关系式中m及表格中a,b的值:
m= ,a= ,b= ;
(2)根据表格中的数据在所给的平面直角坐标系中画出该函数的图象,并根据图象写
出该函数的一条性质: ;
(3)已知函数y= 的图象如图所示,结合你所画的函数图象,直接写出不等式x+|﹣
2x+6|+m> 的解集.【考点】反比例函数与一次函数的交点问题.
【专题】数形结合;应用意识.
【答案】(1)﹣2,3,4;
(2)图象见解答过程,当x=3时函数有最小值y=1(答案不唯一);
(3)x<0或x>4.
【分析】(1)代入一对x、y的值即可求得m的值,然后代入x=1求a值,代入x=4
求b值即可;
(2)利用描点作图法作出图像并写出一条性质即可;
(3)根据图像求出即可.
【解答】解:(1)当x=0时,|6|+m=4,
解得:m=﹣2,
即函数解析式为:y=x+|﹣2x+6|﹣2,
当x=1时,a=1+|﹣2+6|﹣2=3,
当x=4时,b=4+|﹣2×4+6|﹣2=4,
故答案为:﹣2,3,4;
(2)图象如右图,根据图象可知当x=3时函数有最小值y=1;
(3)根据当y=x+|﹣2x+6|﹣2的函数图象在函数y= 的图象上方时,不等式 x+|﹣2x+6|﹣2> 成立,
∴x<0或x>4.
23重庆小面是重庆美食的名片之一,深受外地游客和本地民众欢迎.某面馆向食客推出经
典特色重庆小面,顾客可到店食用(简称“堂食”小面),也可购买搭配佐料的袋装生
面(简称“生食”小面).已知3份“堂食”小面和2份“生食”小面的总售价为31元,
4份“堂食”小面和1份“生食”小面的总售价为33元.
(1)求每份“堂食”小面和“生食”小面的价格分别是多少元?
(2)该面馆在4月共卖出“堂食”小面4500份,“生食”小面2500份.为回馈广大食
客,该面馆从5月1日起每份“堂食”小面的价格保持不变,每份“生食”小面的价格
降低 a%.统计5月的销量和销售额发现:“堂食”小面的销量与4月相同,“生食”
小面的销量在4月的基础上增加 a%,这两种小面的总销售额在4月的基础上增加
a%.求a的值.
【考点】二元一次方程组的应用;一元二次方程的应用.
【专题】一元二次方程及应用;运算能力.
【答案】(1)每份“堂食”小面的价格为7元,每份“生食”小面的价格为5元;
(2)a=8.
【分析】(1)设每份“堂食”小面的价格为x元,每份“生食”小面的价格为y元,根据3份“堂食”小面和2份“生食”小面的总售价为31元,4份“堂食”小面和1份
“生食”小面的总售价为33元列方程组解出可得结论;
(2)根据5月“堂食”小面的销售额+“生食”小面的销售额=4月的总销售额(1+
a%),用换元法解方程可得结论.
【解答】解:(1)设每份“堂食”小面的价格为x元,每份“生食”小面的价格为y元,
根据题意得: ,
解得: ,
答:每份“堂食”小面的价格为7元,每份“生食”小面的价格为5元;
(2)由题意得:4500×7+2500(1+ a%)×5(1﹣ a%)=(4500×7+2500×5)(1+
a%),
设a%=m,则方程可化为:9×7+25(1+ m)(1﹣ m)=(9×7+25)(1+ m),
375m2﹣30m=0,
m(25m﹣2)=0,
解得:m =0(舍),m = ,
1 2
∴a=8.
24对于任意一个四位数m,若千位上的数字与个位上的数字之和是百位上的数字与十位上
的数字之和的2倍,则称这个四位数m为“共生数”.例如:m=3507,因为3+7=2×
(5+0),所以3507是“共生数”;m=4135,因为4+5≠2×(1+3),所以4135不是
“共生数”.
(1)判断5313,6437是否为“共生数”?并说明理由;
(2)对于“共生数”n,当十位上的数字是千位上的数字的2倍,百位上的数字与个位
上的数字之和能被9整除时,记F(n)= .求满足F(n)各数位上的数字之和是偶
数的所有n.
【考点】列代数式;因式分解的应用.
【专题】新定义;运算能力.【答案】(1)5313是“共生数”,6437不是“共生数”;
(2)2148或3069.
【分析】(1)根据题目中的定义,可直接判断5313,6437是否为“共生数”;
(2)根据定义,先用两个未知数表示F(n),然后列出含有n的式子,找出满足要求
的结果即可.
【解答】解:(1)∵5+3=2×(3+1),
∴5313是”共生数“,
∵6+7≠2×(3+4),
∴6437不是“共生数”;
(2)∵n是“共生数”,根据题意,个位上的数字要大于百位上的数字,
设n的千位上的数字为a,则十位上的数字为2a,(1≤a≤4),
设n的百位上的数字为b,
∵个位和百位都是0﹣9的数字,
∴个位上的数字为9﹣b,且9﹣b>b,
∴0≤b≤4
∴n=1000a+100b+20a+9﹣b;
∴F(n)= =340a+33b+3,
由于n是“共生数”,
∴a+9﹣b=2×(2a+b),
即a+b=3,
可能的情况有:
,
∴n的值为1227或2148或3069,
各位数和为偶数的有2148和3069,
∴n的值是2148或3069.
25如图,在平面直角坐标系中,抛物线 y=ax2+bx﹣4(a≠0)与x轴交于点A(﹣1,
0),B(4,0),与y轴交于点C.
(1)求该抛物线的解析式;
(2)直线l为该抛物线的对称轴,点D与点C关于直线l对称,点P为直线AD下方抛
物线上一动点,连接PA,PD,求△PAD面积的最大值.(3)在(2)的条件下,将抛物线y=ax2+bx﹣4(a≠0)沿射线AD平移4 个单位,
得到新的抛物线y ,点E为点P的对应点,点F为y 的对称轴上任意一点,在y 上确定
1 1 1
一点G,使得以点D,E,F,G为顶点的四边形是平行四边形,写出所有符合条件的点
G的坐标,并任选其中一个点的坐标,写出求解过程.
【考点】二次函数综合题.
【专题】二次函数图象及其性质;应用意识.
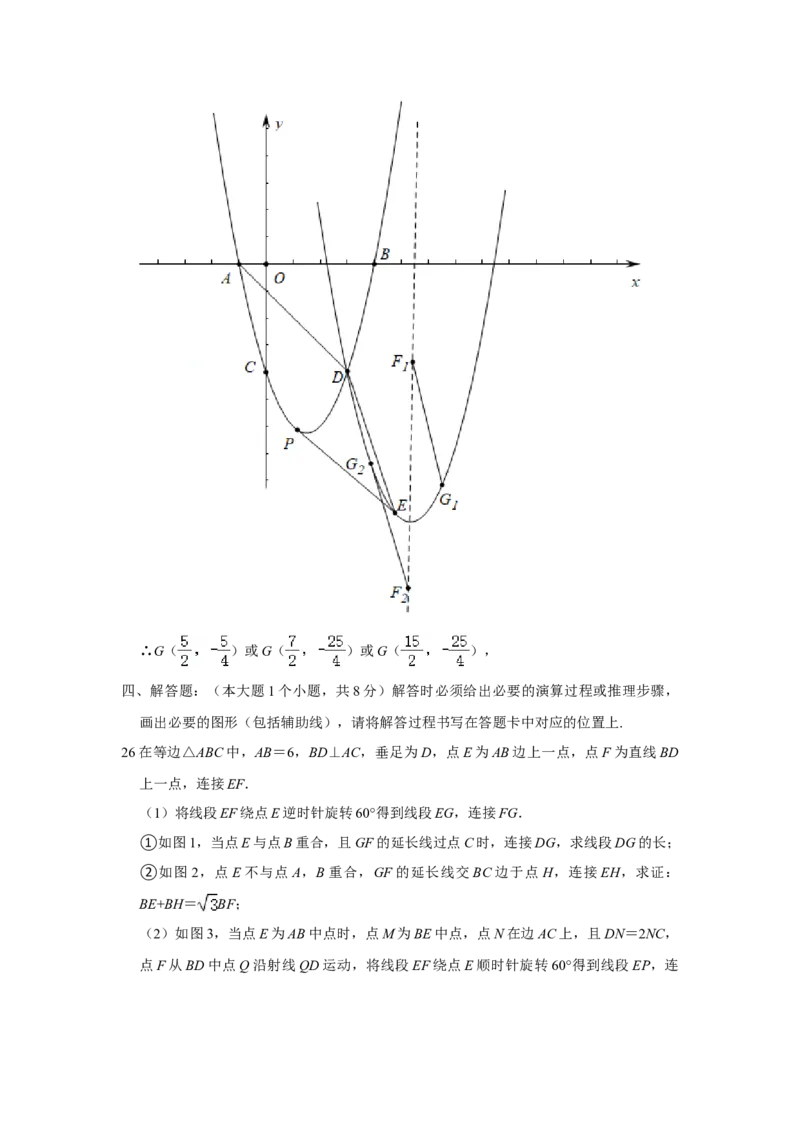
【答案】(1)y=x2﹣3x﹣4;(2)8;(3)G( )或G( )或G(
).
【分析】(1)直角代入点A,B坐标即可;
(2)作PE∥y轴交直线AD于E,通过铅垂高表示出△APD的面积即可求出最大面积;
(3)通过平移距离为4 ,转化为向右平移4个单位,再向下平移4个单位,得出平
移后的抛物线关系式和E的坐标,从而平行四边形中,已知线段 DE,分DE为边还是
对角线,通过点的平移得出G的横坐标即可.
【解答】解:(1)将A(﹣1,0),B(4,0)代入y=ax2+bx﹣4得
,
∴ ,
∴y=x2﹣3x﹣4,
(2)当x=0时,y=﹣4,
∴点C(0,﹣4),∵点D与点C关于直线l对称,
∴D(3,﹣4),
∵A(﹣1,0),
∴直线AD的函数关系式为:y=﹣x﹣1,
设P(m,m2﹣3m﹣4),
作PE∥y轴交直线AD于E,
∴E(m,﹣m﹣1),
∴PE=﹣m﹣1﹣(m2﹣3m﹣4)
=﹣m2+2m+3,
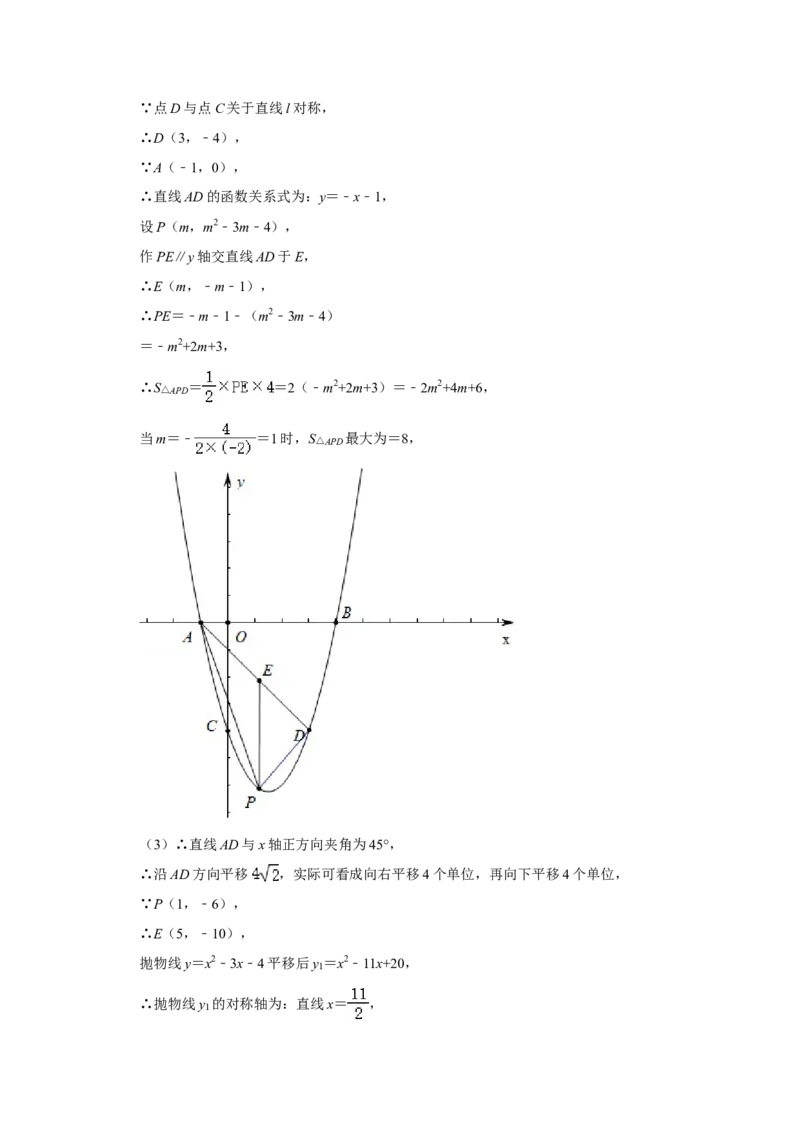
∴S△APD = =2(﹣m2+2m+3)=﹣2m2+4m+6,
当m=﹣ =1时,S△APD 最大为=8,
(3)∴直线AD与x轴正方向夹角为45°,
∴沿AD方向平移 ,实际可看成向右平移4个单位,再向下平移4个单位,
∵P(1,﹣6),
∴E(5,﹣10),
抛物线y=x2﹣3x﹣4平移后y =x2﹣11x+20,
1
∴抛物线y 的对称轴为:直线x= ,
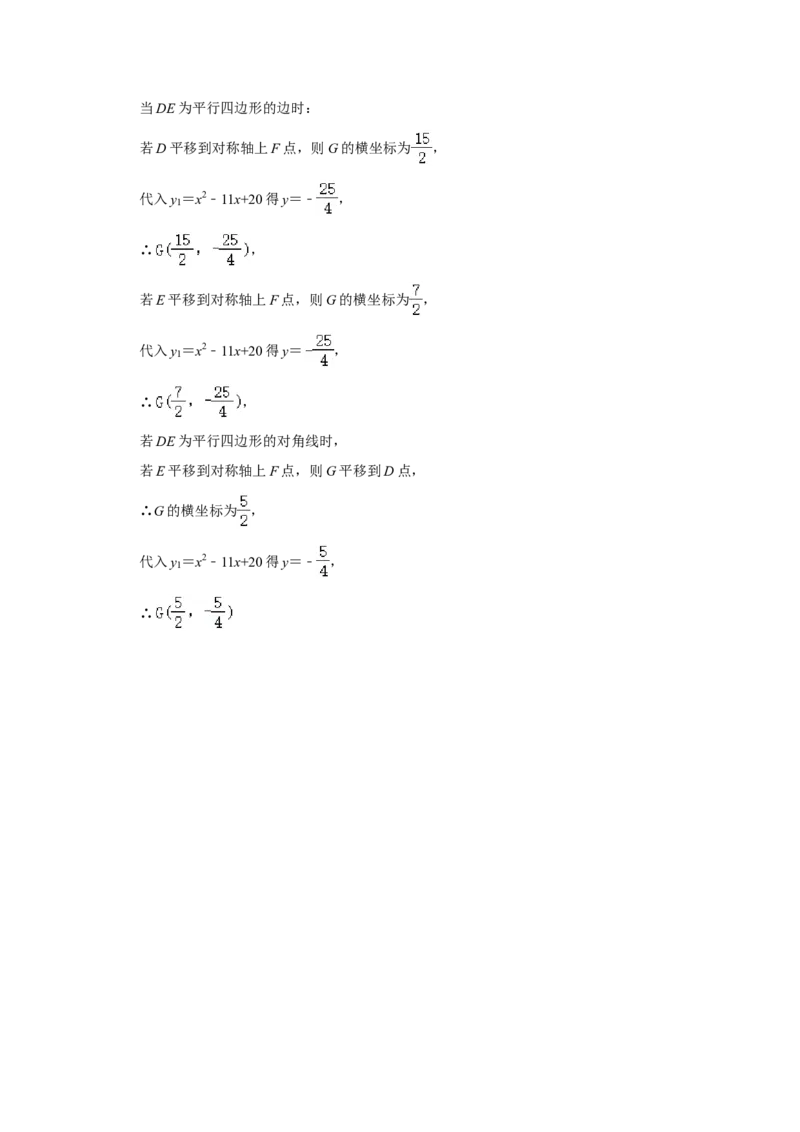
1当DE为平行四边形的边时:
若D平移到对称轴上F点,则G的横坐标为 ,
代入y =x2﹣11x+20得y=﹣ ,
1
∴ ,
若E平移到对称轴上F点,则G的横坐标为 ,
代入y =x2﹣11x+20得y= ,
1
∴ ,
若DE为平行四边形的对角线时,
若E平移到对称轴上F点,则G平移到D点,
∴G的横坐标为 ,
代入y =x2﹣11x+20得y=﹣ ,
1
∴∴G( )或G( )或G( ),
四、解答题:(本大题1个小题,共8分)解答时必须给出必要的演算过程或推理步骤,
画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
26在等边△ABC中,AB=6,BD⊥AC,垂足为D,点E为AB边上一点,点F为直线BD
上一点,连接EF.
(1)将线段EF绕点E逆时针旋转60°得到线段EG,连接FG.
①如图1,当点E与点B重合,且GF的延长线过点C时,连接DG,求线段DG的长;
②如图2,点E不与点A,B重合,GF的延长线交BC边于点H,连接EH,求证:
BE+BH= BF;
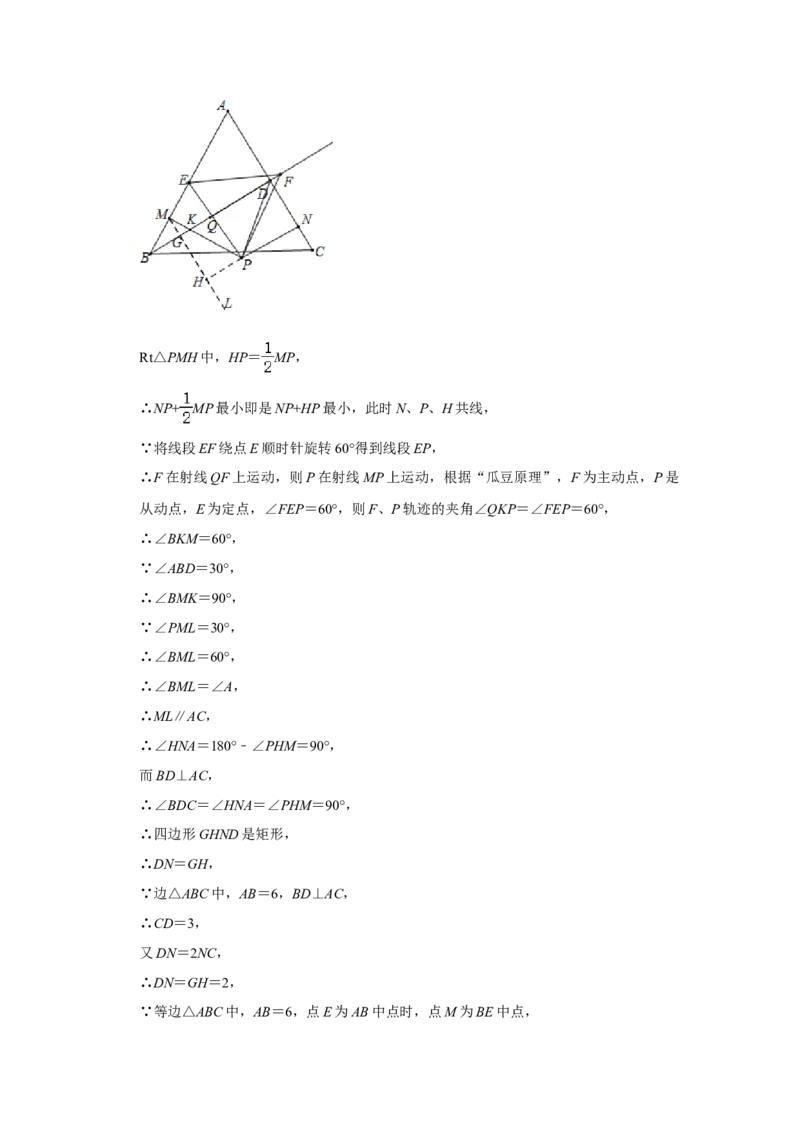
(2)如图3,当点E为AB中点时,点M为BE中点,点N在边AC上,且DN=2NC,
点F从BD中点Q沿射线QD运动,将线段EF绕点E顺时针旋转60°得到线段EP,连接FP,当NP+ MP最小时,直接写出△DPN的面积.
【考点】几何变换综合题.
【专题】图形的全等;等腰三角形与直角三角形;推理能力;模型思想;应用意识.
【答案】(1)① ;
②证明见解答过程;
(2) .
【分析】(1)①过D作DH⊥GC于H,先证明△BGF是等边三角形,求出CD长度,
再证明BF=CF=GF,从而在Rt△BDC中,求出CF= = =2 ,
即得GF,在Rt△CDH中,求出DH=CD•sin30°= 和CH=CD•cos30°= ,可得
GH=GF+FH= ,Rt△GHD中,即可得到DG= = ;
②过E作EP⊥AB交BD于P,过H作MH⊥BC交BD于M,连接PG,作BP中点N,
连接EN,由∠ABC+∠EFH=180°,得B、E、F、H共圆,可得∠FBH=∠FEH,从而
可证HF=GF,由E、P、F、G共圆可得∠BMH=∠GPF=60°,故△GFP≌HFM,PF
=FM,可得 NF=MH,BF=MH+EP,在 Rt△BEP 中,EP=BE•tan30°= BE,
Rt△MHB中,MH=BH•tan30°= BH,即可得到BE+BH= BF;
(2)以M为顶点,MP为一边,作∠PML=30°,ML交BD于G,过P作PH⊥ML于
H,设MP交BD于K,Rt△PMH中,HP= MP,NP+ MP最小即是NP+HP最小,此时N、P、H共线,而将线段EF绕点E顺时针旋转60°得到线段EP,可得∠QKP=
∠FEP=60°,从而可证ML∥AC,四边形GHND是矩形,由DN=2NC,得DN=GH=
2,由等边△ABC中,AB=6,点E为AB中点时,点M为BE中点,可得BM= ,BD
=AB•sinA=3 ,Rt△BGM中,MG= BM= ,BG=BM•cos30°= ,可求MH
=MG+GH= ,GD=BD﹣BG= ,Rt△MHP中,可得HP= ,从而可得
PN=HN﹣HP=GD﹣HP= ,故S△DPN = PN•DN= .
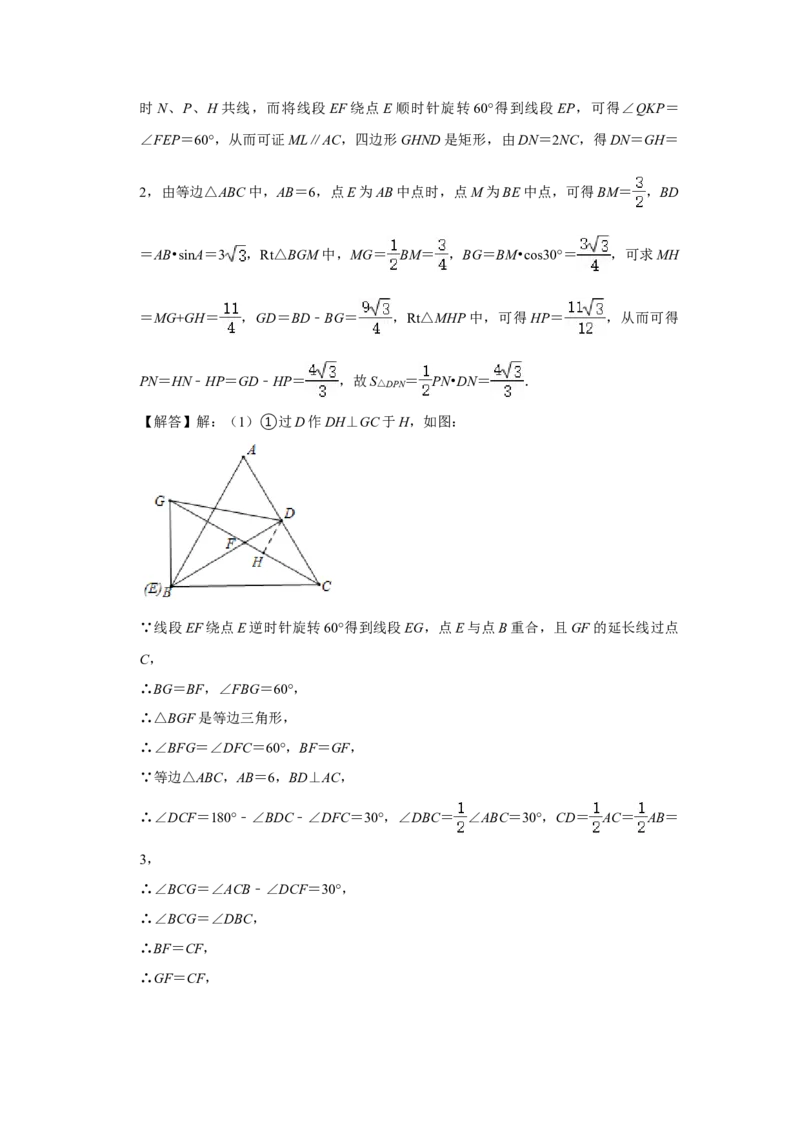
【解答】解:(1)①过D作DH⊥GC于H,如图:
∵线段EF绕点E逆时针旋转60°得到线段EG,点E与点B重合,且GF的延长线过点
C,
∴BG=BF,∠FBG=60°,
∴△BGF是等边三角形,
∴∠BFG=∠DFC=60°,BF=GF,
∵等边△ABC,AB=6,BD⊥AC,
∴∠DCF=180°﹣∠BDC﹣∠DFC=30°,∠DBC= ∠ABC=30°,CD= AC= AB=
3,
∴∠BCG=∠ACB﹣∠DCF=30°,
∴∠BCG=∠DBC,
∴BF=CF,
∴GF=CF,Rt△BDC中,CF= = =2 ,
∴GF=2 ,
Rt△CDH中,DH=CD•sin30°= ,CH=CD•cos30°= ,
∴FH=CF﹣CH= ,
∴GH=GF+FH= ,
Rt△GHD中,DG= = ;
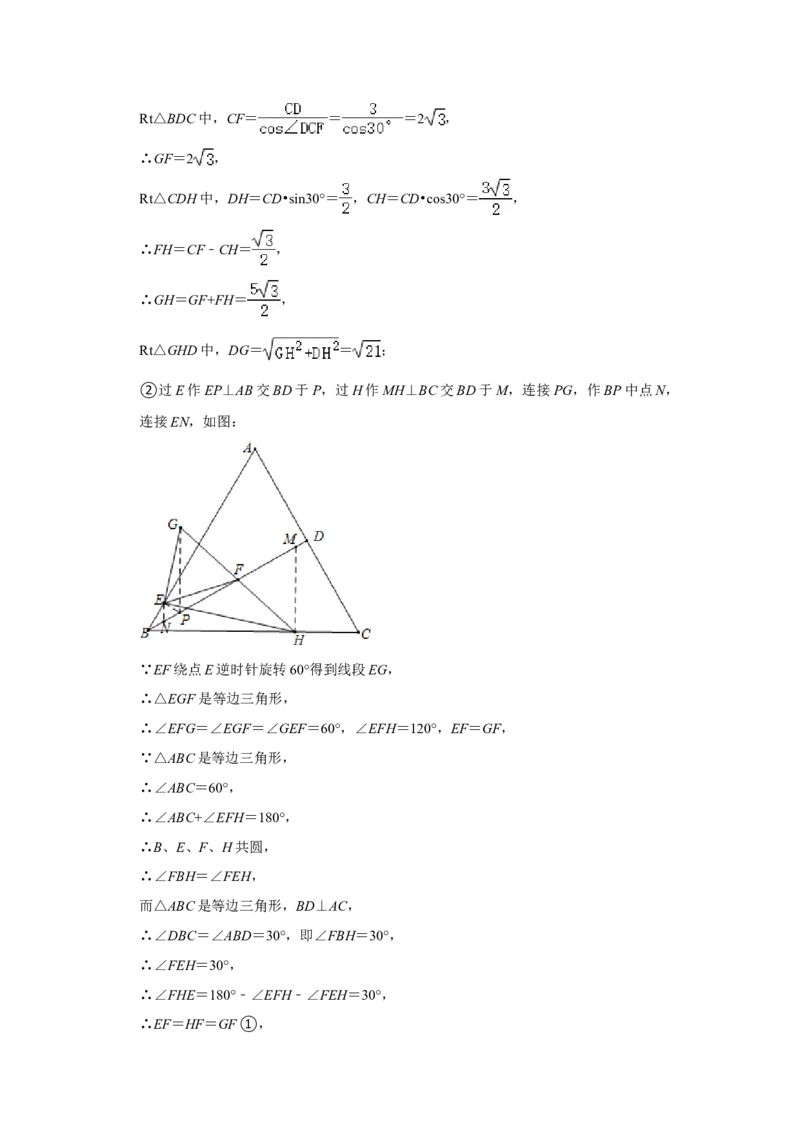
②过E作EP⊥AB交BD于P,过H作MH⊥BC交BD于M,连接PG,作BP中点N,
连接EN,如图:
∵EF绕点E逆时针旋转60°得到线段EG,
∴△EGF是等边三角形,
∴∠EFG=∠EGF=∠GEF=60°,∠EFH=120°,EF=GF,
∵△ABC是等边三角形,
∴∠ABC=60°,
∴∠ABC+∠EFH=180°,
∴B、E、F、H共圆,
∴∠FBH=∠FEH,
而△ABC是等边三角形,BD⊥AC,
∴∠DBC=∠ABD=30°,即∠FBH=30°,
∴∠FEH=30°,
∴∠FHE=180°﹣∠EFH﹣∠FEH=30°,
∴EF=HF=GF①,∵EP⊥AB,∠ABD=30°,
∴∠EPB=60°,∠EPF=120°,
∴∠EPF+∠EGF=180°,
∴E、P、F、G共圆,
∴∠GPF=∠GEF=60°,
∵MH⊥BC,∠DBC=30°,
∴∠BMH=60°,
∴∠BMH=∠GPF②,
而∠GFP=∠HFM③,
由①②③得△GFP≌HFM(AAS),
∴PF=FM,
∵EP⊥AB,BP中点N,∠ABD=30°,
∴EP= BP=BN=NP,
∴PF+NP=FM+BN,
∴NF= BM,
Rt△MHB中,MH= BM,
∴NF=MH,
∴NF+BN=MH+EP,即BF=MH+EP,
Rt△BEP中,EP=BE•tan30°= BE,
Rt△MHB中,MH=BH•tan30°= BH,
∴BF= BE+ BH,
∴BE+BH= BF;
(2)以M为顶点,MP为一边,作∠PML=30°,ML交BD于G,过P作PH⊥ML于
H,设MP交BD于K,如图:Rt△PMH中,HP= MP,
∴NP+ MP最小即是NP+HP最小,此时N、P、H共线,
∵将线段EF绕点E顺时针旋转60°得到线段EP,
∴F在射线QF上运动,则P在射线MP上运动,根据“瓜豆原理”,F为主动点,P是
从动点,E为定点,∠FEP=60°,则F、P轨迹的夹角∠QKP=∠FEP=60°,
∴∠BKM=60°,
∵∠ABD=30°,
∴∠BMK=90°,
∵∠PML=30°,
∴∠BML=60°,
∴∠BML=∠A,
∴ML∥AC,
∴∠HNA=180°﹣∠PHM=90°,
而BD⊥AC,
∴∠BDC=∠HNA=∠PHM=90°,
∴四边形GHND是矩形,
∴DN=GH,
∵边△ABC中,AB=6,BD⊥AC,
∴CD=3,
又DN=2NC,
∴DN=GH=2,
∵等边△ABC中,AB=6,点E为AB中点时,点M为BE中点,∴BM= ,BD=AB•sinA=6×sin60°=3 ,
Rt△BGM中,MG= BM= ,BG=BM•cos30°= ,
∴MH=MG+GH= ,GD=BD﹣BG= ,
Rt△MHP中,HP=MH•tan30°= ,
∴PN=HN﹣HP=GD﹣HP= ,
∴S△DPN = PN•DN= .