文档内容
2024 年高三年级第一次适应性检测
物理答案及评分标准
一、单项选择题:本题共8小题,每小题3分,共24分。
1.B 2.C 3.A 4.D 5.D 6.C 7.B 8.C
二、多项选择题:本题共4小题,每小题4分,共16分。
9.AD 10.BC 11.AD 12.ABC
三、非选择题:本题共6小题,共60分。
Ld(t -t )
1 2
13.(6分) (1)12.9(2分); (2)0.4(2分); (3) (2分)。
ght t
12
14.(8分) (1)78.9(2分); (2)37.6(2分);
1500 1.5
(3)I= (2分)(写成I= 得1分);
157.6+0.38t 157.6+0.38t
(4)不变(2分)。
15.(7分)
(1)充气过程中气囊克服外界大气压强所做的功W=p V··································(2分)
0
3
PV'
PV 5
(2)对气囊内所有的气体由理想气体状态方程得 = ···························(2分)
T T
3
1
从气囊内排出气体的体积为 ΔV=V'-V···············································(1分)
3
Δm ΔV 2
排出气体质量与排气前气体总质量的之比为 = = ·························· (2分)
m V' 5
评分标准:第1问,2分;第2问,5分。共7分。
16.(9 分)
(1)设出水口处水的速度为v,由题意可得ΔV=svt ········································(1分)
解得v=1m/s ···················································································(1分)
1
平抛过程:竖直方向h= gt2 ································································(1分)
2
水平方向x=v t=0.3m·····················································(2分)
0
(2)取水质量m=ρΔV=0.8kg································································(1分)
1
根据能量守恒定律 mv2+mgh=ηPt····················································(2分)
2
P=1.5W····················································································(1分)
评分标准:第1问,5分;第2问,4分。共9 分。
高三物理答案 第1页(共5页)
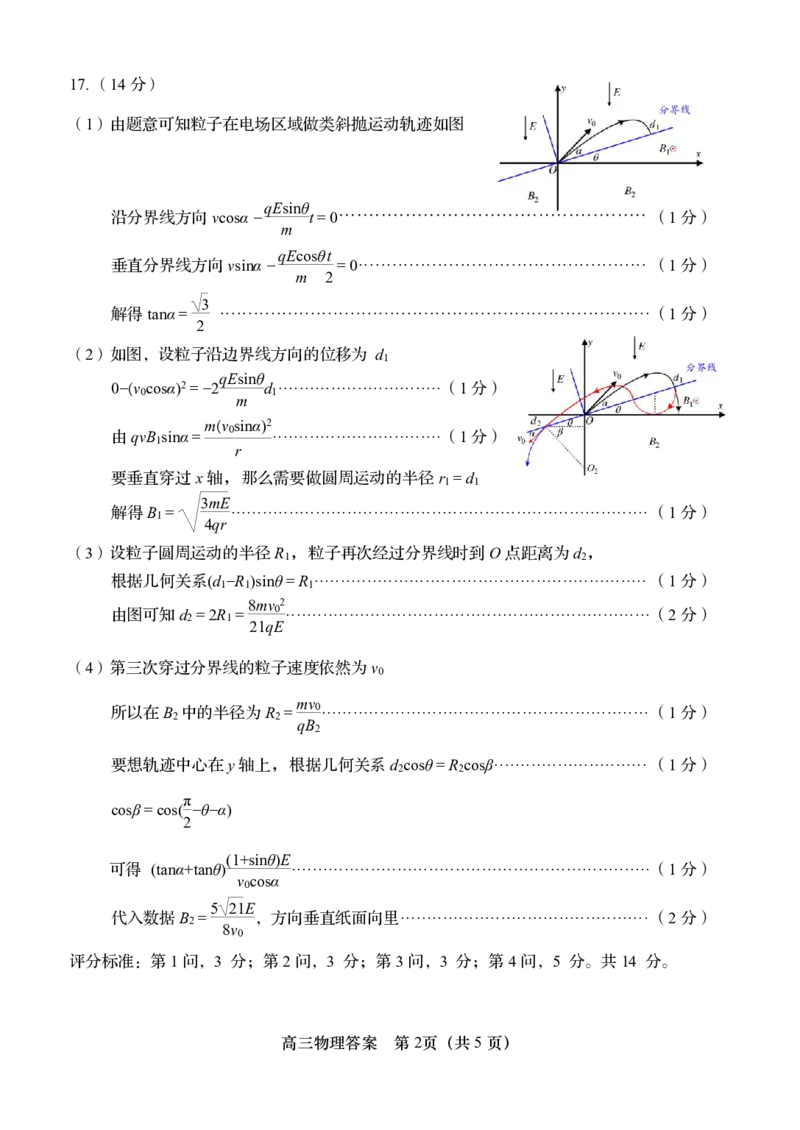
{#{QQABJYqEogggQBBAAQgCEwFqCgCQkBECCAoORBAMsAAACAFABCA=}#}17.(14分)
(1)由题意可知粒子在电场区域做类斜抛运动轨迹如图
qEsinθ
沿分界线方向vcosα- t=0··················································· (1分)
m
qEcosθt
垂直分界线方向vsinα- =0··················································· (1分)
m 2
3
解得tanα= ············································································(1分)
2
(2)如图,设粒子沿边界线方向的位移为 d
1
qEsinθ
0-(v cosα)2=-2 d ·······························(1分)
0 1
m
m(v sinα)2
由qvB sinα= 0 ································(1分)
1
r
要垂直穿过x轴,那么需要做圆周运动的半径r =d
1 1
3mE
解得B = ···············································································(1分)
1
4qr
(3)设粒子圆周运动的半径R ,粒子再次经过分界线时到O点距离为d ,
1 2
根据几何关系(d -R )sinθ=R ······························································· (1分)
1 1 1
8mv 2
由图可知d =2R = 0 ·····································································(2分)
2 1
21qE
(4)第三次穿过分界线的粒子速度依然为v
0
mv
所以在B 中的半径为R = 0······························································(1分)
2 2
qB
2
要想轨迹中心在y轴上,根据几何关系d cosθ=R cosβ····························· (1分)
2 2
π
cosβ=cos( -θ-α)
2
(1+sinθ)E
可得 (tanα+tanθ) ····································································(1分)
v cosα
0
5 21E
代入数据B = ,方向垂直纸面向里···············································(2分)
2
8v
0
评分标准:第1问,3 分;第2问,3 分;第3问,3 分;第4问,5 分。共14 分。
高三物理答案 第2页(共5页)
{#{QQABJYqEogggQBBAAQgCEwFqCgCQkBECCAoORBAMsAAACAFABCA=}#}18.(16分)
1
(1)根据机械能守恒,小球摆到最低点时的速度为v
0
满足 mv
0
2=mgH
2
解得v = 2gH=10 2m/s···································································· (1分)
0
A碰B时,根据动量守恒mv =m v ·······················································(1分)
0 0 1
v m
恢复系数为e= 1 解得e= ·····························································(1分)
v m
0 0
B碰A时根据动量守恒为m v =m v '+mv·······························································(1分)
0 0 0 0
v-v '
恢复系数e'= 0 ·············································································(1分)
v
0
联立得v=v =10 2m/s·······································································(1分)
0
(2)设共速时速度为v ,共速的位置距离小车左端距离为,
共
根据动量守恒mv =(M+m)v ·································································(1分)
0 共
m 1
解得v = v = v =5 2m/s····························································· (1分)
共 M+m 0 2 0
根据能量守恒可得μmgL+F
1
L+F
2
(x-L)+μmg(x-L)=ΔE
k0
································(1分)
1 1 m MmgH
其中ΔE = mv 2- v 2= =100J··············································(1分)
k0 2 0 2M+m 共 M+m
5MH 1 253
可得x= + L>L 代入数据可得x= ≈4.22m···························(1分)
6(M+m) 2 60
(3)当m再次返回到小车左端的时候,具有的可损失动能为
ΔE
k1
=ΔE
k0
-μmg(x+x)·········································································(1分)
MmgH
得ΔE
k1
= -0.4mgL
3(M+m)
MmgH 1
将 代换回ΔE
k0
得ΔE
k1
= ΔE
k0
-0.4mgL
M+m 3
1
其中0.4mgL=0.8J,所以ΔE
k1
= ΔE
k0
-0.8
3
因为每次从左侧挡板出发都会经过类似的过程,所以递推关系为
1
ΔE
k(n+1)
= ΔE
kn
-0.8·················································································(1分)
3
以下列举每次数量关系
1
n=1时,ΔE
k1
= ΔE
k0
-0.8
3
高三物理答案 第3页(共5页)
{#{QQABJYqEogggQBBAAQgCEwFqCgCQkBECCAoORBAMsAAACAFABCA=}#}1 1
n=2时,ΔE
k2
= ΔE
k0
-0.8× -0.8
32 3
1 1 1
n=3时,ΔE
k3
= ΔE
k0
-0.8× -0.8× -0.8
33 32 3
……
1 1 1
n=n时,ΔE
kn
= ΔE
k0
-0.8×( +… +1)
3n 3n-1 3
1 1.2
结合数列求和得ΔE
kn
= ΔE
k0
-(1.2- )····················································(1分)
3n 3n
101.2
由ΔE =100J,整理得ΔE = -1.2
k0 kn
3n
101.2 4
可知当n=4时,ΔE = -1.2= J
k4
34 81
假设此后m相对小车向右运动过程中会停在小车上的L段,设停在x
4
位置处
根据功能关系ΔE =(F +f)x ·································································(1分)
k4 1 4
1
带入数据得:x = m≈4mm
4
243
因为x ≈4mm<0.1m=L,所以假设正确,
4
综上
1
m物块一共跟左侧挡板碰撞4次,最后停在距离左端x = m≈4mm的位置·(1分)
4
243
评分标准:第1问,6分;第2问,5分;第3问,5分。共16分。
高三物理答案 第4页(共5页)
{#{QQABJYqEogggQBBAAQgCEwFqCgCQkBECCAoORBAMsAAACAFABCA=}#}