文档内容
2023 年高考考前押题密卷(五省新高考)
数学·参考答案
1 2 3 4 5 6 7 8 9 10 11 12
C A C B C D D C BCD BCD ACD ABC
13. (答案不唯一) 14.
15. 16
【解答题评分细则】
17.(1) ;
(2) .
【详解】(1)设 的公比为 ,则 ,又 ,
当 时, ,当 时, ,
两式相减可得, ,(1分)
所以 ,所以 或 (舍去),(2分)
所以 ,即 ,(3分)
所以等比数列 的通项公式为 ;(4分)
(2)由 , ,可得 ,(5分)
所以 ,又 ,(6分)
所以 ,当且仅当 时等号成立,
所以 ,(7分)
所以 ,(8分)
所以 .(9分)
即 .(10分)
18.(1)证明见解析
(2)
【详解】(1)由题意得 ,即 .
由正弦定理得 ,(1分)
学科网(北京)股份有限公司又由余弦定理得 ,
所以 ,故 ,(2分)
故 ,整理得 ,(3分)
又 为锐角三角形,则 (4分)
所以 ,因此 .(5分)
(2)在 中,由正弦定理得 ,所以 . (6分)
所以 ,(7分)
因为 为锐角三角形,且 ,所以 ,(8分)
解得 .(9分)
故 ,(10分)
所以 .(11分)
因此线段 长度的取值范围 .(12分)
19.(1)证明见解析;
(2) .
【详解】(1)(1)延长三条侧棱交于点 .因为 所以 , 分别为中点,且
.
因为 ,所以 .
取 的中点 ,则 .(1分)
因为
所以 所以 .(2分)
,则 ,故 ,
即 .(3分)
因为 , , 平面 , 平面 ,(4分)
学科网(北京)股份有限公司所以 平面 .
又 平面 ,故平面 平面 .(5分)
(2)因为 ,所以 .
而 ,
所以 ,解得: .(6分)
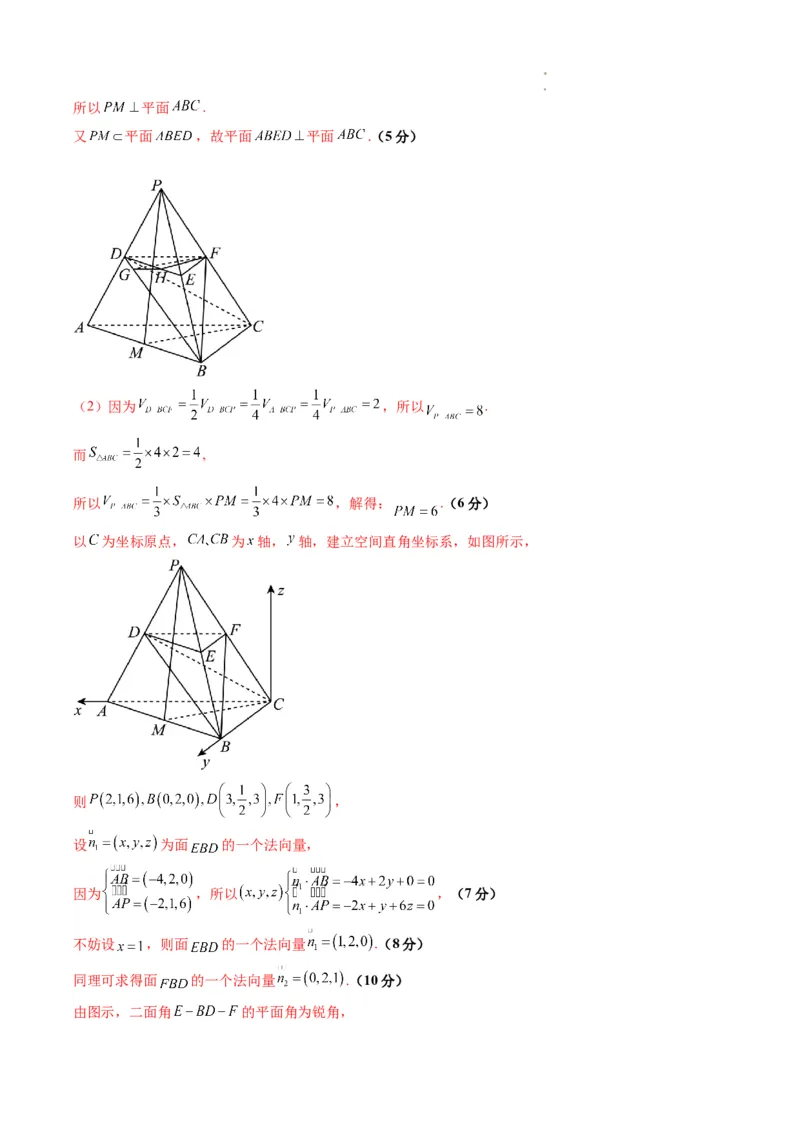
以 为坐标原点, 为 轴, 轴,建立空间直角坐标系,如图所示,
则 ,
设 为面 的一个法向量,
因为 ,所以 ,(7分)
不妨设 ,则面 的一个法向量 .(8分)
同理可求得面 的一个法向量 .(10分)
由图示,二面角 的平面角为锐角,
学科网(北京)股份有限公司所以 ,(11分)
所以二面角 的余弦值为 .(12分)
20.(1)甲、乙获得冠军的实力没有明显差别
(2)分布列见解析,
【详解】(1)解:设教师甲在三个项目中获胜的事件依次为 ,
则教师甲获得冠军的概率
,(1分)
由对立事件的概率公式,可得得 ,(2分)
所以 ,(3分)
解得 ,(4分)
因为 ,(5分)
所以甲、乙获得冠军的实力没有明显差别.(6分)
(2)解:根据题意知, 的可能取值为 ,(7分)
可得 ,
,
,
.
所以随机变量 的分布列为
0 15 30
0.15 0.425 0.35 0.075
(11分,其中算对一个概率给1分,没列表格不扣分)微信搜索“高中试卷君”公众号 领取押题卷联考卷
所以期望为 .(12分)
21.(1)
(2)点 在定直线 上
学科网(北京)股份有限公司【详解】(1)解:设 ,则 ,且 ,所以, (1分)
则 ,(2分)
故 ①,又 ②,
联立①②,解得 , ,(3分)
故椭圆 的方程为 .(4分)
(2)解:结论:点 在定直线上 . (5分没写结论扣1分)
由(1)得, 、 ,设 ,
设直线 的方程为 ,设点 、 ,
联立 ,整理得 ,(6分)
,
, (7分)
直线 的方程为 ,直线 的方程为 ,
所以, ,(8分)
可得
,(10分)
解得 ,(11分)
因此,点 在直线 上.(12分)
22.(1)答案见解析
(2) 微信搜索“高中试卷君”公众号 领取押题卷联考卷
学科网(北京)股份有限公司【详解】(1)因为函数 ,则 , ,
当 时, ,此时 单调递增,无极值;(1分)
当 时,令 ,得 ;令 ,得 ,所以 在 上单调递增,在
上单调递减,所以 ,无极小值;(2分)
当 时,令 ,得 ;令 ,得 ,所以 在 上单调递减,在
上单调递增,所以 ,无极大值.(3分)
综上,当 时,函数 无极值;当 时, ,无极小值;当 时,
,无极大值.(4分)
(2)由 及 ,得 , ,
即 .(5分)
设 , ,
当 时,需 .由 ,得 ,(6分)
,设 ,
则 , ,
当 时,由 ,得 ,因为 ,所以 ,
所以当 时,则 , 即 为增函数,则 ,
为增函数,则 ,所以 符合条件.(10分)
当 时,由 ,得 ,
因为 ,所以 ,所以当 时, ,则 即 为减函数,则
, 为减函数,则 ,不符合条件.(11分)
学科网(北京)股份有限公司综上所述,m的取值范围为 .(12分)
学科网(北京)股份有限公司学科网(北京)股份有限公司