文档内容
2022 年广西桂林市中考数学试卷
一、选择题(共10小题,每小题3分,共30分.在每小题给出的四个选项中只有一项是符
合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑)
1.(3分)在东西向的马路上,把出发点记为0,向东与向西意义相反.若把向东走2km记
做“+2km”,那么向西走1km应记做( )
A.﹣2km B.﹣1km C.1km D.+2km
2.(3分)﹣3的绝对值是( )
A.3 B. C.0 D.﹣3
3.(3分)如图,直线a,b被直线c所截,且a∥b,若∠1=60°,则∠2的度数是( )
A.70° B.60° C.50° D.40°
4.(3分)下列图形中,是中心对称图形的是( )
A.等边三角形 B.圆
C.正五边形 D.扇形
5.(3分)下列调查中,最适合采用全面调查的是( )
A.了解全国中学生的睡眠时间
B.了解某河流的水质情况
C.调查全班同学的视力情况
第1页(共22页)
学科网(北京)股份有限公司D.了解一批灯泡的使用寿命
6.(3分)2022年6月5日,中华民族再探苍穹,神舟十四号载人飞船通过长征二号 F运载
火箭成功升空,并与天和核心舱顺利进行接轨.据报道,长征二号 F运载火箭的重量大约
是500000kg.将数据500000用科学记数法表示,结果是( )
A.5×105 B.5×106 C.0.5×105 D.0.5×106
7.(3分)把不等式x﹣1<2的解集在数轴上表示出来,正确的是( )
A.
B.
C.
D.
8.(3分)化简 的结果是( )
A.2 B.3 C.2 D.2
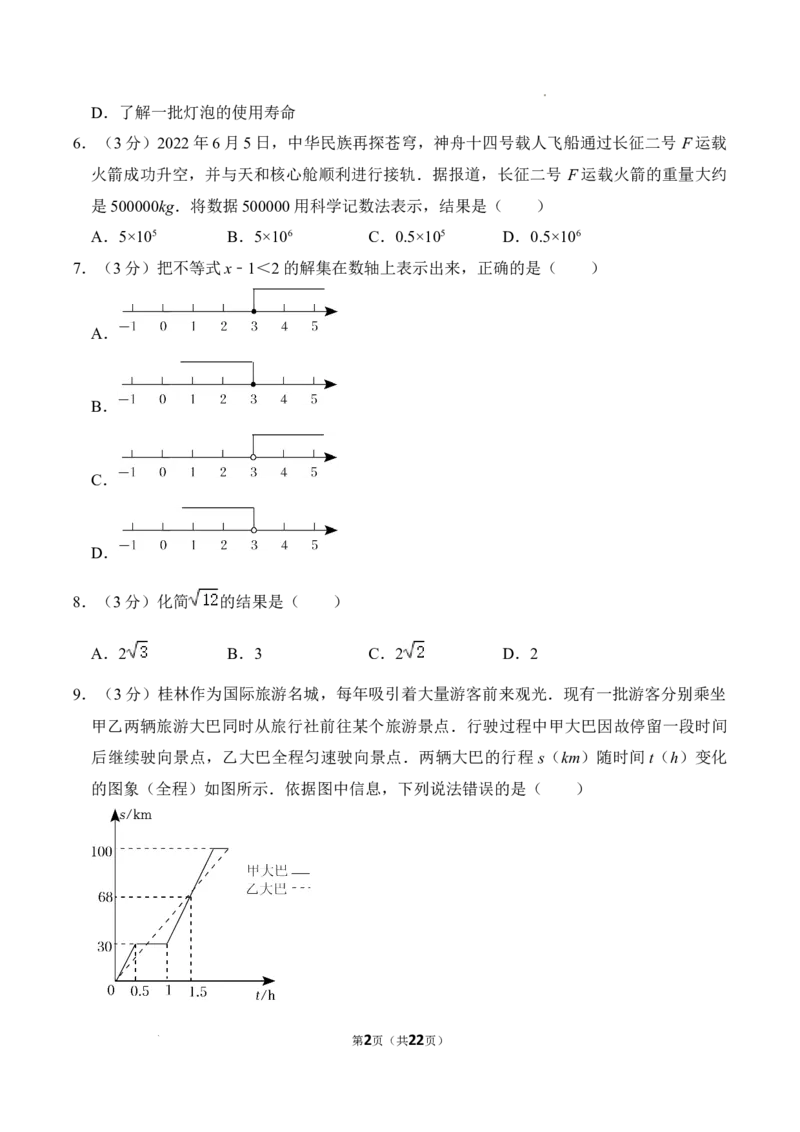
9.(3分)桂林作为国际旅游名城,每年吸引着大量游客前来观光.现有一批游客分别乘坐
甲乙两辆旅游大巴同时从旅行社前往某个旅游景点.行驶过程中甲大巴因故停留一段时间
后继续驶向景点,乙大巴全程匀速驶向景点.两辆大巴的行程 s(km)随时间t(h)变化
的图象(全程)如图所示.依据图中信息,下列说法错误的是( )
第2页(共22页)
学科网(北京)股份有限公司A.甲大巴比乙大巴先到达景点
B.甲大巴中途停留了0.5h
C.甲大巴停留后用1.5h追上乙大巴
D.甲大巴停留前的平均速度是60km/h
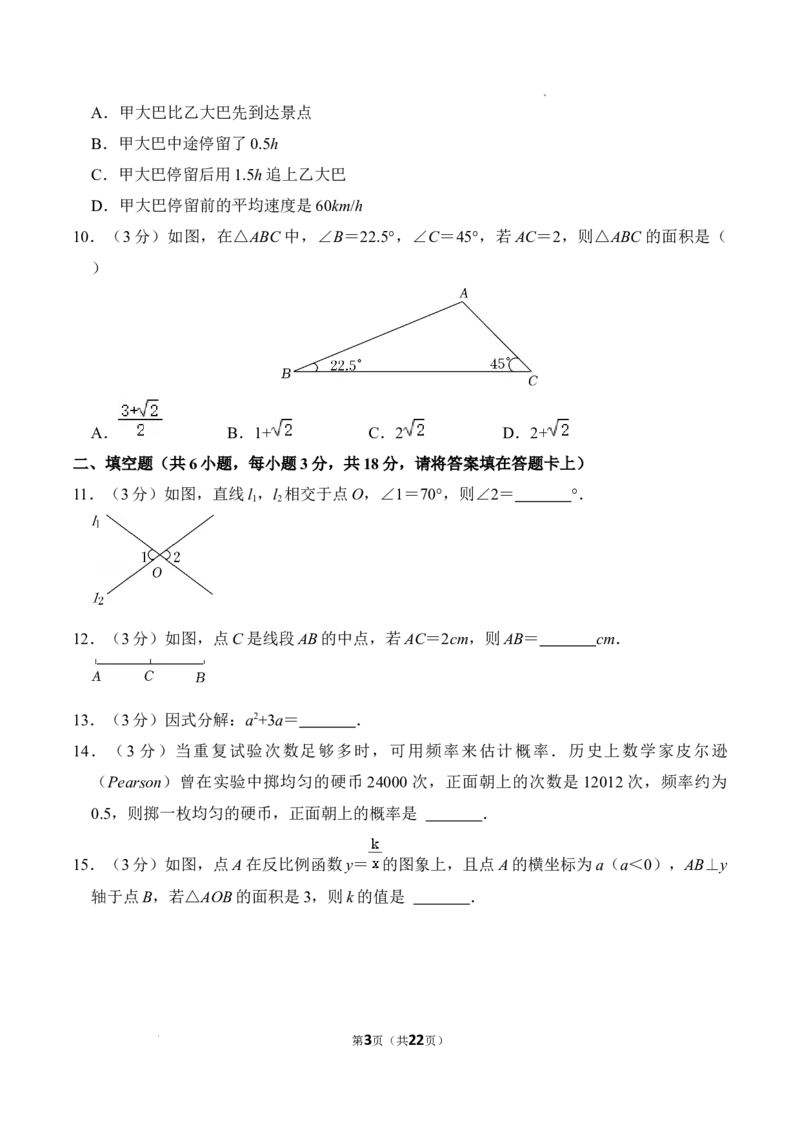
10.(3分)如图,在△ABC中,∠B=22.5°,∠C=45°,若AC=2,则△ABC的面积是(
)
A. B.1+ C.2 D.2+
二、填空题(共6小题,每小题3分,共18分,请将答案填在答题卡上)
11.(3分)如图,直线l ,l 相交于点O,∠1=70°,则∠2= °.
1 2
12.(3分)如图,点C是线段AB的中点,若AC=2cm,则AB= cm.
13.(3分)因式分解:a2+3a= .
14.(3 分)当重复试验次数足够多时,可用频率来估计概率.历史上数学家皮尔逊
(Pearson)曾在实验中掷均匀的硬币 24000次,正面朝上的次数是 12012次,频率约为
0.5,则掷一枚均匀的硬币,正面朝上的概率是 .
15.(3分)如图,点A在反比例函数y= 的图象上,且点A的横坐标为a(a<0),AB⊥y
轴于点B,若△AOB的面积是3,则k的值是 .
第3页(共22页)
学科网(北京)股份有限公司第15题图 第16题图
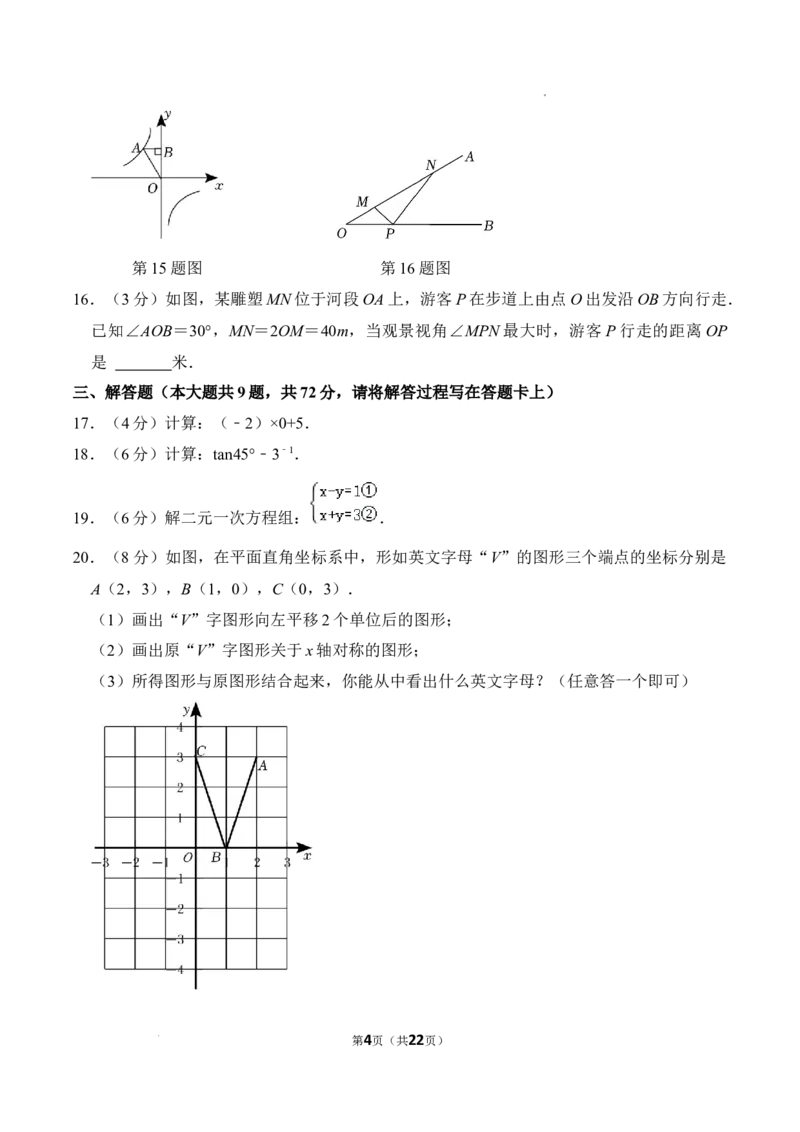
16.(3分)如图,某雕塑MN位于河段OA上,游客P在步道上由点O出发沿OB方向行走.
已知∠AOB=30°,MN=2OM=40m,当观景视角∠MPN最大时,游客P行走的距离OP
是 米.
三、解答题(本大题共9题,共72分,请将解答过程写在答题卡上)
17.(4分)计算:(﹣2)×0+5.
18.(6分)计算:tan45°﹣3﹣1.
19.(6分)解二元一次方程组: .
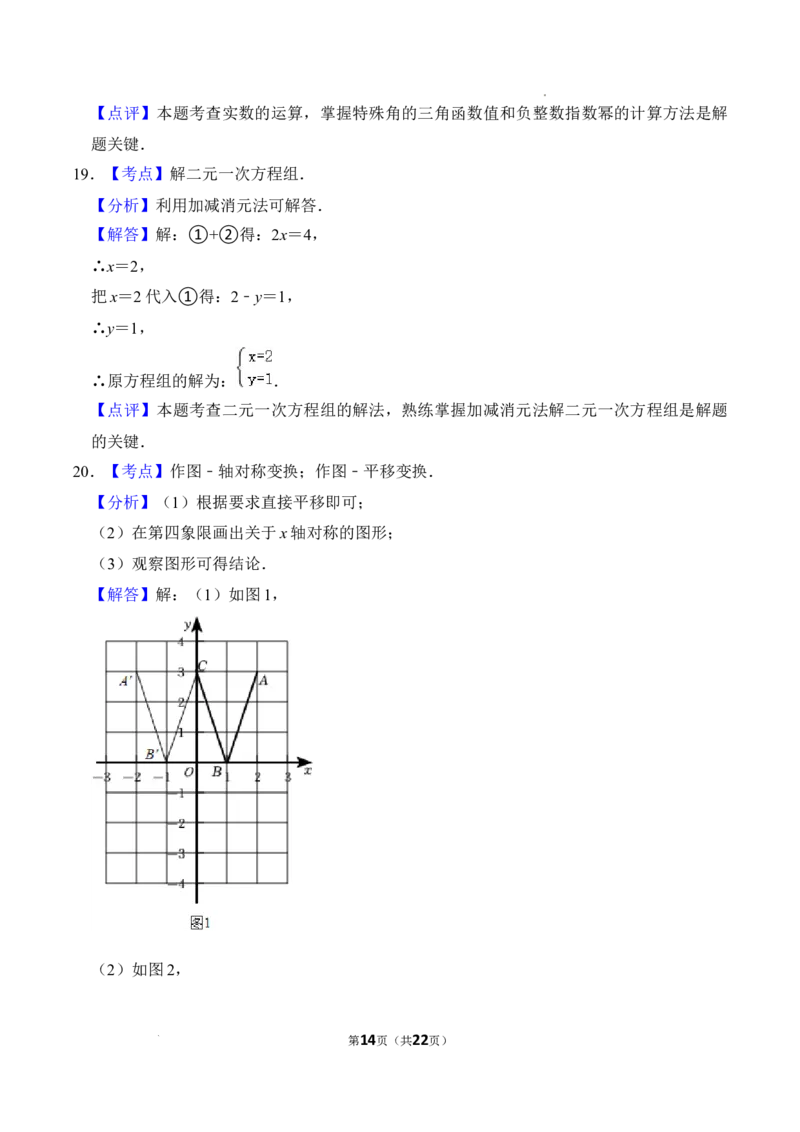
20.(8分)如图,在平面直角坐标系中,形如英文字母“V”的图形三个端点的坐标分别是
A(2,3),B(1,0),C(0,3).
(1)画出“V”字图形向左平移2个单位后的图形;
(2)画出原“V”字图形关于x轴对称的图形;
(3)所得图形与原图形结合起来,你能从中看出什么英文字母?(任意答一个即可)
第4页(共22页)
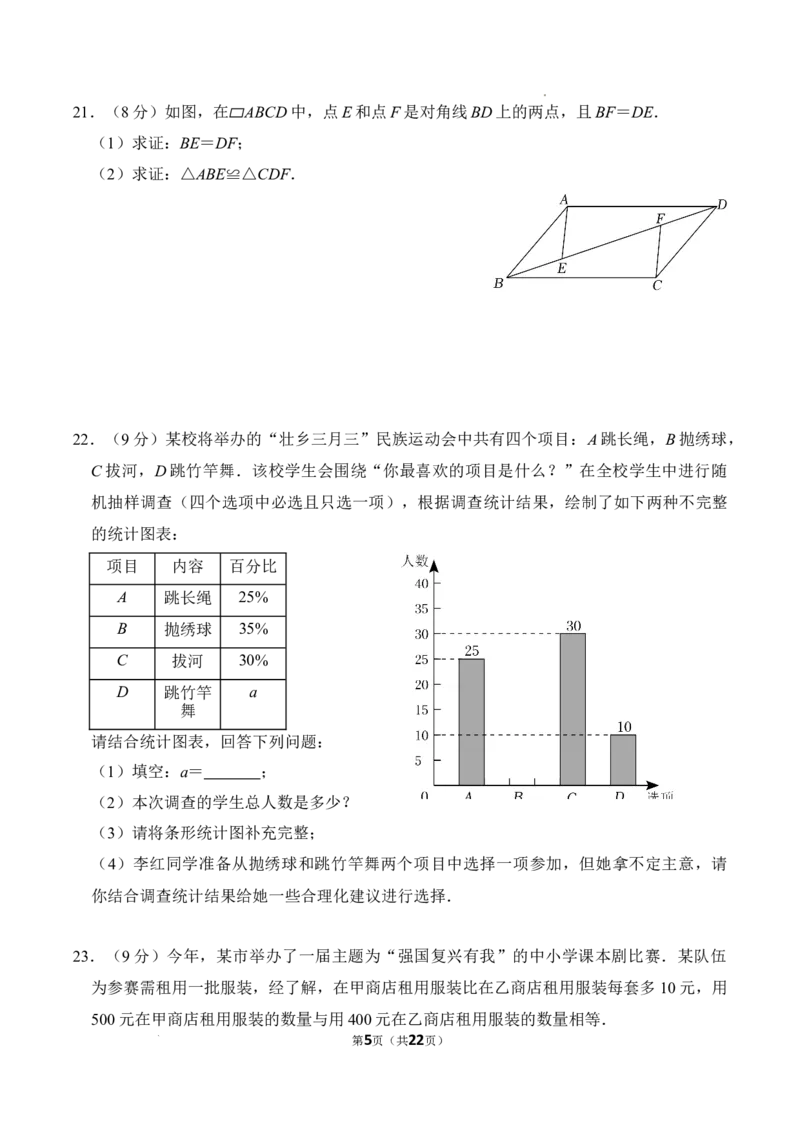
学科网(北京)股份有限公司21.(8分)如图,在 ABCD中,点E和点F是对角线BD上的两点,且BF=DE.
(1)求证:BE=DF;
▱
(2)求证:△ABE≌△CDF.
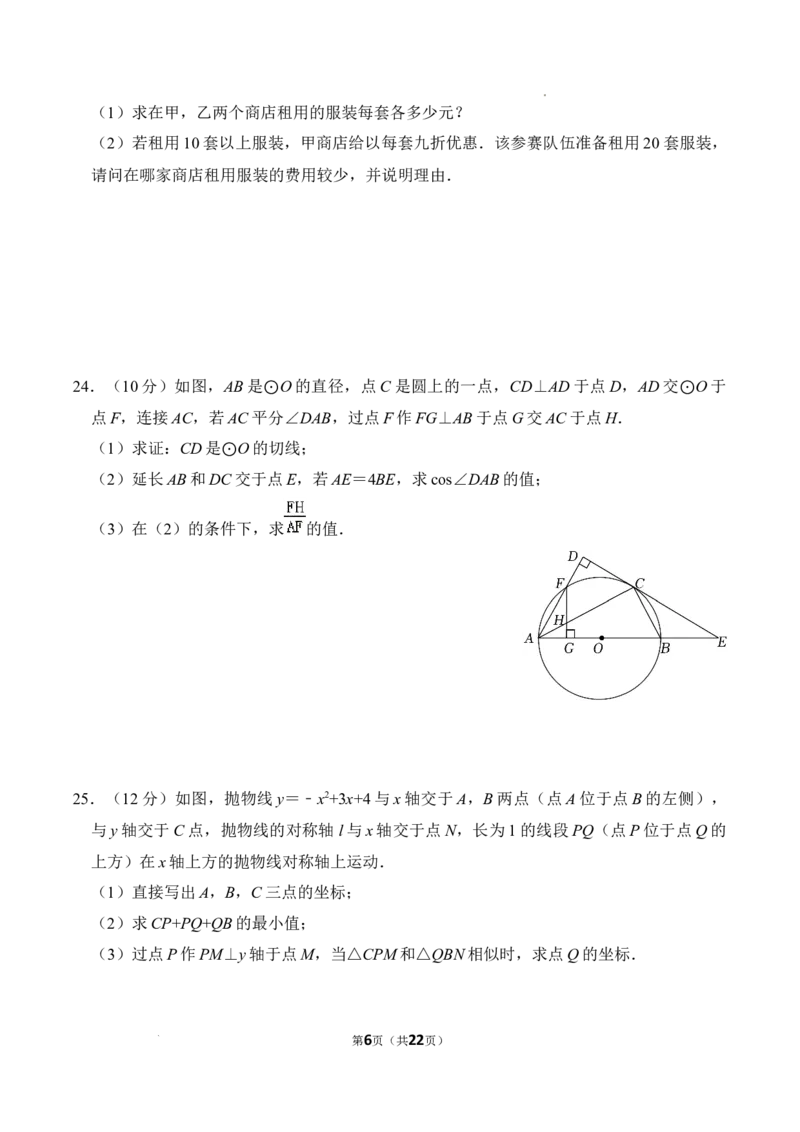
22.(9分)某校将举办的“壮乡三月三”民族运动会中共有四个项目:A跳长绳,B抛绣球,
C拔河,D跳竹竿舞.该校学生会围绕“你最喜欢的项目是什么?”在全校学生中进行随
机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了如下两种不完整
的统计图表:
项目 内容 百分比
A 跳长绳 25%
B 抛绣球 35%
C 拔河 30%
D 跳竹竿 a
舞
请结合统计图表,回答下列问题:
(1)填空:a= ;
(2)本次调查的学生总人数是多少?
(3)请将条形统计图补充完整;
(4)李红同学准备从抛绣球和跳竹竿舞两个项目中选择一项参加,但她拿不定主意,请
你结合调查统计结果给她一些合理化建议进行选择.
23.(9分)今年,某市举办了一届主题为“强国复兴有我”的中小学课本剧比赛.某队伍
为参赛需租用一批服装,经了解,在甲商店租用服装比在乙商店租用服装每套多 10元,用
500元在甲商店租用服装的数量与用400元在乙商店租用服装的数量相等.
第5页(共22页)
学科网(北京)股份有限公司(1)求在甲,乙两个商店租用的服装每套各多少元?
(2)若租用10套以上服装,甲商店给以每套九折优惠.该参赛队伍准备租用20套服装,
请问在哪家商店租用服装的费用较少,并说明理由.
24.(10分)如图,AB是 O的直径,点C是圆上的一点,CD⊥AD于点D,AD交 O于
点F,连接AC,若AC平分∠DAB,过点F作FG⊥AB于点G交AC于点H.
⊙ ⊙
(1)求证:CD是 O的切线;
(2)延长AB和DC交于点E,若AE=4BE,求cos∠DAB的值;
⊙
(3)在(2)的条件下,求 的值.
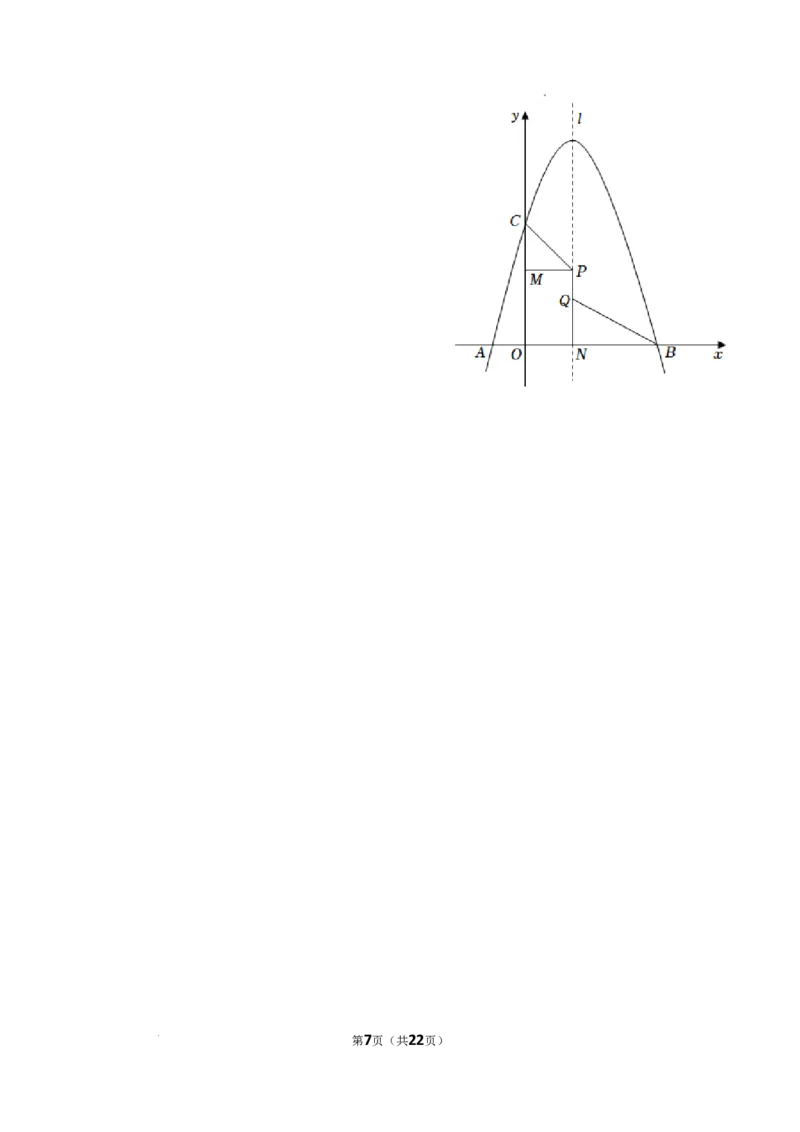
25.(12分)如图,抛物线y=﹣x2+3x+4与x轴交于A,B两点(点A位于点B的左侧),
与y轴交于C点,抛物线的对称轴l与x轴交于点N,长为1的线段PQ(点P位于点Q的
上方)在x轴上方的抛物线对称轴上运动.
(1)直接写出A,B,C三点的坐标;
(2)求CP+PQ+QB的最小值;
(3)过点P作PM⊥y轴于点M,当△CPM和△QBN相似时,求点Q的坐标.
第6页(共22页)
学科网(北京)股份有限公司第7页(共22页)
学科网(北京)股份有限公司2022 年广西桂林市中考数学试卷
参考答案与试题解析
一、选择题(共10小题,每小题3分,共30分.在每小题给出的四个选项中只有一项是符
合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑)
1.【考点】正数和负数.菁优网版权所有
【分析】在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.
【解答】解:若把向东走2km记做“+2km”,那么向西走1km应记做﹣1km.
故选:B.
【点评】本题主要考查正数与负数,理解正数与负数的意义是解题的关键.
2.【考点】绝对值.菁优网版权所有
【分析】利用绝对值的意义解答即可.
【解答】解:﹣3的绝对值是3.
故选:A.
【点评】本题主要考查了绝对值的意义,正确利用绝对值的意义是解题的关键.
3.【考点】平行线的性质.菁优网版权所有
【分析】根据平行线的性质可以得到∠1=∠2,然后根据∠1的度数,即可得到∠2的度数.
【解答】解:∵a∥b,
∴∠1=∠2,
∵∠1=60°,
∴∠2=60°,
故选:B.
【点评】本题考查平行线的性质,解答本题的关键是明确两直线平行,同位角相等.
4.【考点】中心对称图形.菁优网版权所有
【分析】根据中心对称图形的定义进行判断,即可得出答案.把一个图形绕某一点旋转
180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这
个点叫做对称中心.
【解答】解:选项A、C、D均不能找到这样的一个点,使图形绕某一点旋转180度后和原
图形完全重合,所以不是中心对称图形,
第8页(共22页)
学科网(北京)股份有限公司选项B能找到这样的一个点,使图形绕某一点旋转 180度后和原图形完全重合,所以是中
心对称图形,
故选:B.
【点评】本题考查中心对称图形的概念:在同一平面内,如果把一个图形绕某一点旋转
180度,旋转后的图形能和原图形完全重合,那么这个图形就叫做中心对称图形.
5.【考点】全面调查与抽样调查.菁优网版权所有
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查
得到的调查结果比较近似解答.
【解答】解:A.了解全国中学生的睡眠时间,适合进行抽样调查,故本选项不合题意;
B.了解某河流的水质情况,适合进行抽样调查,故本选项不合题意;
C.调查全班同学的视力情况,适合进行全面调查,故本选项符合题意;
D.了解一批灯泡的使用寿命,适合进行抽样调查,故本选项不合题意;
故选:C.
【点评】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考
查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意
义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普
查.
6.【考点】科学记数法—表示较大的数.菁优网版权所有
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值
时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:数据500000用科学记数法表示为5×105.
故选:A.
【点评】此题考查科学记数法的表示方法,表示时关键要正确确定a的值以及n的值.
7.【考点】解一元一次不等式;在数轴上表示不等式的解集.菁优网版权所有
【分析】先移项,合并同类项,把不等式的解集在数轴上表示出来即可.
【解答】解:移项得,x<1+2,
得,x<3.
在数轴上表示为:
第9页(共22页)
学科网(北京)股份有限公司故选:D.
【点评】本题考查了解一元一次不等式,解不等式的基本步骤是关键,尤其需要注意不等
式两边都乘以或除以同一个负数,不等号方向要改变.
8.【考点】算术平方根.菁优网版权所有
【分析】将被开方数12写成平方数4与3的乘积,再将4开出来为2,易知化简结果为2
.
【解答】解: =2 ,
故选:A.
【点评】本题考查了二次根式的化简,关键在于被开方数要写成平方数乘积的形式再进行
化简.
9.【考点】一次函数的应用.菁优网版权所有
【分析】根据函数图象中的数据,可以判断各个选项中的结论是否成立,从而可以解答本
题.
【解答】解:由图象可得,
甲大巴比乙大巴先到达景点,故选项A正确,不符合题意;
甲大巴中途停留了1﹣0.5=0.5(h),故选项B正确,不符合题意;
甲大巴停留后用1.5﹣1=0.5h追上乙大巴,故选项C错误,符合题意;
甲大巴停留前的平均速度是30÷0.5=60(km/h),故选项D正确,不符合题意;
故选:C.
【点评】本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解
答.
10.【考点】三角形的面积;等腰三角形的判定与性质.菁优网版权所有
【分析】如图,过点 A 作 AD⊥AC 于 A,交 BC 于 D,过点 A 作 AE⊥BC 于 E,先证明
△ADC是等腰直角三角形,得AD=AC=2,∠ADC=45°,CD= AC=2 ,再证明AD
=BD,计算AE和BC的长,根据三角形的面积公式可解答.
【解答】解:如图,过点A作AD⊥AC于A,交BC于D,过点A作AE⊥BC于E,
第10页(共22页)
学科网(北京)股份有限公司∵∠C=45°,
∴△ADC是等腰直角三角形,
∴AD=AC=2,∠ADC=45°,CD= AC=2 ,
∵∠ADC=∠B+∠BAD,∠B=22.5°,
∴∠DAB=22.5°,
∴∠B=∠DAB,
∴AD=BD=2,
∵AD=AC,AE⊥CD,
∴DE=CE,
∴AE= CD= ,
∴△ABC的面积= •BC•AE= × ×(2+2 )=2+ .
故选:D.
【点评】本题考查的是勾股定理,等腰直角三角形的性质,三角形的面积,熟知掌握等腰
三角形的性质是解本题的关键.
二、填空题(共6小题,每小题3分,共18分,请将答案填在答题卡上)
11.【考点】对顶角、邻补角.菁优网版权所有
【分析】根据对顶角的性质解答即可.
【解答】解:∵∠1和∠2是一对顶角,
∴∠2=∠1=70°.
故答案为:70.
【点评】本题主要考查了对顶角,熟练掌握对顶角相等是解答本题的关键.
12.【考点】两点间的距离.菁优网版权所有
【分析】根据中点的定义可得AB=2AC=4cm.
【解答】解:根据中点的定义可得:AB=2AC=2×2=4cm,
第11页(共22页)
学科网(北京)股份有限公司故答案为:4.
【点评】本题主要考查中点的定义,熟知中点的定义是解题关键.
13.【考点】因式分解﹣提公因式法.菁优网版权所有
【分析】直接提取公因式a,进而得出答案.
【解答】解:a2+3a=a(a+3).
故答案为:a(a+3).
【点评】此题主要考查了提取公因式法分解因式,正确提取公因式是解题关键.
14.【考点】利用频率估计概率;数学常识.菁优网版权所有
【分析】根据大量重复试验中事件发生的频率可以表示概率解答即可.
【解答】解:当重复试验次数足够多时,频率逐渐稳定在0.5左右,
∴掷一枚均匀的硬币,正面朝上的概率是0.5.
故答案为:0.5.
【点评】本题主要考查了用频率估计概率,熟练掌握大量重复试验中事件发生的频率可以
表示概率是解答本题的关键.
15.【考点】反比例函数系数k的几何意义;反比例函数图象上点的坐标特征.菁优网版权
所有
【分析】根据题意和反比例函数的性质,可以得到k的值.
【解答】解:设点A的坐标为(a, ),
∵△AOB的面积是3,
∴ =3,
解得k=﹣6,
故答案为:﹣6.
【点评】本题考查反比例函数系数k的几何意义、反比例函数图象上点的坐标特征,解答
本题的关键是找出k与三角形面积的关系.
16.【考点】解直角三角形的应用;勾股定理;切线的性质.菁优网版权所有
【分析】先证OB是 F的切线,切点为E,当点P与点E重合时,观景视角∠MPN最大,
由直角三角形的性质可求解.
⊙
【解答】解:如图,取MN的中点F,过点F作FE⊥OB于E,以直径MN作 F,
第12页(共22页) ⊙
学科网(北京)股份有限公司∵MN=2OM=40m,点F是MN的中点,
∴MF=FN=20m,OF=40m,
∵∠AOB=30°,EF⊥OB,
∴EF=20m,OE= EF=20 m,
∴EF=MF,
又∵EF⊥OB,
∴OB是 F的切线,切点为E,
∴当点P与点E重合时,观景视角∠MPN最大,
⊙
此时OP=20 m,
故答案为:20 .
【点评】本题考查了解直角三角形的应用,切线的判定,直角三角形的性质,证明 OB是
F的切线是解题的关键.
三、解答题(本大题共9题,共72分,请将解答过程写在答题卡上)
⊙
17.【考点】有理数的混合运算.菁优网版权所有
【分析】根据有理数的混合运算顺序,先计算乘法,再计算加法即可.
【解答】解:(﹣2)×0+5
=0+5
=5.
【点评】本题考查了有理数的混合运算,掌握相关运算法则是解答本题的关键.
18.【考点】实数的运算;负整数指数幂;特殊角的三角函数值.菁优网版权所有
【分析】根据特殊角的三角函数值、负整数指数幂的计算方法分别化简,再计算即可.
【解答】解:原式=1﹣
= .
第13页(共22页)
学科网(北京)股份有限公司【点评】本题考查实数的运算,掌握特殊角的三角函数值和负整数指数幂的计算方法是解
题关键.
19.【考点】解二元一次方程组.菁优网版权所有
【分析】利用加减消元法可解答.
【解答】解:①+②得:2x=4,
∴x=2,
把x=2代入①得:2﹣y=1,
∴y=1,
∴原方程组的解为: .
【点评】本题考查二元一次方程组的解法,熟练掌握加减消元法解二元一次方程组是解题
的关键.
20.【考点】作图﹣轴对称变换;作图﹣平移变换.菁优网版权所有
【分析】(1)根据要求直接平移即可;
(2)在第四象限画出关于x轴对称的图形;
(3)观察图形可得结论.
【解答】解:(1)如图1,
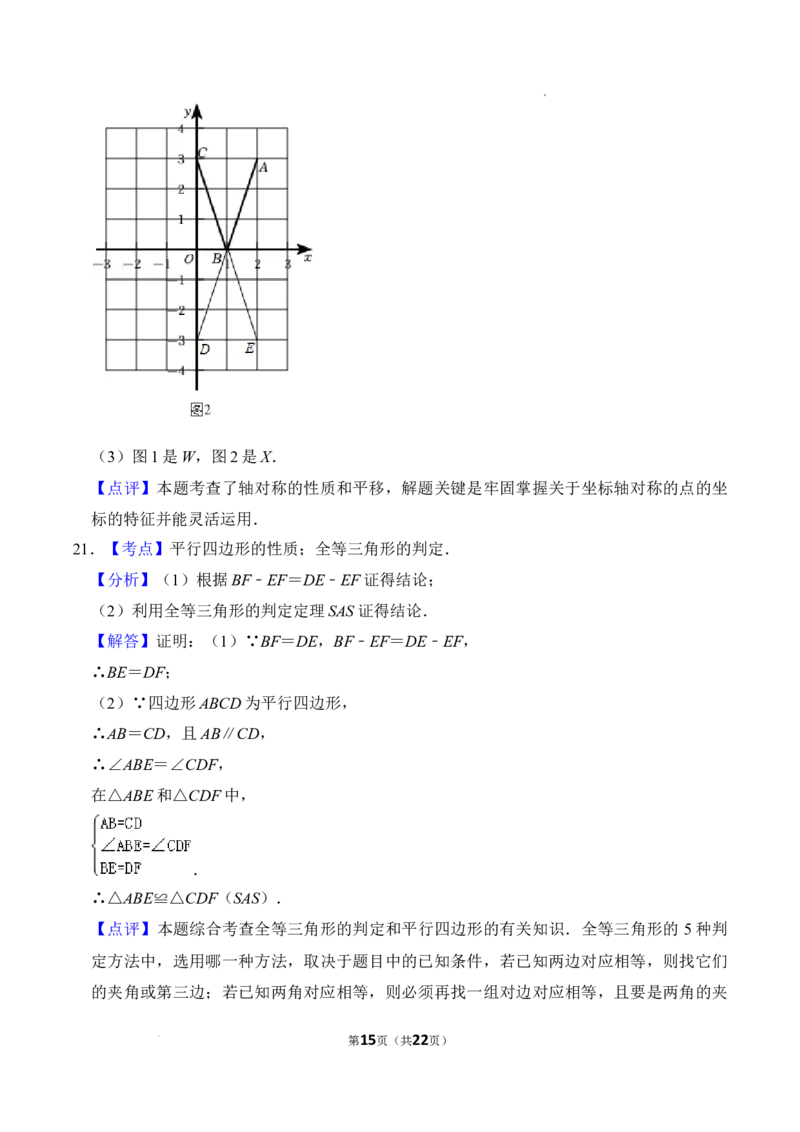
(2)如图2,
第14页(共22页)
学科网(北京)股份有限公司(3)图1是W,图2是X.
【点评】本题考查了轴对称的性质和平移,解题关键是牢固掌握关于坐标轴对称的点的坐
标的特征并能灵活运用.
21.【考点】平行四边形的性质;全等三角形的判定.菁优网版权所有
【分析】(1)根据BF﹣EF=DE﹣EF证得结论;
(2)利用全等三角形的判定定理SAS证得结论.
【解答】证明:(1)∵BF=DE,BF﹣EF=DE﹣EF,
∴BE=DF;
(2)∵四边形ABCD为平行四边形,
∴AB=CD,且AB∥CD,
∴∠ABE=∠CDF,
在△ABE和△CDF中,
.
∴△ABE≌△CDF(SAS).
【点评】本题综合考查全等三角形的判定和平行四边形的有关知识.全等三角形的 5种判
定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们
的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹
第15页(共22页)
学科网(北京)股份有限公司边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.
22.【考点】条形统计图;调查收集数据的过程与方法;统计表.菁优网版权所有
【分析】(1)用1分别减去A、C、D类的百分比即可得到a的值;
(2)用A类学生数除以它所占的百分比即可得到总人数;
(3)用35%乘以总人数得到B类人数,再补全条形统计图画树状图;
(4)根据选择两个项目的人数得出答案.
【解答】解:(1)a=1﹣35%﹣25%﹣30%=10%,
故答案为:10%;
(2)25÷25%=100(人),
答:本次调查的学生总人数是100人;
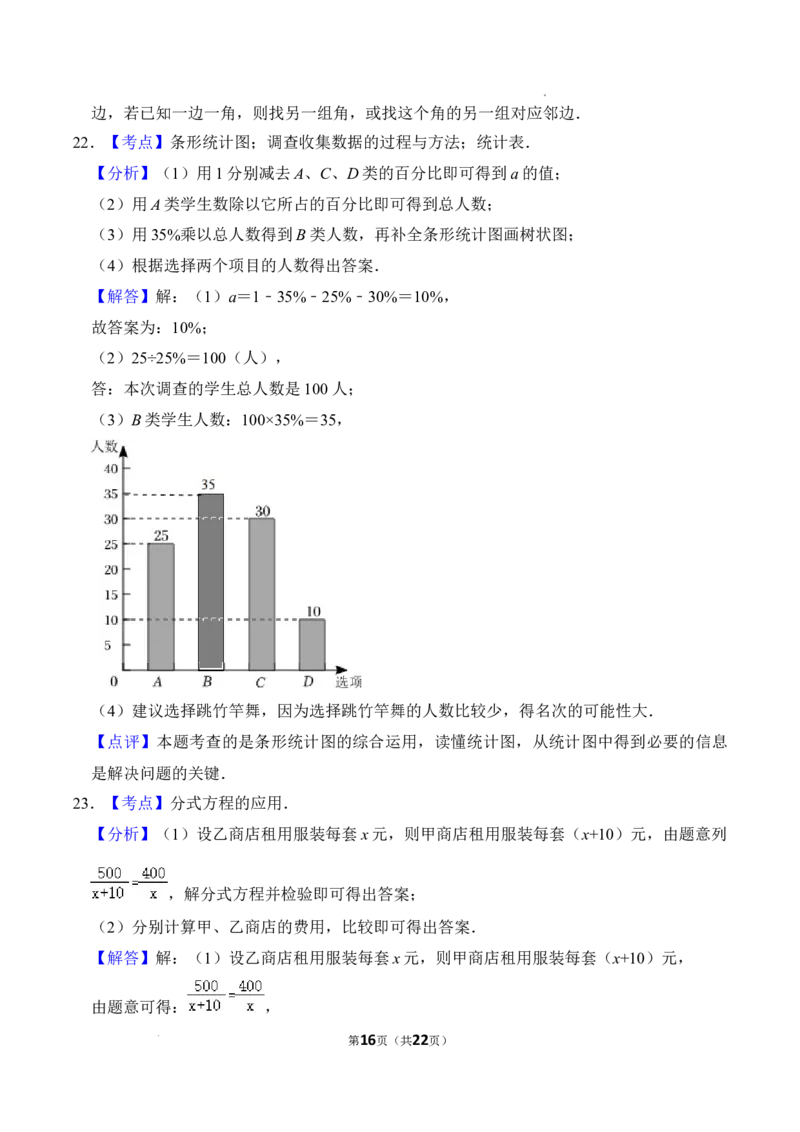
(3)B类学生人数:100×35%=35,
(4)建议选择跳竹竿舞,因为选择跳竹竿舞的人数比较少,得名次的可能性大.
【点评】本题考查的是条形统计图的综合运用,读懂统计图,从统计图中得到必要的信息
是解决问题的关键.
23.【考点】分式方程的应用.菁优网版权所有
【分析】(1)设乙商店租用服装每套x元,则甲商店租用服装每套(x+10)元,由题意列
,解分式方程并检验即可得出答案;
(2)分别计算甲、乙商店的费用,比较即可得出答案.
【解答】解:(1)设乙商店租用服装每套x元,则甲商店租用服装每套(x+10)元,
由题意可得: ,
第16页(共22页)
学科网(北京)股份有限公司解得:x=40,
经检验,x=40是该分式方程的解,并符合题意,
∴x+10=50,
∴甲,乙两个商店租用的服装每套各50元,40元.
(2)该参赛队伍准备租用20套服装时,
甲商店的费用为:50×20×0.9=900(元),
乙商店的费用为:40×20=800(元),
∵900>800,
∴乙商店租用服装的费用较少.
【点评】本题考查了分式方程的应用,根据题意列出分式方程是解决问题的关键.
24.【考点】圆的综合题.菁优网版权所有
【分析】(1)如图1,连接OC,根据等腰三角形的性质得到∠CAO=∠ACO,由角平分
线的定义得到∠DAC=∠OAC,等量代换得到∠DAC=∠ACO,根据平行线的判定定理得
到AD∥OC,由平行线的性质即可得到结论;
(2)设BE=x,则AB=3x,根据平行线的性质得∠COE=∠DAB,由三角函数定义可得
结论;
(3)证明△AHF∽△ACE,列比例式可解答.
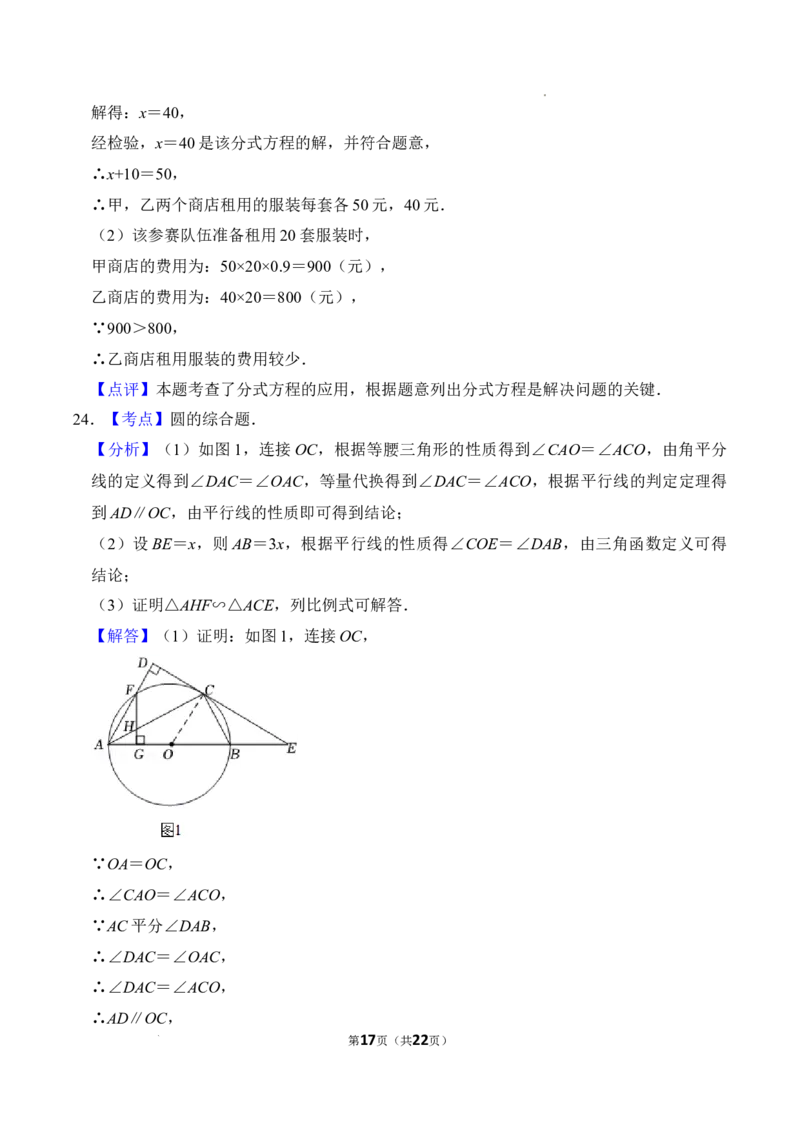
【解答】(1)证明:如图1,连接OC,
∵OA=OC,
∴∠CAO=∠ACO,
∵AC平分∠DAB,
∴∠DAC=∠OAC,
∴∠DAC=∠ACO,
∴AD∥OC,
第17页(共22页)
学科网(北京)股份有限公司∵CD⊥AD,
∴OC⊥CD,
∵OC是 O的半径,
∴CD是 O的切线;
⊙
(2)解:∵AE=4BE,OA=OB,
⊙
设BE=x,则AB=3x,
∴OC=OB=1.5x,
∵AD∥OC,
∴∠COE=∠DAB,
∴cos∠DAB=cos∠COE= = = ;
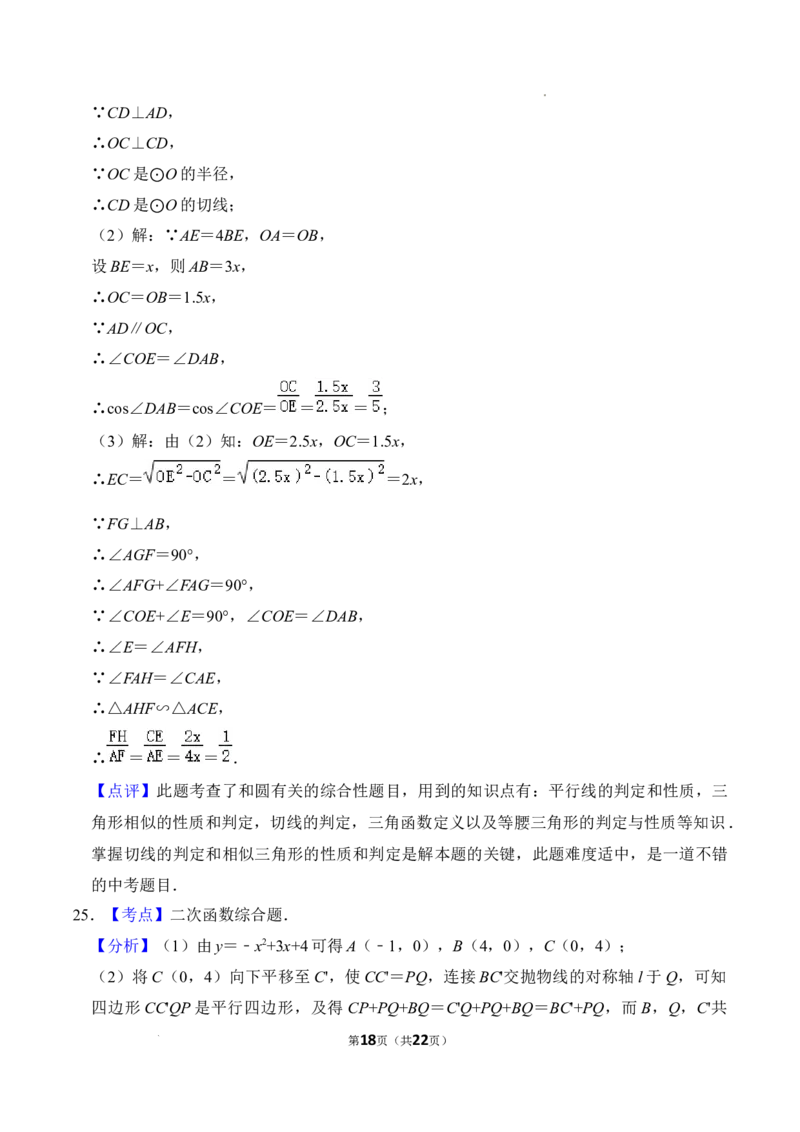
(3)解:由(2)知:OE=2.5x,OC=1.5x,
∴EC= = =2x,
∵FG⊥AB,
∴∠AGF=90°,
∴∠AFG+∠FAG=90°,
∵∠COE+∠E=90°,∠COE=∠DAB,
∴∠E=∠AFH,
∵∠FAH=∠CAE,
∴△AHF∽△ACE,
∴ = = = .
【点评】此题考查了和圆有关的综合性题目,用到的知识点有:平行线的判定和性质,三
角形相似的性质和判定,切线的判定,三角函数定义以及等腰三角形的判定与性质等知识.
掌握切线的判定和相似三角形的性质和判定是解本题的关键,此题难度适中,是一道不错
的中考题目.
25.【考点】二次函数综合题.菁优网版权所有
【分析】(1)由y=﹣x2+3x+4可得A(﹣1,0),B(4,0),C(0,4);
(2)将C(0,4)向下平移至C',使CC'=PQ,连接BC'交抛物线的对称轴l于Q,可知
四边形CC'QP是平行四边形,及得 CP+PQ+BQ=C'Q+PQ+BQ=BC'+PQ,而B,Q,C'共
第18页(共22页)
学科网(北京)股份有限公司线,故此时 CP+PQ+BQ 最小,最小值为 BC'+PQ 的值,由勾股定理可得 BC'=5,即得
CP+PQ+BQ最小值为6;
(3)由在y=﹣x2+3x+4得抛物线对称轴为直线x=﹣ = ,设Q( ,t),则Q( ,
t+1),M(0,t+1),N( ,0),知BN= ,QN=t,PM= ,CM=|t﹣3|,①当
= 时, = ,可解得Q( , )或( , );②当 = 时, =
,得Q( , ).
【解答】解:(1)在y=﹣x2+3x+4中,令x=0得y=4,令y=0得x=﹣1或x=4,
∴A(﹣1,0),B(4,0),C(0,4);
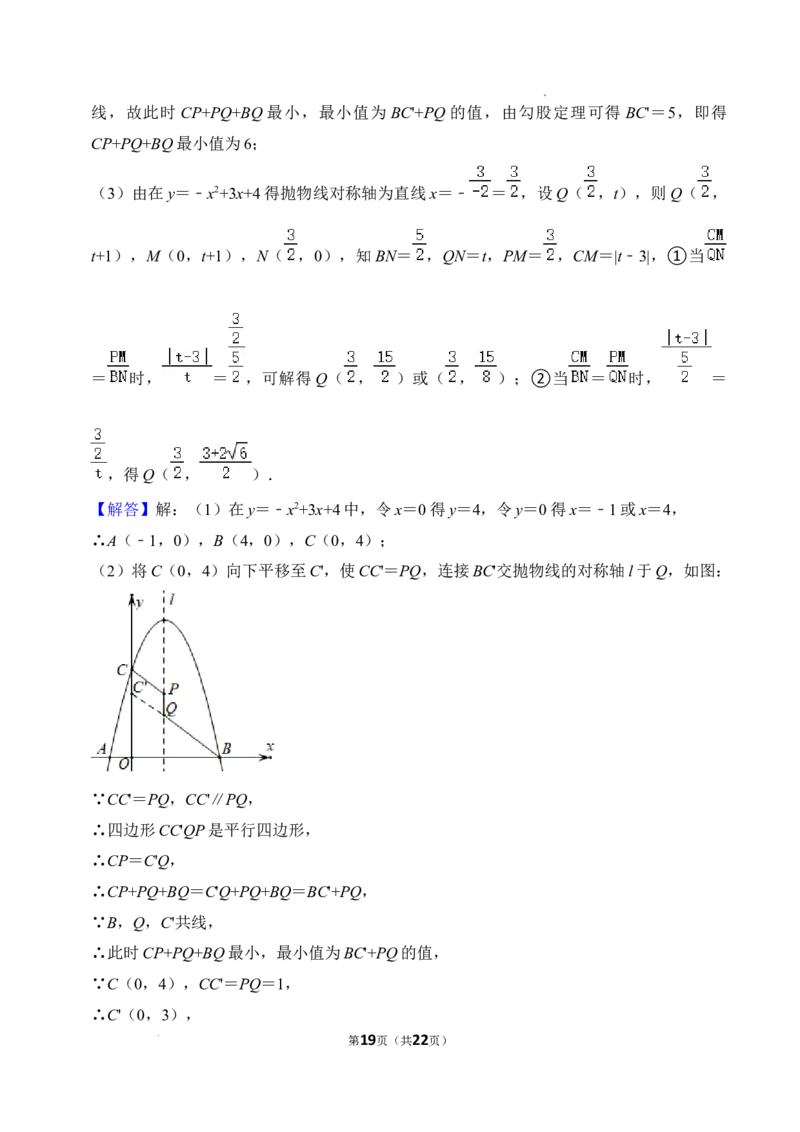
(2)将C(0,4)向下平移至C',使CC'=PQ,连接BC'交抛物线的对称轴l于Q,如图:
∵CC'=PQ,CC'∥PQ,
∴四边形CC'QP是平行四边形,
∴CP=C'Q,
∴CP+PQ+BQ=C'Q+PQ+BQ=BC'+PQ,
∵B,Q,C'共线,
∴此时CP+PQ+BQ最小,最小值为BC'+PQ的值,
∵C(0,4),CC'=PQ=1,
∴C'(0,3),
第19页(共22页)
学科网(北京)股份有限公司∵B(4,0),
∴BC'= =5,
∴BC'+PQ=5+1=6,
∴CP+PQ+BQ最小值为6;
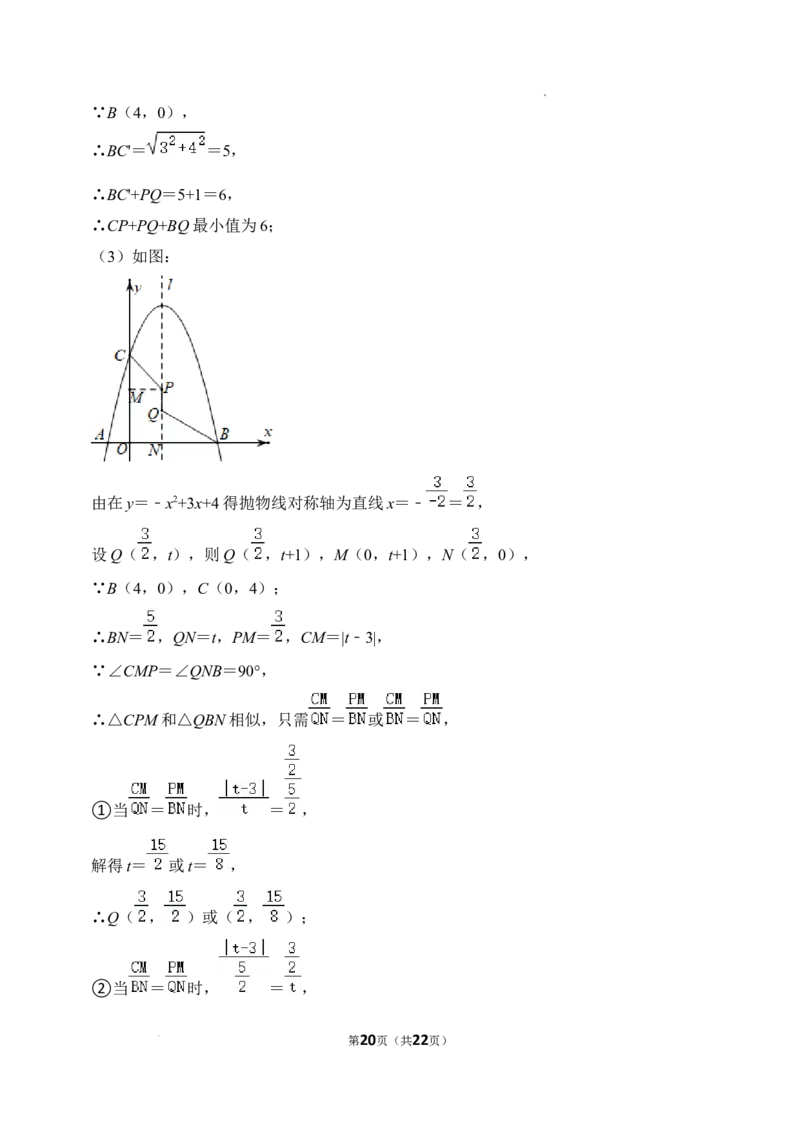
(3)如图:
由在y=﹣x2+3x+4得抛物线对称轴为直线x=﹣ = ,
设Q( ,t),则Q( ,t+1),M(0,t+1),N( ,0),
∵B(4,0),C(0,4);
∴BN= ,QN=t,PM= ,CM=|t﹣3|,
∵∠CMP=∠QNB=90°,
∴△CPM和△QBN相似,只需 = 或 = ,
①当 = 时, = ,
解得t= 或t= ,
∴Q( , )或( , );
②当 = 时, = ,
第20页(共22页)
学科网(北京)股份有限公司解得t= 或t= (舍去),
∴Q( , ),
综上所述,Q的坐标是( , )或( , )或( , ).
【点评】本题考查二次函数综合应用,涉及二次函数图象上点坐标的特征,线段和的最小
值,相似三角形的性质及应用等,解题的关键是分类讨论思想的应用.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2022/6/29
22:42:29;用户:容老师;邮箱:orFmNt4K95kSOOGZHgflQsK;学号:43745164
第21页(共22页)
学科网(北京)股份有限公司第22页(共22页)
学科网(北京)股份有限公司