文档内容
数 学
2024.5
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置。
2.选择题的作答:选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,
用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合
题目要求的.
1.设随机变量𝛽~𝑁(0,σ2),𝑃(𝛽<−2)=0.3,则函数𝑓(𝑥)=𝑥2−𝛽𝑥+1无零点的概率为
A. 0.3 B. 0.4 C. 0.6 D. 0.7
2.已知复数𝑧满足𝑧(2−i)=1+i,则𝑧的虚部是
3 3 3 3
A. − B. C. − i D. i
5 5 5 5
3.已知等差数列{𝑎 }的公差为𝑑,前𝑛项和为𝑆 .设甲:𝑑>0;乙:{𝑆 }是递增数列,则
𝑛 𝑛 𝑛
A. 甲是乙的充分条件但不是必要条件 B. 甲是乙的必要条件但不是充分条件
C. 甲是乙的充要条件 D. 甲既不是乙的充分条件也不是乙的必要条件
4.已知函数𝑓(𝑥)=𝑠𝑖𝑛𝑥 1+ 𝑚 是偶函数,则𝑚的值是
1−𝑒𝑥
A.-2 B. -1 C. 1 D. 2
5.已知双曲线𝐶:𝑥2 −𝑦2 =1(𝑎>0,𝑏>0)的左、右焦点分别为𝐹 ,𝐹 ,𝑂为原点,若以|𝐹 𝐹 |为直径的圆与
1 2 1 2
𝑎2 𝑏2
𝐶的渐近线的一个交点为𝑃,且|𝐹 𝑃|= 3|𝑂𝑃|,则𝐶的离心率为
1
A. 3 B. 2 C. 5 D. 6
6.已知𝑎>0,𝑏>0,且𝑎+𝑏=𝑎𝑏,则下列不等式成立的是
A. 𝑎+𝑏≤4 B. 𝑙𝑜𝑔 𝑎 + 𝑙𝑜𝑔 𝑏 >2 C. 𝑏𝑙𝑛𝑎>1 D. 𝑎+ 𝑏≥3
2 2
7.已知𝑠𝑖𝑛𝑥𝑐𝑜𝑠𝑦+𝑐𝑜𝑠𝑥𝑠𝑖𝑛𝑦= 1 ,𝑐𝑜𝑠2𝑥−𝑐𝑜𝑠2𝑦= 1 ,则𝑠𝑖𝑛(𝑥−𝑦)=
2 4
1 1 3 1
A. B. C.− D. −
2 4 4 4
8.已知函数𝑓(𝑥),𝑔(𝑥)均是定义在𝑅上的连续函数,𝑔′ (𝑥)为𝑔(𝑥)的导函数,且𝑓(𝑥+1)+𝑔(𝑥+2)=2,𝑓
(𝑥−1)−𝑔(4−𝑥)=4,若𝑓(𝑥)为奇函数,则下列说法正确的是
A.𝑓(𝑥)是周期函数 B.𝑦=𝑔(𝑥+2)为奇函数
C.𝑦=𝑔′(𝑥)关于𝑥=2对称 D.存在𝑥∈𝑁,使𝑓(𝑥)=2024
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全
部选对的得6分,部分选对的得部分分,有选错的得0分.
9.抛物线的弦与过弦的端点的两条切线所围成的三角形叫做阿基米德三角形.已知抛物线𝐶:𝑥2=8𝑦,
阿基米德三角形PAB,弦AB过𝐶的焦点𝐹,其中点𝐴在第一象限,则下列说法正确的是
学科网(北京)股份有限公司A.点𝑃的纵坐标为 2 B.𝐶的准线方程为𝑥=−2
−
C.若|𝐴𝐹|=8,则𝐴𝐵的斜率为 3 D.∆𝑃𝐴𝐵面积的最小值为16
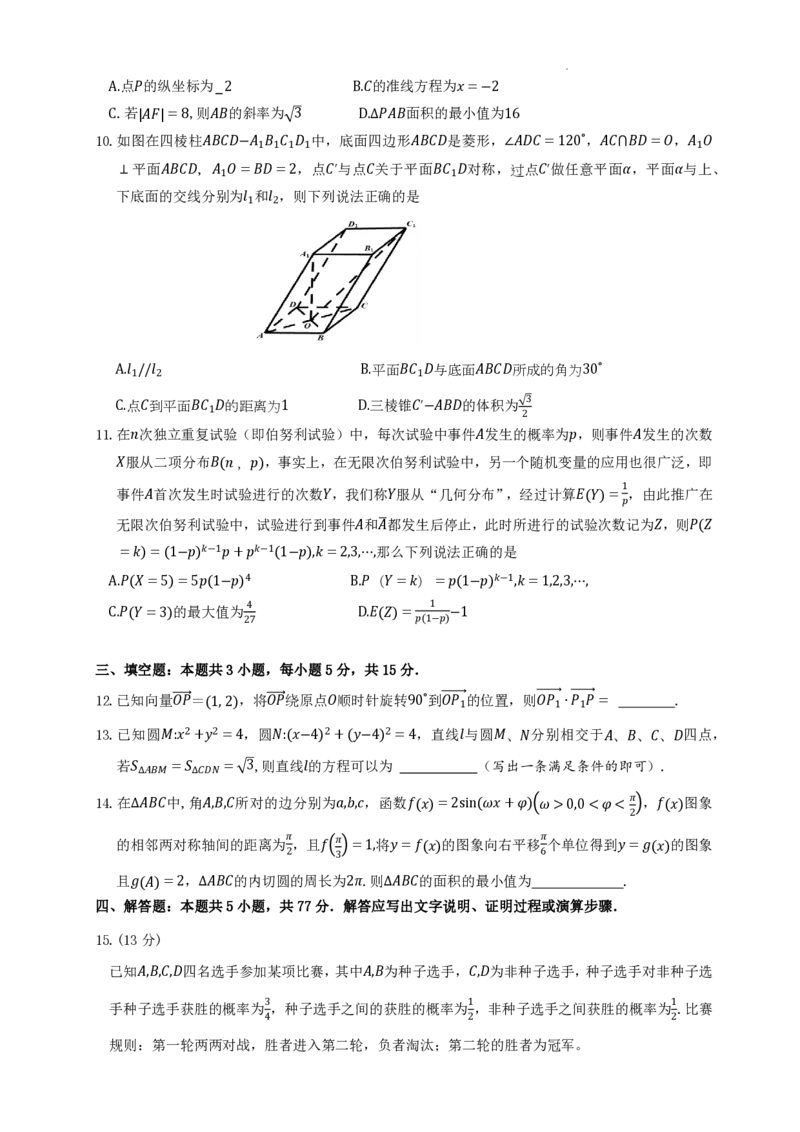
10.如图在四棱柱𝐴𝐵𝐶𝐷−𝐴 𝐵 𝐶 𝐷 中,底面四边形𝐴𝐵𝐶𝐷是菱形,∠𝐴𝐷𝐶=120°,𝐴𝐶⋂𝐵𝐷=𝑂,𝐴 𝑂
1 1 1 1 1
⊥平面𝐴𝐵𝐶𝐷, 𝐴
1
𝑂=𝐵𝐷=2,点𝐶′与点𝐶关于平面𝐵𝐶
1
𝐷对称,过点𝐶′做任意平面𝛼,平面𝛼与上、
下底面的交线分别为𝑙 和𝑙 ,则下列说法正确的是
1 2
A.𝑙 //𝑙 B.平面𝐵𝐶 𝐷与底面𝐴𝐵𝐶𝐷所成的角为30°
1 2 1
C.点𝐶到平面𝐵𝐶
1
𝐷的距离为1 D.三棱锥𝐶′−𝐴𝐵𝐷的体积为 3
2
11.在𝑛次独立重复试验(即伯努利试验)中,每次试验中事件𝐴发生的概率为𝑝,则事件𝐴发生的次数
𝑋服从二项分布𝐵(𝑛,𝑝),事实上,在无限次伯努利试验中,另一个随机变量的应用也很广泛,即
1
事件𝐴首次发生时试验进行的次数𝑌,我们称𝑌服从“几何分布”,经过计算𝐸(𝑌)= ,由此推广在
𝑝
无限次伯努利试验中,试验进行到事件𝐴和𝐴都发生后停止,此时所进行的试验次数记为𝑍,则𝑃(𝑍
=𝑘)=(1−𝑝)𝑘−1𝑝+𝑝𝑘−1(1−𝑝),𝑘=2,3,⋯,那么下列说法正确的是
A.𝑃(𝑋=5)=5𝑝(1−𝑝)4 B.𝑃(𝑌=𝑘)=𝑝(1−𝑝)𝑘−1,𝑘=1,2,3,⋯,
4 1
C.𝑃(𝑌=3)的最大值为 D.𝐸(𝑍)= −1
27 𝑝(1−𝑝)
三、填空题:本题共3小题,每小题5分,共15分.
12.已知向量𝑂𝑃=(1, 2),将𝑂𝑃绕原点𝑂顺时针旋转90°到𝑂𝑃 的位置,则𝑂𝑃 ∙𝑃 𝑃= .
1 1 1
13.已知圆𝑀:𝑥2+𝑦2=4,圆𝑁:(𝑥−4)2+(𝑦−4)2=4,直线𝑙与圆𝑀、𝑁分别相交于𝐴、𝐵、𝐶、𝐷四点,
若𝑆 =𝑆 = 3,则直线𝑙的方程可以为 (写出一条满足条件的即可).
∆𝐴𝐵𝑀 ∆𝐶𝐷𝑁
14.在∆𝐴𝐵𝐶中,角𝐴,𝐵,𝐶所对的边分别为𝑎,𝑏,𝑐,函数𝑓(𝑥)=2sin(𝜔𝑥+𝜑) 𝜔>0,0<𝜑< 𝜋 ,𝑓(𝑥)图象
2
的相邻两对称轴间的距离为 𝜋 ,且𝑓 𝜋 =1,将𝑦=𝑓(𝑥)的图象向右平移 𝜋 个单位得到𝑦=𝑔(𝑥)的图象
2 3 6
且𝑔(𝐴)=2,∆𝐴𝐵𝐶的内切圆的周长为2𝜋.则∆𝐴𝐵𝐶的面积的最小值为 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
已知𝐴,𝐵,𝐶,𝐷四名选手参加某项比赛,其中𝐴,𝐵为种子选手,𝐶,𝐷为非种子选手,种子选手对非种子选
3 1 1
手种子选手获胜的概率为 ,种子选手之间的获胜的概率为 ,非种子选手之间获胜的概率为 .比赛
4 2 2
规则:第一轮两两对战,胜者进入第二轮,负者淘汰;第二轮的胜者为冠军。
学科网(北京)股份有限公司(1)若你是主办方,则第一轮选手的对战安排一共有多少不同的方案?
(2)选手𝐴与选手𝐷相遇的概率为多少?
(3)以下两种方案,哪一种种子选手夺冠的概率更大?
方案一:第一轮比赛种子选手与非种子选手比赛;
方案二:第一轮比赛种子选手与种子选手比赛.
16.(15分)
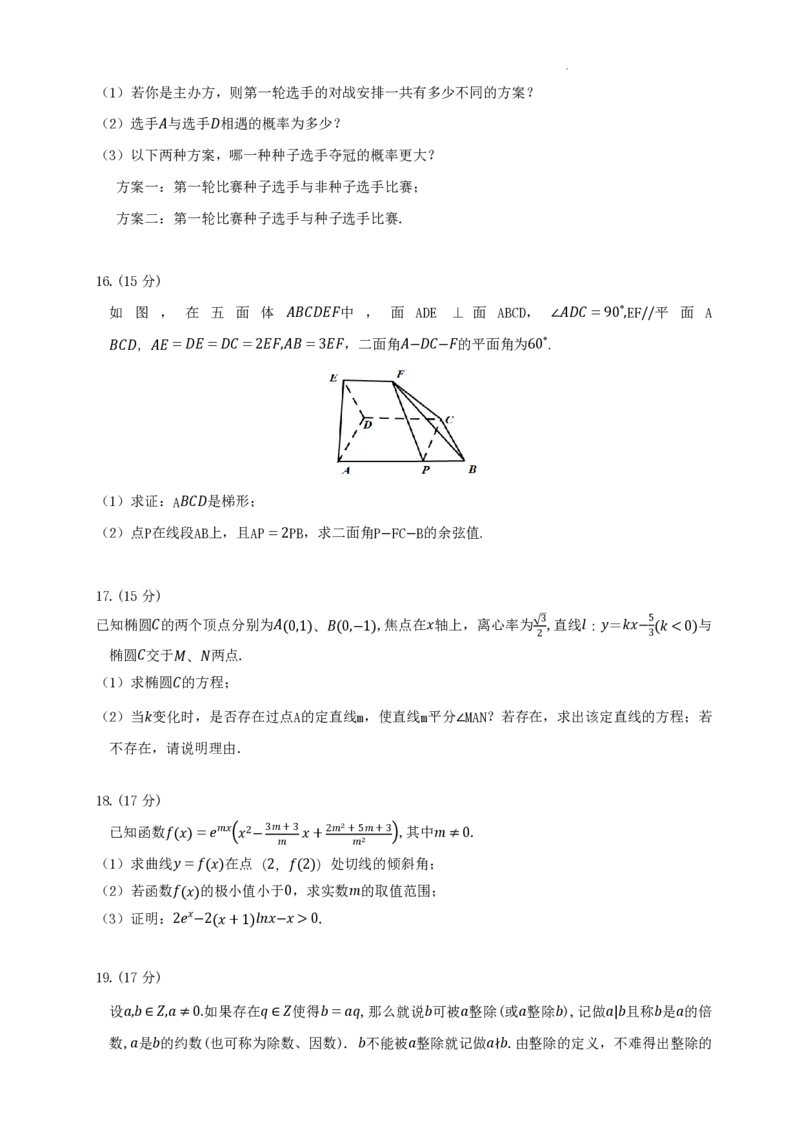
如 图 , 在 五 面 体 𝐴𝐵𝐶𝐷𝐸𝐹中 , 面 ADE ⊥ 面 ABCD, ∠𝐴𝐷𝐶=90°,EF//平 面 A
𝐵𝐶𝐷,𝐴𝐸=𝐷𝐸=𝐷𝐶=2𝐸𝐹,𝐴𝐵=3𝐸𝐹,二面角𝐴−𝐷𝐶−𝐹的平面角为60°.
(1)求证:A𝐵𝐶𝐷是梯形;
(2)点P在线段AB上,且AP=2PB,求二面角P−FC−B的余弦值.
17.(15分)
已知椭圆𝐶的两个顶点分别为𝐴(0,1)、𝐵(0,−1),焦点在𝑥轴上,离心率为 3,直线𝑙:𝑦=𝑘𝑥− 5 (𝑘<0)与
2 3
椭圆𝐶交于𝑀、𝑁两点.
(1)求椭圆𝐶的方程;
(2)当𝑘变化时,是否存在过点A的定直线m,使直线m平分∠MAN?若存在,求出该定直线的方程;若
不存在,请说明理由.
18.(17分)
已知函数𝑓(𝑥)=𝑒𝑚𝑥 𝑥2− 3𝑚+3 𝑥+2𝑚2+5𝑚+3 ,其中𝑚≠0.
𝑚 𝑚2
(1)求曲线𝑦=𝑓(𝑥)在点(2,𝑓(2))处切线的倾斜角;
(2)若函数𝑓(𝑥)的极小值小于0,求实数𝑚的取值范围;
(3)证明:2𝑒𝑥−2(𝑥+1)𝑙𝑛𝑥−𝑥>0.
19.(17分)
设𝑎,𝑏∈𝑍,𝑎≠0.如果存在𝑞∈𝑍使得𝑏=𝑎𝑞,那么就说𝑏可被𝑎整除(或𝑎整除𝑏),记做𝑎|𝑏且称𝑏是𝑎的倍
数,𝑎是𝑏的约数(也可称为除数、因数). 𝑏不能被𝑎整除就记做𝑎∤𝑏.由整除的定义,不难得出整除的
学科网(北京)股份有限公司下面几条性质:①若𝑎|𝑏,𝑏|𝑐,则𝑎|c;②𝑎,𝑏互质,若𝑎|c,𝑏|𝑐,则𝑎b|c;③若𝑎|𝑏
𝑖
,则𝑎|∑𝑛
𝑖=1
𝑐
𝑖
𝑏
𝑖
,其中𝑐
𝑖
∈𝑍,𝑖=1,2,3,⋯,𝑛..
(1)若数列{𝑎 }满足,𝑎 =2𝑛−1,其前n项和为S ,证明:279|S ;
𝑛 𝑛 𝑛 3000
(2)若n为奇数,求证:𝑎𝑛+𝑏𝑛能被a + b整除;
(3)对于整数𝑛与𝑘,𝐹(𝑛,𝑘)=∑𝑛 𝑟2𝑘−1, 求证:𝐹(𝑛,1)可整除𝐹(𝑛,𝑘).
𝑟=1
学科网(北京)股份有限公司