文档内容
更多全科试卷,请关注公众号:高中试卷君
2024 届高三二轮复习“8+3+3”小题强化训练(19)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.已知集合 , ,则 ( )
A. B.
C. D.
【答案】C
【解析】 ,得 或 ,
所以 或 , ,
所以 .
故选:C
2.已知圆锥的底面直径为 ,母线长为 ,则其侧面展开图扇形的圆心角为( )
A. B. C. D.
【答案】C
【解析】由题设,底面周长 ,而母线长为 ,
根据扇形周长公式知:圆心角 .
故选:C.
3.已知 , 均为单位向量,若 ,则 在 上的投影向量为( )
A. B. C. D.
【答案】D
【解析】 ,
在 上的投影向量 ,
故选:D.
4.如图,某种车桩可在左右两侧各停靠一辆单车,每辆单车只能停靠于一个车桩.某站点设有4个均
停满共享单车的这样的车桩.若有两人在该站点各自挑选一辆共享单车骑行,且所挑单车不停靠于同一
车桩,则不同的选法种数是( )更多全科试卷,请关注公众号:高中试卷君
A. 24 B. 36 C. 48 D. 96
【答案】C
【解析】由题有 ,
故选:C.
5.已知函数 ,要得到函数 的图象,
只需将 的图象( )
A. 向左平移 个单位长度 B. 向左平移 个单位长度
C. 向右平移 个单位长度 D. 向右平移 个单位长度
【答案】D
【解析
,
,
故将 的图象向右平移 个单位长度可得 ,即为
的图象.
故选:C
6.已知复数 ,其中 且 ,则 的最小值是( )
A. B. 2 C. D.
【答案】D
【解析】复数 ,其中 且 ,
复数 在复平面内对应的点 ,在直线 上,
的几何意义是点 到点 的距离,
其最小值为点 到直线 的距离,最小值为 .
故选:D更多全科试卷,请关注公众号:高中试卷君
7.已知三棱锥 的体积是 是球 的球面上的三个点,且
, ,则球 的表面积为( )
A. B. C. D.
【答案】A
【解析】因为 ,所以 的外接圆半径为 ,
在 中,由余弦定理可得
,
所以 ,所以 ,
设球心 到平面 的距离为 ,
∵ ,
,
球半径 ,所以球面积 .
故选:A
8.已知双曲线 的右焦点为F,过点F且斜率为 的直线l交双曲线于
A、B两点,线段AB的中垂线交x轴于点D. 若 ,则双曲线的离心率取值范围是
( )
A. B. C. D.
【答案】A
【解析】设双曲线的右焦点为 ,则直线 ,
联立方程 ,消去y得: ,
则可得 ,
则 ,
设线段 的中点 ,则
,更多全科试卷,请关注公众号:高中试卷君
即 ,
且 ,线段 的中垂线的斜率为 ,
则线段 的中垂线所在直线方程为 ,
令 ,则 ,解得 ,
即 ,则 ,
由题意可得: ,即 ,
整理得 ,则 ,
注意到双曲线的离心率 ,
∴双曲线的离心率取值范围是 .
故选:A.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.下列说法中,正确的是( )
A. 若随机变量 ,且 ,则
B. 一组数据6,7,7,9,13,14,16,17,21的第70百分位数为16
C. 盒子中装有除颜色外完全相同的5个黄球和3个蓝球,从袋中有放回地依次抽取2个球,第一次抽
到蓝球的情况下第二次也抽到蓝球的概率为
D. 设随机事件 , ,已知 事件发生的概率为0.3,在 发生的条件下 发生的概率为0.4,在
不发生的条件下 发生的概率为0.2,则 发生的概率为0.26
【答案】BCD
【解析】A选项,根据正态分布的对称性可知 ,A选项错误.
B选项, ,所以第 百分位数是 ,B选项正确.
C选项,由于抽取的方式是有放回,所以“第一次抽到蓝球”与“第二次抽到蓝球”是相互独立事
件,所以第一次抽到蓝球的情况下第二次也抽到蓝球的概率为 ,
所以C选项正确.
D选项, ,所以D选项正确.
故选:BCD
10.已知等差数列 的前 项和为 ,等比数列 的前 项和为 ,则下列结论正确的是(
)更多全科试卷,请关注公众号:高中试卷君
A. 数列 为等差数列 B. 对任意正整数 ,
C. 数列 一定是等差数列 D. 数列 一定是等比数列
【答案】ABC
【解析】设等差数列 的公差为 ,则 ,所以, .
对于A选项, ,所以, 为等差数列,A对;
对于B选项,对任意的 , ,由等比中项的性质可得 ,
由基本不等式可得 ,B对;
对于C选项,令 ,
所以, ,
故数列 一定是等差数列,C对;
对于D选项,设等比数列 的公比为 ,
当 时, ,
此时,数列 不是等比数列,D错.
故选:ABC.
11 . 已 知 定 义 在 上 的 函 数 满 足 : , 都 有 , 且
, ,当 时,有 ,则( )
A. B. C. D.
【答案】ACD
【解析】令 ,则由 ,可得 ,所以 ,故A正
确,
因为 , ,所以 ,可得 ,故B错误,
因为 ,所以 ,故C正确,
又因为当 时,都有 ,且 ,
所以当 时, ,
因为 ;更多全科试卷,请关注公众号:高中试卷君
又 进而 ,
因此 ,所以 .故D正确,
故选:ACD
三、填空题:本题共3小题,每小题5分,共15分.
12.已知 的图象在 处的切线与与函数 的图象也相切,则该切线
的斜率 __________.
【答案】
【解析】函数 的图象在 处的切线的切点为 ,
因为 ,所以切线斜率为 ,切线方程为 ,即 ,
设 的图象的切线的切点为 ,因为 ,所以切线斜率为 ,
切线方程为 ,即 ,
由题 ,解得 , ,斜率为 .
故答案为: .
13.已知圆 ,直线 ,若直线 与圆 交于 两
点,则 的最小值为__________.
【答案】2
【解析】由直线 可得: ,即直线 经过定点 .由
可得: ,即圆心为 ,半径为 ,如图.
连接 ,过点 作 的垂线交圆 于点 ,则此时 取最小值.
(理由如下:过点 作另一条直线交圆 于点 ,过点 作 于点 ,
在 中,显然 ,而 , ,
因 故有 ,即 是最短的弦长)
此时, , .
故答案为:2.更多全科试卷,请关注公众号:高中试卷君
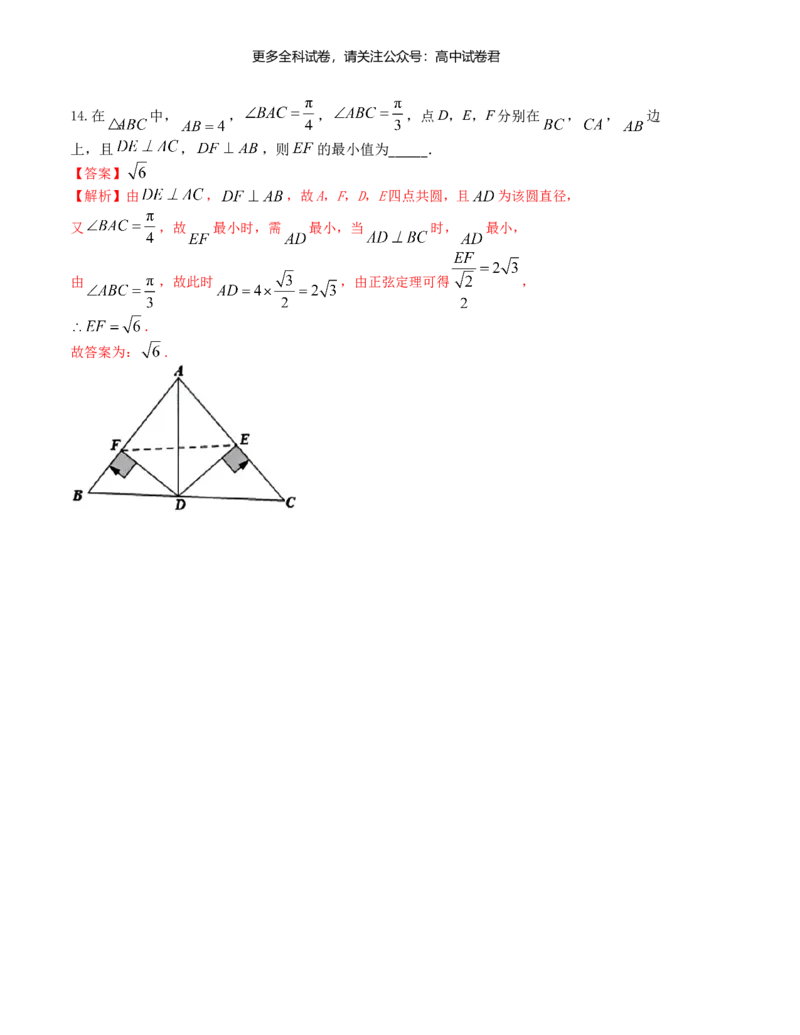
14.在 中, , , ,点D,E,F分别在 , , 边
上,且 , ,则 的最小值为______.
【答案】
【解析】由 , ,故A,F,D,E四点共圆,且 为该圆直径,
又 ,故 最小时,需 最小,当 时, 最小,
由 ,故此时 ,由正弦定理可得 ,
.
故答案为: .