文档内容
沈阳市 2022 年初中学业水平考试
数学试题
试题满分120分,考试时间120分钟.
注意事项:
1.答题前,考生须用0.5mm黑色字迹的签字笔在本试题卷规定位置填写自己的姓名、准考
证号;
2.考生须在答题卡上作答,不能在本试题卷上作答,答在本试题卷上无效;
3.考试结束,将本试题卷和答题卡一并交回;
4.本试题卷包括八道大题,25道小题,共6页.如缺页、印刷不清,考生须声明.
一、选择题(下列各题的备选答案中,只有一个答案是正确的.每小题2分,共20分)
1. 计算 正确的是( )
A. 2 B. C. 8 D.
2. 如图是由4个相同的小立方块搭成的几何体,这个几何体的主视图是( )
A. B. C. D.
3. 下列计算结果正确的是( )
A. B. C. D.
4. 在平面直角坐标系中,点 关于y轴对称的点的坐标是( )
A. B. C. D.
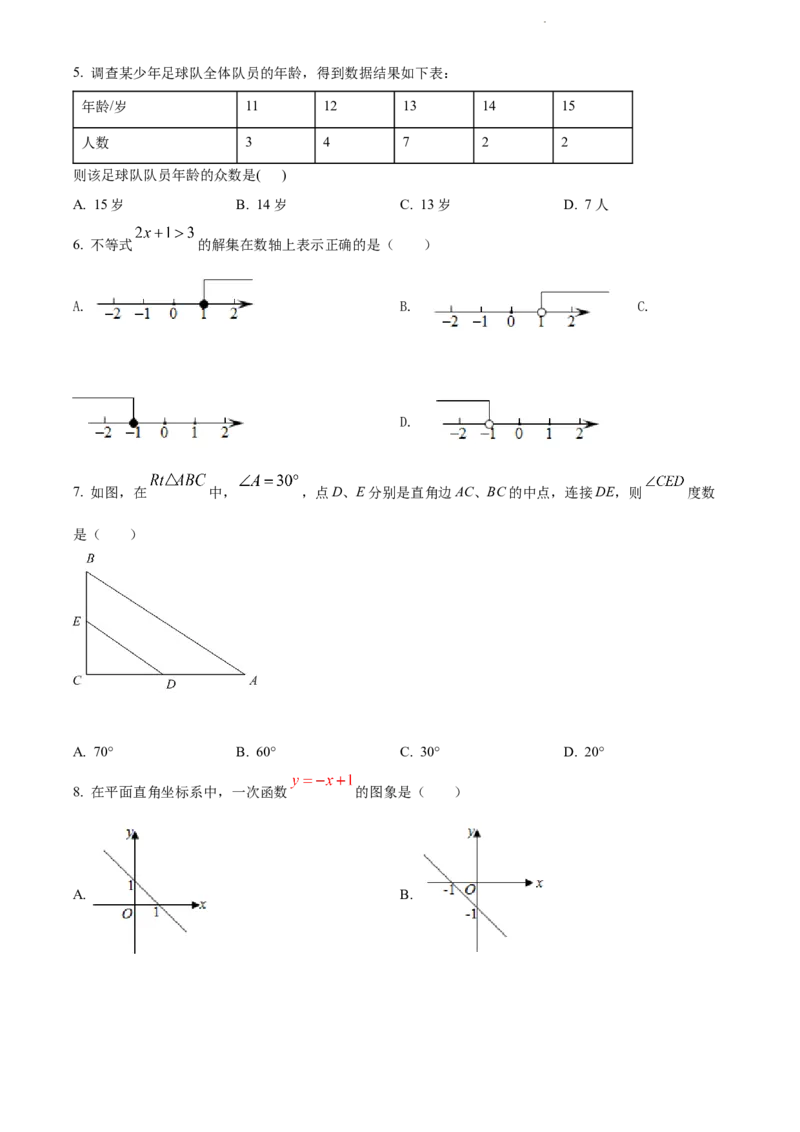
学科网(北京)股份有限公司5. 调查某少年足球队全体队员的年龄,得到数据结果如下表:
年龄/岁 11 12 13 14 15
人数 3 4 7 2 2
则该足球队队员年龄的众数是( )
A. 15岁 B. 14岁 C. 13岁 D. 7人
6. 不等式 的解集在数轴上表示正确的是( )
A. B. C.
D.
7. 如图,在 中, ,点D、E分别是直角边AC、BC的中点,连接DE,则 度数
是( )
A. 70° B. 60° C. 30° D. 20°
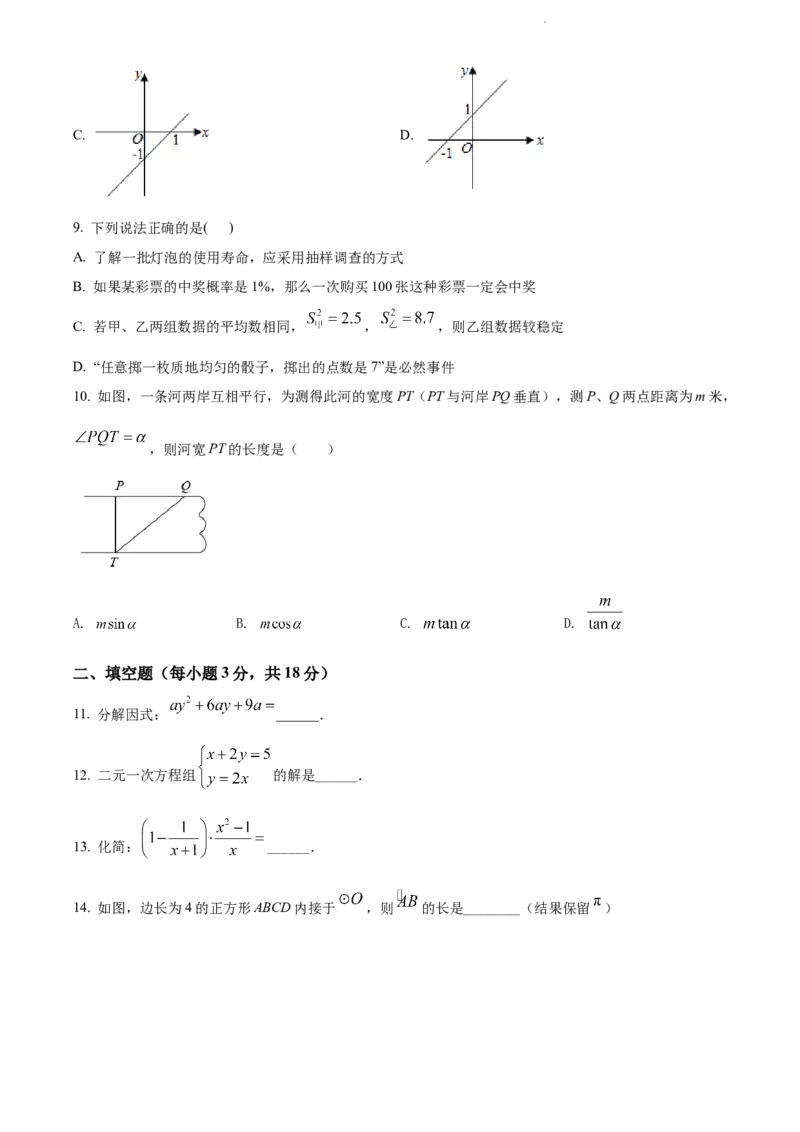
8. 在平面直角坐标系中,一次函数 的图象是( )
A. B.
学科网(北京)股份有限公司C. D.
9. 下列说法正确的是( )
A. 了解一批灯泡的使用寿命,应采用抽样调查的方式
B. 如果某彩票的中奖概率是1%,那么一次购买100张这种彩票一定会中奖
C. 若甲、乙两组数据的平均数相同, , ,则乙组数据较稳定
D. “任意掷一枚质地均匀的骰子,掷出的点数是7”是必然事件
10. 如图,一条河两岸互相平行,为测得此河的宽度PT(PT与河岸PQ垂直),测P、Q两点距离为m米,
,则河宽PT的长度是( )
A. B. C. D.
二、填空题(每小题3分,共18分)
11. 分解因式: ______.
12. 二元一次方程组 的解是______.
13. 化简: ______.
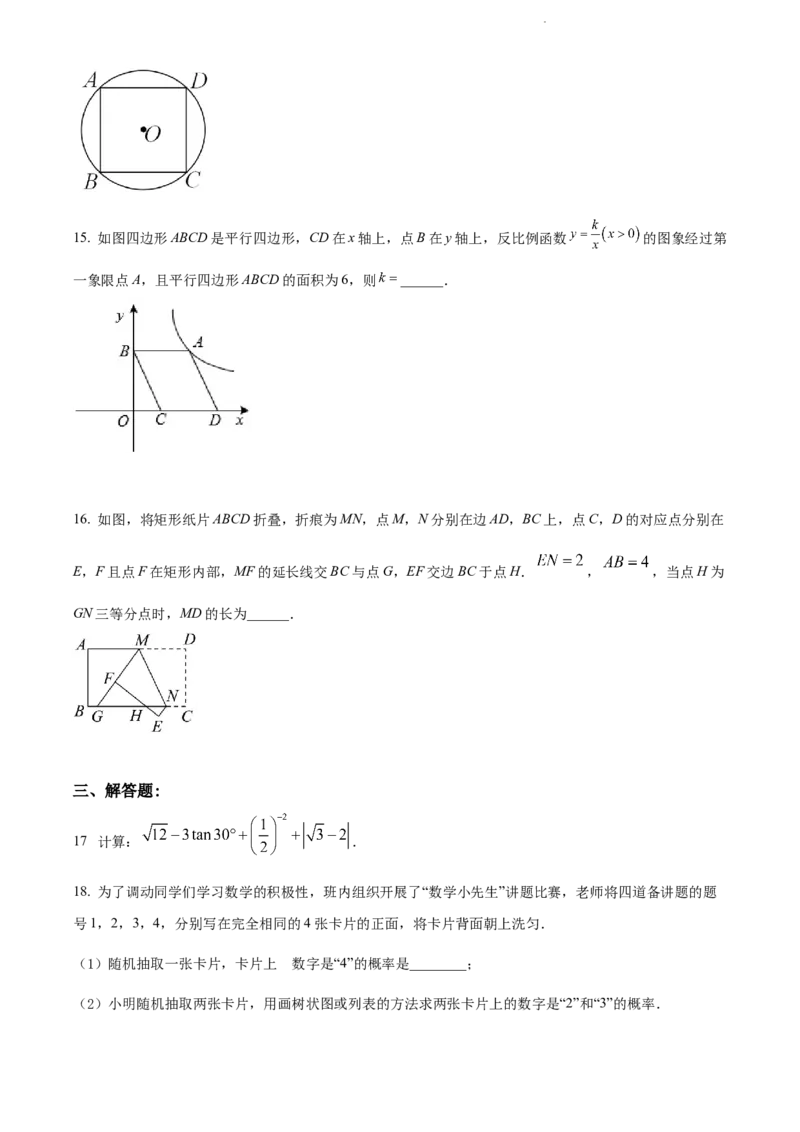
14. 如图,边长为4的正方形ABCD内接于 ,则 的长是________(结果保留 )
学科网(北京)股份有限公司15. 如图四边形ABCD是平行四边形,CD在x轴上,点B在y轴上,反比例函数 的图象经过第
一象限点A,且平行四边形ABCD的面积为6,则 ______.
16. 如图,将矩形纸片ABCD折叠,折痕为MN,点M,N分别在边AD,BC上,点C,D的对应点分别在
E,F且点F在矩形内部,MF的延长线交BC与点G,EF交边BC于点H. , ,当点H为
GN三等分点时,MD的长为______.
三、解答题:
.
17 计算: .
18. 为了调动同学们学习数学的积极性,班内组织开展了“数学小先生”讲题比赛,老师将四道备讲题的题
号1,2,3,4,分别写在完全相同的4张卡片的正面,将卡片背面朝上洗匀.
的
(1)随机抽取一张卡片,卡片上 数字是“4”的概率是________;
(2)小明随机抽取两张卡片,用画树状图或列表的方法求两张卡片上的数字是“2”和“3”的概率.
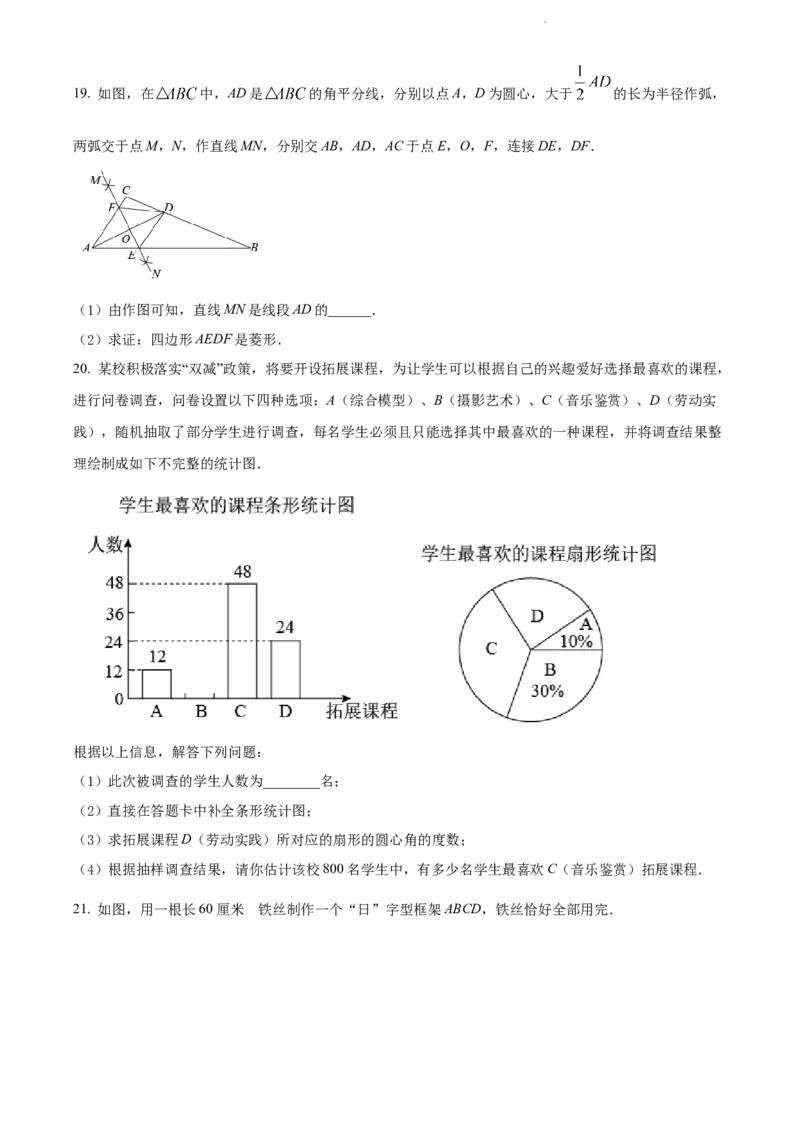
学科网(北京)股份有限公司19. 如图,在 中,AD是 的角平分线,分别以点A,D为圆心,大于 的长为半径作弧,
两弧交于点M,N,作直线MN,分别交AB,AD,AC于点E,O,F,连接DE,DF.
(1)由作图可知,直线MN是线段AD的______.
(2)求证:四边形AEDF是菱形.
20. 某校积极落实“双减”政策,将要开设拓展课程,为让学生可以根据自己的兴趣爱好选择最喜欢的课程,
进行问卷调查,问卷设置以下四种选项:A(综合模型)、B(摄影艺术)、C(音乐鉴赏)、D(劳动实
践),随机抽取了部分学生进行调查,每名学生必须且只能选择其中最喜欢的一种课程,并将调查结果整
理绘制成如下不完整的统计图.
根据以上信息,解答下列问题:
(1)此次被调查的学生人数为________名;
(2)直接在答题卡中补全条形统计图;
(3)求拓展课程D(劳动实践)所对应的扇形的圆心角的度数;
(4)根据抽样调查结果,请你估计该校800名学生中,有多少名学生最喜欢C(音乐鉴赏)拓展课程.
的
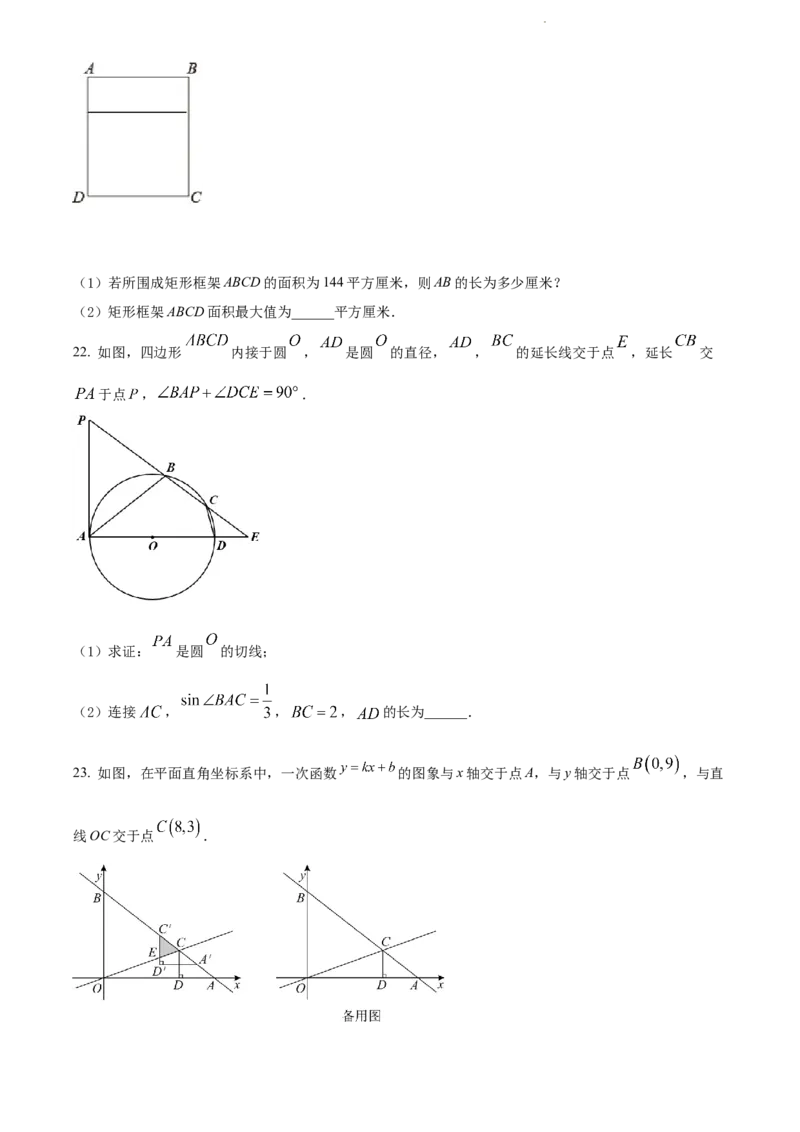
21. 如图,用一根长60厘米 铁丝制作一个“日”字型框架ABCD,铁丝恰好全部用完.
学科网(北京)股份有限公司(1)若所围成矩形框架ABCD的面积为144平方厘米,则AB的长为多少厘米?
(2)矩形框架ABCD面积最大值为______平方厘米.
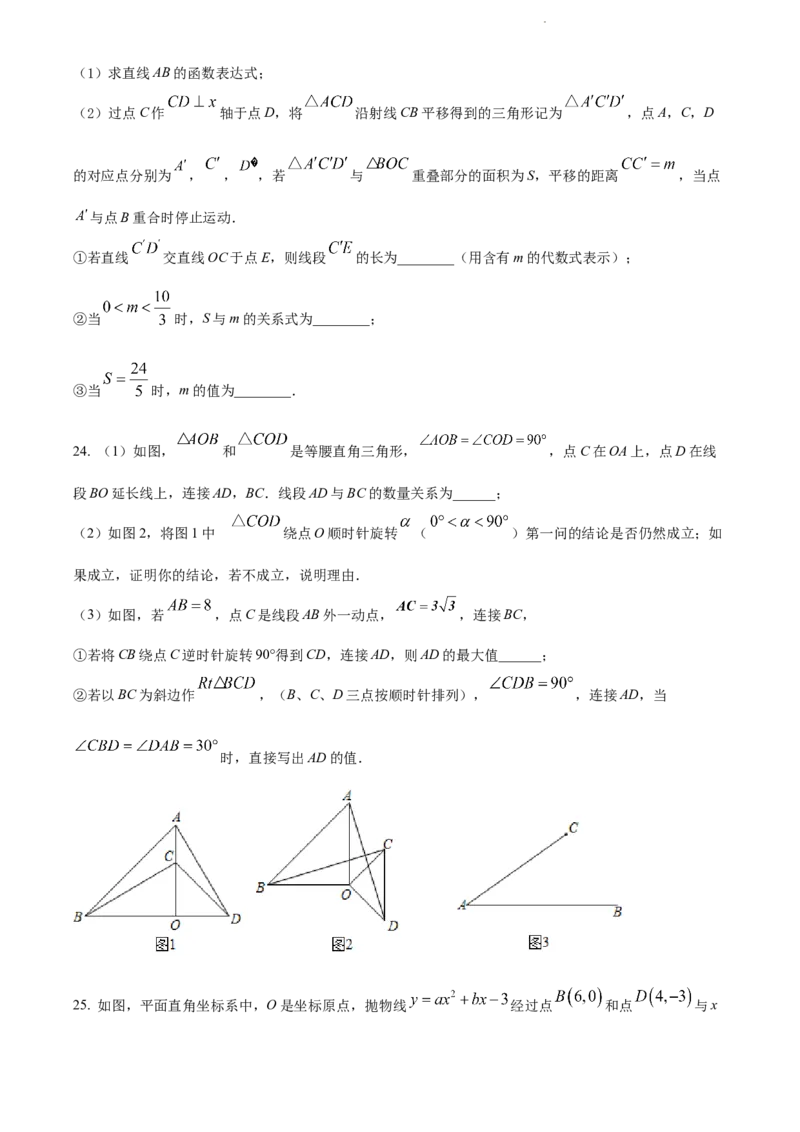
22. 如图,四边形 内接于圆 , 是圆 的直径, , 的延长线交于点 ,延长 交
于点 , .
(1)求证: 是圆 的切线;
(2)连接 , , , 的长为______.
23. 如图,在平面直角坐标系中,一次函数 的图象与x轴交于点A,与y轴交于点 ,与直
线OC交于点 .
学科网(北京)股份有限公司(1)求直线AB的函数表达式;
(2)过点C作 轴于点D,将 沿射线CB平移得到的三角形记为 ,点A,C,D
的对应点分别为 , , ,若 与 重叠部分的面积为S,平移的距离 ,当点
与点B重合时停止运动.
①若直线 交直线OC于点E,则线段 的长为________(用含有m的代数式表示);
②当 时,S与m的关系式为________;
③当 时,m的值为________.
24. (1)如图, 和 是等腰直角三角形, ,点C在OA上,点D在线
段BO延长线上,连接AD,BC.线段AD与BC的数量关系为______;
的
(2)如图2,将图1中 绕点O顺时针旋转 ( )第一问的结论是否仍然成立;如
果成立,证明你的结论,若不成立,说明理由.
(3)如图,若 ,点C是线段AB外一动点, ,连接BC,
①若将CB绕点C逆时针旋转90°得到CD,连接AD,则AD的最大值______;
②若以BC为斜边作 ,(B、C、D三点按顺时针排列), ,连接AD,当
时,直接写出AD的值.
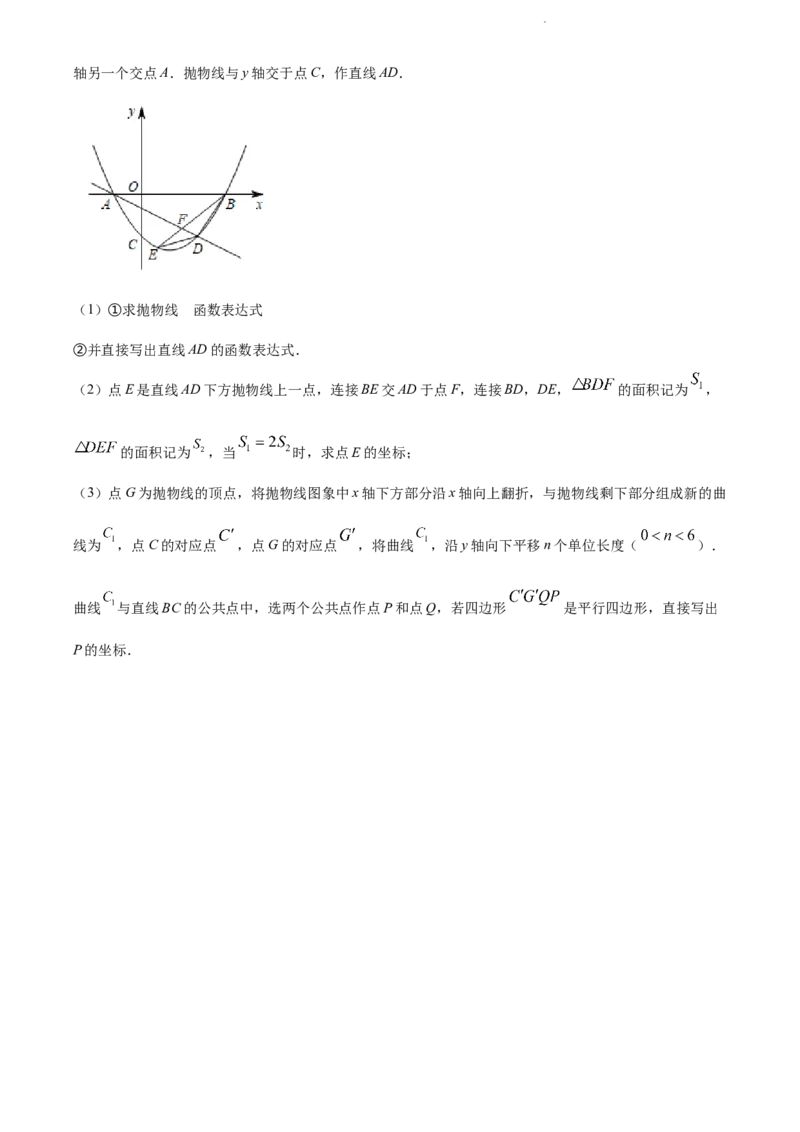
25. 如图,平面直角坐标系中,O是坐标原点,抛物线 经过点 和点 与x
学科网(北京)股份有限公司轴另一个交点A.抛物线与y轴交于点C,作直线AD.
的
(1)①求抛物线 函数表达式
②并直接写出直线AD的函数表达式.
(2)点E是直线AD下方抛物线上一点,连接BE交AD于点F,连接BD,DE, 的面积记为 ,
的面积记为 ,当 时,求点E的坐标;
(3)点G为抛物线的顶点,将抛物线图象中x轴下方部分沿x轴向上翻折,与抛物线剩下部分组成新的曲
线为 ,点C的对应点 ,点G的对应点 ,将曲线 ,沿y轴向下平移n个单位长度( ).
曲线 与直线BC的公共点中,选两个公共点作点P和点Q,若四边形 是平行四边形,直接写出
P的坐标.
学科网(北京)股份有限公司学科网(北京)股份有限公司