吉林省2019年中考数学真题试题_中考真题_2.数学中考真题2015-2024年_2019年全国中考数学206份

吉林省2019年初中毕业生学业水平考试数学试题 数学试题共6题，包括六道大题，共26道小题。全卷满分120分，考试时间为120分钟。考试结束 后，将本试卷和答题卡一并交回。 注意事项： 1．答题前，请您将自己的姓名、准考证号填写在答题卡上，并将条形码准确粘贴在条形码区域内。 2．答题时，请您按照考试要求在答题卡上的指定区域内作答，在草稿纸、试题上答题无效。 一、单项选择题（每小题2分，共12分） 1．如图，数轴上蝴蝶所在点表示的数可能为（ ） 0 （第1题） A．3 B．2 C．1 D．－1 2．如图，由6个相同的小正方体组合成一个立体图形，它的俯视图为（ ） 正面 （第2题） A． B． C． D． 3．若a为实数，则下列各式的运算结果比a小的是（ ） A．a1 B．a1 C．a1 D．a1 4．把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合，则这个旋转角度至少为（ ） A．30° B．90° C．120° D．180° A C O 曲桥 B A P B （第4题） （第5题） (第6题) 5．如图，在⊙O中，AB所对的圆周角∠ACB=50°，若P为AB上一点，∠AOP=55°，则∠POB的度数为 （ ） A．30° B．45° C．55° D．60° 6． 曲桥是我国古代经典建筑之一，它的修建增加了游人在桥上行走的路程，有利于游人更好地观赏 风光。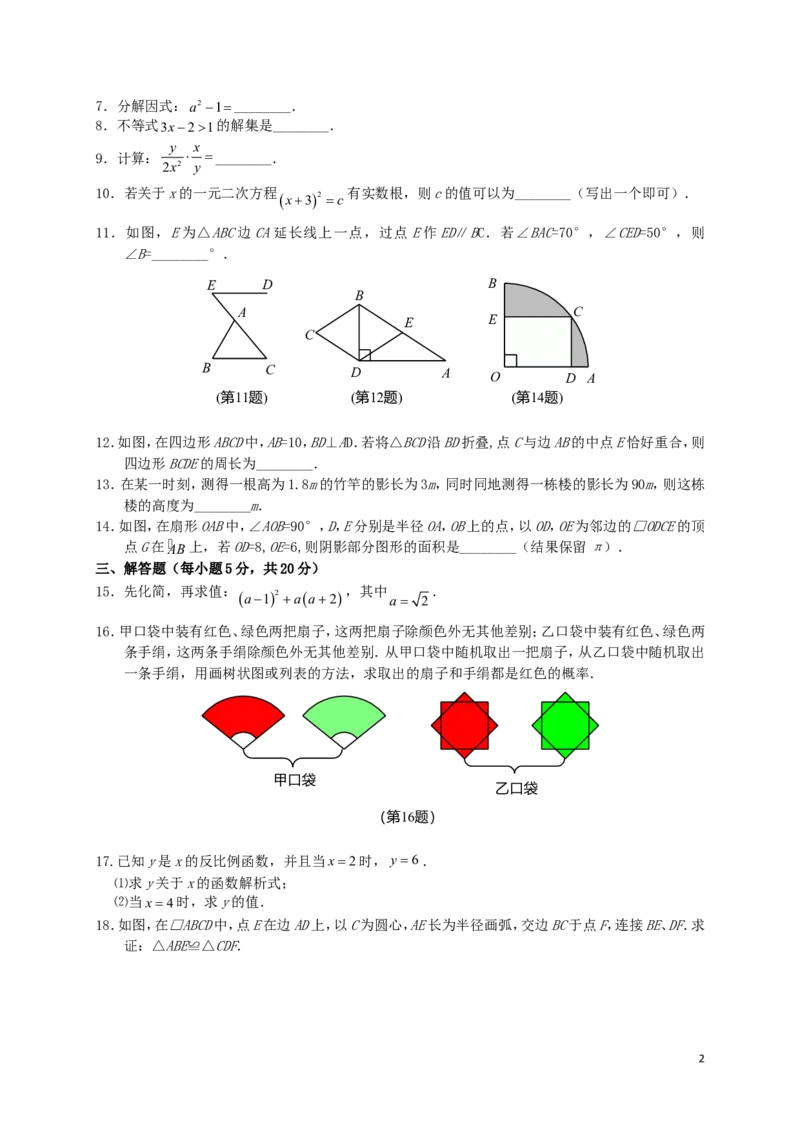如图，A、B两地间修建曲桥与修建直的桥相比，增加了桥的长度，其中蕴含的数学道理是（ ） A．两点之间，线段最短 B．平行于同一条直线的两条直线平行 C．垂线段最短 D．两点确定一条直线 二、填空题（每小题3分，共24分） 17．分解因式：a2 1________． 8．不等式3x21的解集是________． y x 9．计算：  ________． 2x2 y 10．若关于x的一元二次方程 有实数根，则c的值可以为________（写出一个即可）． x32 c 11．如图，E为△ABC边CA延长线上一点，过点E作ED∥BC．若∠BAC=70°，∠CED=50°，则 ∠B=________°． E D B B A C E E C B C D A O D A (第11题) (第12题) (第14题) 12．如图，在四边形ABCD中，AB=10，BD⊥AD．若将△BCD沿BD折叠,点C与边AB的中点E恰好重合，则 四边形BCDE的周长为________． 13．在某一时刻，测得一根高为1.8m的竹竿的影长为3m，同时同地测得一栋楼的影长为90m，则这栋 楼的高度为________m． 14．如图，在扇形OAB中，∠AOB=90°，D，E分别是半径OA，OB上的点，以OD，OE为邻边的□ODCE的顶 点G在AB上，若OD=8,OE=6,则阴影部分图形的面积是________（结果保留π）． 三、解答题（每小题5分，共20分） 15．先化简，再求值： ，其中 ． a12 aa2 a 2 16．甲口袋中装有红色、绿色两把扇子，这两把扇子除颜色外无其他差别；乙口袋中装有红色、绿色两 条手绢，这两条手绢除颜色外无其他差别．从甲口袋中随机取出一把扇子，从乙口袋中随机取出 一条手绢，用画树状图或列表的方法，求取出的扇子和手绢都是红色的概率． 甲口袋 乙口袋 （第16题） 17.已知y是x的反比例函数，并且当x2时，y6． ⑴求y关于x的函数解析式； ⑵当x4时，求y的值． 18．如图，在□ABCD中，点E在边AD上，以C为圆心，AE长为半径画弧，交边BC于点F，连接BE、DF．求 证：△ABE≌△CDF． 2A E D B F C （第18题） 四、解答题（每小题7分，共28分） 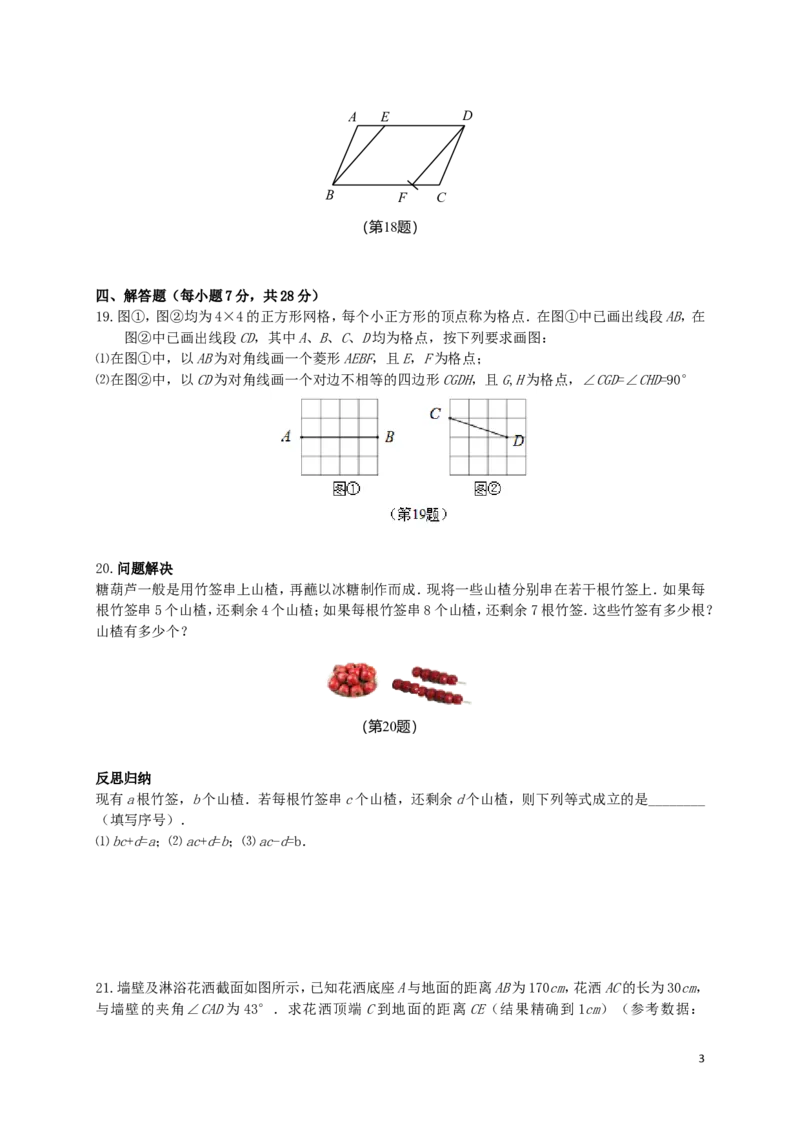19.图①，图②均为4×4的正方形网格，每个小正方形的顶点称为格点．在图①中已画出线段AB，在 图②中已画出线段CD，其中A、B、C、D均为格点，按下列要求画图： ⑴在图①中，以AB为对角线画一个菱形AEBF，且E，F为格点； ⑵在图②中，以CD为对角线画一个对边不相等的四边形CGDH，且G,H为格点，∠CGD=∠CHD=90° 20.问题解决 糖葫芦一般是用竹签串上山楂，再蘸以冰糖制作而成．现将一些山楂分别串在若干根竹签上．如果每 根竹签串5个山楂，还剩余4个山楂；如果每根竹签串8个山楂，还剩余7根竹签．这些竹签有多少根？ 山楂有多少个？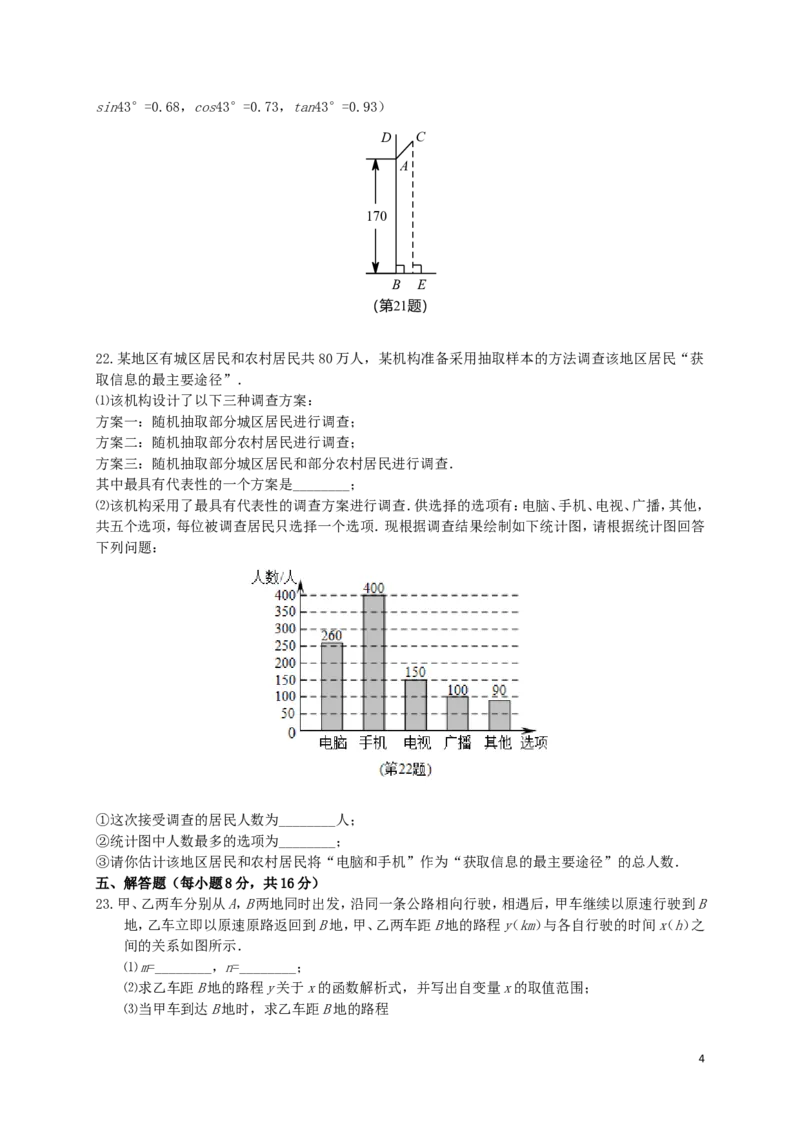 （第20题） 反思归纳 现有a根竹签，b个山楂．若每根竹签串c个山楂，还剩余d个山楂，则下列等式成立的是________ （填写序号）． ⑴bc+d=a；⑵ac+d=b；⑶ac-d=b． 21.墙壁及淋浴花洒截面如图所示，已知花洒底座A与地面的距离AB为170cm，花洒AC的长为30cm， 与墙壁的夹角∠CAD为43°．求花洒顶端C到地面的距离CE（结果精确到1cm）（参考数据： 3sin43°=0.68，cos43°=0.73，tan43°=0.93） D C A 170 B E （第21题） 22.某地区有城区居民和农村居民共80万人，某机构准备采用抽取样本的方法调查该地区居民“获 取信息的最主要途径”． ⑴该机构设计了以下三种调查方案： 方案一：随机抽取部分城区居民进行调查； 方案二：随机抽取部分农村居民进行调查； 方案三：随机抽取部分城区居民和部分农村居民进行调查． 其中最具有代表性的一个方案是________； ⑵该机构采用了最具有代表性的调查方案进行调查．供选择的选项有：电脑、手机、电视、广播，其他， 共五个选项，每位被调查居民只选择一个选项．现根据调查结果绘制如下统计图，请根据统计图回答 下列问题： ①这次接受调查的居民人数为________人； ②统计图中人数最多的选项为________； ③请你估计该地区居民和农村居民将“电脑和手机”作为“获取信息的最主要途径”的总人数． 五、解答题（每小题8分，共16分） 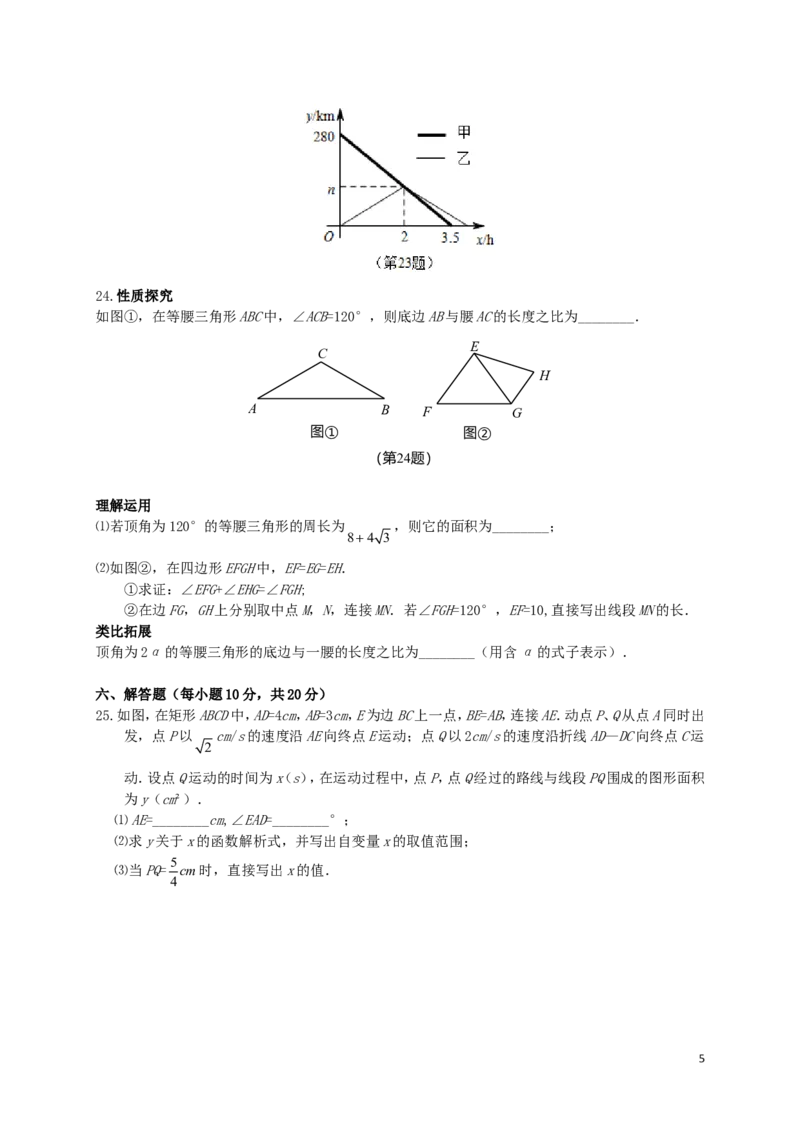23.甲、乙两车分别从A，B两地同时出发，沿同一条公路相向行驶，相遇后，甲车继续以原速行驶到B 地，乙车立即以原速原路返回到B地，甲、乙两车距B地的路程y（km）与各自行驶的时间x（h）之 间的关系如图所示． ⑴m=________，n=________； ⑵求乙车距B地的路程y关于x的函数解析式，并写出自变量x的取值范围； ⑶当甲车到达B地时，求乙车距B地的路程 424.性质探究 如图①，在等腰三角形ABC中，∠ACB=120°，则底边AB与腰AC的长度之比为________． E C H A B F G 图① 图② （第24题） 理解运用 ⑴若顶角为120°的等腰三角形的周长为 ，则它的面积为________； 84 3 ⑵如图②，在四边形EFGH中，EF=EG=EH． ①求证：∠EFG+∠EHG=∠FGH; ②在边FG，GH上分别取中点M，N，连接MN．若∠FGH=120°，EF=10,直接写出线段MN的长． 类比拓展 顶角为2α的等腰三角形的底边与一腰的长度之比为________（用含α的式子表示）． 六、解答题（每小题10分，共20分） 25.如图，在矩形ABCD中，AD=4cm，AB=3cm，E为边BC上一点，BE=AB，连接AE．动点P、Q从点A同时出 发，点P以 cm/s的速度沿AE向终点E运动；点Q以2cm/s的速度沿折线AD—DC向终点C运 2 动．设点Q运动的时间为x（s），在运动过程中，点P，点Q经过的路线与线段PQ围成的图形面积 为y（cm²）． ⑴AE=________cm,∠EAD=________°； ⑵求y关于x的函数解析式，并写出自变量x的取值范围； 5 ⑶当PQ= cm时，直接写出x的值． 4 5C E B C E B P D Q A D A （第25题） （备用图） 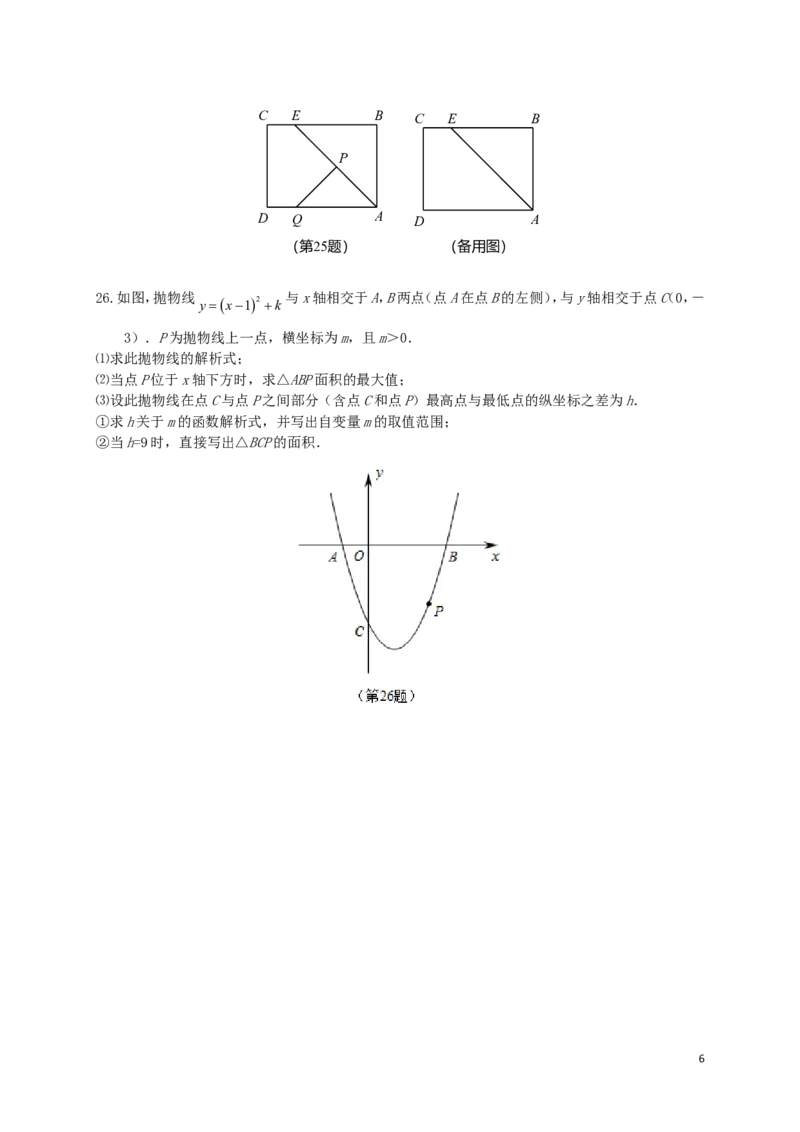26.如图，抛物线 与x轴相交于A，B两点（点A在点B的左侧），与y轴相交于点C（0，－ yx12 k 3）．P为抛物线上一点，横坐标为m，且m＞0． ⑴求此抛物线的解析式； ⑵当点P位于x轴下方时，求△ABP面积的最大值； ⑶设此抛物线在点C与点P之间部分（含点C和点P）最高点与最低点的纵坐标之差为h． ①求h关于m的函数解析式，并写出自变量m的取值范围； ②当h=9时，直接写出△BCP的面积． 6参考答案 1、D 2、D 3、B 4、C 5、B 6、A 1 7、（a1)(a1) 8、x＞1 9、 10、5（答案不唯一，只有c≥0即可） 2x 11、60 12、20 13、54 14、25－48 15、解：原式＝a2 2a1a2 2a2a2 1， 当 时，原式＝5 a  2 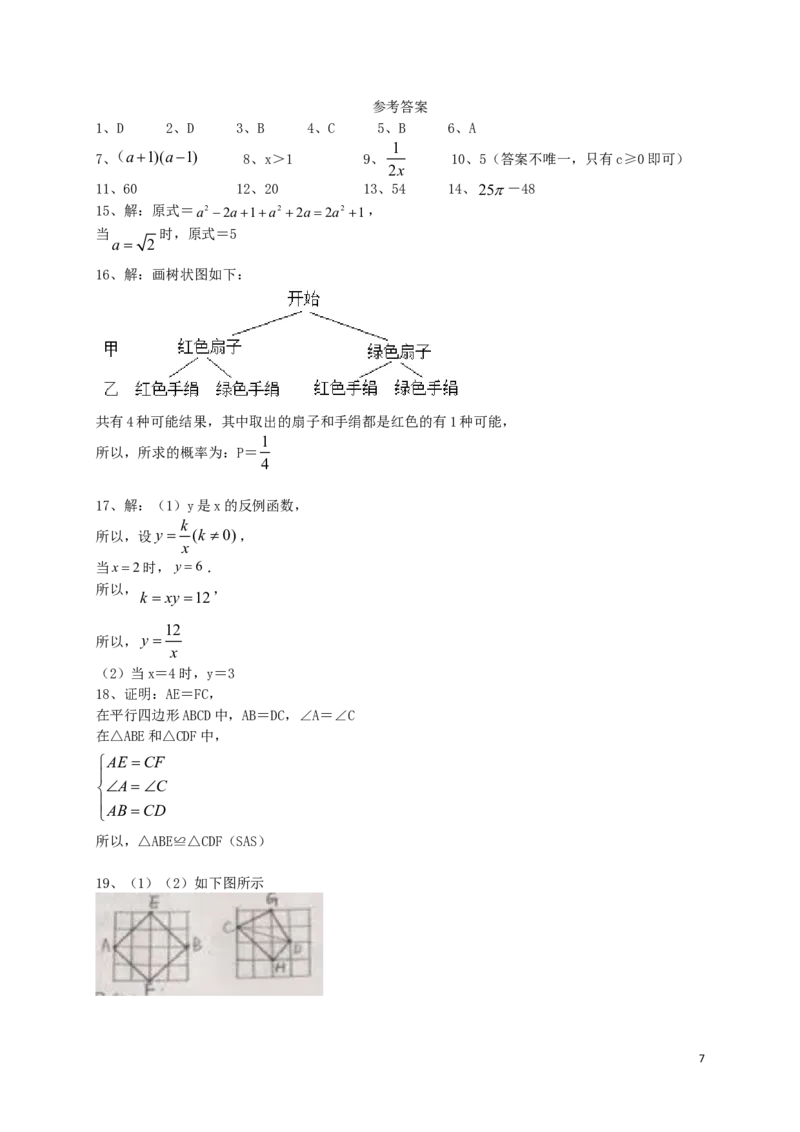16、解：画树状图如下： 共有4种可能结果，其中取出的扇子和手绢都是红色的有1种可能， 1 所以，所求的概率为：P＝ 4 17、解：（1）y是x的反例函数， k 所以，设y  (k 0)， x 当x2时，y6． 所以， ， k  xy 12 12 所以，y  x （2）当x＝4时，y＝3 18、证明：AE＝FC， 在平行四边形ABCD中，AB＝DC，∠A＝∠C 在△ABE和△CDF中， AE CF  AC  ABCD  所以，△ABE≌△CDF（SAS） 19、（1）（2）如下图所示 789101112