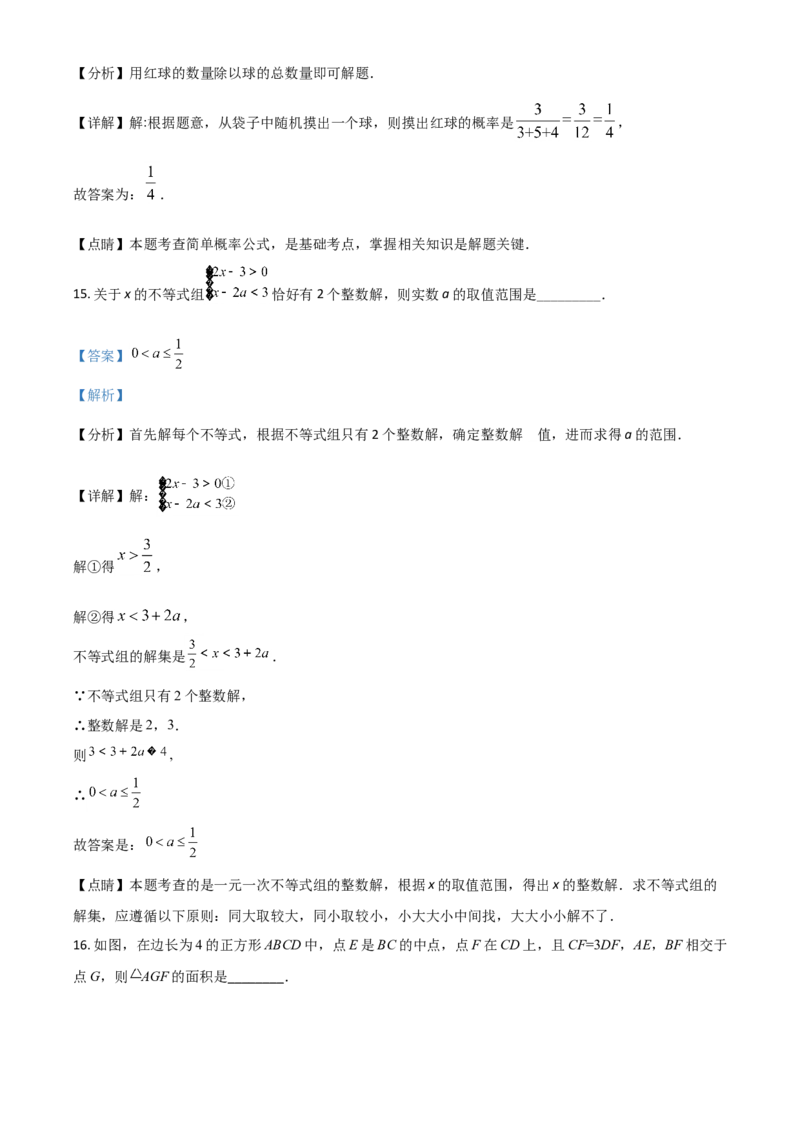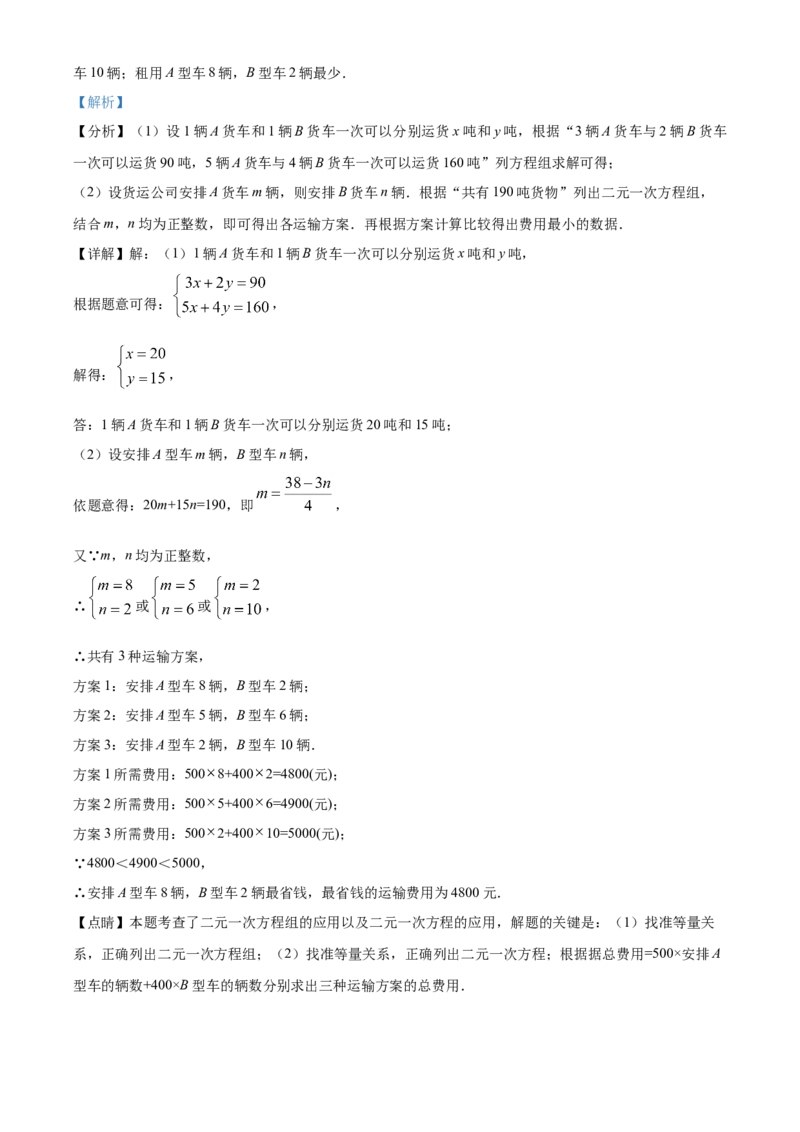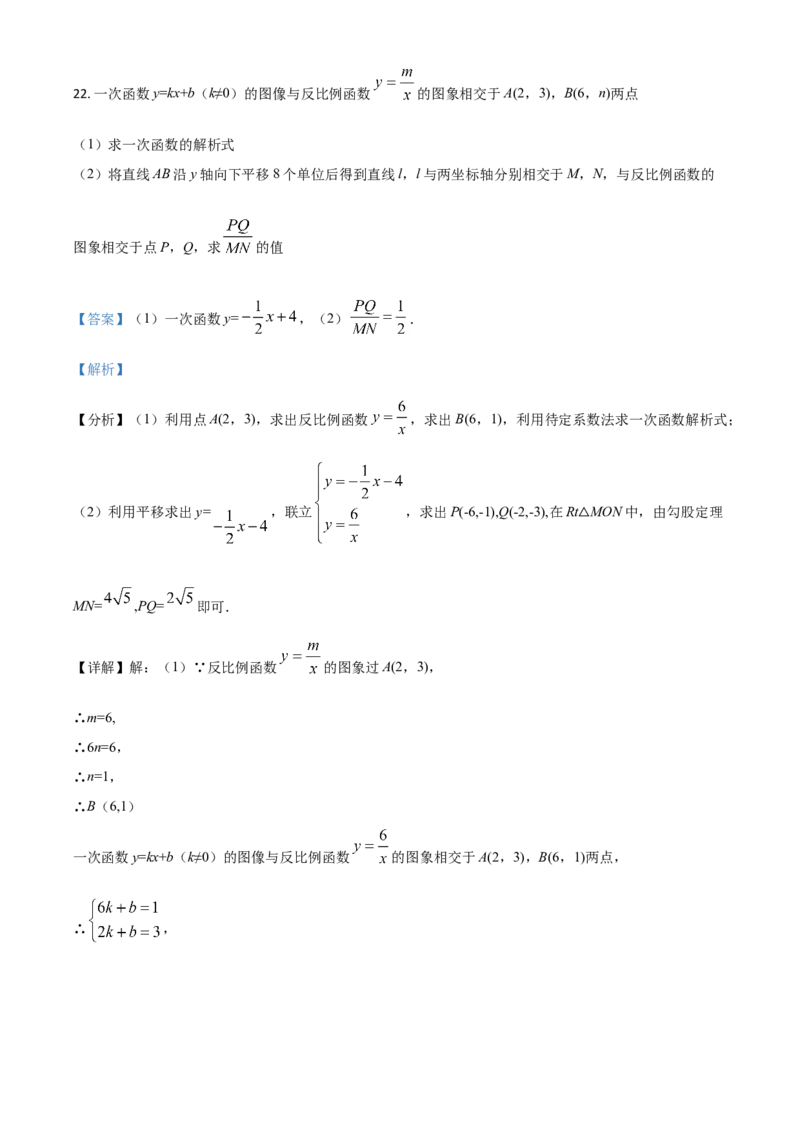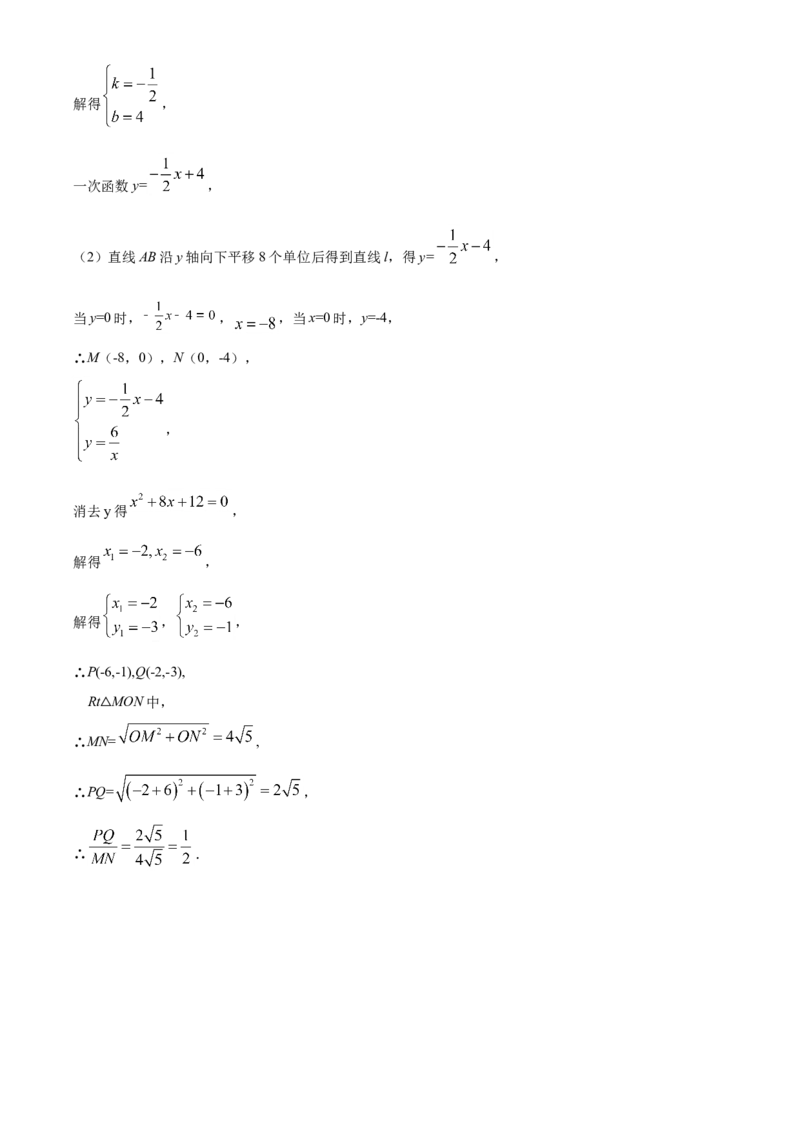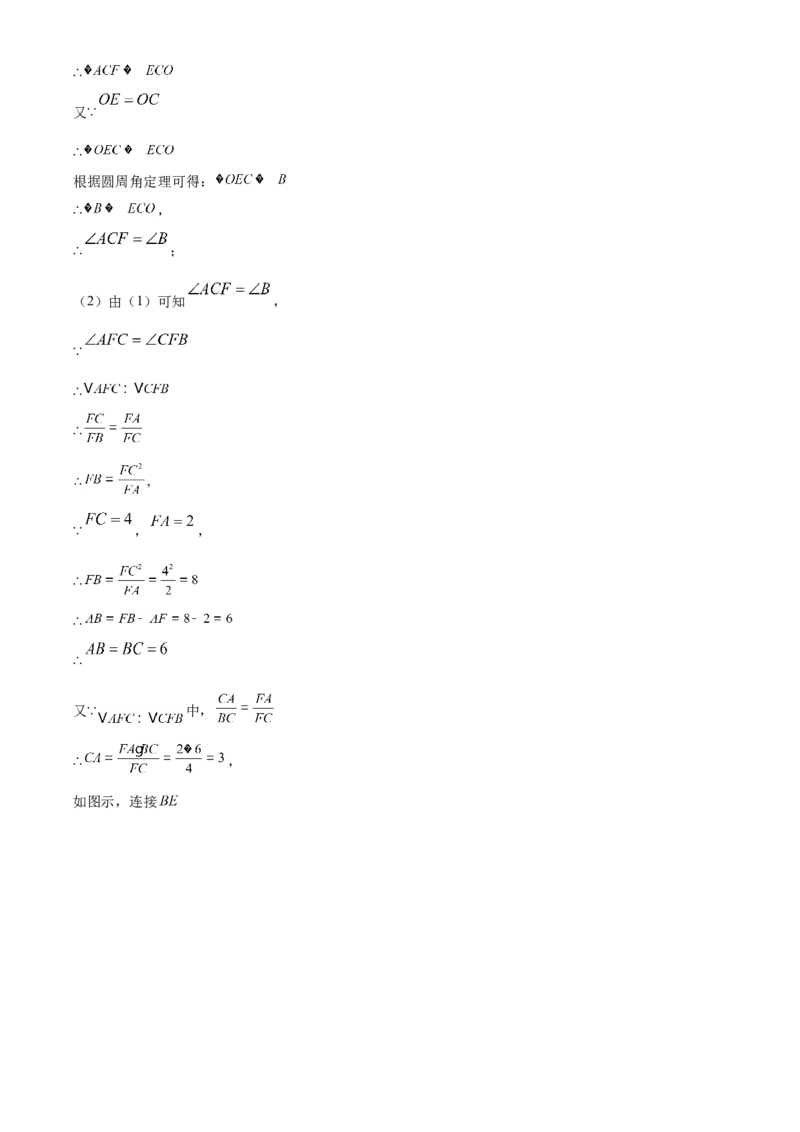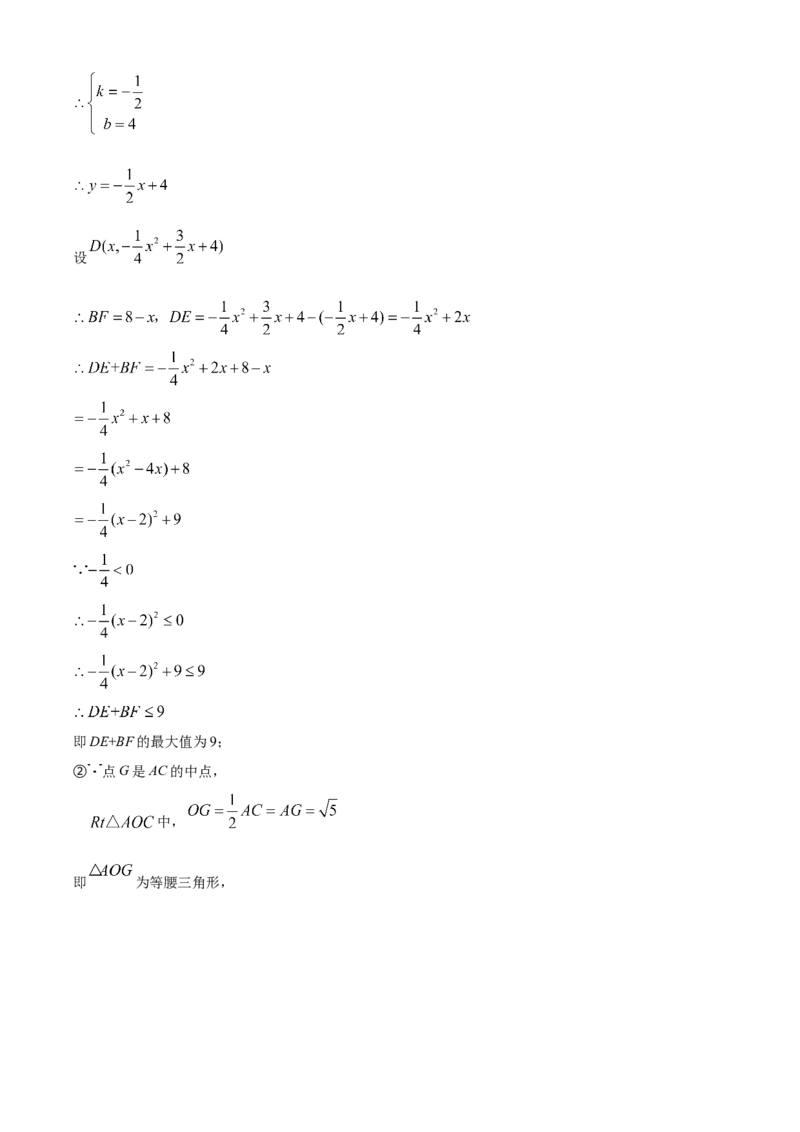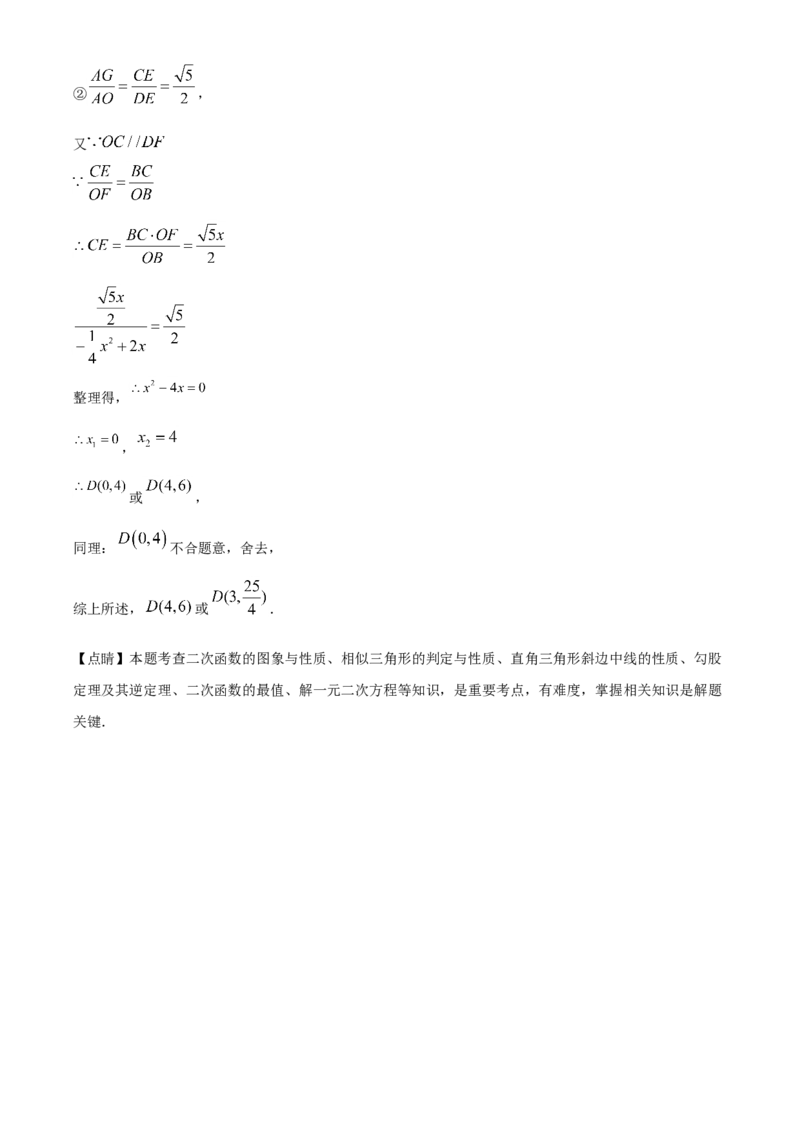文档内容
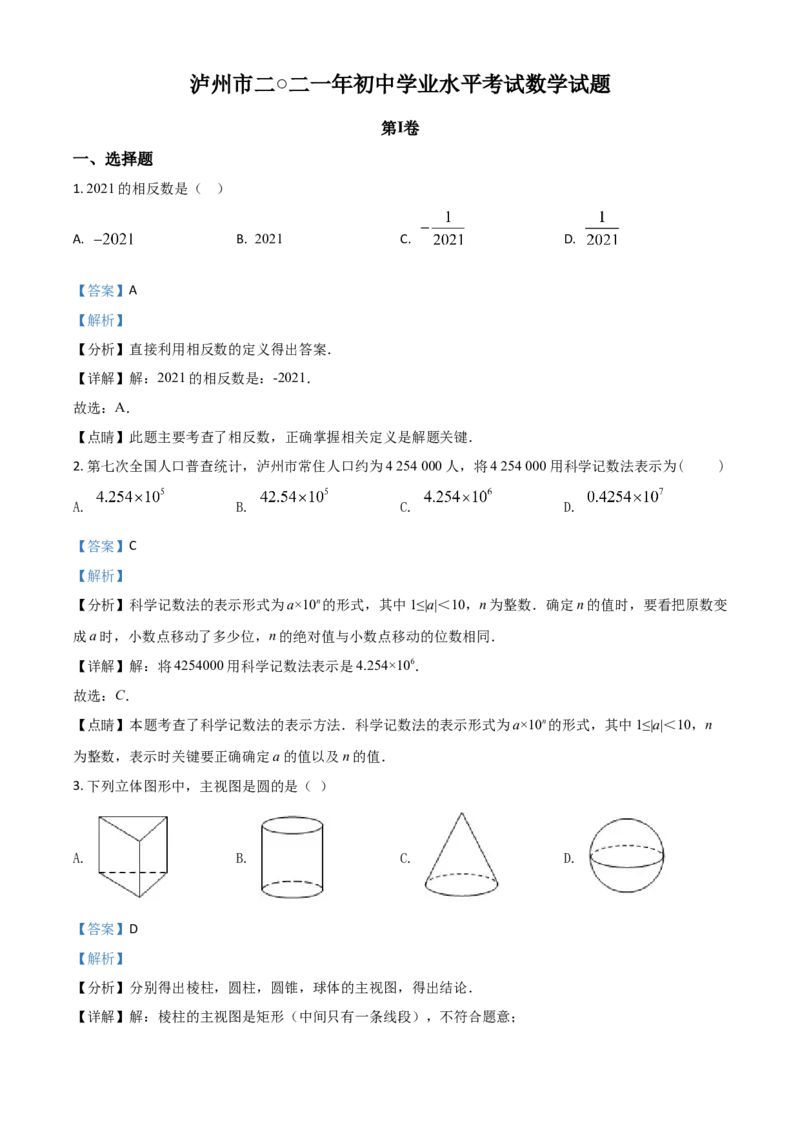
泸州市二○二一年初中学业水平考试数学试题
第Ⅰ卷
一、选择题
1. 2021的相反数是( )
A. B. 2021 C. D.
【答案】A
【解析】
【分析】直接利用相反数的定义得出答案.
【详解】解:2021的相反数是:-2021.
故选:A.
【点睛】此题主要考查了相反数,正确掌握相关定义是解题关键.
2. 第七次全国人口普查统计,泸州市常住人口约为4 254 000人,将4 254 000用科学记数法表示为( )
A. B. C. D.
【答案】C
【解析】
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变
成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
【详解】解:将4254000用科学记数法表示是4.254×106.
故选:C.
【点睛】本题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n
为整数,表示时关键要正确确定a的值以及n的值.
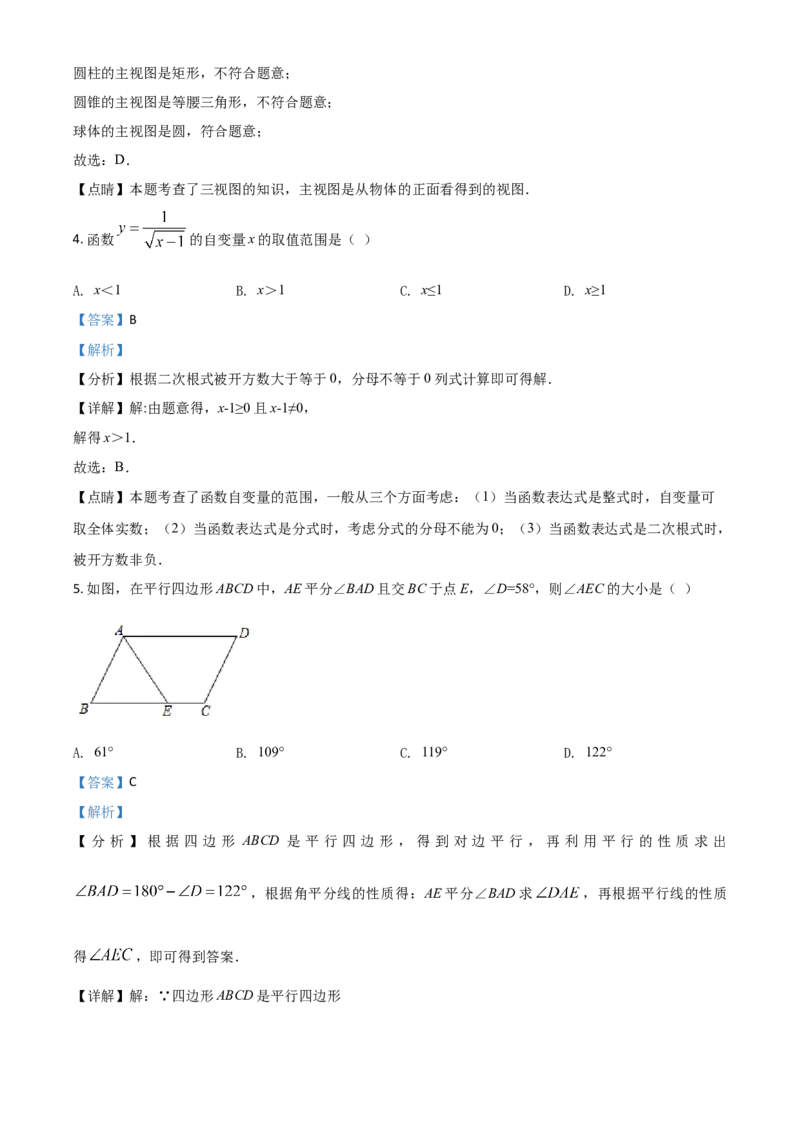
3. 下列立体图形中,主视图是圆的是( )
A. B. C. D.
【答案】D
【解析】
【分析】分别得出棱柱,圆柱,圆锥,球体的主视图,得出结论.
【详解】解:棱柱的主视图是矩形(中间只有一条线段),不符合题意;圆柱的主视图是矩形,不符合题意;
圆锥的主视图是等腰三角形,不符合题意;
球体的主视图是圆,符合题意;
故选:D.
【点睛】本题考查了三视图的知识,主视图是从物体的正面看得到的视图.
4. 函数 的自变量x的取值范围是( )
A. x<1 B. x>1 C. x≤1 D. x≥1
【答案】B
【解析】
【分析】根据二次根式被开方数大于等于0,分母不等于0列式计算即可得解.
【详解】解:由题意得,x-1≥0且x-1≠0,
解得x>1.
故选:B.
【点睛】本题考查了函数自变量的范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可
取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,
被开方数非负.
5. 如图,在平行四边形ABCD中,AE平分∠BAD且交BC于点E,∠D=58°,则∠AEC的大小是( )
A. 61° B. 109° C. 119° D. 122°
【答案】C
【解析】
【 分 析 】 根 据 四 边 形 ABCD 是 平 行 四 边 形 , 得 到 对 边 平 行 , 再 利 用 平 行 的 性 质 求 出
,根据角平分线的性质得:AE平分∠BAD求 ,再根据平行线的性质
得 ,即可得到答案.
【详解】解:∵四边形ABCD是平行四边形∴ ,
∴
∵AE平分∠BAD
∴
∵
∴
故选C.
【点睛】本题考查了平行四边形的性质,角平分线的性质,能利用平行四边形的性质找到角与角的关系,
是解答此题的关键.
6. 在平面直角坐标系中,将点A(-3,-2)向右平移5个单位长度得到点B,则点B关于y轴对称点 的坐标
为( )
A. (2,2) B. (-2,2) C. (-2,-2) D. (2,-2)
【答案】C
【解析】
【分析】根据点的平移规律左减右加可得点B的坐标,然后再根据关于B轴的对称点的坐标特点:横坐标
互为相反数,纵坐标不变可得答案.
【详解】解:点A(-3,-2)向右平移5个单位长度得到点B(2,-2),
点B关于y轴对称点 的坐标为(-2,-2),
故选:C.
【点睛】本题主要考查了点的平移和关于y轴的对称点的坐标特点,关键是掌握点的坐标的变化规律.
7. 下列命题是真命题的是( )
A. 对角线相等的四边形是平行四边形
B. 对角线互相平分且相等的四边形是矩形
C. 对角线互相垂直的四边形是菱形
D. 对角线互相垂直平分的四边形是正方形
【答案】B
【解析】
【分析】A、根据平行四边形的判定定理作出判断;B、根据矩形的判定定理作出判断;C、根据菱形的判定定理作出判断;D、根据正方形的判定定理作出判断.
【详解】解:A、对角线互相平分的四边形是平行四边形;故本选项错误,不符合题意;
B、对角线互相平分且相等的四边形是矩形;故本选项正确,符合题意;
C、对角线互相垂直的平行四边形是菱形;故本选项错误,不符合题意;
D、对角线互相垂直平分且相等的四边形是正方形;故本选项错误,不符合题意;
故选:B.
【点睛】本题综合考查了正方形、矩形、菱形及平行四边形的判定.解答此题时,必须理清矩形、正方形、
菱形与平行四边形间的关系.
8. 在锐角 ABC中,∠A,∠B,∠C所对的边分别为a,b,c,有以下结论:
(其中R为 ABC的外接圆半径)成立.在 ABC中,若∠A=75°,∠B=45°,c=4,则 ABC的外接圆面
积为( )
A. B. C. D.
【答案】A
【解析】
【分析】方法一:先求出∠C,根据题目所给的定理, , 利用圆的面积公式S = .
圆
方法二:设△ABC的外心为O,连结OA,OB,过O作OD⊥AB于D,由三角形内角和可求∠C=60°,由
圆周角定理可求∠AOB=2∠C=120°,由等腰三角形性质,∠OAB=∠OBA= ,由垂径定理可求AD=BD=
,利用三角函数可求OA= ,利用圆的面积公式S = .
圆
【详解】解:方法一:∵∠A=75°,∠B=45°,
∴∠C=180°-∠A-∠B=180°-75°-45°=60°,
有题意可知 ,
∴ ,∴S = .
圆
方法二:设 ABC的外心为O,连结OA,OB,过O作OD⊥AB于D,
∵∠A=75°,△∠B=45°,
∴∠C=180°-∠A-∠B=180°-75°-45°=60°,
∴∠AOB=2∠C=2×60°=120°,
∵OA=OB,
∴∠OAB=∠OBA= ,
∵OD⊥AB,AB为弦,
∴AD=BD= ,
∴AD=OAcos30°,
∴OA= ,
∴S = .
圆
故答案为A.
【点睛】本题考查三角形的外接圆,三角形内角和,圆周角定理,等腰三角形性质,垂径定理,锐角三角
函数,圆的面积公式,掌握三角形的外接圆,三角形内角和,圆周角定理,等腰三角形性质,垂径定理,
锐角三角函数,圆的面积公式是解题关键.
9. 关于x的一元二次方程 的两实数根 ,满足 ,则 的
值是( )
A. 8 B. 16 C. 32 D. 16或40【答案】C
【解析】
【分析】根据一元二次方程根与系数的关系,即韦达定理,先解得 或 ,再分别代入一元二次
方程中,利用完全平方公式变形解题即可.
【详解】解:一元二次方程
或
当 时,
原一元二次方程为
,
,
当 时,原一元二次方程为
原方程无解,不符合题意,舍去,
故选:C.
【点睛】本题考查一元二次方程根与系数的关系,韦达定理等知识,涉及解一元二次方程,是重要考点,
难度较易,掌握相关知识是解题关键.10. 已知 , ,则 的值是( )
A. 2 B. C. 3 D.
【答案】C
【解析】
【分析】根据同底数幂的乘法 ,可求 再整体代入即可.
【详解】解: ∵ , ,
∴ ,
∴ ,
∴ .
故选:C.
【点睛】本题考查幂的乘方,同底数幂的乘法逆运算,代数式求值,掌握幂的乘方,同底数幂的乘法法则,
与代数式值求法是解题关键.
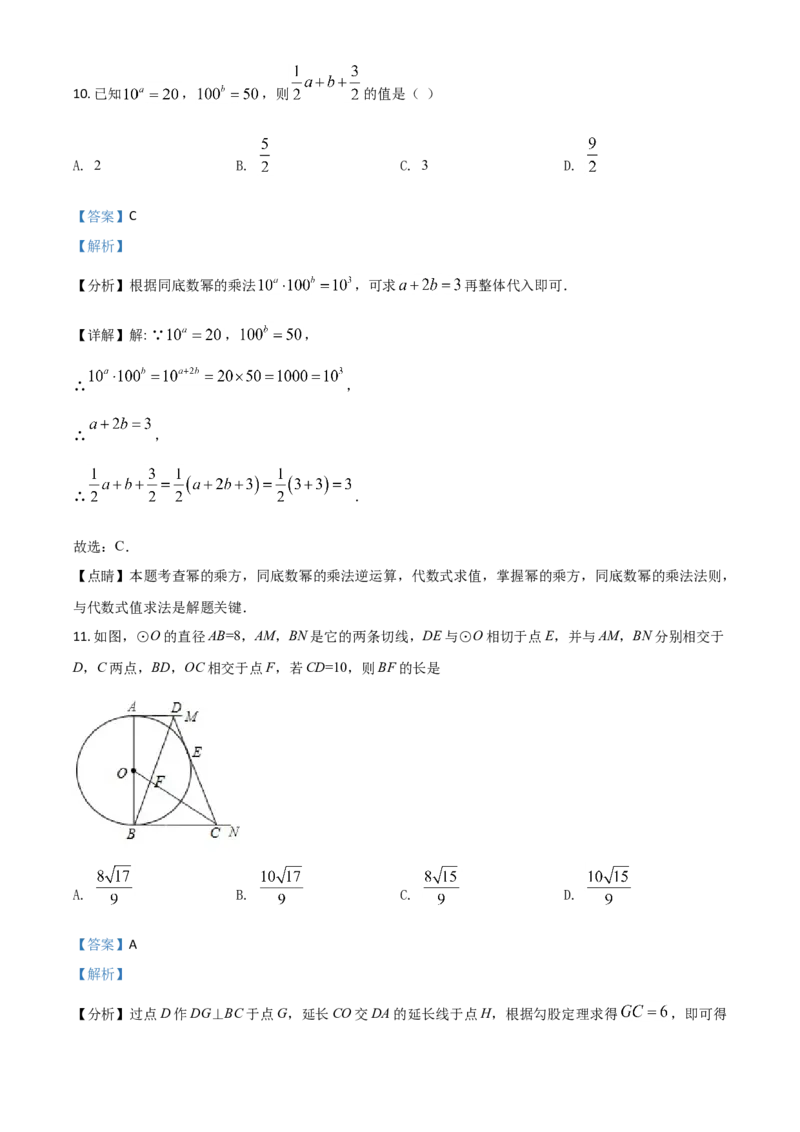
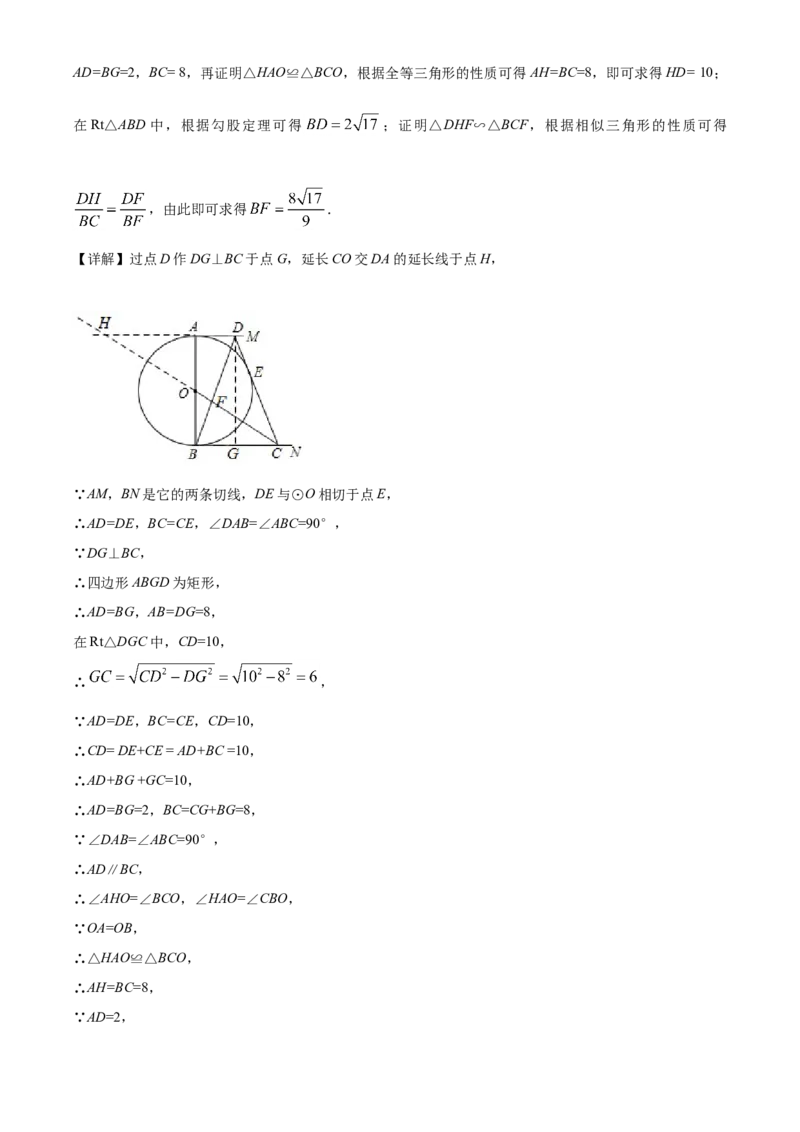
11. 如图,⊙O的直径AB=8,AM,BN是它的两条切线,DE与⊙O相切于点E,并与AM,BN分别相交于
D,C两点,BD,OC相交于点F,若CD=10,则BF的长是
A. B. C. D.
【答案】A
【解析】
【分析】过点D作DG⊥BC于点G,延长CO交DA的延长线于点H,根据勾股定理求得 ,即可得AD=BG=2,BC= 8,再证明△HAO≌△BCO,根据全等三角形的性质可得AH=BC=8,即可求得HD= 10;
在Rt△ABD 中,根据勾股定理可得 ;证明△DHF∽△BCF,根据相似三角形的性质可得
,由此即可求得 .
【详解】过点D作DG⊥BC于点G,延长CO交DA的延长线于点H,
∵AM,BN是它的两条切线,DE与⊙O相切于点E,
∴AD=DE,BC=CE,∠DAB=∠ABC=90°,
∵DG⊥BC,
∴四边形ABGD为矩形,
∴AD=BG,AB=DG=8,
在Rt△DGC中,CD=10,
∴ ,
∵AD=DE,BC=CE,CD=10,
∴CD= DE+CE = AD+BC =10,
∴AD+BG +GC=10,
∴AD=BG=2,BC=CG+BG=8,
∵∠DAB=∠ABC=90°,
∴AD∥BC,
∴∠AHO=∠BCO,∠HAO=∠CBO,
∵OA=OB,
∴△HAO≌△BCO,
∴AH=BC=8,
∵AD=2,∴HD=AH+AD=10;
在Rt△ABD中,AD=2,AB=8,
∴ ,
∵AD∥BC,
∴△DHF∽△BCF,
∴ ,
∴ ,
解得, .
故选A.
【点睛】本题是圆的综合题,考查了切线长定理、勾股定理、全等三角形的判定及性质、相似三角形的判
定于性质,熟练运用相关知识是解决问题的关键.
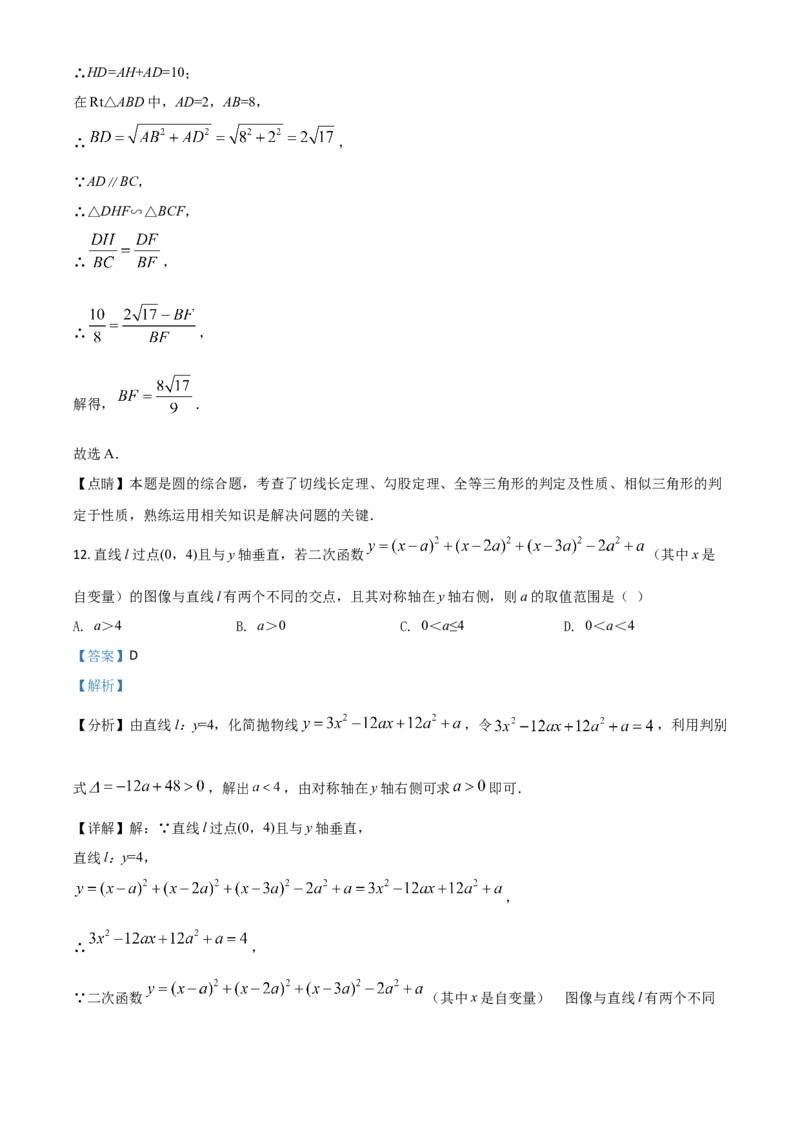
12. 直线l过点(0,4)且与y轴垂直,若二次函数 (其中x是
自变量)的图像与直线l有两个不同的交点,且其对称轴在y轴右侧,则a的取值范围是( )
A. a>4 B. a>0 C. 0<a≤4 D. 0<a<4
【答案】D
【解析】
【分析】由直线l:y=4,化简抛物线 ,令 ,利用判别
式 ,解出 ,由对称轴在y轴右侧可求 即可.
【详解】解:∵直线l过点(0,4)且与y轴垂直,
直线l:y=4,
,
∴ ,
的
∵二次函数 (其中x是自变量) 图像与直线l有两个不同的交点,
∴ ,
,
∴ ,
又∵对称轴在y轴右侧,
,
∴ ,
∴0<a<4.
故选择D.
【点睛】本题考查二次函数与直线的交点问题,抛物线对称轴,一元二次方程两个不等实根,根的判别式,
掌握二次函数与直线的交点问题转化为一元二次方程实根问题,根的判别式,抛物线对称轴公式是解题关
键.
第Ⅱ卷
二、填空题
13. 分解因式: ___________.
【答案】 .
【解析】
【分析】先提取公因式4,再利用平方差公式分解即可.
【详解】解: .
故答案为: .
【点睛】本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再
用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.
14. 不透明袋子重病装有3个红球,5个黑球,4个白球,这些球除颜色外无其他差别,从袋子中随机摸出
一个球,则摸出红球的概率是_________.
【答案】
【解析】【分析】用红球的数量除以球的总数量即可解题.
【详解】解:根据题意,从袋子中随机摸出一个球,则摸出红球的概率是 ,
故答案为: .
【点睛】本题考查简单概率公式,是基础考点,掌握相关知识是解题关键.
15. 关于x的不等式组 恰好有2个整数解,则实数a的取值范围是_________.
【答案】
【解析】
【分析】首先解每个不等式,根据不等式组只有2个整数解,确定整数解 的值,进而求得a的范围.
【详解】解:
解①得 ,
解②得 ,
不等式组的解集是 .
∵不等式组只有2个整数解,
∴整数解是2,3.
则 ,
∴
故答案是:
【点睛】本题考查的是一元一次不等式组的整数解,根据x的取值范围,得出x的整数解.求不等式组的
解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.
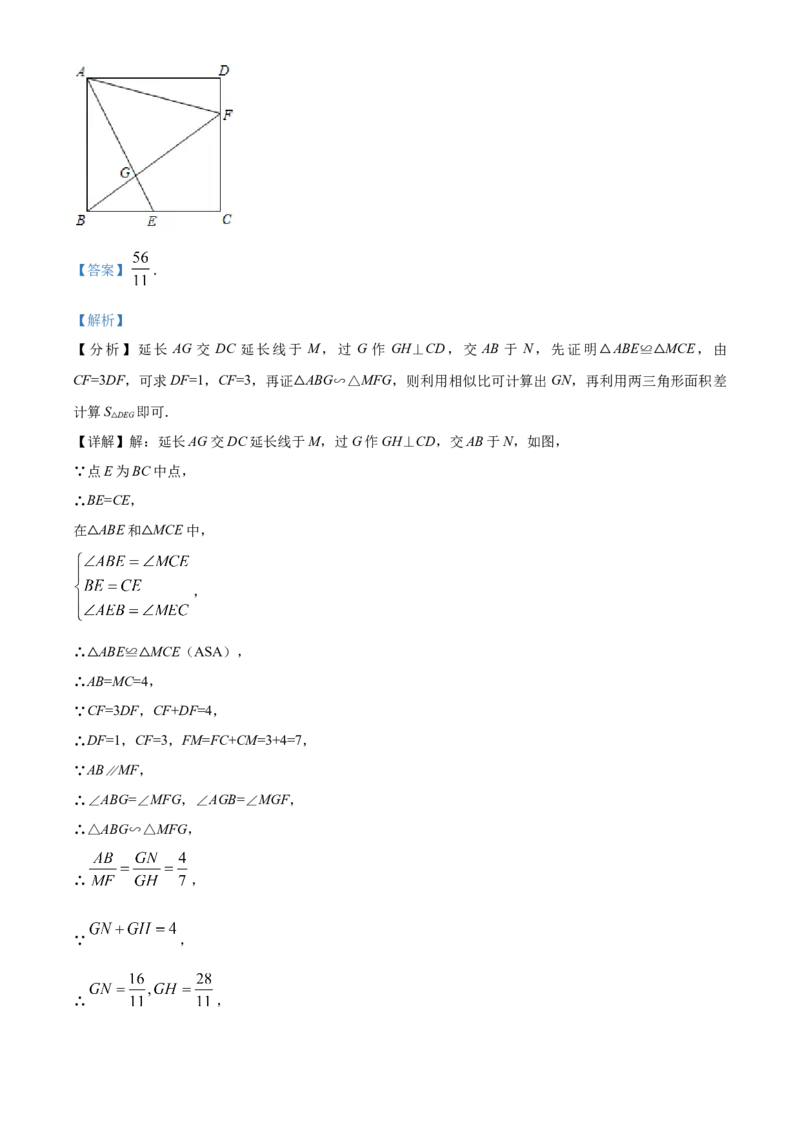
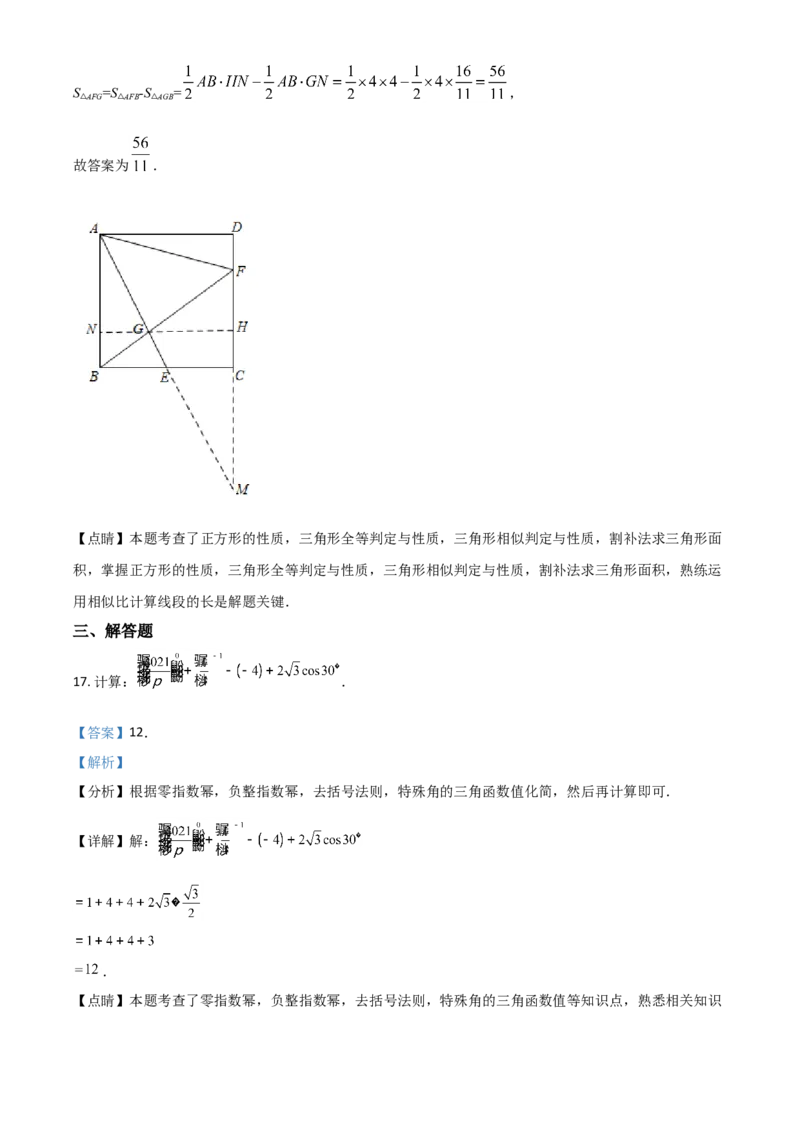
16. 如图,在边长为4的正方形ABCD中,点E是BC的中点,点F在CD上,且CF=3DF,AE,BF相交于
点G,则 AGF的面积是________.【答案】 .
【解析】
【分析】延长 AG 交 DC 延长线于 M,过 G 作 GH⊥CD,交 AB 于 N,先证明 ABE≌ MCE,由
CF=3DF,可求DF=1,CF=3,再证 ABG∽△MFG,则利用相似比可计算出GN,再利△用两三△角形面积差
计算S 即可. △
DEG
△
【详解】解:延长AG交DC延长线于M,过G作GH⊥CD,交AB于N,如图,
∵点E为BC中点,
∴BE=CE,
在 ABE和 MCE中,
△ △
,
∴ ABE≌ MCE(ASA),
∴△AB=MC=△4,
∵CF=3DF,CF+DF=4,
∴DF=1,CF=3,FM=FC+CM=3+4=7,
∵AB∥MF,
∴∠ABG=∠MFG,∠AGB=∠MGF,
∴△ABG∽△MFG,
∴ ,
∵ ,
∴ ,S =S -S = ,
AFG AFB AGB
△ △ △
故答案为 .
【点睛】本题考查了正方形的性质,三角形全等判定与性质,三角形相似判定与性质,割补法求三角形面
积,掌握正方形的性质,三角形全等判定与性质,三角形相似判定与性质,割补法求三角形面积,熟练运
用相似比计算线段的长是解题关键.
三、解答题
17. 计算: .
【答案】12.
【解析】
【分析】根据零指数幂,负整指数幂,去括号法则,特殊角的三角函数值化简,然后再计算即可.
【详解】解:
.
【点睛】本题考查了零指数幂,负整指数幂,去括号法则,特殊角的三角函数值等知识点,熟悉相关知识点是解题的关键
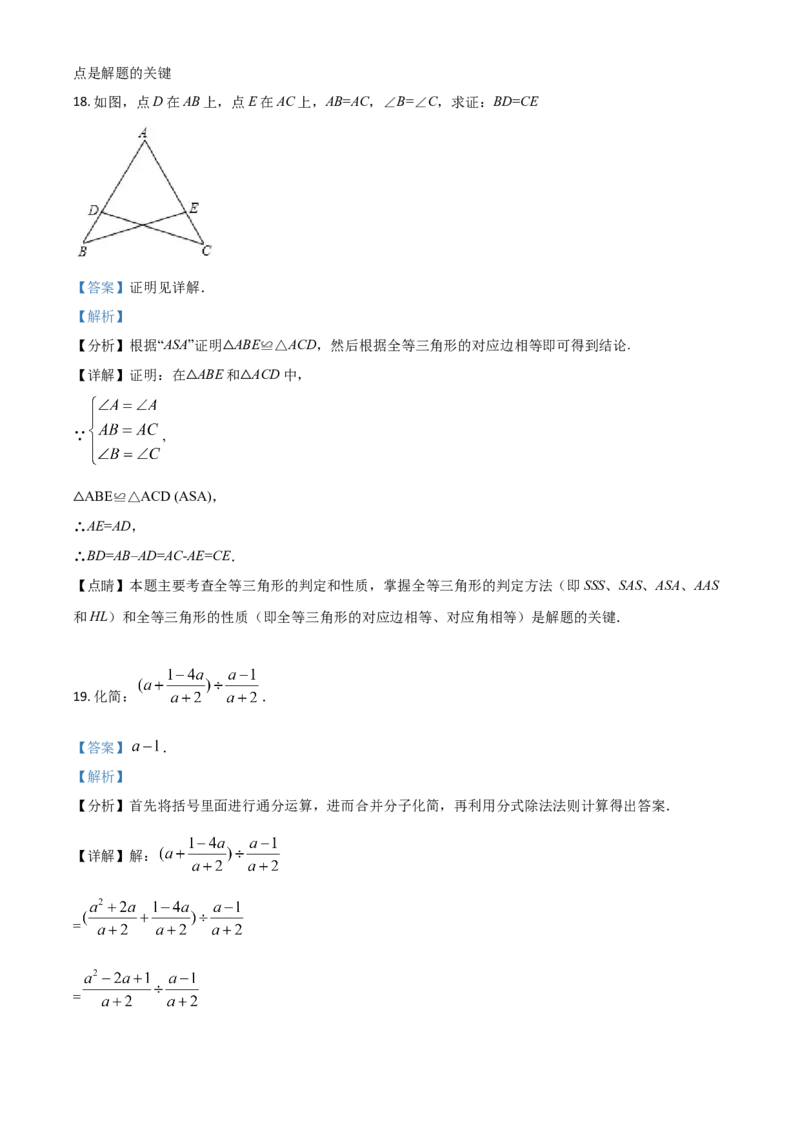
18. 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:BD=CE
【答案】证明见详解.
【解析】
【分析】根据“ASA”证明 ABE≌△ACD,然后根据全等三角形的对应边相等即可得到结论.
【详解】证明:在 ABE△和 ACD中,
△ △
∵ ,
ABE≌△ACD (ASA),
△∴AE=AD,
∴BD=AB–AD=AC-AE=CE.
【点睛】本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS
和HL)和全等三角形的性质(即全等三角形的对应边相等、对应角相等)是解题的关键.
19. 化简: .
【答案】 .
【解析】
【分析】首先将括号里面进行通分运算,进而合并分子化简,再利用分式除法法则计算得出答案.
【详解】解:
=
==
= .
【点睛】此题主要考查了分式的混合运算,正确进行分式的通分运算是解答此题的关键.
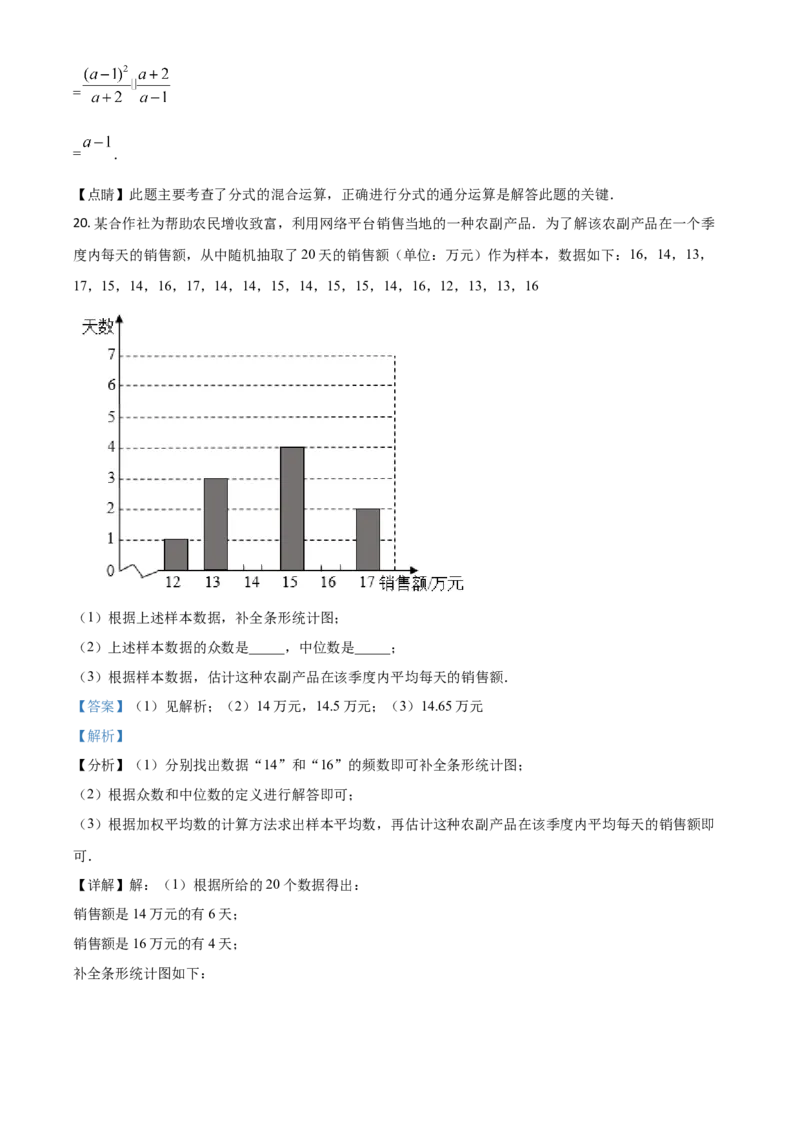
20. 某合作社为帮助农民增收致富,利用网络平台销售当地的一种农副产品.为了解该农副产品在一个季
度内每天的销售额,从中随机抽取了20天的销售额(单位:万元)作为样本,数据如下:16,14,13,
17,15,14,16,17,14,14,15,14,15,15,14,16,12,13,13,16
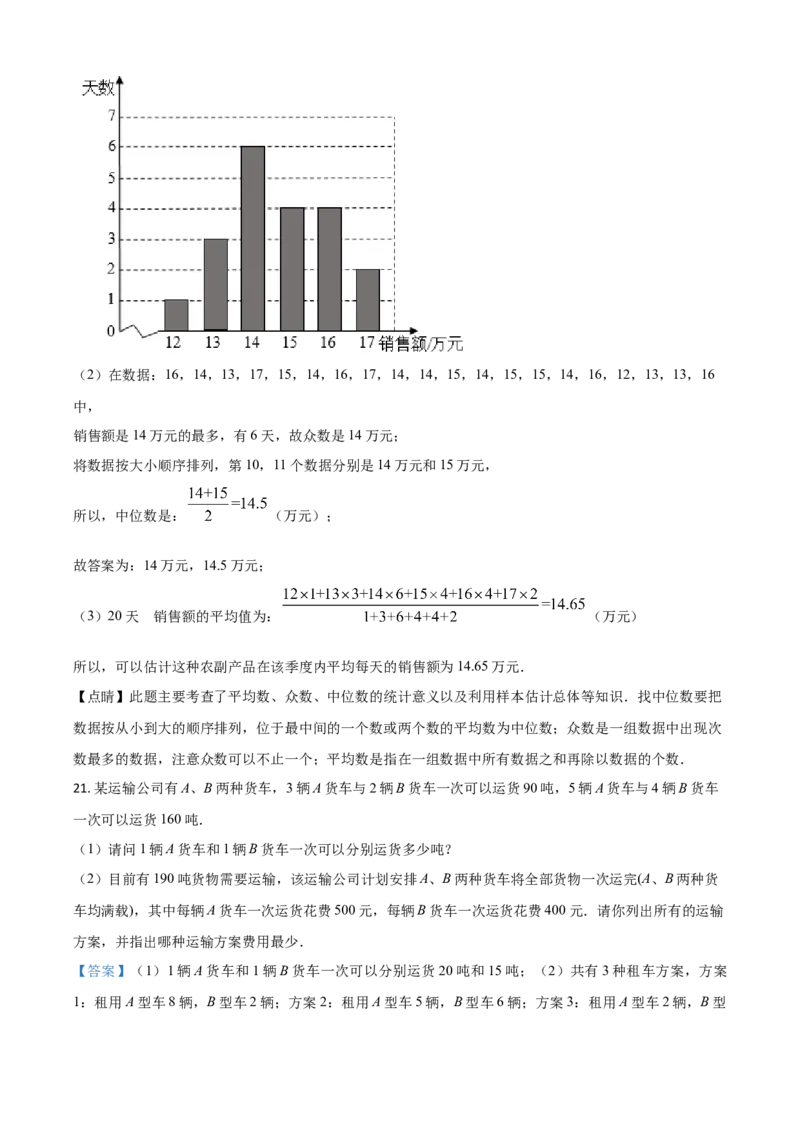
(1)根据上述样本数据,补全条形统计图;
(2)上述样本数据的众数是_____,中位数是_____;
(3)根据样本数据,估计这种农副产品在该季度内平均每天的销售额.
【答案】(1)见解析;(2)14万元,14.5万元;(3)14.65万元
【解析】
【分析】(1)分别找出数据“14”和“16”的频数即可补全条形统计图;
(2)根据众数和中位数的定义进行解答即可;
(3)根据加权平均数的计算方法求出样本平均数,再估计这种农副产品在该季度内平均每天的销售额即
可.
【详解】解:(1)根据所给的20个数据得出:
销售额是14万元的有6天;
销售额是16万元的有4天;
补全条形统计图如下:(2)在数据:16,14,13,17,15,14,16,17,14,14,15,14,15,15,14,16,12,13,13,16
中,
销售额是14万元的最多,有6天,故众数是14万元;
将数据按大小顺序排列,第10,11个数据分别是14万元和15万元,
所以,中位数是: (万元);
故答案为:14万元,14.5万元;
(3)20天 的销售额的平均值为: (万元)
所以,可以估计这种农副产品在该季度内平均每天的销售额为14.65万元.
【点睛】此题主要考查了平均数、众数、中位数的统计意义以及利用样本估计总体等知识.找中位数要把
数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次
数最多的数据,注意众数可以不止一个;平均数是指在一组数据中所有数据之和再除以数据的个数.
21. 某运输公司有A、B两种货车,3辆A货车与2辆B货车一次可以运货90吨,5辆A货车与4辆B货车
一次可以运货160吨.
(1)请问1辆A货车和1辆B货车一次可以分别运货多少吨?
(2)目前有190吨货物需要运输,该运输公司计划安排A、B两种货车将全部货物一次运完(A、B两种货
车均满载),其中每辆A货车一次运货花费500元,每辆B货车一次运货花费400元.请你列出所有的运输
方案,并指出哪种运输方案费用最少.
【答案】(1)1辆A货车和1辆B货车一次可以分别运货20吨和15吨;(2)共有3种租车方案,方案
1:租用A型车8辆,B型车2辆;方案2:租用A型车5辆,B型车6辆;方案3:租用A型车2辆,B型车10辆;租用A型车8辆,B型车2辆最少.
【解析】
【分析】(1)设1辆A货车和1辆B货车一次可以分别运货x吨和y吨,根据“3辆A货车与2辆B货车
一次可以运货90吨,5辆A货车与4辆B货车一次可以运货160吨”列方程组求解可得;
(2)设货运公司安排A货车m辆,则安排B货车n辆.根据“共有190吨货物”列出二元一次方程组,
结合m,n均为正整数,即可得出各运输方案.再根据方案计算比较得出费用最小的数据.
【详解】解:(1)1辆A货车和1辆B货车一次可以分别运货x吨和y吨,
根据题意可得: ,
解得: ,
答:1辆A货车和1辆B货车一次可以分别运货20吨和15吨;
(2)设安排A型车m辆,B型车n辆,
依题意得:20m+15n=190,即 ,
又∵m,n均为正整数,
∴ 或 或 ,
∴共有3种运输方案,
方案1:安排A型车8辆,B型车2辆;
方案2:安排A型车5辆,B型车6辆;
方案3:安排A型车2辆,B型车10辆.
方案1所需费用:500 8+400 2=4800(元);
方案2所需费用:500 5+400 6=4900(元);
方案3所需费用:500 2+400 10=5000(元);
∵4800<4900<5000,
∴安排A型车8辆,B型车2辆最省钱,最省钱的运输费用为4800元.
【点睛】本题考查了二元一次方程组的应用以及二元一次方程的应用,解题的关键是:(1)找准等量关
系,正确列出二元一次方程组;(2)找准等量关系,正确列出二元一次方程;根据据总费用=500×安排A
型车的辆数+400×B型车的辆数分别求出三种运输方案的总费用.22. 一次函数y=kx+b(k≠0)的图像与反比例函数 的图象相交于A(2,3),B(6,n)两点
(1)求一次函数的解析式
(2)将直线AB沿y轴向下平移8个单位后得到直线l,l与两坐标轴分别相交于M,N,与反比例函数的
图象相交于点P,Q,求 的值
【答案】(1)一次函数y= ,(2) .
【解析】
【分析】(1)利用点A(2,3),求出反比例函数 ,求出 B(6,1),利用待定系数法求一次函数解析式;
(2)利用平移求出y= ,联立 ,求出P(-6,-1),Q(-2,-3),在Rt MON中,由勾股定理
△
MN= ,PQ= 即可.
【详解】解:(1)∵反比例函数 的图象过A(2,3),
∴m=6,
∴6n=6,
∴n=1,
∴B(6,1)
一次函数y=kx+b(k≠0)的图像与反比例函数 的图象相交于A(2,3),B(6,1)两点,
∴ ,解得 ,
一次函数y= ,
(2)直线AB沿y轴向下平移8个单位后得到直线l,得y= ,
当y=0时, , ,当x=0时,y=-4,
∴M(-8,0),N(0,-4),
,
消去y得 ,
解得 ,
解得 , ,
∴P(-6,-1),Q(-2,-3),
在Rt MON中,
△
∴MN= ,
∴PQ= ,
∴ .【点睛】本题考查待定系数法求反比例函数解析式与一次函数解析式,利用平移求平移后直线l.,解方程
组,一元二次方程,勾股定理,掌握待定系数法求反比例函数解析式与一次函数解析式,利用平移求平移
后直线l.,解方程组,一元二次方程,勾股定理是解题关键.
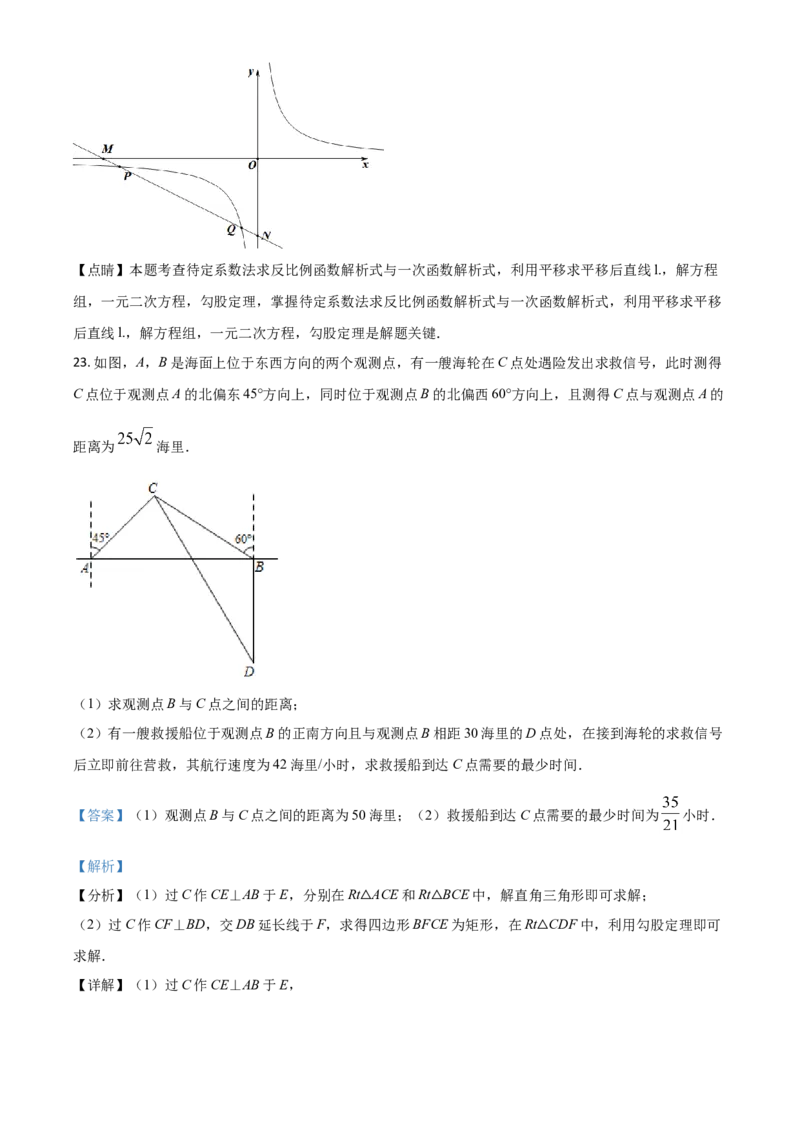
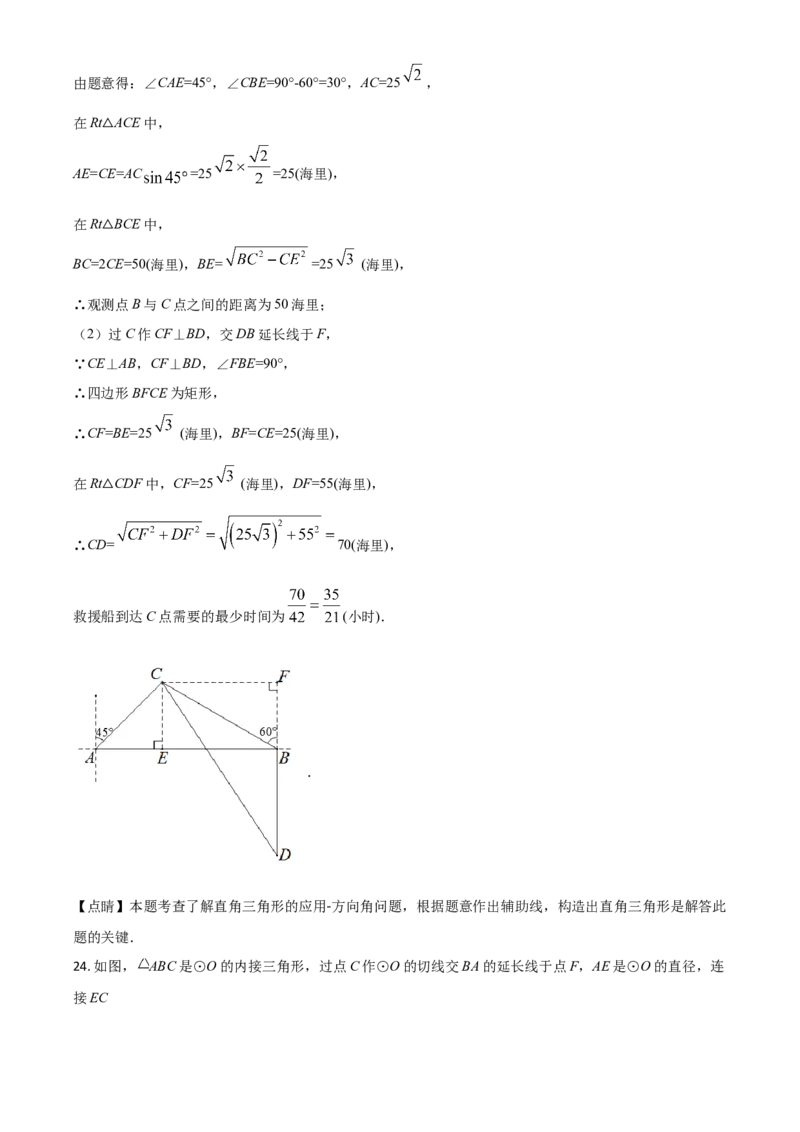
23. 如图,A,B是海面上位于东西方向的两个观测点,有一艘海轮在C点处遇险发出求救信号,此时测得
C点位于观测点A的北偏东45°方向上,同时位于观测点B的北偏西60°方向上,且测得C点与观测点A的
距离为 海里.
(1)求观测点B与C点之间的距离;
(2)有一艘救援船位于观测点B的正南方向且与观测点B相距30海里的D点处,在接到海轮的求救信号
后立即前往营救,其航行速度为42海里/小时,求救援船到达C点需要的最少时间.
【答案】(1)观测点B与C点之间的距离为50海里;(2)救援船到达C点需要的最少时间为 小时.
【解析】
【分析】(1)过C作CE⊥AB于E,分别在Rt ACE和Rt BCE中,解直角三角形即可求解;
(2)过C作CF⊥BD,交DB延长线于F,求得△四边形BFC△E为矩形,在Rt CDF中,利用勾股定理即可
求解. △
【详解】(1)过C作CE⊥AB于E,由题意得:∠CAE=45°,∠CBE=90°-60°=30°,AC=25 ,
在Rt ACE中,
△
AE=CE=AC =25 =25(海里),
在Rt BCE中,
△
BC=2CE=50(海里),BE= =25 (海里),
∴观测点B与C点之间的距离为50海里;
(2)过C作CF⊥BD,交DB延长线于F,
∵CE⊥AB,CF⊥BD,∠FBE=90°,
∴四边形BFCE为矩形,
∴CF=BE=25 (海里),BF=CE=25(海里),
在Rt CDF中,CF=25 (海里),DF=55(海里),
△
∴CD= 70(海里),
救援船到达C点需要的最少时间为 (小时).
.
【点睛】本题考查了解直角三角形的应用-方向角问题,根据题意作出辅助线,构造出直角三角形是解答此
题的关键.
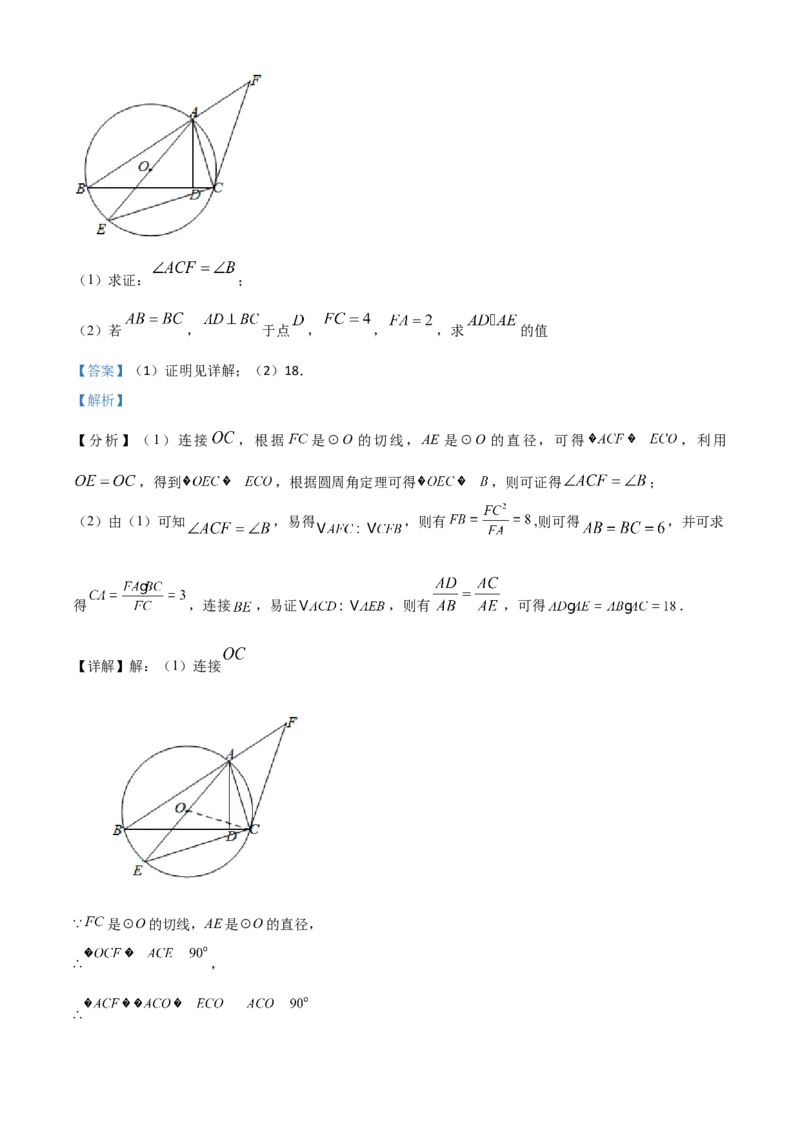
24. 如图, ABC是⊙O的内接三角形,过点C作⊙O的切线交BA的延长线于点F,AE是⊙O的直径,连
接EC(1)求证: ;
(2)若 , 于点 , , ,求 的值
【答案】(1)证明见详解;(2)18.
【解析】
【分析】(1)连接 ,根据 是⊙O 的切线,AE 是⊙O 的直径,可得 ,利用
,得到 ,根据圆周角定理可得 ,则可证得 ;
(2)由(1)可知 ,易得 ,则有 ,则可得 ,并可求
得 ,连接 ,易证 ,则有 ,可得 .
【详解】解:(1)连接
∵ 是⊙O的切线,AE是⊙O的直径,
∴ ,
∴∴
又∵
∴
根据圆周角定理可得:
∴ ,
∴ ;
(2)由(1)可知 ,
∵
∴
∴
∴ ,
∵ , ,
∴
∴
∴
又∵ 中,
∴ ,
如图示,连接∵ ,
∴
∴
∴ .
【点睛】本题考查了圆的性质,等腰三角形的判定与性质,圆周角定理,切线的性质,三角形相似的判定
与性质等知识点,熟悉相关性质是解题的关键.
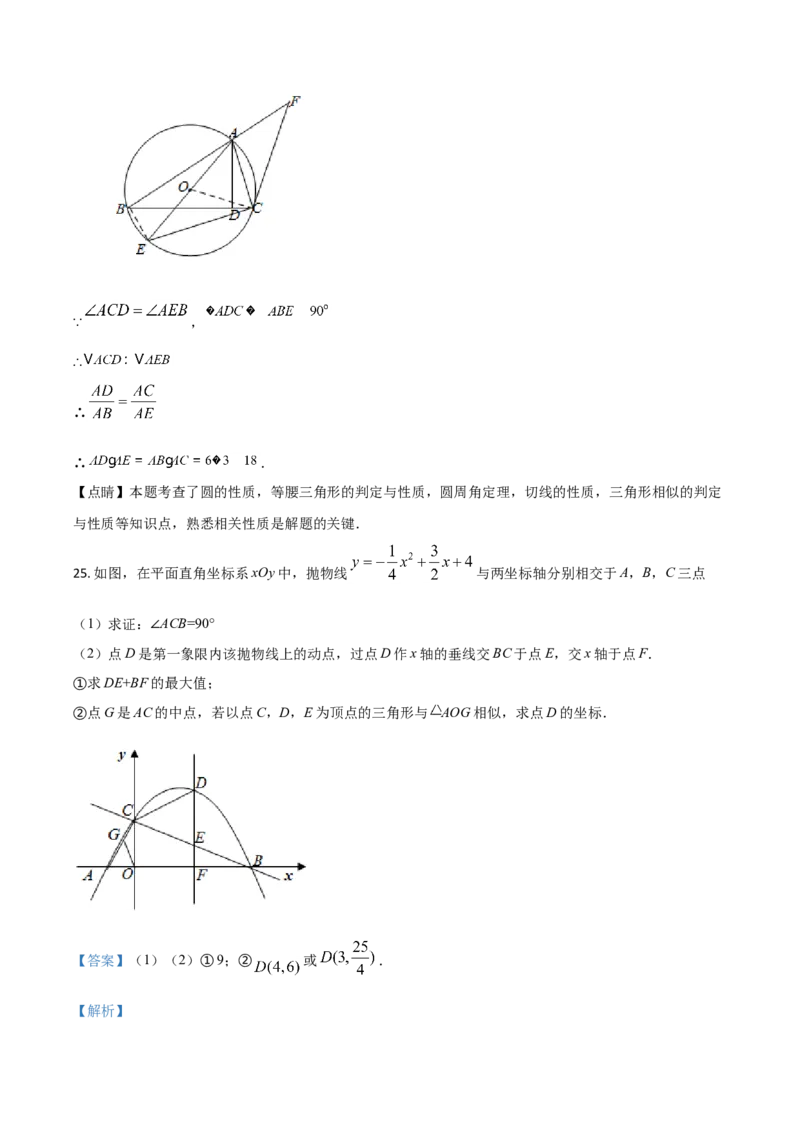
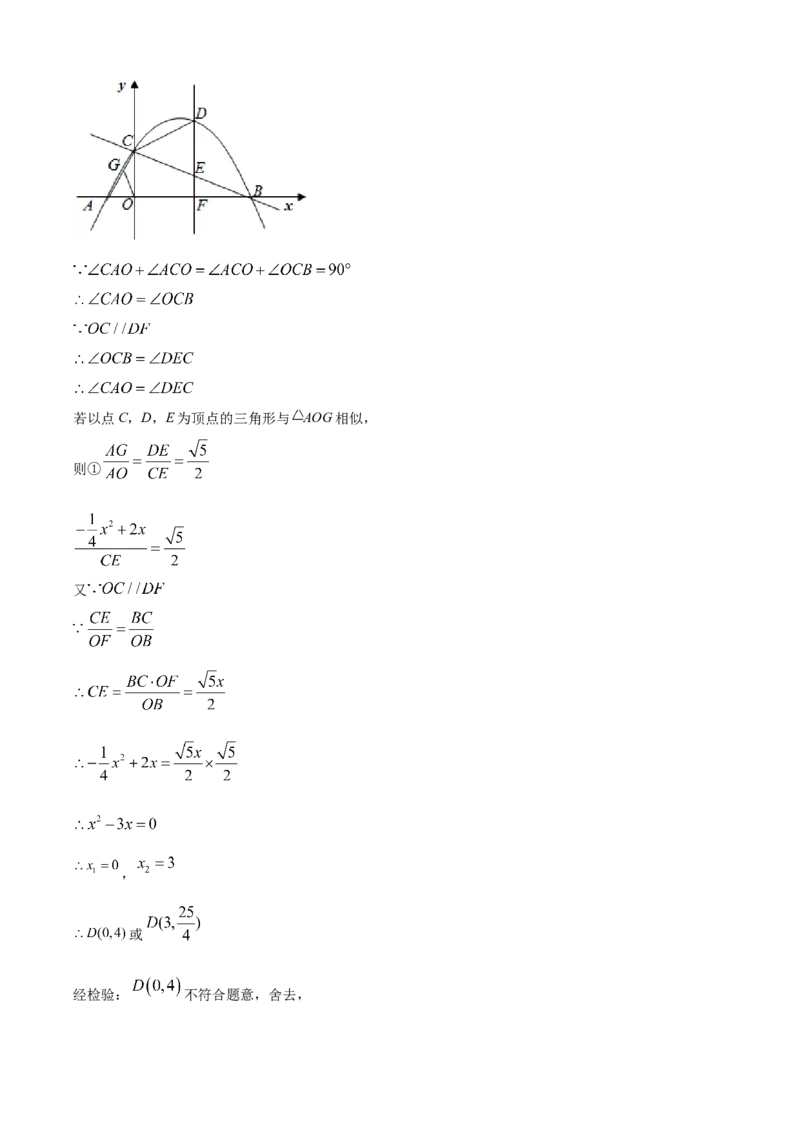
25. 如图,在平面直角坐标系xOy中,抛物线 与两坐标轴分别相交于A,B,C三点
(1)求证:∠ACB=90°
(2)点D是第一象限内该抛物线上的动点,过点D作x轴的垂线交BC于点E,交x轴于点F.
①求DE+BF的最大值;
②点G是AC的中点,若以点C,D,E为顶点的三角形与 AOG相似,求点D的坐标.
【答案】(1)(2)①9;② 或 .
【解析】【分析】(1)分别计算A,B,C三点的坐标,再利用勾股定理求得AB、BC、AC的长,最后利用勾股定
理逆定理解题;
(2)①先解出直线BC的解析式,设 ,接着解出 ,
利用二次函数的配方法求最值;②根据直角三角形斜边的中线性质,解得AG的长,再证明
,再分两种情况讨论以点C,D,E为顶点的三角形与 AOG相似,结合相似三角形对
应边成比例性质解题即可.
【详解】解:(1)令x=0,得
令 得
,
(2)①设直线BC的解析式为: ,代入 , 得设
即DE+BF的最大值为9;
② 点G是AC的中点,
在中,
即 为等腰三角形,若以点C,D,E为顶点的三角形与 AOG相似,
则①
又
,
或
经检验: 不符合题意,舍去,② ,
又
整理得,
,
或 ,
同理: 不合题意,舍去,
综上所述, 或 .
【点睛】本题考查二次函数的图象与性质、相似三角形的判定与性质、直角三角形斜边中线的性质、勾股
定理及其逆定理、二次函数的最值、解一元二次方程等知识,是重要考点,有难度,掌握相关知识是解题
关键.