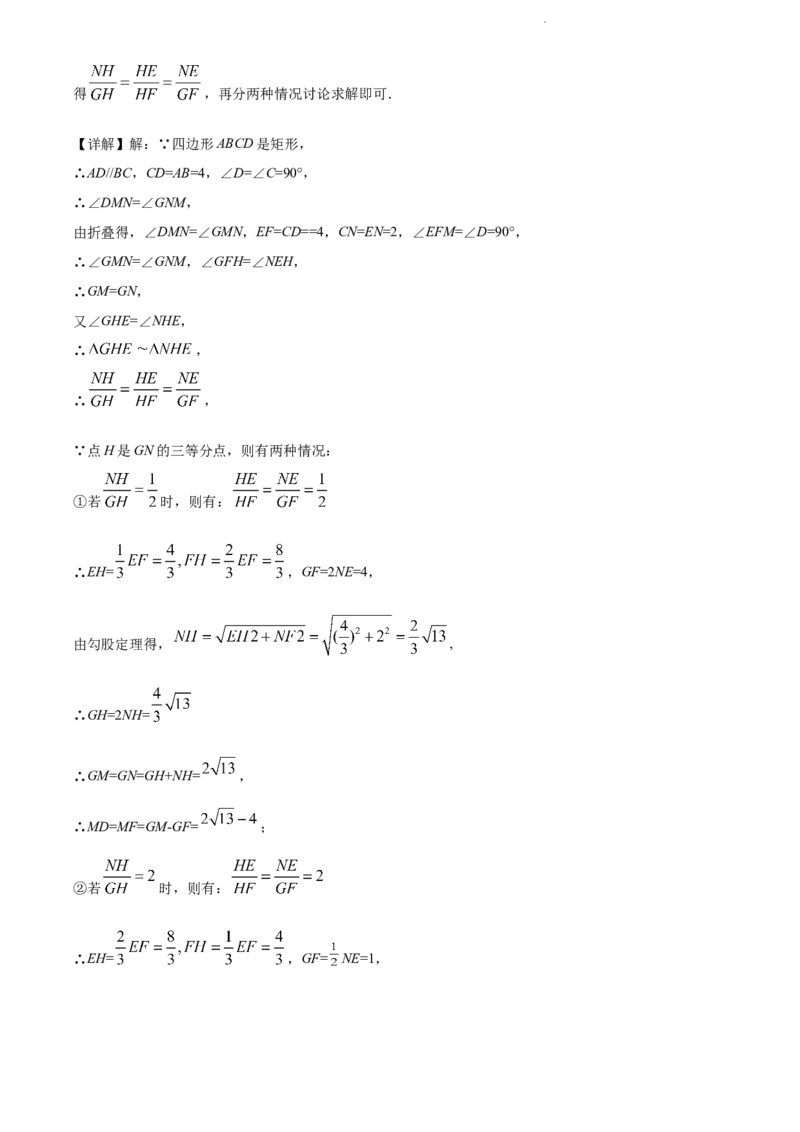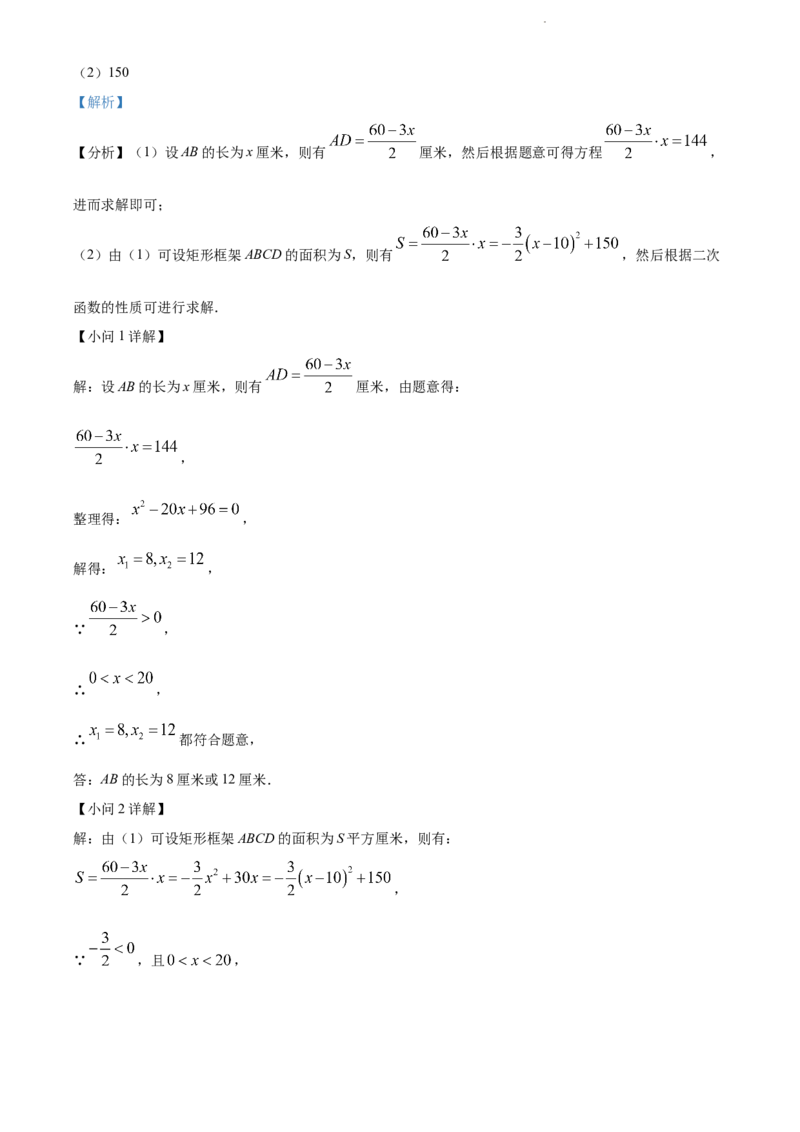文档内容
沈阳市 2022 年初中学业水平考试
数学试题
试题满分120分,考试时间120分钟.
注意事项:
1.答题前,考生须用0.5mm黑色字迹的签字笔在本试题卷规定位置填写自己的姓名、准考
证号;
2.考生须在答题卡上作答,不能在本试题卷上作答,答在本试题卷上无效;
3.考试结束,将本试题卷和答题卡一并交回;
4.本试题卷包括八道大题,25道小题,共6页.如缺页、印刷不清,考生须声明.
一、选择题(下列各题的备选答案中,只有一个答案是正确的.每小题2分,共20分)
1. 计算 正确的是( )
A. 2 B. C. 8 D.
【答案】A
【解析】
【分析】根据有理数的加法运算即可求解.
【详解】解: .
故选:A.
【点睛】本题考查了有理数的加法,掌握有理数的加法法则是解题的关键.
2. 如图是由4个相同的小立方块搭成的几何体,这个几何体的主视图是( )
A. B. C. D.
【答案】D
学科网(北京)股份有限公司【解析】
【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.
【详解】解:从正面看易得上面第一层有1个正方形,第二层左边和右边都有一个正方形,如图所示:
故选:D.
【点睛】本题考查了三视图的知识,主视图是从物体的正面看得到的视图.
3. 下列计算结果正确的是( )
.
A B. C. D.
【答案】D
【解析】
【分析】分别利用幂的乘方法则,同底数幂的除法,积的乘方法则,完全平方公式分别求出即可.
【详解】A. ,故此选项计算错误,不符合题意;
B. ,故此选项计算错误,不符合题意;
C. ,故此选项计算错误,不符合题意;
D. ,故此选项计算正确,符合题意;
故选:D.
【点睛】本题考查幂的乘方法则,同底数幂的除法,积的乘方法则,完全平方公式,熟练掌握相关计算法
则是解答本题的关键.幂的乘方,底数不变,指数相乘;同底数幂相除,底数不变,指数相减;积的乘方,
等于把积的每一个因式分别乘方,再把所得的幂相乘; 与
都叫做完全平方公式,为了区别,我们把前者叫做两数和的完全平方公式,后者
叫做两数差的完全平方公式.
学科网(北京)股份有限公司4. 在平面直角坐标系中,点 关于y轴对称的点的坐标是( )
A. B. C. D.
【答案】B
【解析】
【分析】根据“关于y轴对称的两个点的坐标,纵坐标相同,横坐标互为相反数”即可解答.
【详解】解:点A(2,3)关于y轴对称的点的坐标是(-2,3).
故选B.
【点睛】本题考查了关于坐标轴对称的点的坐标特征,对称点的坐标规律:①关于x轴对称的点,横坐标
相同,纵坐标互为相反数;②关于y轴对称的点,纵坐标相同,横坐标互为相反数;(3)关于原点对称的
点,横坐标与纵坐标都互为相反数.
5. 调查某少年足球队全体队员的年龄,得到数据结果如下表:
年龄/岁 11 12 13 14 15
人数 3 4 7 2 2
则该足球队队员年龄的众数是( )
A. 15岁 B. 14岁 C. 13岁 D. 7人
【答案】C
【解析】
【分析】根据众数的定义即一组数据中出现次数最多的数据,即可得出答案.
【详解】解:∵年龄是13岁的人数最多,有7个人,
∴这些队员年龄的众数是13;
故选:C.
【点睛】本题考查了众数,掌握众数的定义是本题的关键,众数是一组数据中出现次数最多的数据.
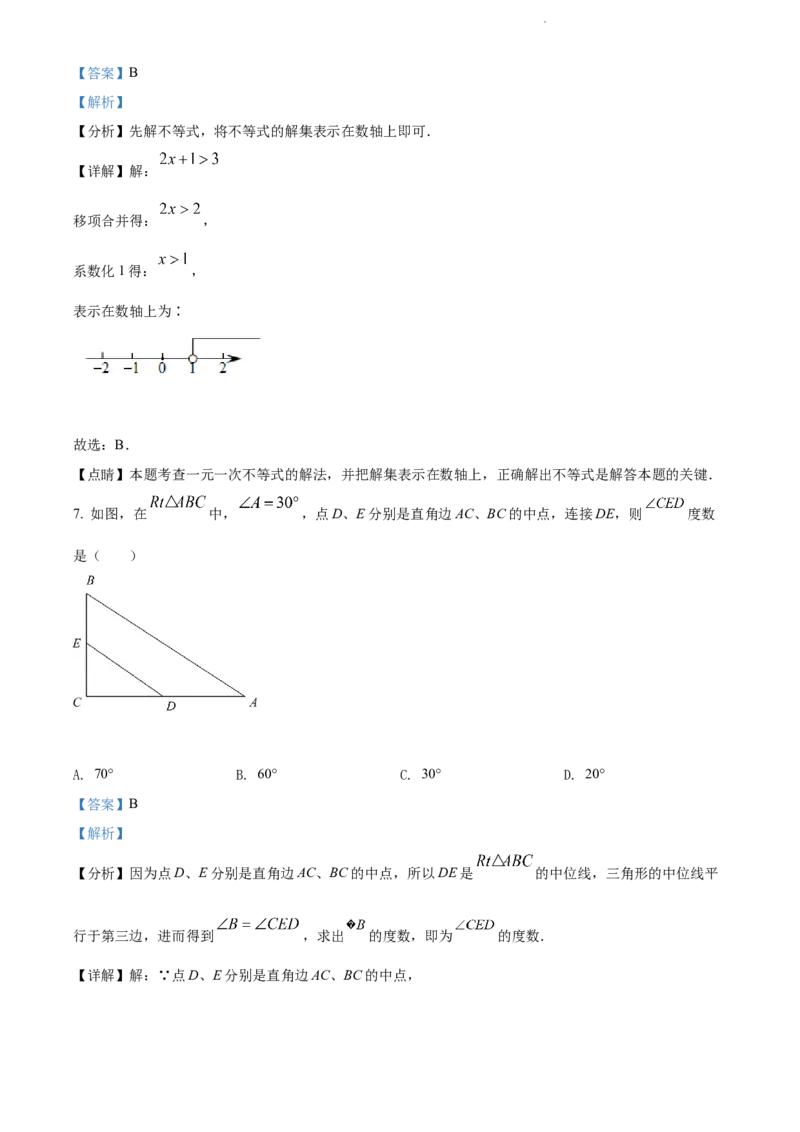
6. 不等式 的解集在数轴上表示正确的是( )
A. B. C.
D.
学科网(北京)股份有限公司【答案】B
【解析】
【分析】先解不等式,将不等式的解集表示在数轴上即可.
【详解】解:
移项合并得: ,
系数化1得: ,
表示在数轴上为∶
故选:B.
【点睛】本题考查一元一次不等式的解法,并把解集表示在数轴上,正确解出不等式是解答本题的关键.
7. 如图,在 中, ,点D、E分别是直角边AC、BC的中点,连接DE,则 度数
是( )
A. 70° B. 60° C. 30° D. 20°
【答案】B
【解析】
【分析】因为点D、E分别是直角边AC、BC的中点,所以DE是 的中位线,三角形的中位线平
行于第三边,进而得到 ,求出 的度数,即为 的度数.
【详解】解:∵点D、E分别是直角边AC、BC的中点,
学科网(北京)股份有限公司∴DE是 的中位线,
∴ ,
∴ ,
∵ , ,
∴ ,
∴ ,
故选:B.
【点睛】本题考查三角形中位线的性质以及三角形内角和,由三角形中位线定义,找到平行线是解答本题
的关键.
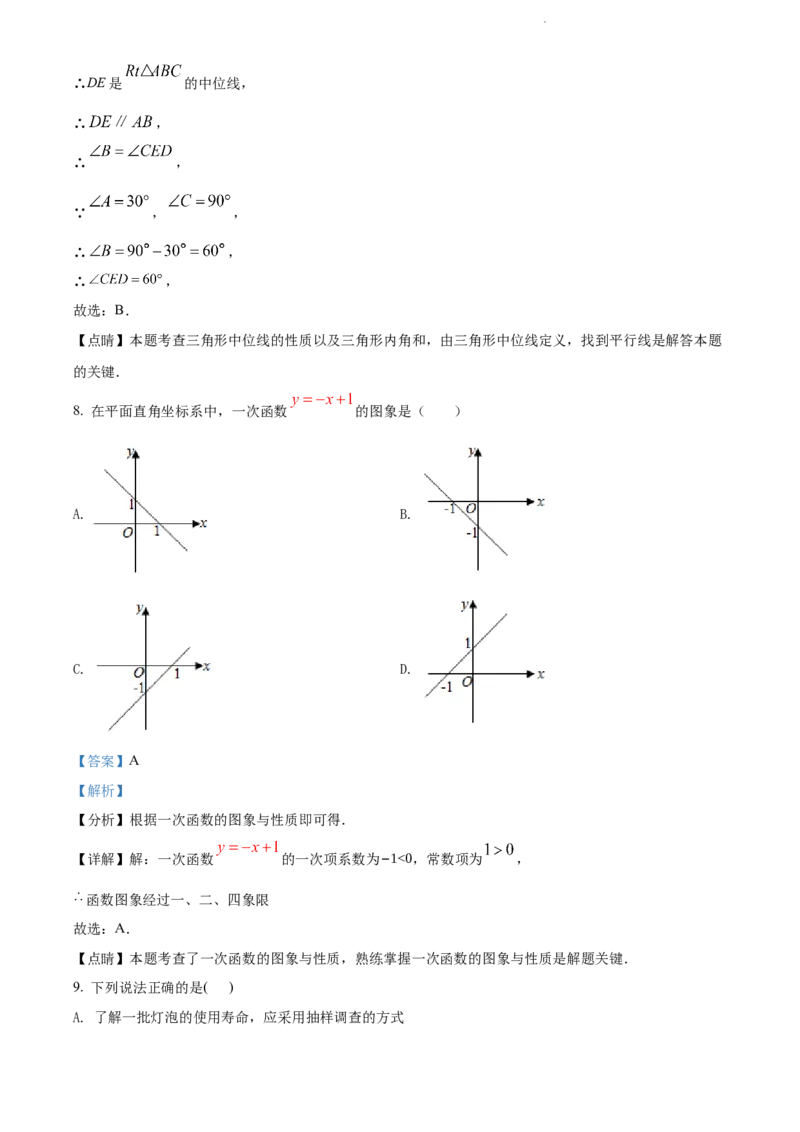
8. 在平面直角坐标系中,一次函数 的图象是( )
A. B.
C. D.
【答案】A
【解析】
【分析】根据一次函数的图象与性质即可得.
【详解】解:一次函数 的一次项系数为−1<0,常数项为 ,
函数图象经过一、二、四象限
故选:A.
【点睛】本题考查了一次函数的图象与性质,熟练掌握一次函数的图象与性质是解题关键.
9. 下列说法正确的是( )
A. 了解一批灯泡的使用寿命,应采用抽样调查的方式
学科网(北京)股份有限公司B. 如果某彩票的中奖概率是1%,那么一次购买100张这种彩票一定会中奖
C. 若甲、乙两组数据的平均数相同, , ,则乙组数据较稳定
D. “任意掷一枚质地均匀的骰子,掷出的点数是7”是必然事件
【答案】A
【解析】
【分析】根据全面调查和抽样调查的意义、概率的意义、方差的意义、事件可能性的大小分别进行判断即
可.
【详解】解:A.要了解一批灯泡的使用寿命,采用普查的方式不合适,破坏性较强,应采用抽样调查,
故此选项正确,符合题意;
B.如果某彩票的中奖概率是1%,那么一次购买100张这种彩票不一定一定会中奖,故选项错误,不符合
题意;
C.若甲、乙两组数据的平均数相同, , ,则 < ,则甲组数据较稳定,故选项错
误,不符合题意;
D.“任意掷一枚质地均匀的骰子,掷出的点数是7” 是不可能事件,故选项错误,不符合题意.
故选:A.
【点睛】此题主要考查了全面调查和抽样调查的意义、概率的意义、方差的意义、事件可能性的大小,关
键是熟练掌握各知识点.
10. 如图,一条河两岸互相平行,为测得此河的宽度PT(PT与河岸PQ垂直),测P、Q两点距离为m米,
,则河宽PT的长度是( )
A. B. C. D.
【答案】C
【解析】
【分析】结合图形利用正切函数求解即可.
【详解】解:根据题意可得:
学科网(北京)股份有限公司,
∴ ,
故选C.
【点睛】题目主要考查解直角三角形的实际应用,理解题意,利用正切函数解直角三角形是解题关键.
二、填空题(每小题3分,共18分)
11. 分解因式: ______.
【答案】
【解析】
【分析】先提取公因式,然后再利用完全平方公式进行因式分解即可.
【详解】解:
=
;
故答案为: .
【点睛】本题主要考查因式分解,熟练掌握因式分解是解题的关键.
12. 二元一次方程组 的解是______.
【答案】 ##
【解析】
【分析】利用代入消元法进行求解方程组的解即可.
【详解】解:
把②代入①得: ,解得: ,
把 代入②得: ;
学科网(北京)股份有限公司∴原方程组的解为 ;
故答案为 .
【点睛】本题主要考查二元一次方程组的解法,熟练掌握二元一次方程组的解法是解题的关键.
13. 化简: ______.
【答案】 ##
【解析】
【分析】根据分式的混合运算可直接进行求解.
【详解】解:原式= ;
故答案为 .
【点睛】本题主要考查分式的运算,熟练掌握分式的加减乘除运算是解题的关键.
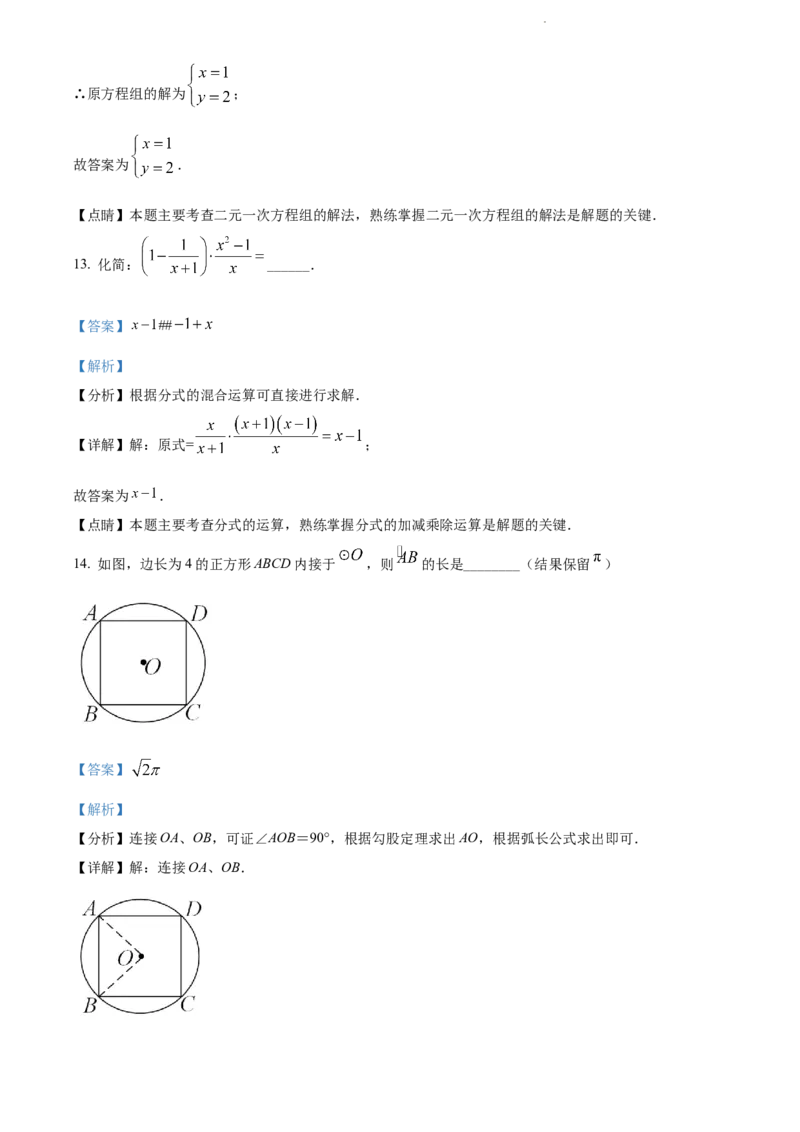
14. 如图,边长为4的正方形ABCD内接于 ,则 的长是________(结果保留 )
【答案】
【解析】
【分析】连接OA、OB,可证∠AOB=90°,根据勾股定理求出AO,根据弧长公式求出即可.
【详解】解:连接OA、OB.
学科网(北京)股份有限公司∵正方形ABCD内接于⊙O,
∴AB=BC=DC=AD=4,AO=BO,
∴ ,
∴∠AOB= ×360°=90°,
在Rt AOB中,由勾股定理得:AO2+BO2=2AO2=42=16,
△
解得:AO=2 ,
∴ 的长= ,
故答案为: .
【点睛】本题考查了弧长公式和正方形的性质,能求出∠AOB的度数和OA的长是解此题的关键.
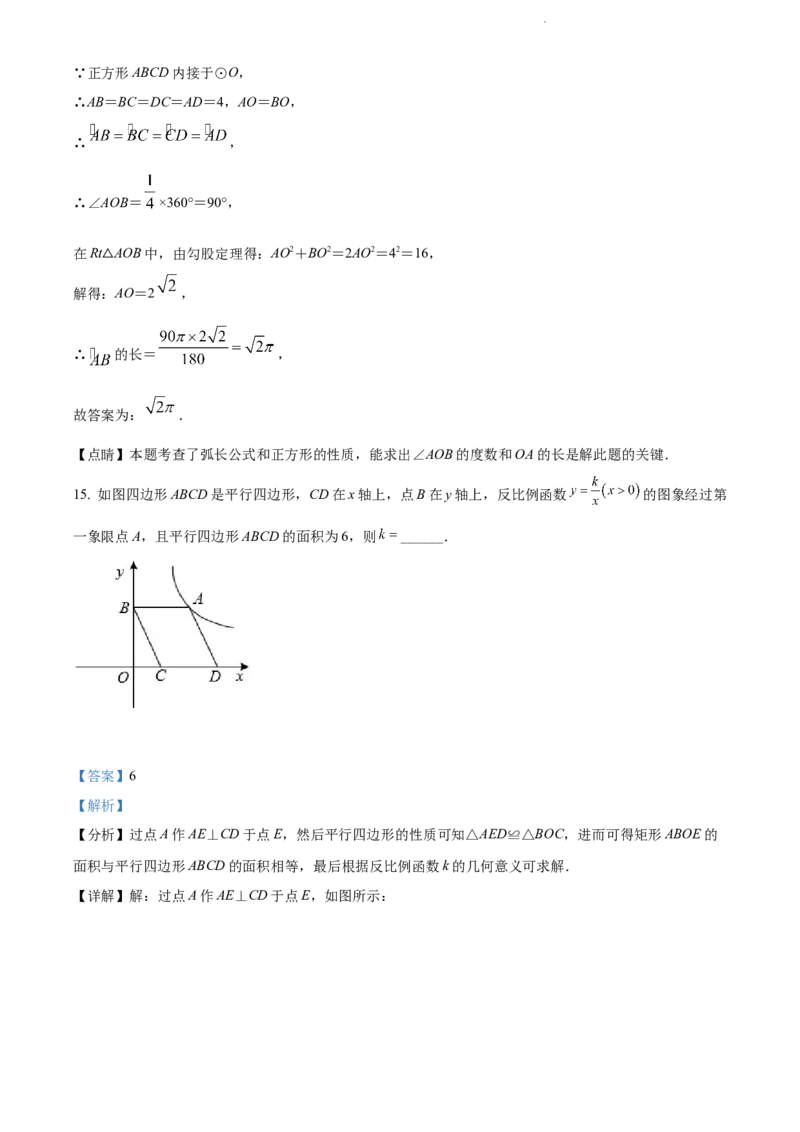
15. 如图四边形ABCD是平行四边形,CD在x轴上,点B在y轴上,反比例函数 的图象经过第
一象限点A,且平行四边形ABCD的面积为6,则 ______.
【答案】6
【解析】
【分析】过点A作AE⊥CD于点E,然后平行四边形的性质可知△AED≌△BOC,进而可得矩形ABOE的
面积与平行四边形ABCD的面积相等,最后根据反比例函数k的几何意义可求解.
【详解】解:过点A作AE⊥CD于点E,如图所示:
学科网(北京)股份有限公司∴ ,
∵四边形ABCD是平行四边形,
∴ ,
∴ ,
∴△AED≌△BOC(AAS),
∵平行四边形ABCD的面积为6,
∴ ,
∴ ;
故答案为6.
【点睛】本题主要考查平行四边形的性质及反比例函数k的几何意义,熟练掌握平行四边形的性质及反比
例函数k的几何意义是解题的关键.
16. 如图,将矩形纸片ABCD折叠,折痕为MN,点M,N分别在边AD,BC上,点C,D的对应点分别在
E,F且点F在矩形内部,MF的延长线交BC与点G,EF交边BC于点H. , ,当点H为
GN三等分点时,MD的长为______.
【答案】 或4
【解析】
【分析】由折叠得,∠DMN=∠GMN,EF=CD==4,CN=EN=2,∠EFM=∠D=90°,证明
学科网(北京)股份有限公司得 ,再分两种情况讨论求解即可.
【详解】解:∵四边形ABCD是矩形,
∴AD//BC,CD=AB=4,∠D=∠C=90°,
∴∠DMN=∠GNM,
由折叠得,∠DMN=∠GMN,EF=CD==4,CN=EN=2,∠EFM=∠D=90°,
∴∠GMN=∠GNM,∠GFH=∠NEH,
∴GM=GN,
又∠GHE=∠NHE,
∴ ,
∴ ,
∵点H是GN的三等分点,则有两种情况:
①若 时,则有:
∴EH= ,GF=2NE=4,
由勾股定理得, ,
∴GH=2NH=
∴GM=GN=GH+NH= ,
∴MD=MF=GM-GF= ;
②若 时,则有:
∴EH= ,GF= NE=1,
学科网(北京)股份有限公司由勾股定理得, ,
∴GH= NH=
∴GM=GN=GH+NH=5;
∴MD=MF=GM-GF=
综上,MD的值为 或4.
【点睛】本题主要考查了矩形的性质,折叠的性质,等腰三角形的判定与性质以及相似三角形的判定与性
质等知识,进行分类讨论是解答本题的关键.
三、解答题:
17. 计算: .
【答案】
【解析】
【分析】根据二次根式的性质,特殊角的三角函数值,负整数指数幂,化简绝对值进行计算即可求解.
【详解】解:原式=
.
【点睛】本题考查了实数的混合运算,掌握二次根式的性质,特殊角的三角函数值,负整数指数幂,化简
绝对值是解题的关键.
18. 为了调动同学们学习数学的积极性,班内组织开展了“数学小先生”讲题比赛,老师将四道备讲题的题
号1,2,3,4,分别写在完全相同的4张卡片的正面,将卡片背面朝上洗匀.
(1)随机抽取一张卡片,卡片上的数字是“4”的概率是________;
(2)小明随机抽取两张卡片,用画树状图或列表的方法求两张卡片上的数字是“2”和“3”的概率.
【答案】(1)
学科网(北京)股份有限公司(2)
【解析】
【分析】(1)直接由概率公式求解即可;
(2)画树状图,共有12种等可能的结果,其中两张卡片上的数字是2和3的结果有2种,再由概率公式
求解即可.
【小问1详解】
解:随机抽取一张卡片,卡片上的数字是4的概率为 ,
故答案为: ;
【小问2详解】
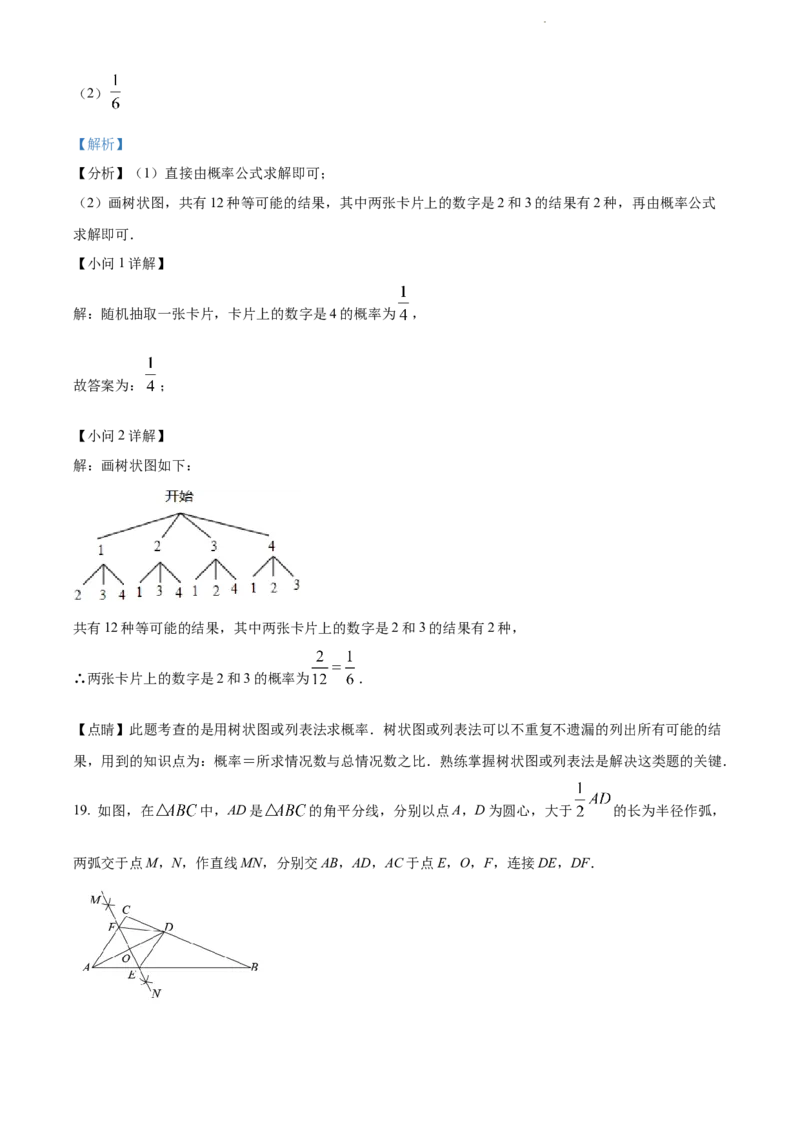
解:画树状图如下:
共有12种等可能的结果,其中两张卡片上的数字是2和3的结果有2种,
∴两张卡片上的数字是2和3的概率为 .
【点睛】此题考查的是用树状图或列表法求概率.树状图或列表法可以不重复不遗漏的列出所有可能的结
果,用到的知识点为:概率=所求情况数与总情况数之比.熟练掌握树状图或列表法是解决这类题的关键.
19. 如图,在 中,AD是 的角平分线,分别以点A,D为圆心,大于 的长为半径作弧,
两弧交于点M,N,作直线MN,分别交AB,AD,AC于点E,O,F,连接DE,DF.
学科网(北京)股份有限公司(1)由作图可知,直线MN是线段AD的______.
(2)求证:四边形AEDF是菱形.
【答案】(1)垂直平分线
(2)见详解
【解析】
【分析】(1)根据线段垂直平分线的尺规作图可直接得出答案;
(2)由题意易得 ,然后可证 ,则有
OF=OE,进而问题可求证.
【小问1详解】
解:由题意得:直线MN是线段AD的垂直平分线;
故答案为:垂直平分线;
【小问2详解】
证明:∵直线MN是线段AD的垂直平分线,
∴ ,
∵AD是 的角平分线,
∴ ,
∵AO=AO,
∴ (ASA),
∴OF=OE,
∵AO=DO,
∴四边形AEDF是平行四边形,
∵ ,
∴四边形AEDF是菱形.
【点睛】本题主要考查线段垂直平分线的尺规作图、全等三角形的性质与判定及菱形的判定,熟练掌握线
段垂直平分线的尺规作图、全等三角形的性质与判定及菱形的判定是解题的关键.
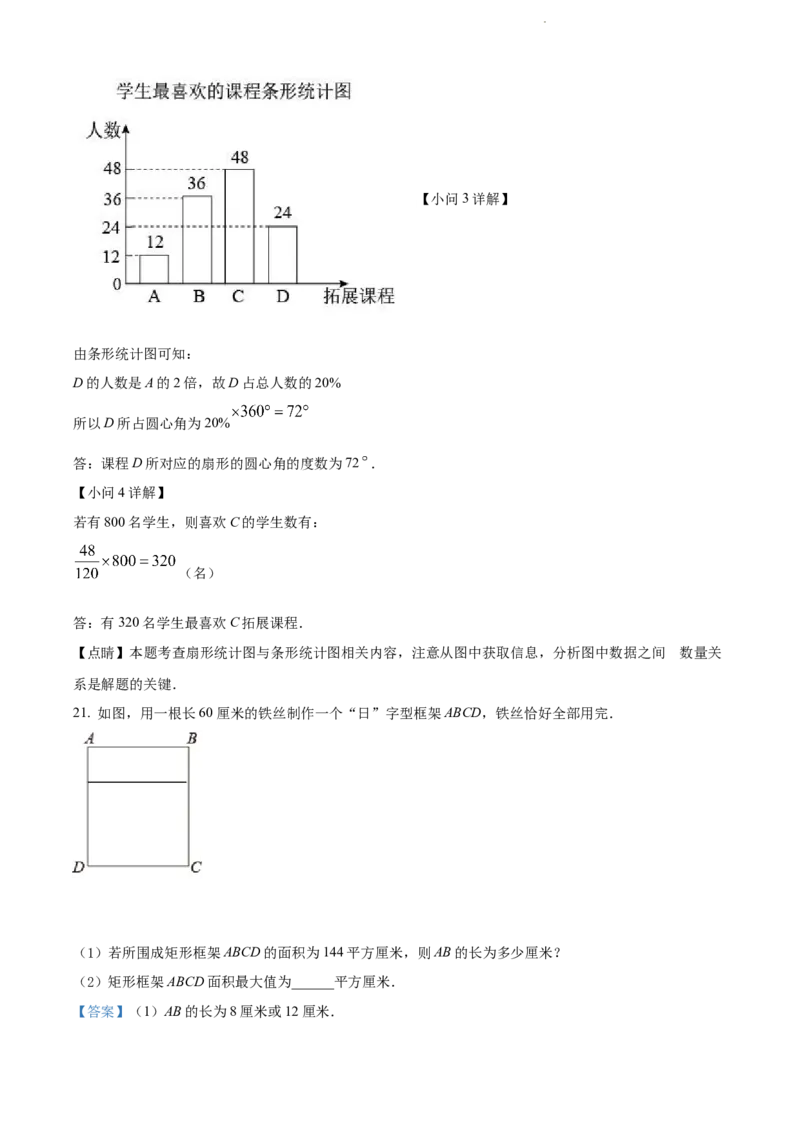
20. 某校积极落实“双减”政策,将要开设拓展课程,为让学生可以根据自己的兴趣爱好选择最喜欢的课程,
进行问卷调查,问卷设置以下四种选项:A(综合模型)、B(摄影艺术)、C(音乐鉴赏)、D(劳动实
践),随机抽取了部分学生进行调查,每名学生必须且只能选择其中最喜欢的一种课程,并将调查结果整
理绘制成如下不完整的统计图.
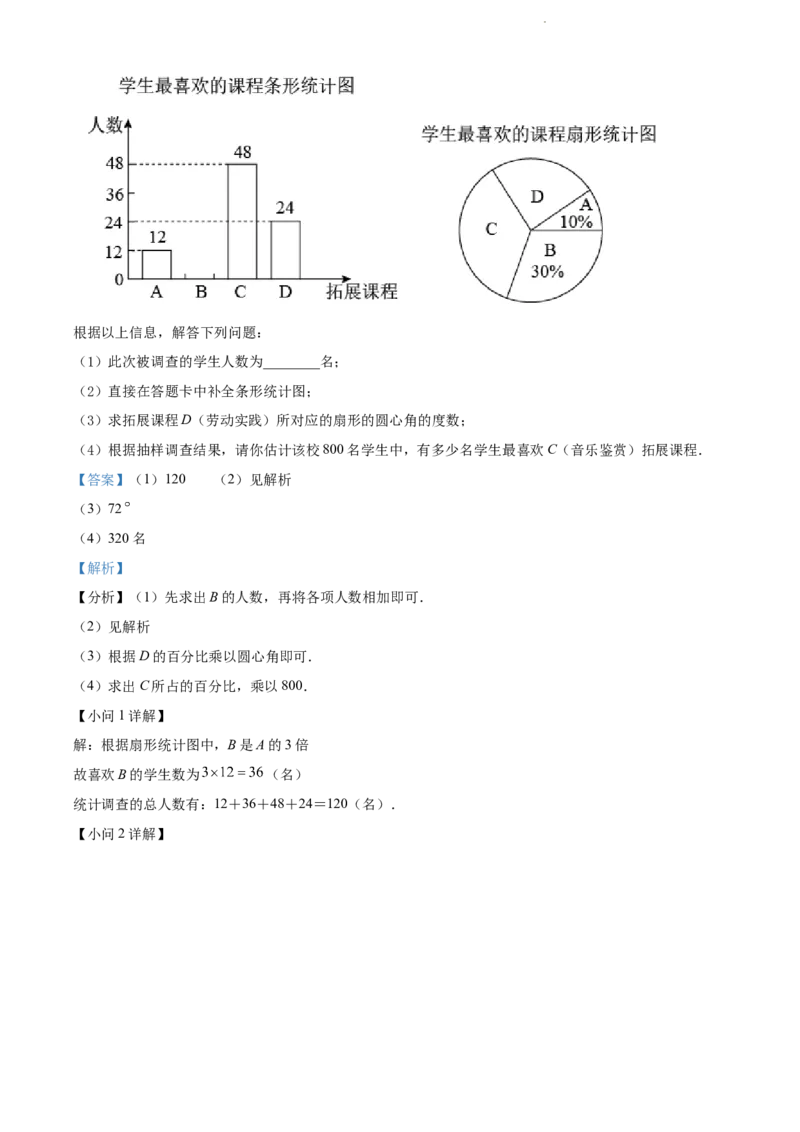
学科网(北京)股份有限公司根据以上信息,解答下列问题:
(1)此次被调查的学生人数为________名;
(2)直接在答题卡中补全条形统计图;
(3)求拓展课程D(劳动实践)所对应的扇形的圆心角的度数;
(4)根据抽样调查结果,请你估计该校800名学生中,有多少名学生最喜欢C(音乐鉴赏)拓展课程.
【答案】(1)120 (2)见解析
(3)72
(4)320名
【解析】
【分析】(1)先求出B的人数,再将各项人数相加即可.
(2)见解析
(3)根据D的百分比乘以圆心角即可.
(4)求出C所占的百分比,乘以800.
【小问1详解】
解:根据扇形统计图中,B是A的3倍
故喜欢B的学生数为 (名)
统计调查的总人数有:12+36+48+24=120(名).
【小问2详解】
学科网(北京)股份有限公司【小问3详解】
由条形统计图可知:
D的人数是A的2倍,故D占总人数的20%
所以D所占圆心角为20%
答:课程D所对应的扇形的圆心角的度数为72 .
【小问4详解】
若有800名学生,则喜欢C的学生数有:
(名)
答:有320名学生最喜欢C拓展课程.
【点睛】本题考查扇形统计图与条形统计图相关内容,注意从图中获取信息,分析图中数据之间 的数量关
系是解题的关键.
21. 如图,用一根长60厘米的铁丝制作一个“日”字型框架ABCD,铁丝恰好全部用完.
(1)若所围成矩形框架ABCD的面积为144平方厘米,则AB的长为多少厘米?
(2)矩形框架ABCD面积最大值为______平方厘米.
【答案】(1)AB的长为8厘米或12厘米.
学科网(北京)股份有限公司(2)150
【解析】
【分析】(1)设AB的长为x厘米,则有 厘米,然后根据题意可得方程 ,
进而求解即可;
(2)由(1)可设矩形框架ABCD的面积为S,则有 ,然后根据二次
函数的性质可进行求解.
【小问1详解】
解:设AB的长为x厘米,则有 厘米,由题意得:
,
整理得: ,
解得: ,
∵ ,
∴ ,
∴ 都符合题意,
答:AB的长为8厘米或12厘米.
【小问2详解】
解:由(1)可设矩形框架ABCD的面积为S平方厘米,则有:
,
∵ ,且 ,
学科网(北京)股份有限公司∴当 时,S有最大值,即为 ;
故答案为:150.
【点睛】本题主要考查一元二次方程及二次函数的应用,解题的关键是找准题干中的等量关系.
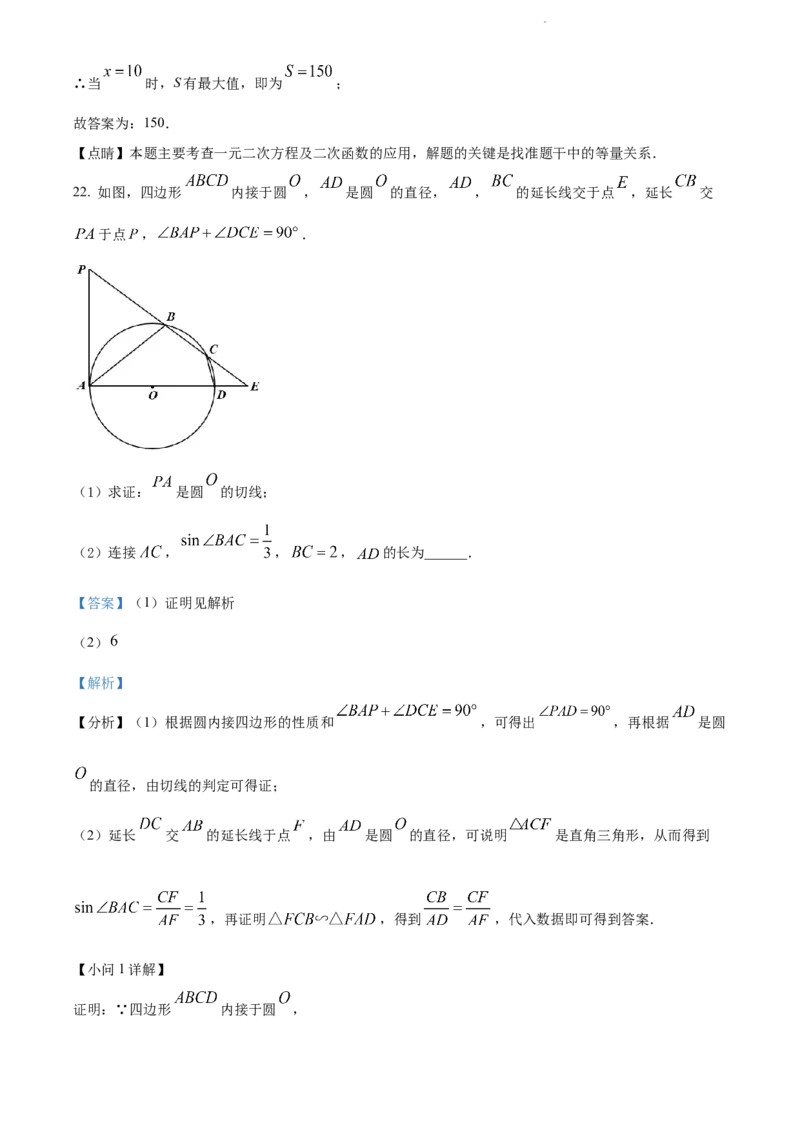
22. 如图,四边形 内接于圆 , 是圆 的直径, , 的延长线交于点 ,延长 交
于点 , .
(1)求证: 是圆 的切线;
(2)连接 , , , 的长为______.
【答案】(1)证明见解析
(2)
【解析】
【分析】(1)根据圆内接四边形的性质和 ,可得出 ,再根据 是圆
的直径,由切线的判定可得证;
(2)延长 交 的延长线于点 ,由 是圆 的直径,可说明 是直角三角形,从而得到
,再证明 ,得到 ,代入数据即可得到答案.
【小问1详解】
证明:∵四边形 内接于圆 ,
学科网(北京)股份有限公司∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∵ 是圆 的直径,
∴ 是圆 的切线.
【小问2详解】
解:延长 交 的延长线于点 ,
∵ 是圆 的直径,
∴ ,
∴ ,
∴ 是直角三角形,
∴ ,
∵四边形 内接于圆 ,
∴ ,
又∵ ,
∴ ,
∴ ,
∵ , ,
∴ ,
∴ .
学科网(北京)股份有限公司为
故答案 : .
【点睛】本题考查了切线的判定,圆内接四边形的性质,圆周角定理推论,相似三角形的判定和性质,三
角函数等知识.通过作辅助线构造相似三角形是解题的关键.
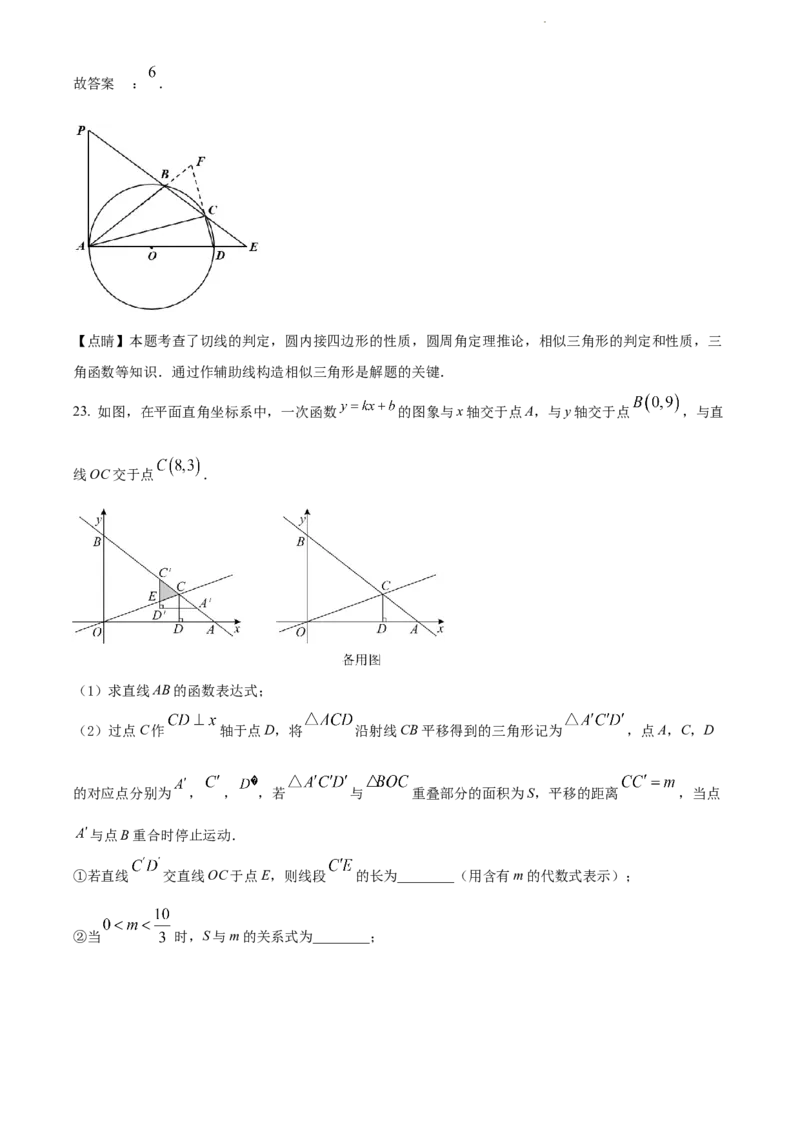
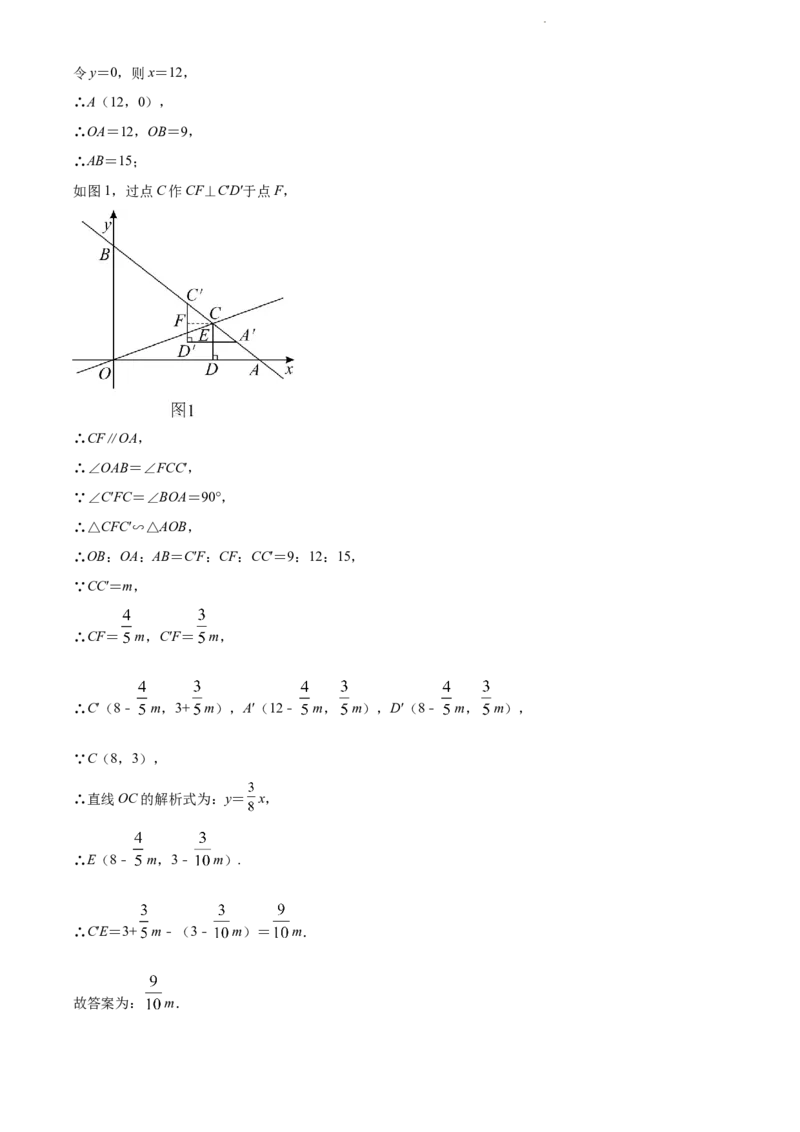
23. 如图,在平面直角坐标系中,一次函数 的图象与x轴交于点A,与y轴交于点 ,与直
线OC交于点 .
(1)求直线AB的函数表达式;
(2)过点C作 轴于点D,将 沿射线CB平移得到的三角形记为 ,点A,C,D
的对应点分别为 , , ,若 与 重叠部分的面积为S,平移的距离 ,当点
与点B重合时停止运动.
①若直线 交直线OC于点E,则线段 的长为________(用含有m的代数式表示);
②当 时,S与m的关系式为________;
学科网(北京)股份有限公司③当 时,m的值为________.
【答案】(1)y=﹣ x+9;
(2)① m;② m2;③ 或15﹣2 .
【解析】
【分析】(1)将点B(0,9),C(8,3)的坐标代入直线解析式,求解即可;
(2)①过点C作CF⊥C′D′,易得 CFC′∽△AOB,可用m表达CF和C′F的长度,进而可表达点C′,D′
的坐标,由点C的坐标可得出直线△OC的解析式,代入可得点E的坐标;
②根据题意可知,当0<m< 时,点D′未到直线OC,利用三角形面积公式可得出本题结果;
③分情况讨论,分别求出当0<m< 时,当 <m<5时,当5<m<10时,当10<m<15时,S与m的
关系式,分别令S= ,建立方程,求出m即可.
【小问1详解】
解:将点B(0,9),C(8,3)的坐标代入直线y=kx+b,
∴ ,
解得 .
∴直线AB的函数表达式为:y=﹣ x+9;
【小问2详解】
①由(1)知直线AB的函数表达式为:y=﹣ x+9,
学科网(北京)股份有限公司令y=0,则x=12,
∴A(12,0),
∴OA=12,OB=9,
∴AB=15;
如图1,过点C作CF⊥C′D′于点F,
∴CF∥OA,
∴∠OAB=∠FCC′,
∵∠C′FC=∠BOA=90°,
∴△CFC′∽△AOB,
∴OB:OA:AB=C′F:CF:CC′=9:12:15,
∵CC′=m,
∴CF= m,C′F= m,
∴C′(8﹣ m,3+ m),A′(12﹣ m, m),D′(8﹣ m, m),
∵C(8,3),
∴直线OC的解析式为:y= x,
∴E(8﹣ m,3﹣ m).
∴C′E=3+ m﹣(3﹣ m)= m.
故答案为: m.
学科网(北京)股份有限公司②当点D′落在直线OC上时,有 m= (8﹣ m),
解得m= ,
∴当0<m< 时,点D′未到直线OC,
此时S= C′E•CF= • m• m= m2;
故答案为: m2.
③分情况讨论,
当0<m< 时,由②可知,S= m2;
令S= m2= ,解得m= > (舍)或m=﹣ (舍);
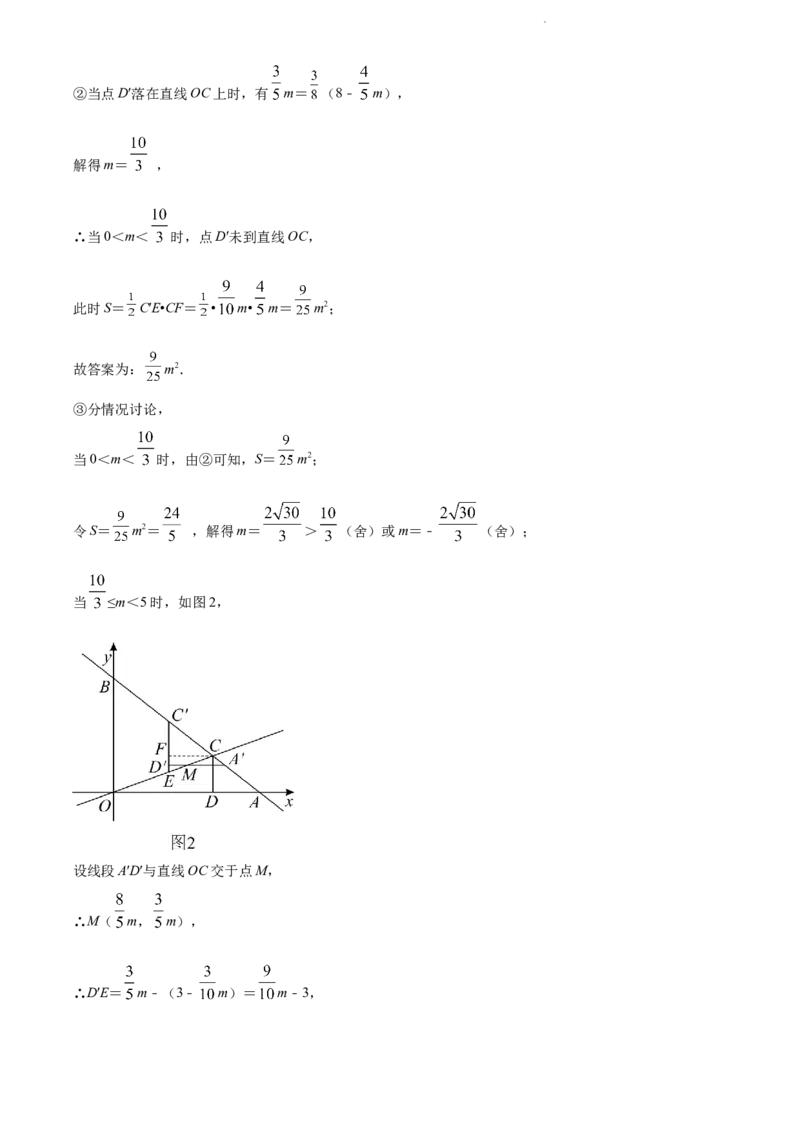
当 ≤m<5时,如图2,
设线段A′D′与直线OC交于点M,
∴M( m, m),
∴D′E= m﹣(3﹣ m)= m﹣3,
学科网(北京)股份有限公司D′M= m﹣(8﹣ m)= m﹣8;
∴S= m2﹣ •( m﹣3)•( m﹣8)
=﹣ m2+ m﹣12,
令﹣ m2+ m﹣12= ;
整理得,3m2﹣30m+70=0,
解得m= 或m= >5(舍);
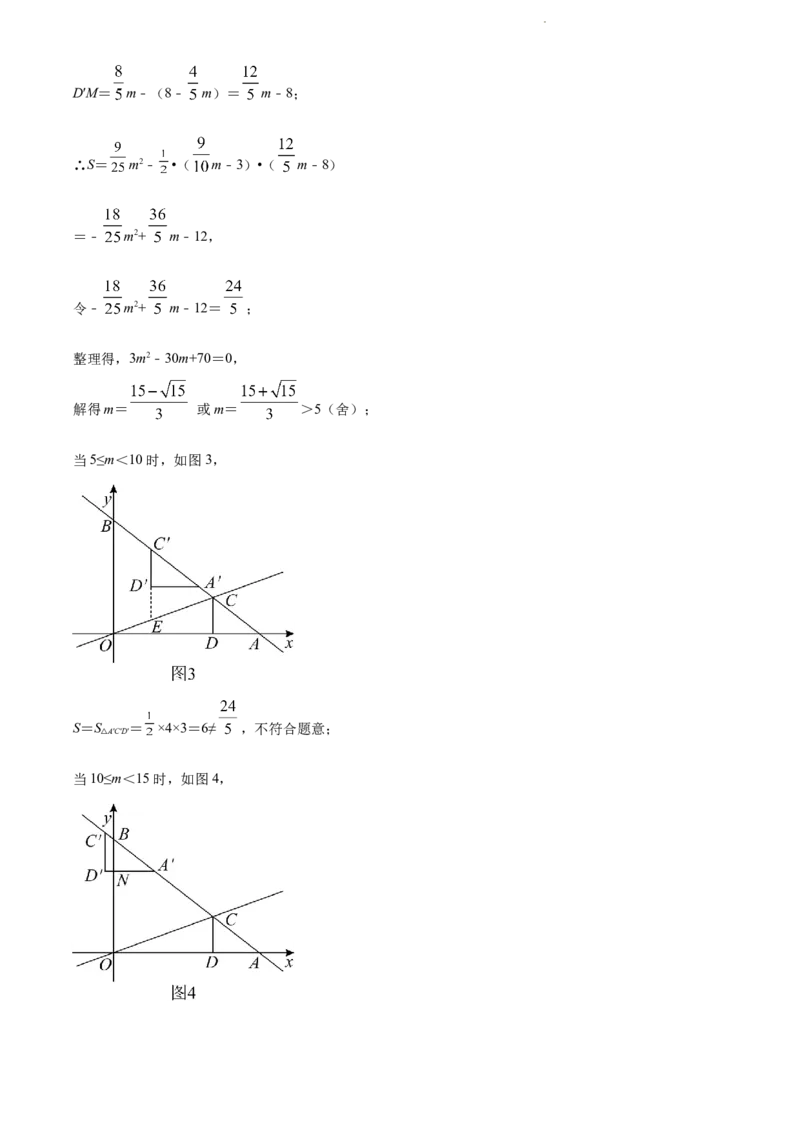
当5≤m<10时,如图3,
S=S = ×4×3=6≠ ,不符合题意;
A′C′D′
△
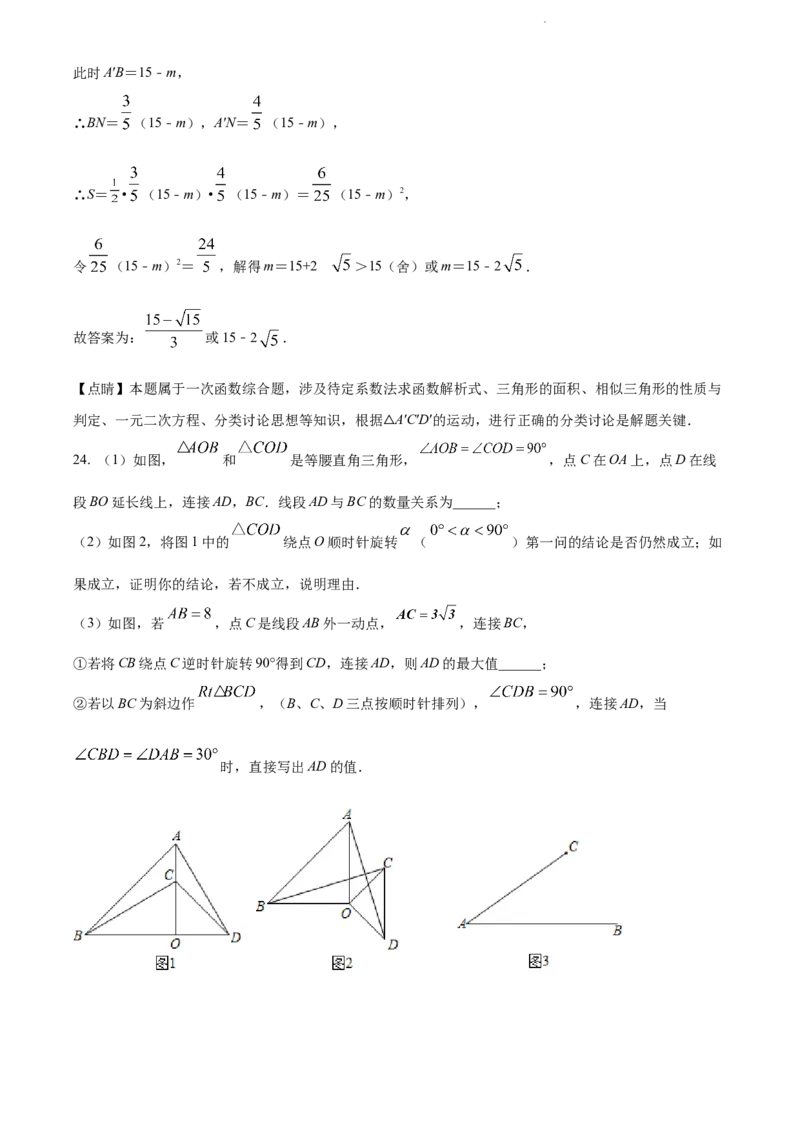
当10≤m<15时,如图4,
学科网(北京)股份有限公司此时A′B=15﹣m,
∴BN= (15﹣m),A′N= (15﹣m),
∴S= • (15﹣m)• (15﹣m)= (15﹣m)2,
令 (15﹣m)2= ,解得m=15+2 >15(舍)或m=15﹣2 .
故答案为: 或15﹣2 .
【点睛】本题属于一次函数综合题,涉及待定系数法求函数解析式、三角形的面积、相似三角形的性质与
判定、一元二次方程、分类讨论思想等知识,根据 A′C′D′的运动,进行正确的分类讨论是解题关键.
△
24. (1)如图, 和 是等腰直角三角形, ,点C在OA上,点D在线
段BO延长线上,连接AD,BC.线段AD与BC的数量关系为______;
(2)如图2,将图1中的 绕点O顺时针旋转 ( )第一问的结论是否仍然成立;如
果成立,证明你的结论,若不成立,说明理由.
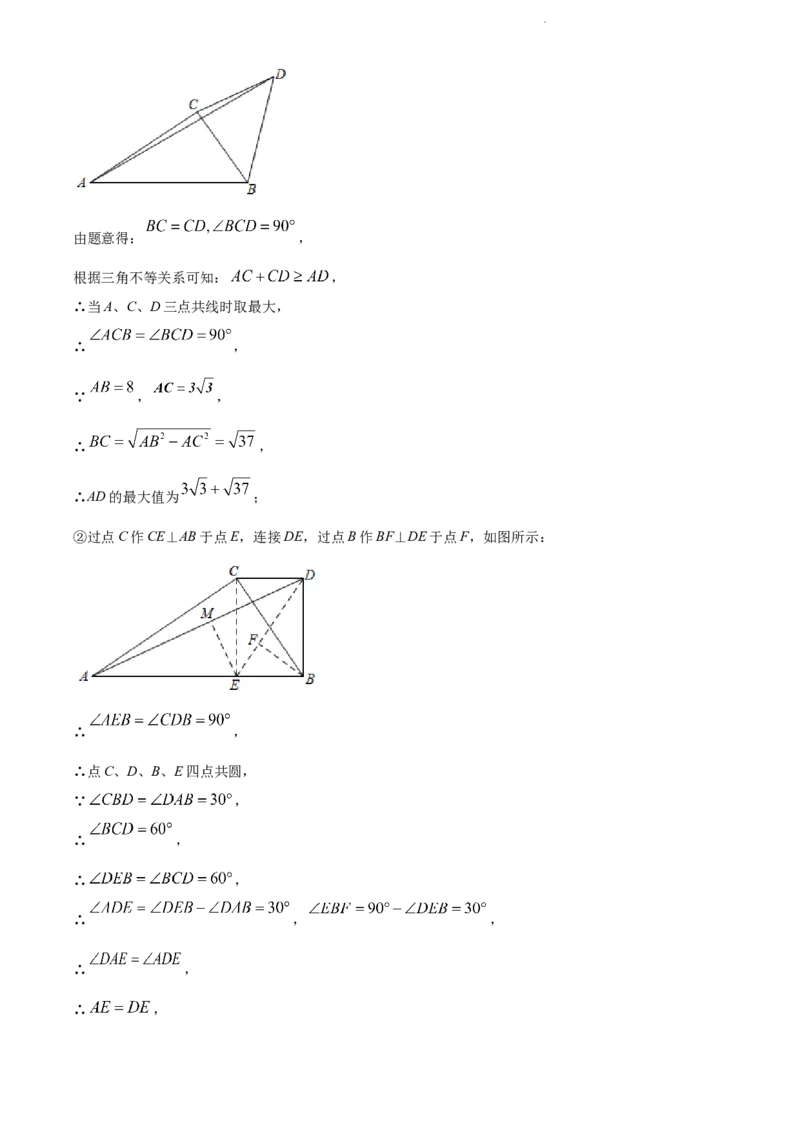
(3)如图,若 ,点C是线段AB外一动点, ,连接BC,
①若将CB绕点C逆时针旋转90°得到CD,连接AD,则AD的最大值______;
②若以BC为斜边作 ,(B、C、D三点按顺时针排列), ,连接AD,当
时,直接写出AD的值.
学科网(北京)股份有限公司【答案】(1)AD=BC;(2)结论仍成立,理由见详解;(3)① ,② .
【解析】
【分析】(1)由题意易得 ,然后可证 ,
进而问题可求解;
(2)由题意易得 ,然后可证 ,进而问题可求证;
(3)①根据题意作出图形,然后根据三角不等关系可得 ,则当A、C、D三点共线时取最
大,进而问题可求解;②过点C作CE⊥AB于点E,连接DE,过点B作BF⊥DE于点F,然后可得点C、
D、B、E四点共圆,则有 ,设 ,则
,进而根据勾股定理可进行方程求解.
【详解】解:(1)AD=BC,理由如下:
∵ 和 是等腰直角三角形, ,
∴ ,
∴ (SAS),
∴AD=BC,
故答案为AD=BC;
(2)结论仍成立,理由如下:
∵ 和 是等腰直角三角形, ,
∴ ,
∴ ,即 ,
∴ (SAS),
∴AD=BC;
(3)①如图,
学科网(北京)股份有限公司由题意得: ,
根据三角不等关系可知: ,
∴当A、C、D三点共线时取最大,
∴ ,
∵ , ,
∴ ,
∴AD的最大值为 ;
②过点C作CE⊥AB于点E,连接DE,过点B作BF⊥DE于点F,如图所示:
∴ ,
∴点C、D、B、E四点共圆,
∵ ,
∴ ,
∴ ,
∴ , ,
∴ ,
∴ ,
学科网(北京)股份有限公司设 ,则 ,
∴ ,
∴ , ,
∴在Rt△AEC和Rt△BEC中,由勾股定理得: ,整理得: ①;
在Rt△BFD中,由勾股定理得: ,整理得: ②,
联立①②得: ,
解得: (不符合题意,舍去),
∴ ,
过点E作EM⊥AD于点M,
∴ , ,
∴ ,
∴ .
【点睛】本题主要考查全等三角形的性质与判定、等腰直角三角形的性质、四点共圆及含30度直角三角形
的性质,熟练掌握全等三角形的性质与判定、等腰直角三角形的性质、四点共圆及含30度直角三角形的性
质是解题的关键.
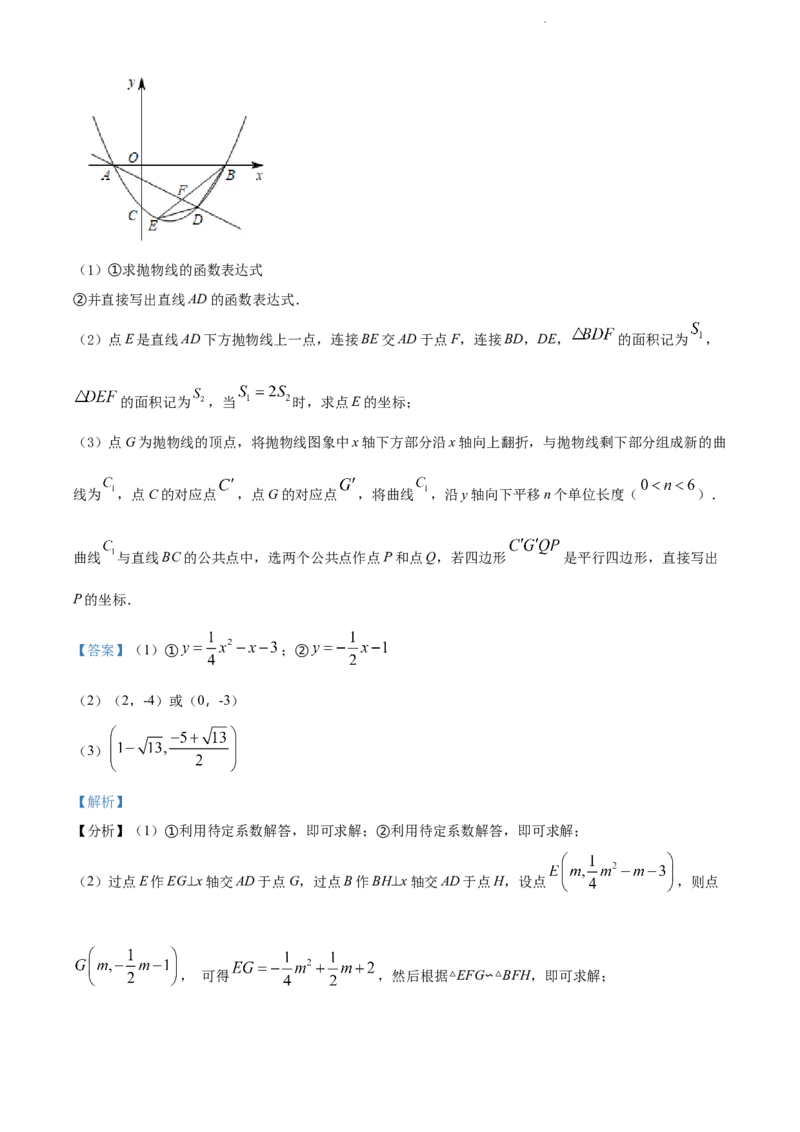
25. 如图,平面直角坐标系中,O是坐标原点,抛物线 经过点 和点 与x
轴另一个交点A.抛物线与y轴交于点C,作直线AD.
学科网(北京)股份有限公司(1)①求抛物线的函数表达式
②并直接写出直线AD的函数表达式.
(2)点E是直线AD下方抛物线上一点,连接BE交AD于点F,连接BD,DE, 的面积记为 ,
的面积记为 ,当 时,求点E的坐标;
(3)点G为抛物线的顶点,将抛物线图象中x轴下方部分沿x轴向上翻折,与抛物线剩下部分组成新的曲
线为 ,点C的对应点 ,点G的对应点 ,将曲线 ,沿y轴向下平移n个单位长度( ).
曲线 与直线BC的公共点中,选两个公共点作点P和点Q,若四边形 是平行四边形,直接写出
P的坐标.
【答案】(1)① ;②
(2)(2,-4)或(0,-3)
(3)
【解析】
【分析】(1)①利用待定系数解答,即可求解;②利用待定系数解答,即可求解;
(2)过点E作EG⊥x轴交AD于点G,过点B作BH⊥x轴交AD于点H,设点 ,则点
, 可得 ,然后根据△EFG∽△BFH,即可求解;
学科网(北京)股份有限公司(3)先求出向上翻折部分的图象解析式为 ,可得向上翻折部分平移后的函数解析式
为 ,平移后抛物线剩下部分的解析式为 ,分别求出直线BC
和直线 的解析式为,可得BC∥C′G′,再根据平行四边形的性质可得点 ,然后分三
种情况讨论:当点P,Q均在向上翻折部分平移后的图象上时;当点P在向上翻折部分平移后的图象上,
点Q在平移后抛物线剩下部分的图象上时;当点P在平移后抛物线剩下部分的图象上,点Q在向上翻折部
分平移后的图象上时,即可求解.
【小问1详解】
解:①把点 和点 代入得:
,解得: ,
∴抛物线解析式为 ;
②令y=0,则 ,
解得: ,
∴点A(-2,0),
设直线AD的解析式为 ,
∴把点 和点A(-2,0)代入得:
,解得: ,
学科网(北京)股份有限公司∴直线AD的解析式为 ;
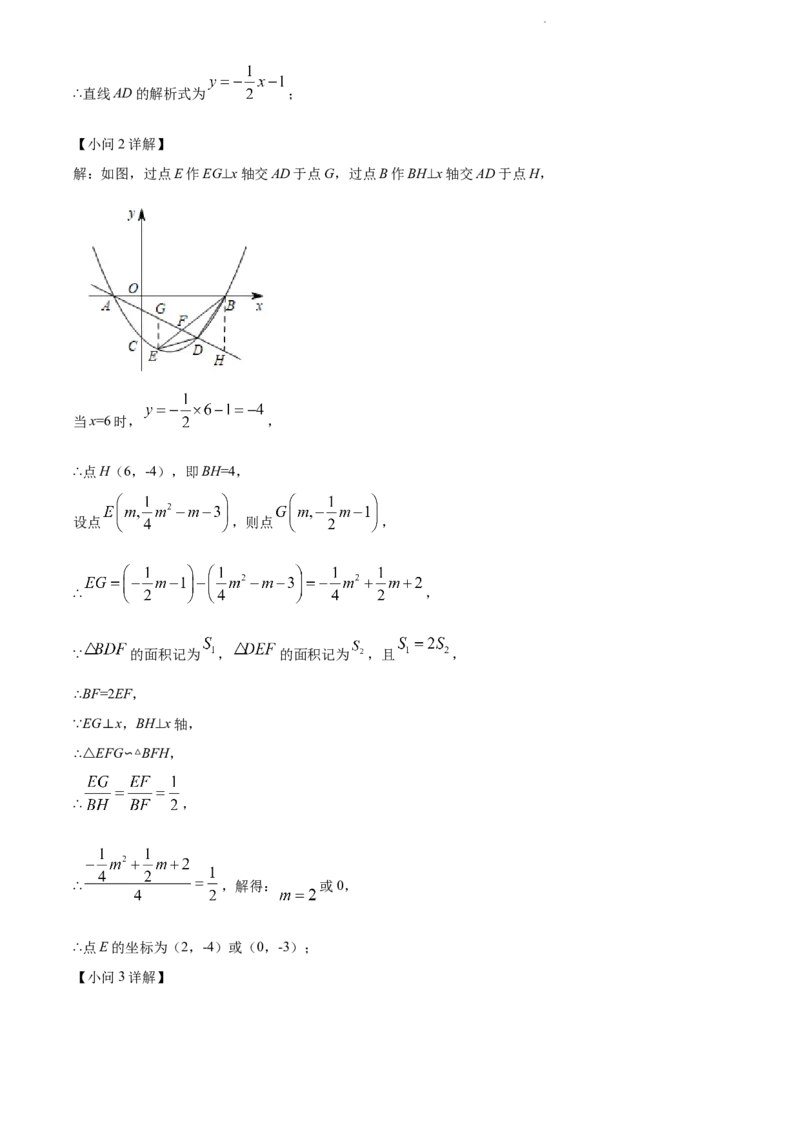
【小问2详解】
解:如图,过点E作EG⊥x轴交AD于点G,过点B作BH⊥x轴交AD于点H,
当x=6时, ,
∴点H(6,-4),即BH=4,
设点 ,则点 ,
∴ ,
∵ 的面积记为 , 的面积记为 ,且 ,
∴BF=2EF,
∵EG⊥x,BH⊥x轴,
∴△EFG∽△BFH,
∴ ,
∴ ,解得: 或0,
∴点E的坐标为(2,-4)或(0,-3);
【小问3详解】
学科网(北京)股份有限公司解: ,
∴点G的坐标为(2,-4),
当x=0时,y=-3,即点C(0,-3),
∴点 ,
∴向上翻折部分的图象解析式为 ,
∴向上翻折部分平移后的函数解析式为 ,平移后抛物线剩下部分的解析式为
,
设直线BC的解析式为 ,
把点B(6,0),C(0,-3)代入得:
,解得: ,
∴直线BC 解析式为 ,
的
同理直线 的解析式为 ,
∴BC∥C′G′,
设点P的坐标为 ,
∵点 ,
∴点 C′向右平移2个单位,再向上平移1个单位得到点 G′,
∵四边形 是平行四边形,
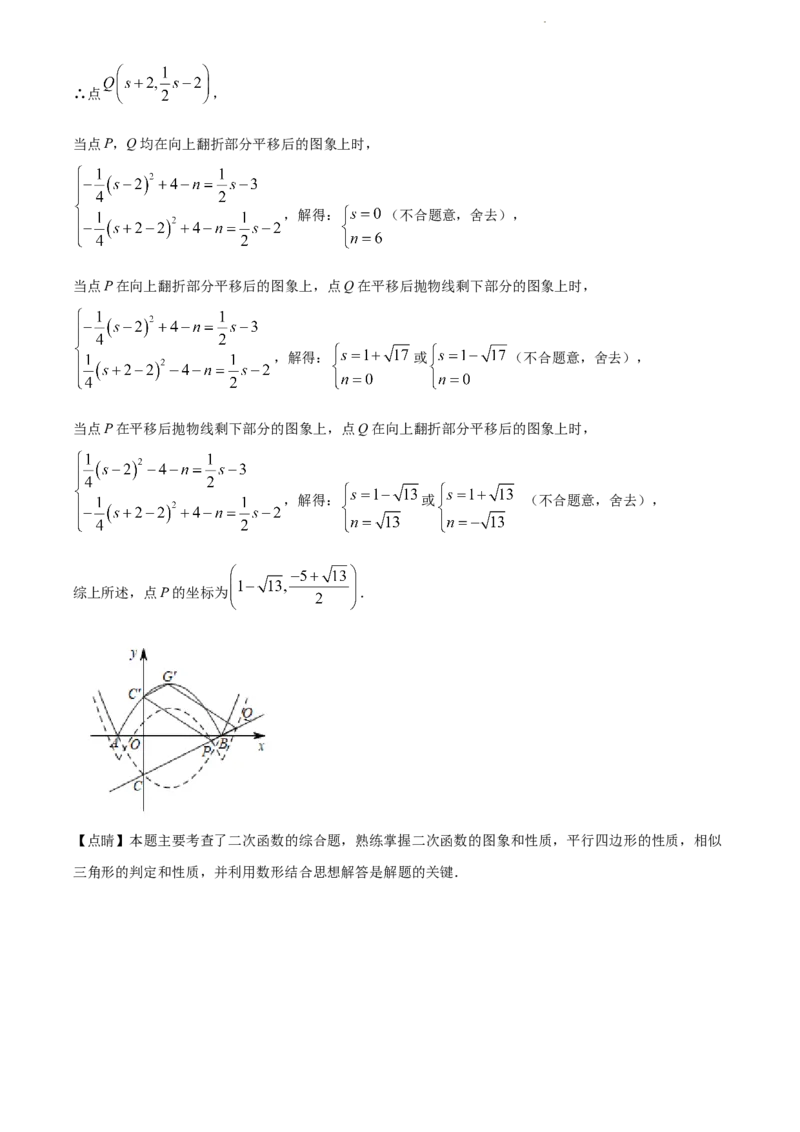
学科网(北京)股份有限公司∴点 ,
当点P,Q均在向上翻折部分平移后的图象上时,
,解得: (不合题意,舍去),
当点P在向上翻折部分平移后的图象上,点Q在平移后抛物线剩下部分的图象上时,
,解得: 或 (不合题意,舍去),
当点P在平移后抛物线剩下部分的图象上,点Q在向上翻折部分平移后的图象上时,
,解得: 或 (不合题意,舍去),
综上所述,点P的坐标为 .
【点睛】本题主要考查了二次函数的综合题,熟练掌握二次函数的图象和性质,平行四边形的性质,相似
三角形的判定和性质,并利用数形结合思想解答是解题的关键.
学科网(北京)股份有限公司学科网(北京)股份有限公司