文档内容
2022年辽宁省鞍山市中考数学试卷
一、选择题(下列各题的备选答案中,只有一个是正确的.每题3分,共24分)
1.(3分)2022的相反数是( )
A. B.﹣ C.2022 D.﹣2022
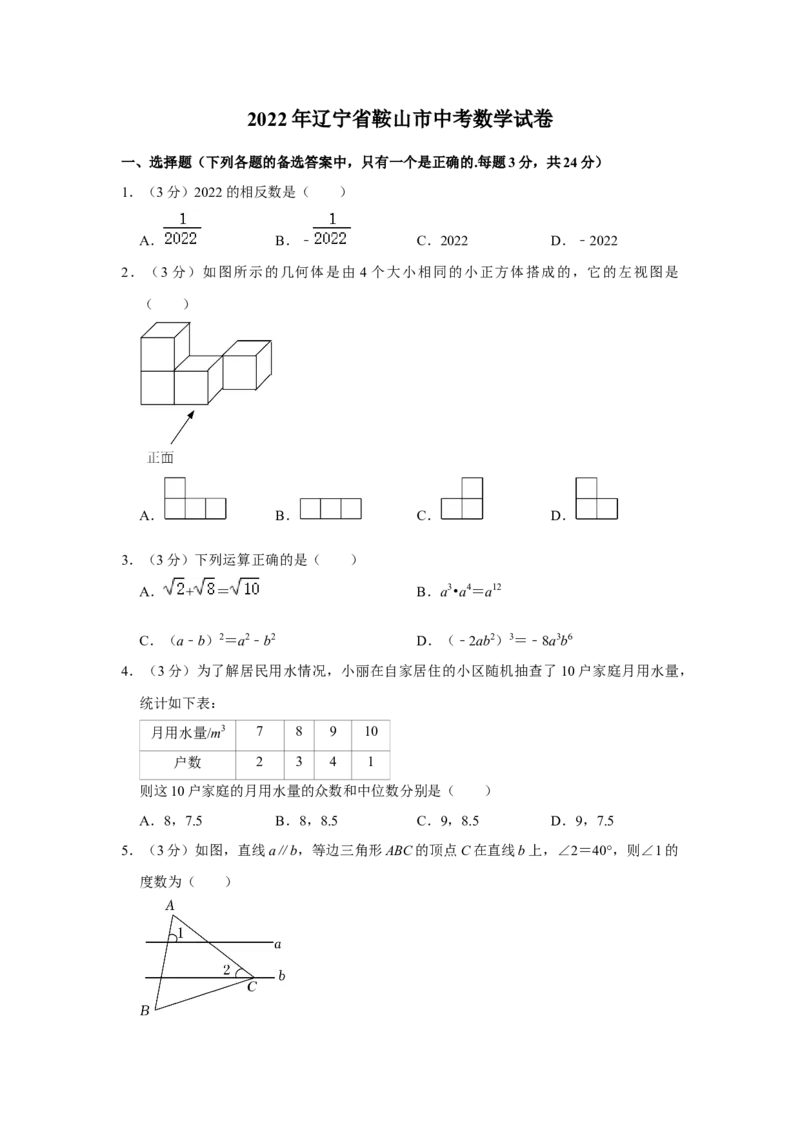
2.(3 分)如图所示的几何体是由 4 个大小相同的小正方体搭成的,它的左视图是
( )
A. B. C. D.
3.(3分)下列运算正确的是( )
A. + = B.a3•a4=a12
C.(a﹣b)2=a2﹣b2 D.(﹣2ab2)3=﹣8a3b6
4.(3分)为了解居民用水情况,小丽在自家居住的小区随机抽查了10户家庭月用水量,
统计如下表:
月用水量/m3 7 8 9 10
户数 2 3 4 1
则这10户家庭的月用水量的众数和中位数分别是( )
A.8,7.5 B.8,8.5 C.9,8.5 D.9,7.5
5.(3分)如图,直线a∥b,等边三角形ABC的顶点C在直线b上,∠2=40°,则∠1的
度数为( )A.80° B.70° C.60° D.50°
6.(3分)如图,在△ABC中,AB=AC,∠BAC=24°,延长BC到点D,使CD=AC,连
接AD,则∠D的度数为( )
A.39° B.40° C.49° D.51°
7.(3分)如图,在矩形ABCD中,AB=2,BC= ,以点B为圆心,BA长为半径画弧,
交CD于点E,连接BE,则扇形BAE的面积为( )
A. B. C. D.
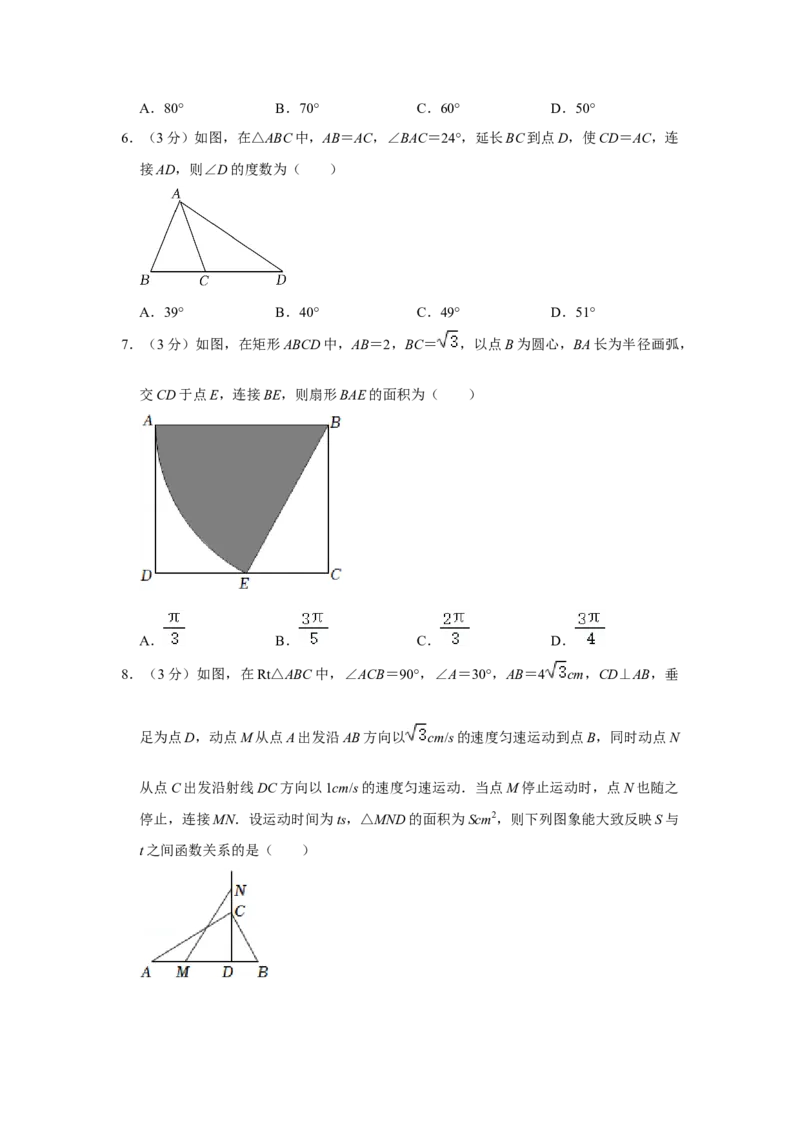
8.(3分)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4 cm,CD⊥AB,垂
足为点D,动点M从点A出发沿AB方向以 cm/s的速度匀速运动到点B,同时动点N
从点C出发沿射线DC方向以1cm/s的速度匀速运动.当点M停止运动时,点N也随之
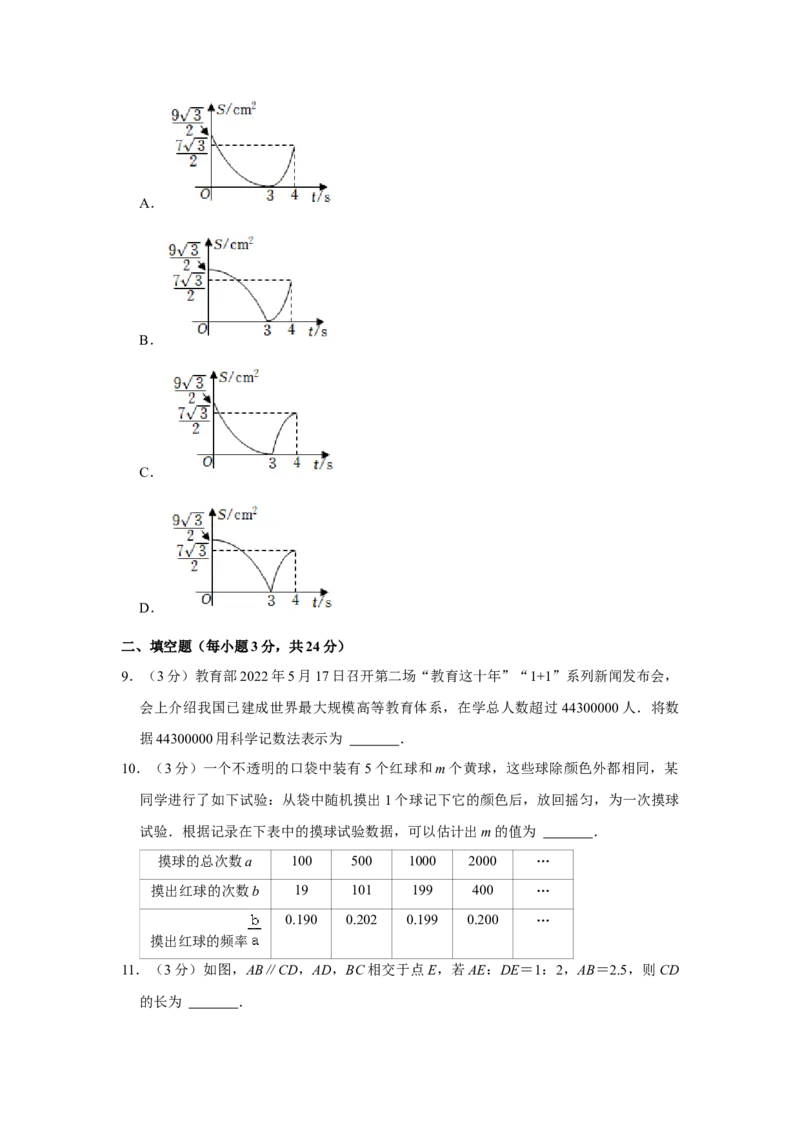
停止,连接MN.设运动时间为ts,△MND的面积为Scm2,则下列图象能大致反映S与
t之间函数关系的是( )A.
B.
C.
D.
二、填空题(每小题3分,共24分)
9.(3分)教育部2022年5月17日召开第二场“教育这十年”“1+1”系列新闻发布会,
会上介绍我国已建成世界最大规模高等教育体系,在学总人数超过 44300000人.将数
据44300000用科学记数法表示为 .
10.(3分)一个不透明的口袋中装有5个红球和m个黄球,这些球除颜色外都相同,某
同学进行了如下试验:从袋中随机摸出1个球记下它的颜色后,放回摇匀,为一次摸球
试验.根据记录在下表中的摸球试验数据,可以估计出m的值为 .
摸球的总次数a 100 500 1000 2000 …
摸出红球的次数b 19 101 199 400 …
0.190 0.202 0.199 0.200 …
摸出红球的频率
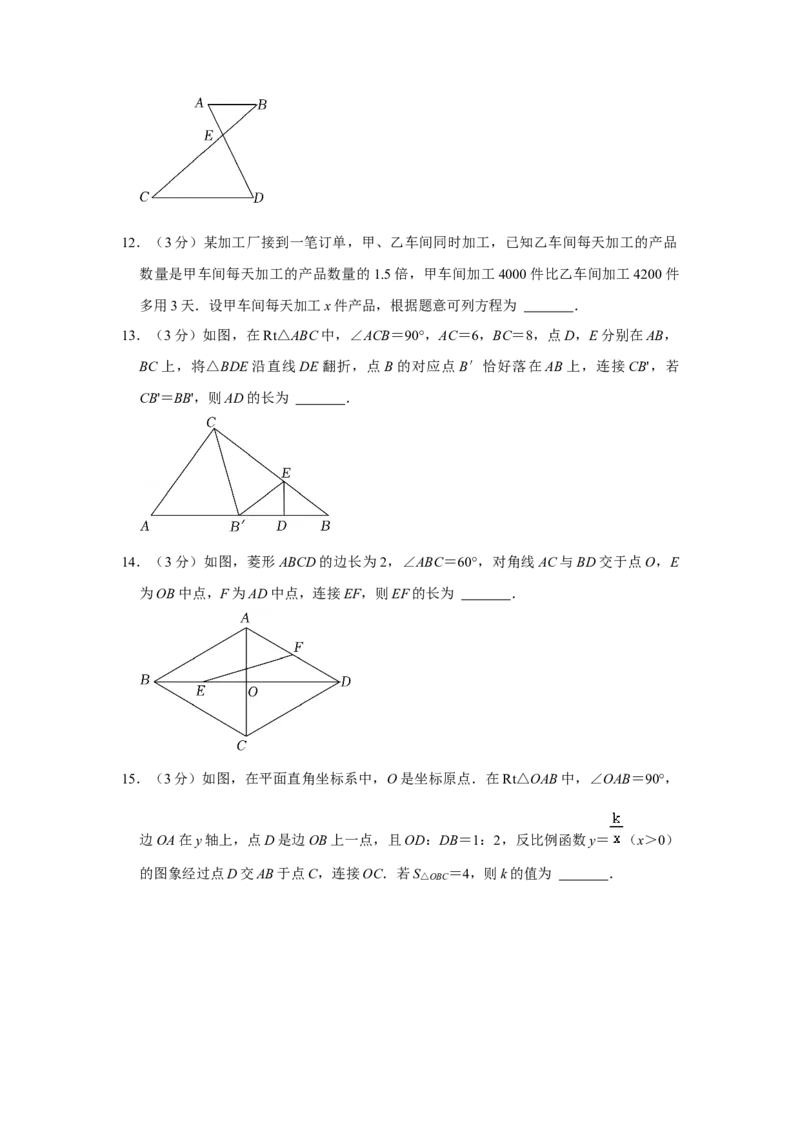
11.(3分)如图,AB∥CD,AD,BC相交于点E,若AE:DE=1:2,AB=2.5,则CD
的长为 .12.(3分)某加工厂接到一笔订单,甲、乙车间同时加工,已知乙车间每天加工的产品
数量是甲车间每天加工的产品数量的1.5倍,甲车间加工4000件比乙车间加工4200件
多用3天.设甲车间每天加工x件产品,根据题意可列方程为 .
13.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D,E分别在AB,
BC上,将△BDE沿直线DE翻折,点B的对应点B′恰好落在AB上,连接CB',若
CB'=BB',则AD的长为 .
14.(3分)如图,菱形ABCD的边长为2,∠ABC=60°,对角线AC与BD交于点O,E
为OB中点,F为AD中点,连接EF,则EF的长为 .
15.(3分)如图,在平面直角坐标系中,O是坐标原点.在Rt△OAB中,∠OAB=90°,
边OA在y轴上,点D是边OB上一点,且OD:DB=1:2,反比例函数y= (x>0)
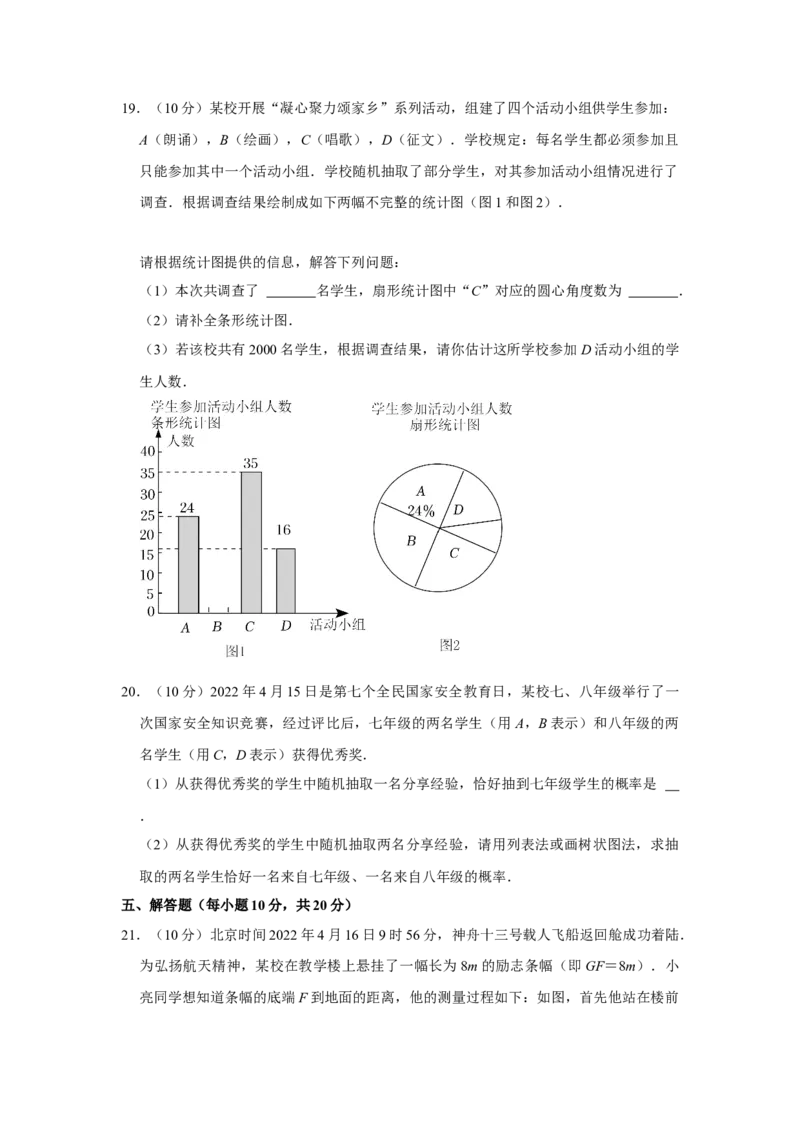
的图象经过点D交AB于点C,连接OC.若S△OBC =4,则k的值为 .16.(3分)如图,在正方形ABCD中,点E为AB的中点,CE,BD交于点H,DF⊥CE
于点F,FM平分∠DFE,分别交AD,BD于点M,G,延长MF交BC于点N,连接
BF.下列结论:①tan∠CDF= ;②S△EBH :S△DHF =3:4;③MG:GF:FN=5:
3:2;④△BEF∽△HCD.其中正确的是 .(填序号即可).
三、解答题(每小题8分,共16分)
17.(8分)先化简,再求值: ÷(1﹣ ),其中m=2.
18.(8分)如图,在四边形ABCD中,AC与BD交于点O,BE⊥AC,DF⊥AC,垂足分
别为点E,F,且BE=DF,∠ABD=∠BDC.求证:四边形ABCD是平行四边形.
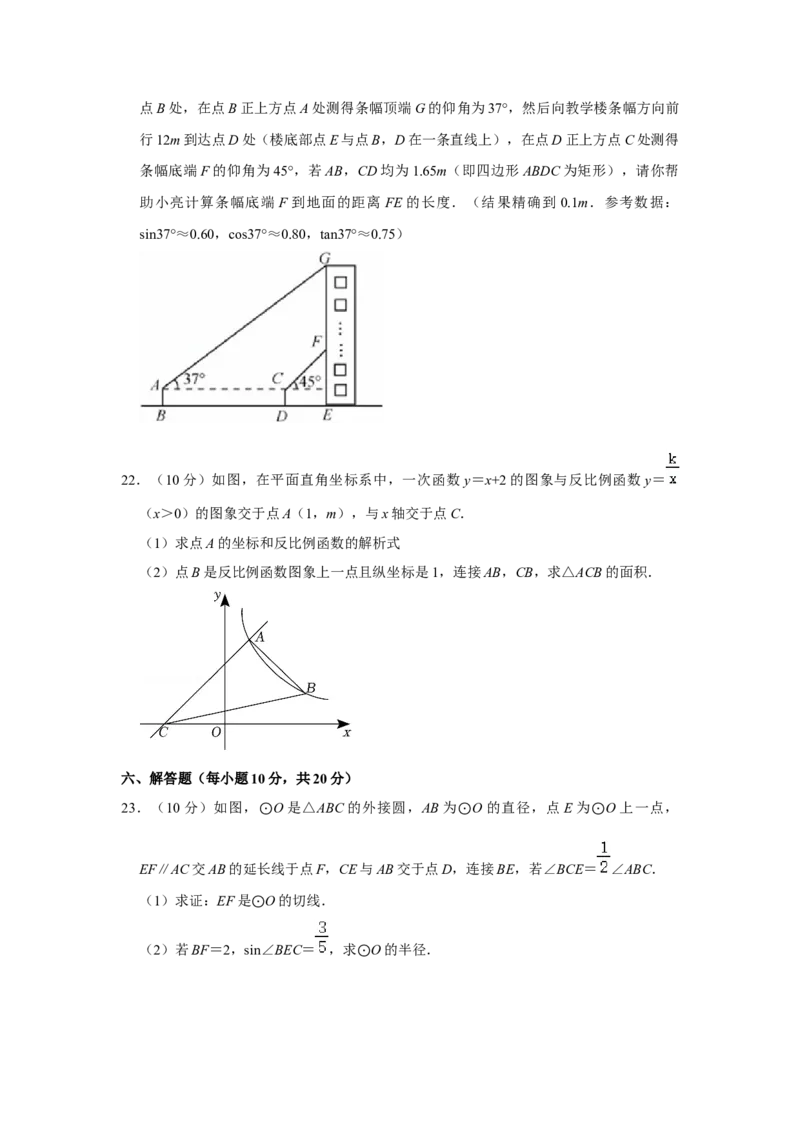
四、解答题(每小题10分,共20分)19.(10分)某校开展“凝心聚力颂家乡”系列活动,组建了四个活动小组供学生参加:
A(朗诵),B(绘画),C(唱歌),D(征文).学校规定:每名学生都必须参加且
只能参加其中一个活动小组.学校随机抽取了部分学生,对其参加活动小组情况进行了
调查.根据调查结果绘制成如下两幅不完整的统计图(图1和图2).
请根据统计图提供的信息,解答下列问题:
(1)本次共调查了 名学生,扇形统计图中“C”对应的圆心角度数为 .
(2)请补全条形统计图.
(3)若该校共有2000名学生,根据调查结果,请你估计这所学校参加D活动小组的学
生人数.
20.(10分)2022年4月15日是第七个全民国家安全教育日,某校七、八年级举行了一
次国家安全知识竞赛,经过评比后,七年级的两名学生(用 A,B表示)和八年级的两
名学生(用C,D表示)获得优秀奖.
(1)从获得优秀奖的学生中随机抽取一名分享经验,恰好抽到七年级学生的概率是
.
(2)从获得优秀奖的学生中随机抽取两名分享经验,请用列表法或画树状图法,求抽
取的两名学生恰好一名来自七年级、一名来自八年级的概率.
五、解答题(每小题10分,共20分)
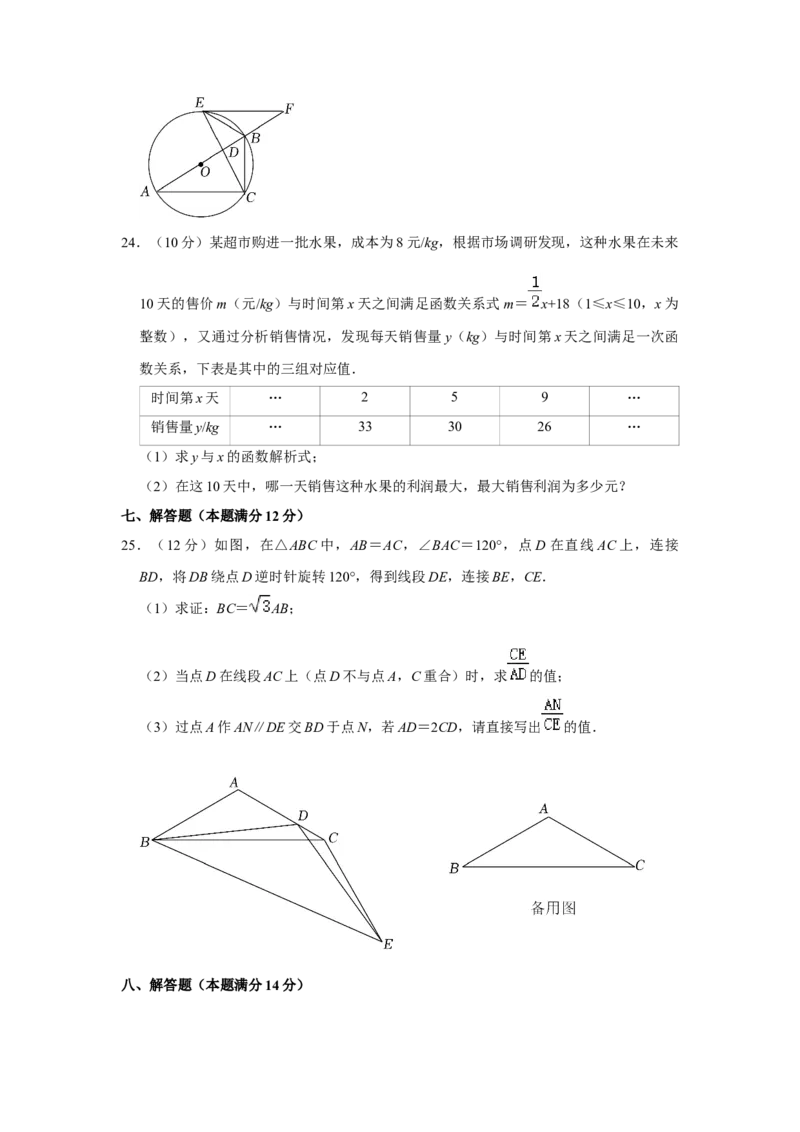
21.(10分)北京时间2022年4月16日9时56分,神舟十三号载人飞船返回舱成功着陆.
为弘扬航天精神,某校在教学楼上悬挂了一幅长为8m的励志条幅(即GF=8m).小
亮同学想知道条幅的底端F到地面的距离,他的测量过程如下:如图,首先他站在楼前点B处,在点B正上方点A处测得条幅顶端G的仰角为37°,然后向教学楼条幅方向前
行12m到达点D处(楼底部点E与点B,D在一条直线上),在点D正上方点C处测得
条幅底端F的仰角为45°,若AB,CD均为1.65m(即四边形ABDC为矩形),请你帮
助小亮计算条幅底端 F到地面的距离 FE的长度.(结果精确到 0.1m.参考数据:
sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
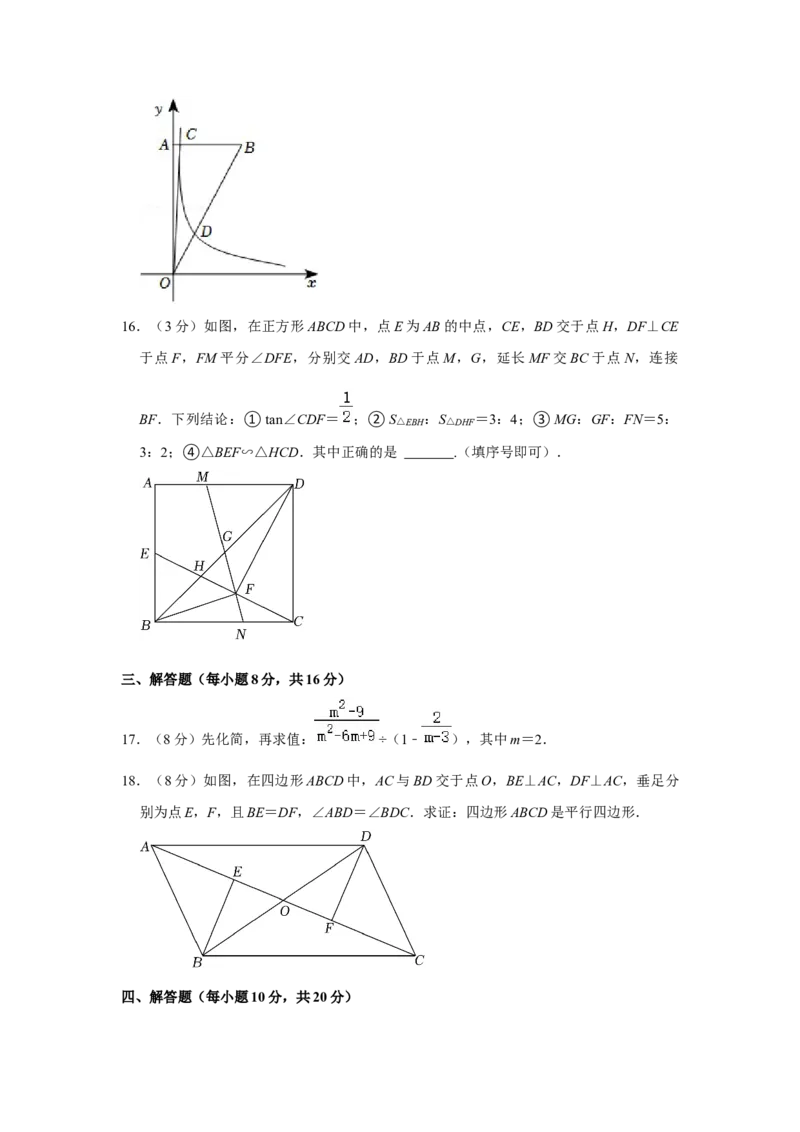
22.(10分)如图,在平面直角坐标系中,一次函数y=x+2的图象与反比例函数y=
(x>0)的图象交于点A(1,m),与x轴交于点C.
(1)求点A的坐标和反比例函数的解析式
(2)点B是反比例函数图象上一点且纵坐标是1,连接AB,CB,求△ACB的面积.
六、解答题(每小题10分,共20分)
23.(10分)如图, O是△ABC的外接圆,AB为 O的直径,点E为 O上一点,
⊙ ⊙ ⊙
EF∥AC交AB的延长线于点F,CE与AB交于点D,连接BE,若∠BCE= ∠ABC.
(1)求证:EF是 O的切线.
⊙
(2)若BF=2,sin∠BEC= ,求 O的半径.
⊙24.(10分)某超市购进一批水果,成本为8元/kg,根据市场调研发现,这种水果在未来
10天的售价m(元/kg)与时间第x天之间满足函数关系式m= x+18(1≤x≤10,x为
整数),又通过分析销售情况,发现每天销售量y(kg)与时间第x天之间满足一次函
数关系,下表是其中的三组对应值.
时间第x天 … 2 5 9 …
销售量y/kg … 33 30 26 …
(1)求y与x的函数解析式;
(2)在这10天中,哪一天销售这种水果的利润最大,最大销售利润为多少元?
七、解答题(本题满分12分)
25.(12分)如图,在△ABC中,AB=AC,∠BAC=120°,点D在直线AC上,连接
BD,将DB绕点D逆时针旋转120°,得到线段DE,连接BE,CE.
(1)求证:BC= AB;
(2)当点D在线段AC上(点D不与点A,C重合)时,求 的值;
(3)过点A作AN∥DE交BD于点N,若AD=2CD,请直接写出 的值.
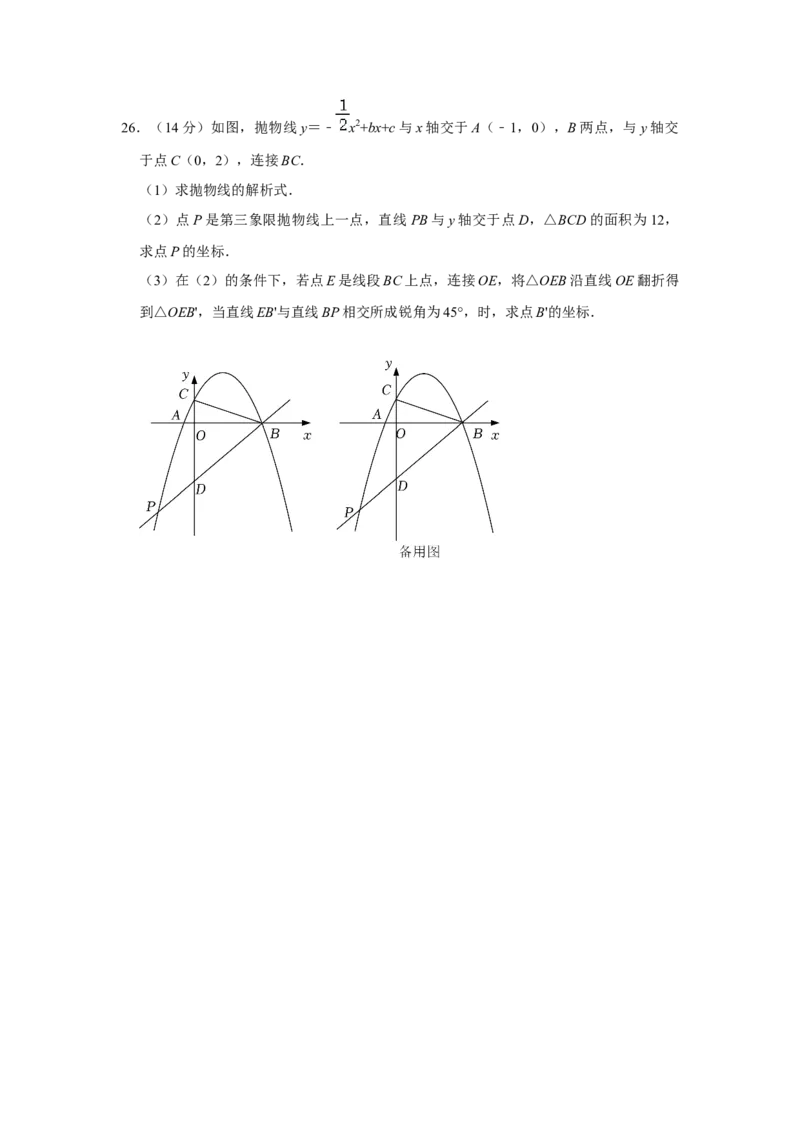
八、解答题(本题满分14分)26.(14分)如图,抛物线y=﹣ x2+bx+c与x轴交于A(﹣1,0),B两点,与y轴交
于点C(0,2),连接BC.
(1)求抛物线的解析式.
(2)点P是第三象限抛物线上一点,直线PB与y轴交于点D,△BCD的面积为12,
求点P的坐标.
(3)在(2)的条件下,若点E是线段BC上点,连接OE,将△OEB沿直线OE翻折得
到△OEB',当直线EB'与直线BP相交所成锐角为45°,时,求点B'的坐标.