文档内容
绵阳市高中2021级第三次诊断性考试
文科数学参考答案及评分意见
一、选择题:本大题共12小题,每小题5分,共60分.
CDACC ACCBD CA
二、填空题:本大题共4小题,每小题5分,共20分.
13.2 14. 15. 16.
三、解答题:本大题共6小题,共70分.
17.解:(1)①当 时, ,则 .································1分
②当 时,由 ,得 ,······························2分
两式相减,得 ,·······················································3分
,即 ,··················································4分
∴
∴数列 是以 为首项, 为公比的等比数列,························5分
∴ .·········································································6分
(2)由(1)得 ,······························8分
可知数列 是以 为首项,4为公比的等比数列,····························9分
∴ ······································································10分
········································································11分
.(也可不计算到此步)·····································12分
18.解:(1)调试前,电池的平均放电时间为:
2.5×0.02×5+7.5×0.06×5+12.5×0.08×5+17.5×0.04×5=11小时,···················4分
调试后的合格率为:0.1×5+0.06×5=0.8,则 ,·······················5分
∴a=48;·····················································································6分
数学(文科)评分标准 第 1 页 共 7 页(2)由列联表可计算 ,·················10分
∴有95%的把握认为参数调试能够改变产品合格率.··························12分
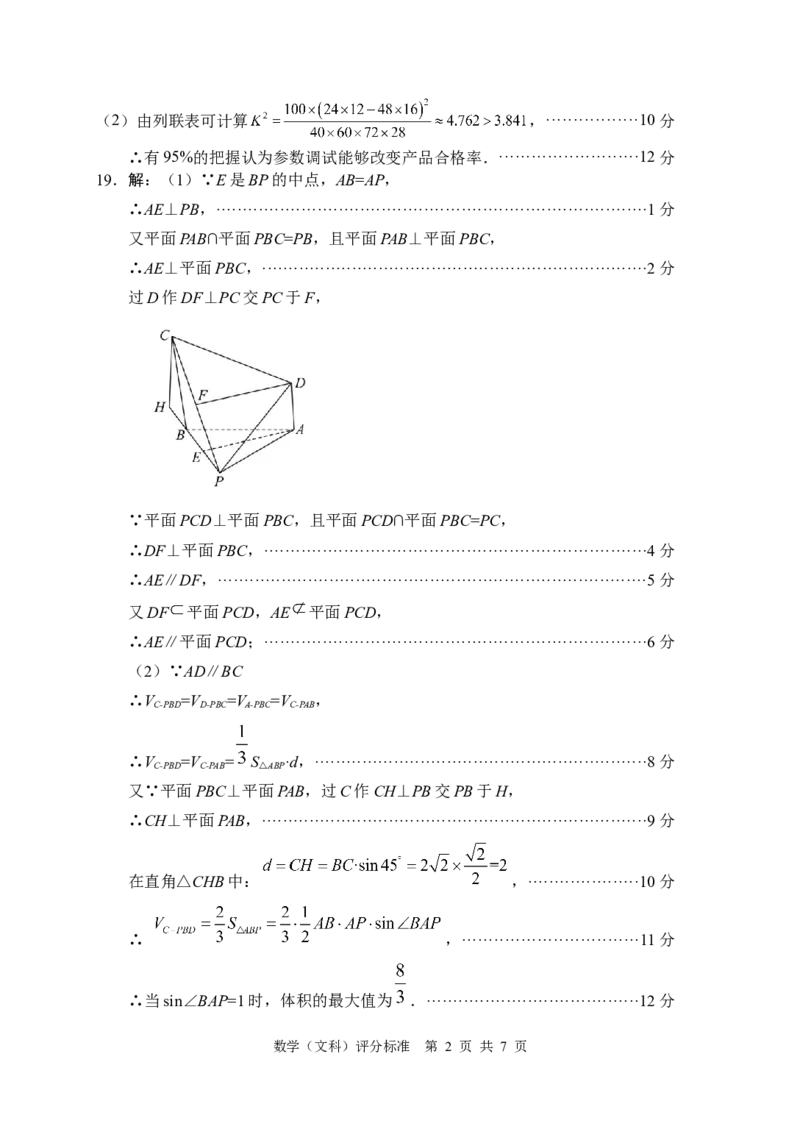
19.解:(1)∵E是BP的中点,AB=AP,
∴AE⊥PB,·················································································1分
又平面PAB∩平面PBC=PB,且平面PAB⊥平面PBC,
∴AE⊥平面PBC,·········································································2分
过D作DF⊥PC交PC于F,
∵平面PCD⊥平面PBC,且平面PCD∩平面PBC=PC,
∴DF⊥平面PBC,········································································4分
∴AE∥DF,·················································································5分
又DF 平面PCD,AE 平面PCD,
∴AE∥平面PCD;········································································6分
(2)∵AD∥BC
∴V =V =V =V ,
C-PBD D-PBC A-PBC C-PAB
∴V =V = S ·d,·······························································8分
C-PBD C-PAB △ABP
又∵平面PBC⊥平面PAB,过C作CH⊥PB交PB于H,
∴CH⊥平面PAB,·········································································9分
在直角△CHB中: ,·····················10分
∴ ,·································11分
∴当sin∠BAP=1时,体积的最大值为 .········································12分
数学(文科)评分标准 第 2 页 共 7 页20.解:(1)解:当 时, ,·······················1分
a=1
,··········································································2分
此时切线斜率为: ;····························································3分
所以曲线 在(e, )处的切线方程: ···············4分
即: ;····························································5分
(2)证明方法一:因为 ,·································6分
由 得到x>a;由 得到0a;由 得到0b>0,所以a−b=2, ②·······················································4分
数学(文科)评分标准 第 6 页 共 7 页由①②得:
a=3,b=1
;··································································5分
√3−at+√bt=√3−3t+√t=√3√1−t+√t
(2) ,·································6分
π
√t=sinθ,0≤θ≤
令 2 ,则
√1−t=cosθ
,··········································7分
π
√3√1−t+√t=√3cosθ+sinθ=2sin(θ+ )
∴ 3 ,··································9分
π 1
θ= t=
∴当 6 时,即 4 时,
√3−at+√bt
的最大值为2.·····················10分
数学(文科)评分标准 第 7 页 共 7 页