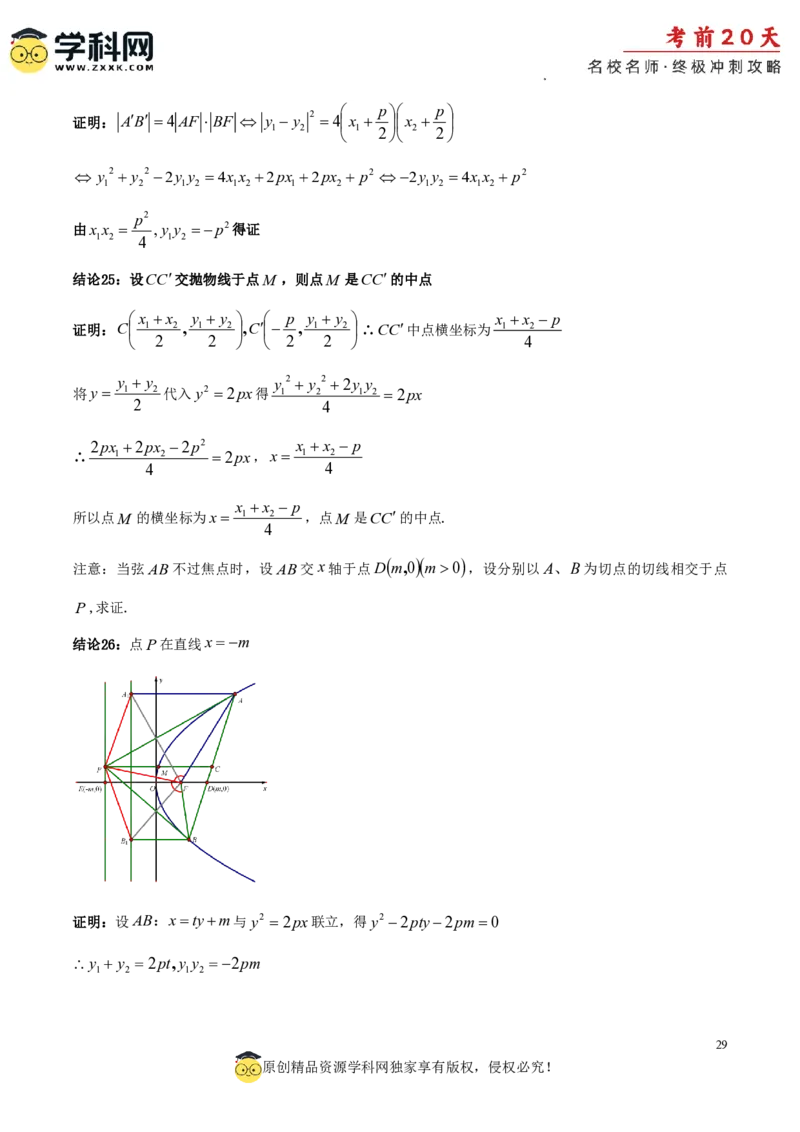
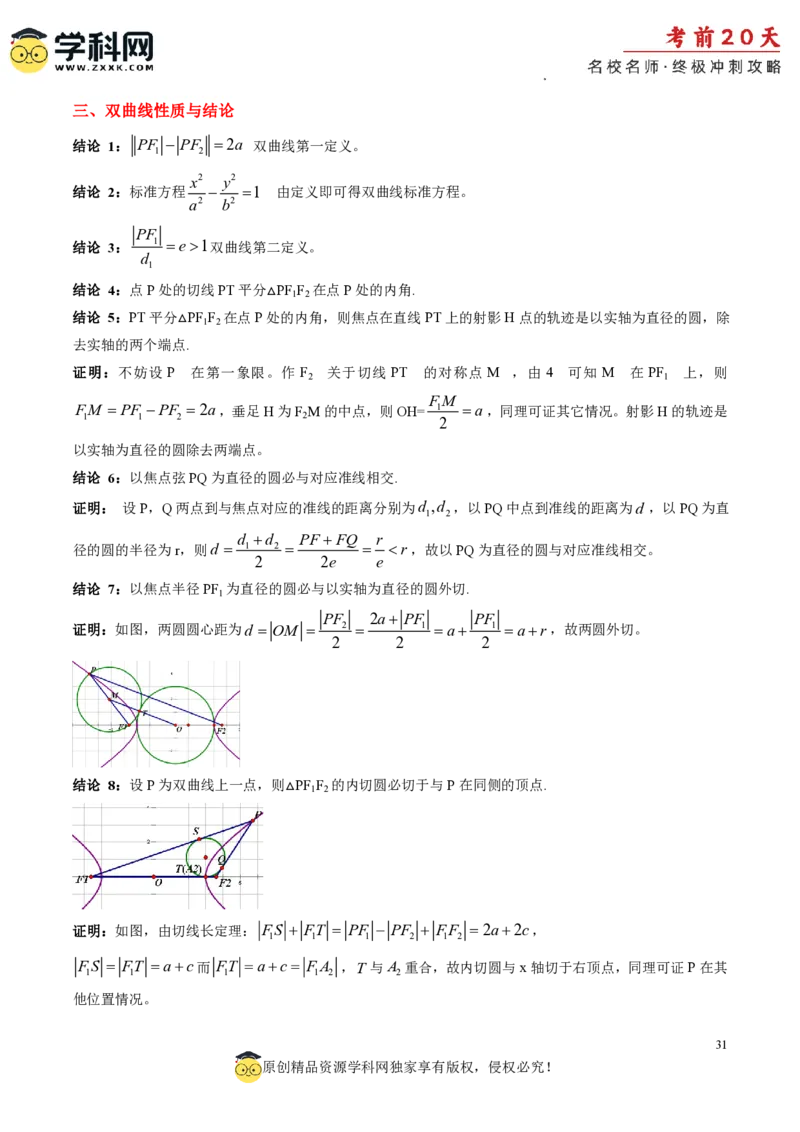
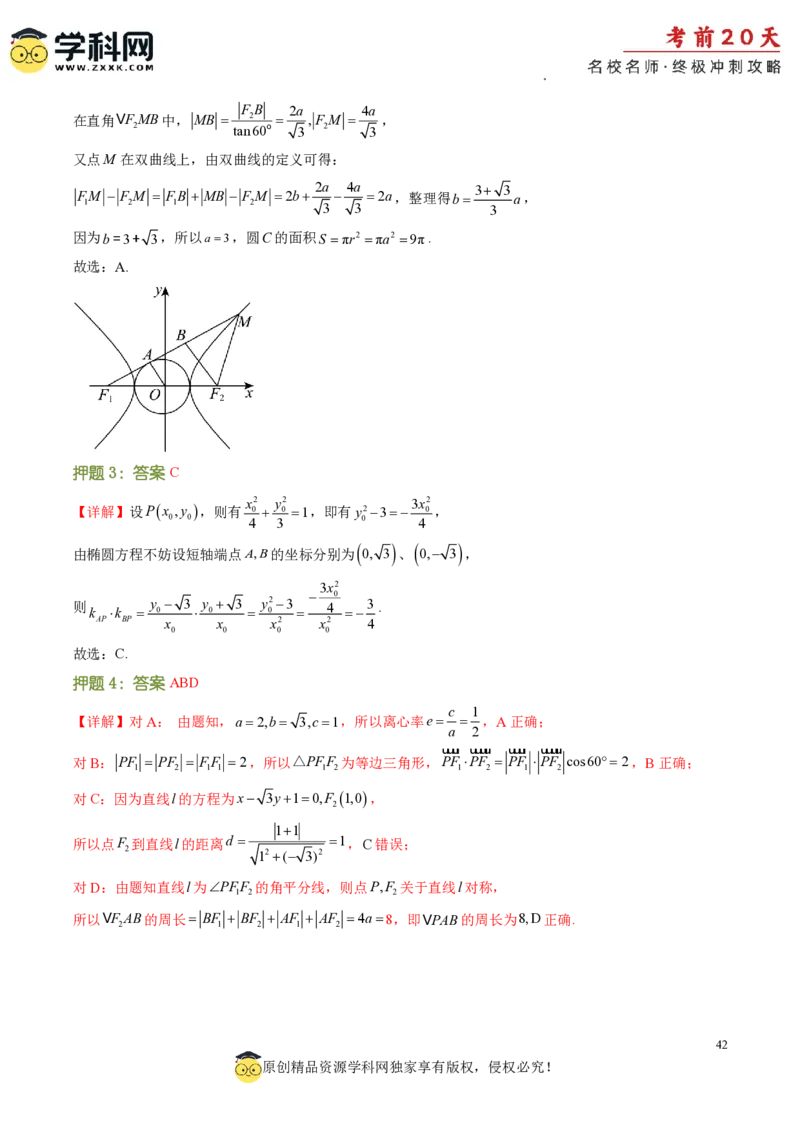
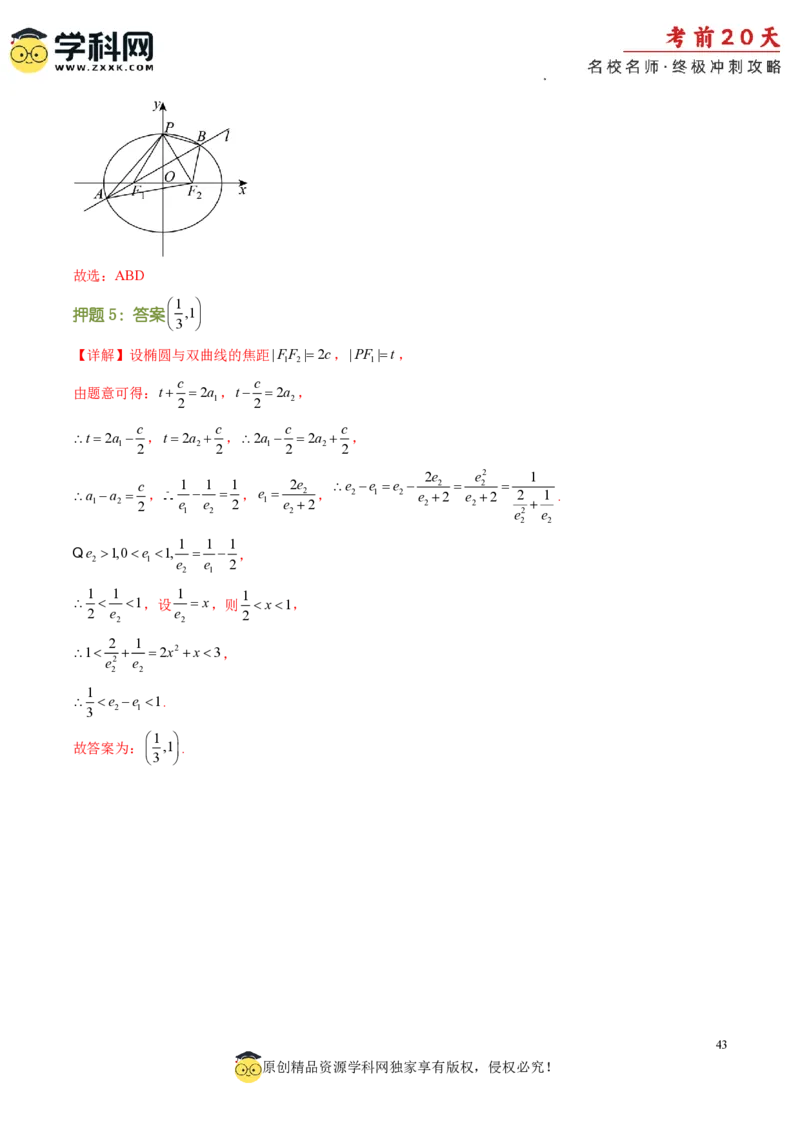
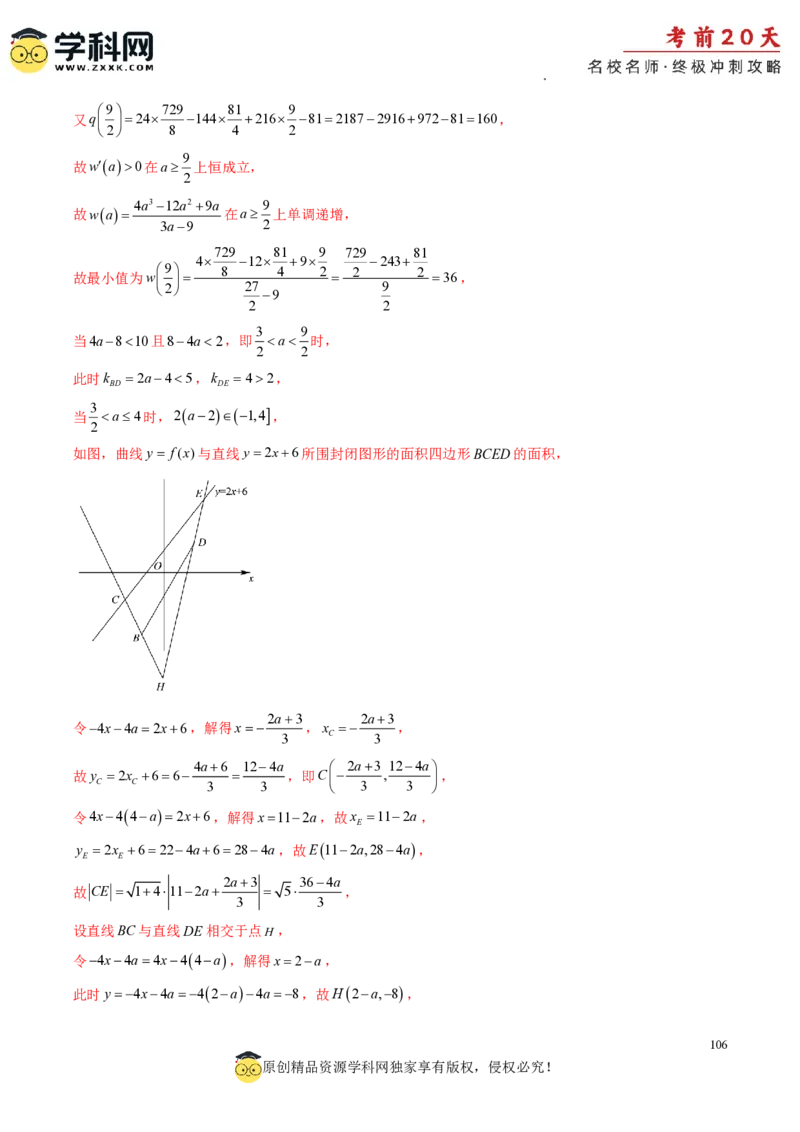文档内容
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司目 录
contents
(一)
统计、排列组合及随机变量及其分布(选填题)…………………………01
圆锥曲线(选填题)…………………………………………………………21
数列(选填题)………………………………………………………………44
空间立体几何(选填题) …………………………………………………62
直线(圆)与方程(选填题)………………………………………………79
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司统计、排列组合及随机变量及其分布(选填题)
年份 题号 知识点 考点
8 事件的独立性 区分独立事件与互斥事件
2021年I卷
①离散型随机变量的均值与变形
9 离散型随机变量
②离散型随机变量的方差与变形
6 正态分布 正态分布均值与标准差在图像中的含义
①离散型随机变量的均值与变形
2021年II
②离散型随机变量的方差与标准差
卷
9 离散型随机变量
③离散型随机变量的中位数
④离散型随机变量的极差
①相同元素与不同元素分配问题
②相邻问题与不相邻问题
5 排列组合
③涂色问题与定序问题
④可重复与限制及正难则反问题
2022年I卷
①二项展开式中的参数及常数项问题
②二项展开式中的系数最值
13 二项式定理
③ 二项展开式中的系数和、各项系数和
与差
①相同元素与不同元素分配问题
②相邻问题与不相邻问题
2022年II 5 排列组合
③涂色问题与定序问题
卷
④可重复与限制及正难则反问题
13 正态分布 正态分布均值与标准差在图像中的含义
2023年新 ①离散型随机变量的均值与变形
9 离散型随机变量
高考1 ②离散型随机变量的方差与标准差
3
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司③离散型随机变量的中位数
④离散型随机变量的极差
①相同元素与不同元素分配问题
②相邻问题与不相邻问题
13 排列组合
③涂色问题与定序问题
④可重复与限制及正难则反问题
①相同元素与不同元素分配问题
②相邻问题与不相邻问题
3 排列组合
2023 年新 ③涂色问题与定序问题
高考2 ④可重复与限制及正难则反问题
①区分独立事件与互斥事件
12 计数原理及事件的独立性 ②计数原理先分类后分步,分类用加分
步用乘
近三年,统计与排列组合在选填中占据两个位置,考查的考点一般来说是:
1、排列组合的四类(①相同元素与不同元素分配问题②相邻问题与不相邻问题③涂色问题与定序问题④可
重复与限制及正难则反问题)
2、离散型随机变量中四组数据(①离散型随机变量的均值与变形②离散型随机变量的方差与标准差③离散
型随机变量的中位数④离散型随机变量的极差)
3、二项式定理中三类(①二项展开式中的参数及常数项问题②二项展开式中的系数最值③ 二项展开式中
的系数和、各项系数和与差)
4、正态分布(正态分布均值与标准差在图像中的含义)
5、计数原理及事件的独立性总方针(计数原理先分类后分步,分类用加分步用乘)
题干的设置一般来说在上述的五项考点中选其两项。排列组合的四类需要认真分析(即完成目标事件
可以分为几类,每一类需要几步可以完成,计算时分步的种数(概率)相乘,最终将几类种数(概率)相
加即为最终答案)其它几类则需要一定的基础和秒杀技巧便可轻松搞定。
统计与排列组合在2024新高考新题型中的考查形式依然以选择或者填空为主(统计大题在后面有讲
解),以考查基本概念和核心方法为主,统计在选填中难度降低,而排列组合选填难度与以往持平,考生
可适当留意常见的排列组合现象并分类,每一类总结出一个固定模板,以便此类题在高考出现时考生能做
到心中有数,快速解答.
4
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司一、万能处理二项展开式中的各项问题
Ⅰ秒杀:确定二项展开式中的参数。
根据条件列出等式,解得所要求的参数。
秒杀公式: ab n展开式中,通项:T Cranrbr,二项展开式的各种题型关键是利用通项求r,r=
r1 n
Nmt
外层指数差/内层指数差。
axm bxn
N展开式中求xt的系数,则有r
。
mn
形如:
2x4x2
5,求x1的系数
破解:分配系数处理
从5次结构中取3次2x和2次4x2,则结果为2342C3 1280
5
形如:
2x3y
3x2y
8的展开式中x2y7的系数为__________
破解:两种括号的情况,一般形式为 1 m和 n m
第一步:分配系数处理
所以分两类情况:第一类情况为:21
3
0C13127C1
1 8
第二类情况为20
3
1C13226C2
1 8
故总的情况为21
3
0C13127C120
3
1C13226C2
1 8 1 8
Ⅱ二项式系数最大问题
二项式系数具备对称性,即Cm Cnm(mn)对于C0,C1,C2,C3 ,Cn大小以二次函数开口向下的图
n n n n n n n
象分析.
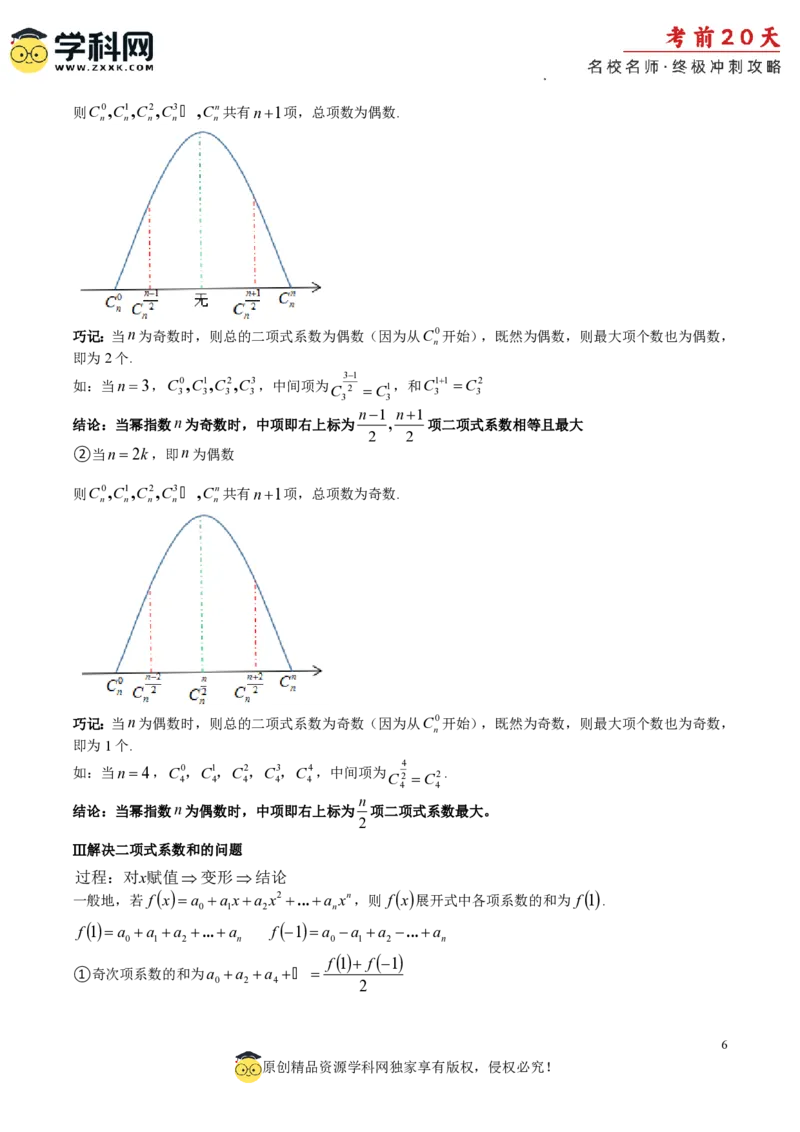
①当n2k1,即n为奇数
5
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司则C0,C1,C2,C3 ,Cn共有n1项,总项数为偶数.
n n n n n
巧记:当n为奇数时,则总的二项式系数为偶数(因为从C0开始),既然为偶数,则最大项个数也为偶数,
n
即为2个.
31
如:当n3,C
3
0,C
3
1,C
3
2,C
3
3,中间项为
C 2
C1,和C
3
11 C
3
2
3 3
n1 n1
结论:当幂指数n为奇数时,中项即右上标为 , 项二项式系数相等且最大
2 2
②当n2k,即n为偶数
则C0,C1,C2,C3 ,Cn共有n1项,总项数为奇数.
n n n n n
巧记:当n为偶数时,则总的二项式系数为奇数(因为从C0开始),既然为奇数,则最大项个数也为奇数,
n
即为1个.
4
如:当n4,C
4
0,C
4
1,C
4
2,C
4
3,C
4
4,中间项为
C2
C2.
4 4
n
结论:当幂指数n为偶数时,中项即右上标为 项二项式系数最大。
2
Ⅲ解决二项式系数和的问题
过程:对x赋值变形结论
一般地,若 f x a a xa x2 ...a xn,则 f x 展开式中各项系数的和为 f 1 .
0 1 2 n
f 1 a a a ...a f 1 a a a ...a
0 1 2 n 0 1 2 n
f 1 f 1
①奇次项系数的和为a a a
0 2 4 2
6
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司
f 1 f 1
偶次项系数的和为a a a
1 3 5 2
②形如 axb n, ax2 bxc m的式子,求展开式的各项系数之和,只需令x1即可.
③形如 axby n的式子求其展开式的各项系数之和,只需令x y 1.
④二项展开式二项式系数和:2n;奇数项与偶数项二项式系数和相等为:2n1。
推导:C0 C1 C2 C3 C4 C5 Cn 11 n 2n
n n n n n n n
押题分向(考察可能性极大)
形如:已知14x5 a axa x2a x5,则a a 2a 3a 4a 5a
0 1 2 5 0 1 2 3 4 5
(带系数利用求导处理)14x5 a axa x2a x5,令x0,a 1;
0 1 2 5 0
两边求导得,2014x4 a 2a x3a x24a x35a x4,
1 2 3 4 5
令x1,a 2a 3a 4a 5a 2034 1620.
1 2 3 4 5
∴a a 2a 3a 4a 5a 1619
0 1 2 3 4 5
Ⅳ展开式系数最大(一道题破解所有)
正规方法:原则:系数最大的这一项,即比前一项大,也比后一项大,从而列不等式组.
①在系数符号相同的前提下,求系数的最大(最小)值只需比较两组相邻两项系数的大小.
T T
r 1 r 1
T T T T T T
不等式组最大值为: r r1 r1 ,最小值为 r r1 r1
T T T T T T
r r1 r 1 r r1 r 1
T T
r1 r1
②当各项系数正负相间时,求系数的最大值应在系数都为正的各项系数间构造不等式
T
r 1
T T T
不等式组最大值为: r r2 r2
T T T
r r2 r 1
T
r2
T
r 1
T T T
求系数的最小值应在系数都为负的各项系数间构造不等式最小值为 r r2 r2
T T T
r r2 r 1
T
r2
秒杀方法:
求展开式中系数最大的项与求二次项系数最大的项是不同的,还需考虑各项系数的正负变化情况,事实上
由于展开式中的各项的系数是离散型变量,因此我们可以考虑类比求数列最大项的方法,即比较第r1项
与相邻两项系数的大小,根据通项构造不等式求解.技巧如下:
形如: 1mx n m0 的二项式展开式,设第r1项的系数为Cr mr最大.
n
7
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司Cr mr Cr1mr1 mn1 mnm
n n r
Cr mr Cr1mr1 m1 m1
n n
Cr mr Cr1mr1 Cr nr1 mr1 1
n n n ,
Cr mr Cr1mr1 Cr1 r mr m
n n n
mnm mn1 mn1 mnm
因为 1,所以不等式组必有解,且当 和 都为整数时,r有两解,且两解
m1 m1 m1 m1
mn1 mnm
分别为 和 ,否则r有一解,因此得出一个结论:
m1 m1
形如
1mx
n
m0
的二项展开式系数最大的项最多只有两项.
mn1
注意:若系数最大的项为最后一项,则 n1mn(Cnmn Cn1mn1)
m1 n n
形如:求
15x
4展开式中系数最大的项时,因为54,所以系数最大的项是最后一项.
mnm
若系数最大的项为第一项,则 1,即mn1
m1
二、排列组合问题
Ⅰ隔板法:解相同元素的组合问题
相同元素的组合问题,即有若干组元素,每组元素相同,将这些元素排成一排的计数问题
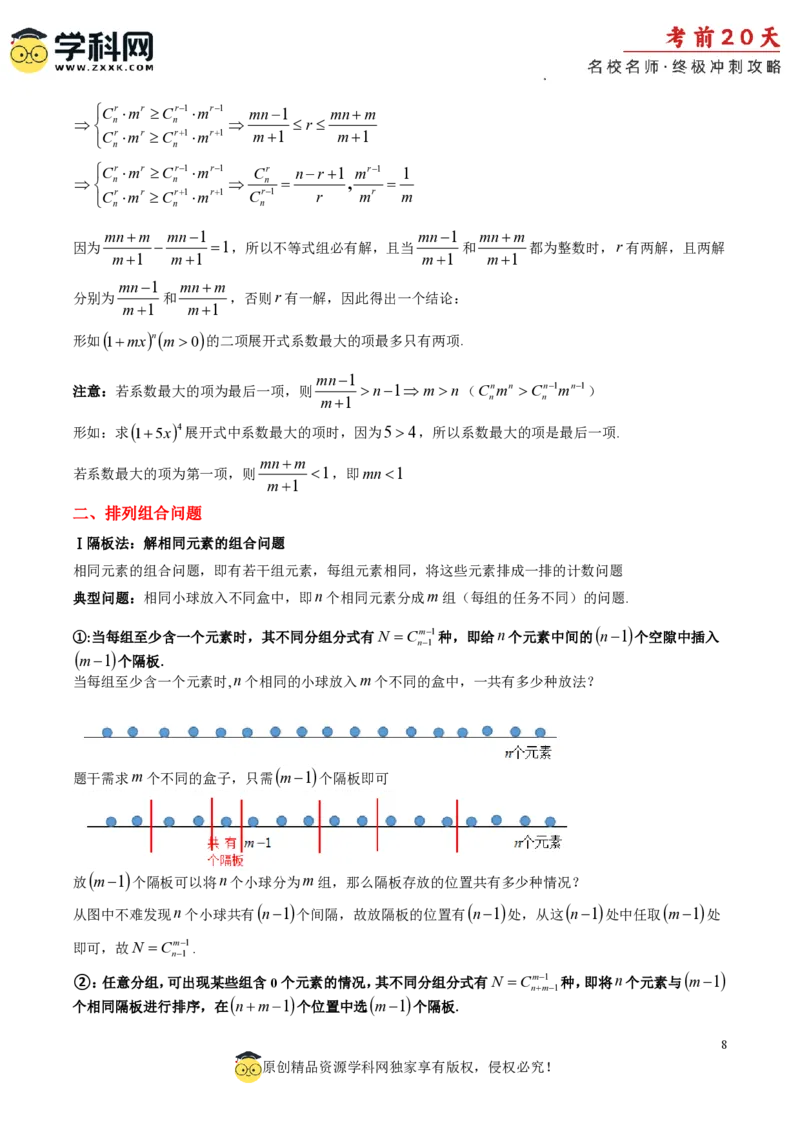
典型问题:相同小球放入不同盒中,即n个相同元素分成m组(每组的任务不同)的问题.
①:当每组至少含一个元素时,其不同分组分式有N Cm1种,即给n个元素中间的 n1 个空隙中插入
n1
m1 个隔板.
当每组至少含一个元素时,n个相同的小球放入m个不同的盒中,一共有多少种放法?
题干需求m个不同的盒子,只需 m1 个隔板即可
放 m1 个隔板可以将n个小球分为m组,那么隔板存放的位置共有多少种情况?
从图中不难发现n个小球共有 n1 个间隔,故放隔板的位置有 n1 处,从这 n1 处中任取 m1 处
即可,故N Cm1.
n1
②:任意分组,可出现某些组含0个元素的情况,其不同分组分式有N Cm1 种,即将n个元素与 m1
nm1
个相同隔板进行排序,在 nm1 个位置中选 m1 个隔板.
8
原创精品资源学科网独家享有版权,侵权必究!
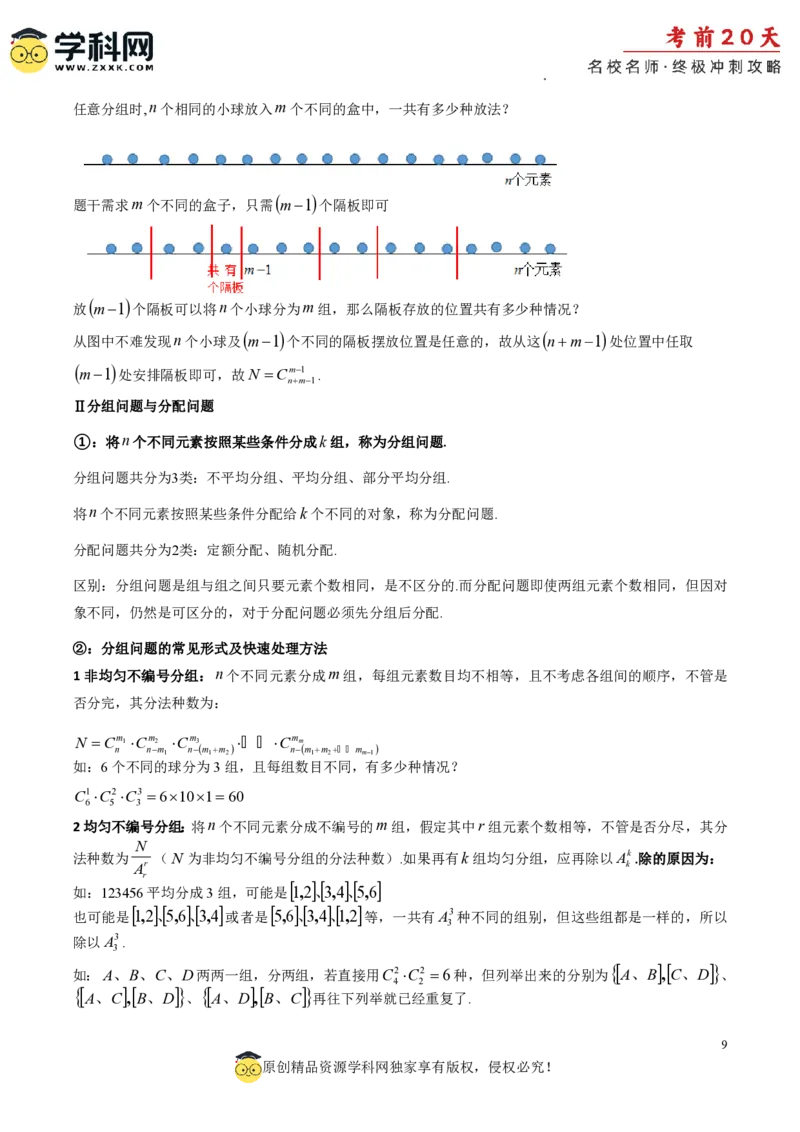
学科网(北京)股份有限公司任意分组时,n个相同的小球放入m个不同的盒中,一共有多少种放法?
题干需求m个不同的盒子,只需 m1 个隔板即可
放 m1 个隔板可以将n个小球分为m组,那么隔板存放的位置共有多少种情况?
从图中不难发现n个小球及 m1 个不同的隔板摆放位置是任意的,故从这 nm1 处位置中任取
m1 处安排隔板即可,故N Cm1 .
nm1
Ⅱ分组问题与分配问题
①:将n个不同元素按照某些条件分成k组,称为分组问题.
分组问题共分为3类:不平均分组、平均分组、部分平均分组.
将n个不同元素按照某些条件分配给k个不同的对象,称为分配问题.
分配问题共分为2类:定额分配、随机分配.
区别:分组问题是组与组之间只要元素个数相同,是不区分的.而分配问题即使两组元素个数相同,但因对
象不同,仍然是可区分的,对于分配问题必须先分组后分配.
②:分组问题的常见形式及快速处理方法
1 非均匀不编号分组:n个不同元素分成m组,每组元素数目均不相等,且不考虑各组间的顺序,不管是
否分完,其分法种数为:
N Cm 1 Cm 2 Cm 3 Cm m
n nm nmm nmm m
1 1 2 1 2 m1
如:6个不同的球分为3组,且每组数目不同,有多少种情况?
C1C2C3 610160
6 5 3
2均匀不编号分组:将n个不同元素分成不编号的m组,假定其中r组元素个数相等,不管是否分尽,其分
N
法种数为 (N 为非均匀不编号分组的分法种数).如果再有k组均匀分组,应再除以Ak.除的原因为:
Ar k
r
如:123456平均分成3组,可能是
1,2
、
3,4
、
5,6
也可能是 1,2 、 5,6 、 3,4 或者是 5,6 、 3,4 、 1,2 等,一共有A3种不同的组别,但这些组都是一样的,所以
3
除以A3.
3
如:A、B、C、D两两一组,分两组,若直接用C2C2 6种,但列举出来的分别为 A、B , C、D 、
4 2
A、C , B、D 、 A、D , B、C 再往下列举就已经重复了.
9
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司如: B、C , A、D 、 B、D , A、C 、 C、D , A、B .
如:6个不同的球分为3组,且每组数目相同,有多少种情况?
N 90
N C2C2C2 90,种数 15.
6 4 2 A3 6
3
3 非均匀编号分组:将n个不同元素分成m组,各组元素数目均不相等,且考虑各组间的顺序,其分法种
数为NAm(N 为非均匀不编号分组的分法种数)
m
4 均匀编号分组:将n个不同元素分成m组,各组元素数目均相等,且考虑各组间的顺序,其分法种数为
NAm
m (N 为非均匀不编号分组的分法种数).
Ar
r
Ⅲ相邻问题与不相邻问题
①相邻问题
1、思路:对于相邻问题,一般采用“捆绑法”解决,即将相邻的元素看做是一个整体,在于其他元素放在
一起考虑.如果设计到顺序,则还应考虑相邻元素的顺序问题,再与其他元素放在一起进行计算.
2、解题步骤:
第一步:把相邻元素看作一个整体(捆绑法),求出排列种数
第二步:求出其余元素的排列种数
第三步:求出总的排列种数
②不相邻问题
1.思路:对于不相邻问题一般采用“插空法”解决,即先将无要求的元素进行全排列,然后将要求不相邻
的元素插入到已排列的元素之间,最后进行计算即可
2.解题步骤:
①先考虑不受限制的元素的排列种数
②再将不相邻的元素插入到已排列元素的空当种(插空法),求出排列种数
③求出总的排列种数
Ⅳ涂色问题与定序问题
①涂色问题
秒杀策略:涂色问题分步(乘法)、分类(加法)处理:尽可能多的找两两相邻的区域,因为这些区域颜色各
不相同,按乘法原理涂色,再按分类涂剩余区域,一般分用剩余颜色与不用剩余颜色。
②定序问题
定序问题作倍缩放:将题干给定的总数n都看成某一个独立的个体(不相同的),进行全排列故为An,其
n
An
次再将有顺序要求的m个元素进行全排列Am个,其中满足要求的顺序必为1个,则总的情况数为 n 。
m Am
m
三、离散型随机变量问题
Ⅰ均值与方差的性质
10
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司
(1)E aX b aE X b.
(2)D aX b a2D X (a,b为常数).(3)D X E X2 E X 2
两点分布、二项分布、超几何分布的期望、方差
(1)若X服从两点分布,则E X p,D X p1 p .
(2)若X服从二项分布,即X ~ B n, p ,则E X np,D X np1 p .
(3)若X服从超几何分布,即X ~ H n,M,N 时,
nM nM N M N n
E X .D X
N
N2
N 1
Ⅱ二项分布之概率最值问题
如果X ~ B n, p ,其中0 p1,求P X k 最大值对应的k值.
P X k
一般是考察 与1的大小关系.
P X k1
P X k nk1 p n1 pk
因为 1 1k n
P X k1 k 1 p k 1 p
所以要使P X k p X k1 ,则k n1 p.故有
⑴如果 n1 p n,则k n时P X k 取得最大值.
⑵如果 n1 p,是不超过n的正整数,则当k n p1 和k n p 时,P X k 取
得最大值.
(3)如果 n1 p是不超过n的非整数,则当k n1 p (注意k n1 p 表示不超
过 n1 p的最大整数)时P X k 取得最大值.
四、正态分布问题
1.正态曲线及其性质
(1)正态曲线:
函数
,
x
2
1
e x 2 2 2 ,x,,其中实数μ,σ(σ>0)为参数,我们称φ μ,σ (x)的图象为正态分布
密度曲线,简称正态曲线.
(2)正态曲线的性质:
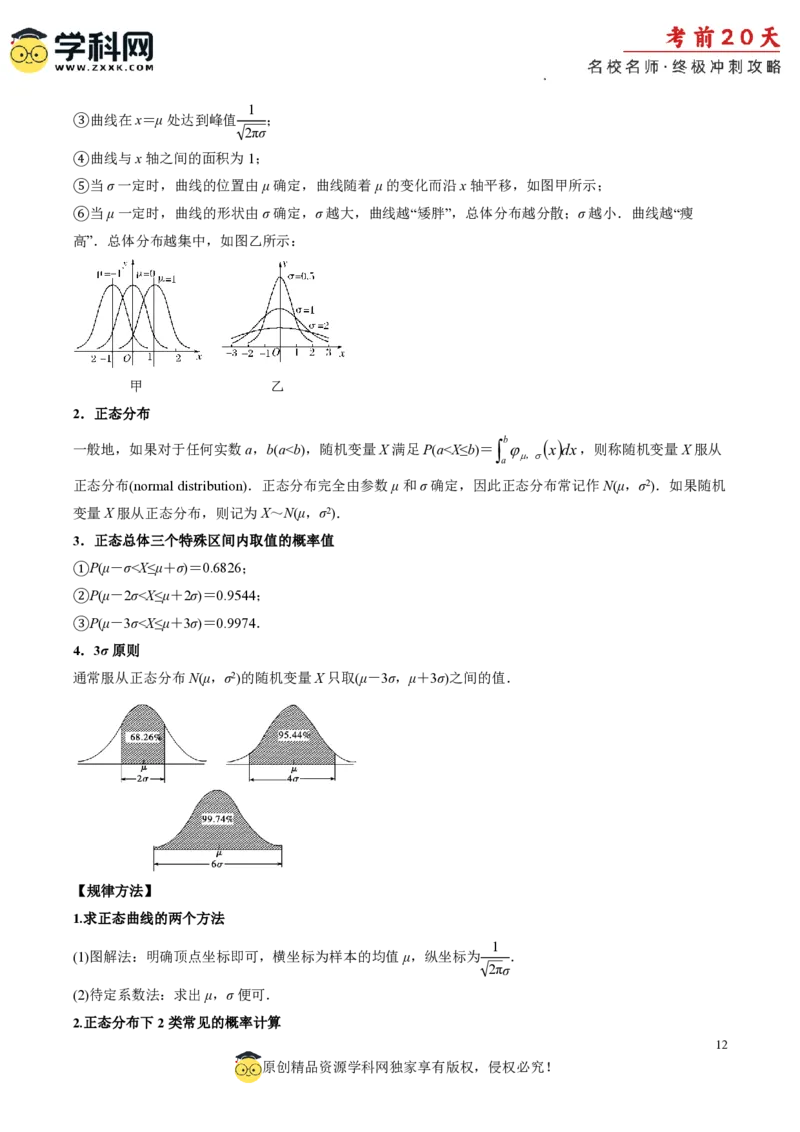
①曲线位于x轴上方,与x轴不相交;
②曲线是单峰的,它关于直线x=μ对称;
11
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司1
③曲线在x=μ处达到峰值 ;
2πσ
④曲线与x轴之间的面积为1;
⑤当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移,如图甲所示;
⑥当μ一定时,曲线的形状由σ确定,σ越大,曲线越“矮胖”,总体分布越分散;σ越小.曲线越“瘦
高”.总体分布越集中,如图乙所示:
甲 乙
2.正态分布
b
一般地,如果对于任何实数a,b(a0, f x单调递增,
当0x1时, fx0, f x单调递减,
从而 f x f 30或 f 12 f x f 00,
这表明了a q33q2的范围是2a 0或a 0.
4 4 4
所以A错误,B正确,C正确,D正确.
故选:BCD.
押题2:答案BCD
【详解】对A:若数列a ta nN* 为等差数列,则有a ta a ta d,
n1 n n2 n1 n1 n
即a 1ta ta d,由a a a nN* ,
n2 n1 n n2 n1 n
1t 1
故有a a 1ta ta d恒成立,即有t 1 ,无解,
n1 n n1 n
d 0
故不存在这样的实数t,故A错误;
a ta
对B:若数列a ta nN* 为等比数列,则有 n2 n1 q,
n1 n a ta
n1 n
即a qta qta ,由a a a nN* ,
n2 n1 n n2 n1 n
59
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司qt 1
故有a a qta qta 恒成立,即有 ,
n1 n n1 n qt 1
1 5
即t2 t10,解得t ,此时a ta 11 5 50,
2 2 1
故存在非零实数t,使得a ta nN* 为等比数列,故B正确;
n1 n
对C:由a a a
nN*
,
n2 n1 n
则a a a a a a a a a 3a ,
n4 n n3 n2 n n2 n1 n2 n n2
即有3a a a
nN*
,故C正确;
n2 n4 n
对D:由a a a
nN*
,
n2 n1 n
故1n2a 1n2a 1n2a 1n1a 1na ,
n2 n1 n n1 n
2024
故1ia 1a 12a 13a L 12024a
i 1 2 3 2024
i1
1212112a 1a 13a 12a 14a 13a L 12023a 12022a
2 1 3 2 4 3 2023 2022
211a 12023 a a 3,故D正确.
1 2023 2023
故选:BCD.
押题3:答案BC
【详解】设数列a 的首项为a ,公比为 q ,
n 1
3
aq2 18 q3 q
由题有 1 ,解得 或 4,
a
1
a
1
qa
1
q2 26 a
1
2
a 32
1
3
q
对于选项A,当 4,n为奇数时,a 0,所以选项A错误,
n
a 32
1
3
a (1qn) q q3
对于选项B,因为S 1 ,当 4,显然有S 0,当 时,
n 1q
a 32
n a
1
2
1
1q0,1qn 0,所以S 0,故选项B正确,
n
对于选项C,当q3时,数列
a
是首项为2,公比为3的递增数列,
n
3 3
当q 时,数列
a
是首项为32,公比为 的递减数列,所以选项C正确,
4 n 4
对于选项D,由选项B知S 0,所以 S S ,
n n n
60
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司3
3 32(1( )n)
当 q 4时,S 4 128 [1( 3 )n],此时S 不具有单调性,所以选项D错误,
n 3 7 4 n
a 32 1
1 4
故选:BC.
押题4:答案16
【详解】设等差数列a 的公差为d,
n
a 4da 8d 14 a 5
则有 1 1 ,解得: 1 ,
a d 3 d 2
1
87
所以S 85 216.
8 2
故答案为:16
1
押题5:答案 /0.25
4
【详解】Qa a a a 2,又a a 3,a ,a 是方程x23x20的两根,
3 7 4 6 4 6 4 6
又a 为单增等比数列,a 1,a 2q2 2
n 4 6
π π
又cos2x 2cos2xsin2xcos2x1 2sin2x 1,
2 4
π π 2
2sin2x 12sin2x ,
4 4 2
π π 9π π π 3π π
Qx0,π,2x , , 2x 0x ,
4 4 4 4 4 4 4
π
0
所求概率 4 1.
P
π0 4
1
故答案为: .
4
61
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司空间立体几何(选填题)
年份 题号 知识点 考点
①截面周长与面积定值问题
2021年I卷 12 三棱柱 ②动点构成体积定值
③动点参与的垂直问题
2021年II
10 正方体 动点满足要求所存在的情况
卷
①线与线夹角问题
2022年I卷 9 正方体
②线与面夹角问题
2022年II 体积之间的关系
11 空间多边形
卷
2023年新
12 正方体 立体几何的包裹问题
高考1
2023 年新
①锥体的侧面积问题
高考2 9 椎体
②锥体的体积问题
近三年,空间几何体在选填中占据一个位置,考查的考点一般来说是:
4、空间几何体的表面积与体积(①锥体的表面积与体积②柱体的表面积与体积③组合体的表面积与体积)
2、空间几何体涉及夹角与位置问题(①线与线、线与面及面与面的夹角问题②线与面平行关系③线与面垂
直关系)
3、动点与截面问题(①以动点为导火索求新平面图、几何体的各种参数②截面所截面积与周长定值最值问
题)
题干的设置一般来说在上述的三项考点中选其一项或两项。有关表面积与体积考生需熟记公式,有关
截面问题考生需要掌握截面的作法,针对计算可以用几何法也可借助空间向量,对于动点完全需要利用空
62
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司间向量求出轨迹方程进而求其它。
从近三年的全国卷的考查情况以及新高考新题型标准来看,空间几何体是高考选填方向必不可少的一
类题,类型1:正方体探究截面与动点问题,类型2:空间中线与面的位置关系。类型3:组合体表面积与
体积(实际应用)问题,尤其是台体的表面积与体积,类型1相对有难度,其它两类相对简单.
一、立体几何截面问题
①作出空间几何体的截面
1、作截面应遵循的三个原则:(1)在同一平面上的两点可引直线;(2)凡是相交的直线都要画出它们的
交点;(3)凡是相交的平面都要画出它们的交线;
2、作交线的方法有如下两种:(1)利用基本事实3作直线;(2)利用线面平行及面面平
行的性质定理去寻找线面平行及面面平行,然后根据性质作出交线。
②判断截面多边形的形状
判断截面多边形形状时需要注意以下几点:
1、截面与几何体表面相交,交线不会超过几何体表面个数。
2、不会与同一个表面有两条交线。
3、与一对平行表面相交,交线平行(不一定等长)
4、截面截内切球或者外接球时,区分与面相切和与棱相切之间的关系
③求解截面多边形的周长
求解截面多边形的周长有两个思路:(1)利用多面体展开图进行求解;(2)在各个表面
确定交线,分别利用解三角形进行求解。
④求解截面多边形的面积
求解截面多边形的面积问题的步骤:(1)通过解三角形求得截面多边形各边的长度;(2)
判断多边形的形状是否规则,若为规则图形可直接使用面积公式求解;否则可通过切割法
将多边形分为多个三角形求解。
⑤截面分割几何体的体积问题
截面分割后的几何体易出现不规则的几何体,对此往往采用“切割法”或“补形法”进行
体积的求解。
⑥截面最值的相关问题
截面最值问题的计算,主要由以下三种方法:
1、极限法:通过假设动点运动至两端,计算最值(需注意判断是否单调);
2、坐标法:通过建系设坐标,构造对应的函数进行求解;
3、化归法:通过图形转化,把立体图形转化为平面图形,寻找平面图形中的最值计算。
63
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司二、垂直与平行命题判断
技巧总结
结论:①要证线∥面,条件为3个,其中必有《线面》
②要证线⊥面,条件为2个,其中必有《线∥线或面∥面》
③要证线∥线(面∥面),条件为2或3个,其中必有《两个线⊥面》
④要证线⊥线(面⊥面),条件为2个,其中必有《⊥、∥()》
、、
⑤要证线⊥线(面⊥面),条件为3个,其中必有《 》
线面、∥∥
三、空间几何体表面积与体积
1、空间几何体的表面积和体积公式
名称
表面积 体积
几何体
柱体(棱柱和圆柱) S =S +2S V=S h
表面积 侧 底 底
1
锥体(棱锥和圆锥) S =S +S V= S h
表面积 侧 底 底
3
S =S +S +S 1
台体(棱台和圆台) 表面积 侧 上 V= (S 上 +S 下 + S上S下)h
3
下
4
球 S=4πR2 V= πR3
3
几何体的表面积和侧面积的注意点
①几何体的侧面积是指(各个)侧面面积之和,而表面积是侧面积与所有底面面积之和.
②组合体的表面积应注意重合部分的处理.
2、柱体、锥体、台体侧面积间的关系
(1)当正棱台的上底面与下底面全等时,得到正棱柱;当正棱台的上底面缩为一个点时,得到正棱锥,
c′=c 1 c′=0 1
则S
正棱柱侧
=ch′←―― S
正棱台侧
= (c+c′)h′――→S
正棱锥侧
= ch′.
2 2
(2)当圆台的上底面半径与下底面半径相等时,得到圆柱;当圆台的上底面半径为零时,得到圆锥,
r′=r r′=0
则S
圆柱侧
=2πrl←―― S
圆台侧
=π(r+r′)l――→S
圆锥侧
=πrl.
①求空间几何体表面积的常见类型及思路
1、求多面体的表面积:只需将它们沿着棱“剪开”展成平面图形,利用求平面图形面积的方法求多面体的表
面积;
2、求旋转体的表面积:可以从旋转体的形成过程及其几何特征入手,将其展开后求表面积,但要搞清它们
的底面半径、母线长与对应侧面展开图中的边长关系
3、求不规则几何体的表面积:通常将所给几何体分割成基本的柱体、锥体、台体,先求出这些基本的柱体、
64
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司锥体、台体的表面积,再通过求和或作差,求出所给几何体的表面积;
②空间几何体的体积
1、处理空间几何体体积的基本思路
(1)转:转换底面与高,将原本不容易求面积的底面转换为容易求面积的底面,或将原来不容易看出的高
转换为容易看出并容易求解的高;
(2)拆:将一个不规则的几何体拆成几个规则的几何体,便于计算;
(3)拼:将小几何体嵌入一个大几何体中,如有时将一个三棱锥复原成一个三棱柱,将一个三棱柱复原乘
一个四棱柱,还台位锥,这些都是拼补的方法。
2、求体积的常用方法
(1)直接法:对于规则的几何体,利用相关公式直接计算;
(2)割补法:把不规则的几何体分割成规则的几何体,然后进行体积计算;或者把不规则的几何体补成规
则的几何体,不熟悉的几何体补成熟悉的几何体,便于计算;
(3)等体积法:选择合适的底面来求几何体的体积,常用于求三棱锥的体积,即利用三棱锥的任一个面作
为三棱锥的底面进行等体积变换
③平移法求异面直线所成角的步骤
第一步平移:平移的方法一般有三种类型:(1)利用图中已有的平行线平移;(2)利用特殊点(线段的端点或中
点)作平行线平移;(3)补形平移
第二步证明:证明所作的角是异面直线所成的角或其补角
第三步寻找:在立体图形中,寻找或作出含有此角的三角形,并解之
第四步取舍:因为异面直线所成角θ的取值范围是0°<θ≤90°,所以所作的角为钝角时,应取它的补角作为
异面直线所成的角
三、空间几何体动态问题
立体几何中的动态问题主要包括:空间动点轨迹的判断,求解轨迹的长度及动角的范围等问题;
立体几何中的动点轨迹问题一般有四种,即线段型,平面型,二次曲线型,球型,空间中轨迹问题的解答
思路:
(1)根据已知条件确定和待求点相关的平行、垂直等关系;
(2)用动点Q的坐标x、y、z表示相关点P的坐标x 、y 、z ,然后代入点P的坐标x ,y,z 所满足
0 0 0 0 0 0
的曲线方程,整理化简可得出动点Q的轨迹方程;
(3)根据轨迹形状即可求解出轨迹的长度等其他量.
立体几何最值:
1、计算多面体或旋转体的表面上的最值问题时,一般采用转化的方法来进行,即将侧面展开化为平面图形,
即“化折为直”或“化曲为直”来解决,要熟练掌握多面体与旋转体的侧面展开图的形状;
2、对于几何体内部的折线的最值,可采用转化法,转化为两点间的距离,结合勾股定理求解.
65
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司空间中动线段的距离和的最值问题,可以类比平面中的距离和的最值处理利用对称性来处理于转化,另外
异面直线间的公垂线段的长度可利用点到平面的距离来处理.计算多面体或旋转体的表面上折线段的最值
问题时,一般采用转化的方法进行,即将侧面展开化为平面图形,即“化折为直”或“化曲为直”来解决,
要熟练掌握多面体与旋转体的侧面展开图的形状;
典例1【2023新高考1卷】下列物体中,能够被整体放入棱长为1(单位:m)的正方体容器(容器壁厚度
忽略不计)内的有( )
A. 直径为0.99m的球体
B. 所有棱长均为1.4m的四面体
C. 底面直径为0.01m,高为1.8m的圆柱体
D. 底面直径为1.2m,高为0.01m的圆柱体
【答案】ABD
【解析】对于选项A:因为0.99m1m,即球体的直径小于正方体的棱长,
所以能够被整体放入正方体内,故A正确;
对于选项B:因为正方体的面对角线长为 2m,且 2 1.4,
所以能够被整体放入正方体内,故B正确;
对于选项C:因为正方体的体对角线长为 3m,且 3 1.8,
所以不能够被整体放入正方体内,故C不正确;
对于选项D:因为1.2m1m,可知底面正方形不能包含圆柱的底面圆,
如图,过AC 的中点O作OE AC ,设OEI AC E,
1 1
3 CC OE
可知AC 2,CC 1,AC 3,OA= ,则tanCAC 1 ,
1 1 2 1 AC AO
1 OE
6
即 2 3 ,解得OE ,
4
2
2
6 3 9 9 6
且 0.62,即 0.6,
4 8 24 25 4
故以AC 为轴可能对称放置底面直径为1.2m圆柱,
1
若底面直径为1.2m的圆柱与正方体的上下底面均相切,设圆柱的底面圆心O ,与正方体的下底面的切点
1
为M ,
66
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司CC OM
可知:AC OM,OM 0.6,则tanCAC 1 1 ,
1 1 1 1 AC AO
1
1 0.6
即 ,解得AO 0.6 2 ,
2 AO 1
1
根据对称性可知圆柱的高为 320.6 2 1.7321.21.4140.03520.01,
所以能够被整体放入正方体内,故D正确;
故选:ABD.
典例2【2023新高考全国Ⅱ卷】 已知圆锥的顶点为P,底面圆心为O,AB为底面直径,APB120,
PA2,点C在底面圆周上,且二面角PACO为45°,则( ).
A. 该圆锥的体积为π B. 该圆锥的侧面积为4 3π
C. AC 2 2 D. △PAC 的面积为 3
【答案】AC
【解析】依题意,APB120,PA2,所以OP1,OAOB 3,
1 2
A选项,圆锥的体积为 π 3 1π,A选项正确;
3
B选项,圆锥的侧面积为π 322 3π,B选项错误;
C选项,设D是AC的中点,连接OD,PD,
则AC OD,AC PD,所以PDO是二面角PACO的平面角,
则PDO 45,所以OPOD1,
故ADCD 31 2,则AC 2 2,C选项正确;
1
D选项,PD 12 12 2,所以S 2 2 2 2,D选项错误.
VPAC 2
故选:AC.
67
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司典例3【2022新高考全国Ⅰ卷】南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某
水库.已知该水库水位为海拔148.5m时,相应水面的面积为140.0km2;水位为海拔157.5m时,相应水面
的面积为180.0km2,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5m上升到
157.5m时,增加的水量约为( 7 2.65)( )
A. 1.0109m3 B. 1.2109m3 C. 1.4109m3 D. 1.6109m3
【答案】 C
【解析】依题意可知棱台的高为MN 157.5148.59(m),所以增加的水量即为棱台的体积V .
棱台上底面积S 140.0km2 140106m2,下底面积S180.0km2 180106m2,
1 1
∴V h S S SS 9 140106 180106 1401801012
3 3
3 32060 7 106 96182.65107 1.437109 1.4109(m3).
故选:C.
典例4【2022新高考全国Ⅱ卷】 如图,四边形ABCD为正方形,ED平面ABCD,
FB∥ED,AB ED 2FB,记三棱锥EACD,F ABC ,F ACE 的体积分别为V,V ,V ,则( )
1 2 3
68
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司A. V 2V B. V V
3 2 3 1
C. V V V D. 2V 3V
3 1 2 3 1
【答案】CD
【解析】
1 1 1 4
设ABED2FB2a,因为ED平面ABCD,FBPED,则V EDS 2a 2a2 a3,
1 3 VACD 3 2 3
1 1 1 2
V FBS a 2a2 a3,连接BD交AC于点M ,连接EM,FM ,易得BD AC,
2 3 VABC 3 2 3
又ED平面ABCD,AC平面ABCD,则ED AC,又EDI BD D,ED,BD平面BDEF ,
则AC 平面BDEF ,
1
又BM DM BD 2a,过F 作FG DE 于G,易得四边形BDGF为矩形,则
2
FGBD2 2a,EGa,
则EM 2a2 2a 2 6a,FM a2 2a 2 3a,EF a2 2 2a 2 3a,
1 3 2
EM2 FM2 EF2,则EM FM ,S EMFM a2,AC 2 2a,
VEFM 2 2
1
则V V V ACS 2a3,则2V 3V ,V 3V ,V V V ,故A、B错误;C、D
3 AEFM CEFM 3 VEFM 3 1 3 2 3 1 2
正确.故选:CD.
典例5【2021新高考全国Ⅱ卷】 正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为( )
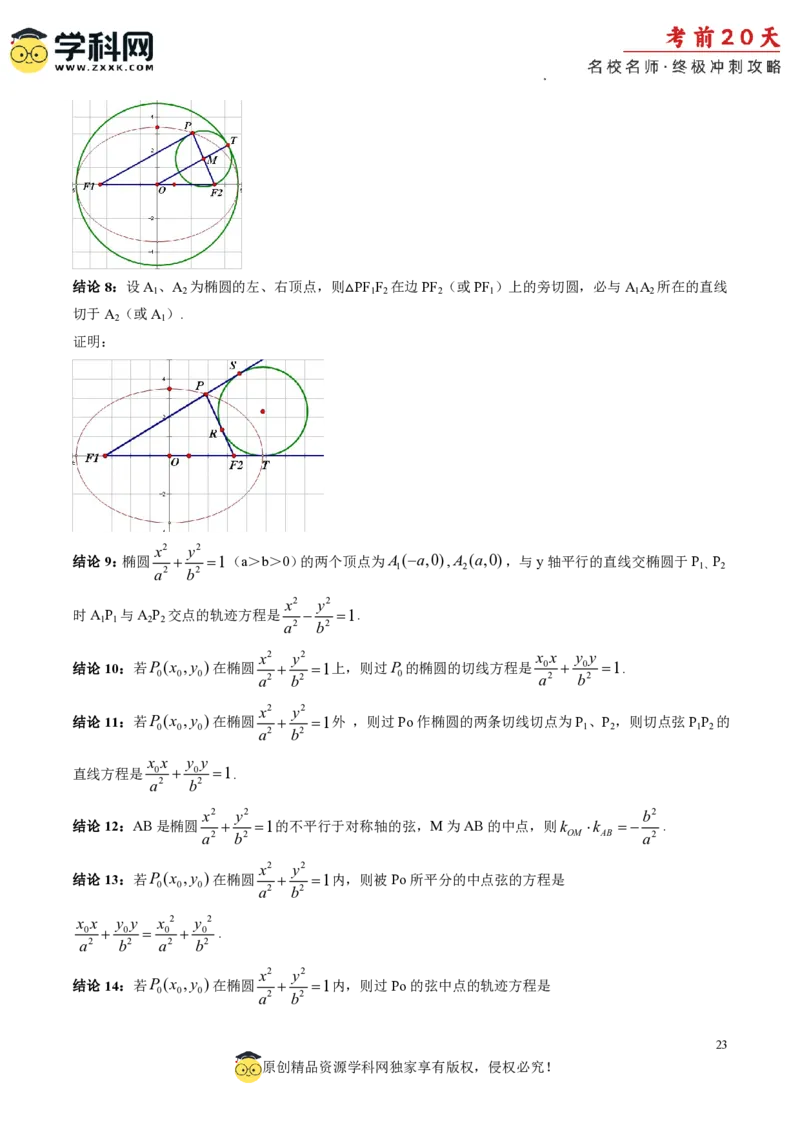
56 28 2
A. 2012 3 B. 28 2 C. D.
3 3
【答案】D
69
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司【解析】作出图形,连接该正四棱台上下底面的中心,如图,
因为该四棱台上下底面边长分别为2,4,侧棱长为2,
2
所以该棱台的高h 22 2 2 2 2,
下底面面积S 16,上底面面积S 4,
1 2
1 1 28
所以该棱台的体积V h S S S S 2 164 64 2 .
3 1 2 1 2 3 3
故选:D.
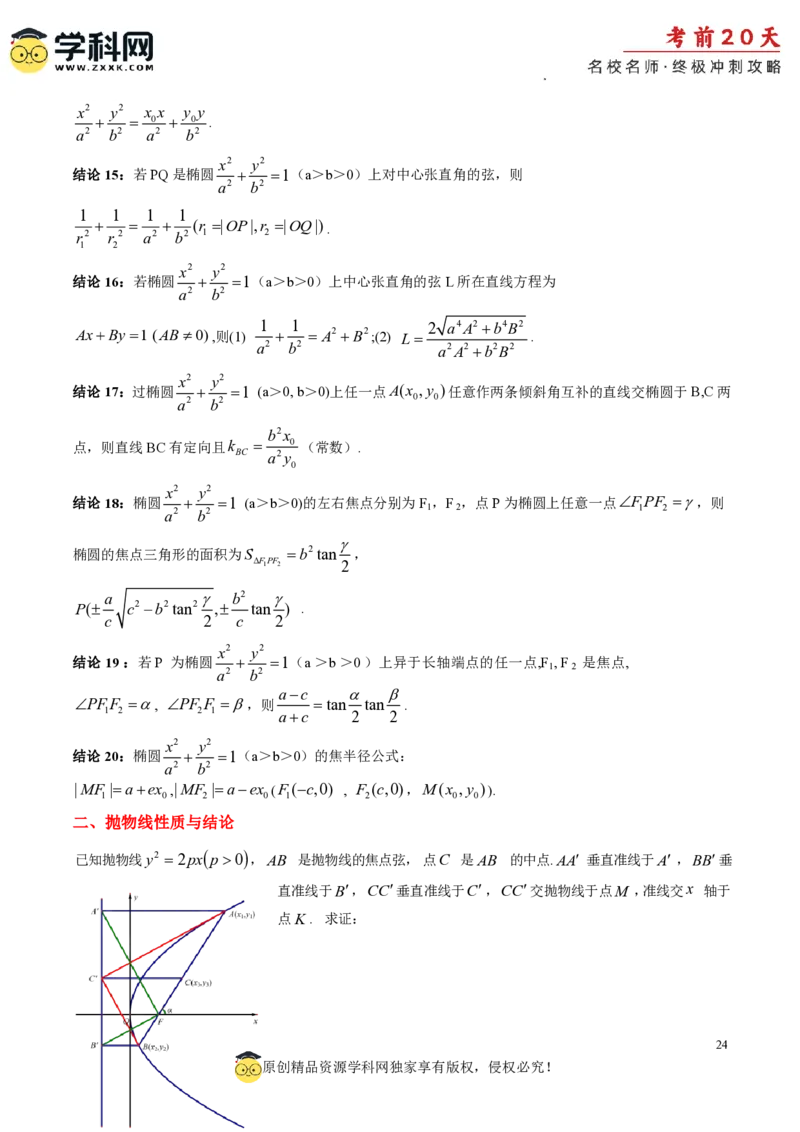
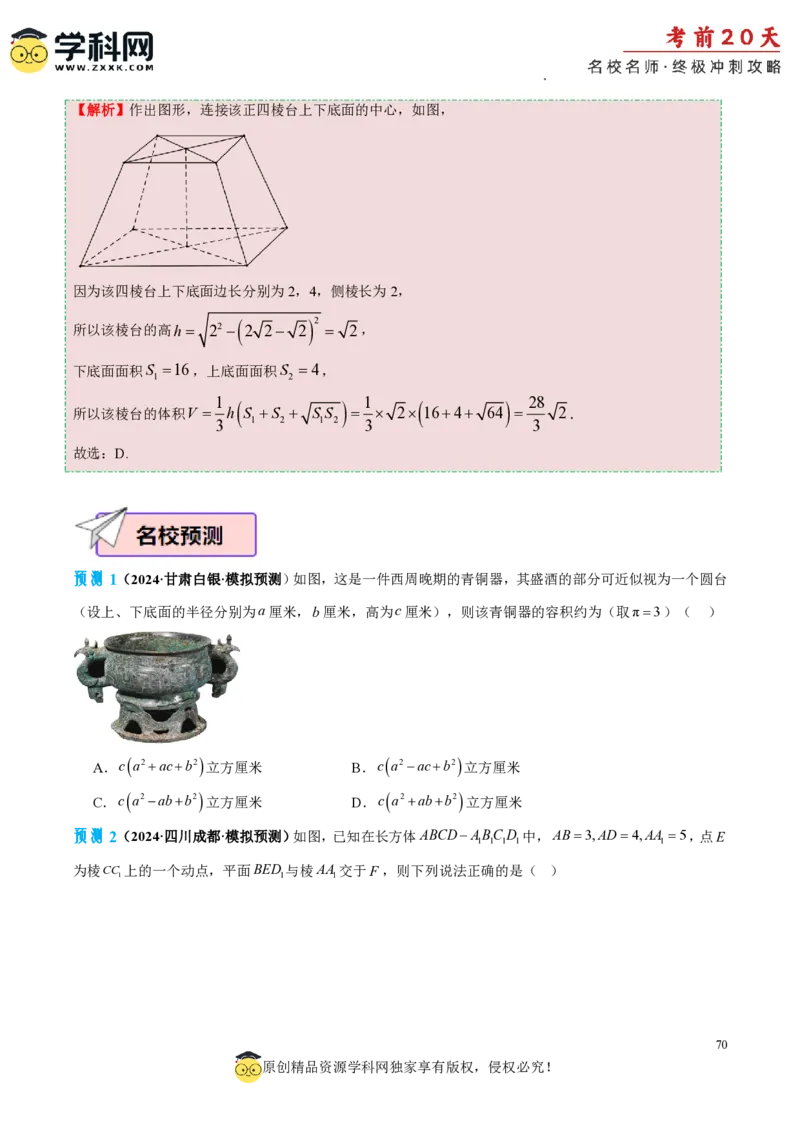
预测1(2024·甘肃白银·模拟预测)如图,这是一件西周晚期的青铜器,其盛酒的部分可近似视为一个圆台
(设上、下底面的半径分别为a厘米,b厘米,高为c厘米),则该青铜器的容积约为(取π3)( )
A.c
a2acb2
立方厘米 B.c
a2acb2
立方厘米
C.c
a2abb2
立方厘米 D.c
a2abb2
立方厘米
预测2(2024·四川成都·模拟预测)如图,已知在长方体ABCDABCD 中,AB3,AD4,AA 5,点E
1 1 1 1 1
为棱CC 上的一个动点,平面BED 与棱AA 交于F ,则下列说法正确的是( )
1 1 1
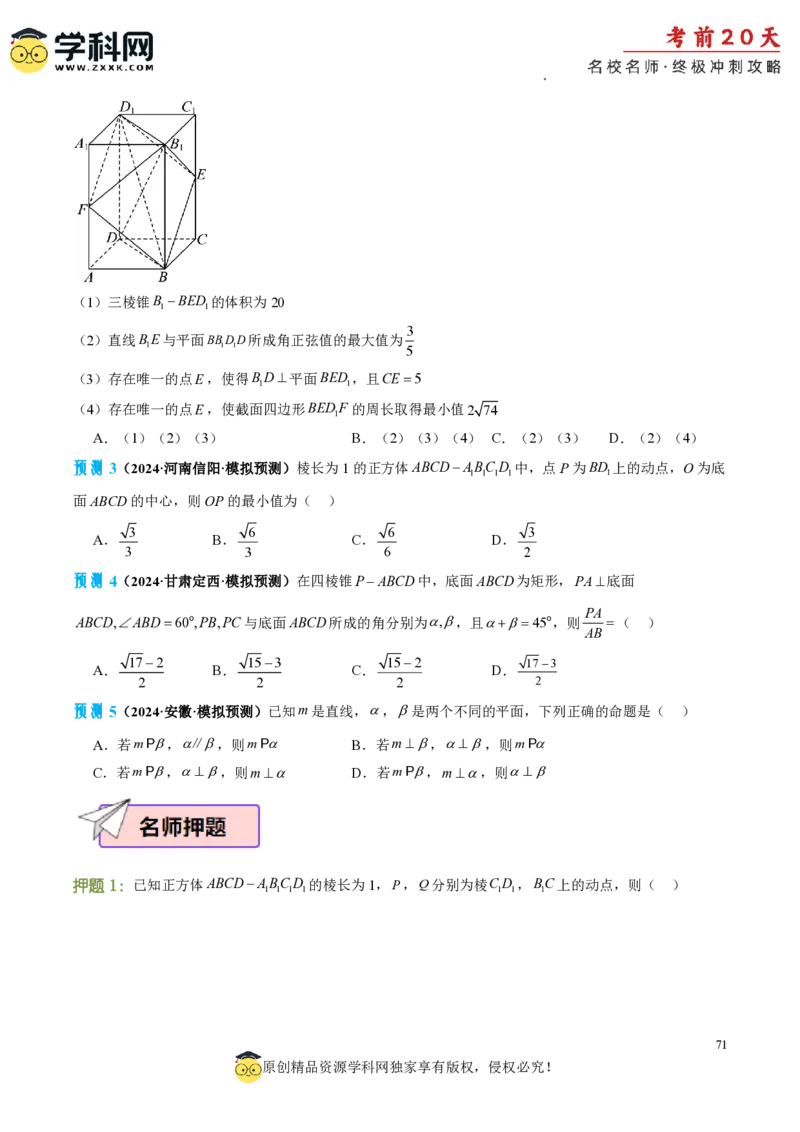
70
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司(1)三棱锥B BED 的体积为20
1 1
3
(2)直线BE与平面BBDD所成角正弦值的最大值为
1 1 1 5
(3)存在唯一的点E,使得BD平面BED ,且CE5
1 1
(4)存在唯一的点E,使截面四边形BEDF 的周长取得最小值2 74
1
A.(1)(2)(3) B.(2)(3)(4) C.(2)(3) D.(2)(4)
预测3(2024·河南信阳·模拟预测)棱长为1的正方体ABCDABCD 中,点P为BD 上的动点,O为底
1 1 1 1 1
面ABCD的中心,则OP的最小值为( )
3 6 6 3
A. B. C. D.
3 3 6 2
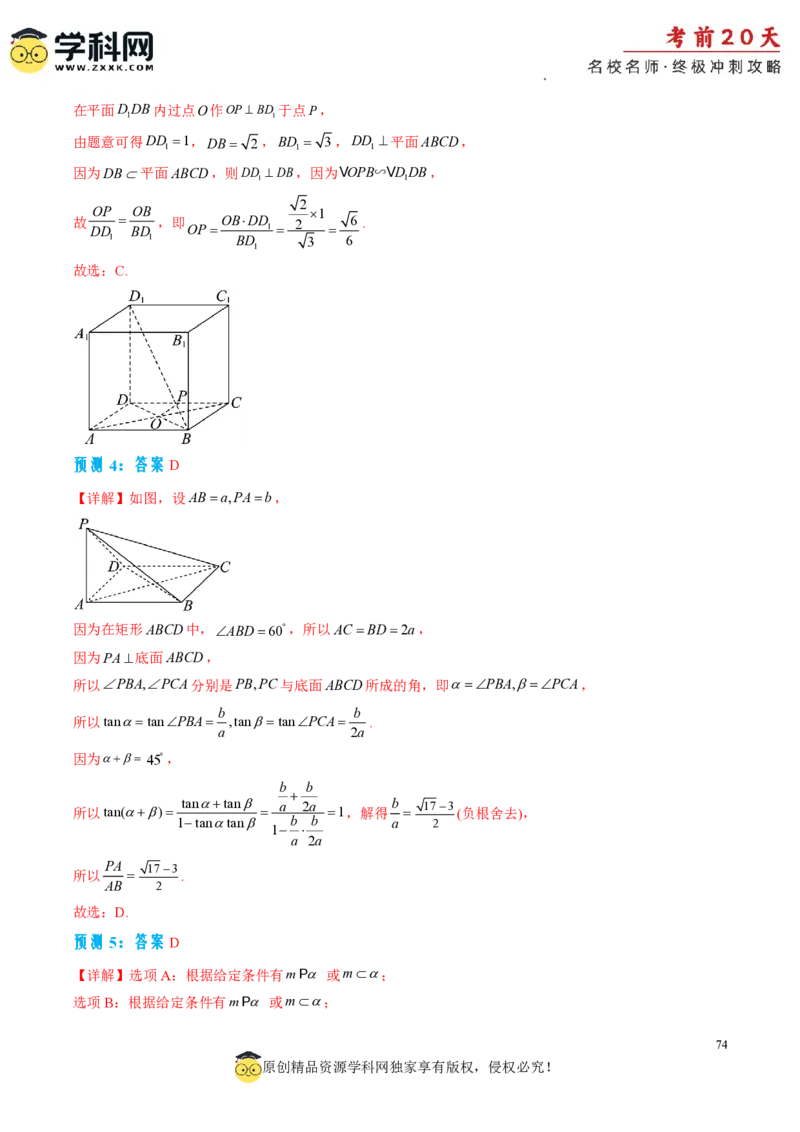
预测4(2024·甘肃定西·模拟预测)在四棱锥PABCD中,底面ABCD为矩形,PA底面
PA
ABCD,ABD60o,PB,PC与底面ABCD所成的角分别为,,且45o,则 ( )
AB
172 153 152 173
A. B. C. D.
2 2 2 2
预测5(2024·安徽·模拟预测)已知m是直线,,是两个不同的平面,下列正确的命题是( )
A.若mP,∥,则mP B.若m,,则mP
C.若mP,,则m D.若mP,m,则
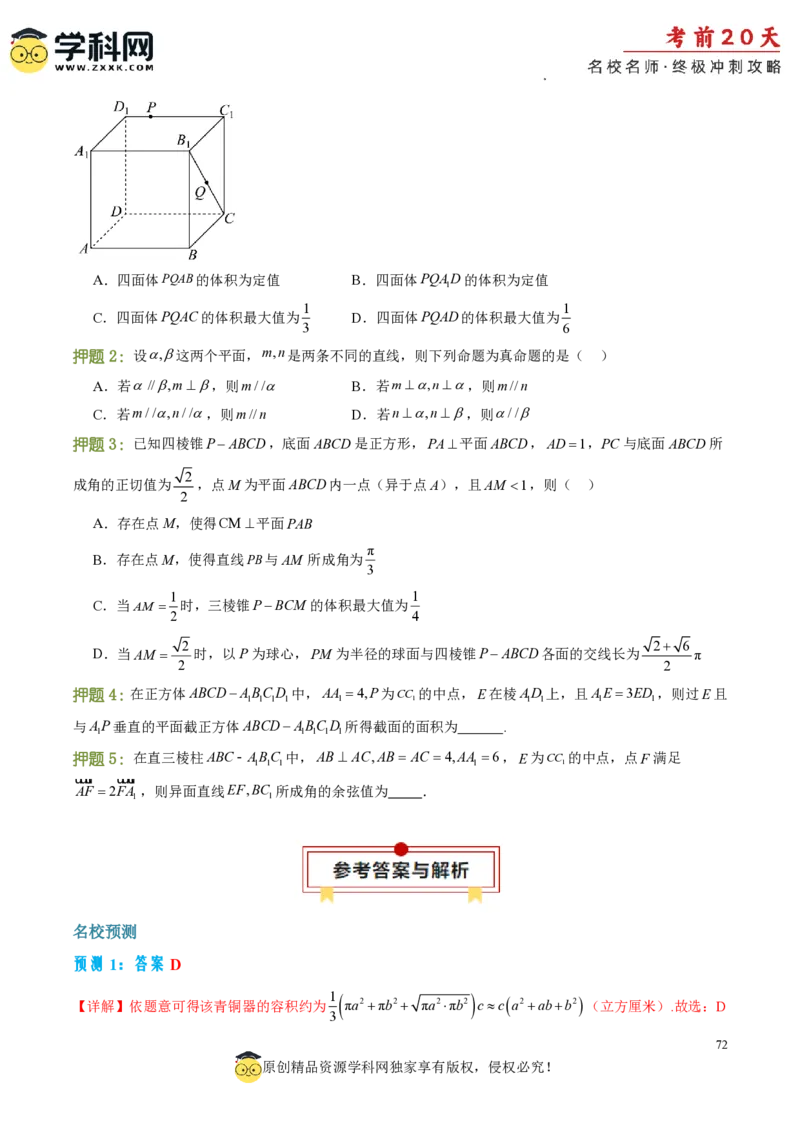
押题1:已知正方体ABCDABCD 的棱长为1,P,Q分别为棱CD ,BC上的动点,则( )
1 1 1 1 1 1 1
71
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司A.四面体PQAB的体积为定值 B.四面体PQAD的体积为定值
1
1 1
C.四面体PQAC的体积最大值为 D.四面体PQAD的体积最大值为
3 6
押题2:设,这两个平面,m,n是两条不同的直线,则下列命题为真命题的是( )
A.若//,m,则m// B.若m,n,则m//n
C.若m//,n//,则m//n D.若n,n,则//
押题3:已知四棱锥PABCD,底面ABCD是正方形,PA平面ABCD,AD1,PC与底面ABCD所
2
成角的正切值为 ,点M为平面ABCD内一点(异于点A),且AM 1,则( )
2
A.存在点M,使得CM平面PAB
π
B.存在点M,使得直线PB与AM 所成角为
3
1 1
C.当AM 时,三棱锥PBCM 的体积最大值为
2 4
2 2 6
D.当AM 时,以P为球心,PM 为半径的球面与四棱锥PABCD各面的交线长为 π
2 2
押题4:在正方体ABCDABCD 中,AA 4,P为CC 的中点,E在棱AD 上,且AE3ED ,则过E且
1 1 1 1 1 1 1 1 1 1
与AP垂直的平面截正方体ABCDABCD 所得截面的面积为 .
1 1 1 1 1
押题5:在直三棱柱ABC- ABC 中,AB AC,AB AC 4,AA 6,E为CC 的中点,点F 满足
1 1 1 1 1
uuur uuur
AF 2FA ,则异面直线EF,BC 所成角的余弦值为 .
1 1
名校预测
预测1:答案D
【详解】依题意可得该青铜器的容积约为 1 πa2πb2 πa2πb2 cc a2abb2 (立方厘米).故选:D
3
72
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司预测2:答案D
12
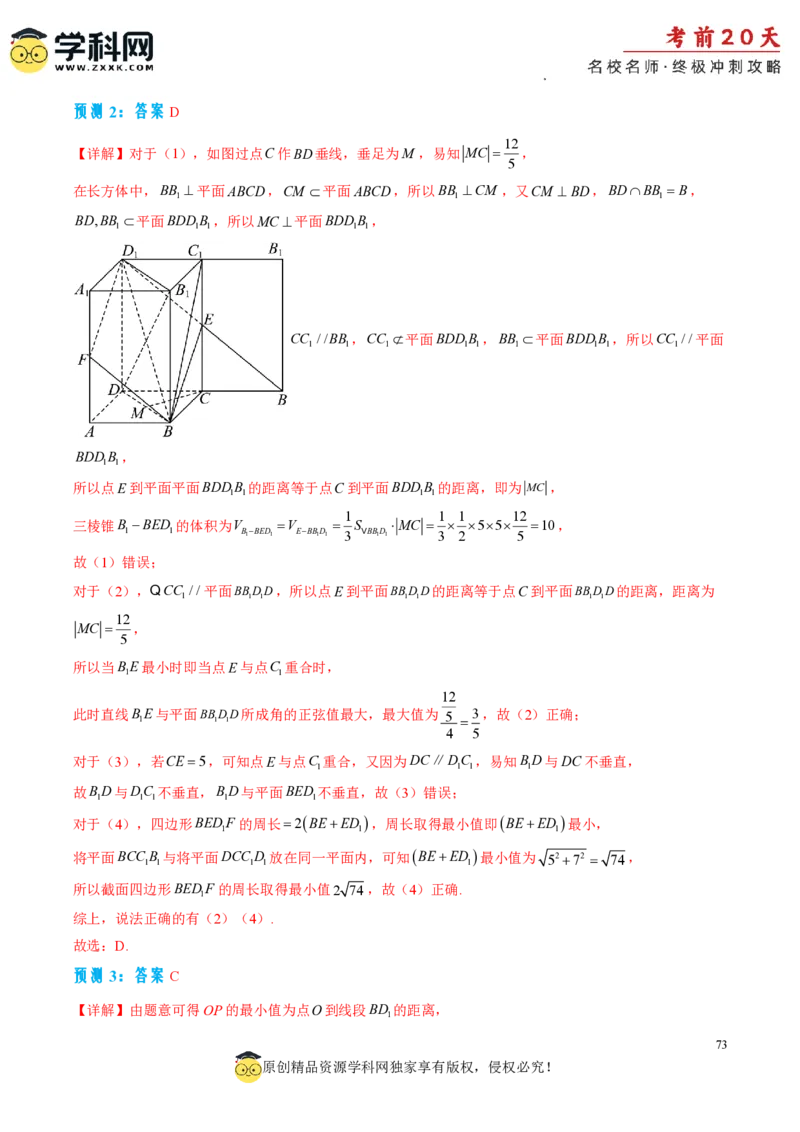
【详解】对于(1),如图过点C作BD垂线,垂足为M ,易知 MC ,
5
在长方体中,BB 平面ABCD,CM 平面ABCD,所以BB CM ,又CM BD,BDBB B,
1 1 1
BD,BB 平面BDDB ,所以MC 平面BDDB ,
1 1 1 1 1
CC //BB ,CC 平面BDDB ,BB 平面BDDB ,所以CC //平面
1 1 1 1 1 1 1 1 1
BDDB ,
1 1
所以点E到平面平面BDDB 的距离等于点C到平面BDDB 的距离,即为 MC ,
1 1 1 1
1 1 1 12
三棱锥B BED 的体积为V V S MC 55 10,
1 1 B1BED1 EBB1D1 3 VBB1D1 3 2 5
故(1)错误;
对于(2),QCC //平面BBDD,所以点E到平面BBDD的距离等于点C到平面BBDD的距离,距离为
1 1 1 1 1 1 1
12
MC ,
5
所以当BE最小时即当点E与点C 重合时,
1 1
12
此时直线BE与平面BBDD所成角的正弦值最大,最大值为 5 3,故(2)正确;
1 1 1
4 5
对于(3),若CE5,可知点E与点C 重合,又因为DC∥DC ,易知BD与DC不垂直,
1 1 1 1
故BD与DC 不垂直,BD与平面BED 不垂直,故(3)错误;
1 1 1 1 1
对于(4),四边形BEDF 的周长2BEED ,周长取得最小值即BEED 最小,
1 1 1
将平面BCCB 与将平面DCCD 放在同一平面内,可知BEED 最小值为 5272 74,
1 1 1 1 1
所以截面四边形BEDF 的周长取得最小值2 74,故(4)正确.
1
综上,说法正确的有(2)(4).
故选:D.
预测3:答案C
【详解】由题意可得OP的最小值为点O到线段BD 的距离,
1
73
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司在平面DDB内过点O作OPBD 于点P,
1 1
由题意可得DD 1,DB 2,BD 3,DD 平面ABCD,
1 1 1
因为DB平面ABCD,则DD DB,因为VOPB∽VDDB,
1 1
2
OP OB 1
故 ,即 OBDD 2 6 .
DD BD OP 1
1 1 BD 3 6
1
故选:C.
预测4:答案D
【详解】如图,设ABa,PAb,
因为在矩形ABCD中,ABD60,所以ACBD2a,
因为PA底面ABCD,
所以PBA,PCA分别是PB,PC与底面ABCD所成的角,即PBA,PCA,
b b
所以tantanPBA ,tantanPCA .
a 2a
因为 45,
b b
tantan a 2a b 173
所以tan() 1,解得 (负根舍去),
1tantan b b a 2
1
a 2a
PA 173
所以 .
AB 2
故选:D.
预测5:答案D
【详解】选项A:根据给定条件有mP 或m;
选项B:根据给定条件有mP 或m;
74
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司选项C:根据给定条件有m与的位置可能平行、相交或m在α内;
选项D:因为mP,所以存在直线m' 使得m' Pm,
又因为m,所以m' ,因为m' ,所以.
故选:D.
名师押题
押题1:答案BCD
1 2
【详解】A:因为VABP的面积为 ABBC ,Q到平面ABP的距离不是定值,
2 1 2
所以四面体PQAB的体积不是定值,故A错误;
1 2 2
B:因为△ADQ的面积为 ADDC ,P到矩形ABCD的距离为定值 ,
1 2 1 2 1 1 2
2 1 2 1
所以P到平面ADQ的距离为 ,则四面体PQAD的体积为 S ,故B正确;
1 2 1 3 VA1DQ 2 6
1 3
C:当Q与B 重合时,S 取得最大值,为 AB CB sin60 ,
1 △QAC 2 1 1 2
当P与D 重合时,P到平面ACQ的距离d取得最大值,
1
在正VACB 1 中,其外接圆的半径为r 2sin 2 60 3 6 ,则d ( 2)2r2 2 3 3 ,
1 3 2 3 1
故四面体PQAC的体积最大值为 ,故C正确;
3 2 3 3
D:过点Q作GH∥BC,PM DG,PN CD,
设CGt,PD s,则t,s0,1,
1
S 1 ADDG 1 1t2 ,PM DG 1t2 ,OM DMsinCDGts t ,
△ADQ 2 2 1t2
t 1st
OP 1t2 st ,
1t2 1t2
故四面体PQAD的体积为V 1 1 1t2 1st 1 1st ,其最大值为 1 ,故D正确.
3 2 1t2 6 6
故选:BCD
75
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司押题2:答案BD
【详解】对于选项A,因为//,m,则m,所以选项A错误,
对于选项B,因为m,n,由线面垂直的性质知,m//n,所以选项B正确,
对于选项C,因为m//,n//,则m与n可能是异面直线,也可能是相交直线,所以选项C错误,
对于选项D,因为n,n,垂直同一直线的两个平面互相平行,所以选项D正确,
故选:BD.
押题3:答案BC
【详解】对于A,假设存在点M,使得CM平面PAB,
由于PA平面ABCD,PA平面PAB,则平面PAB平面ABCD,
平面PAB平面ABCD AB,CM 平面ABCD,则CM AB,
由于CB AB,CM,CB平面ABCD,故直线CM,CB重合,
即M点落在CB上,由于AM 1,即M落在以A为圆心,以AB1为半径的圆面内(不包含圆),
这与M点落在CB上矛盾,A错误;
对于B,以A为坐标原点,AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系,
PA平面ABCD,则PCA即为PC与底面ABCD所成角,
PA 2
故tanPCA ,而AC 2,故PA1,
AC 2
uuur
则P(0,0,1),B(1,0,0),PB(1,0,1),
uuur uuuur 1
uuuur 1 1 uuur uuuur PBAM 2 1
结合A的分析,可取AM ( , ,0),则cosPB,AM uuur uuuur ,
2 2 |PB||AM | 2 2
2
2
π π
由于直线PB与AM 所成角范围为(0, ],故此时直线PB与AM 所成角为 ,
2 3
π
即存在点M,使得直线PB与AM 所成角为 ,B正确;
3
76
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司1 3
对于C,当AM 时,当M位于BA的延长线时,VBCM 的高最大为 ,
2 2
1 3 3 1 3 1
此时面积最大,最大值为 1 ,则三棱锥PBCM 的体积最大值为 1 ,C正确;
2 2 4 3 4 4
2
2 2 6
对于D,当AM 时,PM 12 ,
2 2 2
以P为球心,PM 为半径的球面与四棱锥PABCD各面的交线是以P为圆心,
6
为半径的圆与侧面展开图的交线,如下图E ¼ MF,
2
由于PB 2,PC 12 3,则PC2 PB2BC2,即PBCB,
2 1 π
则tanAPF tanBPC ,则APF BPC,APFFPB ,
2 2 4
π π
则FPC BPCFPB ,根据对称性有FPC CPE,FPE ,
4 2
1 6 6π
故E ¼ MF的长为 2π ,
4 2 4
2 1 2 2π
又球与底面ABCD的交线是以A为圆心, 为半径的四分之一圆,故长度为 2π ,
2 4 2 4
2 6
故以P为球心,PM 为半径的球面与四棱锥PABCD各面的交线长为 π,D错误,
4
故选:BC
押题4:答案12
77
原创精品资源学科网独家享有版权,侵权必究!
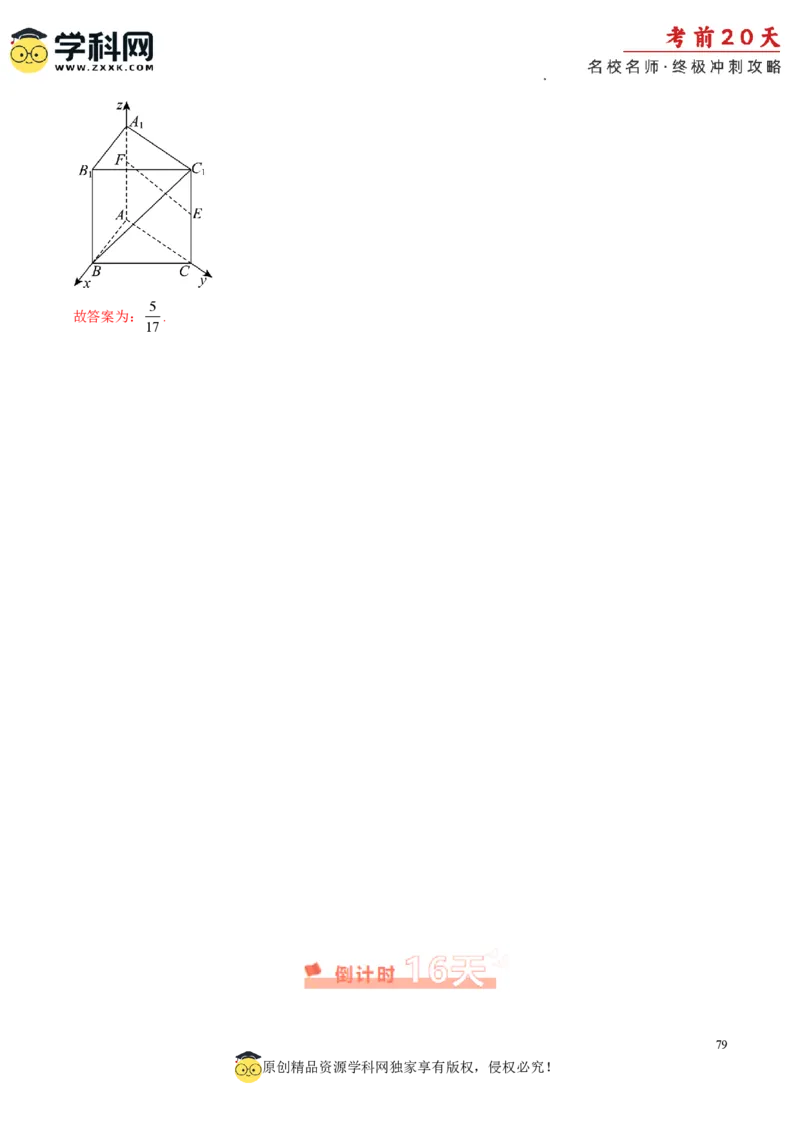
学科网(北京)股份有限公司【详解】
如图所示,取AF 3FB ,连接AC,AC ,易知AA 面ABCD ,
1 1 1 1 1 1 1 1
而EF 面ABCD ,故AA EF ,连接BD,且BD AC 显然成立,
1 1 1 1 1 1 1 1 1 1 1
AF AE
由已知得 1 1 3,故EF // BD,则C A EF ,
FB ED 1 1 1 1
1 1
而C A AA A ,C A,AA 面AACC,
1 1 1 1 1 1 1 1 1
所以EF平面AACC,且AP面AACC,所以EF AP,
1 1 1 1 1 1
取Q为DD的中点,DH 3HA,则EH AQ且EH PQ,
1 1
AQPQQ,AQ,PQ面APQ,
1 1 1
所以EH 平面APQ,因为AP平面APQ,EH AP,同理可得BG3GA,
1 1 1 1
所以等腰梯形HGFE为所得截面,
又HG 1212 2,EF 3232 3 2,EH 2242 2 5,
作EF HK ,显然HK 42( 2)2 3 2,则梯形的高为3 2,
1
所以等腰梯形HGFE的面积为 ( 23 2)3 2 12.
2
故答案为:12
5
押题5:答案
17
【详解】如图,以A为坐标原点,建立空间直角坐标系,
则B4,0,0,C 0,4,6,E0,4,3,F0,0,4,
1
uuuur uuur
所以BC 4,4,6,EF (0,4,1),
1
uuur uuuur
EFBC
5
1
设异面直线EF,BC 所成的角为,则cos uuur uuuur .
1 EF BC 17
1
78
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司5
故答案为: .
17
79
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司直线(圆)与方程(选填题)
年份 题号 知识点 考点
①点线距
2021年I卷 11 圆
②角度最值时求其它
2021年II
11 直线与圆 直线与圆的位置关系
卷
①圆与圆的位置关系
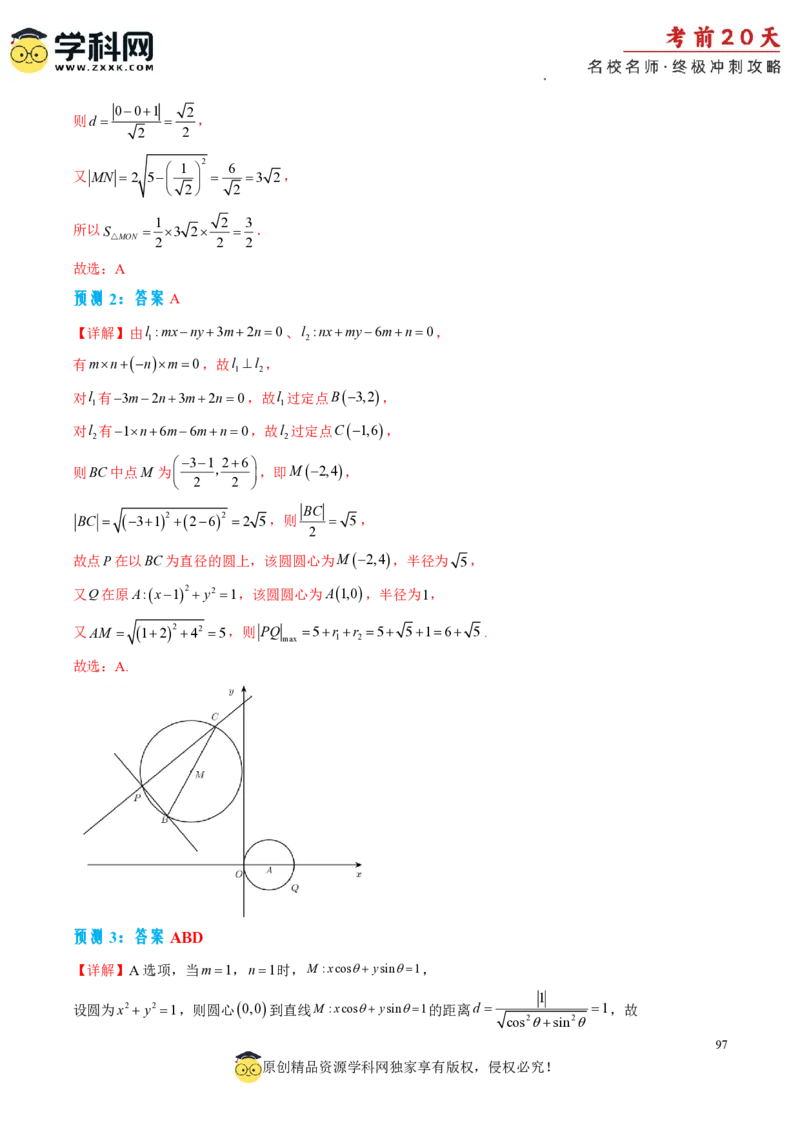
2022年I卷 14 圆
②圆与圆的公切线问题
2022年II ①直线与圆的位置关系
15 直线与圆
卷 ②线关于线对称
2023年新
6 圆 圆的切线问题
高考1
2023 年新
高考2 9 直线与圆 直线与圆的位置关系
近三年,直线与圆在选填中占据一个位置,考查的考点一般来说是:
5、直线(①直线:倾斜角与斜率、斜率求算、夹角公式②平行与垂直定理及直线求法、对称、距离及最值
问题)
2、圆(①各种方程、直线(圆)与圆的位置关系②四点共圆、三类切线、弦长、最值)
题干的设置一般来说在上述的多项考点中选其一项或两项。直线与圆有关定值与最值需考生需熟悉技
巧,其次掌握直线与圆及圆与圆的位置关系,对称也是高考的重点内容,设置此类题难度一般,用心研究
必能夺分。
从近三年的全国卷的考查情况以及新高考新题型标准来看,直线与圆是高考选填方向必不可少的一类
题,类型1:圆上的动点到定直线的最值问题。类型2:圆的三类切线。类型3:对称及阿波罗尼斯圆,尤
其是阿波罗尼斯圆,考生需从多方面认识,类型3相对有难度,其它两类相对简单.此类题目一定采用数形
结合.
80
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司一、圆的取值范围与最值问题
涉及与圆有关的最值,可借助图形性质,利用数形结合求解.一般地:
yb
(1)形如 的最值问题,可转化为动直线斜率的最值问题.
xa
(2)形如t axby的最值问题,可转化为动直线截距的最值问题.
(3)形如m(xa)2 (yb)2的最值问题,可转化为曲线上的点到点(a,b)的距离平方的最值问
题
解决圆中的范围与最值问题常用的策略:
(1)数形结合
(2)多与圆心联系
(3)参数方程
(4)代数角度转化成函数值域问题
二、直线的交点坐标与距离公式
①:直线的交点
求两直线AxB yC 0(ABC 0)与A xB yC 0(A B C 0)的交点坐标,只需求两直线方程
1 1 1 1 1 1 2 2 2 2 2 2
AxB yC 0 A B C
联立所得方程组 1 1 1 的解即可.若有 1 1 1 ,则方程组有无穷多个解,此时两直线重
A xB yC 0 A B C
2 2 2 2 2 2
A B C A B
合;若有 1 1 1 ,则方程组无解,此时两直线平行;若有 1 1 ,则方程组有唯一解,此时两直线
A B C A B
2 2 2 2 2
相交,此解即两直线交点的坐标.
求两直线的交点坐标实际上就是解方程组,看方程组解的个数.
②过两条直线交点的直线系方程
一般地,具有某种共同属性的一类直线的集合称为直线系,它的方程叫做直线系方程,直线系方程中
除含有x,y以外,还有根据具体条件取不同值的变量,称为参变量,简称参数.由于参数取法不同,从而得
到不同的直线系.
过两直线的交点的直线系方程:经过两直线l :AxB yC 0,l :A xB yC 0交点的直线方程为
1 1 1 1 2 2 2 2
AxB yC (A xB yC )0,其中是待定系数.在这个方程中,无论取什么实数,都得不到
1 1 1 2 2 2
A xB yC 0,因此它不能表示直线l .
2 2 2 2
③两点间的距离公式
两点P(x,y ),P(x ,y )间的距离公式为 PP (x x )2 (y y )2 .
1 1 1 2 2 2 1 2 2 1 2 1
81
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司此公式可以用来求解平面上任意两点之间的距离,它是所有求距离问题的基础,点到直线的距离和两平行
直线之间的距离均可转化为两点之间的距离来解决.另外在下一章圆的标准方程的推导、直线与圆、圆与
圆的位置关系的判断等内容中都有广泛应用,需熟练掌握.
④:点到直线的距离公式
Ax By C
点P(x ,y )到直线AxByC 0的距离为d 0 0 .
0 0 A2 B2
(1)点P(x ,y )到直线AxByC 0的距离为直线上所有的点到已知点P的距离中最小距离;
0 0
(2)使用点到直线的距离公式的前提条件是:把直线方程先化为一般式方程;
(3)此公式常用于求三角形的高、两平行线间的距离及下一章中直线与圆的位置关系的判断等.
⑤两平行线间的距离
本类问题常见的有两种解法:①转化为点到直线的距离问题,在任一条直线上任取一点,此点到另一条直
线的距离即为两直线之间的距离;②距离公式:直线 AxByC 0与直线 AxByC 0的距离为
1 2
C C
d 2 1 .
A2 B2
(1)两条平行线间的距离,可以看作在其中一条直线上任取一点,这个点到另一条直线的距离,此点一般
可以取直线上的特殊点,也可以看作是两条直线上各取一点,这两点间的最短距离;
|C C |
(2)利用两条平行直线间的距离公式d 1 2 时,一定先将两直线方程化为一般形式,且两条直线中
A2 B2
x,y的系数分别是相同的以后,才能使用此公式.
圆:①:圆的标准方程
(xa)2 (yb)2 r2,其中Ca,b为圆心,r 为半径.
(1)如果圆心在坐标原点,这时a0,b0,圆的方程就是x2 y2 r2.有关图形特征与方程的转化:如:
圆心在x轴上:b0;圆与y轴相切时:|a|r ;圆与x轴相切时:|b|r;与坐标轴相切时:|a||b|r;过
原点:a2 b2 r2
(2)圆的标准方程(xa)2 (yb)2 r2 圆心为a,b,半径为r ,它显现了圆的几何特点.
(3)标准方程的优点在于明确指出了圆心和半径.由圆的标准方程可知,确定一个圆的方程,只需要a、b、r
这三个独立参数,因此,求圆的标准方程常用定义法和待定系数法.
②:点和圆的位置关系
如果圆的标准方程为(xa)2 (yb)2 r2,圆心为Ca,b,半径为r ,则有
(1)若点Mx ,y 在圆上|CM |r x a2 y b2 r2
0 0 0 0
(2)若点Mx ,y 在圆外|CM |r x a2 y b2 r2
0 0 0 0
(3)若点Mx ,y 在圆内|CM |r x a2 y b2 r2
0 0 0 0
82
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司③:圆的一般方程
D E
当 D2 E2 4F 0时,方程 x2 y2 DxEyF 0叫做圆的一般方程. , 为圆心,
2 2
1
D2 E2 4F 为半径.
2
D 2 E 2 D2 E2 4F
由方程x2 y2 DxEyF 0得 x y
2 2 4
D E D E
(1)当D2 E2 4F 0时,方程只有实数解x ,y .它表示一个点( , ).
2 2 2 2
(2)当D2 E2 4F 0时,方程没有实数解,因而它不表示任何图形.
D E 1
(3)当D2 E2 4F 0时,可以看出方程表示以 , 为圆心, D2 E2 4F 为半径的圆.
2 2 2
④:用待定系数法求圆的方程的步骤
求圆的方程常用“待定系数法”.用“待定系数法”求圆的方程的大致步骤是:
(1)根据题意,选择标准方程或一般方程.
(2)根据已知条件,建立关于a、b、r或D、E、F的方程组.
(3)解方程组,求出a、b、r或D、E、F的值,并把它们代入所设的方程中去,就得到所求圆的方
程.
三、对称全覆盖
①点关于线对称的点的求算
Ax By C Ax By C
点A x ,y 关于直线l:AxByC 0的对称点为x 2A 0 0 ,y 2B 0 0
0 0 0 A2 B2 0 A2 B2
②线关于点对称的直线求算
直线l:AxByC 0关于点A x ,y 对称的直线为l:AxBy 2Ax 2By C 0
0 0 0 0
③线关于线对称的直线方程求算
直线l :AxB yC 0关于直线l:AxByC 0对称直线为AxB yC AxByC 0
1 1 1 1 1 1 1
2AABB
其中 1 1
A2 B2
注意:特殊情况
Ⅰ:点A(x ,y
)关于直线l:xm对称的点坐标为A
2mx ,y
.
0 0 0 0
点A(x ,y )关于直线l: y
n对称的点坐标为A
x ,2n y
.
0 0 0 0
直线l :AxByC 0关于直线l:xm对称的直线方程为l :A 2mx ByC 0.
1 2
直线l :AxByC 0关于直线l: y n对称的直线方程为l :AxB 2n y C 0.
1 2
83
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司Ⅱ:点A
x ,y
关于直线l:x yC
0对称的点坐标为A
C y ,Cx
.
0 0 0 0
点A
x ,y
关于直线l:x yC
0对称的点坐标为A
C y ,Cx
.
0 0 0 0
直线l :AxByC0关于直线l:x yC 0对称的直线方程为l :A C y B Cx C0;
1 2
直线l :AxByC0关于直线l:x yC 0对称的直线方程为l :A C y B Cx C0;
1 2
x yC 0 y Cx x yC 0 y Cx
《记忆方法》 0 0 或者 0 0
x y C 0 xC y x y C 0 xC y
0 0 0 0
④正规方法
点关于直线成轴对称问题(所有对称都可以转化为点关于线对称)
由轴对称定义知,对称轴即为两对称点连线的“垂直平分线”利用“垂直”“平分”这两个条件建立方程
组,就可求出对顶点的坐标一般情形如下:设点P(x , y )关于直线 y kxb的对称点为P'(x', y'),则
0 0
有
y' y
0 k 1
x'x
0 ,可求出x'、y'.
y' y x x'
0 k 0 b
2 2
⑤万能对称原理(曲线关于直线对称的原理)
曲线(或直线 )C:F(x,y)0关于直线l: f(x,y) AxByC 0的对称曲线C'(或直线 )的方程为:
2A 2B
F[x f(x,y), y f(x,y)]0.
A2 B2 A2 B2
证明:设M(x,y)是曲线C'上的任意一点M(x,y),它关于l的对称点为M'(x', y'),则M'C
于是F(x',y')0 ①
∵M 与M'关于直线l对称.
2A
B(xx')A(y y')0 x' x f(x,y)
A2 B2
∴ xx' y y' ②
A B C 0 2B
2 2 y' y f(x,y)
A2 B2
2A 2B
②代入①,得F[x f(x, y) , y f(x,y)]0,此即为曲线C'的方程.
A2 B2 A2 B2
四、最值问题
Ⅰ求直线上一点到两定点的距离之差的最大值的方法
当两点A,B在直线l的两侧时,可以在直线l上找到一点P,使得 PA PB 最大.
理由如下:作点B关于直线l的对称点B,连接AB并延长交l于点P,连接PB,则点P即为所求点,此时
84
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司PA PB 最大.且 PA PB PA PB AB
max
若在直线l上取不同于点P的点P,连接PA、PB、PB,则 PB PB .在APB中,
PA PB<AB (三角形中两边之差小于第三边)即 PA PB<AB
②求直线上一点到两定点的距离之和的最小值的方法
当两点A,B在直线l的同侧时,可以在直线l上找到一点P,使得 PA PB 最小.
理由如下:作点B关于直线l的对称点B,连接AB交l于点P,连接PB,则点P即为所求点,此时
PA PB 最小.且 PA PB PA PB AB
min
若在直线l上取不同于点P的点P,连接PA、PB、PB,则 PB PB .在APB中,
PA PB>AB (三角形中两边之和大于第三边)即 PA PB>AB
y
Ⅱ形如:若P x,y 是定圆C:xa2 yb2 r2上的一动点,则求mxny和 这两种形式的最值
x
思路1:几何法
manbt
① mxny的最值,设mxny t,圆心C a,b 到直线mxny t的距离为d ,由d r
m2 n2
即可解得两个t值,一个为最大值,一个为最小值
y y
② 的最值: 即点P与原点连线的斜率,数形结合可求得斜率的最大值和最小值
x x
思路2:代数法
①
mxny的最值,设mxny t,与圆的方程联立,化为一元二次方程,由判别式等于0,求得t的两
个值,一个为最大值,一个为最小值.
y y
② 的最值:设t ,则y tx,与圆的方程联立,化为一元二次方程,由判别式等于0,求得t的两个
x x
值,一个为最大值,一个为最小值.
五、圆的三类切线问题
第一类:求过圆上一点 x ,y 的圆的切线方程的方法
0 0
正规方法:
第一步:求切点与圆心的连线所在直线的斜率k
1
第二步:利用垂直关系求出切线的斜率为
k
第三步:利用点斜式y y k xx 求出切线方程
0 0
注意:若k 0则切线方程为x x ,若k不存在时,切线方程为y y
0 0
85
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司秒杀方法:
①经过圆x2 y2 r2上一点P x ,y 的切线方程为x x y y r2
0 0 0 0
②经过圆xa2 yb2 r2上一点P x ,y 的切线方程为 x axa y byb r2
0 0 0 0
③经过圆x2 y2 DxEyF 0上一点P x ,y 的切线方程为
0 0
xx y y
x x y yD 0 E 0 F 0
0 0 2 2
第二类:求过圆外一点 x ,y 的圆的切线方程的方法
0 0
方法一:几何法
第一步:设切线方程为y y k xx ,即kx ykx y 0,
0 0 0 0
第二步:由圆心到直线的距离等于半径长,可求得k,切线方程即可求出
方法二:代数法
第一步:设切线方程为y y k xx ,即y kxkx y ,
0 0 0 0
第二步:代入圆的方程,得到一个关于x的一元二次方程,由 0可求得k,切线方程即可求出
注意:过圆外一点的切线必有两条,当上面两种方法求得的k只有一个时,则另一条切线的斜率一定不存
在,可得数形结合求出.
第三类:求斜率为k且与圆相切的切线方程的方法
方法一:几何法
第一步:设切线方程为y kxm,即kx ym0
第二步:由圆心到直线的距离等于半径长,可求得m,切线方程即可求出.
方法二:代数法
第一步:设切线方程为y kxm,
第二步:代入圆的方程,得到一个关于x的一元二次方程,由 0可求得m,切线方程即可求出
方法三:秒杀方法
已知圆x2 y2 r2的切线的斜率为k,则圆的切线方程为y kxr k2 1
已知圆xa2 yb2 r2的切线的斜率为k,则圆的切线方程为y kxr k2 1bka
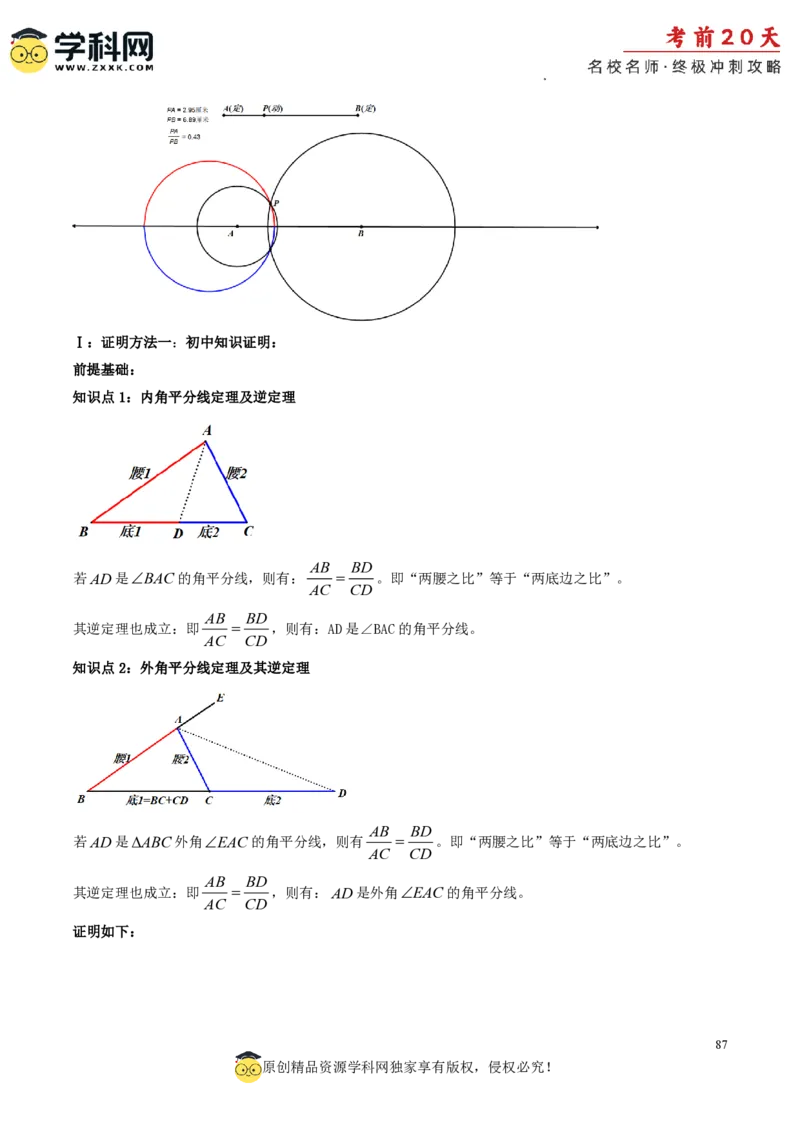
六、阿波罗尼斯圆考点
阿氏圆是指:平面上的一个动点P到两个定点A,B的距离的比值等于k,且k 1的点P的轨迹称之为阿
PA
氏圆。即: k(k 1),如下图所示:
PB
86
原创精品资源学科网独家享有版权,侵权必究!
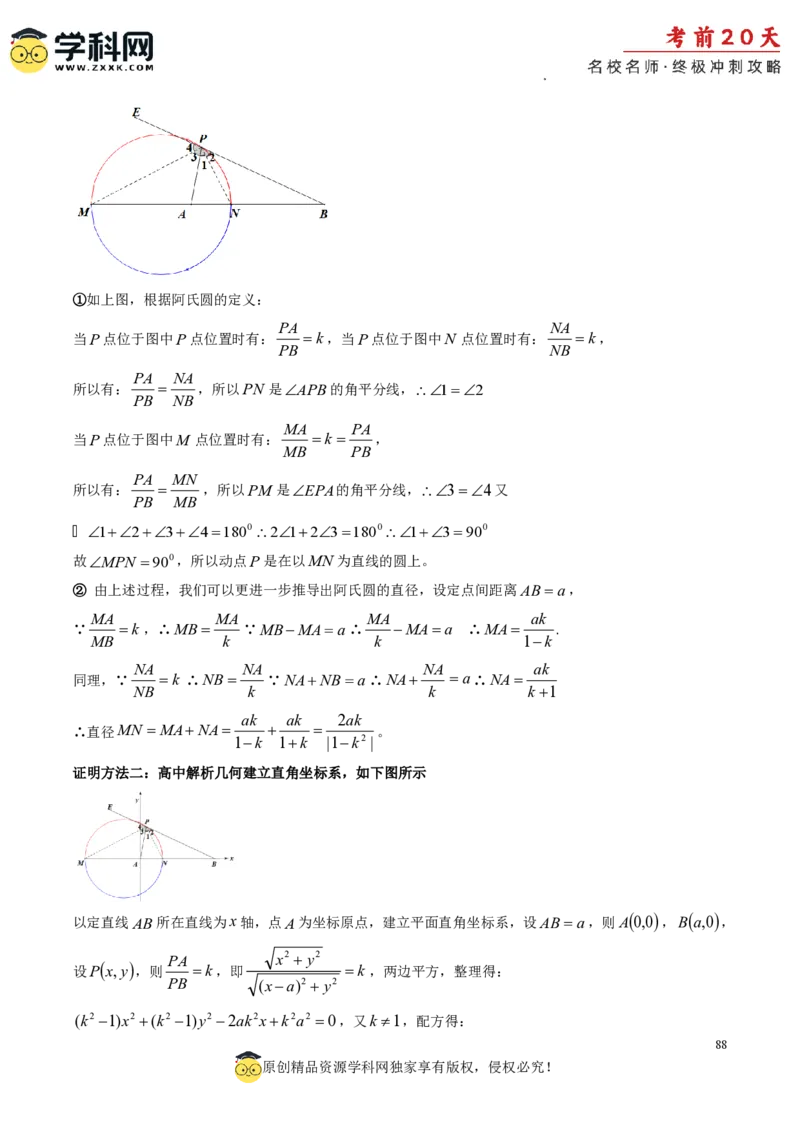
学科网(北京)股份有限公司Ⅰ:证明方法一:初中知识证明:
前提基础:
知识点1:内角平分线定理及逆定理
AB BD
若AD是BAC的角平分线,则有: 。即“两腰之比”等于“两底边之比”。
AC CD
AB BD
其逆定理也成立:即 ,则有:AD是∠BAC的角平分线。
AC CD
知识点2:外角平分线定理及其逆定理
AB BD
若AD是ABC外角EAC的角平分线,则有 。即“两腰之比”等于“两底边之比”。
AC CD
AB BD
其逆定理也成立:即 ,则有:AD是外角EAC的角平分线。
AC CD
证明如下:
87
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司①如上图,根据阿氏圆的定义:
PA NA
当P点位于图中P点位置时有: k,当P点位于图中N 点位置时有: k,
PB NB
PA NA
所以有: ,所以PN 是APB的角平分线,12
PB NB
MA PA
当P点位于图中M 点位置时有: k ,
MB PB
PA MN
所以有: ,所以PM 是EPA的角平分线,34又
PB MB
123418002123180013900
故MPN 900,所以动点P是在以MN 为直线的圆上。
② 由上述过程,我们可以更进一步推导出阿氏圆的直径,设定点间距离ABa,
MA MA MA ak
∵ k ,∴MB ∵MBMAa∴ MAa ∴MA .
MB k k 1k
NA NA NA ak
同理,∵ k ∴NB ∵NANB a∴NA a∴NA
NB k k k1
ak ak 2ak
∴直径MN MANA 。
1k 1k |1k2 |
证明方法二:高中解析几何建立直角坐标系,如下图所示
以定直线AB所在直线为x轴,点A为坐标原点,建立平面直角坐标系,设ABa,则A 0,0 ,B a,0 ,
PA x2 y2
设P x,y ,则 k,即 k ,两边平方,整理得:
PB (xa)2 y2
(k2 1)x2 (k2 1)y2 2ak2xk2a2 0,又k 1,配方得:
88
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司ak2 k2a2
(x )2 y2
k2 1 (k2 1)2
ak2 ak
由圆的方程可知:此方程表示是以( ,0)为圆心, 为半径的圆。
k2 1 |k2 1|
Ⅱ:阿氏圆常用于解决形如:PAkPB(k 1)类线段最值问题:其中P是动点,A,B是定点,且动点P
在阿氏圆上运动,我们总结出更加一般的解题步骤,使这种题变成套路题,直接秒杀。
PAkPB(k 1)类问题解题步骤:
运用:动点在圆上运动,两线段(带系数)相加求最小值。
形如:ABkBP的最小值 (k为系数),
原理:构造共边共角相似,转移带系数的边,利用两点间线段最短求最小值,
解题步骤:
第一步: 计算出动点所在圆的半径r;
r
第二步:在题中寻找: k (相似比),若找不到,则需要将系数k提到括号外边再寻找相似比;比如
定边
3
PA PB,找不到相似比为3:5时,需要经过如下变形:
5
3 3 5
PA PB ( PAPB),对带系数的线段PA去寻找相似比为5:3。
5 5 3
第三步:利用共边共角模型,在第2步:定边所在的三角形中构造共边共角相似模型,此时定边与动点构成
一个三角形(此步非常重要,是核心);
第四步:利用相似转移带系数的边;
第五步:由两点间线段最短求最小值。
Ⅲ:其他结论
BN
①k 当k>1时,A在圆内,B在圆外,当0<k<1时,A在圆外,B在圆内,
NA
②BP2 BNBM
③过点B作圆的切线BP,则PN,PM 分别为BPA的内,外角平分线.
典例1【2023新高考1卷】过点 0,2 与圆x2 y2 4x10相切的两条直线的夹角为,则sin( )
15 10 6
A. 1 B. C. D.
4 4 4
【答案】B
89
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司【解析】方法一:因为x2 y2 4x10,即x22 y2 5,可得圆心C2,0 ,半径r 5,
过点P0,2 作圆C的切线,切点为A,B,
因为 PC 22 22 2 2,则 PA PC 2 r2 3,
5 10 3 6
可得sinAPC ,cosAPC ,
2 2 4 2 2 4
10 6 15
则sinAPBsin2APC 2sinAPCcosAPC 2 ,
4 4 4
2 2
6 10 1
cosAPBcos2APC cos2APCsin2APC 0,
4 4 4
即APB为钝角,
15
所以sinsinπAPBsinAPB ;
4
法二:圆x2 y2 4x10的圆心C2,0 ,半径r 5,
过点P0,2 作圆C的切线,切点为A,B,连接AB,
可得 PC 22 22 2 2,则 PA PB PC 2 r2 3,
2 2 2 2
因为 PA PB 2 PA PB cosAPB CA CB 2 CA CB cosACB
且ACBπAPB,则336cosAPB5510cosπAPB
,
1
即3cosAPB55cosAPB,解得cosAPB 0,
4
1
即APB为钝角,则coscosπAPBcosAPB ,
4
15
且为锐角,所以sin 1cos2 ;
4
方法三:圆x2 y2 4x10的圆心C2,0 ,半径r 5,
若切线斜率不存在,则切线方程为x0,则圆心到切点的距离d 2r,不合题意;
若切线斜率存在,设切线方程为y kx2,即kx y20,
2k2
则 5,整理得k2 8k10,且644600
k2 1
设两切线斜率分别为k ,k ,则k k 8,k k 1,
1 2 1 2 1 2
90
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司可得 k k k k 2 4k k 2 15,
1 2 1 2 1 2
k k sin sin
所以tan 1 2 15,即 15 ,可得cos ,
1k k cos 15
1 2
sin2
则sin2cos2sin2 1,
15
15
且0,π
,则sin0,解得sin .
4
故选:B.
典例2【2023新高考全国Ⅱ卷】 已知直线l:xmy10与eC:x12 y2 4交于A,B两点,写出
8
满足“VABC面积为 ”的m的一个值______.
5
1 1
【答案】2(2,2, , 中任意一个皆可以)
2 2
【解析】设点C到直线AB的距离为d,由弦长公式得 AB 2 4d2 ,
1 8 4 5 2 5
所以S d2 4d2 ,解得:d 或d ,
△ABC 2 5 5 5
11 2 2 4 5 2 2 5 1
由d ,所以 或 ,解得:m2或m .
1m2 1m2 1m2 5 1m2 5 2
1 1
故答案为:2(2,2, , 中任意一个皆可以).
2 2
典例3【2022新高考全国Ⅰ卷】写出与圆x2 y2 1和(x3)2 (y4)2 16都相切的一条直线的方程
________________.
3 5 7 25
【答案】 y x 或y x 或x=1
4 4 24 24
91
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司【解析】[方法一]:
显然直线的斜率不为0,不妨设直线方程为x+by+c=0,
|c| |34bc|
于是 1, 4.
1b2 1b2
故c2 1b2①,|34bc||4c|.于是34bc4c或34bc4c,
24 4
b b
b0 7 3
再结合①解得 或 或 ,
c1
25
5
c c
7 3
所以直线方程有三条,分别为x10,7x24y250,3x4y50.
[方法二]:
设圆x2 y2 1的圆心O(0,0),半径为r 1,
1
圆(x3)2 (y4)2 16的圆心C(3,4),半径r 4,
2
则|OC|5r r ,因此两圆外切,
1 2
由图像可知,共有三条直线符合条件,显然x10符合题意;
又由方程(x3)2 (y4)2 16和x2 y2 1相减可得方程3x4y50,
即为过两圆公共切点的切线方程,
又易知两圆圆心所在直线OC的方程为4x3y0,
4
直线OC与直线x10的交点为(1, ),
3
4
4 k 7
设过该点的直线为 y k(x1),则 3 ,解得k ,
3 1 24
k2 1
从而该切线的方程为7x24y 25 0.(填一条即可)
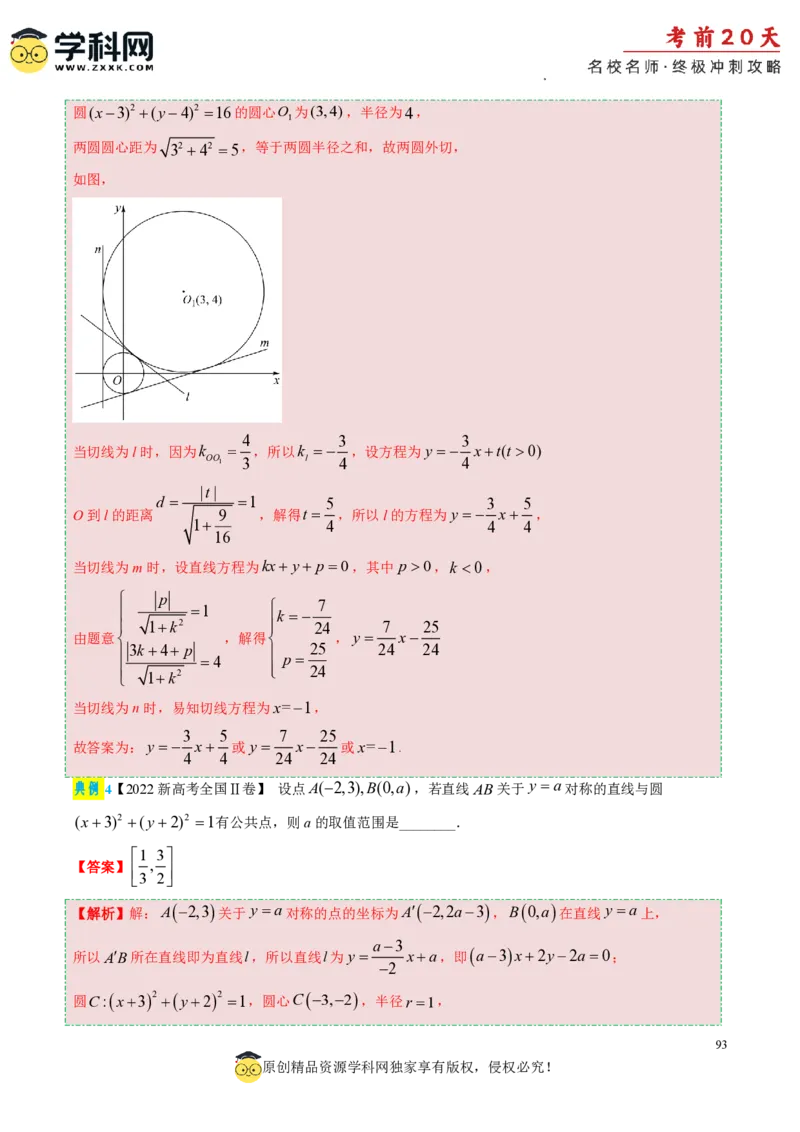
[方法三]:
圆x2 y2 1的圆心为O0,0 ,半径为1,
92
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司圆(x3)2 (y4)2 16的圆心O 为(3,4),半径为4,
1
两圆圆心距为 32 42 5,等于两圆半径之和,故两圆外切,
如图,
4 3 3
当切线为l时,因为k ,所以k ,设方程为y xt(t 0)
OO 1 3 l 4 4
|t|
d 1 5 3 5
O到l的距离 9 ,解得t ,所以l的方程为y x ,
1 4 4 4
16
当切线为m时,设直线方程为kx y p 0,其中 p 0,k 0,
p
7
1 k
1k2 24 7 25
由题意 ,解得 ,y x
3k4 p 25 24 24
4 p
1k2
24
当切线为n时,易知切线方程为x=1,
3 5 7 25
故答案为:y x 或y x 或x=1.
4 4 24 24
典例4【2022新高考全国Ⅱ卷】 设点A(2,3),B(0,a),若直线AB关于y a对称的直线与圆
(x3)2 (y2)2 1有公共点,则a的取值范围是________.
1 3
【答案】 ,
3 2
【解析】解:A2,3 关于y a对称的点的坐标为A2,2a3 ,B0,a 在直线y a上,
a3
所以AB所在直线即为直线l,所以直线l为y xa,即 a3x2y2a 0;
2
圆C:x32 y22 1,圆心C3,2
,半径r 1,
93
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司3a342a
d 1
依题意圆心到直线l的距离 ,
a32 22
1 3 1 3
即55a2 a32 22,解得 a ,即a , ;
3 2 3 2
1 3
故答案为: ,
3 2
典例5【2021新高考全国Ⅱ卷】 已知直线l:axbyr2 0与圆C:x2 y2 r2,点A(a,b),则下列说
法正确的是( )
A. 若点A在圆C上,则直线l与圆C相切 B. 若点A在圆C内,则直线l与圆C相离
C. 若点A在圆C外,则直线l与圆C相离 D. 若点A在直线l上,则直线l与圆C相切
【答案】ABD
r2
【解析】圆心C0,0 到直线l的距离d ,
a2 b2
r2
若点Aa,b 在圆C上,则a2 b2 r2,所以d = r ,
a2 b2
则直线l与圆C相切,故A正确;
r2
若点Aa,b 在圆C内,则a2 b2 r2,所以d > r ,
a2 b2
则直线l与圆C相离,故B正确;
r2
若点Aa,b 在圆C外,则a2 b2 r2,所以d < r ,
a2 b2
则直线l与圆C相交,故C错误;
若点Aa,b 在直线l上,则a2 b2 r2 0即a2 b2=r2,
r2
所以d = r ,直线l与圆C相切,故D正确.
a2 b2
故选:ABD.
预测1(2024·辽宁抚顺·模拟预测)已知直线yx1与圆C:x2y2 5相交于M,N两点,O为坐标原点,
则△MON 的面积为( )
94
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司3 5
A. B.2 C. D.4
2 2
预测2(2024·辽宁葫芦岛·模拟预测)已知Q为圆A:x12y2 1上动点,直线l :mxny3m2n0
1
和直线l :nxmy6mn0(m,nR,m2n2 0)的交点为P,则PQ的最大值是( )
2
A.6 5 B.4 5 C.5 5 D.1 5
预测3(2024·辽宁·模拟预测)设直线系M:xcosmysinn1(其中0,m,n均为参数,02π,
m,n1,2),则下列命题中是真命题的是( )
A.当m1,n1时,存在一个圆与直线系M中所有直线都相切
B.存在m,n,使直线系M中所有直线恒过定点,且不过第三象限
2
C.当mn时,坐标原点到直线系M中所有直线的距离最大值为1,最小值为
2
D.当m2,n1时,若存在一点Aa,0,使其到直线系M中所有直线的距离不小于1,则a0
预测4(2024·全国·模拟预测)已知直线l:mxnyr2 0与圆C:x2y2 r2,点Pm,n,则下列命题
中是假命题的是( ).
A.若点P在圆C外,则直线l与圆C相离B.若点P在圆C内,则直线l与圆C相交
C.若点P在圆C上,则直线l与圆C相切D.若点P在直线l上,则直线l与圆C相切
预测5(2024·全国·模拟预测)在平面直角坐标系xOy中,A2,0,动点P满足 PA 3 PO ,得到动
点P的轨迹是曲线C.则下列说法正确的是( )
A.曲线C的方程为x12y2 3
B.若直线ykx1与曲线C相交,则弦最短时k 1
C.当O,A,P三点不共线时,若点D 1 3,0 ,则射线PD平分APO
D.过A作曲线C的切线,切点分别为M,N,则直线MN的方程为x0
押题1:如图,在平面直角坐标系中,已知点A4,0,B0,2,C0,1,D是线段OA上的动点,点O与点P
关于直线CD对称.则下列结论正确的是( )
95
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司4 8
A.当CD∥AB时,点P的坐标为 ,
5 5
uuur uuur
B.OPOA的最大值为4
C.当点P在直线AB上时,直线DP的方程为4x3y80
4
D.OAP正弦的最大值为
5
uuur uuur
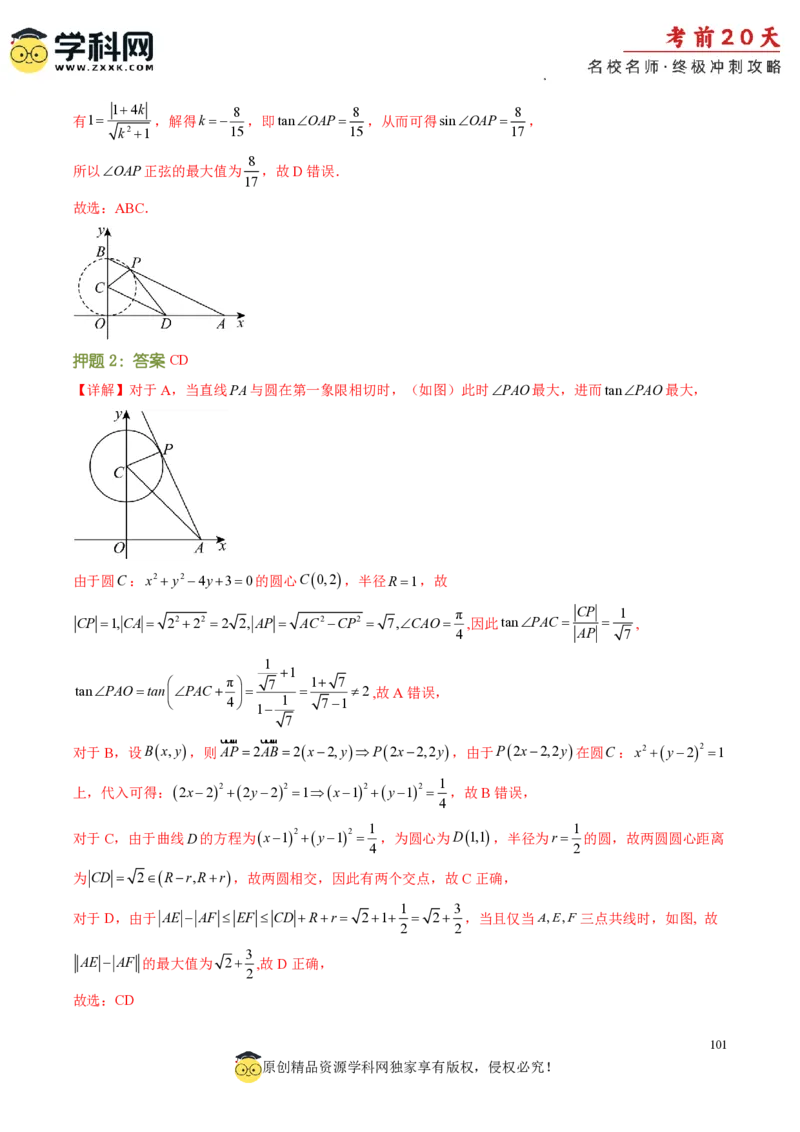
押题2:已知点P为圆C:x2y24y30上的动点,点A的坐标为2,0,AP2AB,设B点的轨迹
为曲线D,O为坐标原点,则下列结论正确的有( )
A.tanPAO的最大值为2
B.曲线D的方程为x12y12 1
C.圆C与曲线D有两个交点
3
D.若E,F 分别为圆C和曲线D上任一点,则 AE AF 的最大值为 2
2
押题3:已知a,bÎ R,O为坐标原点,函数 f(x)a x2 b x2 2(ab).下列说法中正确的是( )
A.当ab1时,若 f xx的解集是,2,则b0
B.当ab2时,若 f(x)x2有5个不同实根,则a32 2
C.当ab 3时,若ab,曲线y f(x)与半径为4的圆O有且仅有3个交点,则b2
D.当ab4时,曲线y f(x)与直线y2x6所围封闭图形的面积的最小值是33
押题4:已知圆C :(x3)2y2 1,C :x2(ya)2 16,则下列结论正确的有( )
1 2
A.若圆C 和圆C 外离,则a4
1 2
B.若圆C 和圆C 外切,则a4
1 2
C.当a0时,圆C 和圆C 有且仅有一条公切线
1 2
D.当a2时,圆C 和圆C 相交
1 2
押题5:已知直线l:m2xm1y10与圆O:x2y2 4交于A,B两点,则 AB 的最小值
为 .
名校预测
预测1:答案A
【详解】设点O到直线MN的距离为d,
96
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司001 2
则d ,
2 2
2
1 6
又 MN 2 5 3 2,
2 2
1 2 3
所以S 3 2 .
△MON 2 2 2
故选:A
预测2:答案A
【详解】由l :mxny3m2n0、l :nxmy6mn0,
1 2
有mnnm0,故l l ,
1 2
对l 有3m2n3m2n0,故l 过定点B3,2,
1 1
对l 有1n6m6mn0,故l 过定点C1,6,
2 2
31 26
则BC中点M 为 , ,即M2,4,
2 2
BC
BC 312 262 2 5,则 5,
2
故点P在以BC为直径的圆上,该圆圆心为M2,4,半径为 5,
又Q在原A:x12y2 1,该圆圆心为A1,0,半径为1,
又AM 122 42 5,则 PQ 5r r 5 516 5.
max 1 2
故选:A.
预测3:答案ABD
【详解】A选项,当m1,n1时,M:xcosysin1,
1
设圆为x2y2 1,则圆心0,0到直线M:xcosysin1的距离d 1,故
cos2sin2
97
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司M:xcosysin1与x2y2 1总相切,A正确;
B选项,当mn2时,M:xcos2ysin21,
由于cos2sin21,故直线M :xcos2ysin21恒过1,1,
若sin0时,直线为M:x1,
cos2
若sin0时,直线M:xcos2ysin21的斜率为 0,
sin2
故直线M:xcos2ysin21不过第三象限,
所以存在m,n,使直线系M中所有直线恒过定点,且不过第三象限,B正确;
C选项,当mn1时,M:xcosysin1,
1
坐标原点到直线系M的距离为d 1,
1 cos2sin2
当当mn2时,M:xcos2ysin21,
1
坐标原点到直线系M的距离为d
2 cos4sin4
其中cos4sin4cos2cos2sin2sin2cos2sin21,
1
故d 1,C错误.
2 cos4sin4
D选项,当m2,n1时,M:xcos2ysin1,
acos21
点Aa,0到直线系M中所有直线的距离d 1,
3 cos4sin2
化简得 a21 cos22a1恒成立,
由于cos20,1,
若a210,解得a1,
当a1时,01,不合要求,舍去,
当a1时,01,满足要求,
若a210,即a1或a1,此时 a21 cos2的最小值为0,
1
则02a1,解得a ,故此时a1,
2
若a210,即1a1,此时 a21 cos2的最小值为a21,
则a212a1,解得a2或a0,故此时1a0,
综上,a0,D正确.
故选:ABD
预测4:答案AB
98
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司【详解】对于A,因为点Pm,n在圆C外,所以m2n2 r2,
0m0nr2 r2
则圆心C0,0到直线l的距离为d r,
m2n2 m2n2
所以直线l与圆C相交,故命题A是假命题;
对于B,因为点Pm,n在圆C内,所以m2n2 r2,
0m0nr2 r2
则圆心C0,0到直线l的距离为d r,
m2n2 m2n2
所以直线l与圆C相离,故命题B是假命题;
对于C,因为点Pm,n在圆C上,所以m2n2 r2,
0m0nr2 r2
则圆心C0,0到直线l的距离为d r,
m2n2 m2n2
所以直线l与圆C相切,故命题C是真命题;
对于D,因为点Pm,n在直线l上,所以m2n2r2 0,即m2n2 r2,
0m0nr2 r2
则圆心C0,0到直线l的距离为d r,
m2n2 m2n2
所以直线l与圆C相切,故命题D是真命题;
故选:AB.
预测5:答案ACD
【详解】A:设Px,y,因为A2,0,动点P满足 PA 3 PO ,
所以 x22 y2 3 x2y2 ,化简可得x12y2 3,故A正确;
k1
B:由选项A可知,圆心1,0,半径r 3,设圆心到直线的距离为d ,则d ,
1 1 1k2
1k2 2k22k2 1
设弦长为d 2 ,由弦长公式得
d
2
2 r2d
1
2 2 3
1k2
2
1k2
2 2 1
1 ,
k
k
1 1
因为k 2 k 2,当且仅当k1,取等号,
k k
所以弦最短时k1,故B错误;
99
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司C:
PA
因为 PA 3 PO ,则 3,又D 1 3,0 ,
PO
AD 3 3 PA
所以 AD 3 3,OD 31,则 3 ,
OD 31 PO
所以由角平分线定理的逆定理可知射线PD平分APO,故C正确;
D:过A作曲线C的切线,切点分别为M,N,
AC 3 1
则由集合关系可知M,N在以AC为直径的圆上,半径为 ,圆心为 ,0,
2 2 2
1 2 9
此圆方程为 x y2 ,
2 4
两圆方程相减可得公共线MN的方程为x0,故D正确;
故选:ACD.
名师押题
押题1:答案ABC
【详解】如图,由题意可得点P在以C为圆心,半径为1的圆上,
设POB,0 π ,则P 2sincos,2cos2 ,
2
对于A,当CD//AB时,可得POBOAB,
5 2 5 4 8
sin ,cos ,此时点P的坐标为 , ,故A正确;
5 5 5 5
uuur uuur π
对于B,OPOA2sincos44sin24,当且仅当 时等号成立,故B正确;
4
4 8
对于C,当点P在直线AB上时,可得POBOAB,此时点P的坐标为 , ,
5 5
1 4
直线DP与圆C:x2y12 1相切,所以k ,所以直线DP的方程为4x3y80,故C正
DP k 3
CP
确;
对于D,当直线AP与圆C相切时,OAP正弦的最大,设直线AP的斜率为k,则直线AP的方程为
ykx4,
100
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司14k 8 8 8
有1 ,解得k ,即tanOAP ,从而可得sinOAP ,
k21 15 15 17
8
所以OAP正弦的最大值为 ,故D错误.
17
故选:ABC.
押题2:答案CD
【详解】对于A,当直线PA与圆在第一象限相切时,(如图)此时PAO最大,进而tanPAO最大,
由于圆C:x2y24y30的圆心C0,2,半径R1,故
π CP 1
CP 1,CA 2222 2 2, AP AC2CP2 7,CAO ,因此tanPAC ,
4 AP 7
1
1
π 7 1 7
tanPAOtanPAC 2,故A错误,
4 1 71
1
7
uuur uuur
对于B,设Bx,y,则AP2AB2x2,yP2x2,2y,由于P2x2,2y在圆C:x2y22
1
1
上,代入可得:2x222y22 1x12y12 ,故B错误,
4
1 1
对于C,由于曲线D的方程为x12y12 ,为圆心为D1,1,半径为r 的圆,故两圆圆心距离
4 2
为CD 2Rr,Rr,故两圆相交,因此有两个交点,故C正确,
1 3
对于D,由于 AE AF EF CD Rr 21 2 ,当且仅当A,E,F 三点共线时,如图, 故
2 2
3
AE AF 的最大值为 2 ,故D正确,
2
故选:CD
101
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司押题3:答案BD
abx4a,x2
【详解】A选项,由题意, f(x) abx,2x2 ,
abx4b,x2
2b1x4b1,x2
当ab1时, f(x)x,2x2 ,
2b1x4b,x2
若 f xx的解集是,2,
当2x2时, f(x)x显然成立,
当x2时,令 f(x)2b1x4b1x,
即2b2x4b42b1x4b1在x2上恒成立,
则要2b10,解得b1,
且x2时,2b1x4bx恒成立,即2bx4b恒成立,
故2b0,解得b0,
综上,1b0,A错误;
2a1x4a,x2
B选项,当ab2时, f(x)2x,2x2 ,
2a1x4a2,x2
因为 f(x)x2有5个不同实根,
当2x2时,2x x2,得x0或x2,有两个根,
当x2时,2a1x4a2x2,即x2x2a20,
得x2a2或x2,
当x<2时,2a1x4ax2,方程最多两个根,
要想保证有5个不同实根,故x2a22为其中一个根,故a3,
此时x2a22,满足要求,
102
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司而x22a1x4a0,方程需要在,2有两个不同的实数根,
设g(x)x22a1x4a,
g(2)8
则Δ4a12 16a0,解得a32 2,B正确;
1a2
3x4b1,x2
C选项,当ab 3时, f(x) 2b 3 x,2x2,
3x4b,x2
若ab,则b0,
且曲线y f(x)与半径为4的圆O有且仅有3个交点,
如下图,可能是y 3x4b,x2与圆相切,
004b
则d 4 ,得b2或b2(舍),
13
也可能,点2, f(2)在圆上,如下图,
2
则2222 2b 3 42,解得b 3或b0(舍)
所以C错误;
103
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司4x4a,x2
D选项,当ab4时, f(x)2a2x,2x2,
4x44a,x2
且 f(2)84a, f(2)4a8,
当x2时,y 226 2,当x2时,y22610,
f 22 3
当 ,即a 时,画出两函数图象如下:
f 210 2
曲线y f(x)与直线y2x6所围封闭图形的面积三角形ACD的面积,
令2a2x2x6,解得x 3 ,故x 3
a3 C a3
令4x44a2x6,解得x112a,故x 112a,
A
3 92a4a
则 AC 14112a 5 ,
a3 3a
4a864 184a
点D2,4a8到直线y2x6的距离为h ,
14 5
1 1 92a4a 184a 92a24a
故S AC h 5 ,
VACD 2 2 3a 5 3a
92a24a 3
令ua ,a ,
3a 2
492a4a92a23a92a24a
则ua
3a2
3926a4a292a
0,
3a2
92a24a 3
故ua 在a 上单调递减,
3a 2
104
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司932
4
3
3 2
故最小值为u 60,
2 3
3
2
9
当4a8226,即a 时,此时k 2a45,k 42,
2 BD DE
如图,曲线y f(x)与直线y2x6所围封闭图形的面积三角形ABC的面积,
2a3 2a3
令4x4a2x6,解得x ,x ,
3 C 3
令2a2x2x6,解得x 3 ,故x 3 ,
a3 A a3
9 3 2a3 2a23a
因为a ,所以 AC 14 5 ,
2 a3 3 3a9
2284a6
4a6
故点B2,84a到直线y2x6的距离d ,
221 5
故此时曲线y f(x)与直线y2x6所围封闭图形的面积为
1 1 2a23a 4a6 4a312a29a
AC d 5 ,
2 2 3a9 5 3a9
4a312a29a
令wa ,
3a9
4a312a29a 12a224a9 3a93 4a312a29a
则wa
3a92 3a92
24a3144a2216a81
,
3a92
令qa24a3144a2216a81,
则qa72a2288a21672 a24a3 0在a 9 上恒成立,
2
9
故qa24a3144a2216a81在a 单调递增,
2
105
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司9 729 81 9
又q 24 144 216 812187291697281160,
2 8 4 2
9
故wa0在a 上恒成立,
2
4a312a29a 9
故wa 在a 上单调递增,
3a9 2
729 81 9 729 81
4 12 9 243
9 8 4 2 2 2
故最小值为w 36,
2 27 9
9
2 2
3 9
当4a810且84a2,即 a 时,
2 2
此时k 2a45,k 42,
BD DE
3
当 a4时,2a21,4,
2
如图,曲线y f(x)与直线y2x6所围封闭图形的面积四边形BCED的面积,
2a3 2a3
令4x4a2x6,解得x ,x ,
3 C 3
4a6 124a 2a3 124a
故y 2x 66 ,即C , ,
C C 3 3 3 3
令4x44a2x6,解得x112a,故x 112a,
E
y 2x 6224a6284a,故E112a,284a,
E E
2a3 364a
故CE 14112a 5 ,
3 3
设直线BC与直线DE相交于点H,
令4x4a4x44a,解得x2a,
此时y4x4a42a4a8,故H2a,8,
106
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司22a68
182a
点H到直线y2x6的距离为d ,
1 14 5
1 1 364a 182a
182a2
故S CE d 5 ,
VECH 2 1 2 3 5 3
其中B2,84a,D2,4a8,
故 BD 222 4a884a2 168a162 64a2256a272,
2a42a8 2aa4
点H到直线BD的距离为d
2
12a42
4a216a17
,
1 1
2aa4
故S BD d 64a2256a272 4 aa4 ,
VBDH 2 2 2 4a216a17
182a2
则四边形BCED的面积为S S 4 aa4,
VECH VBDH 3
当
3
a4时,S S
182a2
4 a24a
16a2
40a108
16
a
15
2
33,
2 VECH VBDH 3 3 3 4
15
当a 时,面积取得最小值,最小值为33,
4
9
当4a 时,2a24,5,画出图象如下:
2
四边形BCED的面积为S S
182a2
4 a24a
16a2
40a108
16
a
15
2
33,
VECH VBDH 3 3 3 4
9 16 15 2
当4a 时, a 3333,
2 3 4
综上,当ab4时,曲线y f(x)与直线y2x6所围封闭图形的面积的最小值是33,D正确.
故选:BD
押题4:答案BCD
107
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司【详解】C 3,0,C 0,a,CC 9a2,r 1,r 4.
1 2 1 2 1 2
若C 和C 外离,则CC 9a2 r r 5,解得a4或a<-4,故A错误;
1 2 1 2 1 2
若C 和C 外切,CC 9a2 5,解得a4,故B正确;
1 2 1 2
当a0时,CC 3r r,C 和C 内切,故C正确;
1 2 2 1 1 2
当a2时,3 CC 135,C 和C 相交,故D正确.
1 2 1 2
故选:BCD
押题5:答案2 2
【详解】由l:m2xm1y10,得l:mxy2xy10,
xy0 x1
由 ,解得 ,则直线l过定点(1,1),
2xy10 y1
又1212 4,所以该定点在圆O:x2y2 4内,
由圆O:x2y2 4可得圆心O0,0,半径r 2,
当圆心O与定点(1,1)的连线垂直于AB时,|AB|取得最小值,
圆心O0,0与定点(1,1)的距离为d 1212 2,
则|AB|的最小值为2 r2d2 2 42 2 2.
故答案为:2 2.
108
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司海量资源免费下载公众号《良学小屋》
√书虫致力于提供高考名师课程和全国各地名校试卷
√收费群仅在公众号进行售卖进群,其他平台购买均
属倒卖,倒卖有断更、更新延迟、遗漏等问题不提供
售后服务
扫码关注良学小屋
领取免费资源
如果搜索不到可以搜索微信号:lxxw64787822