文档内容
2023年陕西省中考数学试卷(A卷)
一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题意的)
1.(3分)计算:3﹣5=( )
A.2 B.﹣2 C.8 D.﹣8
2.(3分)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
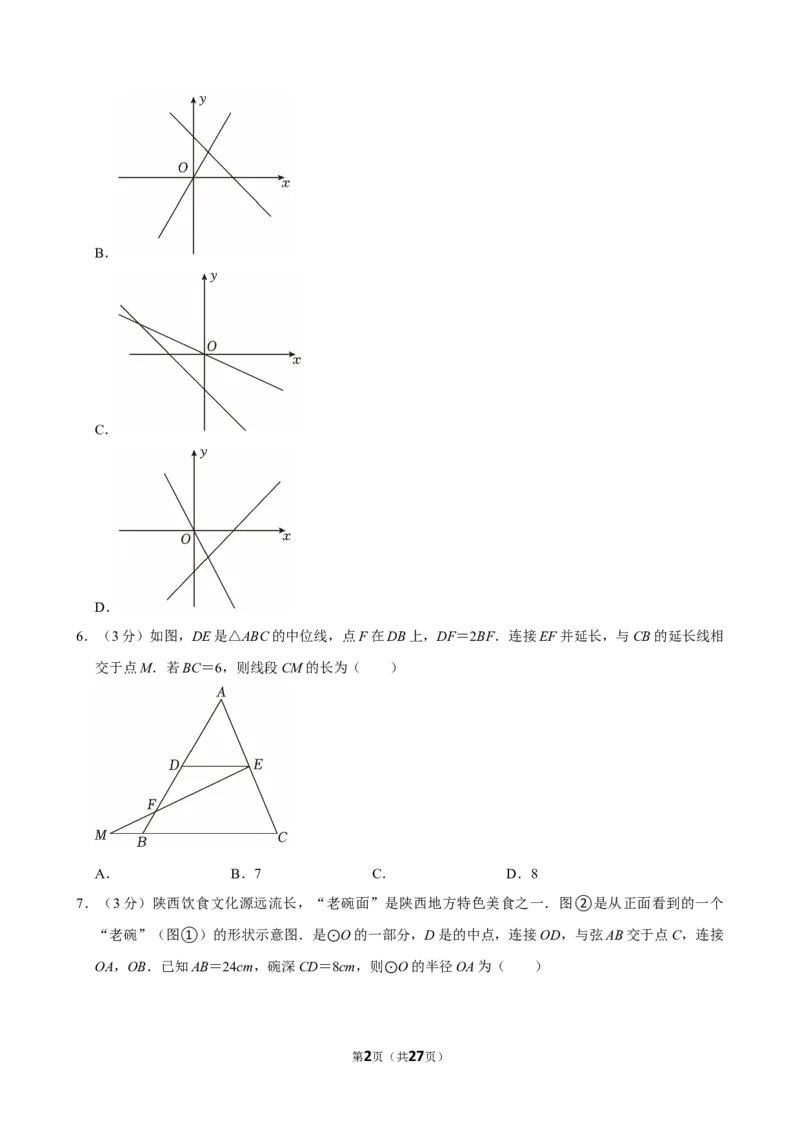
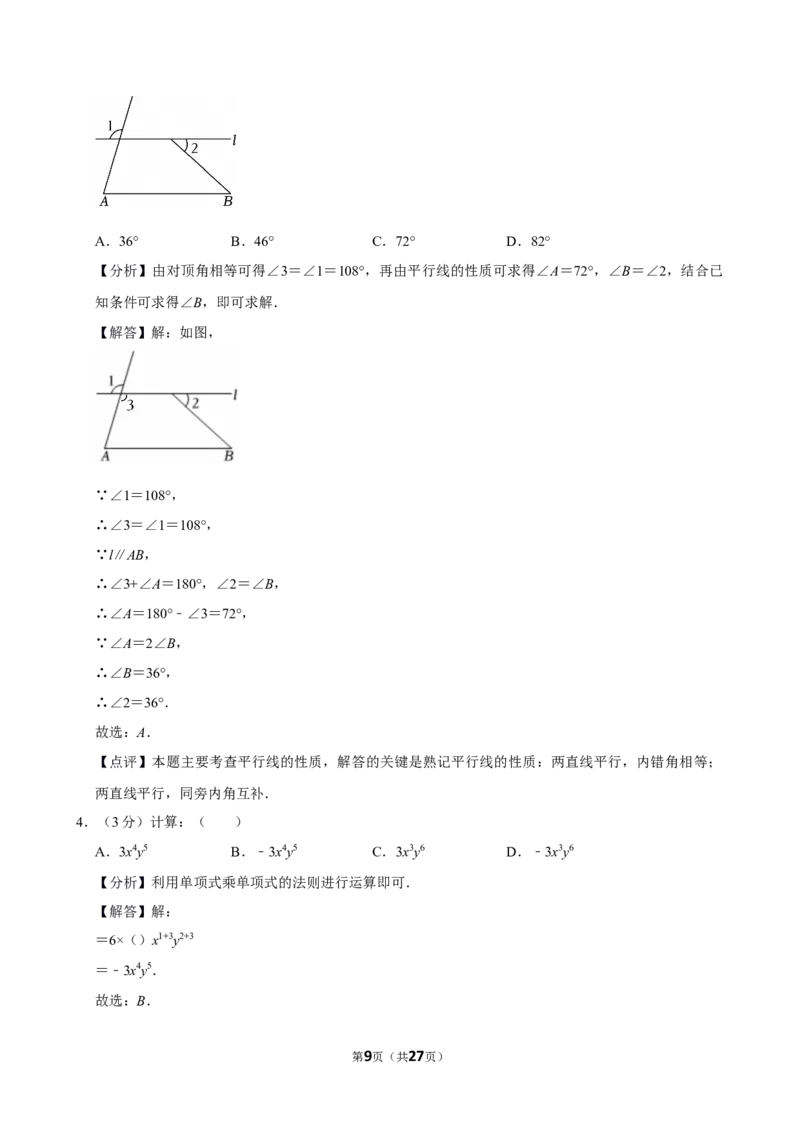
3.(3分)如图,l∥AB,∠A=2∠B.若∠1=108°,则∠2的度数为( )
A.36° B.46° C.72° D.82°
4.(3分)计算:( )
A.3x4y5 B.﹣3x4y5 C.3x3y6 D.﹣3x3y6
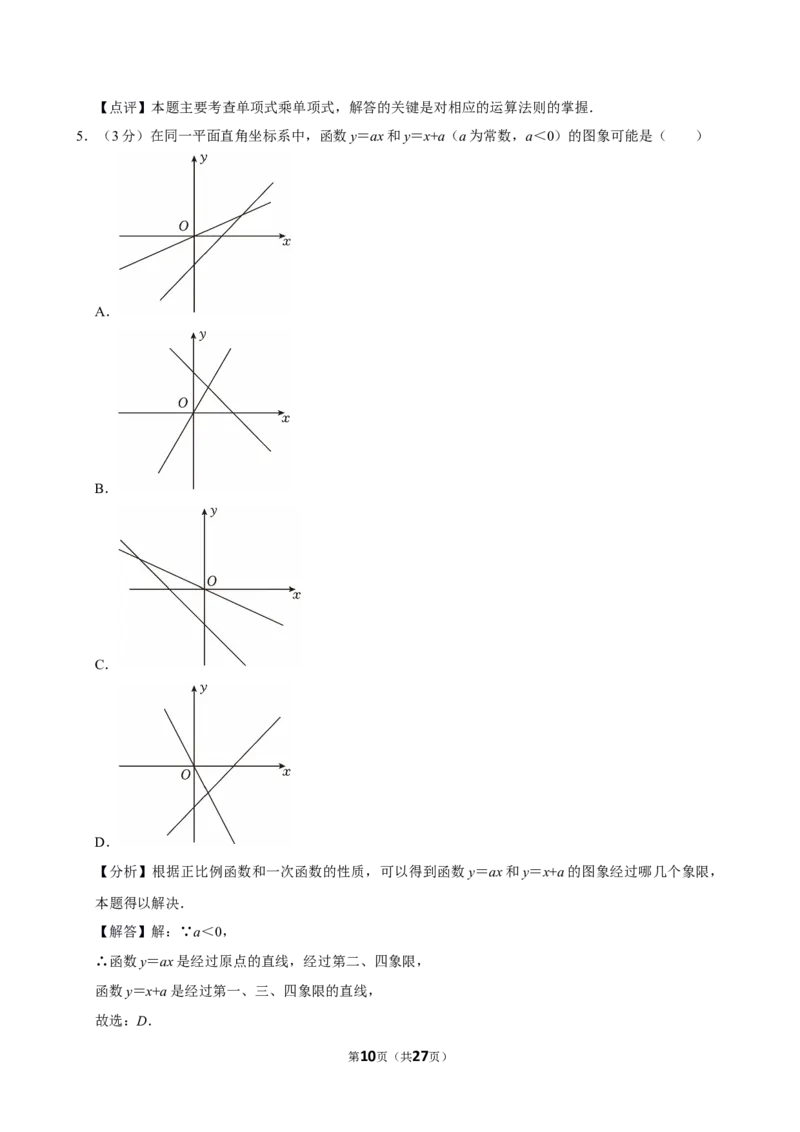
5.(3分)在同一平面直角坐标系中,函数y=ax和y=x+a(a为常数,a<0)的图象可能是( )
A.
第1页(共27页)B.
C.
D.
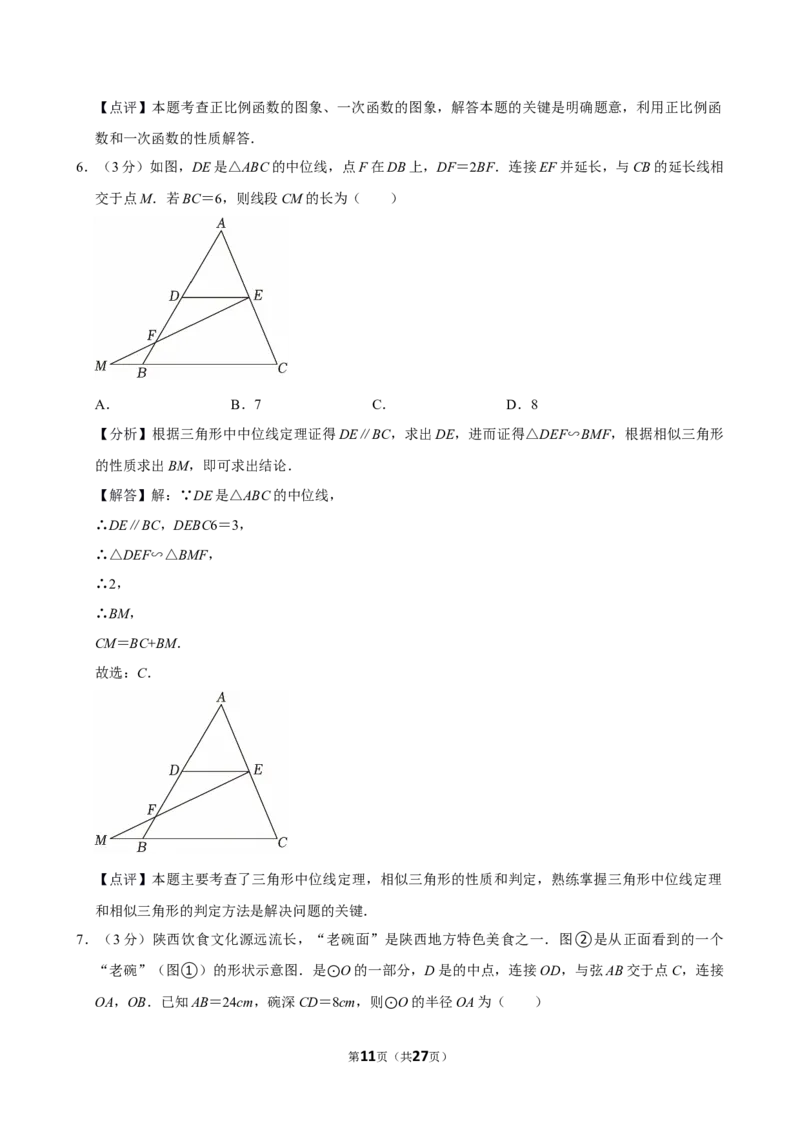
6.(3分)如图,DE是△ABC的中位线,点F在DB上,DF=2BF.连接EF并延长,与CB的延长线相
交于点M.若BC=6,则线段CM的长为( )
A. B.7 C. D.8
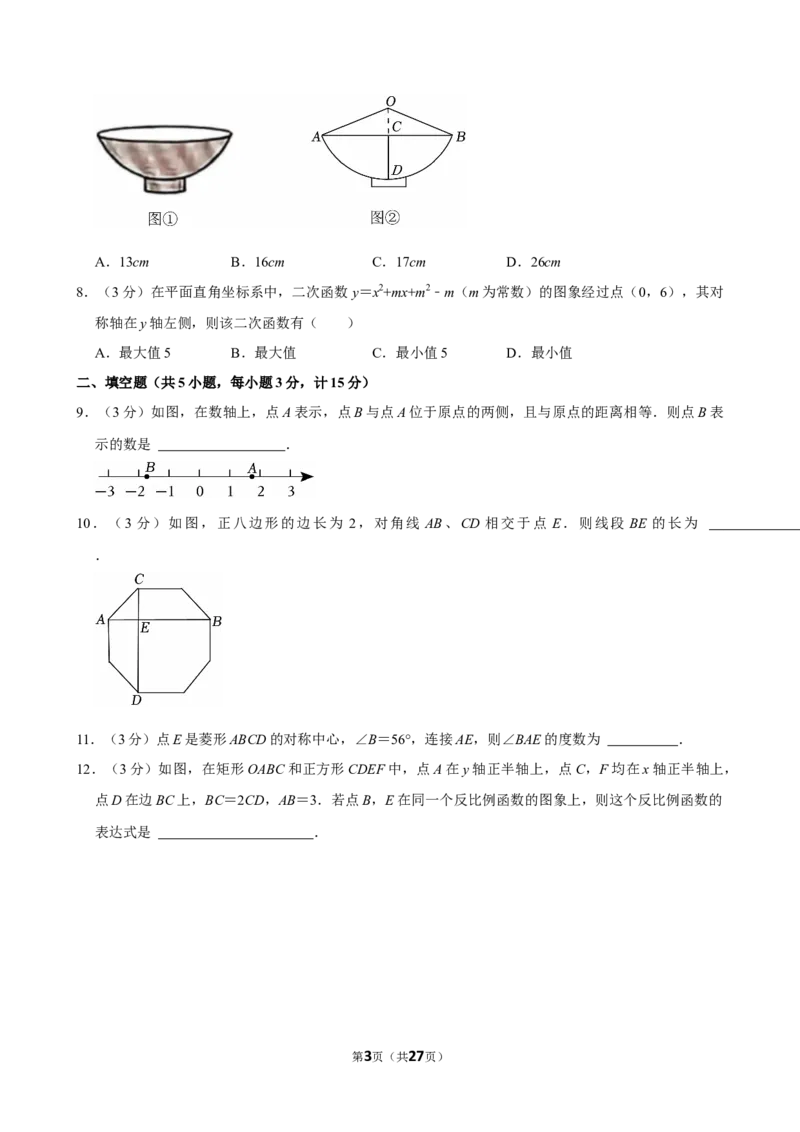
7.(3分)陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一.图②是从正面看到的一个
“老碗”(图①)的形状示意图.是 O的一部分,D是的中点,连接OD,与弦AB交于点C,连接
OA,OB.已知AB=24cm,碗深CD=⊙8cm,则 O的半径OA为( )
⊙
第2页(共27页)A.13cm B.16cm C.17cm D.26cm
8.(3分)在平面直角坐标系中,二次函数y=x2+mx+m2﹣m(m为常数)的图象经过点(0,6),其对
称轴在y轴左侧,则该二次函数有( )
A.最大值5 B.最大值 C.最小值5 D.最小值
二、填空题(共5小题,每小题3分,计15分)
9.(3分)如图,在数轴上,点A表示,点B与点A位于原点的两侧,且与原点的距离相等.则点B表
示的数是 .
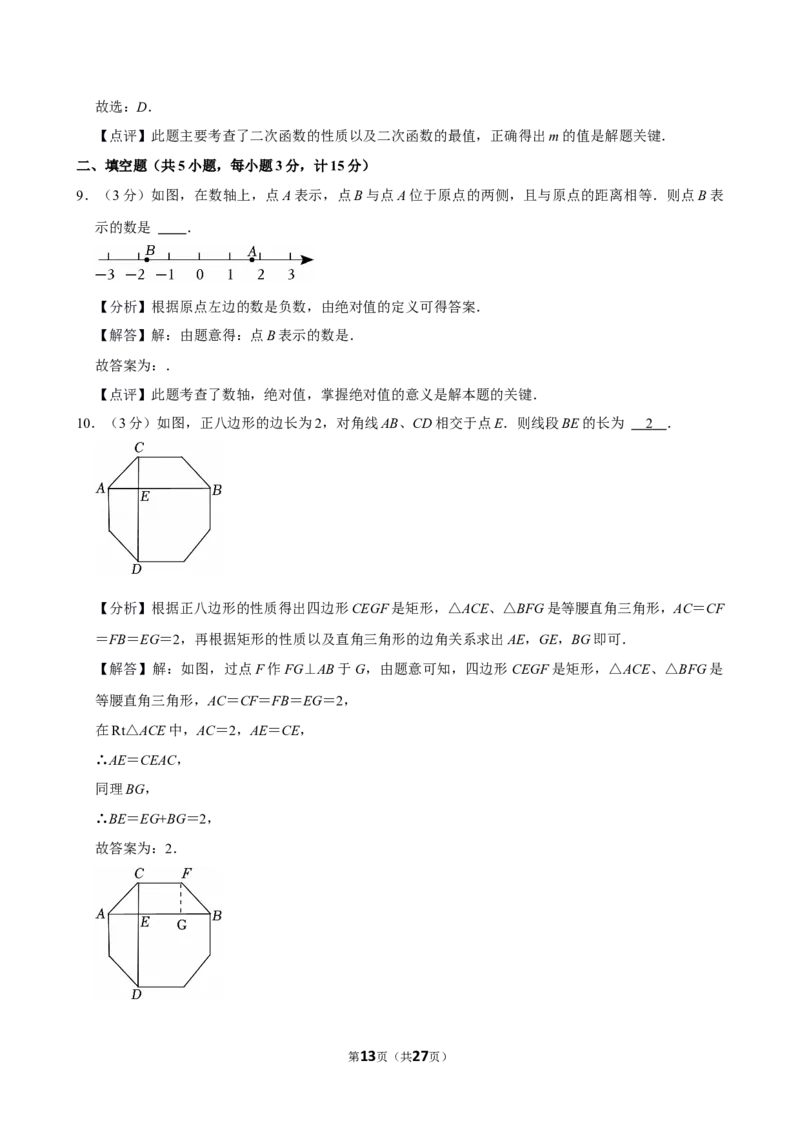
10.(3 分)如图,正八边形的边长为 2,对角线 AB、CD 相交于点 E.则线段 BE 的长为
.
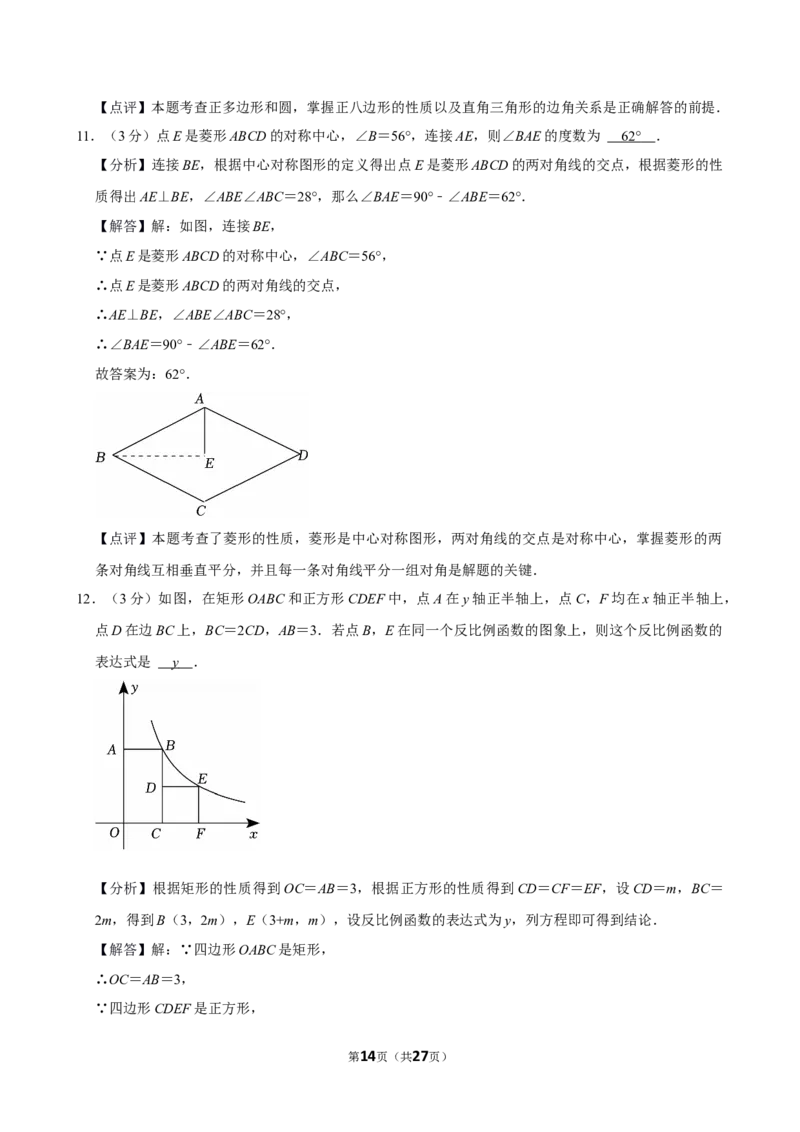
11.(3分)点E是菱形ABCD的对称中心,∠B=56°,连接AE,则∠BAE的度数为 .
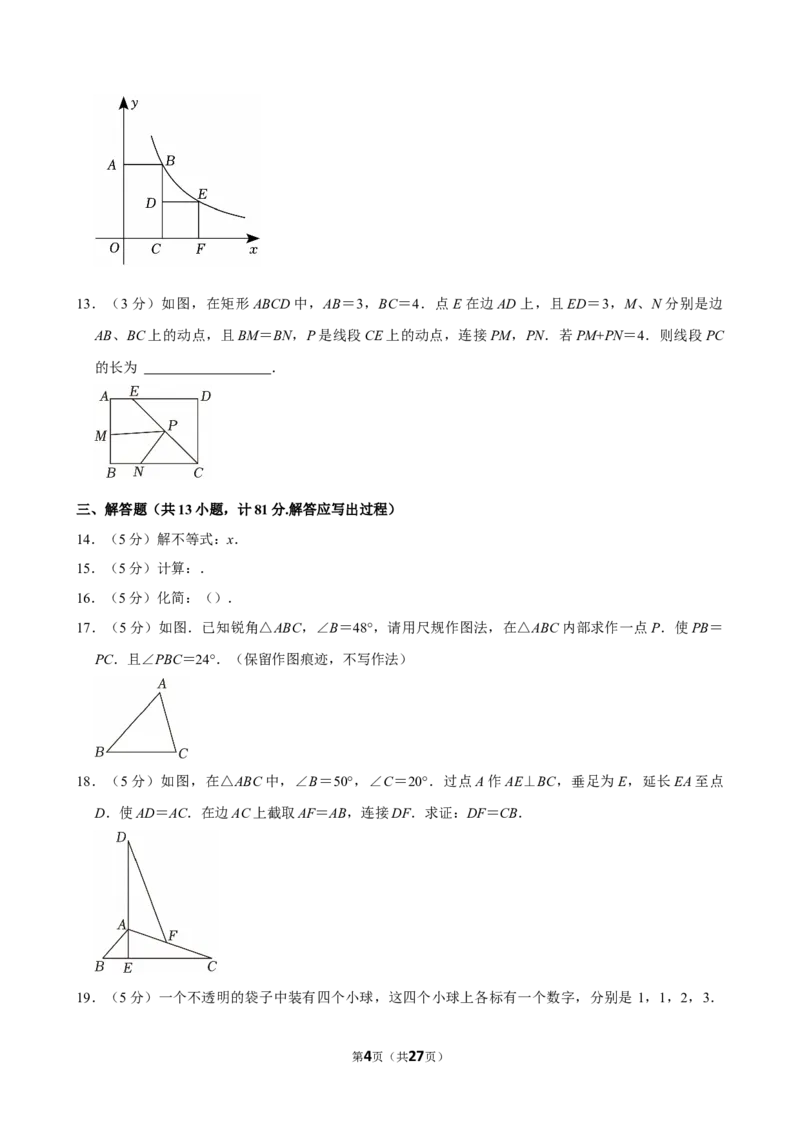
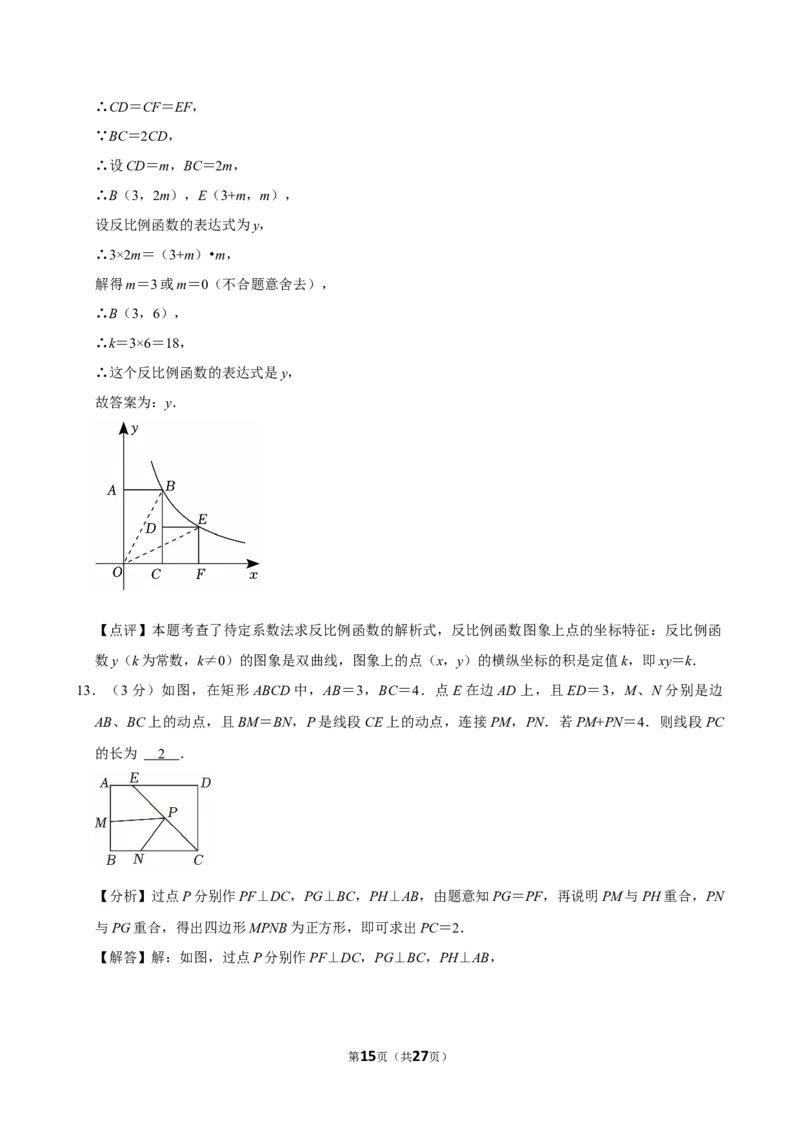
12.(3分)如图,在矩形OABC和正方形CDEF中,点A在y轴正半轴上,点C,F均在x轴正半轴上,
点D在边BC上,BC=2CD,AB=3.若点B,E在同一个反比例函数的图象上,则这个反比例函数的
表达式是 .
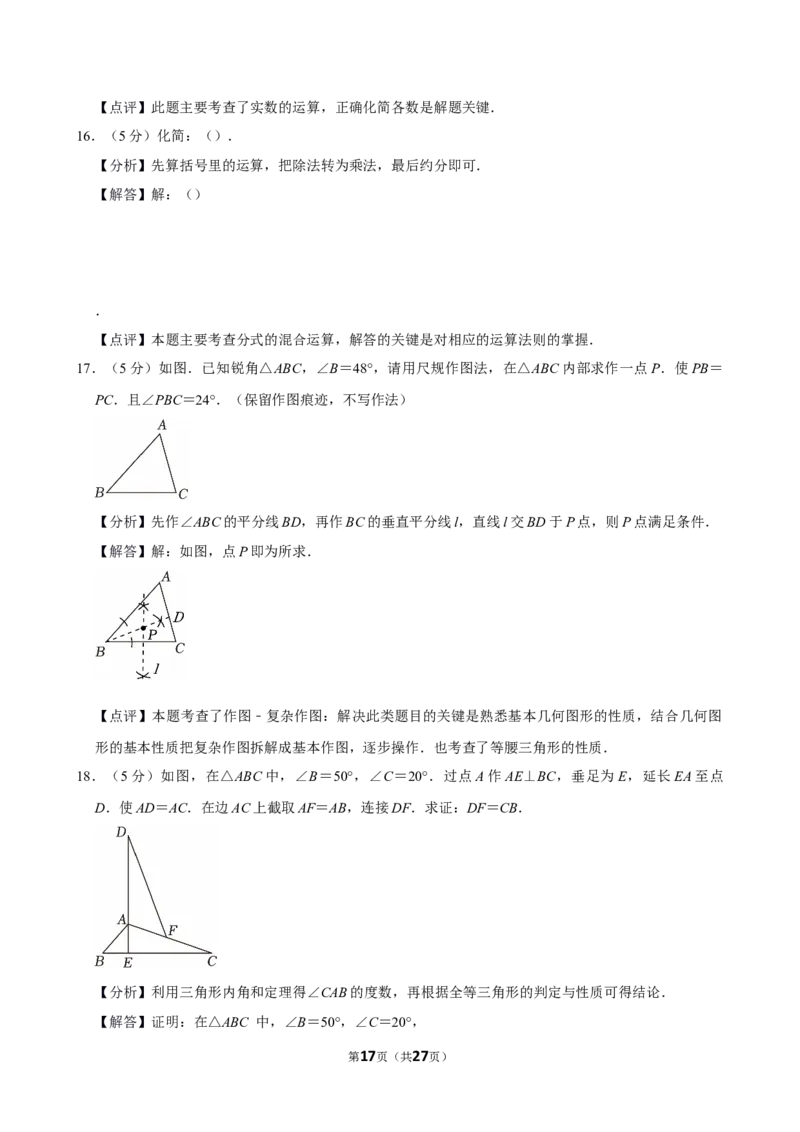
第3页(共27页)13.(3分)如图,在矩形ABCD中,AB=3,BC=4.点E在边AD上,且ED=3,M、N分别是边
AB、BC上的动点,且BM=BN,P是线段CE上的动点,连接PM,PN.若PM+PN=4.则线段PC
的长为 .
三、解答题(共13小题,计81分.解答应写出过程)
14.(5分)解不等式:x.
15.(5分)计算:.
16.(5分)化简:().
17.(5分)如图.已知锐角△ABC,∠B=48°,请用尺规作图法,在△ABC内部求作一点P.使PB=
PC.且∠PBC=24°.(保留作图痕迹,不写作法)
18.(5分)如图,在△ABC中,∠B=50°,∠C=20°.过点A作AE⊥BC,垂足为E,延长EA至点
D.使AD=AC.在边AC上截取AF=AB,连接DF.求证:DF=CB.
19.(5分)一个不透明的袋子中装有四个小球,这四个小球上各标有一个数字,分别是 1,1,2,3.
第4页(共27页)这些小球除标有的数字外都相同.
(1)从袋中随机摸出一个小球,则摸出的这个小球上标有的数字是 1 的概率为
;
(2)先从袋中随机摸出一个小球,记下小球上标有的数字后,放回,摇匀,再从袋中随机摸出一个小
球,记下小球上标有的数字,请利用画树状图或列表的方法、求摸出的这两个小球上标有的数字之积
是偶数的概率.
20.(5分)小红在一家文具店买了一种大笔记本 4个和一种小笔记本6个,共用了62元.已知她买的
这种大笔记本的单价比这种小笔记本的单价多3元,求该文具店中这种大笔记本的单价.
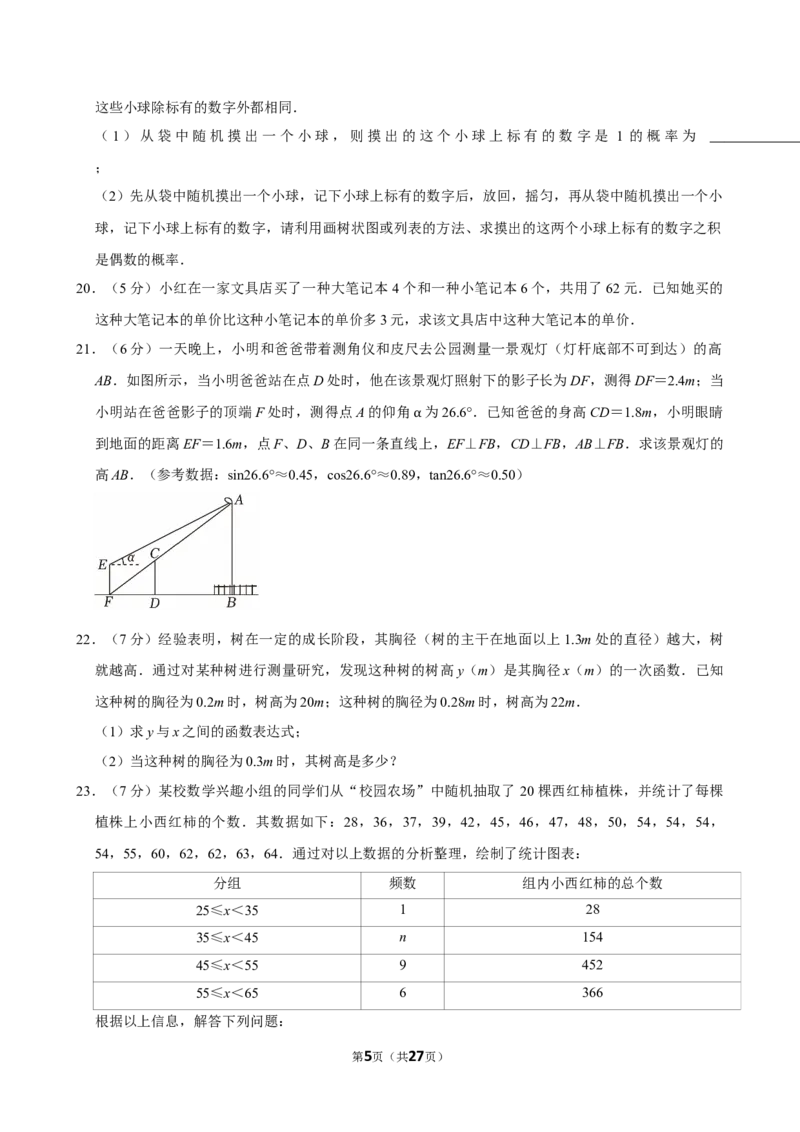
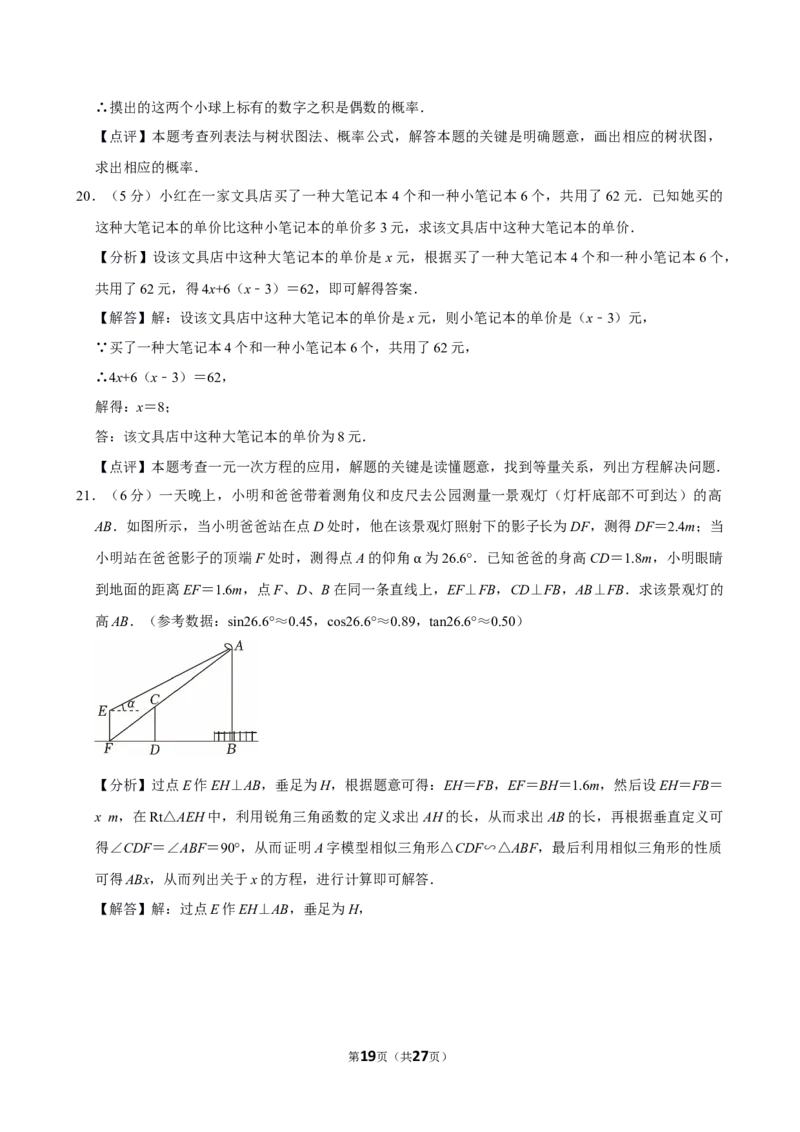
21.(6分)一天晚上,小明和爸爸带着测角仪和皮尺去公园测量一景观灯(灯杆底部不可到达)的高
AB.如图所示,当小明爸爸站在点D处时,他在该景观灯照射下的影子长为DF,测得DF=2.4m;当
小明站在爸爸影子的顶端F处时,测得点A的仰角 为26.6°.已知爸爸的身高CD=1.8m,小明眼睛
到地面的距离EF=1.6m,点F、D、B在同一条直线α上,EF⊥FB,CD⊥FB,AB⊥FB.求该景观灯的
高AB.(参考数据:sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50)
22.(7分)经验表明,树在一定的成长阶段,其胸径(树的主干在地面以上1.3m处的直径)越大,树
就越高.通过对某种树进行测量研究,发现这种树的树高y(m)是其胸径x(m)的一次函数.已知
这种树的胸径为0.2m时,树高为20m;这种树的胸径为0.28m时,树高为22m.
(1)求y与x之间的函数表达式;
(2)当这种树的胸径为0.3m时,其树高是多少?
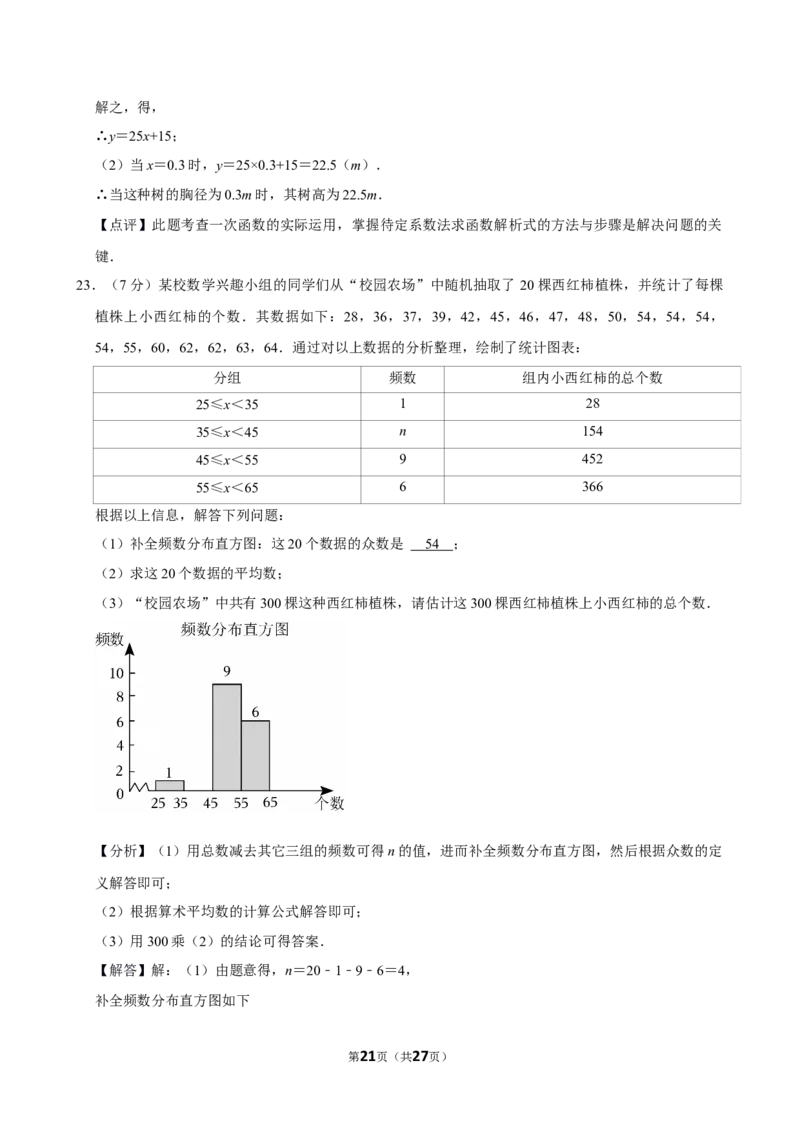
23.(7分)某校数学兴趣小组的同学们从“校园农场”中随机抽取了 20棵西红柿植株,并统计了每棵
植株上小西红柿的个数.其数据如下:28,36,37,39,42,45,46,47,48,50,54,54,54,
54,55,60,62,62,63,64.通过对以上数据的分析整理,绘制了统计图表:
分组 频数 组内小西红柿的总个数
25≤x<35 1 28
35≤x<45 n 154
45≤x<55 9 452
55≤x<65 6 366
根据以上信息,解答下列问题:
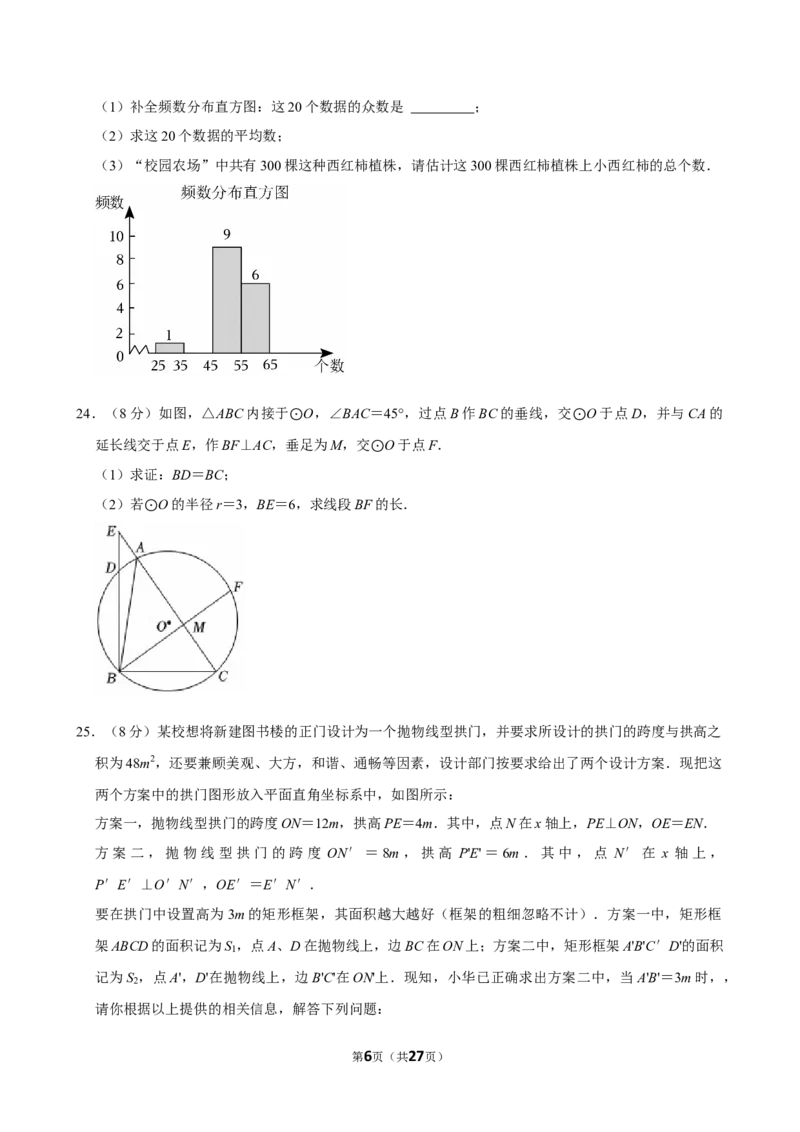
第5页(共27页)(1)补全频数分布直方图:这20个数据的众数是 ;
(2)求这20个数据的平均数;
(3)“校园农场”中共有300棵这种西红柿植株,请估计这300棵西红柿植株上小西红柿的总个数.
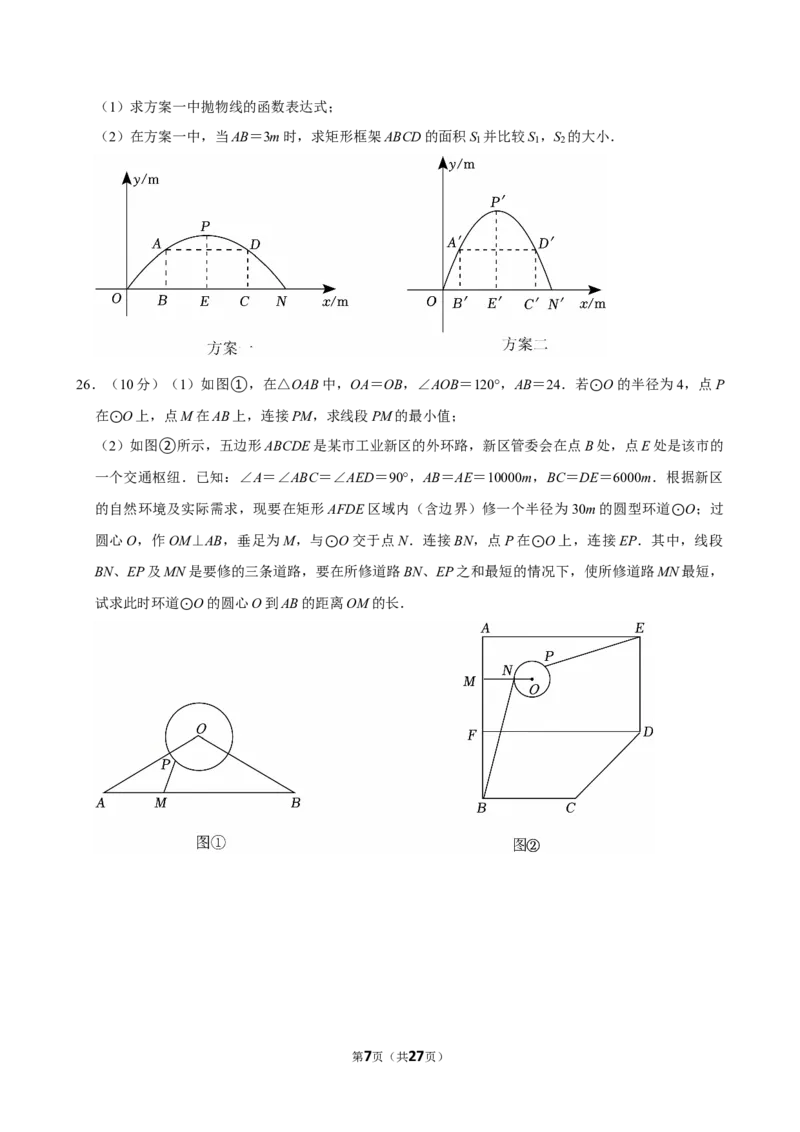
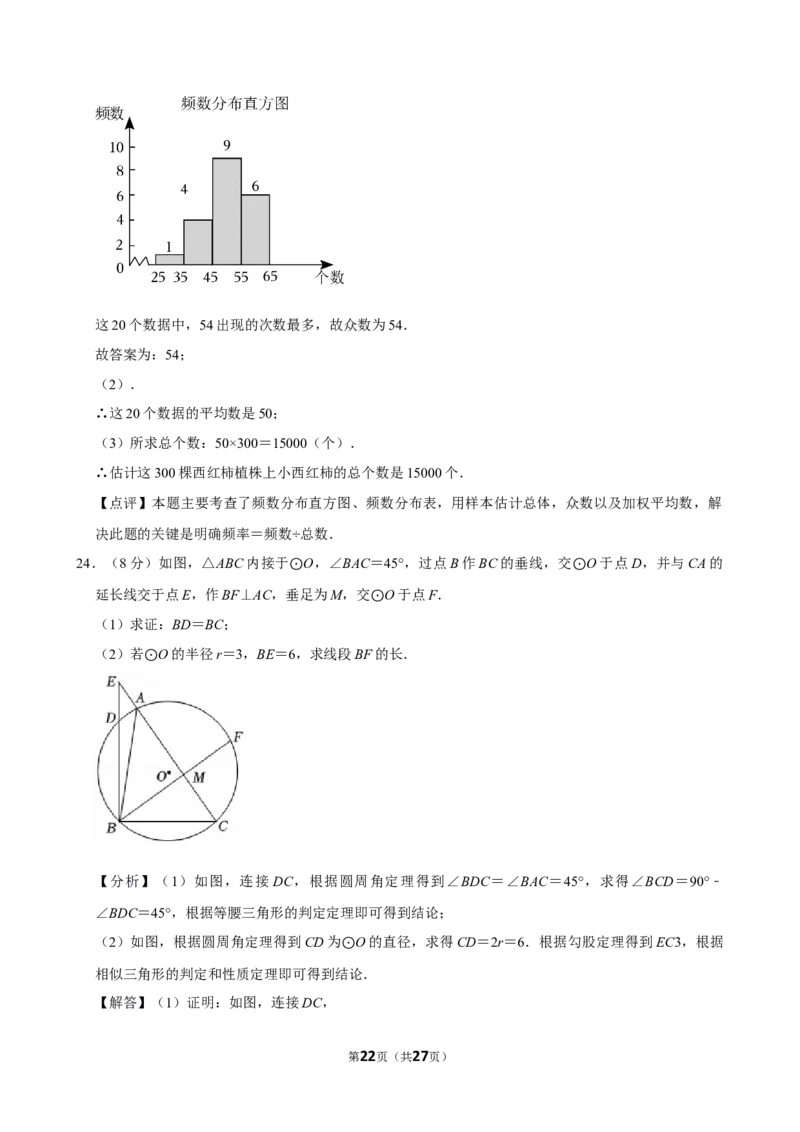
24.(8分)如图,△ABC内接于 O,∠BAC=45°,过点B作BC的垂线,交 O于点D,并与CA的
延长线交于点E,作BF⊥AC,垂⊙足为M,交 O于点F. ⊙
(1)求证:BD=BC; ⊙
(2)若 O的半径r=3,BE=6,求线段BF的长.
⊙
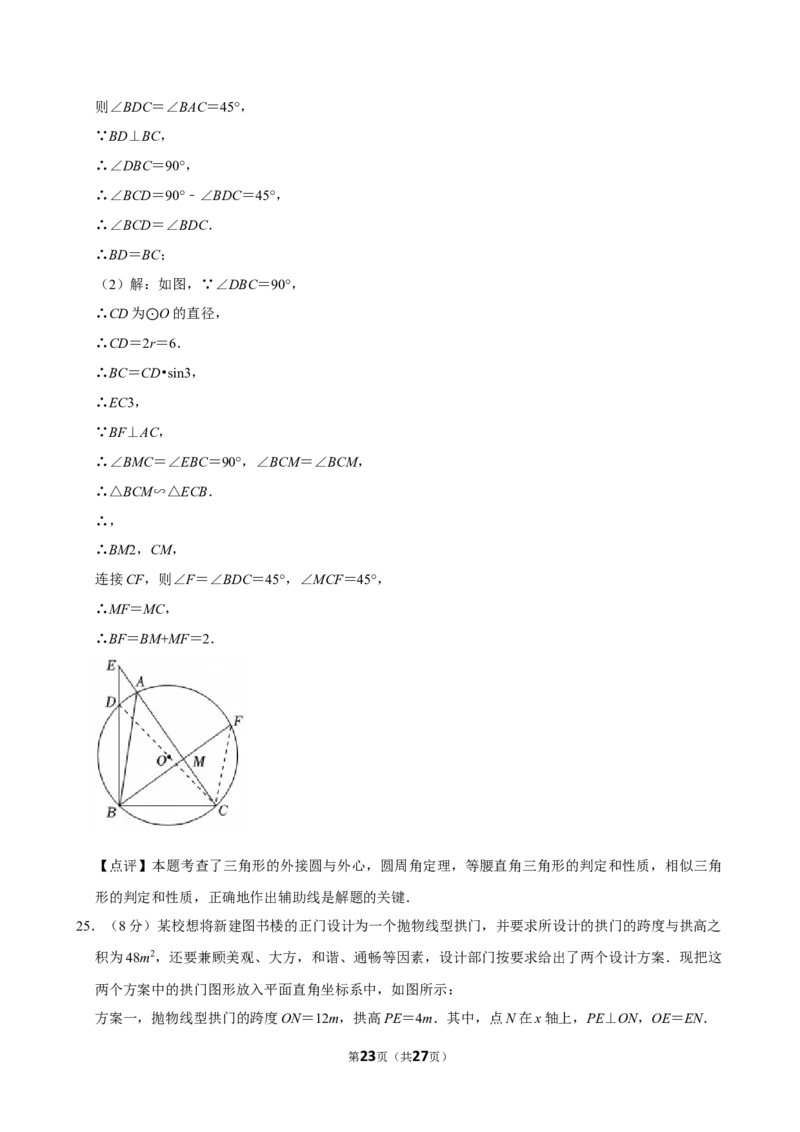
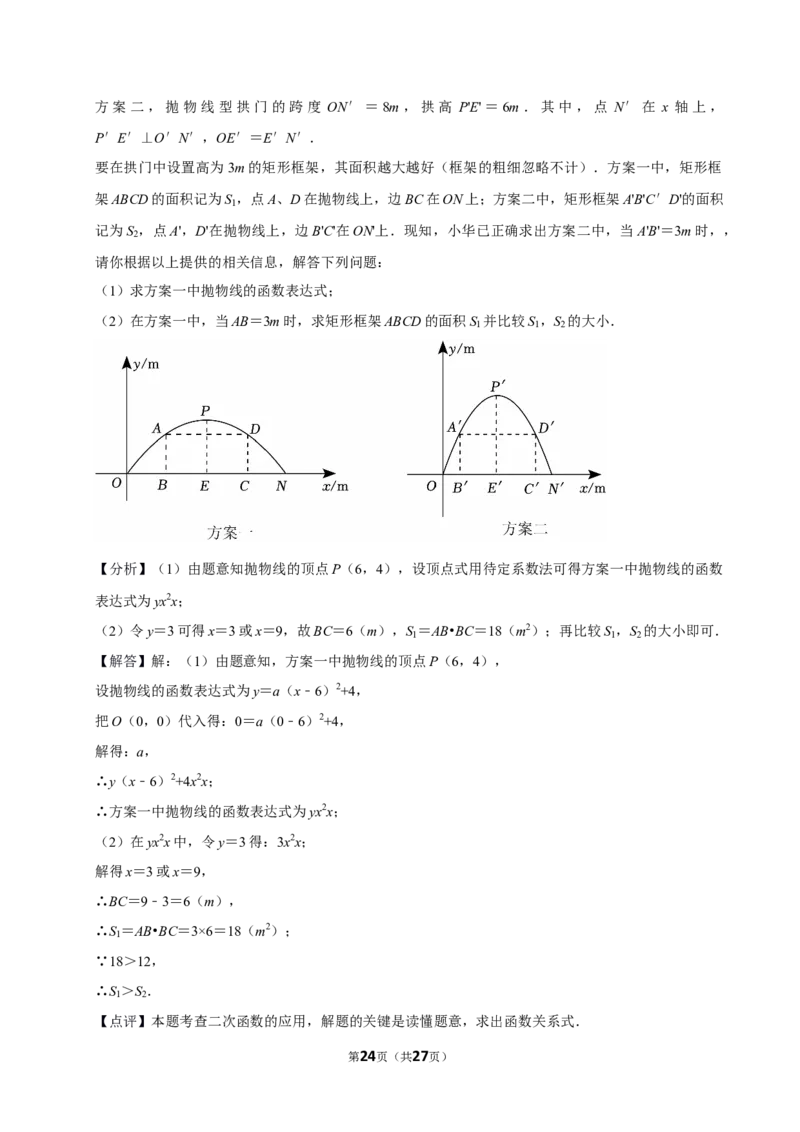
25.(8分)某校想将新建图书楼的正门设计为一个抛物线型拱门,并要求所设计的拱门的跨度与拱高之
积为48m2,还要兼顾美观、大方,和谐、通畅等因素,设计部门按要求给出了两个设计方案.现把这
两个方案中的拱门图形放入平面直角坐标系中,如图所示:
方案一,抛物线型拱门的跨度ON=12m,拱高PE=4m.其中,点N在x轴上,PE⊥ON,OE=EN.
方案二,抛物线型拱门的跨度 ON′=8m,拱高 P'E'=6m.其中,点 N′在 x 轴上,
P′E′⊥O′N′,OE′=E′N′.
要在拱门中设置高为3m的矩形框架,其面积越大越好(框架的粗细忽略不计).方案一中,矩形框
架ABCD的面积记为S ,点A、D在抛物线上,边BC在ON上;方案二中,矩形框架A'B'C′D'的面积
1
记为S ,点A',D'在抛物线上,边B'C'在ON'上.现知,小华已正确求出方案二中,当A'B'=3m时,,
2
请你根据以上提供的相关信息,解答下列问题:
第6页(共27页)(1)求方案一中抛物线的函数表达式;
(2)在方案一中,当AB=3m时,求矩形框架ABCD的面积S 并比较S ,S 的大小.
1 1 2
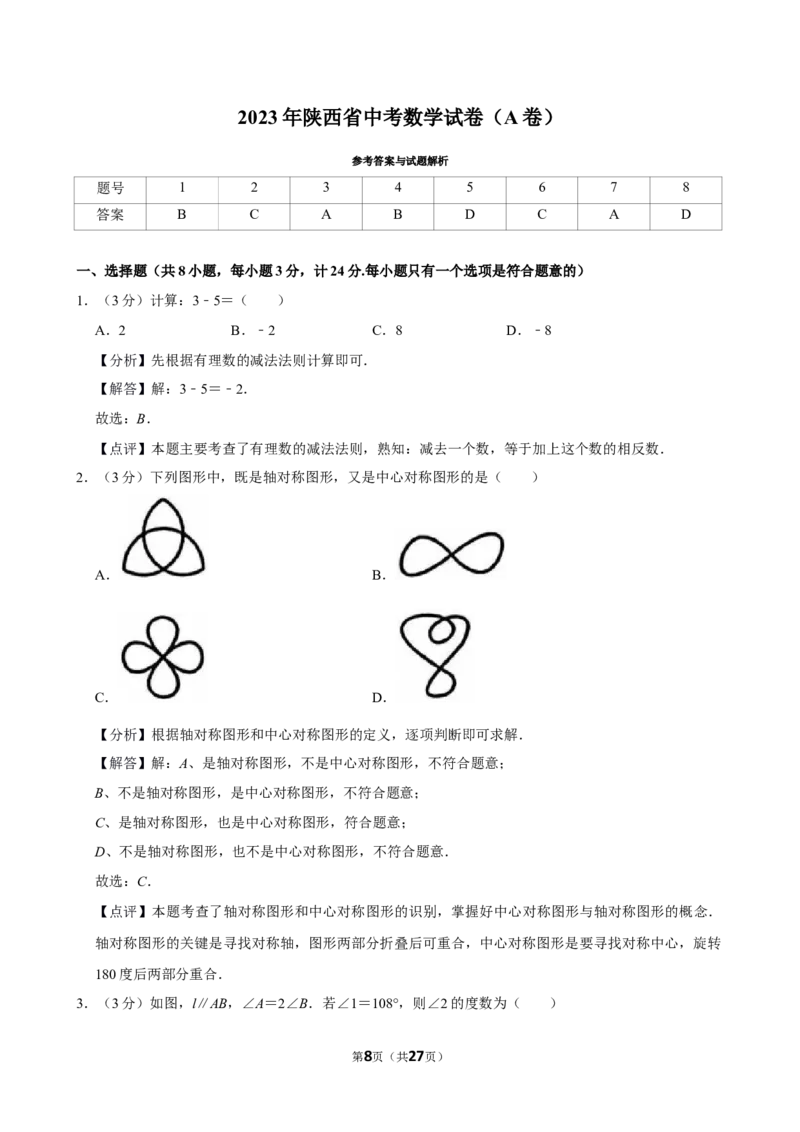
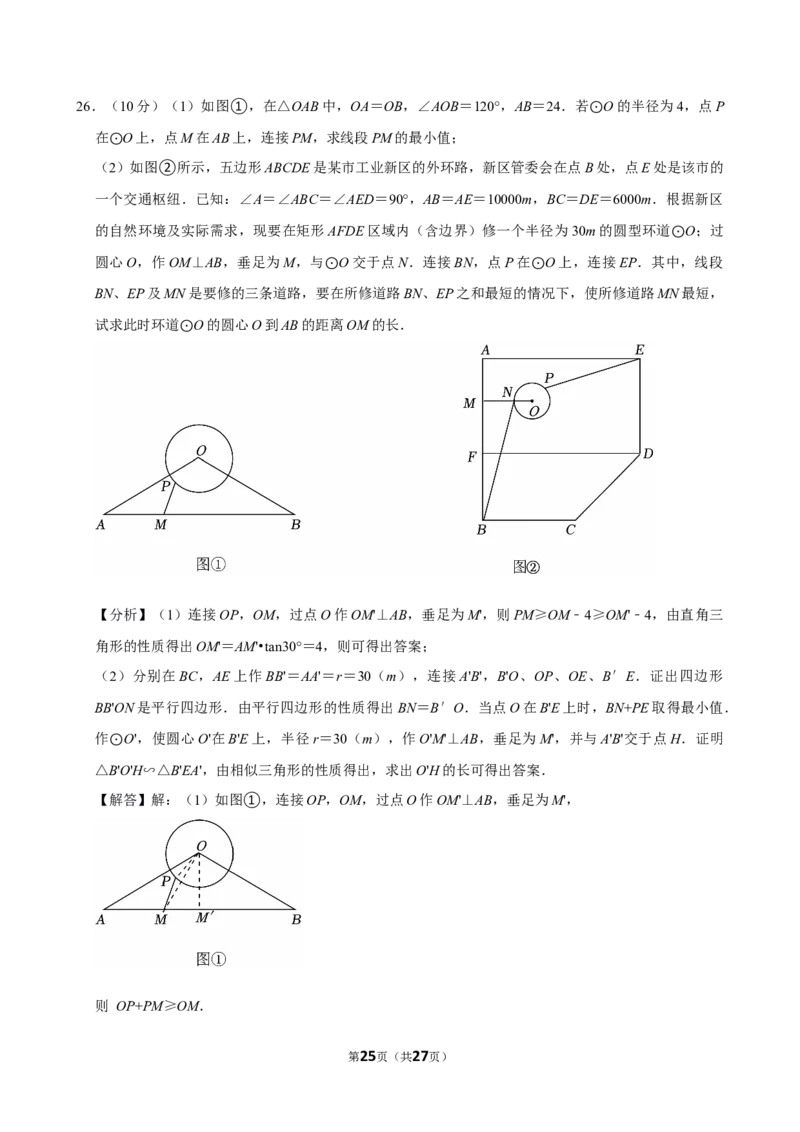
26.(10分)(1)如图①,在△OAB中,OA=OB,∠AOB=120°,AB=24.若 O的半径为4,点P
在 O上,点M在AB上,连接PM,求线段PM的最小值; ⊙
(⊙2)如图②所示,五边形ABCDE是某市工业新区的外环路,新区管委会在点B处,点E处是该市的
一个交通枢纽.已知:∠A=∠ABC=∠AED=90°,AB=AE=10000m,BC=DE=6000m.根据新区
的自然环境及实际需求,现要在矩形AFDE区域内(含边界)修一个半径为30m的圆型环道 O;过
圆心O,作OM⊥AB,垂足为M,与 O交于点N.连接BN,点P在 O上,连接EP.其中⊙,线段
BN、EP及MN是要修的三条道路,要⊙在所修道路BN、EP之和最短的情⊙况下,使所修道路MN最短,
试求此时环道 O的圆心O到AB的距离OM的长.
⊙
第7页(共27页)2023年陕西省中考数学试卷(A卷)
参考答案与试题解析
题号 1 2 3 4 5 6 7 8
答案 B C A B D C A D
一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题意的)
1.(3分)计算:3﹣5=( )
A.2 B.﹣2 C.8 D.﹣8
【分析】先根据有理数的减法法则计算即可.
【解答】解:3﹣5=﹣2.
故选:B.
【点评】本题主要考查了有理数的减法法则,熟知:减去一个数,等于加上这个数的相反数.
2.(3分)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形和中心对称图形的定义,逐项判断即可求解.
【解答】解:A、是轴对称图形,不是中心对称图形,不符合题意;
B、不是轴对称图形,是中心对称图形,不符合题意;
C、是轴对称图形,也是中心对称图形,符合题意;
D、不是轴对称图形,也不是中心对称图形,不符合题意.
故选:C.
【点评】本题考查了轴对称图形和中心对称图形的识别,掌握好中心对称图形与轴对称图形的概念.
轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转
180度后两部分重合.
3.(3分)如图,l∥AB,∠A=2∠B.若∠1=108°,则∠2的度数为( )
第8页(共27页)A.36° B.46° C.72° D.82°
【分析】由对顶角相等可得∠3=∠1=108°,再由平行线的性质可求得∠A=72°,∠B=∠2,结合已
知条件可求得∠B,即可求解.
【解答】解:如图,
∵∠1=108°,
∴∠3=∠1=108°,
∵l∥AB,
∴∠3+∠A=180°,∠2=∠B,
∴∠A=180°﹣∠3=72°,
∵∠A=2∠B,
∴∠B=36°,
∴∠2=36°.
故选:A.
【点评】本题主要考查平行线的性质,解答的关键是熟记平行线的性质:两直线平行,内错角相等;
两直线平行,同旁内角互补.
4.(3分)计算:( )
A.3x4y5 B.﹣3x4y5 C.3x3y6 D.﹣3x3y6
【分析】利用单项式乘单项式的法则进行运算即可.
【解答】解:
=6×()x1+3y2+3
=﹣3x4y5.
故选:B.
第9页(共27页)【点评】本题主要考查单项式乘单项式,解答的关键是对相应的运算法则的掌握.
5.(3分)在同一平面直角坐标系中,函数y=ax和y=x+a(a为常数,a<0)的图象可能是( )
A.
B.
C.
D.
【分析】根据正比例函数和一次函数的性质,可以得到函数y=ax和y=x+a的图象经过哪几个象限,
本题得以解决.
【解答】解:∵a<0,
∴函数y=ax是经过原点的直线,经过第二、四象限,
函数y=x+a是经过第一、三、四象限的直线,
故选:D.
第10页(共27页)【点评】本题考查正比例函数的图象、一次函数的图象,解答本题的关键是明确题意,利用正比例函
数和一次函数的性质解答.
6.(3分)如图,DE是△ABC的中位线,点F在DB上,DF=2BF.连接EF并延长,与CB的延长线相
交于点M.若BC=6,则线段CM的长为( )
A. B.7 C. D.8
【分析】根据三角形中中位线定理证得DE∥BC,求出DE,进而证得△DEF∽BMF,根据相似三角形
的性质求出BM,即可求出结论.
【解答】解:∵DE是△ABC的中位线,
∴DE∥BC,DEBC6=3,
∴△DEF∽△BMF,
∴2,
∴BM,
CM=BC+BM.
故选:C.
【点评】本题主要考查了三角形中位线定理,相似三角形的性质和判定,熟练掌握三角形中位线定理
和相似三角形的判定方法是解决问题的关键.
7.(3分)陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一.图②是从正面看到的一个
“老碗”(图①)的形状示意图.是 O的一部分,D是的中点,连接OD,与弦AB交于点C,连接
OA,OB.已知AB=24cm,碗深CD=⊙8cm,则 O的半径OA为( )
⊙
第11页(共27页)A.13cm B.16cm C.17cm D.26cm
【分析】首先利用垂径定理的推论得出OD⊥AB,AC=BCAB=12cm,再设 O的半径OA为R cm,
则OC=(R﹣8)cm.在Rt△OAC中根据勾股定理列出方程R2=122+(R﹣8⊙)2,求出R即可.
【解答】解:∵是 O的一部分,D是的中点,AB=24cm,
∴OD⊥AB,AC=B⊙CAB=12cm.
设 O的半径OA为R cm,则OC=OD﹣CD=(R﹣8)cm.
在⊙Rt△OAC中,∵∠OCA=90°,
∴OA2=AC2+OC2,
∴R2=122+(R﹣8)2,
∴R=13,
即 O的半径OA为13cm.
故⊙选:A.
【点评】本题考查了垂径定理、勾股定理的应用,设 O的半径OA为R cm,列出关于R的方程是解
题的关键. ⊙
8.(3分)在平面直角坐标系中,二次函数y=x2+mx+m2﹣m(m为常数)的图象经过点(0,6),其对
称轴在y轴左侧,则该二次函数有( )
A.最大值5 B.最大值 C.最小值5 D.最小值
【分析】将(0,6)代入二次函数解析式,进而得出m的值,再利用对称轴在y轴左侧,得出m=3,
再利用公式法求出二次函数最值.
【解答】解:由题意可得:6=m2﹣m,
解得:m =3,m =﹣2,
1 2
∵二次函数y=x2+mx+m2﹣m,对称轴在y轴左侧,
∴m>0,
∴m=3,
∴y=x2+3x+6,
∴二次函数有最小值为:.
第12页(共27页)故选:D.
【点评】此题主要考查了二次函数的性质以及二次函数的最值,正确得出m的值是解题关键.
二、填空题(共5小题,每小题3分,计15分)
9.(3分)如图,在数轴上,点A表示,点B与点A位于原点的两侧,且与原点的距离相等.则点B表
示的数是 .
【分析】根据原点左边的数是负数,由绝对值的定义可得答案.
【解答】解:由题意得:点B表示的数是.
故答案为:.
【点评】此题考查了数轴,绝对值,掌握绝对值的意义是解本题的关键.
10.(3分)如图,正八边形的边长为2,对角线AB、CD相交于点E.则线段BE的长为 2 .
【分析】根据正八边形的性质得出四边形CEGF是矩形,△ACE、△BFG是等腰直角三角形,AC=CF
=FB=EG=2,再根据矩形的性质以及直角三角形的边角关系求出AE,GE,BG即可.
【解答】解:如图,过点F作FG⊥AB于G,由题意可知,四边形CEGF是矩形,△ACE、△BFG是
等腰直角三角形,AC=CF=FB=EG=2,
在Rt△ACE中,AC=2,AE=CE,
∴AE=CEAC,
同理BG,
∴BE=EG+BG=2,
故答案为:2.
第13页(共27页)【点评】本题考查正多边形和圆,掌握正八边形的性质以及直角三角形的边角关系是正确解答的前提.
11.(3分)点E是菱形ABCD的对称中心,∠B=56°,连接AE,则∠BAE的度数为 62 ° .
【分析】连接BE,根据中心对称图形的定义得出点E是菱形ABCD的两对角线的交点,根据菱形的性
质得出AE⊥BE,∠ABE∠ABC=28°,那么∠BAE=90°﹣∠ABE=62°.
【解答】解:如图,连接BE,
∵点E是菱形ABCD的对称中心,∠ABC=56°,
∴点E是菱形ABCD的两对角线的交点,
∴AE⊥BE,∠ABE∠ABC=28°,
∴∠BAE=90°﹣∠ABE=62°.
故答案为:62°.
【点评】本题考查了菱形的性质,菱形是中心对称图形,两对角线的交点是对称中心,掌握菱形的两
条对角线互相垂直平分,并且每一条对角线平分一组对角是解题的关键.
12.(3分)如图,在矩形OABC和正方形CDEF中,点A在y轴正半轴上,点C,F均在x轴正半轴上,
点D在边BC上,BC=2CD,AB=3.若点B,E在同一个反比例函数的图象上,则这个反比例函数的
表达式是 y .
【分析】根据矩形的性质得到OC=AB=3,根据正方形的性质得到CD=CF=EF,设CD=m,BC=
2m,得到B(3,2m),E(3+m,m),设反比例函数的表达式为y,列方程即可得到结论.
【解答】解:∵四边形OABC是矩形,
∴OC=AB=3,
∵四边形CDEF是正方形,
第14页(共27页)∴CD=CF=EF,
∵BC=2CD,
∴设CD=m,BC=2m,
∴B(3,2m),E(3+m,m),
设反比例函数的表达式为y,
∴3×2m=(3+m)•m,
解得m=3或m=0(不合题意舍去),
∴B(3,6),
∴k=3×6=18,
∴这个反比例函数的表达式是y,
故答案为:y.
【点评】本题考查了待定系数法求反比例函数的解析式,反比例函数图象上点的坐标特征:反比例函
数y(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
13.(3分)如图,在矩形ABCD中,AB=3,BC=4.点E在边AD上,且ED=3,M、N分别是边
AB、BC上的动点,且BM=BN,P是线段CE上的动点,连接PM,PN.若PM+PN=4.则线段PC
的长为 2 .
【分析】过点P分别作PF⊥DC,PG⊥BC,PH⊥AB,由题意知PG=PF,再说明PM与PH重合,PN
与PG重合,得出四边形MPNB为正方形,即可求出PC=2.
【解答】解:如图,过点P分别作PF⊥DC,PG⊥BC,PH⊥AB,
第15页(共27页)∵DE=CD=3,∠D=90°,
∴∠ECD=45°,
∴∠ECB=45°,
∴PG=PF,
∵PM≥PH,PN≥PG,
∴PM+PN≥PH+PG=4,
∵PM+PN=4,
∴PM与PH重合,PN与PG重合,
∴四边形PHBG为正方形,
∴PH=PG=2,
∴PC=2.
故答案为:2.
【点评】本题考查矩形的性质和等腰直角三角形的性质,作出适当的辅助线是解题关键.
三、解答题(共13小题,计81分.解答应写出过程)
14.(5分)解不等式:x.
【分析】去分母,移项,合并同类项,系数化成1即可.
【解答】解:x,
去分母,得3x﹣5>4x,
移项,得3x﹣4x>5,
合并同类项,得﹣x>5,
不等式的两边都除以﹣1,得x<﹣5.
【点评】本题考查了解一元一次不等式,能正确根据不等式的性质进行变形是解此题的关键.
15.(5分)计算:.
【分析】直接利用二次根式的乘法运算法则以及负整数指数幂的性质、绝对值的性质分别化简,进而
得出答案.
【解答】解:原式=﹣57+|﹣8|
=﹣51.
第16页(共27页)【点评】此题主要考查了实数的运算,正确化简各数是解题关键.
16.(5分)化简:().
【分析】先算括号里的运算,把除法转为乘法,最后约分即可.
【解答】解:()
.
【点评】本题主要考查分式的混合运算,解答的关键是对相应的运算法则的掌握.
17.(5分)如图.已知锐角△ABC,∠B=48°,请用尺规作图法,在△ABC内部求作一点P.使PB=
PC.且∠PBC=24°.(保留作图痕迹,不写作法)
【分析】先作∠ABC的平分线BD,再作BC的垂直平分线l,直线l交BD于P点,则P点满足条件.
【解答】解:如图,点P即为所求.
【点评】本题考查了作图﹣复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图
形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了等腰三角形的性质.
18.(5分)如图,在△ABC中,∠B=50°,∠C=20°.过点A作AE⊥BC,垂足为E,延长EA至点
D.使AD=AC.在边AC上截取AF=AB,连接DF.求证:DF=CB.
【分析】利用三角形内角和定理得∠CAB的度数,再根据全等三角形的判定与性质可得结论.
【解答】证明:在△ABC 中,∠B=50°,∠C=20°,
第17页(共27页)∴∠CAB=180°﹣∠B﹣∠C=110°.
∵AE⊥BC.
∴∠AEC=90°.
∴∠DAF=∠AEC+∠C=110°,
∴∠DAF=∠CAB.
在△DAF和△CAB中,
,
∴△DAF≌△CAB(SAS).
∴DF=CB.
【点评】此题考查的是全等三角形的判定与性质,掌握其性质定理是解决此题的关键.
19.(5分)一个不透明的袋子中装有四个小球,这四个小球上各标有一个数字,分别是 1,1,2,3.
这些小球除标有的数字外都相同.
(1)从袋中随机摸出一个小球,则摸出的这个小球上标有的数字是1的概率为 ;
(2)先从袋中随机摸出一个小球,记下小球上标有的数字后,放回,摇匀,再从袋中随机摸出一个小
球,记下小球上标有的数字,请利用画树状图或列表的方法、求摸出的这两个小球上标有的数字之积
是偶数的概率.
【分析】(1)根据题意和题目中的数据,可以计算出从袋中机摸出一个小球,则摸出的这个小球上标
有的数字是1的概率;
(2)根据题意可以画出相应的树状图,然后即可求出摸出的这两个小球上标有的数字之积是偶数的概
率.
【解答】解:(1)由题意可得,
从袋中机摸出一个小球,则摸出的这个小球上标有的数字是1的概率为,
故答案为:;
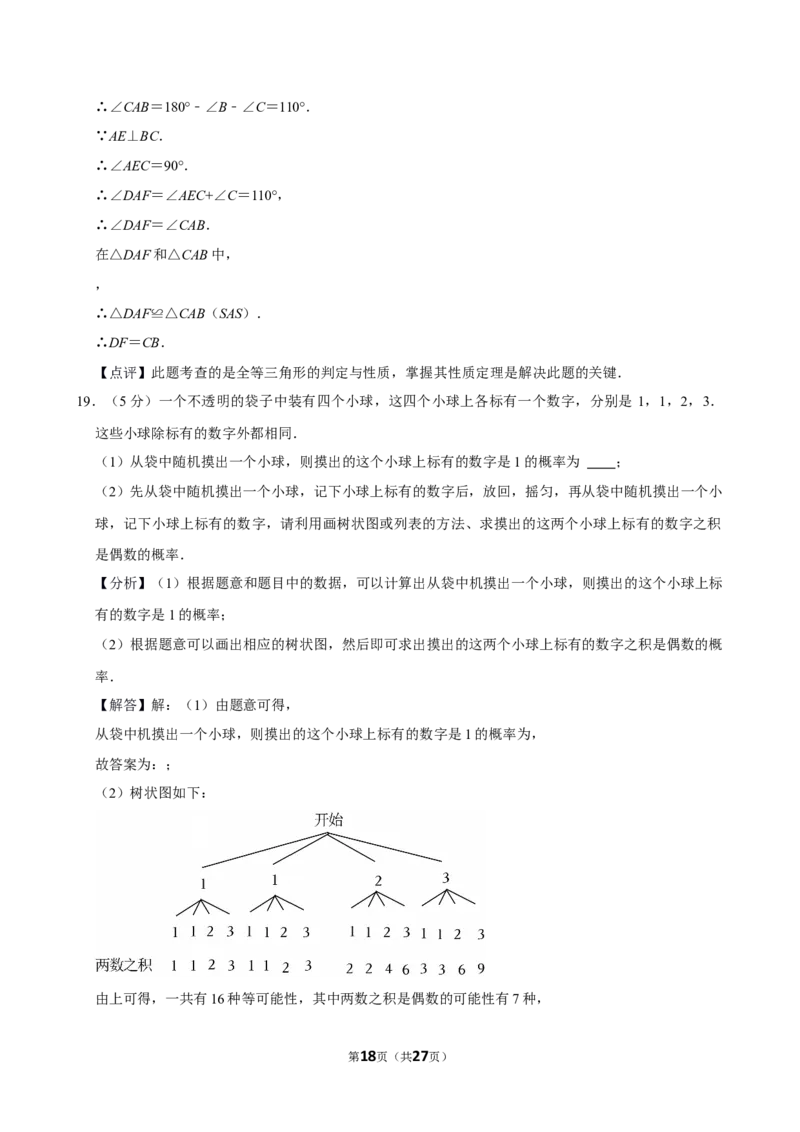
(2)树状图如下:
由上可得,一共有16种等可能性,其中两数之积是偶数的可能性有7种,
第18页(共27页)∴摸出的这两个小球上标有的数字之积是偶数的概率.
【点评】本题考查列表法与树状图法、概率公式,解答本题的关键是明确题意,画出相应的树状图,
求出相应的概率.
20.(5分)小红在一家文具店买了一种大笔记本 4个和一种小笔记本6个,共用了62元.已知她买的
这种大笔记本的单价比这种小笔记本的单价多3元,求该文具店中这种大笔记本的单价.
【分析】设该文具店中这种大笔记本的单价是x元,根据买了一种大笔记本4个和一种小笔记本6个,
共用了62元,得4x+6(x﹣3)=62,即可解得答案.
【解答】解:设该文具店中这种大笔记本的单价是x元,则小笔记本的单价是(x﹣3)元,
∵买了一种大笔记本4个和一种小笔记本6个,共用了62元,
∴4x+6(x﹣3)=62,
解得:x=8;
答:该文具店中这种大笔记本的单价为8元.
【点评】本题考查一元一次方程的应用,解题的关键是读懂题意,找到等量关系,列出方程解决问题.
21.(6分)一天晚上,小明和爸爸带着测角仪和皮尺去公园测量一景观灯(灯杆底部不可到达)的高
AB.如图所示,当小明爸爸站在点D处时,他在该景观灯照射下的影子长为DF,测得DF=2.4m;当
小明站在爸爸影子的顶端F处时,测得点A的仰角 为26.6°.已知爸爸的身高CD=1.8m,小明眼睛
到地面的距离EF=1.6m,点F、D、B在同一条直线α上,EF⊥FB,CD⊥FB,AB⊥FB.求该景观灯的
高AB.(参考数据:sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50)
【分析】过点E作EH⊥AB,垂足为H,根据题意可得:EH=FB,EF=BH=1.6m,然后设EH=FB=
x m,在Rt△AEH中,利用锐角三角函数的定义求出AH的长,从而求出AB的长,再根据垂直定义可
得∠CDF=∠ABF=90°,从而证明A字模型相似三角形△CDF∽△ABF,最后利用相似三角形的性质
可得ABx,从而列出关于x的方程,进行计算即可解答.
【解答】解:过点E作EH⊥AB,垂足为H,
第19页(共27页)由题意得:EH=FB,EF=BH=1.6m,
设EH=FB=x m,
在Rt△AEH中,∠AEH=26.6°,
∴AH=EH•tan26.6°≈0.5x(m),
∴AB=AH+BH=(0.5x+1.6)m,
∵CD⊥FB,AB⊥FB,
∴∠CDF=∠ABF=90°,
∵∠CFD=∠AFB,
∴△CDF∽△ABF,
∴,
∴,
∴ABx,
∴x=0.5x+1.6,
解得:x=6.4,
∴ABx=4.8(m),
∴该景观灯的高AB约为4.8m.
【点评】本题考查了解直角三角形的应用﹣仰角俯角问题,相似三角形的应用,平行投影,根据题目
的已知条件并结合图形添加适当的辅助线是解题的关键.
22.(7分)经验表明,树在一定的成长阶段,其胸径(树的主干在地面以上1.3m处的直径)越大,树
就越高.通过对某种树进行测量研究,发现这种树的树高y(m)是其胸径x(m)的一次函数.已知
这种树的胸径为0.2m时,树高为20m;这种树的胸径为0.28m时,树高为22m.
(1)求y与x之间的函数表达式;
(2)当这种树的胸径为0.3m时,其树高是多少?
【分析】(1)设y=kx+b(k≠0),利用待定系数法解答即可;
(2)把x=0.3代入(1)的结论解答即可.
【解答】解:(1)设y=kx+b(k≠0),
根据题意,得,
第20页(共27页)解之,得,
∴y=25x+15;
(2)当x=0.3时,y=25×0.3+15=22.5(m).
∴当这种树的胸径为0.3m时,其树高为22.5m.
【点评】此题考查一次函数的实际运用,掌握待定系数法求函数解析式的方法与步骤是解决问题的关
键.
23.(7分)某校数学兴趣小组的同学们从“校园农场”中随机抽取了 20棵西红柿植株,并统计了每棵
植株上小西红柿的个数.其数据如下:28,36,37,39,42,45,46,47,48,50,54,54,54,
54,55,60,62,62,63,64.通过对以上数据的分析整理,绘制了统计图表:
分组 频数 组内小西红柿的总个数
25≤x<35 1 28
35≤x<45 n 154
45≤x<55 9 452
55≤x<65 6 366
根据以上信息,解答下列问题:
(1)补全频数分布直方图:这20个数据的众数是 5 4 ;
(2)求这20个数据的平均数;
(3)“校园农场”中共有300棵这种西红柿植株,请估计这300棵西红柿植株上小西红柿的总个数.
【分析】(1)用总数减去其它三组的频数可得n的值,进而补全频数分布直方图,然后根据众数的定
义解答即可;
(2)根据算术平均数的计算公式解答即可;
(3)用300乘(2)的结论可得答案.
【解答】解:(1)由题意得,n=20﹣1﹣9﹣6=4,
补全频数分布直方图如下
第21页(共27页)这20个数据中,54出现的次数最多,故众数为54.
故答案为:54;
(2).
∴这20个数据的平均数是50;
(3)所求总个数:50×300=15000(个).
∴估计这300棵西红柿植株上小西红柿的总个数是15000个.
【点评】本题主要考查了频数分布直方图、频数分布表,用样本估计总体,众数以及加权平均数,解
决此题的关键是明确频率=频数÷总数.
24.(8分)如图,△ABC内接于 O,∠BAC=45°,过点B作BC的垂线,交 O于点D,并与CA的
延长线交于点E,作BF⊥AC,垂⊙足为M,交 O于点F. ⊙
(1)求证:BD=BC; ⊙
(2)若 O的半径r=3,BE=6,求线段BF的长.
⊙
【分析】(1)如图,连接 DC,根据圆周角定理得到∠BDC=∠BAC=45°,求得∠BCD=90°﹣
∠BDC=45°,根据等腰三角形的判定定理即可得到结论;
(2)如图,根据圆周角定理得到CD为 O的直径,求得CD=2r=6.根据勾股定理得到EC3,根据
相似三角形的判定和性质定理即可得到结⊙论.
【解答】(1)证明:如图,连接DC,
第22页(共27页)则∠BDC=∠BAC=45°,
∵BD⊥BC,
∴∠DBC=90°,
∴∠BCD=90°﹣∠BDC=45°,
∴∠BCD=∠BDC.
∴BD=BC;
(2)解:如图,∵∠DBC=90°,
∴CD为 O的直径,
∴CD=2⊙r=6.
∴BC=CD•sin3,
∴EC3,
∵BF⊥AC,
∴∠BMC=∠EBC=90°,∠BCM=∠BCM,
∴△BCM∽△ECB.
∴,
∴BM2,CM,
连接CF,则∠F=∠BDC=45°,∠MCF=45°,
∴MF=MC,
∴BF=BM+MF=2.
【点评】本题考查了三角形的外接圆与外心,圆周角定理,等腰直角三角形的判定和性质,相似三角
形的判定和性质,正确地作出辅助线是解题的关键.
25.(8分)某校想将新建图书楼的正门设计为一个抛物线型拱门,并要求所设计的拱门的跨度与拱高之
积为48m2,还要兼顾美观、大方,和谐、通畅等因素,设计部门按要求给出了两个设计方案.现把这
两个方案中的拱门图形放入平面直角坐标系中,如图所示:
方案一,抛物线型拱门的跨度ON=12m,拱高PE=4m.其中,点N在x轴上,PE⊥ON,OE=EN.
第23页(共27页)方案二,抛物线型拱门的跨度 ON′=8m,拱高 P'E'=6m.其中,点 N′在 x 轴上,
P′E′⊥O′N′,OE′=E′N′.
要在拱门中设置高为3m的矩形框架,其面积越大越好(框架的粗细忽略不计).方案一中,矩形框
架ABCD的面积记为S ,点A、D在抛物线上,边BC在ON上;方案二中,矩形框架A'B'C′D'的面积
1
记为S ,点A',D'在抛物线上,边B'C'在ON'上.现知,小华已正确求出方案二中,当A'B'=3m时,,
2
请你根据以上提供的相关信息,解答下列问题:
(1)求方案一中抛物线的函数表达式;
(2)在方案一中,当AB=3m时,求矩形框架ABCD的面积S 并比较S ,S 的大小.
1 1 2
【分析】(1)由题意知抛物线的顶点P(6,4),设顶点式用待定系数法可得方案一中抛物线的函数
表达式为yx2x;
(2)令y=3可得x=3或x=9,故BC=6(m),S =AB•BC=18(m2);再比较S ,S 的大小即可.
1 1 2
【解答】解:(1)由题意知,方案一中抛物线的顶点P(6,4),
设抛物线的函数表达式为y=a(x﹣6)2+4,
把O(0,0)代入得:0=a(0﹣6)2+4,
解得:a,
∴y(x﹣6)2+4x2x;
∴方案一中抛物线的函数表达式为yx2x;
(2)在yx2x中,令y=3得:3x2x;
解得x=3或x=9,
∴BC=9﹣3=6(m),
∴S =AB•BC=3×6=18(m2);
1
∵18>12,
∴S >S .
1 2
【点评】本题考查二次函数的应用,解题的关键是读懂题意,求出函数关系式.
第24页(共27页)26.(10分)(1)如图①,在△OAB中,OA=OB,∠AOB=120°,AB=24.若 O的半径为4,点P
在 O上,点M在AB上,连接PM,求线段PM的最小值; ⊙
(⊙2)如图②所示,五边形ABCDE是某市工业新区的外环路,新区管委会在点B处,点E处是该市的
一个交通枢纽.已知:∠A=∠ABC=∠AED=90°,AB=AE=10000m,BC=DE=6000m.根据新区
的自然环境及实际需求,现要在矩形AFDE区域内(含边界)修一个半径为30m的圆型环道 O;过
圆心O,作OM⊥AB,垂足为M,与 O交于点N.连接BN,点P在 O上,连接EP.其中⊙,线段
BN、EP及MN是要修的三条道路,要⊙在所修道路BN、EP之和最短的情⊙况下,使所修道路MN最短,
试求此时环道 O的圆心O到AB的距离OM的长.
⊙
【分析】(1)连接OP,OM,过点O作OM'⊥AB,垂足为M',则PM≥OM﹣4≥OM'﹣4,由直角三
角形的性质得出OM'=AM'•tan30°=4,则可得出答案;
(2)分别在BC,AE上作BB'=AA'=r=30(m),连接A'B',B'O、OP、OE、B′E.证出四边形
BB'ON是平行四边形.由平行四边形的性质得出BN=B′O.当点O在B'E上时,BN+PE取得最小值.
作 O',使圆心O'在B'E上,半径r=30(m),作O'M'⊥AB,垂足为M',并与A'B'交于点H.证明
△B⊙'O'H∽△B'EA',由相似三角形的性质得出,求出O'H的长可得出答案.
【解答】解:(1)如图①,连接OP,OM,过点O作OM'⊥AB,垂足为M',
则 OP+PM≥OM.
第25页(共27页)∵ O半径为4,
∴⊙PM≥OM﹣4≥OM'﹣4,
∵OA=OB.∠AOB=120°,
∴∠A=30°,
∴OM'=AM'•tan30°=12tan30°=4,
∴PM≥OM'﹣4=44,
∴线段PM的最小值为44;
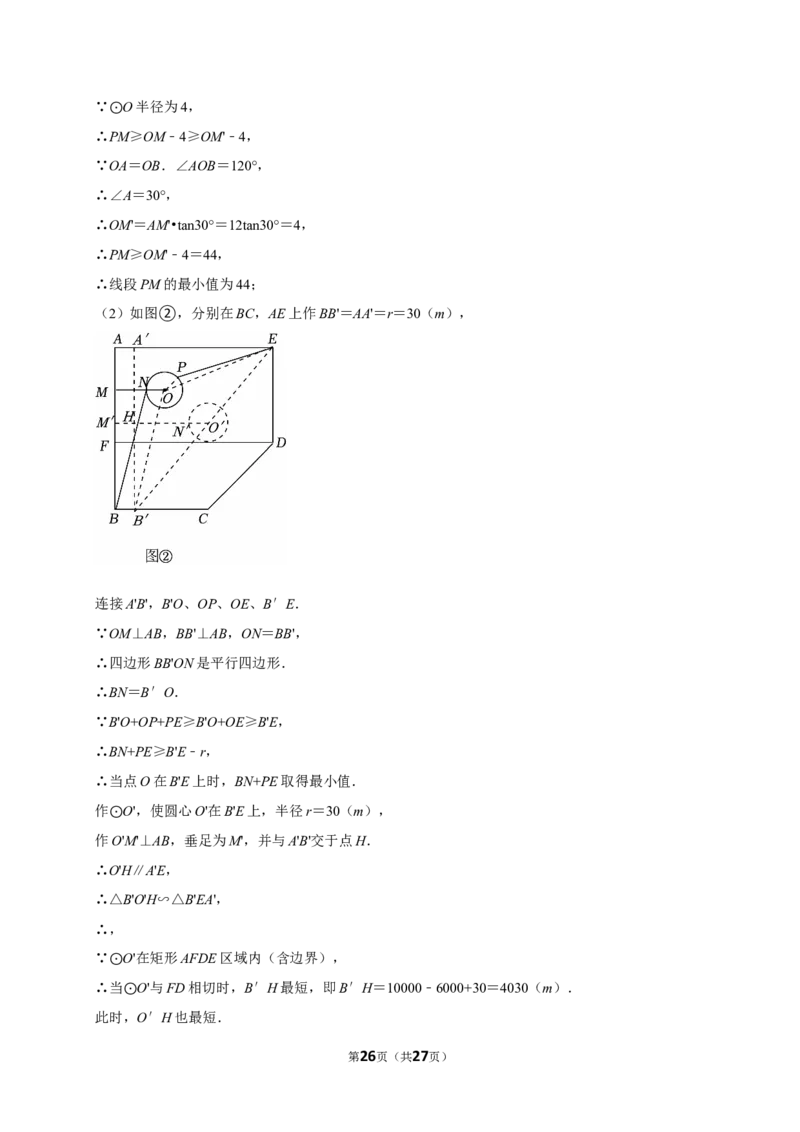
(2)如图②,分别在BC,AE上作BB'=AA'=r=30(m),
连接A'B',B'O、OP、OE、B′E.
∵OM⊥AB,BB'⊥AB,ON=BB',
∴四边形BB'ON是平行四边形.
∴BN=B′O.
∵B'O+OP+PE≥B'O+OE≥B'E,
∴BN+PE≥B'E﹣r,
∴当点O在B'E上时,BN+PE取得最小值.
作 O',使圆心O'在B'E上,半径r=30(m),
作⊙O'M'⊥AB,垂足为M',并与A'B'交于点H.
∴O'H∥A'E,
∴△B'O'H∽△B'EA',
∴,
∵ O'在矩形AFDE区域内(含边界),
∴⊙当 O'与FD相切时,B′H最短,即B′H=10000﹣6000+30=4030(m).
此时⊙,O′H也最短.
第26页(共27页)∵M'N'=O'H,
∴M'N'也最短.
∴O'H4017.91(m),
∴O'M'=O'H+30=4047.91(m),
∴此时环道 O的圆心O到AB的距离OM的长为4047.91m.
【点评】本⊙题是圆的综合题,考查了等腰三角形的性质,切线的性质,平行四边形的判定与性质,相
似三角形的判定与性质,解直角三角形,熟练掌握以上知识是解题的关键.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2025/1/12 21:58:29;用户:庞俊梅;邮箱:18715777852;学号:54801167
第27页(共27页)