数学（三）-2024年高考考前20天终极冲刺攻略_2024高考押题卷_62024学科网全系列_21学科网高考考前终极攻略_数学-2024年高考考前20天终极冲刺攻略

学学学科科科网网网（（（北北北京京京）））股股股份份份有有有限限限公公公司司司目 录 contents （三） 复数（选填题）…………………………………………………………………03 函数与导数（选填题）…………………………………………………………15 不等式（选填题）………………………………………………………………39 球（选填题） …………………………………………………………………53 数列、统计与概率（解答题）…………………………………………………71 学学学科科科网网网（（（北北北京京京）））股股股份份份有有有限限限公公公司司司复数（选填题） 年份 题号 知识点 考点 ①共轭复数的表示 2021年I卷 2 复数 ②复数的乘法运算 ①复数分式的化解 2021年II卷 1 复数 ②标准形式对应点所在象限 ①共轭复数的表示 2022年I卷 2 复数 ②复数的乘法运算 2022年II卷 2 复数 复数的乘法运算 2023年新高考 ①共轭复数的表示 2 复数 1 ②复数分式的化解 2023 年新高考 ①标准形式对应点所在象限 1 复数 2 ②复数的乘法运算 近三年，复数在选填中占据一个位置，考查的考点一般来说是： 1、复数的概念（①虚部的探究②复数相等求参及范围问题③复数的几何意义象限问题④复数的模及其应用） 2、复数的四则运算（①复数形式的加、减运算②复数模最值问题秒杀③复数形式的乘除法运算（分数形式 秒化解）④复数范围内解方程（结论）） 题干的设置一般来说在上述的两项考点中选其一项。复数需要认真分析，明确复数是一类重要的运算 对象，即一对有序实数，复数有三种表达形式，复数与复平面内的点一一对应，计算时注意虚部的正负以 及分式形式模长的快速求算，此类题目需要一定的基础和秒杀技巧便可轻松搞定。 复数在2024新高考新题型中的考查形式依然以选择或者填空为主，以考查基本概念和核心方法为主， 复数在选填中偏重于多选，抽象复数需要设一个标准格式参与求算，考生可适当留意常见的复数乘积组合 形式，切记复数不能比较大小. 3 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司一、虚部的探究 Ⅰ：虚数单位i 数i叫倣虚数单位，它的平方等于1，即i2 1． 注意：i是1的一个平方根，即方程x2 1的一个根，方程x2 1的另一个根是i； Ⅱ：复数的摡念 形如abi(a,bR)的数叫复数，记作：zabi(a,bR)； 其中：a叫复数的实部，b叫复数的虚部，i是虚数单位． Ⅲ：复数的分类（纯虚数及纯实数） 对于复数zabi (a,bR) 若b0，则abi为实数，若b0，则abi为虚数，若a0且b0，则abi为纯虚数．  实数 b0   分类如下：zabi (a,bR)  实数 b0    当a 0时为纯虚数    当a 0时为非纯虚数 Ⅳ：共轭复数： 当两个复数的实部相等，虚部互为相反数时，这两个复数叫做互为共轭复数．虚部不等于0的两个共 轭复数也叫做共轭虚数．通常记复数z的共轭复数为z． 形如：z abi z abi 二、复数相等求参及范围问题 Ⅰ：两个复数相等的定义：如果两个复数的实部和虚部分别相等，那么我们就说这两个复数相等．即： a c abi cdi bd 特别地：abi0ab0． ①根据复数 abi与 cdi相等的定义，可知在 ac,bd 两式中，只要有一个不成立，那么就有 abicdi（a，b,c,dR）． ②一般地，两个复数只能说相等或不相等，而不能比较大小如果两个复数都是实数，就可以比较大小；也 只有当两个复数全是实数时才能比较大小． Ⅱ：复数相等问题的解题策略 ①必须是复数的代数形式才可以根据实部与实部相等，虚部与虚部相等列方程组求解． ②根据复数相等的条件，将复数问题转化为实数问题． 4 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司③如果两个复数都是实数，可以比较大小，否则是不能比较大小的． 三、复数的几何意义象限问题 复数的几何意义 Ⅰ：复平面、实轴、虚轴： 如图所示，复数zabi(a,bR)可用点Z(a,b)表示，这个建立了直角坐标系来表示复数的平面叫做 复平面，也叫高斯平面，x轴叫做实轴，y轴叫做虚轴 注意：实轴上的点都表示实数．除了原点外，虚轴上的点都表示纯虚数． Ⅱ：复数集与复平面内点的对应关系 复数的几何表示法，每一个复数有复平面内唯一的一个点与之对应；反过来，复平面内的每一个点， 有唯一的一个复数和它对应．   故z abi a,b 四、复数的模及其应用 Ⅰ：复数的模 uuur uuur 设OZ abi(a,bR)，则向量OZ 的长度叫做复数zabi的模，记作|abi|． uuur |z||OZ| a2 b2 0 Ⅱ：计算模长的步骤： zabi 第一步：根据题干已知条件将复数化为标准形式 第二步：标出坐标形式（模长即为坐标到坐标原点的距离） 第三步：勾股定理 五：复数形式的加、减运算 Ⅰ：复数的加法、减法运算法则： 设z abi，z cdi（a,b,c,dR），我们规定： 1 2 z z (abi)(cdi)(ac)(bd)i 1 2 z z (ca)(d b)i 2 1 注意：复数加法中的规定是实部与实部相加，虚部与虚部相加，减法同样．很明显， 两个复数的和（差）仍然是一个复数，复数的加（减）法可以推广到多个复数相加（减）的情形． Ⅱ：复数的加法运算律： 交换律：z z z z 1 2 2 1 结合律：(z z )z z (z z ) 1 2 3 1 2 3 5 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司技巧：两个复数相加（减），就是把两个复数的实部相加（减），虚部相加（减）．复数的减法是加 法的逆运算．当多个复数相加（减）时，可将这些复数的所有实部相加（减），所有虚部相加（减）． 复数模最值问题秒杀 Ⅰ：工具 uuur uuuur 如果复数z 、z 分别对应于向量OP 、OP ，那么以OP、OP 为两边作平行四边形OPSP ，对角线OS 1 2 1 2 1 2 1 2 uuur uuuur 表示的向量OS就是z z 的和所对应的向量．对角线PP表示的向量PP 就是两个复数的差z z 所对应 1 2 2 1 2 1 1 2 的向量． uuuur uuuur uuuur uuuur 设复数z abi，z cdi，在复平面上所对应的向量为OZ 、OZ ，即OZ 、OZ 的坐标形式为 1 2 1 2 1 2 uuuur uuuur uuuur uuuur uuur OZ (a,b)，OZ (c,d) 以OZ 、OZ 为邻边作平行四边形OZ ZZ ，则对角线OZ 对应的向量是OZ ， 1 2 1 2 1 2 uuur uuuur uuuur uuuur uuuur 由于OZ OZ OZ (a,b)(c,d)(ac,bd)，所以OZ 和OZ 的和就是与复数(ac)(bd)i对 1 2 1 2 应的向量． Ⅱ秒杀：|z z |表示复平面内z ，z 对应的两点间的距离．利用此性质，可把复数模的问题转化为复平 1 2 1 2 面内两点间的距离问题，从而进行数形结合，把复数问题转化为几何图形问题求解． 复数形式的乘除法运算（分数形式秒化解） Ⅰ：乘法运算法则： 设z abi，z cdi（a,b,c,dR），我们规定： 1 2 z z (abi)(cdi)(acbd)(bcad)i 1 2 (abi)2 a2 b2 2abi(a,bR)． (abi)(abi)a2 b2(a,bR)． (1i)2 2i． Ⅱ：乘法运算律： （1）交换律：z z z z z z 1 2 3 1 2 3 （2）结合律：z z z z z z z 1 2 3 1 2 1 3 （3）分配律：z z z z z z z 1 2 3 1 2 1 3 Ⅲ：分式形式秒化解： 6 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司z abi (abi)(cdi) acbd bcad 1     i z cdi (cdi)(cdi) c2 d2 c2 d2 2 口诀：分子分别为（竖×相加，交叉之差） 1 1i 1i 常用公式需记忆① i；② i；③ i． i 1i 1i Ⅳ：①两个复数代数形式乘法的解题步骤： 第一步：首先按多项式的乘法展开． 第二步：再将i2换成1． 第三步：然后再讲行复数的加、减运簯． ②两个复数代数形式的除法运算步骤 第一步：首先将除式写为分式． 第二步：再将分子、分母同乘以分母的共轭复数． 第三步：然后将分子、分母分别进行乘法运算，并将其化为复数的代数形式． 复数范围内解方程（结论） 结论：当一元二次方程中0时，在复数范围内有两根且互为共轭复数． mni 形如：ax2 bxc0在0前提下两根分别为  然后利用韦达定理 mni 正规方法：已知一元二次方程根时，需要将根带入一元二次方程，利用复数相等求解参数 1i 典例1【2023新高考1卷】已知z  ，则zz （ ） 22i A. i B. i C. 0 D. 1 【答案】A 1i 1i1i 2i 1 1 【解析】因为z     i，所以z  i，即zz i． 22i 21i1i 4 2 2 故选：A． 典例2【2023新高考全国Ⅱ卷】 在复平面内， 13i3i 对应的点位于（ ）． A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 【答案】A 7 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司【解析】因为 13i3i38i3i2 68i， 则所求复数对应的点为 6,8 ，位于第一象限. 故选：A. 典例3【2022新高考全国Ⅰ卷】若i(1z)1，则zz （ ） A. 2 B. 1 C. 1 D. 2 【答案】D 1 i 【解析】由题设有1z   i，故z 1+i，故zz 1i1i2， i i2 故选：D 典例4【2022新高考全国Ⅱ卷】 (22i)(12i)（ ） A. 24i B. 24i C. 62i D. 62i 【答案】D 【解析】22i12i244i2i62i， 故选：D. 典例5【2021新高考全国Ⅰ卷】 已知z 2i，则zz i（ ） A. 62i B. 42i C. 62i D. 42i 【答案】C 【解析】因为 z 2i，故z 2i，故z  zi  2i22i=4+4i2i2i2 62i 故选：C. 预测1（2024·广东韶关·模拟预测）已知复数z ,z ，则下列命题正确的是（ ） 1 2 2 A．若 z  z ，则z z B．若z  z ，则 zz  z 1 2 1 2 1 2 1 2 1 1 C．若z 是非零复数，且z2 z z ，则z  z D．若z 是非零复数，则z  0 1 1 1 2 1 2 1 1 z 1 预测2（2024·浙江杭州·模拟预测）已知关于x的方程x2tx10(2t2)的两根为z 和z ，则（ ） 1 2 8 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司A．z z B．z z 1 1 2 1 2 z  z  C． z 1  z 2 D． 1  1  z z  2 2 预测3（2024·河南信阳·模拟预测）设z为复数（i为虚数单位），下列命题正确的有（ ） A．若(1i)zi，则 z 1 B．对任意复数z ，z ，有 z z  z  z 1 2 1 2 1 2 C．对任意复数z ，z ，有z z z z 1 2 1 2 1 2 D．在复平面内，若M {z| z2 2}，则集合M所构成区域的面积为6π 预测4（2024·湖南·模拟预测）已知i为虚数单位，下列说法正确的是（ ） 1i A．若复数z ，则z30 1 1i B．若 z  z ，则z2 z2 1 2 1 2 z z C．若z 0，则 1  1 2 z z 2 2 D．复数z在复平面内对应的点为Z，若 zi  zi 2，则点Z的轨迹是一个椭圆 预测5（2024·黑龙江·模拟预测）已知复数z 2i和z，则下列命题是真命题的有（ ） 0 A．若z满足 zz z z ，则其在复平面内对应点的轨迹是圆． 0 0 0 B．若z满足 zz  zz 4，则其在复平面内对应点的轨迹是椭圆． 0 0 C．若z满足 zz  zz 2，则其在复平面内对应点的轨迹是双曲线． 0 0 D．若z满足 zz z  zz ，则其在复平面内对应点的轨迹是抛物线． 0 0 0 押题1若z 、z 为复数，则（ ） 1 2 A． z z  z  z B．z z  z z 1 2 1 2 1 2 1 2 C．zn  z n nN D．z z  z  z 1 1 1 1 1 1 押题2已知z ,z 为复数，则（ ） 1 2 A．若z z z z ，则z z 为实数 1 2 1 2 1 2 B． z2z z  z  z z 1 1 2 1 2 1 9 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司C．若z2 z ，则z z2 1 2 1 2 D．若z2 z2，则复数z 在复平面内所对应的点位于坐标轴上 1 1 1 押题3已知非零复数z ，z ，其共轭复数分别为 z，z，则下列选项正确的是（ ） 1 2 1 2 A．z2 z 2 1 1 B．z z  z z 1 2 1 2 C．若 z 1 1，则 z 1的最小值为2 2 2 z z D． 1  1 z z 2 2 押题4若复数z满足zi1i，则下列命题正确的有（ ） A．z的虚部是－1 B． z  2 C．z2 2 D．z是方程x22x20的一个根 押题5设z1i，则（ ） A．zz  2 B．zzi0 C． z2 z 2 D． zzz2 名校预测 预测1：答案 BC 【详解】对于A项，若z 1i，z  2i，显然满足 z  z ，但z z ，故A项错误； 1 2 1 2 1 2 对于B项，设z abia,bR，则z abi，z z (abi)(abi)=a2b2，故|z z |a2b2而|z |2a2b2， 1 2 1 2 1 2 1 故B项正确； 对于C项，由z2 z z 可得：z2z z  z (z z )0，因z 是非零复数，故z z 0，即z  z，故C 1 1 2 1 1 2 1 1 2 1 1 2 1 2 项正确； 1 1 对于D项，当z i时，z 是非零复数，但 z  i ii0，故D项错误. 1 1 1 z i 1 故选：BC. 预测2：答案ABC 【详解】关于x的方程x2tx10(2t2)， 10 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司t 4t2i 则t240，x ， 2 t 4t2 t 4t2 不妨设z   i，z   i， 1 2 2 2 2 2 z z ，故A正确； 1 2 由韦达定理可得z z 1，故B正确； 1 2 2  t  2  4t2  z 1  z 2     2     2   1，故C正确；   Qzz 1， 1 2 2 z z2  t 4t2  t22 t 4t2  1  1 z2   i   i， z zz 1  2 2  2 2 2 1 2   则   z 1   t22  t 4t2 i，当t0时， z 1 R，此时 z 1    z 1  ，故D错误． z 2  2 2 z 2 z 2 z 2  故选：ABC． 预测3：答案BC i i1i 1i 【详解】对A：由(1i)zi，故z   ， 1i 1i1i 2  1 2  1 2 2 故 z       ，故A错误；  2  2 2 对B：设z abi a,bR、z cdic,dR， 1 2 则 z z  abicdi  acbdadbci  acbd2 adbc2 1 2  a2c22abcdb2d2a2d22abcdb2c2  a2c2b2d2a2d2b2c2 ， z  z  a2b2  c2d2   a2b2 c2d2  a2c2b2d2a2d2b2c2 ， 1 2 故 z z  z  z ，故B正确； 1 2 1 2 对C：设z abi a,bR、z cdic,dR， 1 2 有z z abicdiacbdadbci，则z z acbdadbci， 1 2 1 2 z z abicdiacbdadbci，故z z z z ，故C正确； 1 2 1 2 1 2 对D：设zxyi x,yR，则有x22y2 4， 集合M所构成区域为以2,0为圆心，半径为2的圆， 故S πr2 4π，故D错误. 故选：BC. 11 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司预测4：答案AC 1i (1i)2 【详解】对于A，因为z  i， 1i (1i)(1i) 所以z30 i30 i472 i2 1，故A正确； 对于B，令z 2i,z 1，满足 z  z ，但z2 z2，故B错误； 1 2 1 2 1 2 对于C，设z abi(a,bR),z cdi(c,dR且不同时为0)， 1 2 z abi (abi)(cdi) acbd(bcad)i 则 1    z cdi (cdi)(cdi) c2d2 2 1 1  (acbd)2(bcad)2   a2b2 c2d2 c2d2 c2d2 a2b2 z   1 ，故C正确； c2d2 z 2 对于D，设复数zxyi，则点Zx,y， 由 zi  zi 2，得 x2 y12  x2 y12 2， 则点Z到点0,1与点0,1的距离和为2， 故点Z的轨迹是线段，故D错误. 故选：AC. 预测5：答案AB 【详解】设zxyix,yR，由z 2i可得z 2i； 0 0 对于A，若z满足 zz z z 2i2i4，即可得 x2y1i 4，所以x22y12 16， 0 0 0 因此其在复平面内对应点的轨迹表示以2,1为圆心，半径为4的圆，即A正确； 对于B，若z满足 zz  zz 4，在复平面内表示点x,y到2,1与(2,-1)的距离之和为4， 0 0 又因为2,1与(2,-1)之间的距离为24，根据椭圆定义可得其在复平面内对应点的轨迹是椭圆，即B正确； 对于C，若z满足 zz  zz 2，在复平面内表示点x,y到2,1与(2,-1)的距离之差为2， 0 0 又因为2,1与(2,-1)之间的距离为22，不满足双曲线定义，即C错误； 对于D，若z满足 zz z  zz ，可化为 z4  zz ， 0 0 0 0 在复平面内表示点x,y到4,0与(2,-1)的距离相等，其在复平面内对应点的轨迹是直线，即D错误； 故选：AB 名师押题 押题1：答案BD 12 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司【详解】对于A选项，取z 1i，z 1i，则z z 2，z z 2， 1 2 1 2 1 2 所以，z 1i，z 1i，所以， z  z  2， 1 2 1 2 所以， z  z 2 2， z z 2，故 z z  z  z ，A错； 1 2 1 2 1 2 1 2 对于B选项，设z abi，z cdia,b,c,dR， 1 2 则z z acbdi，z z acbdi， 1 2 1 2 z abi，z cdi，则z z abcdi，所以，z z  z z ，B对； 1 2 1 2 1 2 1 2 对于C选项，不妨取z 1i，n2，则z2 1i2 2i， z  2， z 2 2， 1 1 1 1 所以，z2  z 2，故zn  z n nN ，C错； 1 1 1 1 对于D选项，设z abia,bR，则z abi，所以， z  z  a2b2 ， 1 1 1 1 所以，z z abiabia2b2  z  z ，D对. 1 1 1 1 故选：BD. 押题2：答案ABD 【详解】设z abi,z cdia,b,c,dR,z z z z  z z z z 2bi2dibd ，故 1 2 1 2 1 2 1 1 2 2 z z ac为实数，故A正确； z2z z  z z z   z  z z  z  z z ，故B正确； 1 2 1 1 2 1 1 2 1 1 2 1 2 1 令z 1i,z 2i，故z2 z ，但z  z2，故C错误； 1 2 1 2 1 2 若z2 z2，则(abi)2 (abi)2，故ab0，即a0或b0，故D正确. 1 1 故选：ABD 押题3：答案BD 【详解】设z abi，z cdia,b,c,dR， 1 2 对A，z2 a22abib2，z 2 abi2 a22abib2， 1 1 当a,b至少一个为0时，z2 z 2，当a,b均不等于0，z2  z 2，故A错误； 1 1 1 1 对B，z z acbdi，则z z acbdi， 1 2 1 2 而z z abicdiacbdi，故z z  z z ，故B正确； 1 2 1 2 1 2 对C，若 z 1 1，即c1di 1，即 c12 d2 1， 2 即c12d2 1，则c,d在复平面上表示的是以1,0为圆心，半径r1的圆， z 1的几何意义表示为点c,d到点1,0的距离，显然11202 41， 2 则点1,0在圆外，则圆心到定点1,0的距离d 2， 13 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司则点1,0与圆上点距离的最小值为dr211，故C错误； z z z abi abicdi acbdadbci 对D， 1  1 ， 1    ， z z z cdi c2d2 c2d2 2 2 2 z acbd  2 adbc 2  a2b2 c2d2 a2b2 1        ， z c2d2  c2d2   c2d22 c2d2 2 z a2b2 z z 而 1  ，故 1  1 ，故D正确； z c2d2 z z 2 2 2 故选：BD. 押题4：答案ABD 1i 【详解】zi1iz 1i，则 z  2，故A，B正确； i z2 (1i)2 2i，故C错误； 而(1i)22(1i)20成立，故D正确. 故选：ABD. 押题5：答案AB 【详解】由z1i可得z1i， 所以zz1i1i1i2 2，即A正确； 可得zzi1i1ii1iii2 0，即B正确； z2 1212 2，z 2 1i2 12ii2 2i，显然 z2 z 2 错误，即C错误； zz1i1i2i，而 z21i21i1i ，所以D错误. 故选：AB 14 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司函数与导数（选填题） 年份 题号 知识点 考点 7 函数与导数 函数切线问题 2021年I卷 15 函数与导数 函数最值问题 8 函数 函数奇偶性 ①抽象函数 2021年II卷 14 函数与导数 ②函数奇偶性 16 函数与导数 函数切线问题 ①三次函数的极值问题 ②三次函数的零点问题 10 函数与导数 ③三次函数的切线问题 2022年I卷 ④三次函数的对称中心问题 ①抽象函数问题 12 函数与导数 ②函数的奇偶性 8 函数 抽象函数问题 2022年II卷 14 函数与导数 函数切线问题 2023年新高考 11 函数 抽象函数问题 1 2023 年新高考 6 函数与导数 已知函数单调性求参数问题 2 11 函数与导数 函数极值问题 近三年，函数在选填中占据两个位置，考查的考点一般来说是： 1、函数的单调性与奇偶性（①抽象函数具体化②常见的结论(函数性质)包括③根据函数奇偶性的规律④判 定抽象函数的奇偶性⑤函数单调性与奇偶性综合求不等式范围问题） 2、函数的对称性与周期性（①函数周期性的妙解②分段函数的类周期性③函数对称性的妙解④不同函数的 15 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司对称性） 3、嵌套函数与零点问题（①函数嵌套原理求函数解析式.②函数嵌套中的不动点与稳定点问题③导函数求解 集或比较大小） 4、导数构造新函数求解集或比较大小（①正规方法②秒杀技巧） 题干的设置一般来说在上述的三项考点中选其一项或两项。函数与导数题目中首先分类找准类型选择 小技巧，另外考生们要想灵活应用小技巧则需在有限的时间内同类型题多做几遍，考场中便可轻松搞定。 从近三年的全国卷的考查情况来看，本节是高考的难点，其中导数构造和分段函数零点问题及抽象函 数考查比较频繁.抽象函数一般以多选题的形式考察，导数构造和分段函数零点问题则以单选题的形式考察， 因小结论偏多，试题灵活，考生在考场中以不变应万变. 一、抽象函数具体化 使用前提：题中没有给出具体函数的解析式，但是可以根据所给的函数特征确定函数模型，属于抽象函数 的内容延伸和实例化. 解题步骤： 第一步：由函数的解析式确定函数所属的模型； 常见函数模型包括： Ⅰ：若 f  mn   f  m  f  n  ，可认为函数为幂函数 f  x   xa(a的范围或数值需要其他条件确定)； Ⅱ：若 f  mn   f  m   f  n  ，可认为函数为对数函数 f  x  log x(a的范围或数值需要其他条件确定)； a Ⅲ：若 f  mn   f  m  f  n  ，可认为函数为指数函数 f  x  ax(a的范围或数值需要其他条件确定)；             Ⅳ：若 f mn  f m  f n ，可认为函数为正比例函数 f x kx或 f x  xf 1     f m  f n Ⅴ：若 f  mn   ，可认为函数为正切函数 f  x  tanx；     1 f m f n Ⅵ：若 f x y f x y f x f y，可认为是余弦函数 f xcosx.             Ⅶ：若 f mn  f m  f n m，可认为函数为一次函数 f x kxb或 f x  xf 1 m 第二步：结合函数模型和函数的单调性的定义确定函数的单调性. 结论法(函数性质法) 使用前提：将所给的函数进行“庖丁解牛”后每一部分都是一个很明显可以判断单调性的函数. 解题步骤： 16 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司第一步：确定所给函数是由哪些可以判断单调性的简单函数组合而成的. 第二步：结合函数的性质即可确定函数的单调性. 常见的结论(函数性质)包括：     (1) f x 与 f x C 单调性相同.(C为常数)         (2)当k 0时， f x 与kf x 具有相同的单调性；当k 0时， f x 与kf x 具有相反的单调性 (3)当 1     f x 恒不等于零时， f x 与 其有相反的单调性. f x         (4)当 f x 、g x 在D上都是增(减)函数时，则 f x g x 在D上是增(减)函数.         (5)当 f x 、g x 在D上都是增(减)函数，且两者都恒大于0 时， f x g x 在D上是增(减)函数；当         f x 、g x 在D上都是增(减)函数，且两者都恒小于0时， f x g x 在D上是减(增)函数.   (6)设 y  f x ,xD为严格增(减)函数，则函数必有反函数，且反函数在其定义域D上也是严格增(减)函 数. (7)奇(或偶)函数的单调性： 由奇偶函数定义易知：奇函数在对称的区间上有相同的单调性；偶函数在对称的区间上有相反的单调性. (8)周期函数的单调性：            若 f x 是周期为T 的函数，且 f x 在 a,b 单调递增或单调递减，则 f x 在 akT,bkT kZ 上单 调递增或单调递减. 根据函数奇偶性的规律判定 使用前提：函数解析式比较复杂，由若干基本函数经过运算之后的函数判定奇偶性. 解题步骤： 第一步：确定所给函数的结构特征，应用奇函数的性质进行判断； 第二步：结合基本函数的奇偶性和函数奇偶性的相关结论确定所给函数的奇偶性. 常见的结论包括： (1)几个奇函数的代数和是奇函数；几个偶函数的代数和是偶函数；奇函数与偶函数的代数和是非奇非偶函 数. (2)奇函数的乘积或商是偶函数，偶函数的乘积或商是偶函数，奇函数与偶函数的乘积或商是奇函数. 常见基本函数的奇偶性：   (1)一次函数y kxb k 0 ，当b0时，是奇函数，当b0时，是非奇非偶函数. (2)二次函数y ax2 bxc  a0  ，当b0时，是偶函数；当b0时，是非奇非偶函数. k (3)反比例函数y  k 0,x0是奇函数. x (4)指数函数y ax(a0且a 1)是非奇非偶函数 17 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司(5)对数函数y log x(a0且a 1，x0)是非奇非偶函数. a    (6)三角函数 y sinx  xR  是奇函数， y cosx  xR  是偶函数， y tanx  xk ,kZ 是奇  2  函数.   (7)常值函数 f x a，当a0时，是偶函数，当a0时，既是奇函数又是偶函数. 特殊函数的奇偶性： 奇函数：两指两对 ax 1 2m ax 1 2m ⑴ f  x  m m  x0  ， f  x  m m  mR       ax 1  ax 1  ax 1  ax 1 ⑵函数 f  x    ax ax    ax  1    a2x 1      ax   ax  xm  2m   xm  2m  ⑶ fx log  log 1 ， fx log  log 1  a  xm a  xm a xm a  xm ⑷函数 f  x  log    mx 2 1mx  ，函数 f  x  log    mx 2 1mx  a  a  ax  ax a2x  1   ⑸函数 f x   ax ax a2x 1      f x  f x 0 考点：形如①已知 f  x  奇函数，则  0   0  M 最大值 m 最小值 0      f x  f x 2a ②已知 f  x  奇函数a，则  0   0  M 最大值 m 最小值 2a 偶函数： ⑴函数 f  x    ax ax  ⑵函数 fx log  amx 1   mx a 2   ⑶函数 f x 类型的一切函数. 判定抽象函数的奇偶性 使用前提：所给的函数没有解析式，需要利用所给的条件判定函数的奇偶性. 解题步骤： 第一步：确定函数的定义域，猜想函数模型，从而确定函数的奇偶性方向； Ⅰ：若 f  mn   f  m  f  n  ，可认为函数为幂函数 f  x   xa(a的范围或数值需要其他条件确定)； Ⅱ：若 f  mn   f  m   f  n  ，可认为函数为对数函数 f  x  log x(a的范围或数值需要其他条件确定)； a Ⅲ：若 f  mn   f  m  f  n  ，可认为函数为指数函数 f  x  ax(a的范围或数值需要其他条件确定)； 18 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司            Ⅳ：若 f mn  f m  f n ，可认为函数为正比例函数 f x kx或 f x  xf 1     f m  f n Ⅴ：若 f  mn   ，可认为函数为正切函数 f  x  tanx；     1 f m f n Ⅵ：若 f x y f x y f x f y，可认为是余弦函数 f xcosx.             Ⅶ：若 f mn  f m  f n m，可认为函数为一次函数 f x kxb或 f x  xf 1 m 第二步：利用所猜想的函数模型，使用赋值法结合所给的条件得出 f x与 f x的关系； 第三步：得出结论. 函数单调性与奇偶性综合求不等式范围问题 技巧总结   结论1：奇函数单调性不改变，若函数 f x 为定义在R上的奇函数时         ①若x0时， f x 为单调递增，则x0时， f x 为也为单调递增，即 f m  f n 0mn0.         ②若x0时， f x 为单调递减，则x0时， f x 为也为单调递减，即 f m  f n 0mn0.     结论2：奇函数单调性不改变，若定义在R上函数 f x 关于点 a,b 对称时 ①若xa时， f  x  为单调递增，则xa时， f  x  为也为单调递增，即     f m  f n 2bmn2a. ②若xa时， f  x  为单调递减，则xa时， f  x  为也为单调递减，即     f m  f n 2bmn2a.   结论3：偶函数单调性改变，若函数 f x 为定义在R上的偶函数时     ①若x0时， f x 为单调递增，则x0时， f x 为单调递减，           即 f m  f n  m  n ， f x  f x 2f m  x m.     ②若x0时， f x 为单调递减，则x0时， f x 为单调递增，           即 f m  f n  m  n ， f x  f x 2f m  x m. 结论4：偶函数单调性改变，若定义在R上函数 f  x  关于直线xa对称时 ①若xa时， f  x  为单调递增，则xa时， f  x  为单调递减，           即 f m  f n  ma  na ， f ax  f ax 2f m  xa m. ②若xa时， f  x  为单调递减，则xa时， f  x  为单调递增，           即 f m  f n  ma  na ， f ax  f ax 2f m  xa m. 二、函数周期性的妙解 技巧总结 19 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司类型一：抽象函数的周期性 使用前提：函数的解析式不确定，给出抽象函数的性质，来确定函数的周期 解题步骤： 第一步：合理利用已知函数关系并进行适当地变形； 第二步：熟记常见结论，准确求出函数的周期性； 常见的结论包括： 结论1：若对于非零常数m和任意实数x，等式 f  xm  f  x  恒成立，则 f  x  是周期函数，且2m是 它的一个周期.         证明： f x2m  f xmm f xm  f x T 2m 也可理解为：平移m个单位到谷底，再平移一个单位到巅峰，再平移一个单位又到谷底，则谷底与谷底的 距离为2m，T 2m 结论2：定义在R上的函数 f x，对任意的xR，若有 f xa f xb (其中a,b为常数，a b)， 则函数 f x是周期函数， ab 是函数的一个周期.         证明： f xaa  f xab  f x  f xba T  ba 口诀：同号差（周期）异号加（对称轴）只研究x前的正负. 结论 3 ：定义在 R上的函数 f x，对任意的 xR，若有 f xaf xb ( 其中a,b为常数， a b)，则函数 f x是周期函数，2 ab 是函数的一个周期. 证明： f xaf xb先向左平移a个单位得 f  xaa  f  xab   f  x  f  xba  令ba m  f  x  f  xm 如同结论1 1 1 结论4：定义在R上的函数 f x，对任意的xR，若有 f(xa) ，(或 f(xa) )(其中 f(x) f(x) a为常数，a  0)，则函数 f x是周期函数，2 a 是函数的一个周期. 1 1 证明： f  xa   ， f  x2a   f  xaa    f  x T 2a     f x f xa 结论5:定义在R上的函数 f x，对任意的xR，有 f  ax   f  ax  且 f  bx   f  bx  ，   (其中a,b是常数，ab)则函数y  f x 是周期函数，2ab 是函数的一个周期. 另一种题干出现的信息：①若y  f x的图象关于直线xa,xb都对称，则等价于 f  ax   f  ax  且 f  bx   f  bx  ，则y  f x为周期函数且T 2ab . ②若y  f x为偶函数且图象关于直线xa对称，则y  f x为周期函数且T 2a 20 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司证明： f  ax   f  ax  向左平移a个单位，得 f  xaa   f  a  xa               f x  f 2ax ，同理 f x  f 2bx ， f 2ax  f 2bx 利用口诀：同号差（周期）异号加（对称轴）只研究x前的正负.秒出周期 结论6:若定义在R上的函数y  f x对任意实数xR，恒有 f  x   f  ax   f  xa  成立(a0)，则 f x是周期函数，且6a 是它的一个周期.             证明：由函数 f x  f ax  f xa  f xa  f x2a  f x  f  x   f  x2a   f  x   f  xa   f  xa  f  x2a  ，向右平移a个单位得           f x f x3a  f x3a3a f x3a  f x T 6a 口诀：内同号，外异号，内部只差需2倍，出现周期很easy. 1 f(x) 结论7:若对于非零常数m和任意实数x，等式 f(xm) 成立，则 f x是周期函数，且4m是 1 f(x) 它的一个周期. 1 f(x) 1 1 f(x) 1 f(xm) 1 f(x) 1 证明： f(xm)  f(x2m)   1 f(x) 1 f(xm) 1 f(x) f x 1 1 f(x) 1 1 f  x2m   如同结论4， f  x2m2m    f  x T 4m     f x f x2m 1 f(x) 结论8:若对于非零常数m和任意实数x，等式 f(xm) 成立，则 f x是周期函数，且2m是 1 f(x) 它的一个周期. 1 f(x) 1 1 f(x) 1 f(xm) 1 f(x) 证明： f(xm)  f(x2m)   f x 1 f(x) 1 f(xm) 1 f(x) 1 1 f(x) T 2m 1 结论9:若对于非零常数m和任意实数x，等式 f(xm)1  f(x)0成立，则 f x是周期函数， f(x) 且3m是它的一个周期. 1 证明： f(xm)1  f(x)0得 f(x) 1 1 1 1 f(x3m)1 1    f x f(x2m) 1 f(xm)1 1 1 1 1 f(xm) f x 21 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司T 3m 结论10:①若定义在R上的函数y  f x的图象关于两点A  a,y  ,B  b,y  都对称，则 f x是周期函数， 0 0 且2ba 是它的一个周期. ②若奇函数y  f x的图象关于点A  a,0  对称，则 f x是周期函数，且2a 是它的一个周期. 证明：函数y  f  x  满足 f  ax   f  ax  2y 且 f  bx   f  bx  2y ， 0 0           则 f x 2y  f 2ax 2y  f 2bx  f 2ax  f 2bx 0 0 利用口诀：同号差（周期）异号加（对称轴）只研究x前的正负.秒出周期 结论11:①若定义在R上的函数y  f x的图象关于点A  a,y  和直线xb都对称，则 f x是周期函数， 0 且4ba 是它的一个周期. ②若奇函数y  f x的图象关于直线xa对称，则 f x是周期函数，且4a 是它的一个周期. 证明：函数y  f  x  满足 f  ax   f  ax  2y 且 f  bx   f  bx  ， 0             则 f x 2y  f 2ax  f 2bx  f x 2y  f 2b2ax 2y  f 2ax 0 0 0          f 2bx 2y  f 2ax  f x 2y  f 2b2ax 0 0  f  x  2y  f  2b2ax  2y  f  4b4ax  2y T 4ba 0 0 0 秒记：模仿三角函数 第三步:运用函数的周期性求解问题.           注意：偶函数 f x2m  f x  f m ，一定有 f m  f m 0T 2m. 分段函数的类周期性 使用前提：所给的函数不具有周期性，但是可以经过伸缩变换将所给的函数变形为周期函数 解题步骤： 第一步：确定函数在一个区间上的函数图像 第二步：结合所给的递推关系式和伸缩变换的结论确定函数在定义域内的图象性质 常见的伸缩变换结论包括： 1 结论1：若 f  x  kf  xm  ，即 fxm  fxm0,k 0 ，则只需将函数在一个“周期”内的图象 k 1 向右平移m个单位的同时，函数值变为原来的 倍；向左平移m个单位的同时函数值变为原来的k倍. k           结论2：若 f x  f xm k，即 f xm  f x k m0,k 0 ，则只需将函数在一个“周期”内的图 象向右平移m个单位的同时，向下平移k个单位；向左平移m个单位的同时，向上平移k个单位.          结论3：若 f x  f mx ，即 f mx  f x m0,k 0 ，则只需将函数在一个“周期”内的图象的横坐标 22 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司伸长为原来的m倍时，函数值不变. 1 结论4：若 f  x  kf  mx  ，即 f mx f x  m0,k 0  ，则只需将函数在一个“周期”内的图象的横 k 1 1 坐标伸长为原来的m倍时，函数值变为原来的 ，横坐标缩短为为原来的 时，函数值变为原来的k倍. k m 结论5：若 f  xm  kf  x  , f  x  kf  xm  ，则只需将函数在一个“周期”内的图象横坐标每增加m个 单位的同时，函数值变为原来的k倍；  x  结论6：若 fx kf  ，则只需将函数在一个“周期”内的图象横坐标每扩大m倍的同时，函数值变为 m 原来的k倍；此函数称为倍增函数. 第三步：解决所给的问题，得到结论 三、函数对称性的妙解 技巧总结 类型一：函数自身的对称性 使用前提：单一的函数本身具有轴对称或中心对称的特征 解题步骤： 第一步：由所给的函数性质确定函数的对称性 常见函数的对称性包括：         定理 1 ：函数 y  f x 的图像关于点 A a,b 对称的充要条件是 f x  f 2ax 2b. 或         f 2ax  f x 2b或 f ax  f ax 2b       推论1：函数y  f x 的图像关于原点O对称的充要条件是 f x  f x 0.           证明：设点 x ,y 在y  f x 上，即y  f x ，通过 f x  f 2ax 2b可知 1 1 1 1             f x  f 2ax 2b， f 2ax 2b f x 2b y ，所以点 2ax ,2b y 也在y  f x 上， 1 1 1 1 1 1 1       而点 2ax ,2b y 与 x ,y 关于 a,b 对称，得证. 1 1 1 1 定理2：函数y  f  x  的图像关于直线xa对称的充要条件是 f  ax   f  ax  ，即 f  x   f  2ax  .       推论2：函数y  f x 的图像关于 y轴对称的充要条件是 f x  f x .           证明：设点 x ,y 在y  f x 上，即y  f x ，通过y  f x  f 2ax 可知 1 1 1 1 1 1 1 点  2ax ,y  ，也在y  f  x  上，而点  2ax ,y  与  x ,y  关于xa对称，得证. 1 1 1 1 1 1 第二步：结合函数的对称性确定结论 不同函数的对称性 使用前提：解析式有关系的两个函数具有轴对称或中心对称的特征 解题步骤： 23 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司第一步：由所给的函数性质确定函数的对称性 常见函数的对称性包括：       结论1：函数y  f x 与函数2b y  f 2ax 关于点 a,b 对称，           等价于函数y  f x 与函数y  g x 关于点 a,b 对称，则g x 2b f 2ax ， 结构特征是：横坐标之和为2a，纵坐标之和为2b。       特别地，函数y  f x 与函数 y  f x 关于点 0,0 对称。 结论2：函数y  f  x  与函数y  f  2ax  关于直线xa对称， 结构特征是：横坐标之和为2a，纵坐标相等。 特别地，函数y  f  x  与函数y  f  x  关于直线x0，即 y轴对称。     结论3：函数y  f x 与函数2b y  f x 关于直线y b对称， 结构特征是：横坐标相等，纵坐标之和为2b. 特别地，函数y  f  x  与函数 y  f  x  关于直线y 0，即x轴对称。     结论4：函数y  f x 与函数x f y 关于直线y  x对称， 结构特征是：横坐标，纵坐标互换。 ba     结论5：函数y  f ax 与函数y  f bx 的图像关于直线x 对称。 2     结论6：函数y  f x 与ax f a y 的图像关于直线x y a成轴对称     结论7：函数y  f x 与xa  f ya 的图像关于直线x y a成轴对称 抽象函数奇偶性性的妙解 技巧总结 抽象函数奇偶性：           f xm 奇函数：则 f xm f xm  f xm  f xm 0   所以对称中心为 m,0 f  xm  偶函数：则 f  xm   f  xm   x m 对称轴 四：函数嵌套原理求函数解析式 技巧总结    定义：①函数里调用另一个函数 f g x 简称函数嵌套.    ②函数里调用函数本身 f f x 简称递归嵌套. 函数嵌套原理求函数解析式步骤如下：     形如： f f x  A  B     第一步：令 f x  Am f x mA 24 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司第二步：令xm， f  m  mA,解出m?   第三步：求出 f x 的解析式. 函数嵌套中的不动点与稳定点问题 技巧总结 不动点：对于函数 f  x  ，xR,则 f  x   x的解x称为函数 f  x  的不动点，即y  f  x  与y  x图象交 点的横坐标. 稳定点：对于函数 f  x  ，xR,则 f  f  x   x的解x称为函数 f  x  的稳定点，即y  f  f  x  与y  x图 象交点的横坐标. 不动点与稳定点关系的结论： 若x 为函数y  f  x  的不动点，即 f  x   x ，则若x 必为函数y  f  x  的稳定点点. 0 0 0 0 证明： x 为函数y  f  x  的不动点，即 f  x   x ， f  f  x   f  x   x . 0 0 0 0 0 0 不动点定理1：（三条线一交点）        若函数 f x 为定义域内的单调增函数，则 f f x  x有解等价于 f x  x有解.       证明：若 f x  x无解，则必有 f x  x或 f x  x恒成立.             ①当 f x  x时， 函数 f x 为定义域内的单调增函数，则 f f x  f x  x，显然 f f x  x无解.             ②当 f x  x时， 函数 f x 为定义域内的单调增函数，则 f f x  f x  x，显然 f f x  x无解.        若函数 f x 为定义域内的单调增函数，则 f f x  x有解等价于 f x  x有解. 不动点定理2：（三条线无交点）                ①当 f f x  x时，则 f f x  f x  x.② f x  x时，则 f f x  f x  x. 函数嵌套的零点问题 技巧总结       结论：若函数 f g x  x有解，则g f x  x必有解. 证明： f  g  x   x，两边同时取反函数得g  x   f 1 x  ，故 f  x  与g  x  为反函数（ f  x  与g  x  关于 y  x对称） 同理 g  f  x   x，两边同时取反函数得 f  x   g1 x  故 f  x  与g  x  为反函数（ f  x  与g  x  关于 y  x对称） 五：构造函数的正规运算 ' f'(x)g(x) f(x)g'(x)  f(x) 形如1： f'(x)g(x) f(x)g'(x)[f(x)g(x)]'与   g2(x) g(x) '  f(x) 推论1：xf'(x) f(x)0[xf(x)]'0；xf'(x) f(x)0 0    x  25 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司' xf'(x) f(x)  f(x) 证明如下： xf'(x) f(x)[xf(x)]'；  x2   x   f(x) xf'(x) f(x)0，则函数yxf(x)单调递增；xf'(x) f(x)0，则y 单调递减． x '  f(x) 推论2：当x0时，xf'(x)nf(x)0[xnf(x)]'0；xf'(x)nf(x)0 0   xn   xnf'(x)nxn1f(x)  f(x) ' 证明如下： xnf'(x)nxn1f(x)[xnf(x)]'；  x2n   xn   f(x) xf'(x)nf(x)0，则函数yxnf(x)单调递增；xf'(x)nf(x)0，则y 单调递减． xn 关于 f'(x) f(x) '  f(x) 推论3： f'(x) f(x)0[exf(x)]'0； f'(x) f(x)0 0   ex   证明如下：Q f xex   exfx+f x,   f x    fx f x ，  ex  ex f(x) f(x) f'(x) f(x)0，则y f(x)ex ；反之y f(x)ex ； f'(x) f(x),则y  ；反之y   ex ex ' (f(x)a) 推论4：由于 f'(x) f(x)a[ex(f(x)a)]'0； f'(x) f(x)a 0   ex   [ex(f(x)a)]' (f(x)a) ' 证明如下： f'(x) f(x)a ； f'(x) f(x)ae2x ex   ex   f(x)a f'(x) f(x)a，则y ex(f(x)a)，反之y ex(f(x)a)；若 f'(x) f(x)a，则y  ， ex f(x)a 反之y   ex 形如2：关于sinxf'(x)cosxf(x)或cosxf'(x)sinxf(x) 推论：口诀：正弦同号，余弦反号 sinxf'(x)cosxf(x)0[sinxf(x)]'0；    当x ,  tanxf'(x) f(x)0[sinxf(x)]'0  2 2    f(x)     f(x) sinxfxcosxf(x)0   0 ; 当x ,  ，tanxfx f(x)0   0 sinx  2 2 sinx 26 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司cosxfxsinxf(x)0cosxf(x) 0 ; 当x    ,   ，fxtanxf(x)0cosxf(x) 0  2 2 形如3 ：    f(x)     f(x) cosxfxsinxf(x)0   0 ; 当x ,  ，fxtanxf(x)0   0 cosx  2 2 cosx xlnx  推论： fxxlnx f(x)0lnxf(x) 0; fxxlnx f(x)0  f(x) 0    lnx   fxxlnx1lnx f(x)0xlnx f(x) 0; fxxlnx1lnx f(x)0  f(x) 0   xlnx   lnx  xf(x) fxxlnx1lnx f(x)0  f(x) 0 ; fxxlnx1lnx f(x)0 0秒记方法：      x   lnx  满足导数构造中加乘减除符号不变性  ①若括号内无lnx则是lnxf(x)或  f(x) ；    lnx   ②若括号内是1+lnx，则是xlnxf(x)或  f(x) ；   xlnx   lnx  xf(x) ③若括号内是1- lnx，则是 f(x) 或      x   lnx  构造函数的变形运算 技巧总结 形如1： xmfx  fx 0 xmfx 0   f  x    xm  f x   f  x  0 0    xm  形如2： f x  nf  x  0  enx f  x   enx f x  nf  x    f  x    f x  nf  x  f x  nf  x  0     enx  enx 形如3： f x   f  x  aex f x   f  x  aex   ex f  x   aex   ex f  x     aex    ex fx    aex  ex fx aex exfx a 0   f x   f  x  a  f  x    a  形如4： f x   f  x  a       ex ex  ex   ex             f x   a  f x a f x a       0    ex   ex  ex ex ex 27 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司形如5：xf x  nf  x  ax xn1 xf x  nf  x   xn1ax  xnf  x   axn axn1 axn1  xnf  x  axndx xnf  x    xnf  x   0 n1 n1  xf x  nf  x  ax  f  x   a 形如6：xf x  nf  x  ax      xn xn  xn  xn f  x   a  f  x  ax1n f  x  ax1n   dx    0 xn xn  xn 1n xn 1n 典例1【2023新高考1卷】已知函数 f x 的定义域为R， f xy y2f x x2f y ，则（ ）． A. f 00 B. f 10 C. f x 是偶函数 D. x0为 f x 的极小值点 【答案】ABC 【解析】方法一： 因为 f(xy) y2f(x)x2f(y)， 对于A，令x y 0， f(0)0f(0)0f(0)0，故A正确. 对于B，令x y 1， f(1)1f(1)1f(1)，则 f(1)0，故B正确. 对于C，令x y 1， f(1) f(1) f(1)2f(1)，则 f(1)0， 令y 1, f(x) f(x)x2f(1) f(x)， 又函数 f(x)的定义域为R，所以 f(x)为偶函数，故C正确， 对于D，不妨令 f(x)0，显然符合题设条件，此时 f(x)无极值，故D错误. 方法二： 因为 f(xy) y2f(x)x2f(y)， 对于A，令x y 0， f(0)0f(0)0f(0)0，故A正确. 对于B，令x y 1， f(1)1f(1)1f(1)，则 f(1)0，故B正确. 对于C，令x y 1， f(1) f(1) f(1)2f(1)，则 f(1)0， 令y 1, f(x) f(x)x2f(1) f(x)， 又函数 f(x)的定义域为R，所以 f(x)为偶函数，故C正确， 对 于 D ， 当 x2y2 0时 ， 对 f(xy) y2f(x)x2f(y)两 边 同 时 除 以 x2y2， 得 到 28 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司f(xy) f(x) f(y)   ， x2y2 x2 y2 f(x) x2ln x ,x0 故可以设 ln x (x0)，则 f(x) ， x2 0,x0 1 当x0肘， f(x) x2lnx，则 fx2xlnxx2  x(2lnx1)， x 令 fx0，得  1 ；令 f¢(x)>0，得 1 ； 0 xe 2 xe 2  1   1    故 f(x)在0,e 2 上单调递减，在e 2,上单调递增，      1   1    因为 f(x)为偶函数，所以 f(x)在e 2,0上单调递增，在,e 2 上单调递减，     显然，此时x0是 f(x)的极大值，故D错误. 故选：ABC. 典例2【2023新高考全国Ⅱ卷】 已知函数 f xaex lnx在区间 1,2 上单调递增，则a的最小值为 （ ）． A. e2 B. e C. e1 D. e2 【答案】C 1 1 【解析】依题可知， fxaex  0在 1,2 上恒成立，显然a0，所以xex  ， x a 设gx xex,x1,2 ，所以gxx1ex 0，所以gx 在 1,2 上单调递增， 1 1 gx g1e，故e ，即a e1，即a的最小值为e1． a e 故选：C． b c 典例3【2023新高考全国Ⅱ卷】若函数 f xalnx  a 0既有极大值也有极小值，则 x x2 （ ）． 29 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司A. bc0 B. ab0 C. b2 8ac0 D. ac0 【答案】BCD b c a b 2c ax2 bx2c 【解析】函数 f(x)alnx  的定义域为(0,)，求导得 f(x)    ， x x2 x x2 x3 x3 因为函数 f(x)既有极大值也有极小值，则函数 f(x)在(0,)上有两个变号零点，而a0， 因此方程ax2 bx2c0有两个不等的正根x,x ， 1 2  Δb2 8ac0   b 于是x x  0 ，即有b2 8ac0，ab0，ac0，显然a2bc0，即bc0，A错误，BCD 1 2 a   2c x x  0   1 2 a 正确. 故选：BCD 典例4【2022新高考全国Ⅰ卷】 已知函数 f(x) x3 x1，则（ ） A. f(x)有两个极值点 B. f(x)有三个零点 C. 点(0,1)是曲线y f(x)的对称中心 D. 直线y 2x是曲线y f(x)的切线 【答案】AC 3 3 【解析】由题， fx3x2 1，令 f¢(x)>0得x 或x ， 3 3 3 3 令 f(x)0得  x ， 3 3 3 3 3 3 3 所以 f(x)在(, )，( ,)上单调递增，( , )上单调递减，所以x 是极值点， 3 3 3 3 3 故A正确； 3 2 3 3 2 3 因 f( )1 0， f( )1 0， f 250， 3 9 3 9  3 所以，函数 f x 在, 上有一个零点，   3   3  3  3  当x 时， f x f  0，即函数 f x 在 ,+上无零点，     3  3   3  综上所述，函数 f(x)有一个零点，故B错误； 30 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司令h(x) x3x，该函数的定义域为R，hxx3 xx3 xhx， 则h(x)是奇函数，(0,0)是h(x)的对称中心， 将h(x)的图象向上移动一个单位得到 f(x)的图象， 所以点(0,1)是曲线y f(x)的对称中心，故C正确； 令 fx3x2 12，可得x1，又 f(1) f 11， 当切点为(1,1)时，切线方程为y 2x1，当切点为(1,1)时，切线方程为y  2x3，故D错误. 故选：AC. 典例5【2022新高考全国Ⅱ卷】 已知函数 f(x)的定义域为R，且 22 f(x y) f(x y) f(x)f(y), f(1)1，则  f(k)（ ） k1 A. 3 B. 2 C. 0 D. 1 【答案】A 【解析】[方法一]：赋值加性质 因为 f x y f x y f x f y ，令x1,y 0可得，2f 1 f 1 f 0 ，所以 f 02， 令x0可得， f y f y2f y，即 f y f y ，所以函数 f x 为偶函数，令y 1得， f x1 f x1 f x f 1 f x ，即有 f x2 f x f x1 ，从而可知 f x2f x1 ， f x1f x4 ，故 f x2 f x4，即 f x f x6 ，所以 函数 f x 的一个周期为6．因为 f 2 f 1 f 0121， f 3 f 2 f 1112， f 4 f 2 f 21， f 5 f 1 f 11， f 6 f 02，所以 一个周期内的 f 1 f 2L  f 60．由于22除以6余4， 22 所以  f k f 1 f 2 f 3 f 411213．故选：A． k1 [方法二]：【最优解】构造特殊函数 由 f x y f x y f x f y ，联想到余弦函数和差化积公式 cosx ycosx y2cosxcosy，可设 f xacosx，则由方法一中 f 02, f 11知 1  a2,acos1，解得cos ，取 ， 2 3  所以 f x2cos x，则 3 31 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司        f x y f x y2cos  x y  2cos  x y  4cos xcos y  f x f y ，所以  3 3   3 3  3 3 2  T  6 f x2cos x符合条件，因此 f(x)的周期  ， f 02, f 11，且 3 3 f 21, f 32, f 41, f 51, f 62，所以 f(1) f(2) f(3) f(4) f(5) f(6)0， 由于22除以6余4， 22 所以  f k f 1 f 2 f 3 f 411213．故选：A． k1 预测1（2024·重庆·模拟预测）已知直线yaxb与曲线yex相切于点  x ,ex0  ，若x ,3，则ab 0 0 的取值范围为（ ） A．,e B．  e3,e C．0,e D．  0,e3    e a ,x0 预测2（2024·贵州贵阳·模拟预测）已知函数 f x x ，若方程 f xex0存在三个不相等的  ex,x0 实根，则实数a的取值范围是（ ） A．,e B．,e C．,2e D．,2e 8 π  预测3（2024·贵州遵义·模拟预测）已知直线nxy20与函数 f(x) cos xx12的图象在x1处的 π 2  切线没有交点，则n（ ） A．6 B．7 C．8 D．12 预测4（2024·河南·模拟预测）已知函数 f x的定义域为R，对于任意实数x，y满足 f xy f xy2f x1 f y，且 f 02，则下列结论错误的是（ ） A． f 11 B． f x为偶函数 1 C． f x是周期函数 D． f 10 512 预测5（2024·陕西西安·模拟预测）若方程ax2lnx0在1,上有两个不同的根，则a的取值范围为 （ ） 32 原创精品资源学科网独家享有版权，侵权必究！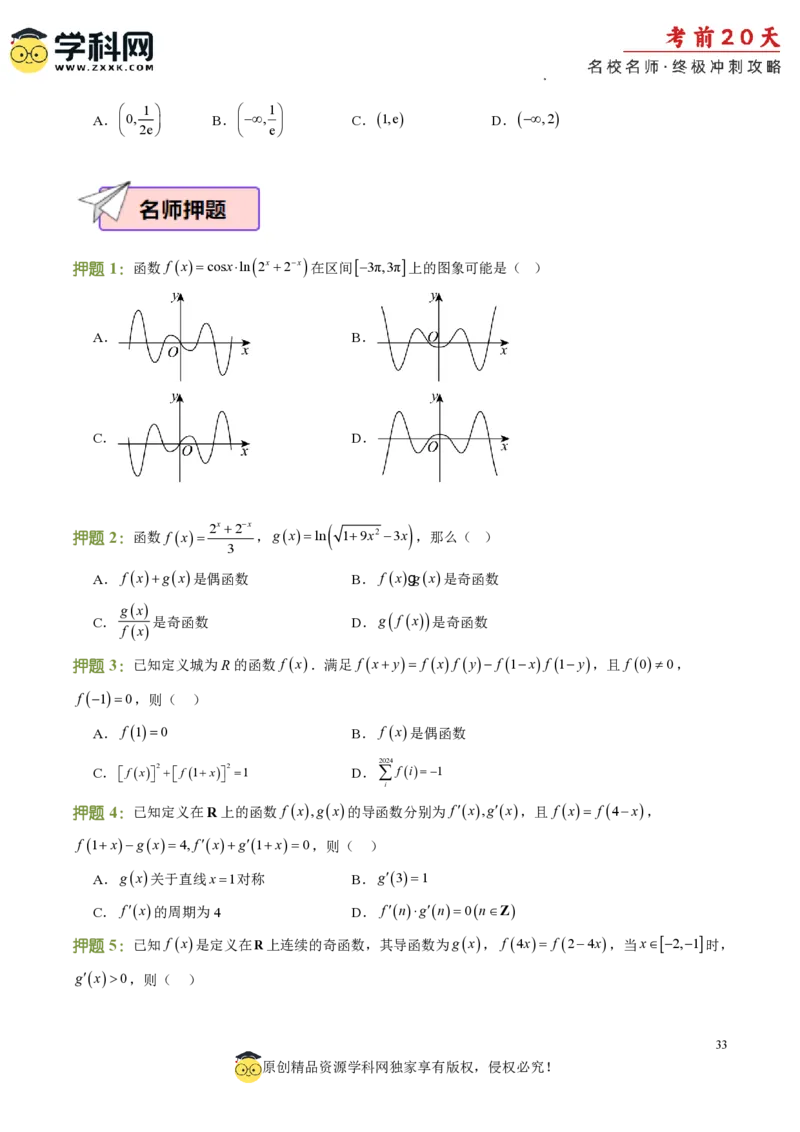 学科网（北京）股份有限公司 1   1 A．0,  B．,  C．1,e D．,2  2e  e 押题1：函数 f xcosxln  2x2x 在区间3π,3π上的图象可能是（ ） A． B． C． D． 2x2x   押题2：函数 f x ，gxln 19x2 3x ，那么（ ） 3 A． f xgx是偶函数 B． f xggx是奇函数 gx C． 是奇函数 D．gf x 是奇函数 f x 押题3：已知定义城为R的函数 f x．满足 f xy f x f y f 1x f 1y，且 f 00， f 10，则（ ） A． f 10 B． f x是偶函数 2024 C．fx 2 f1x 2 1 D． fi1     i 押题4：已知定义在R上的函数 f x,gx的导函数分别为 fx,gx，且 f x f 4x， f 1xgx4, fxg1x0，则（ ） A．gx关于直线x1对称 B．g31 C． fx的周期为4 D． fngn0nZ 押题5：已知 f x是定义在R上连续的奇函数，其导函数为gx， f 4x f 24x，当x2,1时， gx0，则（ ） 33 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司1 A．gx为偶函数 B． f x的图象关于直线x 对称 2 C．4为gx的周期 D．gx在x2026处取得极小值 名校预测 预测1：答案 B 【详解】因为yex，所以yex，∴aex0． 又∵切点  x ,ex0  在直线yaxb上， 0 ∴ex0 ax bx ex0 b，解得b1x ex 0．∴ab2x ex 0． 0 0 0 0 令gx2xex，则gx1xex，x,3， 令gx0，解得：x1；令gx0，解得：1x3； 可得gx在,1上单调递增，在1,3上单调递减， x2时，gx0，2x3时，gx0， 当x趋近负无穷时，gx趋近0，g3e3；gx g1e， max 故ab的取值范围为  e3,e．  故选：B． 预测2：答案C 【详解】因为方程 f xex0存在三个不相等的实根，所以函数gx f xex有三个零点， 当x,0时，gx f xexexex，所以gxexe， 所以当x,1时，gx0；当x1,0时，gx0， 所以gx在,1上单调递减，在1,0单调递增，gxg10， 又当x0时，gx1；当x时，gx，所以gx图象如图； e 当x0,时，gx f xexa ex， x e ex1x1 所以gx e ，所以当x0,1时，gx0；当x1,时，gx0， x2 x2 所以gx在0,1上单调递减，在1,单调递增，gxg1a2e， 又当x0时，gx；当x时，gx，所以gx图象如图， 34 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司所以当a2e0即a2e时函数gx f xex有三个零点， 即方程 f xex0存在三个不相等的实根， 故选：C. 预测3：答案C 8 π  8 π 【详解】 f(x) cos xx12， f(1) cos 11， π 2  π 2 8 π  π π  f(x) sin x 12x11 4sin x12x11 π 2  2 2  π f(1)4sin 128， 2 8 π  所以函数 f(x) cos xx12的图象在x1处的切线方程为： π 2  y18x1，则y8x7， 因为直线nxy20与直线y8x7没有交点， 所以直线nxy20与直线y8x7平行， 则n8. 故选：C. 预测4：答案C 【详解】令x y0，得2f 02f 0 f 1，因为 f 02，所以 f 11，A正确; 令x0，则 f y f y2f 1 f y2f y，所以 f y f y，则 f x为偶函数，B正确； 1 令y0，得2f x2f x1 f 04f x1，即 f x1 f x，所以 f x不是周期函数，C错误； 2 1 1 n 1 n 1 9 1 当x取正整数n时， f n1 f nL   f 1  ，则 f 10   ，D正确. 2 2 2 2 512 故选：C. 预测5：答案A 35 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司lnx 【详解】ax2lnx0a ，x1， x2 lnx 令 f x ，x1， x2 lnx 即ya与 f x ，x1有两个不同的交点， x2 x2xlnx 12lnx 则 fx  ，x1， x4 x3 令 f¢(x)>0，即12lnx0，解得 1 ， 1xe2 令 fx0，即12lnx0，解得 1， xe2 lnx  1  1  故 f x 在1,e2上单调递增，在e2,上单调递减， x2     lnx  1 1 故 f x 在 1 处取得极大值，也是最大值， f e2 ， x2 xe2   2e lnx 且当x1时， f x 0，当x1时， f 10， x2 lnx 当x时， f x 趋向于0， x2  1  故a0, ,  2e 故选：A 名师押题 押题1：答案D 【详解】因为 f x的定义域为R，且 f xcosxln  2x2x cosxln  2x2x  f x， 所以 f x为偶函数，其函数图象关于y轴对称，故排除A，C． 因为 f 0ln20，故排除B． 故选：D． 押题2：答案BC 2x2x 2x2x 【详解】因为 f(x)  f(x)，所以 f x 为偶函数， 3 3        因为g(x)g(x)ln 19x2 3x +ln 19x2 3x ln 19x2 3x 19x2 3x ln10，   即g(x)g(x)，所以gxln 19x2 3x 为奇函数， 36 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司所以 f xgx为非奇非偶函数，A错误； f xggx[f xggx]，所以 f xgx为奇函数，B正确； gx gx gx gx   ，所以 是奇函数，C正确； f x f x f x f x 令Hxgf x ，Hxgf xgf xHx，Hx为偶函数，D错误. 故选：BC． 押题3：答案ABC 【详解】对于A项，由 f xy f x f y f 1x f 1y， 1  1 2  1 2 令x y ，则 f 1  f     f   0，故A项正确； 2  2  2 对于B项，令x y0，则 f 0f 0 2 f 1 2 f 0 2 ，       因 f 00，故 f 01， 令y1，则 f x1 f x f 1 f 1x f 0f 1x①， 所以函数 f x关于点1,0成中心对称， 令x y1，则 f 2f 1 2 f 0 2 1，     令y2，则 f x2 f x f 2 f 1x f 1f x②， 由①可得： f x2f x③，由②③可知： f x f x， 且函数 f x的定义域为R，则函数 f x是偶函数，故B项正确； 对于C项，令yx，则 f 0 f x f x f 1x f 1x， 因为 f 01， f x f x， f x1f 1x，代入上式中得， 故得：f x 2 f 1x 2 1，故C项正确；     对于D项，由上可知： f x2f x，则 f x4f x2 f x， 故函数 f x的一个周期为4，故 f 4 f 01， 令x2,y1，则 f 3 f 2 f 1 f 1 f 00， 所以 f 1 f 2 f 3 f 401010， 2024 则 f(i)25400，故D项错误． i1 故选：ABC． 押题4：答案ACD 37 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司【详解】由 f(x) f(4x)，得 f(1x) f(3x)①， f(1x)g(x)4②，得 f(3x)g(2x)4③， 由①②③，得g(x)g(2x)，所以函数g(x)图象关于直线x1对称，故A正确； 由g(x)g(2x)，得g(x)g(2x)，令x1，得g(1)0； 由 f(1x)g(x)4，得 f(1x)g(x)0， 令x1，得 f(2)g(1)0， ∴ f(2x)g(1x)0④， 又 f(x)g(1x)0⑤，令x2，得 f(2)g(3)0，故B错误； ④⑤两式相加，得 f(2x) f(x)0，得 f(4x) f(2x)0， 所以 f(x) f(4x)，即函数 f(x)的周期为4，故C正确； 由 f(2x) f(x)0，令x2，得 f(4) f(2)0，所以 f(4)0， 所以 f(1)g(1) f(2)g(2) f(3)g(3) f(4)g(4)L  f(n)g(n)0(nZ)，故D正确. 故选：ACD 押题5：答案ACD 【详解】对于A， f(x)是定义在R上连续的奇函数，则 f xf x， 两边求导可得fxfx，所以 fx fx， 因为g(x)为 f(x)的导函数，所以有g(x) fx fxg(x)，即g(x)为偶函数，故A正确； 对于B，若 f(4x) f(24x)，则 f(x) f(2x)，则 f(1x) f(1x)， 所以 f(x)的图象关于直线x1对称，故B错误； 对于C，因为 f(x) f(2x)，所以 fxf2x，即g(x)g(2x)， 又g(x)为偶函数，所以g(x)g(x2)，所以g(x2)g(x)， 所以g(x4)g(x2)g(x)，故4为g(x)的周期，故C正确； 对于D，当x2,1时，g(x)0，则g(x)在区间2,1上为增函数， 由g(x)为偶函数，可得g(x)在区间1,2上为减函数， 由4为g(x)的周期，可得g(x)在区间2,3上为增函数 则g(x)在区间2025,2026上为减函数，在2026,2027上单调递增， 故g(x)在x2026处取得极小值，故D正确． 故选：ACD． 38 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司不等式（选填题） 年份 题号 知识点 考点 ①基本不等式 2021年I卷 5 椭圆与不等式 ②椭圆的几何性质 2021年II卷 无 ①解基础不等式 1 集合与不等式 ②集合的运算 2022年I卷 ①球体综合问题 8 立体几何与不等式 ②基本不等式 ①绝对值不等式 1 集合与不等式 2022年II卷 ②集合的运算 12 不等式 基本不等式 2023年新高考 ①一元二次不等式 1 集合与不等式 1 ②集合的运算 2023年新高考 2 11 不等式 基础不等式 近三年，不等式在选填中与其它知识综合占据一个位置，考查的考点一般来说是： 1、基本不等式（①热点不等式②均值不等式③等价转化④1的整体代换） 2、一元二次不等式（①一元二次不等式与二次函数、韦达定理、判别式②含参、乘除的等价穿根法③对勾 函数、定动区间定动轴） 3、绝对值不等式（①三长三短求解②大于取两边小于取中间） 题干的设置一般来说在上述的三项考点中选其一项。不等式常用于圆锥曲线、集合中解决最值问题， 考生们需要多掌握不等式的目标形式并合理采用不等式技巧（柯西不等式、热点不等式、基本不等式等 等），多理解理解不等式的二次结论是怎么来的。 39 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司从近三年的全国卷的考查情况以及新高考新题型标准来看，不等式是高考选填方向必不可少的一部分， 不等式能够有效的解决最值问题，类型1：单纯的不等式，类型2：将以圆锥曲线为导火索设置最值问题， 类型3：将会以集合元素满足要求涉及基础不等式，不等式结论偏难理解，试题相对综合，此类题目必须熟 练即可拿分. 一、一元二次不等式与二次函数关系 技巧总结 ①ax2 bxc0意味着y ax2 bxc中y 0部分， ②ax2 bxc0意味着y ax2 bxc中y0部分 ， 处理技巧：ax2 bxca(xx )(xx )，求出两个根x ，x ；根据图像可知：开口向上时，大于取两 1 2 1 2 边，小于取中间，开口向下时，大于取中间，小于取两边. 注意：处理此题时，主要确定a的正负及快速画出图象 一元二次不等式与韦达定理 技巧总结 模型一：已知关于x的不等式ax2 bxc0的解集为(m,n)，解关于x的不等式cx2 bxa 0． 1 1 1 1 由ax2 bxc0的解集为(m,n)，得:a( )2 b c0的解集为( , )，即关于x的不等式 x x n m 1 1 cx2 bxa 0的解集为( , )． n m 已知关于x的不等式ax2 bxc0的解集为(m,n)，解关于x的不等式cx2 bxa0． 1 1 1 1 由ax2 bxc0的解集为(m,n)，得:a( )2 b c0的解集为(, ] [ ,)即关于x的不等式 x x n m 1 1 cx2 bxa0的解集为(, ] [ ,)． n m 模型二：已知关于x的不等式ax2 bxc0的解集为(m,n)，解关于x的不等式cx2 bxa0． 1 1 1 1 由ax2 bxc0的解集为(m,n)，得:a( )2 b c0的解集为( , )即关于x的不等式 x x m n 1 1 cx2 bxa0的解集为( , )． m n 40 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司已知关于x的不等式ax2 bxc0的解集为(m,n)，解关于x的不等式cx2 bxa0． 1 1 1 1 由ax2 bxc0的解集为(m,n)，得:a( )2 b c0的解集为(, ] [ ,)即关于x的不 x x m n 1 1 等式cx2 bxa0的解集为(, ] [ ,)， m n 一元二次不等式与判别式 技巧总结 a 0 ①已知关于x的不等式ax2 bxc0的解集为R，则约束条件一定满足 ． 0 a0 ②已知关于x的不等式ax2 bxc0的解集为，则约束条件一定满足 ． 0 a0 ③已知关于x的不等式ax2 bxc0的解集为R，则约束条件一定满足 ． 0 a 0 ④已知关于x的不等式ax2 bxc0的解集为，则约束条件一定满足 ． 0 注意：此类题画出符合要求的图象更加直观 乘除的等价原理和穿根法 技巧总结 f(x) ①若 0，则 f(x)与g(x)异号， f(x)g(x)0． g(x) ②若 f(x) ，则 f(x)与g(x)异号， f(x)g(x)0，且g(x)0． 0 g(x) ③若 f(x) 0，则 f x与gx同号， f(x)g(x)0． g(x) ④若 f(x) 0，则 f x与gx同号， f(x)g(x)0，且g(x)0． g(x) 数轴穿根法 f(x)(xx )(xx )...(xx )0或 f(x)(xx )(xx )...(xx )0 1 2 n 1 2 n 口诀：高系为正上穿下，右穿左，奇穿偶回上为正. 二、基本不等式常用模型 技巧总结 41 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司n n 形式一：mx 2 mn(m0,n0)，当且仅当x 时等号成立. x m n n n 形式二：mx m(xa) ma2 mn ma(m0,n0)，当且仅当xa  时等号 xa xa m 成立. x 1 1 c 形式三：   (a0,c0)，当且仅当x 时等号成立. ax2bxc c 2 acb a axb x mx(nmx) 1 mxnmx n2 n n 形式四：x(nmx)  （ )2  (m0,n0,0 x )，当且仅当x m m 2 4m m 2m 时等号成立. 柯西不等式（二元式） 技巧总结 a b 柯西不等式：设a，b，c，d R，有(ab)(cd)( ac  bd)2 当且仅当  时等号成立． c d 形式一：一次与分式模型 m n 1 1 1 1 (ab)(  )( m  n)2其中a,bR，例如(ab)(  )( a  b )2 4； a b a b a b 形式二：分式与分式模型（分母和为定值） a b a b  [(x)(1x)](  )( a  b)2 x 1x x 1x 形式三：高低和积配凑模型 已知x2  y2的值，求x y的取值范围，或者已知x y的值，求2x2 3y2的最值或者求 x  y 的最值 即(x2  y2)(m2 n2)(mxny)2，其中m，nR 例：(a2 b2)(11)(ab)2 形式四：同次和积配凑模型 已知xy的值，求(xm)(yn)(m,nR )的最值，利用(xm)(yn)( xy  mn)2求最值．  热点基本不等式 技巧总结 a2 b2 a2 b2 (ab)2 通过对柯西不等式变形可知(  )(x y)(ab)2在a,b,x,y 0时，就存在   当 x y x y x y a b a2 b2 c2 (abc)2 a b c  时，等号成立．同理    ,当   时，等号成立． x y x y z x yz x y z 权方和不等式 技巧总结 权方和不等式也称热点不等式的延伸 42 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司(a )m1 (a )m1 (a )m1  a a  a m1 若a 0,b 0,m0.则 1  2   n  1 2 n i i (b )m (b )m (b )m  b b  b m 1 2 n 1 2 n a a a 当仅当 1  2   n 时，等号成立.m为该不等式的和，它的特证是分子的幂比分母的幂多一次. b b b 1 2 n 3 1 关于齐次分式，将分子变为平方式，再用权方和不等式，关于带根号式子，将分子变为 次，分母为 次. 2 2 三、绝对值不等式证明 技巧总结 工具： ①热点不等式： a2 b2 a2 b2 (ab)2 通过对柯西不等式变形可知(  )(x y)(ab)2在a,b,x,y 0时，就存在   当 x y x y x y a b a2 b2 c2 (abc)2 a b c  时，等号成立．同理    ,当   时，等号成立． x y x y z x yz x y z ②柯西不等式 (x2  y2)(m2 n2)(mxny)2 x y  当 等号成立 m n ③1的整体代换 h f abm  形如： ，求 的最小值 a b ab a b h f  h f   a b  1  1  1     破解： m m m a b  a b  m m 随后利用基本不等式求解即可. ④ f  x   xa  xb  xc  xd 取最值时，必须在绝对值零点处取到.    f a     f b  比较，最大的为最大值，最小的为最小值 故   f c   f  d  糖水变甜分式不等式 技巧总结 bm b am a 定理：若ab0，m0，则一定有  ，或者  同号取倒反序 am a bm b 通俗的理解就是a克的不饱和糖水里含有b克糖，往糖水里面加入m克糖，则糖水更甜； 43 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司bm b abamabbm (ab)m 证明：①    0 am a a2 am a2 am am a abbmabam (ab)m ②    0 bm b b2 bm b2 bm b c 典例1【2023新高考Ⅱ卷】若函数 f xalnx  a 0既有极大值也有极小值，则（ ）． x x2 A. bc0 B. ab0 C. b2 8ac0 D. ac0 【答案】BCD b c a b 2c ax2 bx2c 【解析】函数 f(x)alnx  的定义域为(0,)，求导得 f(x)    ， x x2 x x2 x3 x3 因为函数 f(x)既有极大值也有极小值，则函数 f(x)在(0,)上有两个变号零点，而a0， 因此方程ax2 bx2c0有两个不等的正根x,x ， 1 2  Δb2 8ac0   b 于是x x  0 ，即有b2 8ac0，ab0，ac0，显然a2bc0，即bc0，A错误，BCD 1 2 a   2c x x  0   1 2 a 正确. 故选：BCD 典例2【2022新高考全国Ⅱ卷】 若x，y满足x2  y2 xy 1，则（ ） A. x y1 B. x y2 C. x2  y2 2 D. x2  y2 1 【答案】BC ab 2 a2 b2 【解析】因为ab    （a,bÎ R），由x2  y2 xy 1可变形为，  2  2 2  x y x y2 13xy3 ，解得2 x y  2，当且仅当x y 1时，x y 2，当且仅当    2  x y 1时，x y 2，所以A错误，B正确； 44 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司x2  y2 由x2  y2 xy 1可变形为  x2  y2 1 xy ，解得x2  y2 2，当且仅当x y 1时取 2 等号，所以C正确； 2  y 3 y 3 因为x2  y2 xy 1变形可得  x   y2 1，设x cos, y sin，所以  2 4 2 2 1 2 xcos sin,y  sin，因此 3 3 5 2 1 1 1 x2  y2 cos2 sin2 sincos1 sin2 cos2 3 3 3 3 3 4 2  π 2  3 3   sin  2    ,2  ，所以当x ,y  时满足等式，但是x2  y2 1不成立，所以D 3 3  6 3  3 3 错误． 故选：BC． 典例3【2022新高考全国Ⅰ卷】已知正四棱锥的侧棱长为l，其各顶点都在同一球面上.若该球的体积为36， 且3l 3 3，则该正四棱锥体积的取值范围是（ ）  81 27 81 27 64 A.  18,  B.  ,  C.  ,  D. [18,27]  4   4 4   4 3  【答案】C 【解析】∵球的体积为36，所以球的半径R 3, [方法一]：导数法 设正四棱锥的底面边长为2a，高为h， 则l2 2a2 h2，32 2a2 (3h)2, 所以6hl2，2a2 l2 h2 1 1 2 l4 l2 1 l6  所以正四棱锥的体积V  Sh 4a2h (l2  ) = l4  ， 3 3 3 36 6 9 36 45 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司1 l5  1 24l2  所以V 4l3  l3  ， 9 6  9  6  当3l 2 6时，V0，当2 6 l 3 3时，V0， 64 所以当l 2 6 时，正四棱锥的体积V 取最大值，最大值为 ， 3 27 81 又l 3时，V  ，l 3 3时，V  , 4 4 27 所以正四棱锥的体积V 的最小值为 ， 4 27 64 所以该正四棱锥体积的取值范围是  ， .  4 3  故选：C. [方法二]：基本不等式法 4 2 1 1 122hhh 3 64 由方法一故所以V  a2h  6hh2 h 122hhh„    (当且仅当 3 3 3 3 3 3   h4取到)， 3 3 3 1 1 3 3 3 27 当h  时，得a  ，则V  a2h ( )2  ; 2 2 min 3 3 2 2 4 3 9 当l 3 3时，球心在正四棱锥高线上，此时h 3 ， 2 2 2 3 3 3 3 1 1 3 3 9 81 64 a  a  ，正四棱锥体积V  a2h ( )2   ，故该正四棱锥体积的取 2 2 2 1 3 3 2 2 4 3 27 64 值范围是[ , ]. 4 3   M 2,1,0,1,2 N  x x2 x60 典例 4【2023 新高考全国Ⅰ卷】 已知集合 ， ，则M N  （ ） A. 2,1,0,1 B. 0,1,2 C. 2 D. 2 【答案】C 46 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司【解析】方法一：因为N   x x2 x60  ,23, ，而M 2,1,0,1,2 ， 所以M N  2 ． 故选：C． 方法二：因为M 2,1,0,1,2 ，将2,1,0,1,2代入不等式x2 x60，只有2使不等式成立， 所以M N  2 ． 故选：C．  2 15 5 2sin x, x   5 4 4 预测1（2024·陕西西安·模拟预测）已知函数 f x ，若存在实数 5  log x1,x  2 4 x,x ,x ,x x x x x 满足 f x  f x  f x  f x m，则错误的是（ ） 1 2 3 4 1 2 3 4 1 2 3 4 5 A．x2x2 8 B．x x  C．x x x x 0 D．0m2 3 4 1 2 2 3 4 3 4  x3  预测2（2024·山西朔州·模拟预测）已知集合M x 0,xZ,N x1x4 ，则M N （ ）  x3  A． x1x3 B．1,2 C．2 D．2,3,4 预测3（2024·河北沧州·模拟预测）已知抛物线T:y2 2pxp0的焦点为F，直线l交抛物线T于A，B MN 两点，M为线段AB的中点，过点M作抛物线T的准线的垂线，垂足为N，若 MF  AM ，则 的最大 AB 值为（ ） 2 1 1 A．1 B． C． D． 2 2 3 2ab 预测4（2024·黑龙江·模拟预测）已知实数a，b且ab0，则 取得最大值时，ab的值 a2b2a2b29 为（ ） A． 3 B．2 3 C．2 3 D．2 3或2 3 预测5（2024·广东·模拟预测）已知集合Ax lnx10 ，集合B  x x23x0  ，则AB（ ） A．0,2 B．2,3 C．0, D．2, 47 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司押题1：已知VABC的内角A，B，C对边分别为a，b，c，满足asinAcsinAsinC2sinB，若b2， 则VABC面积的最大值为（ ） 3 3 3 3 A． B． C． D． 4 6 3 2 T 押题2：已知正项数列{a }的前n项和为S ，前n项积为T ，且满足a  n (nN)，则不等式S 11 n n n n 3T 1 n n 成立的n的最小值为（ ） A．11 B．12 C．13 D．10 押题3：已知集合A  xx1x90  ,Bx 2x11 ，则AB（ ） A．2,9 B．2,11 C．1,9 D．1,11 PB 押题4：已知抛物线C：y2 6x，P为C上一点，A3,0，B3,0，当 最小时， PB （ ） PA A．3 6 B．3 2 C．2 2 D．18 押题5：函数ylog x11(a0,a1)的图象恒过定点P，若点P在直线mxny10(m0,n0)上， a 则（ ） 1 1 1 1 2 8 A．mm B．4m2n2  C．m2n D．   8 2 4 m1 n 3 名校预测 预测1：答案 A  2π 15 5 2sin x, x  5 4 4   5 【详解】 f xlog x1, x2， 2 4  log x1,x2 2   故 f x的图象如图所示， 48 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司考虑直线ym与y f x图象的交点， 5 5 则x x 2  ，且log x 1log x 1m，0m2，故BD正确. 1 2 4 2 2 3 2 4 1 由log x 1log x 1m可得 x 1即x 1x 11， 2 3 2 4 x 1 4 3 4 3 整理得到x x x x 0，故C正确. 3 4 3 4 又x2x2 x x 22x x x x 22x x ， 3 4 3 4 3 4 3 4 3 4 由x x x x 2 x x 可得x x 4，但x  x ，故x x 4， 3 4 3 4 3 4 3 4 3 4 3 4 故x2x2 1688，故A错误. 3 4 故选：A. 预测2：答案C 【详解】M x|3x3,xZ3,2,1,0,1,2 , 故M N 2， 故选：C. 预测3：答案B 【详解】设 AF m， BF n，因为 MF  AM  MB ，所以AF BF， 所以 AB  m2n2 ，过点A，B分别作AG，BW 垂直准线于点G，W， 由抛物线的定义可知 AF  AG ， BF  BW ， AG  BW AF  BF mn 由梯形的中位线可知 MN    ． 2 2 2 因为m2n2 2mn，所以2  m2n2 2mnm2n2 mn2 ， 49 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司mn 当且仅当mn时，等号成立，所以 AB  m2n2   2 MN 2 MN 2 MN 2 所以  ，故 的最大值为 ． AB 2 AB 2 故选：B 预测4：答案D 2ab 2ab 2   【详解】a2b2a2b29 2aba2b29 9 ， 2ab ab 9 9 又ab0，所以ab 2 ab 6， ab ab 2ab 1 所以  ， a2b2a2b29 4 当且仅当ab3，即ab 3，或ab 3取等号， 所以ab2 3或ab2 3. 故选：D 预测5：答案C 【详解】由lnx10可得：x2，所以A2,， 由x23x0可得：0x3，所以B0,3， 所以AB 0, . 故选：C. 名师押题 押题1：答案C 【详解】由asinAcsinAsinC2sinB， a b c 由正弦定理得sinA ,sinB ,sinC  ， 2R 2R 2R 又asinAcsinAsinC2sinB，且b2， a2c2b2 1 所以a2c2 b2ac，故cosB  ， 2ac 2 2π 又B0,π，所以B ， 3 4 由a2c2 2ac，即a2c2 b2ac4ac2ac，得ac ， 3 1 2π 3 3 VABC面积的最大值为 acsin  ac ， 2 3 4 3 50 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司故选：C． 押题2：答案B T T T 【详解】Q a  n (nN)，a  n1  n1， n 3T 1 n1 3T 1 T n n1 n 1 1 1 3T T 1，则T   T  ， n1 n n1 2 3 n 2 T a 2 1 1 1 Q n1时，a  1  1 ，a  ，则T  a   0， 1 3T 1 3a 1 1 3 1 2 1 2 6 1 1 1 T  n1 2 1 故  ， 1 3 T  n 2 1 1 1 因此{T  }是以 为首项， 为公比的等比数列. n 2 6 3 1 1 1 1 1 1 所以T   ( )n1，即T  ( )n . n 2 6 3 n 2 3 2 1 1 1 ( )n T 2 3 2 3n1 2 根据题中条件a  n   1 ， n 3T 1 3 1 3 3n3 3n3 n ( )n 1 2 3 2 2 2 则a 1，a 1 1 ， n n 3n3 3n 1 1  1 1 1 1 3 3n1 1 因此a a a L a n2(   L  )n2 n1 . 1 2 3 n 3 32 33 3n 1 3n 1 3 当n11时，a a a L a 11； 1 2 3 11 1 1 当n12时，a a a L a 121 11 11. 1 2 3 12 312 312 综上，不等式S 11成立的n的最小值为12. n 故选：B 押题3：答案D 【详解】A  xx1x90  {x|1x9}，又Bx 2x11 ， 则AB{x|1x11}. 故选：D. 押题4：答案B 【详解】依题意，设Pm,nm0，则n2 6m， 51 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司 PB  2 m32n2 m26m96m m29 1 所以   PA     m32n2  m26m96m  m212m9  1 12m ， m29 PB 当m0时， 1； PA 12m 12 12   2 当m0时，m29 9 9 ， m 2 m m m 9 当且仅当m ，即m3时，等号成立， m 2  PB  1 1 1 PB 3 所以  PA    12m  12  3 ，即  ，   1 PA 3 m29 PB 3   综上， 取最小值 时，m3，则P 3,3 2 ， PA 3 所以 PB  332  3 2 2 3 2. 故选：B. 押题5：答案BCD 1 【详解】由题得点P2,1，即2mn1,0m ,0n1， 2 1 1 所以2mn12 2mn，即mn ，当且仅当2mn 时取等号，故A错误； 8 2 (2mn)2 1 1 4m2n2   ，当且仅当2mn 时取等号，故B正确； 2 2 2 1  2 1 m2nm22m1(m1)2  1  ，故C正确； 2  4  1 2 1 1  n 4m1 1 8 由2mn1，2(m1)n3，    2m1n    22   44 ， m1 n 3 3  m1 n  3 3 1 2 8 且取不到等号，故   ，故D正确． m1 n 3 故选：BCD 52 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司球（选填题） 年份 题号 知识点 考点 2021年I卷 无 2021年II卷 4 球 球的表面积与体积 2022年I卷 8 球 球的表面积与体积 2022年II卷 7 球 球的表面积与体积 2023年新高考1 12 球 球的表面积与体积 2023年新高考2 无 近三年，球在选填中偶尔占据一个位置，考查的考点一般来说是： 1、外接球的表面积与体积（①侧棱垂直于底面②侧面垂直于底面③正棱锥模型④正规勾股） 2、内切球的表面积与体积（等体积法求内切球的半径） 题干的设置一般来说在上述的三项考点中选其一项。有关球体表面积与体积考生需熟记公式，有关球 体的求算关键在于半径的求算，下面应试必备给大家详细总结。 从近三年的全国卷的考查情况以及新高考新题型标准来看，球体是高考选填方向必不可少的一类题， 类型1：几何体的外接球，类型2：几何体的内切球。外接球考生需要记住模型及结论，内切球只能采用等 体积法处理，此类题相对有难度，考生多熟练. 53 原创精品资源学科网独家享有版权，侵权必究！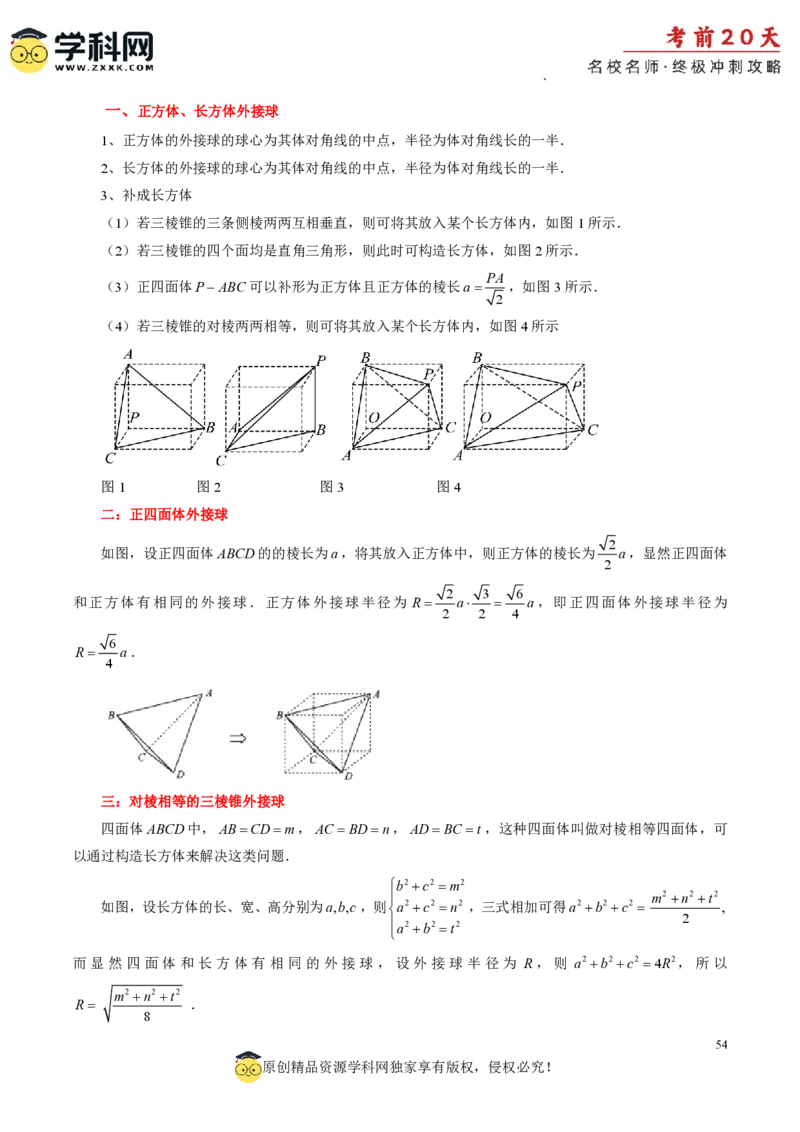 学科网（北京）股份有限公司一、正方体、长方体外接球 1、正方体的外接球的球心为其体对角线的中点，半径为体对角线长的一半． 2、长方体的外接球的球心为其体对角线的中点，半径为体对角线长的一半． 3、补成长方体 （1）若三棱锥的三条侧棱两两互相垂直，则可将其放入某个长方体内，如图1所示． （2）若三棱锥的四个面均是直角三角形，则此时可构造长方体，如图2所示． PA （3）正四面体PABC可以补形为正方体且正方体的棱长a ，如图3所示． 2 （4）若三棱锥的对棱两两相等，则可将其放入某个长方体内，如图4所示 图1 图2 图3 图4 二：正四面体外接球 2 如图，设正四面体ABCD的的棱长为a，将其放入正方体中，则正方体的棱长为 a，显然正四面体 2 2 3 6 和正方体有相同的外接球．正方体外接球半径为 R a  a，即正四面体外接球半径为 2 2 4 6 R a． 4 三：对棱相等的三棱锥外接球 四面体ABCD中，ABCDm，AC BDn，ADBC t，这种四面体叫做对棱相等四面体，可 以通过构造长方体来解决这类问题． b2 c2 m2  m2 n2 t2 如图，设长方体的长、宽、高分别为a,b,c，则a2 c2 n2 ，三式相加可得a2 b2 c2  , 2  a2 b2 t2  而显然四面体和长方体有相同的外接球，设外接球半径为 R，则 a2 b2 c2 4R2，所以 m2 n2 t2 R ． 8 54 原创精品资源学科网独家享有版权，侵权必究！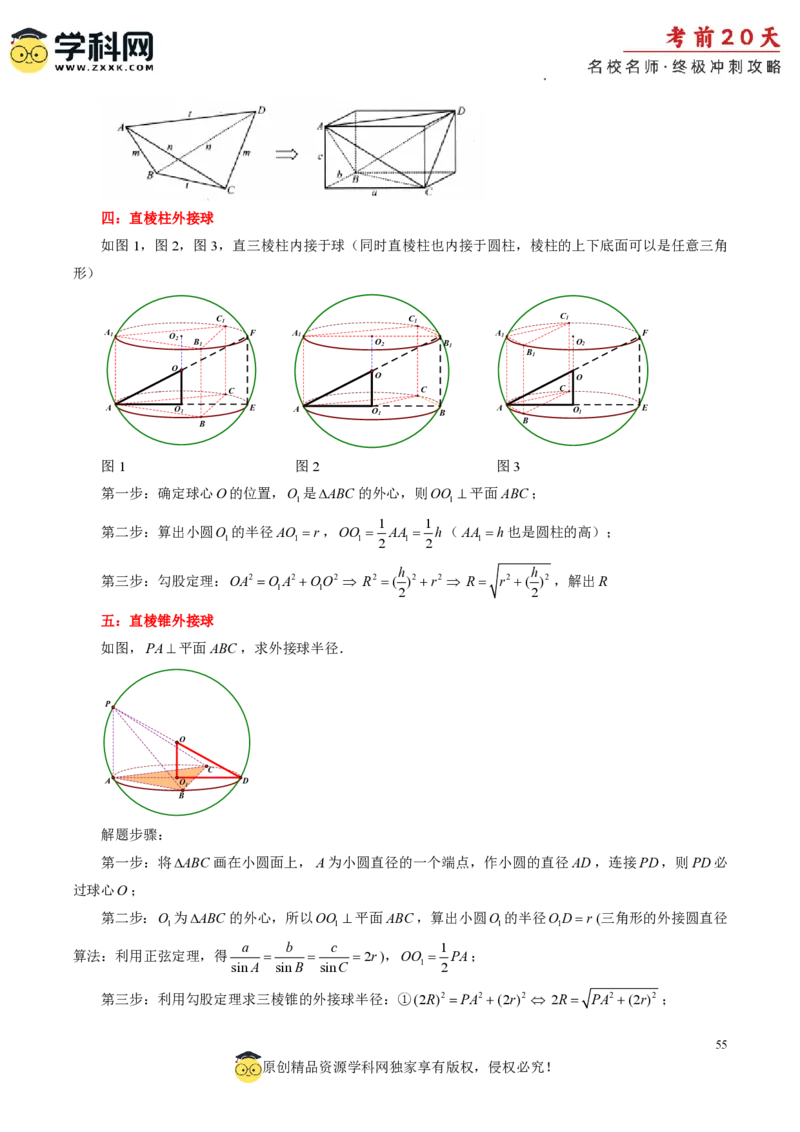 学科网（北京）股份有限公司四：直棱柱外接球 如图1，图2，图3，直三棱柱内接于球（同时直棱柱也内接于圆柱，棱柱的上下底面可以是任意三角 形） C1 C1 C1 A1 O2 B1 F A1 O2 B1 A1 O2 F B1 O O O C C C A O1 E A O1 B A O1 E B B 图3-1 图3-2 图3-3 图1 图2 图3 第一步：确定球心O的位置，O 是ABC 的外心，则OO 平面ABC； 1 1 1 1 第二步：算出小圆O 的半径AO r，OO  AA  h（AA h也是圆柱的高）； 1 1 1 2 1 2 1 h h 第三步：勾股定理：OA2 OA2 OO2  R2 ( )2 r2  R r2 ( )2 ，解出R 1 1 2 2 五：直棱锥外接球 如图，PA平面ABC，求外接球半径． P O C A O1 D B 图5 解题步骤： 第一步：将ABC 画在小圆面上，A为小圆直径的一个端点，作小圆的直径AD，连接PD，则PD必 过球心O； 第二步：O 为ABC 的外心，所以OO 平面ABC，算出小圆O 的半径ODr(三角形的外接圆直径 1 1 1 1 a b c 1 算法：利用正弦定理，得   2r)，OO  PA； sinA sinB sinC 1 2 第三步：利用勾股定理求三棱锥的外接球半径：①(2R)2 PA2 (2r)2  2R PA2 (2r)2 ； 55 原创精品资源学科网独家享有版权，侵权必究！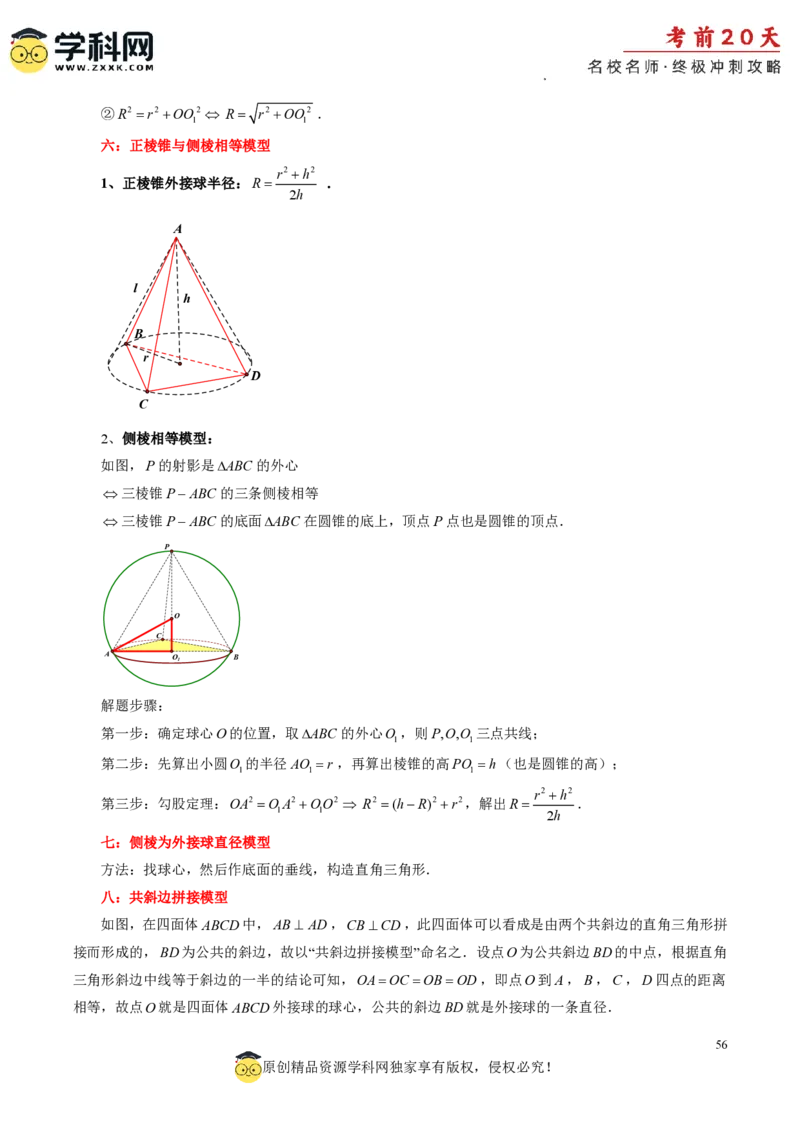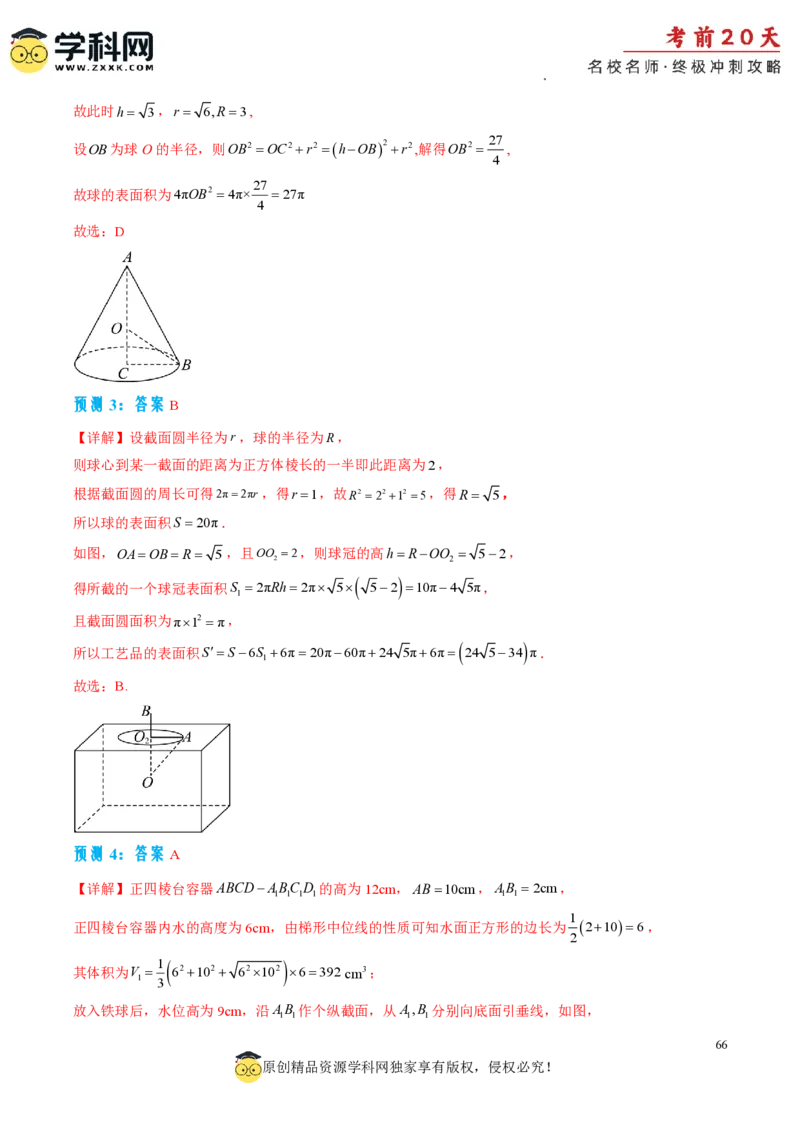 学科网（北京）股份有限公司②R2 r2 OO2  R r2 OO2 ． 1 1 六：正棱锥与侧棱相等模型 r2 h2 1、正棱锥外接球半径：R ． 2h A l h B r D C 2、侧棱相等模型： 如图，P的射影是ABC 的外心 三棱锥PABC的三条侧棱相等 三棱锥PABC的底面ABC 在圆锥的底上，顶点P点也是圆锥的顶点． P O C A O1 B 图5-1 解题步骤： 第一步：确定球心O的位置，取ABC 的外心O ，则P,O,O 三点共线； 1 1 第二步：先算出小圆O 的半径AO r，再算出棱锥的高PO h（也是圆锥的高）； 1 1 1 r2 h2 第三步：勾股定理：OA2 OA2 OO2  R2 (hR)2 r2，解出R ． 1 1 2h 七：侧棱为外接球直径模型 方法：找球心，然后作底面的垂线，构造直角三角形． 八：共斜边拼接模型 如图，在四面体ABCD中，AB AD，CBCD，此四面体可以看成是由两个共斜边的直角三角形拼 接而形成的，BD为公共的斜边，故以“共斜边拼接模型”命名之．设点O为公共斜边BD的中点，根据直角 三角形斜边中线等于斜边的一半的结论可知，OAOC OBOD，即点O到A，B，C，D四点的距离 相等，故点O就是四面体ABCD外接球的球心，公共的斜边BD就是外接球的一条直径． 56 原创精品资源学科网独家享有版权，侵权必究！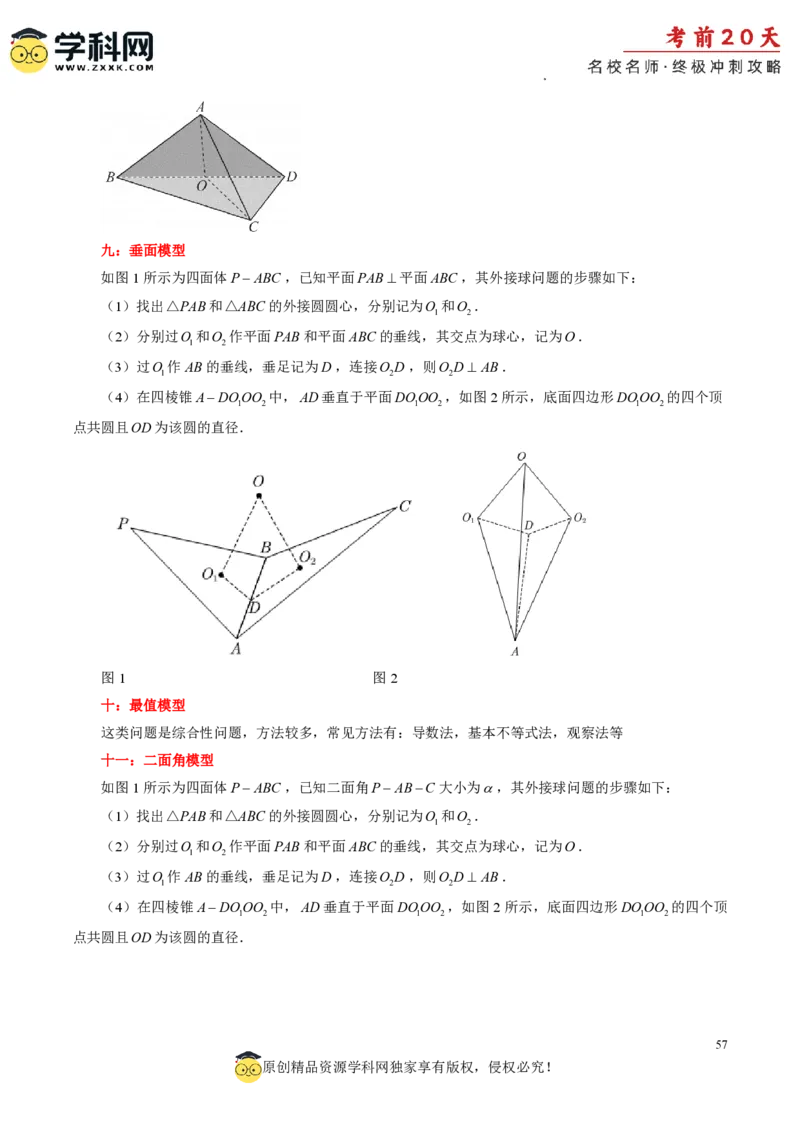 学科网（北京）股份有限公司九：垂面模型 如图1所示为四面体PABC，已知平面PAB平面ABC，其外接球问题的步骤如下： （1）找出△PAB和△ABC的外接圆圆心，分别记为O 和O ． 1 2 （2）分别过O 和O 作平面PAB和平面ABC的垂线，其交点为球心，记为O． 1 2 （3）过O 作AB的垂线，垂足记为D，连接O D，则O D AB． 1 2 2 （4）在四棱锥ADOOO 中，AD垂直于平面DOOO ，如图2所示，底面四边形DOOO 的四个顶 1 2 1 2 1 2 点共圆且OD为该圆的直径． 图1 图2 十：最值模型 这类问题是综合性问题，方法较多，常见方法有：导数法，基本不等式法，观察法等 十一：二面角模型 如图1所示为四面体PABC，已知二面角PABC大小为，其外接球问题的步骤如下： （1）找出△PAB和△ABC的外接圆圆心，分别记为O 和O ． 1 2 （2）分别过O 和O 作平面PAB和平面ABC的垂线，其交点为球心，记为O． 1 2 （3）过O 作AB的垂线，垂足记为D，连接O D，则O D AB． 1 2 2 （4）在四棱锥ADOOO 中，AD垂直于平面DOOO ，如图2 所示，底面四边形DOOO 的四个顶 1 2 1 2 1 2 点共圆且OD为该圆的直径． 57 原创精品资源学科网独家享有版权，侵权必究！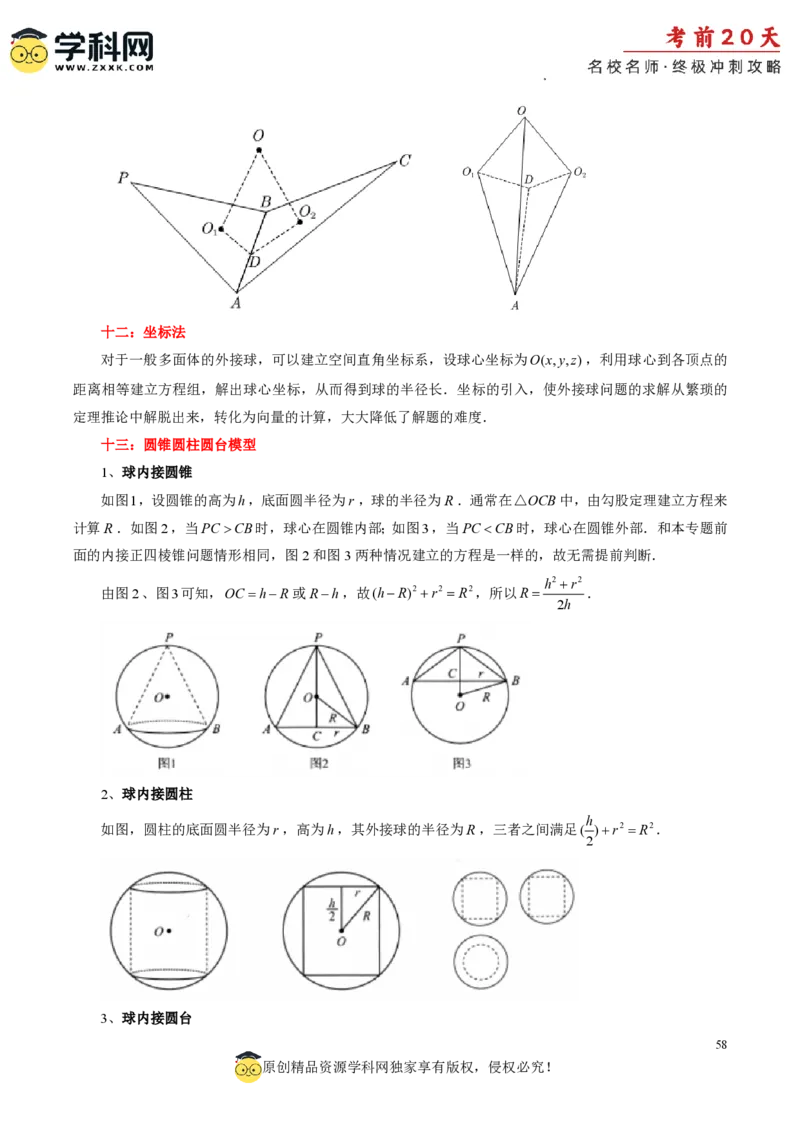 学科网（北京）股份有限公司十二：坐标法 对于一般多面体的外接球，可以建立空间直角坐标系，设球心坐标为O(x,y,z)，利用球心到各顶点的 距离相等建立方程组，解出球心坐标，从而得到球的半径长．坐标的引入，使外接球问题的求解从繁琐的 定理推论中解脱出来，转化为向量的计算，大大降低了解题的难度． 十三：圆锥圆柱圆台模型 1、球内接圆锥 如图1，设圆锥的高为h，底面圆半径为r ，球的半径为R．通常在△OCB中，由勾股定理建立方程来 计算R．如图2，当PC CB时，球心在圆锥内部；如图3，当PCCB时，球心在圆锥外部．和本专题前 面的内接正四棱锥问题情形相同，图2和图3两种情况建立的方程是一样的，故无需提前判断． h2 r2 由图2、图3可知，OC hR或Rh，故(hR)2 r2 R2，所以R ． 2h 2、球内接圆柱 h 如图，圆柱的底面圆半径为r ，高为h，其外接球的半径为R，三者之间满足( )r2 R2． 2 3、球内接圆台 58 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司r2 r2 h2  2 R2 r2  2 1  ，其中r,r ,h分别为圆台的上底面、下底面、高． 2  2h  1 2 十四：锥体内切球 3V 方法：等体积法，即R 体积 S 表面积 十五：棱切球 方法：找切点，找球心，构造直角三角形 典例1【2023新高考1卷】下列物体中，能够被整体放入棱长为1（单位：m）的正方体容器（容器壁厚度 忽略不计）内的有（ ） A. 直径为0.99m的球体 B. 所有棱长均为1.4m的四面体 C. 底面直径为0.01m，高为1.8m的圆柱体 D. 底面直径为1.2m，高为0.01m的圆柱体 【答案】ABD 【解析】对于选项A：因为0.99m1m，即球体的直径小于正方体的棱长， 所以能够被整体放入正方体内，故A正确； 对于选项B：因为正方体的面对角线长为 2m，且 2 1.4， 所以能够被整体放入正方体内，故B正确； 对于选项C：因为正方体的体对角线长为 3m，且 3 1.8， 所以不能够被整体放入正方体内，故C不正确； 对于选项D：因为1.2m1m，可知底面正方形不能包含圆柱的底面圆， 如图，过AC 的中点O作OE  AC ，设OEI AC  E， 1 1 3 CC OE 可知AC  2,CC 1,AC  3,OA= ，则tanCAC  1  ， 1 1 2 1 AC AO 1 OE  6 即 2 3 ，解得OE  ， 4 2 2  6  3 9 9 6 且     0.62，即 0.6，   4 8 24 25 4   故以AC 为轴可能对称放置底面直径为1.2m圆柱， 1 59 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司若底面直径为1.2m的圆柱与正方体的上下底面均相切，设圆柱的底面圆心O ，与正方体的下底面的切点 1 为M ， CC OM 可知：AC OM,OM 0.6，则tanCAC  1  1 ， 1 1 1 1 AC AO 1 1 0.6 即  ，解得AO 0.6 2 ， 2 AO 1 1 根据对称性可知圆柱的高为 320.6 2 1.7321.21.4140.03520.01， 所以能够被整体放入正方体内，故D正确； 故选：ABD. 典例2【2022新高考全国Ⅱ卷】 已知正三棱台的高为1，上、下底面边长分别为3 3和4 3，其顶点都在 同一球面上，则该球的表面积为（ ） A. 100π B. 128π C. 144π D. 192π 【答案】A 3 3 4 3 【解析】设正三棱台上下底面所在圆面的半径r,r ，所以2r  ,2r  ，即r 3,r 4， 1 2 1 sin60o 2 sin60o 1 2 设球心到上下底面的距离分别为d ,d ，球的半径为R，所以d  R2 9，d  R2 16，故 1 2 1 2 d d 1或d d 1，即 R2 9 R2 16 1或 R2 9 R2 16 1，解得R2 25符合题 1 2 1 2 意，所以球的表面积为S 4πR2 100π． 故选：A． 典例3【2022新高考全国Ⅰ卷】已知正四棱锥的侧棱长为l，其各顶点都在同一球面上.若该球的体积为36， 且3l 3 3，则该正四棱锥体积的取值范围是（ ）  81 27 81 27 64 A.  18,  B.  ,  C.  ,  D. [18,27]  4   4 4   4 3  【答案】 C 60 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司【解析】∵球的体积为36，所以球的半径R 3, [方法一]：导数法 设正四棱锥的底面边长为2a，高为h， 则l2 2a2 h2，32 2a2 (3h)2, 所以6hl2，2a2 l2 h2 1 1 2 l4 l2 1 l6  所以正四棱锥的体积V  Sh 4a2h (l2  ) = l4  ， 3 3 3 36 6 9 36 1 l5  1 24l2  所以V 4l3  l3  ， 9 6  9  6  当3l 2 6时，V0，当2 6 l 3 3时，V0， 64 所以当l 2 6 时，正四棱锥的体积V 取最大值，最大值为 ， 3 27 81 又l 3时，V  ，l 3 3时，V  , 4 4 27 所以正四棱锥的体积V 的最小值为 ， 4 27 64 所以该正四棱锥体积的取值范围是  ， .  4 3  故选：C. [方法二]：基本不等式法 4 2 1 1 122hhh 3 64 由方法一故所以V  a2h  6hh2 h 122hhh„    (当且仅当 3 3 3 3 3 3   h4取到)， 3 3 3 1 1 3 3 3 27 当h  时，得a  ，则V  a2h ( )2  ; 2 2 min 3 3 2 2 4 61 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司3 9 当l 3 3时，球心在正四棱锥高线上，此时h 3 ， 2 2 2 3 3 3 3 1 1 3 3 9 81 64 a  a  ，正四棱锥体积V  a2h ( )2   ，故该正四棱锥体积的取 2 2 2 1 3 3 2 2 4 3 27 64 值范围是[ , ]. 4 3 典例4【2021新高考全国Ⅱ卷】 北斗三号全球卫星导航系统是我国航天事业的重要成果．在卫星导航系统 中，地球静止同步卫星的轨道位于地球赤道所在平面，轨道高度为36000km（轨道高度是指卫星到地球表 面的距离）．将地球看作是一个球心为O，半径r为6400km的球，其上点A的纬度是指OA与赤道平面所 成角的度数．地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为，记卫星信号覆盖 地球表面的表面积为S 2r2(1cos)（单位：km2），则S占地球表面积的百分比约为（ ） A. 26% B. 34% C. 42% D. 50% 【答案】C 【解析】由题意可得，S占地球表面积的百分比约为： 6400 1 2r2(1cos) 1cos 640036000 .   0.4242% 4r2 2 2 故选：C. 预测1（2024·宁夏固原·模拟预测）已知四面体ABCD的各顶点均在球O的球面上，平面ABC平面 BCD，ABBC  AC CD2,BC CD，则球O的表面积为（ ） 28π A． B．14π C．28π D．32π 3 预测2（2024·陕西安康·模拟预测）一种锥底孵化桶常用于鱼虾类的孵化，其桶底采用上大下小的漏斗状设 计，底部设计成锥形便于收集幼苗.铁匠老张准备用一个半径R为的扇形铁片作为圆锥的侧面，制作成一个 圆锥形无盖漏斗（接缝处忽略不计）.若该漏斗的容积为2 3π，且漏斗的顶点及底面圆周都在球O的表面 上，则当R最小时，球O的表面积为（ ） 9π A． B．9π C．18π D．27π 2 预测3（2024·四川成都·模拟预测）球面被平面所截得的一部分叫做球冠（如图）.球冠是曲面，是球面的 一部分.截得的圆叫做球冠的底，垂直于截面的直径被截得的一段叫做球冠的高.阿基米德曾在著作《论球与 62 原创精品资源学科网独家享有版权，侵权必究！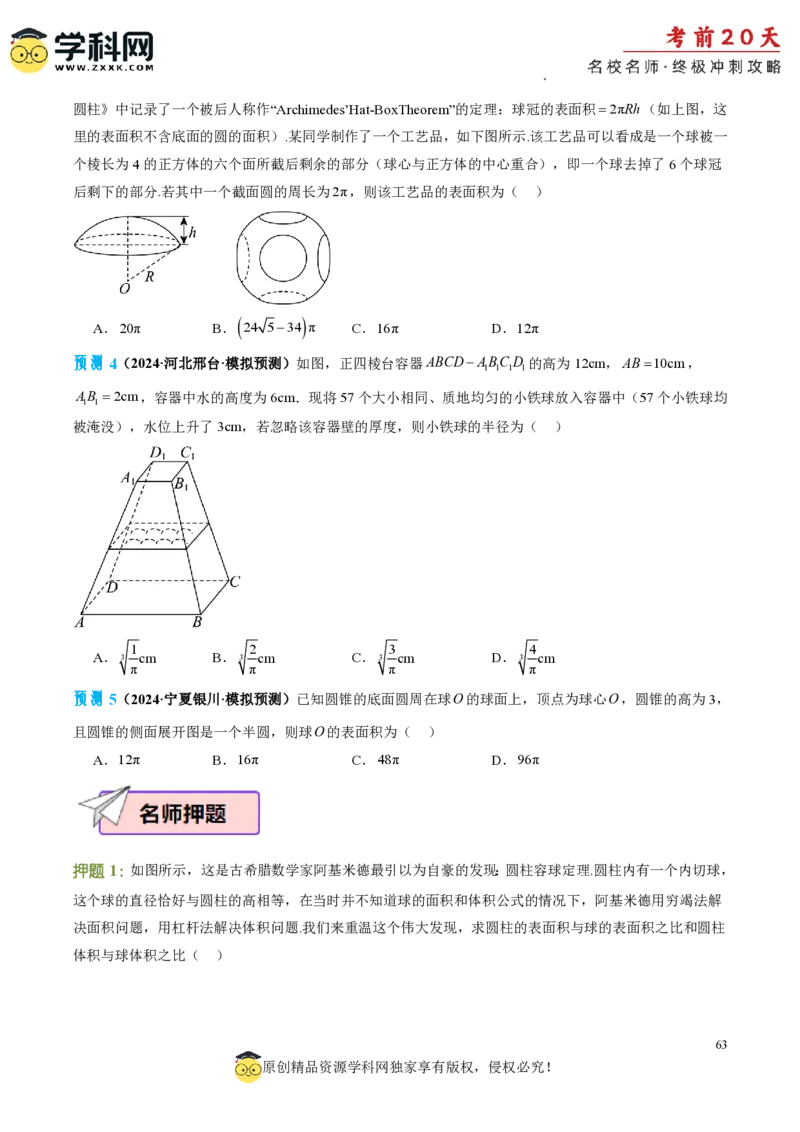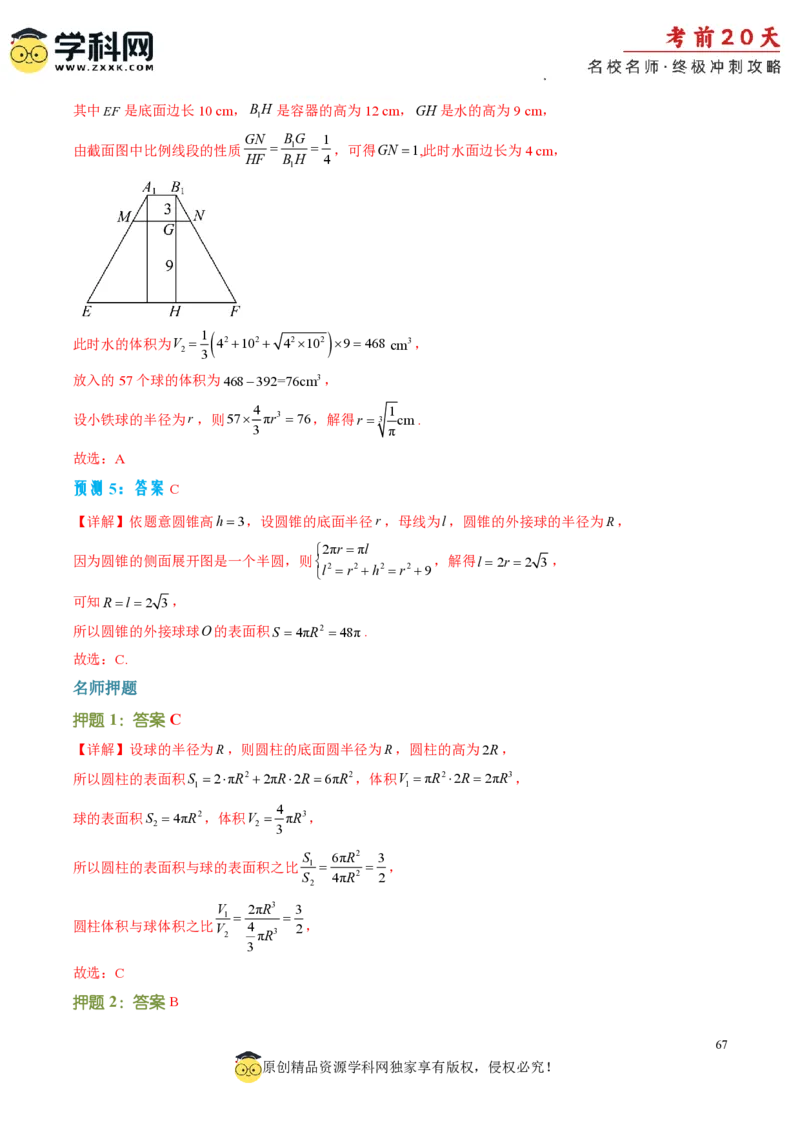 学科网（北京）股份有限公司圆柱》中记录了一个被后人称作“Archimedes’Hat-BoxTheorem”的定理：球冠的表面积2πRh（如上图，这 里的表面积不含底面的圆的面积）.某同学制作了一个工艺品，如下图所示.该工艺品可以看成是一个球被一 个棱长为4的正方体的六个面所截后剩余的部分（球心与正方体的中心重合），即一个球去掉了6个球冠 后剩下的部分.若其中一个截面圆的周长为2π，则该工艺品的表面积为（ ）   A．20π B． 24 534 π C．16π D．12π 预测4（2024·河北邢台·模拟预测）如图，正四棱台容器ABCDABCD 的高为12cm，AB10cm， 1 1 1 1 AB 2cm，容器中水的高度为6cm．现将57个大小相同、质地均匀的小铁球放入容器中（57个小铁球均 1 1 被淹没），水位上升了3cm，若忽略该容器壁的厚度，则小铁球的半径为（ ） 1 2 3 4 A．3 cm B．3 cm C．3 cm D．3 cm π π π π 预测5（2024·宁夏银川·模拟预测）已知圆锥的底面圆周在球O的球面上，顶点为球心O，圆锥的高为3， 且圆锥的侧面展开图是一个半圆，则球O的表面积为（ ） A．12π B．16π C．48π D．96π 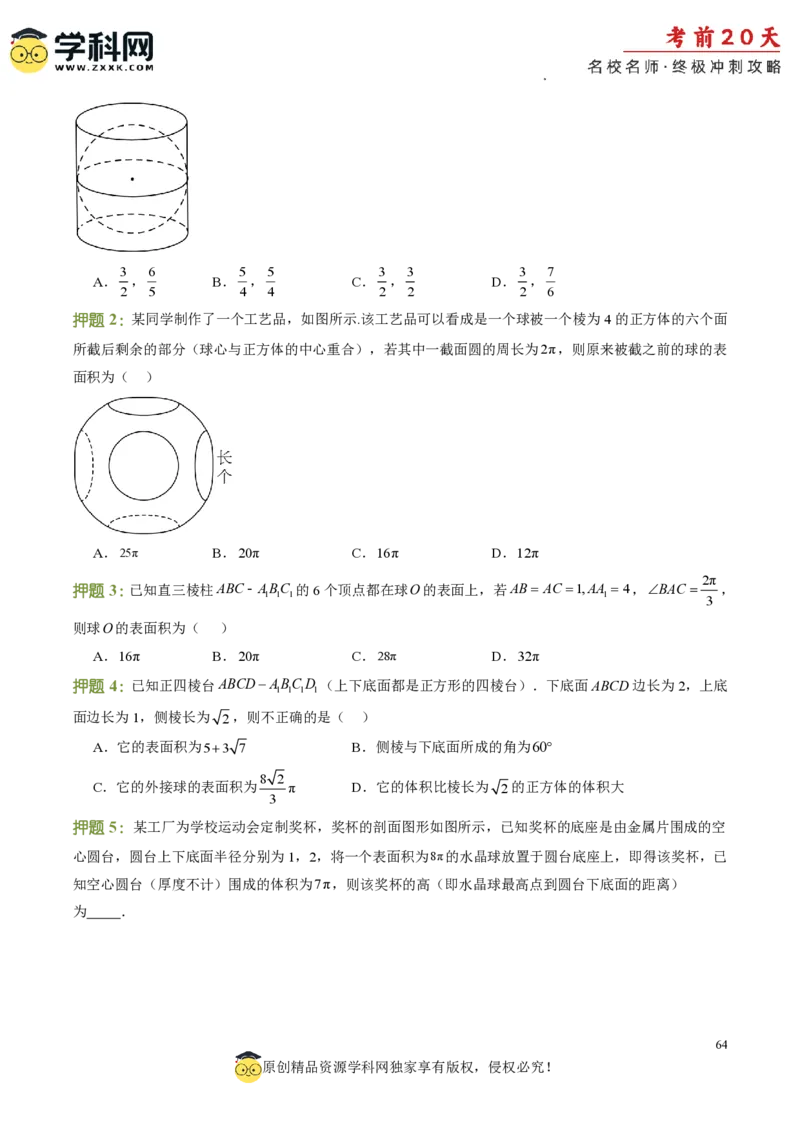押题1：如图所示，这是古希腊数学家阿基米德最引以为自豪的发现：圆柱容球定理.圆柱内有一个内切球， 这个球的直径恰好与圆柱的高相等，在当时并不知道球的面积和体积公式的情况下，阿基米德用穷竭法解 决面积问题，用杠杆法解决体积问题.我们来重温这个伟大发现，求圆柱的表面积与球的表面积之比和圆柱 体积与球体积之比（ ） 63 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司3 6 5 5 3 3 3 7 A． ， B． ， C． ， D． ， 2 5 4 4 2 2 2 6 押题2：某同学制作了一个工艺品，如图所示.该工艺品可以看成是一个球被一个棱为4的正方体的六个面 所截后剩余的部分（球心与正方体的中心重合），若其中一截面圆的周长为2π，则原来被截之前的球的表 面积为（ ） A．25π B．20π C．16π D．12π 2π 押题3：已知直三棱柱ABC- ABC 的6个顶点都在球O的表面上，若AB AC 1,AA 4，BAC  ， 1 1 1 1 3 则球O的表面积为（ ） A．16π B．20π C．28π D．32π 押题4：已知正四棱台ABCDABCD （上下底面都是正方形的四棱台）．下底面ABCD边长为2，上底 1 1 1 1 面边长为1，侧棱长为 2，则不正确的是（ ） A．它的表面积为53 7 B．侧棱与下底面所成的角为60 8 2 C．它的外接球的表面积为 π D．它的体积比棱长为 2的正方体的体积大 3 押题5：某工厂为学校运动会定制奖杯，奖杯的剖面图形如图所示，已知奖杯的底座是由金属片围成的空 心圆台，圆台上下底面半径分别为1，2，将一个表面积为8π的水晶球放置于圆台底座上，即得该奖杯，已 知空心圆台（厚度不计）围成的体积为7π，则该奖杯的高（即水晶球最高点到圆台下底面的距离） 为 ． 64 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司名校预测 预测1：答案A 【详解】因为平面ABC平面BCD，ABBC  AC CD2,BC CD， 所以可将四面体ABCD看作底面是等边三角形的直三棱柱的一部分，如图所示： 则四面体ABCD的外接球即直三棱柱的外接球， 2 2 3 因为底面三角形ABC的外心到三角形ABC的顶点的长度为  22 12  ， 3 3 2 2 3 7 所以直三棱柱的外接球的半径r 12   ，   3 3   2  7 28π 则球O的表面积S 4πr2 4π   ，  3 3   故选：A. 预测2：答案D 【详解】设圆锥的底面圆半径以及圆锥的高分别为r,h， 1 故V  πr2h2 3π，所以r2h6 3， 3 6 3 3 3 3 3 3 3 3 3 由于R2 r2h2  h2   h2 33  h2 9， h h h h h 3 3 当且仅当 h2，即h 3时等号成立， h 65 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司故此时h 3，r 6,R3, 27 设OB为球O的半径，则OB2 OC2r2 hOB2r2,解得OB2  , 4 27 故球的表面积为4πOB2 4π× 27π 4 故选：D 预测3：答案B 【详解】设截面圆半径为r，球的半径为R， 则球心到某一截面的距离为正方体棱长的一半即此距离为2， 根据截面圆的周长可得2π2πr，得r1，故R2 2212 5，得R 5， 所以球的表面积S 20π． 如图，OAOBR 5，且OO 2，则球冠的高hROO  52， 2 2   得所截的一个球冠表面积S 2πRh2π 5 52 10π4 5π， 1 且截面圆面积为π12 π，   所以工艺品的表面积SS6S 6π20π60π24 5π6π 24 534 π． 1 故选：B. 预测4：答案A 【详解】正四棱台容器ABCDABCD 的高为12cm，AB10cm，AB 2cm， 1 1 1 1 1 1 1 正四棱台容器内水的高度为6cm，由梯形中位线的性质可知水面正方形的边长为 2106， 2 1  其体积为V  62102 62102 6392 cm3； 1 3 放入铁球后，水位高为9cm，沿AB 作个纵截面，从A,B 分别向底面引垂线，如图， 1 1 1 1 66 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司其中EF 是底面边长10 cm，BH 是容器的高为12 cm，GH是水的高为9 cm， 1 GN BG 1 由截面图中比例线段的性质  1  ，可得GN 1,此时水面边长为4 cm， HF BH 4 1 1  此时水的体积为V  42102 42102 9468 cm3， 2 3 放入的57个球的体积为468392=76cm3， 4 1 设小铁球的半径为r，则57 πr3 76，解得r 3 cm. 3 π 故选：A 预测5：答案C 【详解】依题意圆锥高h3，设圆锥的底面半径r，母线为l，圆锥的外接球的半径为R， 2πrπl 因为圆锥的侧面展开图是一个半圆，则 ，解得l 2r2 3， l2 r2h2 r29 可知Rl2 3， 所以圆锥的外接球球O的表面积S 4πR2 48π. 故选：C. 名师押题 押题1：答案C 【详解】设球的半径为R，则圆柱的底面圆半径为R，圆柱的高为2R， 所以圆柱的表面积S 2πR22πR2R6πR2，体积V πR22R2πR3， 1 1 4 球的表面积S 4πR2，体积V  πR3， 2 2 3 S 6πR2 3 所以圆柱的表面积与球的表面积之比 1   ， S 4πR2 2 2 V 2πR3 3 1   圆柱体积与球体积之比V 4 2， 2 πR3 3 故选：C 押题2：答案B 67 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司【详解】设球的半径为R，截面圆的半径为r，两个截面圆间的距离为2d， 因为截面圆的周长为2π，可得2πr2π，解得r1， 又因为该工艺品可以看成是一个球被一个棱为4的正方体的六个面所截后剩余的部分， 所以两截面圆之间的距离为2d 4，解得d 2， 根据球的截面的性质，可得R2 r2d2 1222 5， 所以球的表面积为S4πR2 20π. 故选：B. 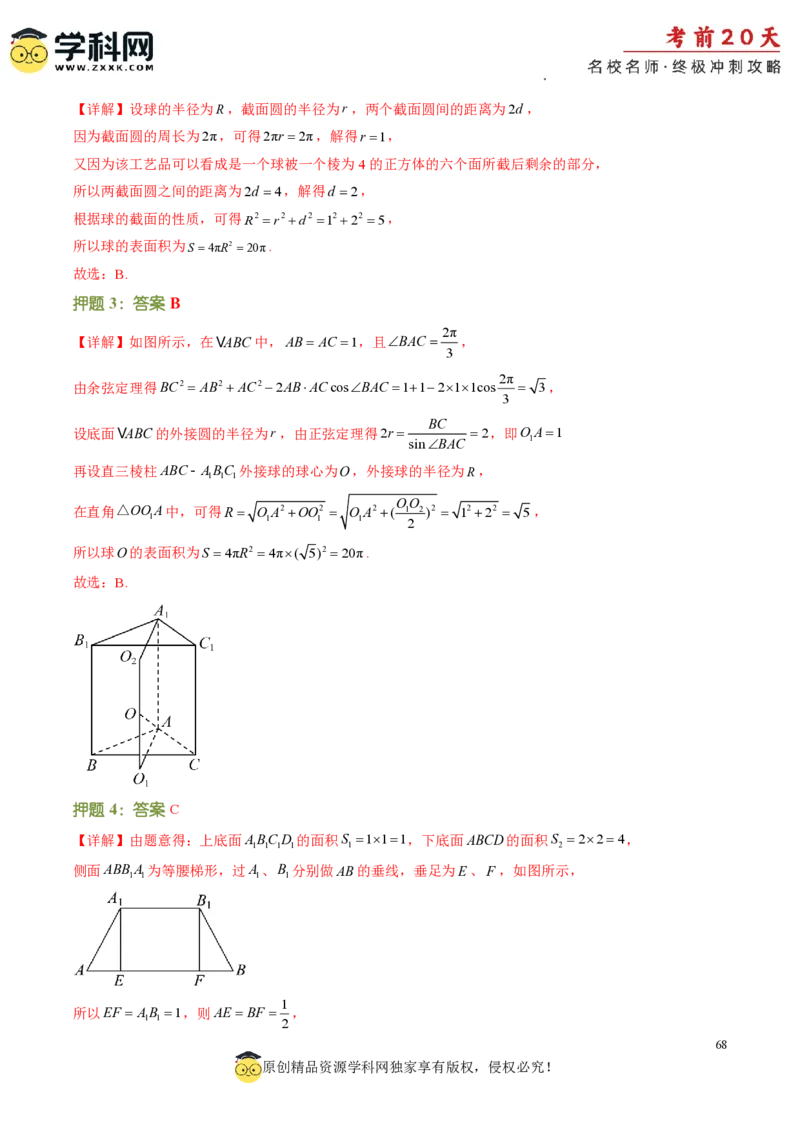押题3：答案B 2π 【详解】如图所示，在VABC中，AB AC 1，且BAC  ， 3 2π 由余弦定理得BC2  AB2AC22ABACcosBAC 11211cos  3， 3 BC 设底面VABC的外接圆的半径为r，由正弦定理得2r 2，即OA1 sinBAC 1 再设直三棱柱ABC- ABC 外接球的球心为O，外接球的半径为R， 1 1 1 OO 在直角△OOA中，可得R OA2OO2  OA2( 1 2)2  1222  5， 1 1 1 1 2 所以球O的表面积为S 4πR2 4π( 5)2 20π. 故选：B. 押题4：答案C 【详解】由题意得：上底面ABCD 的面积S 111，下底面ABCD的面积S 224， 1 1 1 1 1 2 侧面ABBA 为等腰梯形，过A、B 分别做AB的垂线，垂足为E、F ，如图所示， 1 1 1 1 1 所以EF  AB 1，则AEBF  ， 1 1 2 68 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司7 所以BF  BB2BF2  ， 1 1 2 1 7 3 7 所以梯形ABBA 的面积为S  (12)  ， 1 1 3 2 2 4 所以正四棱台ABCDABCD 的表面积S S S 4S 53 7，故A正确； 1 1 1 1 1 2 3 连接AC ，BD，且交于点O ，连接AC，BD交于点O ，连接OO ， 1 1 1 1 1 2 1 2 则OO 垂直底面ABCD， 1 2 过A作AG AO 于G，则AG底面ABCD，则四边形AGOO 为矩形， 1 1 2 1 1 2 1 2 由题意得AC  AB BC  2，所以AO  ， 1 1 1 12 1 12 1 1 2 同理AC 2 2,AO  2， 2 2 又AO GO ，所以AG ， 1 1 2 2 2 在RtVAGA中， AG 2 1， 1 cosAAG   1 AA 2 2 1 所以AAG60，即侧棱与下底面所成的角为60，故B正确； 1 6 所以AG AA2AG2  ． 1 1 2 连接CO ，在RtVCOO 中，CO  OO2CO  2， 1 2 1 1 2 1 2 1 2 1 12 所以点O 到A、B、C、D、A、B 、C 、D 的距离相等，均为 2， 2 1 1 1 1 所以点O 即为正四棱台ABCDABCD 外接球的球心，且外接球半径R 2， 2 1 1 1 1 所以外接球的表面积S4π( 2)2 8π，故C错误； 1 1 6 7 6 正四棱台的体积V  (S S  SS )OO  (14 14)  ， 1 3 1 2 1 2 1 2 3 2 6 棱长为 2的正方体的体积V ( 2)3 2 2， 2 7 6 所以V 6 7 3 147 ，所以V V ， 1    1 1 2 V 2 2 12 144 2 69 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司所以正四棱台ABCDABCD 的体积比棱长为 2的正方体的体积大，故D正确. 1 1 1 1 故选：C． 押题5：答案4 2/ 24 【详解】如图所示， 设水晶球的半径为r，则4πr2 8π，解得r 2， h  设圆台的高为h，则7π π12π22π 1222 ，解得h3， 3  2 又因为水晶球球心到圆台上底面的距离OA  2 12 1， 所以该奖杯的高为hr14 2． 故答案为：4 2. 70 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司数列、统计与概率（解答题） 年份 题号 知识点 考点 ①数列求通项 17 数列 ②数列求和 2021年I卷 ①分布列 18 统计与概率 ②期望 ①数列求通项 17 等差数列 ②数列求和求最值 2021年II卷 ①独立重复试验 21 统计与概率 ②二项分布 ①递推关系求通项 17 数列 ②裂项相消求和 2022年I卷 ①2×2列表 20 统计与概率 ②条件概率 17 数列 求通项 2022年II卷 ①频率分布直方图 19 统计与概率 ②二项分布 ①数列求通项 20 数列 ②数列求和 2023年新高考1 ①两点分布 21 统计与概率 ②二项分布 ①数列求通项 18 数列 ②数列求和求最值 2023年新高考2 ①频率分布直方图 19 统计与概率 ②二项分布 近三年，数列和统计与概率在解答题占据两个位置，考查的考点一般来说是： 1、数列（①递推关系求通项②数列求和） 71 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司2、统计与概率（①频率分布直方图② 2×2列联表及独立性检验③二项分布④超几何分布⑤简单随机抽样即 及回归分析） 题干的设置一般来说在上述的多项考点中选其一项或两项。数列和统计与概率需考生需理解题意，其 次掌握各项技巧，设置此类题难度一般，用心研究必能夺分。 从近三年的全国卷的考查情况以及新高考新题型标准来看，统计与概率是高考解答题方向必不可少的 一类题，类型1：二项分布。类型2：超几何分布。类型3：条件概率，今年高考大概率数列与统计融为一 体，考生需从多方面认识，把握数列各项求和，争取快速拿下. 一、数列求和 一．公式法 n(a a ) n(n1) （1）等差数列a 的前n项和S  1 n na  d ，推导方法：倒序相加法． n n 2 1 2 na ，q1 1  （2）等比数列a 的前n项和S a (1qn) ，推导方法：乘公比，错位相减法． n n 1 ，q1   1q （3）一些常见的数列的前n项和： n 1 n ①k 123L n n(n1)；2k 246L 2nn(n1) 2 k1 k1 n ②(2k1)135L (2n1)n2； k1 n 1 ③k2 12 22 32 L n2  n(n1)(2n1)； 6 k1 n n(n1) ④k3 13 23 33 L n3 [ ]2 2 k1 二．几种数列求和的常用方法 （1）分组转化求和法：一个数列的通项公式是由若干个等差或等比或可求和的数列组成的，则求和时 可用分组求和法，分别求和后相加减． （2）裂项相消法：把数列的通项拆成两项之差，在求和时中间的一些项可以相互抵消，从而求得前n 项和． （3）错位相减法：如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，那么 72 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司求这个数列的前n项和即可用错位相减法求解． （4）倒序相加法：如果一个数列a 与首末两端等“距离”的两项的和相等或等于同一个常数，那么求 n 这个数列的前n项和即可用倒序相加法求解． 三．常见的裂项技巧 积累裂项模型1：等差型 1 1 1 （1）   n(n1) n n1 1 1 1 1 （2）  (  ) n(nk) k n nk 1 1 1 1 （3）  (  ) 4n2 1 2 2n1 2n1 1 1 1 1  （4）     n(n1)(n2) 2n(n1) (n1)(n2) 1 1 1 1 1 （5）   (  ) n(n2 1) n(n1)(n1) 2 (n1)n n(n1) n2 1 1  （6）  1   4n2 1 4 (2n1)(2n1) 3n1 4(n1)(n3) 1 1 1 1 （7）  4(  )(  ) (n1)(n2)(n3) (n1)(n2)(n3) n2 n3 n1 n2 1 （8）n(n1) n(n1)(n2)(n1)n(n1). 3 1 （9）n(n1)(n2) n(n1)(n2)(n3)(n1)n(n1)(n2) 4 1 1 1 1  （10）     n(n1)(n2)(n3) 3n(n1)(n2) (n1)(n2)(n3) 2n1 1 1 （11）   n2(n1)2 n2 (n1)2 n1 1 1 1  （12）     n2(n2)2 4n2 (n2)2  积累裂项模型2：根式型 1 （1）  n1 n n1 n 1 1 （2）  ( nk  n) nk  n k 1 1 （3）  ( 2n1 2n1) 2n1 2n1 2 73 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司1 1 n(n1)1 1 1 （4） 1   1  n2 (n1)2 n(n1) n n1 1 （5） 3 n2 2n1 3 n2 1 3 n2 2n1 3 n13 n  3 n13 n1(3 n2 2n1 3 n2 1 3 n2 2n1) 2 1 (n1) nn n1 (n1) nn n1 1 1 （6）     (n1) nn n1 (n1) n 2 (n n1)2 n(n1) n n1   积累裂项模型3：指数型 2n (2n11)(2n 1) 1 1 （1）    (2n11)(2n 1) (2n11)(2n 1) 2n 1 2n11 3n 1 1 1 （2）  (  ) (3n 1)(3n11) 2 3n 1 3n11 n2 2(n1)n 2 1  1 1 1 （3）       n(n1)2n n(n1)2n n n1 2n n2n1 (n1)2n (4n1)3n1 1 9 1 1 3n1 3n1 （4）     3n1     n(n2) 2(n2) n 2n2 n  (2n1)(1)n (1)n (1)n1 （5）   n(n1) n n1 1 1 （6）a  n3n1，设a (anb)3n [a(n1)b]3n1，易得a ,b ， n n 2 4 1 1 于是a  (2n1)3n  (2n3)3n1 n 4 4 (1)n(n2 4n2)2n (1)n(n2 4n2) (1)n  n2 n2(n1)n  （7）   n2n(n1)2n1 n(n1)2n1 n(n1)2n1 (1)n  1 1  1 1 (1)n (1)n1   (1)n     ( )n    2n1 n2n (n1)2n1  2 2 n2n (n1)2n1  积累裂项模型4：对数型 a log n1 logan1log a a a a a n n 积累裂项模型5：三角型 1 1 （1）  (tantan) coscos sin() 1 1 （2）  tan(n1)tann cosncos(n1) sin1 74 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司1 （3）tantan (tantan)1 tan() tanntan(n1) （4）a tantan(n1);tan1tann(n1) ， n 1tanntan(n1) tanntan(n1) tanntan(n1) 则tanntan(n1) 1,a  1 tan1 n tan1 二、统计与概率 两点分布 两点分布：是很简单的一种概率分布，其实验结果只有两种可能，且概率和为1；两点分布列又称01 分布列或佰努利分布列；两点分布能清晰的反映出事件的正反两面.两点分布的应用十分广泛，如抽取的彩 票是否中奖，买回的意见产品是否为正品，新生儿的鉴定，投篮是否命中等.（想象成扔硬币问题） 超几何分布 超几何分布：一般地，在含有M 件次品的N 件产品中，任取n件，其中恰有 X 件次品数，则事件 Ck Cnk {X k}发 生 的 概 率 为 P(X k) M NM ,k 0,1,2,L ,m, 其 中 mmin{M,n}， 且 Cn N n N,M  N,n,M,NN．称分布列 X 0 1 … m C0Cn C1 Cn1 CmCnm M NM M NM M NM p Cn Cn … Cn N N N 为超几何分布列．如果随机变量X 的分布列为超几何分布列，则称随机变量X 服从超几何分布. 注意：若有N 件产品，其中M 件为次品，无放回地任意抽取n件，则其中恰有的次品件数X 是服出超几 何分布. 二项分布 1．n重伯努利试验的概念 只包含两个可能结果的试验叫做伯努利试验，将一个伯努利试验独立地重复进行n 次所组成的随机试验 称为n重伯努利试验． 2．n重伯努利试验具有如下共同特征 (1)同一个伯努利试验重复做n次； (2)各次试验的结果相互独立． 3．二项分布（若有N 件产品，其中M 件是次品，有放回地任意抽取n件，则其中恰有的次品件数X 是 服从二项分布的） 一般地，在n重伯努利试验中，设每次试验中事件A发生的概率为p(00，我们称P(B|A)＝ 为在事件A发生的条件下，事件B P（A） 发生的条件概率，简称条件概率． 2．概率的乘法公式 由条件概率的定义，对任意两个事件A与B，若P(A)>0，则P(AB)＝P(A)P(B|A)．我们称上式为概率的乘 法公式． 3．条件概率的性质 设P(A)>0，则 (1)P(Ω|A)＝1； (2)如果B与C是两个互斥事件，则P((B∪C)|A)＝P(B|A)＋P(C|A)； － － (3)设B和B互为对立事件，则P(B |A )＝1－P(B|A )． 4．全概率公式 在全概率的实际问题中我们经常会碰到一些较为复杂的概率计算，这时，我们可以用 “化整为零”的思想 将它们分解为一些较为容易的情况分别进行考虑 一般地，设A ，A ，…，A 是一组两两互斥的事件，A ∪A ∪…∪A ＝Ω，且P(A)>0，i＝1，2，…，n， 1 2 n 1 2 n i n 则对任意的事件B⊆Ω，有P(B)＝ ∑ P(A)P(B|Ai） . i＝ 1 i 我们称上面的公式为全概率公式，全概率公式是概率论中最基本的公式之一． 5．贝叶斯公式 设A ，A ，…，A 是一组两两互斥的事件，A ∪A ∪…∪A ＝Ω，且P(A)>0，i＝1，2，…，n，则对任 1 2 n 1 2 n i 意事件B⊆Ω，P(B)>0， P（Ai）P（B|Ai） P  A  P  B/ A  有P(A|B） ＝ = i i i＝1，2，…，n. i P（B） n P  A  P  B/ A  k k k1 6.在贝叶斯公式中，P(A)和P(A |B)分别称为先验概率和后验概率． i i 离散型随机变量的均值与方差 技巧总结 Ⅰ：随机变量的数字特征 76 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司1．离散型随机变量的均值的概念 一般地，若离散型随机变量X的分布列为 X x x … x … x 1 2 i n P p p … p … p 1 2 i n n 则称E(X)＝x p ＋x p ＋…＋xp＋…＋x p ＝x p 为随机变量X的均值或数学期望． 1 1 2 2 i i n n i i i1 2．离散型随机变量的均值的意义 均值是随机变量可能取值关于取值概率的加权平均数，它综合了随机变量的取值和取值的概率，反映了随 机变量取值的平均水平． 3．离散型随机变量的均值的性质 若Y＝aX＋b，其中a，b均是常数(X是随机变量)，则Y也是随机变量，且有E(aX＋b)＝aE(X)＋b. 证明如下：如果Y＝aX＋b，其中a，b为常数，X是随机变量，那么Y也是随机变量．因此P(Y＝ax＋b)＝ i P(X＝x)，i＝1,2,3，…，n，所以Y的分布列为 i Y ax ＋b ax ＋b … ax＋b … ax ＋b 1 2 i n P p p … p … p 1 2 i n 于是有E(Y)＝(ax ＋b)p ＋(ax ＋b)p ＋…＋(ax＋b)p＋…＋(ax ＋b)p ＝a(x p ＋x p ＋…＋xp＋…＋x p )＋ 1 1 2 2 i i n n 1 1 2 2 i i n n b(p ＋p ＋…＋p＋…＋p )＝aE(X)＋b，即E(aX＋b)＝aE(X)＋b. 1 2 i n n 方差：．称D(X)(x E(X))2p 为随机变量X 的方差，它反映了离散型随机变量X 相对于期望的平均波 i i i1 动大小(或说离散程度)，其算术平方根 DX为随机变量X 的标准差，记作X，方差(或标准差)越小表 明X 的取值相对于期望越集中，否则越分散． Ⅱ： 均值与方差的性质     (1)E aX b aE X b． (2)D  aX b  a2D  X  (a,b为常数)．（3）D  X   E  X2    E  X 2 两点分布、二项分布、超几何分布的期望、方差       (1)若X服从两点分布，则E X  p，D X  p1 p ．         (2)若X服从二项分布，即X ~ B n, p ，则E X np,D X np1 p ．   (3)若X服从超几何分布，即X ~ H n,M,N 时，    nM nM N M N n     E X  ．D X  N N2 N 1  方法总结： 求离散型随机变量的均值、方差的基本步骤： 第一步：判断取值：先根据随机变量的意义，确定随机变量可以取哪些值； 77 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司第二步：探求概率：利用排列组合、枚举法、概率公式(常见的有古典概型公式、几何概型公式、互斥 事件的概率和公式、独立事件的概率积公式，以及对立事件的概率公式)等，求出随机变量取每个值时的概 率； 第三步：写分布列：按规范形式写出分布列，并注意用分布列的性质(概率总和为1)检验所求的分布列 是否正确； 第四步：求期望值和方差：利用数学期望和方差的公式分别求期望和方差的值．对于有些实际问题中 的随机变量，如果能够断定它服从某常见的典型分布(如二项分布X～B(n，p))，则此随机变量的期望可直 接利用这种典型分布的期望公式(E(X)＝np)求得．因此，应熟记常见的典型分布的期望与方差公式，可加快 解题速度． 正态分布 技巧总结 1．正态曲线及其性质 (1)正态曲线： 函数 , x 2 1  e  x 2    2 2 ，x,，其中实数μ，σ(σ>0)为参数，我们称φ μ，σ (x)的图象为正态分布 密度曲线，简称正态曲线． (2)正态曲线的性质： ①曲线位于x轴上方，与x轴不相交； ②曲线是单峰的，它关于直线x＝μ对称； 1 ③曲线在x＝μ处达到峰值 ； 2πσ ④曲线与x轴之间的面积为1； ⑤当σ一定时，曲线的位置由μ确定，曲线随着μ的变化而沿x轴平移，如图甲所示； ⑥当μ一定时，曲线的形状由σ确定，σ越大，曲线越“矮胖”，总体分布越分散；σ越小．曲线越“瘦高”．总 体分布越集中，如图乙所示： 甲 乙 2．正态分布 b   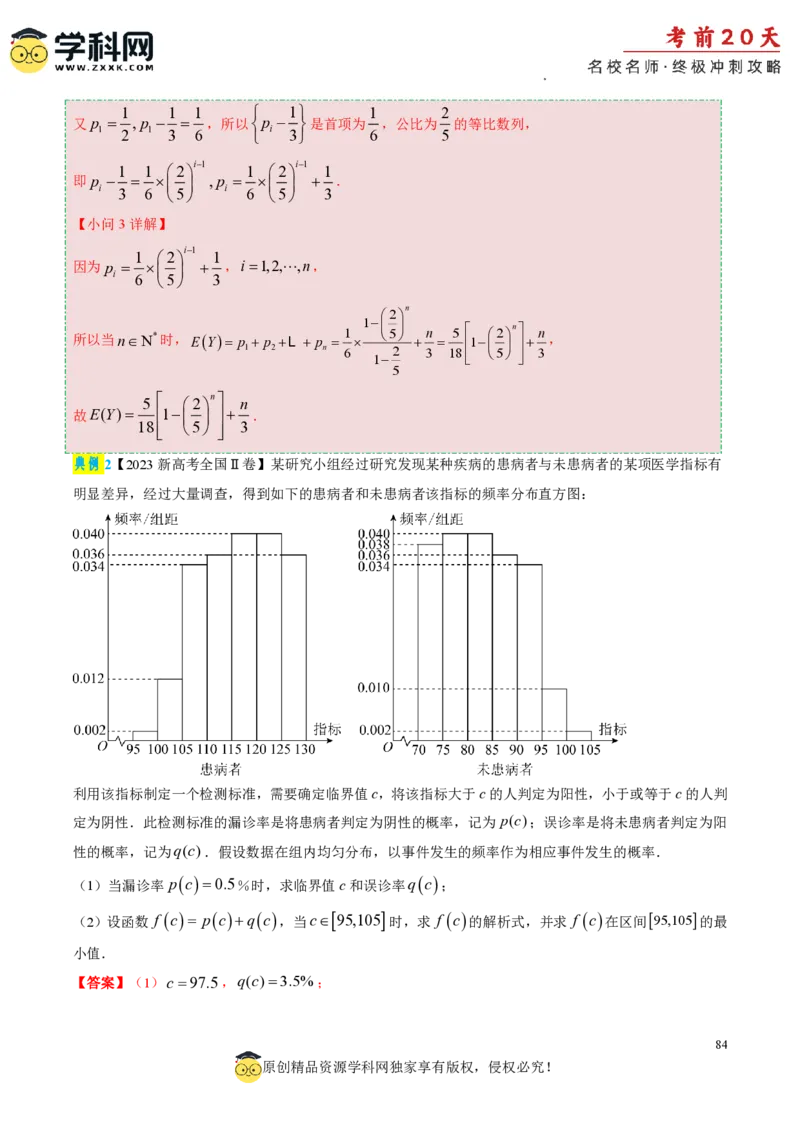一般地，如果对于任何实数a，b(a2且mN*）人组成一组，负责人从某组中任选2人进行询问，若选出的2人的购票类型相同，则该 组标为A，否则该组标为B，记询问的某组被标为B的概率为p． （i）试用含m的代数式表示p； （ii）若一共询问了5组，用gp表示恰有3组被标为B的概率，试求gp的最大值及此时m的值． 押题3：甲、乙、丙三人进行传球游戏，每次投掷一枚质地均匀的正方体骰子决定传球的方式:当球在甲手 中时，若骰子点数大于3，则甲将球传给乙，若点数不大于3，则甲将球保留；当球在乙手中时，若骰子点 数大于4，则乙将球传给甲，若点数不大于4，则乙将球传给丙；当球在丙手中时，若骰子点数大于3，则 丙将球传给甲，若骰子点数不大于3，则丙将球传给乙.初始时，球在甲手中. (1)求投掷3次骰子后球在乙手中的概率； (2)设前三次投掷骰子后，球在甲手中的次数为X ，求随机变量X 的分布列和数学期望. 押题4：某公司计划在员工团建活动中设置一个抽奖环节．工作人员在仓库中随机抽取了20个规格相同的 礼盒，各礼盒中均有1个质地相同的小球，礼盒和小球的颜色为红色或黑色，且颜色分布如下表所示． 礼盒颜色 小球颜色 合计 红色 黑色 红色 m n mn 黑色 2 6 8 合计 m2 n6 20 10 已知从上述礼盒中随机选取2个礼盒，红色与黑色礼盒恰好各1个的概率为 ． 19 (1)求m,n的值． (2)为提高活动的趣味性，设抽奖过程及中奖规则如下： ①将20个礼盒放在1个箱子中，每人有放回地分两次抽取，每次抽取1个礼盒，并记录礼盒和该礼盒中的 小球的颜色． ②两次抽取后的结果分四种情况：礼盒与礼盒中的小球的颜色两次均相同；2个礼盒的颜色相同，但2个小 球的颜色不同；2个礼盒的颜色不同，但2个小球的颜色相同；礼盒与礼盒中的小球的颜色两次均不相同． ③按②抽取后的结果的可能性大小，设概率越小，对应奖项的奖金越高． ④活动奖励分四个等级，奖金额分别为一等奖800元，二等奖400元，三等奖200元，四等奖100元． 若预计有60名员工参与抽奖活动（每人抽奖1次），求抽奖活动的奖金总额的数学期望． 押题5：某地区工会利用“健步行APP”开展健步走活动.为了解会员的健步走情况，工会在某天从系统中抽 取了100名会员，统计了当天他们的步数（千步为单位），并将样本数据分为3,5，5,7，7,9，…， 17,19，19,21九组，整理得到如图所示的频率分布直方图. 91 原创精品资源学科网独家享有版权，侵权必究！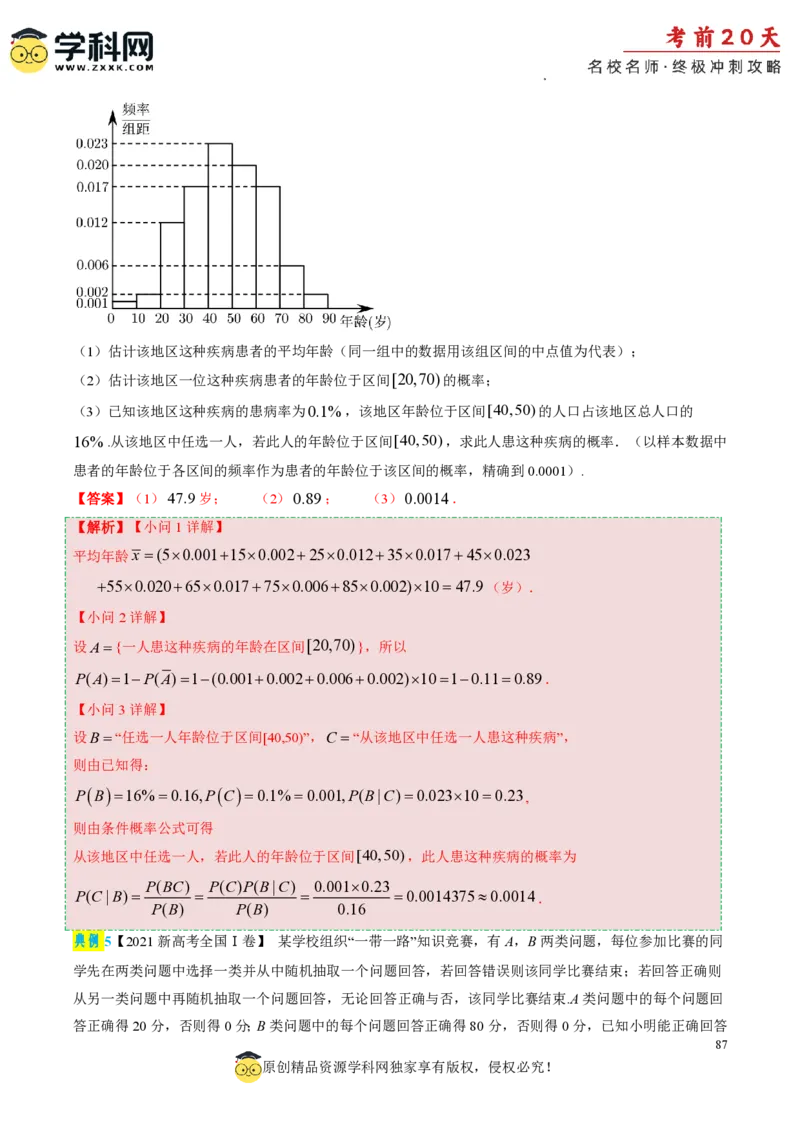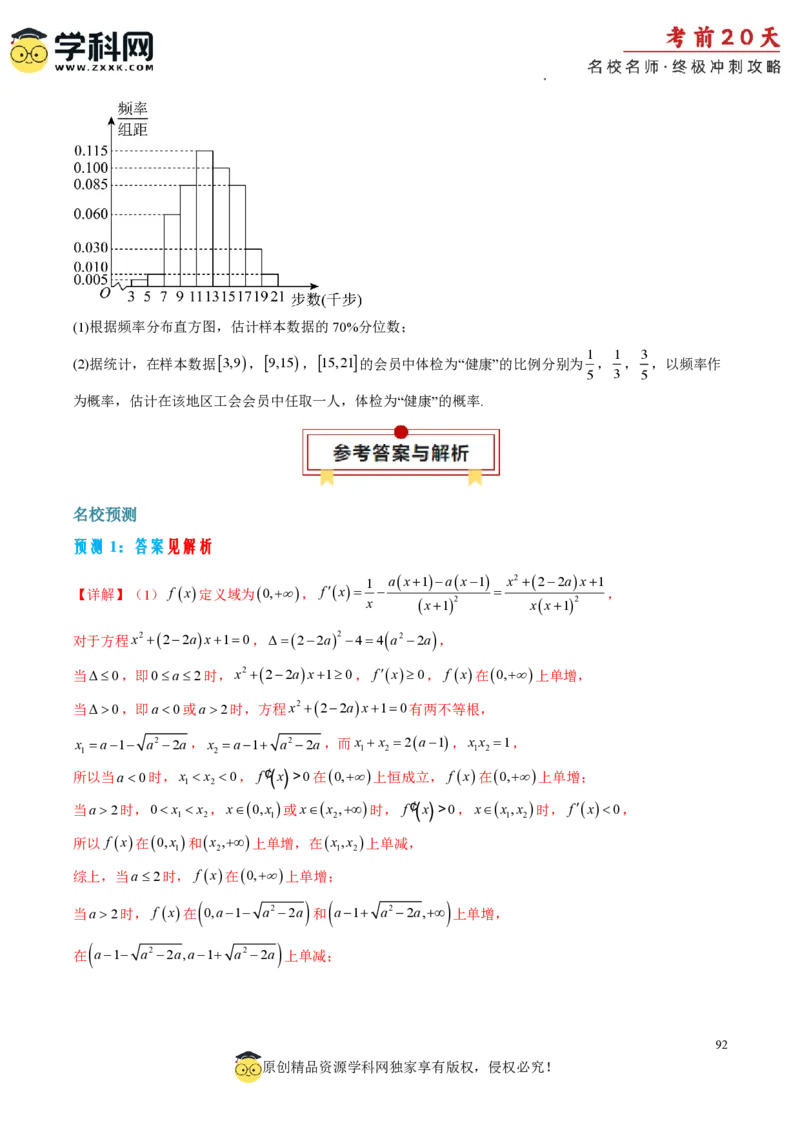 学科网（北京）股份有限公司(1)根据频率分布直方图，估计样本数据的70%分位数； 1 1 3 (2)据统计，在样本数据3,9，9,15，15,21的会员中体检为“健康”的比例分别为 ， ， ，以频率作 5 3 5 为概率，估计在该地区工会会员中任取一人，体检为“健康”的概率. 名校预测 预测1：答案见解析 1 ax1ax1 x222ax1 【详解】（1） f x定义域为0,， fx   ， x x12 xx12 对于方程x222ax10，22a244  a22a  ， 当0，即0a2时，x222ax10， fx0， f x在0,上单增， 当0，即a0或a2时，方程x222ax10有两不等根， x a1 a22a ，x a1 a22a，而x x 2a1，xx 1， 1 2 1 2 1 2 所以当a0时，x x 0， f¢(x)>0在0,上恒成立， f x在0,上单增； 1 2 当a2时，0x x ，x0,x 或xx ,时， f¢(x)>0，xx,x 时， fx0， 1 2 1 2 1 2 所以 f x在0,x 和x ,上单增，在x,x 上单减， 1 2 1 2 综上，当a2时， f x在0,上单增；     当a2时， f x在 0,a1 a22a 和 a1 a22a, 上单增，   在 a1 a22a,a1 a22a 上单减； 92 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司 ax 1  ax 1 lnx  1 lnx  2  （2） f x  f x   1 x 1   2 x 1  k  1 2  1 2 x x x x 1 2 1 2 x 2ax x  x 2ax x  ln 1  1 2 ln 1  1 2 x x 1x 1 x xx x x 1  2 1 2  2 1 2 1 2 x x x x 1 2 1 2 x ln 1 x 2a lnx lnx ，  2   1 2 1 x x 12a21 x x 1 2 1 2 2a lnx lnx 1 lnx lnx 2 所以要证k  ，即证 1 2 1 1，即证 1 2  ， a1 x x a1 x x x x 1 2 1 2 1 2  x  2 1 1 x 2x x  x x  也即证ln 1  1 2 ln 1  2 0（*）成立． x x x x x 2 1 2 2 1 1 x 2 x 2t1 设t 1 0,1 ，函数htlnt ，由（1）知ht在0,上单增，且h10， x t1 2 所以t0,1时，ht0，所以（*）成立，原不等式得证； A20 100998281 （3）由题可得p 100  ， 10020 10020 因为998190292 902，988290282 902，…，918990212 902，  9  19 所以p  ， 10 2t1 又由（2）知t1,，htlnt 0， t1 10  2 1 10 10  9  10 2 取t ，有ln  ln  0， 9 9 10 9 19 1 9 10 19 10 19 即ln  2，即   e2，  9   9   9  19 1 所以p   ． 10 e2 1 2  预测2：答案(1) (2)p ,1 4 3  【详解】（1）4秒后质点移动到点1，则质点需向右移动3次，向左移动1次， 1 4 1 故PX 1C3    ． 4 2 4 93 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司（2）由题意，X可能的取值为4,2,0,2， 则PX 41 p3， PX 2C21 p2 p3p1 p2， 3 PX 0C11 p1 p2 3p21 p， 3 PX 2 p3， 2 所以EX41 p323p1 p22p3 23p20，解得p ， 3 2  又因为p0,1，所以p ,1． 3  11 预测3：答案(1) (2)分布列见解析；EX1 24 【详解】（1）记“射击一次获得‘优秀射击手’称号”为事件A；射击一次获得一等奖为事件B； 1 射击一次获得一等奖为事件C，所以有ABUC，所以PB ， 3 1 1 1 1 1 11 PC   ，所以PAPBCPBPC   . 4 2 8 3 8 24 （2）获得三等奖的次数为X ，X 的可能取值为0，1，2，3，4； 1 1 1 1 记“获得三等奖”为事件D，所以PD    ， 8 4 2 4 1 0 3 4 81 1 1 3 3 27 所以PX 0C0      ，PX 1C1      ， 4 4 4 256 4 4 4 64 1 2 3 2 54 27 1 3 3 12 3 PX 2C2       ，PX 3C3      ， 4 4 4 256 128 4 4 4 256 64 1 4 3 0 1 PX 4C0      ，所以 4 4 4 256 X 0 1 2 3 4 81 27 27 3 1 P 256 64 128 64 256  1 1 显然X B4， ，EX4 1.  4 4 预测4：答案(1)有99.9%的把握认为学生选择《红楼梦》还是《三国演义》与性别有关； (2)见解析 2 【详解】（1）男､女生各100人，选择《红楼梦》的有90人，其中女生有 9060. 3 补全二联表： 94 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司《红楼梦》 《三国演义》 合计 男生 30 70 100 女生 60 40 100 合计 90 110 200 200304060702 200 所以K2   10.828， 90100110100 11 故有99.9%的把握认为学生选择《红楼梦》还是《三国演义》与性别有关； 2 （2）依题意~B(3, )． 3 2 1 1 P(0)C0( )0( )3  ， 3 3 3 27 2 1 6 2 P(1)C1( )( )2   ， 3 3 3 27 9 2 1 12 4 P(2)C2( )2( )  ， 3 3 3 27 9 2 8 P(3)C3( )3  ． 3 3 27 的分布列为：  0 1 2 3 1 2 4 8 P 27 9 9 27 2 E()3 2． 3 8 预测5：答案(1)有关(2) 15 55(2020105)2 1177 539 【详解】（1）由表中数据，可得K2    11.9787.879， 30252530 335 45 所以能在犯错误的概率不超过0.005的前提下认为喜欢“应用统计”课程与性别有关． 6 m （2）设所抽样本中有m个男生，则 ＝ ，得m4， 30 20 所以样本中有4个男生，2个女生，分别记作B ，B ，B ，B ，G ，G ， 1 2 3 4 1 2 从中任选2人的基本事件有(B ，B )，(B ，B )，(B ，B )，(B ，G )，(B ，G )， 1 2 1 3 1 4 1 1 1 2 (B ，B )，(B ，B )，(B ，G )，(B ，G )，(B ，B )，(B ，G )，(B ，G )， 2 3 2 4 2 1 2 2 3 4 3 1 3 2 (B ，G )，(B ，G )，(G ，G )，共15个， 4 1 4 2 1 2 其中恰有1个男生和1个女生的事件有(B ，G )，(B ，G )，(B ，G )，(B ，G )， 1 1 1 2 2 1 2 2 95 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司(B ，G )，(B ，G )，(B ，G )，(B ，G )，共8个， 3 1 3 2 4 1 4 2 8 所以恰有1个男生和1个女生的概率为 . 15 名师押题 押题1：答案(1)n6.(2)分布列见解析，E(Y)1. 4 2 【详解】（1）因为P(X5)  ，所以n6. n 3 （2）样本空间{(m,t∣) m,t{1,2,3,4,5,6}}，共有36个样本点. 记事件A“数字之和小于7”，事件B“数字之和等于7"， 事件C “数字之和大于7”. A{(1,1),(1,2),(2,1),(1,3),(3,1),(2,2),(1,4),(4,1),(2,3),(3,2)， (1,5),(5,1),(2,4),(4,2),(3,3)}，共15种， 15 5 故P(Y0)P(A)  36 12 B{(1,6),(6,1),(2,5),(5,2),(3,4),(4,3)}，共6种， 6 1 故P(Y1)P(B)  ； 36 6 C {(2,6),(6,2),(3,5),(5,3),(4,4),(3,6),(6,3),(4,5),(5,4)， (4,6),(6,4),(5,5),(5,6),(6,5),(6,6)}，共15种， 15 5 故P(Y2)P(C)  ； 36 12 从而Y的分布列为： Y 0 1 2 5 1 5 P 12 6 12 5 1 5 故E(Y)0 1 2 1 12 6 12 3 押题2：答案(1) 10 4m 216 (2)（i）p ；（ii）m3时，gp  ． m23m2 max 625 【详解】（1）因为购买单程上山票、单程下山票和双程票的人数之比为3:5:2，所以这10人中，购买单程 3 5 2 上山票、单程下山票和双程票的人数分别为：10 3，10 5，10 2， 10 10 10 C2C2 3 故随机抽取的4人中恰有2人购买单程上山票的概率P 7 3  ． C4 10 10 96 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司（2）（i）从m2人中任选2人，有C2 种选法，其中购票类型相同的有C2 C2种选法，则询问的某组被 m2 m 2 C2 C2 m2m2 4m 标为B的概率p1 m 2 1  ． C2 m23m2 m23m2 m2 （ii）由题意，5组中恰有3组被标为B的概率g(p)C3p3(1 p)2 10p3(12p p2)10(p32p4 p5)， 5 所以g(p)10(3p28p35p4)10p2(p1)(5p3)，0 p1，  3 所以当p0, 时，gp0，函数gp单调递增，  5 3  当p ,1时，gp0，函数gp单调递减， 5  所以当p 3 时，gp取得最大值，且最大值为g   3 C3   3  3   1 3  2  216 ． 5 5 5 5  5 625 4m 3 由p  ，m>2且mN*，得m3． m23m2 5 216 当m3时，5组中恰有3组被标为B的概率最大，且gp的最大值为 ． 625 3 11 押题3：答案(1) (2)分布列见解析，期望为 8 8 【详解】（1）解：由题意得；若投掷3次骰子后球在乙手中， 1 3 第一类是第一次甲保留，第二次甲保留，第三次甲传给乙，其概率为：P   ； 1 2 1 1 1 第二类是第一次甲传给乙，第二次乙传给甲，第三次甲传给乙，其概率为P    ； 2 2 3 2 1 2 1 第三类是第一次甲传给乙，第二次乙传给丙，第三次丙传给乙，其概率为P    ； 3 2 3 2 1 3 1 1 1 1 2 1 3 所以投掷3次骰子后球在乙手中的概率为：PP P P          ； 1 2 3 2 2 3 2 2 3 2 8 （2）由题意得，X的可能取值为：0，1，2，3， 1 3 1 3 1 1 1 1 1 1 7 则PX 3  ， PX 2         ， 2 2 2 3 2 2 2 3 24 1 1 2 1 1 1 1 2 1 5 1 2 1 1 PX 1          ，PX 0    ， 2 2 3 2 3 2 2 3 2 12 2 3 2 6 故X的分布列为： X 0 1 2 3 1 5 7 1 P 6 12 24 8 97 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司1 5 7 1 11 EX0 1 2 3  6 12 24 8 8 押题4：答案(1)m8,n4(2)20040元 【详解】（1）由表中数据可得：红色礼盒共有2m个，黑色礼盒有n6个， 2mn6 10 所以从上述礼盒中随机选取2个礼盒，红色与黑色礼盒恰好各1个的概率为  ，又 C2 19 20 mn12，解得m8,n4 （2）颜色分布如下表所示． 礼盒颜色 小球颜色 合计 红色 黑色 红色 8 4 12 黑色 2 6 8 合计 10 10 20 8 2 因此礼盒为红色，里面的球也为红色的概率为  ， 20 5 2 1 礼盒为红色，里面的球为黑色的概率为  ， 20 10 4 1 礼盒为黑色，里面的球为红色的概率为  ， 20 5 6 3 礼盒为黑色，里面的球也为黑色的概率为  ， 20 10 2 2  1  2 1 2  3  2 3 故礼盒与礼盒中的小球的颜色两次均相同的概率为          ； 5 10 5 10 10 2  1  1  3  1 2礼盒的颜色相同，但2个小球的颜色不同的概率为2  2   ； 5 10 5 10 5 2 1  1   3  11 2个礼盒的颜色不同，但2个小球的颜色相同2  2   ； 5 5 10 10 50 2  3  1  1  7 礼盒与礼盒中的小球的颜色两次均不相同2  2   ． 5 10 5 10 25 进而可得一个员工在抽奖活动中的所得奖金X 的分布列为 X 800 400 200 100 1 11 7 3 P 5 50 25 10 98 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司1 11 7 3 一个员工抽奖的奖金期望为EX800 400 200 100 334, 5 50 25 10 则60个人奖活动的奖金总额的数学期望60EX3346020040元. 押题5：答案(1)14.5 (2)0.38 【详解】（1）解：（1）由于在3,13的样本数据比例为：0.010.020.120.170.230.55 0.70.55 ∴样本数据的70%分位数在13,15内∴估计为：132 14.5. 0.750.55 （2）（2）设任取的会员数据在3,9，9,15，15,21中分别为事件A，A ，A ， 1 2 3 ∴PA0.010.020.120.15，PA 0.170.20.230.6，PA 0.170.060.020.25 1 2 3 设事件A在该地区工会会员中任取一人体检为“健康” 1 1 3 PA0.15 0.6 0.25 0.38. 5 3 5 99 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司