文档内容
专题4.9 曲线运动综合问题
【考纲解读与考频分析】
曲线运动综合问题考查的知识点多,综合性强,成为高考命题热点。
【高频考点定位】
曲线运动 综合问题
考点一:曲线运动综合问题
【3年真题链接】
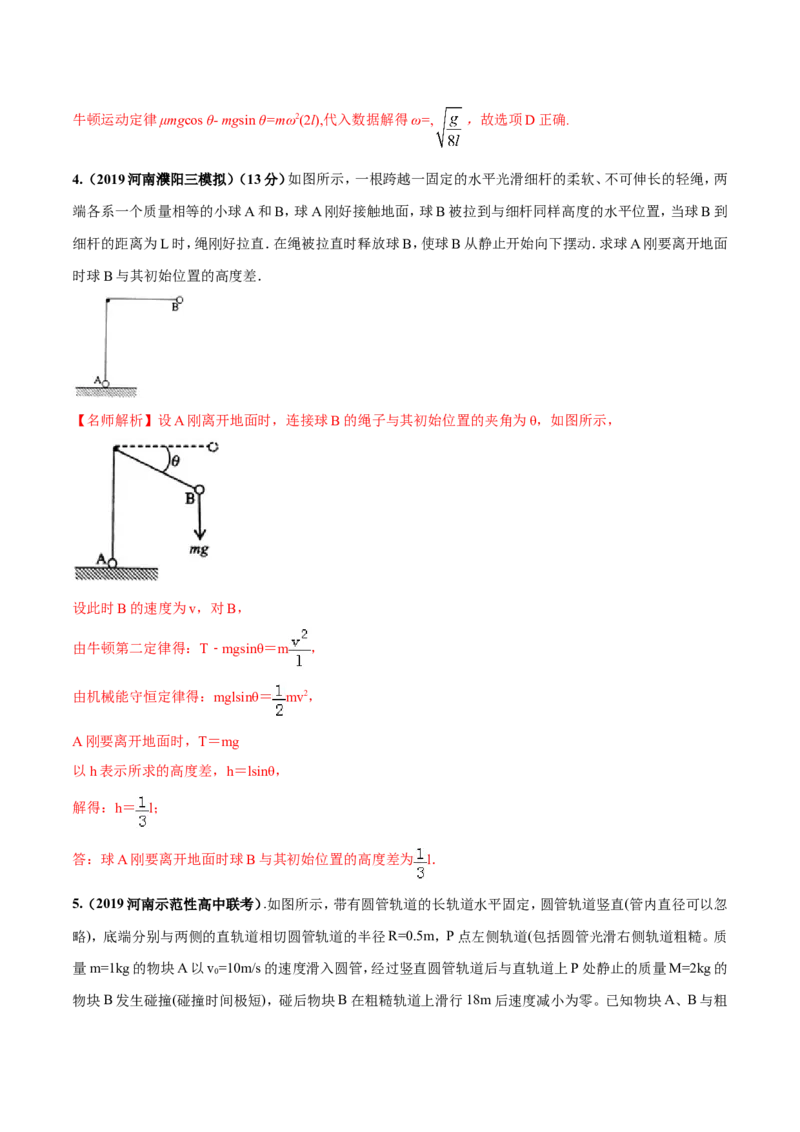
1.(2019海南物理·10)三个小物块分别从3条不同光滑轨道的上端由静止开始滑下。已知轨道1、轨道2、轨
道3的上端距水平地面的高度均为 ;它们的下端水平,距地面的高度分别为 、 、 ,
如图所示。若沿轨道1、2、3下滑的小物块的落地点到轨道下端的水平距离分别记为 、 、 ,则( )
A. B. C. D.
【参考答案】BC
【名师解析】沿轨道1下滑,由机械能守恒定律,mg(4h-h)= mv2,下滑至轨道1末端时速度v= ,从
0 0 1 1
轨道1末端飞出做平抛运动,由平抛运动规律,s=vt,h= gt2,联立解得s=2 h;沿轨道2下滑,由机械
1 11 0 1 1 0能守恒定律,mg(4h-2h)= mv2,下滑至轨道2末端时速度v= ,从轨道2末端飞出做平抛运动,由
0 0 2 2
平抛运动规律,s=vt,2h= gt2,联立解得s=4 h;沿轨道3下滑,由机械能守恒定律,mg(4h-3h)=
2 22 0 2 2 0 0 0
mv2,下滑至轨道3末端时速度v= ,从轨道3末端飞出做平抛运动,由平抛运动规律,s=vt,3h=
3 3 3 33 0
gt2,联立解得s=2 h;显然,s> s ,s> s ,s= s ,选项BC正确。
3 3 0 2 1 2 3 1 3
2.(2017·江苏卷·5)如图所示,一小物块被夹子夹紧,夹子通过轻绳悬挂在小环上,小环套在水平光滑细杆上,
物块质量为M,到小环的距离为L,其两侧面与夹子间的最大静摩擦力均为F.小环和物块以速度v向右匀速
运动,小环碰到杆上的钉子P后立刻停止,物块向上摆动.整个过程中,物块在夹子中没有滑动.小环和夹子的
质量均不计,重力加速度为g.下列说法正确的是( )
(A)物块向右匀速运动时,绳中的张力等于2F (B)小环碰到钉子P时,绳中的张力大于2F
(C)物块上升的最大高度为2v2 (D)速度v不能超过 (2F Mg)L
g M
【参考答案】D
【名师解析】物块向右匀速运动时,则夹子与物体M,处于平衡状态,那么绳中的张力等于Mg,与2F大小关
系不确定,选项A错误;小环碰到钉子P时,物体M做圆周运动,依据最低点由拉力与重力的合力提供向心
力,因此绳中的张力大于Mg,而与2F大小关系不确定,选项B错误;依据机械能守恒定律,减小的动能转化为重力势能,则有: mv2=mgh,那么物块上升的最大高度为h= ,选项C错误;因夹子对物体M的最大静
摩擦力为 2F,依据牛顿第二定律,结合向心力表达式,对物体 M,则有:2F-Mg=M ,解得:v=
(2F Mg)L ,选项D正确。
M
【名师点睛】在分析问题时,要细心。题中给的力F是夹子与重物间的最大静摩擦力,而在物体运动的过程中,
没有信息表明夹子与物体间静摩擦力达到最大。另小环碰到钉子后,重物绕钉子做圆周运动,夹子与重物间
的静摩擦力会突然增大。
3(. 2017全国II卷·17)如图,半圆形光滑轨道固定在水平地面上,半圆的直径与地面垂直,一小物块以速度
从轨道下端滑入轨道,并从轨道上端水平飞出,小物块落地点到轨道下端的距离与轨道半径有关,此距离最
大时,对应的轨道半径为(重力加速度为g)( )
A. B. C. D.
【参考答案】B
【名师解析】设小物块运动到最高点的速度为 ,半圆形光滑轨道半径为R,小物块由最低点运动到最高点,
由机械能守恒定律, ;小物块从最高点飞出做平抛运动,x=vt,2R= gt2,联立解得,
t
x=2 =4 .当R= 时,x最大,选项B正确。
4(. 2019年4月浙江选考)某砂场为提高运输效率,研究砂粒下滑的高度与砂粒在传送带上运动的关系,建立
如图所示的物理模型。竖直平面内有一倾角θ=370的直轨道AB,其下方右侧放置一水平传送带,直轨道末端B与传送带间距可近似为零,但允许砂粒通过。转轮半径R=0.4m、转轴间距L=2m的传送带以恒定的线速度
逆时针转动,转轮最低点离地面的高度H=2.2m。现将一小物块放在距离传送带高h处静止释放,假设小物块
从直轨道B端运动到达传送带上C点时,速度大小不变,方向变为水平向右。已知小物块与直轨道和传送带
间的动摩擦因数均为μ=0.5。(sin370=0.6)
(1)若h=2.4m,求小物块到达B端时速度的大小;
(2)若小物块落到传送带左侧地面,求h需要满足的条件
(3)改变小物块释放的高度h,小物块从传送带的D点水平向右抛出,求小物块落地点到D点的水平距离x
与h的关系式及h需要满足的条件。
【参考答案】(1) ;(2) ;(3)
【名师解析】
(1)物块由静止释放到B的过程中:
解得v =4m/s
B
(2)左侧离开,D点速度为零时高为h
1
解得h