文档内容
2024年高考押题预测卷【全国卷02】
文科数学·全解全析
第一部分(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1.已知集合 ,则 ( )
A. B.
C. D.
【答案】B
【详解】因为 或 ,
则 ,又 ,
所以 .
故选:B
2.已知复数 满足 ( 为虚数单位),则 的虚部为( )
A. B. C. D.
【答案】A
【详解】由 可得 ,
故虚部为 ,
故选:A
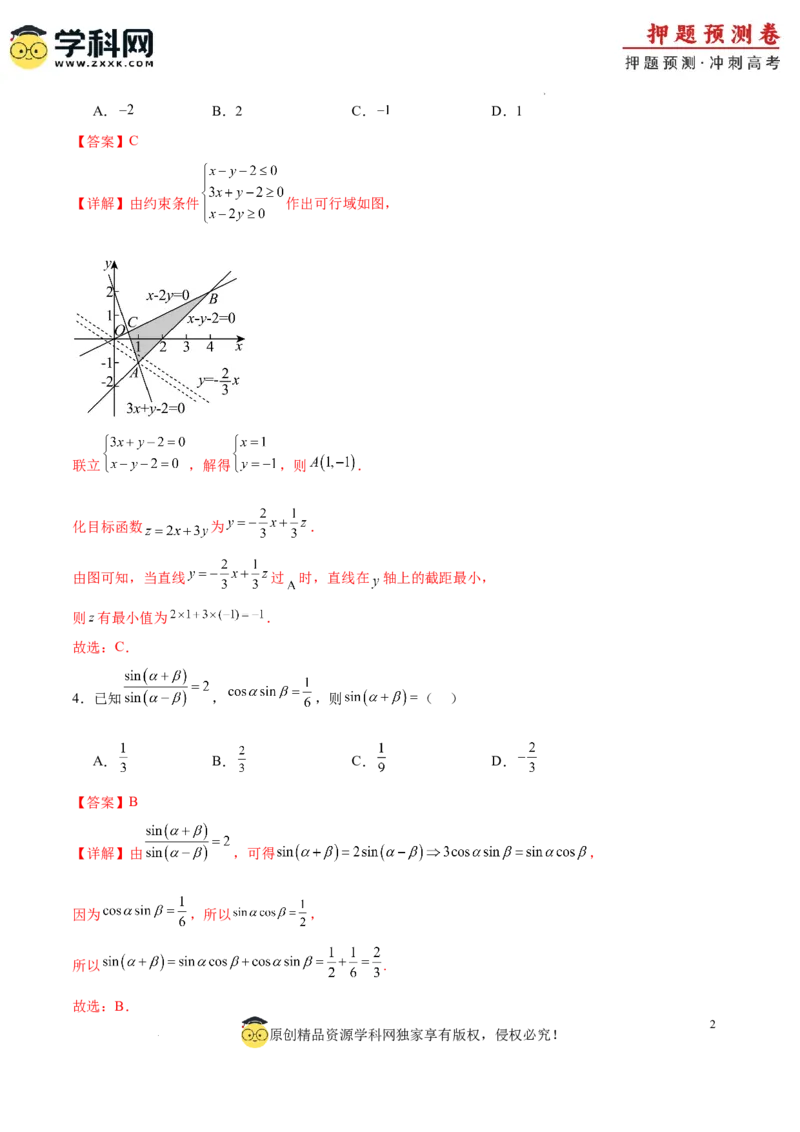
3.若实数 , 满足约束条件 ,则 的最小值为( )
1
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司A. B.2 C. D.1
【答案】C
【详解】由约束条件 作出可行域如图,
联立 ,解得 ,则 .
化目标函数 为 .
由图可知,当直线 过 时,直线在 轴上的截距最小,
则 有最小值为 .
故选:C.
4.已知 , ,则 ( )
A. B. C. D.
【答案】B
【详解】由 ,可得 ,
因为 ,所以 ,
所以 .
故选:B.
2
原创精品资源学科网独家享有版权,侵权必究!
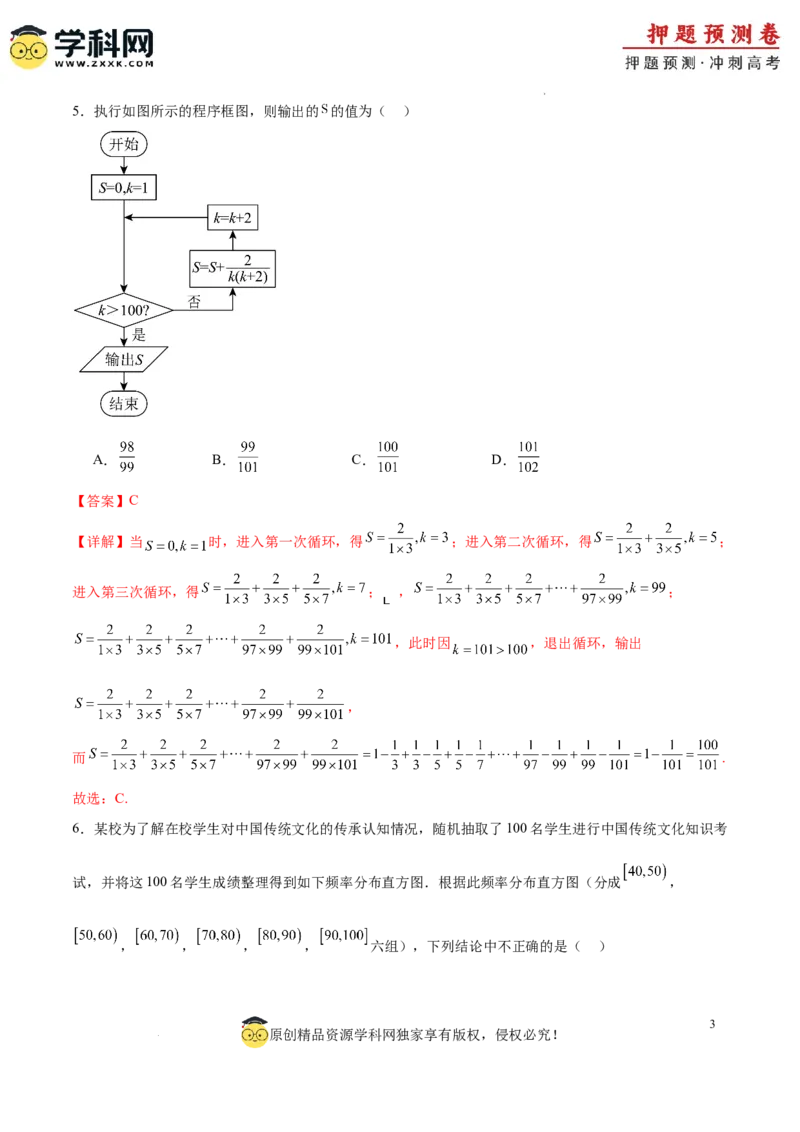
学科网(北京)股份有限公司5.执行如图所示的程序框图,则输出的 的值为( )
A. B. C. D.
【答案】C
【详解】当 时,进入第一次循环,得 ;进入第二次循环,得 ;
进入第三次循环,得 ; , ;
,此时因 ,退出循环,输出
,
而 .
故选:C.
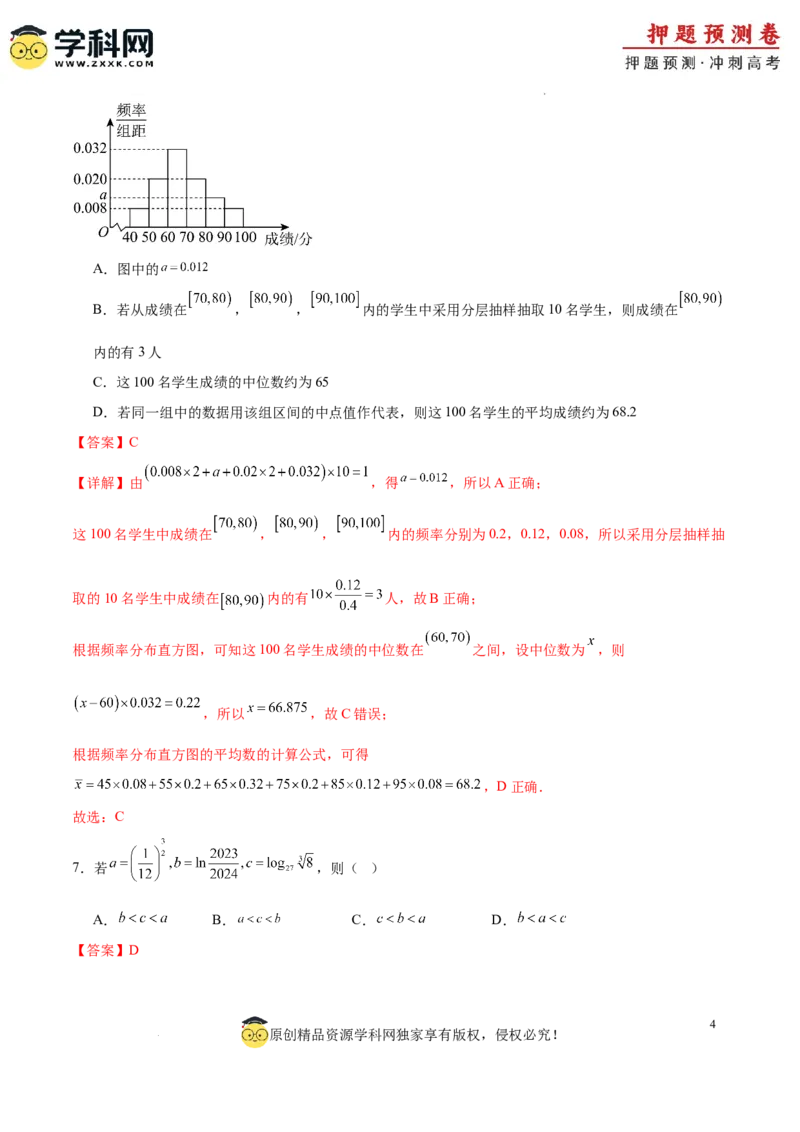
6.某校为了解在校学生对中国传统文化的传承认知情况,随机抽取了100名学生进行中国传统文化知识考
试,并将这100名学生成绩整理得到如下频率分布直方图.根据此频率分布直方图(分成 ,
, , , , 六组),下列结论中不正确的是( )
3
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司A.图中的
B.若从成绩在 , , 内的学生中采用分层抽样抽取10名学生,则成绩在
内的有3人
C.这100名学生成绩的中位数约为65
D.若同一组中的数据用该组区间的中点值作代表,则这100名学生的平均成绩约为68.2
【答案】C
【详解】由 ,得 ,所以A正确;
这100名学生中成绩在 , , 内的频率分别为0.2,0.12,0.08,所以采用分层抽样抽
取的10名学生中成绩在 内的有 人,故B正确;
根据频率分布直方图,可知这100名学生成绩的中位数在 之间,设中位数为 ,则
,所以 ,故C错误;
根据频率分布直方图的平均数的计算公式,可得
,D正确.
故选:C
7.若 ,则( )
A. B. C. D.
【答案】D
4
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司【详解】因为 , ,
因为 ,可知 ,
又因为 ,所以 .
故选:D
8.已知函数 满足 ,且函数 为偶函数,若 ,则
( )
A.0 B.1012 C.2024 D.3036
【答案】B
【详解】由题意函数 为偶函数,所以 , 的图象关于直线 对称,
所以 ,
所以函数 的周期为4,在 中,分别令 和1,
得 , ,即 ,
所以 ,
所以 .
故选:B.
9.攒尖是我国古代建筑中屋顶的一种结构形式,通常有圆形攒尖、三角攒尖、四角攒尖,多见于亭阁式
建筑、园林建筑.下面以四角攒尖为例,如图1,它的屋顶部分的轮廓可以近似看作如图2所示的正四棱
锥 ,其中底面边长和攒尖高的比值为 ,若点 是棱 的中点,则异面直线 与 所成角的
正切值为( )
5
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司A. B. C. D.
【答案】C
【详解】解:如图,连接 ,设 为 的中点, ,
异面直线 与 所成角为 或其补角.
连接 ,
所以,在正四棱锥 中, , ,
平面 ,
,设 ,则由题意得 ,
在 中, .
故选:C.
6
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司10.已知点P为直线 与直线 的交点,点Q为圆
上的动点,则 的取值范围为( )
A. B. C. D.
【答案】A
【详解】因为点 为直线 与直线 的交点,
所以由 可得 ,且 过定点 , 过定点 ,
所以点 的轨迹是以点 与点 为直径端点的圆,圆心为 ,半径 .
而圆 的圆心为 ,半径为 ,
所以两个圆心的距离 ,且 ,所以两圆相离,
所以 的最大值为: , 的最小值为: ,
所以 的取值范围是 .
故选:A.
【点睛】关键点点睛:本题解决的关键是,根据直线 垂直以及过定点得到点 的轨迹是圆,从而得解.
7
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司11.设等比数列 中, 使函数 在 时取得极值 ,则 的值是
( )
A. 或 B. 或 C. D.
【答案】D
【详解】由题意知: ,
在 处取得极值 , ,
解得: 或 ;
当 , 时, ,
在 上单调递增,不合题意;
当 , 时, ,
当 时, ;当 时, ;
在 上单调递增,在 上单调递减,
是 的极小值点,满足题意;
,又 与 同号, .
故选:D.
12.已知抛物线 的准线方程为 , , , 为 上两点,且
,则下列选项错误的是( )
A. B.
8
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司C.若 ,则 D.若 ,则
【答案】C
【详解】由抛物线 的准线方程为 ,可得 ,解得 ,
所以抛物线 ,
设直线 ,且 , ,
联立方程组 ,整理得 ,
则 ,解得 ,且 , ,
由 ,所以A正确;
由 ,所以B正确;
当 时,由 ,可得 ,
则 , 或 , ,所以 ,所以C错误;
由 ,
解得 ,所以 ,则 ,所以D正确.
9
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司故选:C
第二部分(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分
13.已知函数 ( 是 的导函数),则曲线 在 处的切线方程
为 .
【答案】 .
【详解】由题意设切点 ,因为 ,
令 ,得 ,
由导数几何意义知: ,
又 ,所以 ,
故曲线 在 处的切线方程为: ,
整理得: .
故答案为: .
14.已知 是双曲线 上任意一点,若 到 的两条渐近线的距离之积为 ,则 上的
点到焦点距离的最小值为 .
【答案】
1
原创精品资源学科网独家享有版权,侵权必究!
0
学科网(北京)股份有限公司【详解】所求的双曲线方程为 ,则渐近线方程为 ,
设点 ,则 ,
点 到 的两条浙近线的距离之积为 ,
解得: ,故双曲线 方程为: ,
故 ,故双曲线 上的点到焦点距离的最小值为 .
故答案为: .
15.已知长方体 中,侧面 的面积为2,若在棱 上存在一点 ,使得 为
等边三角形,则四棱锥 外接球表面积的最小值为 .
【答案】
【详解】如图,由对称性可知,点 是 的中点,设 ,则 , ,点 是 的中
点,
由底面矩形 的对角线的交点 作底面 的垂线,过等边三角形 的中心 作平面 的
垂线,两条垂线交于点 ,点 是四棱锥 外接球的球心,
, ,则
1
原创精品资源学科网独家享有版权,侵权必究!
1
学科网(北京)股份有限公司,
当 ,即 时,等号成立,则 的最小值为 ,
所以四棱锥 外接球表面积的最小值为 .
故答案为:
16.若 的内角 的对边分别为 , , ,点 在边 上,
且 的面积为 ,则 .
【答案】
【详解】因为 ,所以 ,
所以 ,所以 ,
即 ,所以 ,
因为 ,所以 ,
因为 ,
所以 ,
又 ,所以 ,
因为点 在边 上, ,所以 ,
因为 , ,所以 ,
所以 ,
1
原创精品资源学科网独家享有版权,侵权必究!
2
学科网(北京)股份有限公司所以 ,得 ,
在 中, ,
由余弦定理可得 ,
得 .
故答案为: .
【点睛】方法点睛:在处理三角形中的边角关系时,一般全部化为角的关系,或全部化为边的关系.题中
若出现边的一次式一般采用到正弦定理,出现边的二次式一般采用到余弦定理.应用正、余弦定理时,注
意公式变式的应用.解决三角形问题时,注意角的限制范围.
三、解答题:本大题共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试
题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.陕西省从2022年秋季启动新高考,新高考“3+1+2”模式中“3”为全国统一高考科目的语文、数学、外
语,“1”为首选科目.要求从物理、历史2门科目中确定1门,“2”为再选科目,要求从思想政治、地理、
化学、生物学4门科目中确定2门,共计产生12种组合.某班有学生50名,在选科时,首选科目选历史
和物理的统计数据如下表所示:
历史 物理 合计
男生 1 24 25
女生 9 16 25
合计 10 40 50
附: ,其中 .
0.100 0.050 0.01 0.005 0.001
1
原创精品资源学科网独家享有版权,侵权必究!
3
学科网(北京)股份有限公司0
6.63
2.706 3.841 7.879 10.828
5
(1)根据表中的数据,判断是否有99.5%的把握认为学生选择历史与性别有关;
(2)从选择物理类的40名学生中按照分层抽样,任意抽取5名同学成立学习小组,该小组设正、副组长各
一名,求正、副组长中至少有一名女同学的概率.
【详解】(1)
将表中的数据带入,得到
...............................................................3分
所以有99.5%的把握认为学生选择历史与性别有关...............................................................................5分
(2)
由题意知,抽取的5名同学中,男生有3名,设为A,B,C,女生2名,设为D,E,....................6分
从这5名同学中选取2名同学担任正副组长,所有的可能情况有:
, , , , , , , , , ,共计10种基本情况,且每种情况的发生是等
可能的,..........................................................................................................................................................8分
其中至少有一名女生的情况有 , , , , , , ,共计有7种情况,.........10分
所以 (至少有一名女生) ............................................................................................................12分
18.设等差数列 的公差为 ,记 是数列 的前 项和,若 , .
(1)求数列 的通项公式;
(2)若 ,数列 的前 项和为 ,求证: .
【详解】(1)由 , ,得 ,解得 ,.........................1分
由 , ,所以 ,所以 或 ,...........................3分
1
原创精品资源学科网独家享有版权,侵权必究!
4
学科网(北京)股份有限公司当 时 ,此时 ;...................................................................4分
当 时 ,此时 ;....................................................................5分
综上可得数列 的通项公式为 或 ;.......................................................................6分
(2)因为 ,所以 ,则 ,...............................................................7分
则
,.............................................................................................9分
所以
.....................................................................................................12分
19.如图,四棱锥 中,底面ABCD为菱形, ,侧面 是边长为4的正三角形,
.
(1)证明:平面 平面ABCD;
(2)求点A到平面SBC的距离.
【详解】(1)证明:取CD中点E,连接SE,AE,BE,......................................................................1分
1
原创精品资源学科网独家享有版权,侵权必究!
5
学科网(北京)股份有限公司易得 , ,因为 , ,
所以 , , ,故 ,................................................................3分
又 , ,
所以 ,故 ,.........................................................................................................4分
因为 平面ABCD, 平面ABCD, ,
所以 平面ABCD,又因为 平面SCD,
所以平面 平面ABCD..........................................................................................................................6分
(2)由(1)知 平面ABCD,且 ,
在 中, ,
所以 ,
故 ...............................................................................................8分
在 中, , ,
所以SB边上的高 ,
所以 ..............................................................................................................10分
设点A到平面SBC的距离为d,
则 ,即 ,解得 ,
所以点A到平面SBC的距离为 .........................................................................................................12分
1
原创精品资源学科网独家享有版权,侵权必究!
6
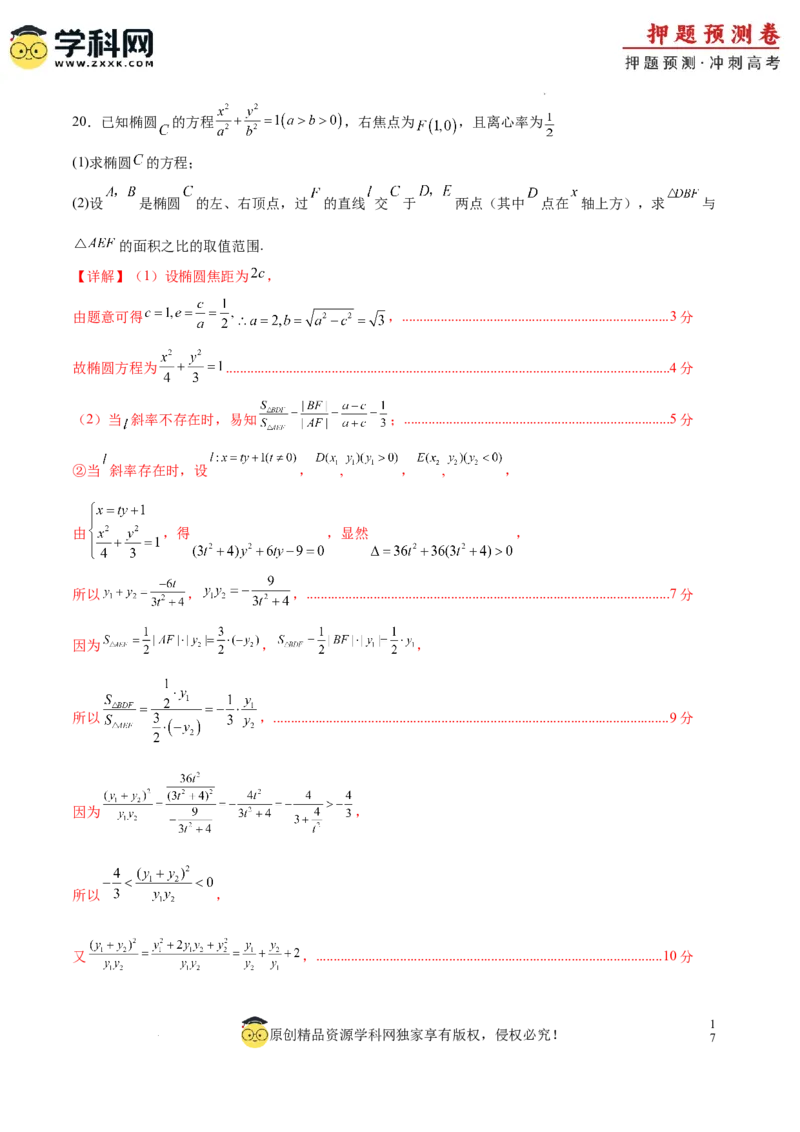
学科网(北京)股份有限公司20.已知椭圆 的方程 ,右焦点为 ,且离心率为
(1)求椭圆 的方程;
(2)设 是椭圆 的左、右顶点,过 的直线 交 于 两点(其中 点在 轴上方),求 与
的面积之比的取值范围.
【详解】(1)设椭圆焦距为 ,
由题意可得 ,............................................................................3分
故椭圆方程为 ..............................................................................................................................4分
(2)当 斜率不存在时,易知 ;............................................................................5分
②当 斜率存在时,设 , , , , ,
由 ,得 ,显然 ,
所以 , ,.......................................................................................................7分
因为 , ,
所以 ,.................................................................................................................9分
因为 ,
所以 ,
又 ,...................................................................................................10分
1
原创精品资源学科网独家享有版权,侵权必究!
7
学科网(北京)股份有限公司设 ,则 , ,解得 且 ,
所以 ,
综上可得 的取值范围为 .........................................................................................................12分
21.已知函数 ,
(1)当 时,讨论 的单调性;
(2)若函数 有两个极值点 ,求 的最小值.
【详解】(1)因为 ,
所以 ,........................................................................................................1分
令 ,则 ,
因为 ,
当 时, ,则 ,即 ,
此时 在 上单调递增,.................................................................................................................3分
当 时, ,由 ,得 ,且 ,
当 或 时, ,即 ;
1
原创精品资源学科网独家享有版权,侵权必究!
8
学科网(北京)股份有限公司当 时, ,即 ,
所以 在 , 上单调递增,在 上单调递减;..........................................................5分
综上,当 时, 在 上单调递增,
当 时, 在 , 上单调递增,在 上单调递减,
其中 ..........................................................................................................6分
(2)由(1)可知, 为 的两个极值点,且 ,
所以 ,且 是方程 的两不等正根,
此时 , , ,
所以 , ,且有 , ,............................................8分
则
.............................................................10分
令 ,则 ,令 ,
则 ,
当 时, ,则 单调递减,
当 时, ,则 单调递增,
1
原创精品资源学科网独家享有版权,侵权必究!
9
学科网(北京)股份有限公司所以 ,
所以 的最小值为 ...............................................................................................12分
(二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
选修4-4:坐标系与参数方程
22.已知在平面直角坐标系 中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线
的极坐标方程为 ;在平面直角坐标系 中,曲线 的参数方程为 ( 为参
数),点 的极坐标为 且点 在曲线 上.
(1)求曲线 的普通方程以及曲线 的极坐标方程;
(2)已知直线 与曲线 分别交于 , 两点,其中 , 异于原点 ,求 的面积.
【详解】(1)因为曲线 的极坐标方程为 ,所以 ,
由 ,得曲线 的直角坐标方程为 ;
由曲线 的参数方程为 ( 为参数),又 ,
得 ,..........................................................................................................................................2分
因为 ,所以 ,即 ,
即曲线 的极坐标方程为 .
2
原创精品资源学科网独家享有版权,侵权必究!
0
学科网(北京)股份有限公司又点 在曲线 上,所以 ,解得 ,
所以曲线 的极坐标方程为 ;.................................................................................................4分
(2)因为点 ,则 ,即点 的直角坐标为 ,.................................5分
由(1)得曲线 的直角坐标方程为 ,
联立 ,解得 或 ,所以 ,
联立 ,解得 或 ,所以 ,............................................................8分
则 ,
点 到直线 的距离 ,.................................................................9分
所以 .........................................................................................................................10分
选修4-5:不等式选讲
23.已知函数 .
(1)当 时,求不等式 的解集;
(2)若 恒成立,求 的取值范围.
【详解】(1)当 时, 可化为 ......................................................................1分
2
原创精品资源学科网独家享有版权,侵权必究!
1
学科网(北京)股份有限公司当 时, ,解得 ;
当 时, ,解得 ;
当 时, ,解得 ................................................................................................4分
故当 时,不等式 的解集为 .......................................................................................5分
(2)因为 ,
所以 等价于 ........................................................................................7分
因为 ,当且仅当 时取等号,....................................8分
所以 的最小值为 ,所以 ,
解得 或 ,
故 的取值范围是 ..............................................................................................................10分
2
原创精品资源学科网独家享有版权,侵权必究!
2
学科网(北京)股份有限公司