数学（全国卷文科02）（考试版A3）_2024高考押题卷_62024学科网全系列_24学科网高考押题预测卷_2024年高考数学押题预测卷_数学（全国卷文科02）-2024年高考押题预测卷

……………… ○ ……………… 内 ……………… ○ ……………… 装 ……………… ○ ……………… 订 ……………… ○ ……………… 线 ……………… ○ … ……………… 学 校 ： ______________ 姓 名 ： _____________ 班 级 ： _______________ 考 号 ： ______________________ 绝密★启用前 2024 年高考押题预测卷【全国卷 02】 文科 数学 （考试时间：120分钟 试卷满分：150分） 注意事项： 1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。 2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦 干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。 98 99 100 101 3．考试结束后，将本试卷和答题卡一并交回。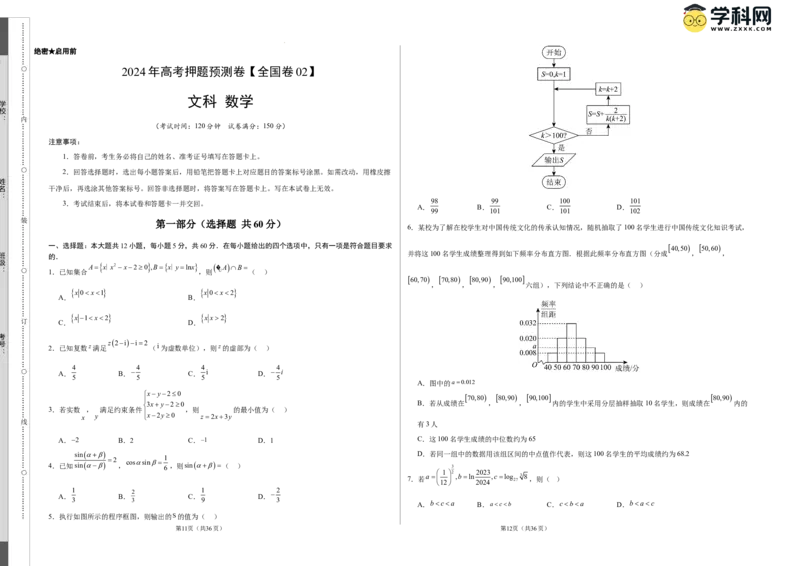 A． B． C． D． 99 101 101 102 第一部分（选择题 共60分） 6．某校为了解在校学生对中国传统文化的传承认知情况，随机抽取了100名学生进行中国传统文化知识考试， 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求 40,50 50,60 并将这100名学生成绩整理得到如下频率分布直方图．根据此频率分布直方图（分成 ， ， 的． A  x∣x2x20  ,Bx∣ylnx � AB 1．已知集合 ，则 U （ ） 60,70 70,80 80,90 90,100 ， ， ， 六组），下列结论中不正确的是（ ） x 0x1 x 0x2 A． B． x 1x2 x x2 C． D． z2ii2 2．已知复数z满足 （ i 为虚数单位），则z的虚部为（ ） 4 4 4 4 A． B． C． i D． i 5 5 5 5 A．图中的a0.012 xy20 70,80 80,90 90,100 80,90  3xy20 B．若从成绩在 ， ， 内的学生中采用分层抽样抽取10名学生，则成绩在 内的 3．若实数 ， 满足约束条件 ，则 的最小值为（ ）  x y x2y0 z2x3y 有3人 A．2 B．2 C．1 D．1 C．这100名学生成绩的中位数约为65 sin D．若同一组中的数据用该组区间的中点值作代表，则这100名学生的平均成绩约为68.2 2 1 4．已知sin ， cossin 6 ，则sin（ ） 3  1 2 2023 7．若 a 12   ,bln 2024 ,clog 27 38 ，则（ ） 1 2 1 2 A． B． C． D． 3 3 9 3 A．bca B．acb C．cba D．bac 5．执行如图所示的程序框图，则输出的S的值为（ ） 第11页（共36页） 第12页（共36页） 学科网（北京）股份有限公司……………… ○ ……………… 外 ……………… ○ ……………… 装 ……………… ○ ……………… 订 ……………… ○ ……………… 线 ……………… ○ ……………… ……………… ○ ……………… 内 ……………… ○ ……………… 装 ……………… ○ ……………… 订 ……………… ○ ……………… 线 ……………… ○ ……………… (cid:2) (cid:2) (cid:2) (cid:2) f x f x31 f 1x f x1 f 11 OPOQ5 APAQ8 8．已知函数 满足 ，且函数 为偶函数，若 ，则 A． B． 15 f 1 f 2 f 3 f 2024 （ ） C．若2，则 PQ  2 D．若 S △PQO 4 2 ，则 PQ 16 5 此 A．0 B．1012 C．2024 D．3036 卷 9．攒尖是我国古代建筑中屋顶的一种结构形式，通常有圆形攒尖、三角攒尖、四角攒尖，多见于亭阁式建筑、 只 园林建筑．下面以四角攒尖为例，如图1，它的屋顶部分的轮廓可以近似看作如图2所示的正四棱锥PABCD， 第二部分（非选择题 共90分） 装 1 其中底面边长和攒尖高的比值为2，若点E是棱PD的中点，则异面直线PB与CE所成角的正切值为（ ） 二、填空题：本大题共4小题，每小题5分，共20分 订 13．已知函数 f x4ex f0x2 （ fx 是 f x 的导函数），则曲线 y f x 在 x0 处的切线方程为 不 ． 密 x2 y2 C:  (0) 2 封 14．已知P是双曲线 8 4 上任意一点，若P到C的两条渐近线的距离之积为3，则C上的点到 焦点距离的最小值为 ． 15．已知长方体 ABCDA 1 B 1 C 1 D 1中，侧面 BCC 1 B 1的面积为2，若在棱 AD 上存在一点 M ，使得 MBC 为等边三 3 3 3 2 A．4 B． 2 C．3 D．2 M BCCB 角形，则四棱锥 1 1外接球表面积的最小值为 . l :mx2ym60 l :2xmym60(mR) cosCsinC 10．已知点P为直线 1 与直线 2 的交点，点Q为圆 16．若 的内角 的对边分别为 ，tanB ， ，点 在边 上， 且 ABC A,B,C a,b,c cosCsinC a 2c D BC AD=b C:(x3)2(y3)2 8 |PQ| 2 3 上的动点，则 的取值范围为（ ） 的面积为 ，则 ． ADB 2 CD [2 2,8 2] (2 2,8 2] [ 2,6 2] ( 2,6 2] 三、解答题：本大题共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考 A． B． C． D． 生都必须作答．第22、23题为选考题，考生根据要求作答． 11．设等比数列 a n  中， a 3 ,a 7使函数 f xx33a 3 x2a 7 xa 3 2 在 x=1 时取得极值0，则 a 5的值是（ ） （一）必考题：共60分． 17．陕西省从2022年秋季启动新高考，新高考“3+1+2”模式中“3”为全国统一高考科目的语文、数学、外语，  3 3 2 3 3 2 3 2 3 2 A． 或 B． 或 C． D． “1”为首选科目．要求从物理、历史2门科目中确定1门，“2”为再选科目，要求从思想政治、地理、化学、生 (cid:2) (cid:2) 12．已知抛物线 C:y2 2pxp0 的准线方程为 x=1 ， A1,0 ，P， Q 为 C 上两点，且 APAQ1 ， 物学4门科目中确定2门，共计产生12种组合．某班有学生50名，在选科时，首选科目选历史和物理的统计数 据如下表所示： 历史 物理 合计 则下列选项错误的是（ ） 第23页（共36页） 第24页（共36页）……………… ○ ……………… 内 ……………… ○ ……………… 装 ……………… ○ ……………… 订 ……………… ○ ……………… 线 ……………… ○ … ……………… 学 校 ： ______________ 姓 名 ： _____________ 班 级 ： _______________ 考 号 ： ______________________ 男生 1 24 25 (2)求点A到平面SBC的距离. 女生 9 16 25 合计 10 40 50 nadbc2 附： 2  abcdacbd，其中 nabcd ． 20．已知椭圆C的方程a x2 2  b y 2 2 1ab0 ，右焦点为 F1,0 ，且离心率为 1 2  0.100 0.050 0.01 0.005 0.001 (1)求椭圆C的方程； 0 A，B C F l C D，E D x DBF (2)设 是椭圆 的左、右顶点，过 的直线 交 于 两点（其中 点在 轴上方），求 与 6.63 x 2.706 3.841 7.879 10.828  5 △AEF 的面积之比的取值范围. (1)根据表中的数据，判断是否有99.5%的把握认为学生选择历史与性别有关； (2)从选择物理类的40名学生中按照分层抽样，任意抽取5名同学成立学习小组，该小组设正、副组长各一名， 求正、副组长中至少有一名女同学的概率. f xlnxx22ax,aR 21．已知函数 ， f x a0 (1)当 时，讨论 的单调性； 18．设等差数列 a n  的公差为d，记 S n是数列 a n  的前 n 项和，若 S 5 a 3 20 ， S 15 a 2 a 3 a 8. f x x,x x x  2f x  f x  (2)若函数 有两个极值点 1 2 1 2 ，求 1 2 的最小值. a  (1)求数列 n 的通项公式； (2)若 d 0,b n  a n 4  S a n n1  nN* ，数列 b n  的前n项和为T n ，求证： T n n 1 2. （二）选考题：共10分．请考生在22、23题中任选一题作答，如果多做，则按所做的第一题计分． 选修4-4：坐标系与参数方程 19．如图，四棱锥 中，底面ABCD为菱形，DAB π ，侧面 是边长为4的正三角形， 22．已知在平面直角坐标系 xOy 中，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，曲线 C 1的极 SABCD 3 SCD SA2 10 .  xm 3cos  坐标方程为 ；在平面直角坐标系 中，曲线 的参数方程为 （ 为参数），点 2sin xOy C 2 y 3sin  A  π  6,  的极坐标为 4且点A在曲线C 2 上. (1)证明：平面SCD平面ABCD； 第31页（共36页） 第32页（共36页） 学科网（北京）股份有限公司……………… ○ ……………… 外 ……………… ○ ……………… 装 ……………… ○ ……………… 订 ……………… ○ ……………… 线 ……………… ○ ……………… ……………… ○ ……………… 内 ……………… ○ ……………… 装 ……………… ○ ……………… 订 ……………… ○ ……………… 线 ……………… ○ ……………… C C (1)求曲线 1的普通方程以及曲线 2的极坐标方程； (2)已知直线 l:x 3y0 与曲线 C 1 ,C 2分别交于 P ， Q 两点，其中 P ， Q 异于原点 O ，求 △APQ 的面积. 此 卷 只 选修4-5：不等式选讲 装 f x x  x2 xa 23．已知函数 . 订 a2 f x14 不 (1)当 时，求不等式 的解集； 密 f x x28 x 16 (2)若 恒成立，求a的取值范围. 封 第43页（共36页） 第44页（共36页）