文档内容
2023 年高考考前押题密卷
数学·全解全析
一、选择题(本题共9小题,每小题5分,共45分.在每小题给出的四个选项中,只有一项是符合题目要
求的.)
1.【原创】集合 , ,则 ( ).
A. B.
C. D.
【答案】A
【分析】根据函数定义域求出 ,再根据交集定义即可求出 .
【详解】因为 ,解得 ,且 ,
所以 ,
所以 ,
故选:A.
2.【原创】已知向量 , , ,则“ ”是“ ”的( ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】B
【分析】由 得出 的关系,进而可得出答案.
【详解】由 得 ,进而得出 ,即 或 ;
所以由 不能推出 ,反之则成立;
所以“ ”是“ ”的必要不充分条件.
故选:B
1
学科网(北京)股份有限公司3.函数 的大致图象为( )
A. B.
C. D.
【答案】A
【分析】由函数的奇偶性排除BD选项,再根据 时 排除C得A.
【详解】解:因为当 时, ,则 ,当 时, ,
所以函数为奇函数,图像关于原点对称,故排除BD;
因为当 时, , ,故 ,
所以C选项不满足,A选项满足.
故选:A
4.已知 , , ,则 的大小关系是( )
A. B. C. D.
【答案】C
【分析】将 化为同底的对数形式,根据对数函数单调性可知 ;利用 可得 ,由
此可得结论.
【详解】 , ,
2
学科网(北京)股份有限公司又 , ;
, ,又 , ;
综上所述: .
故选:C.
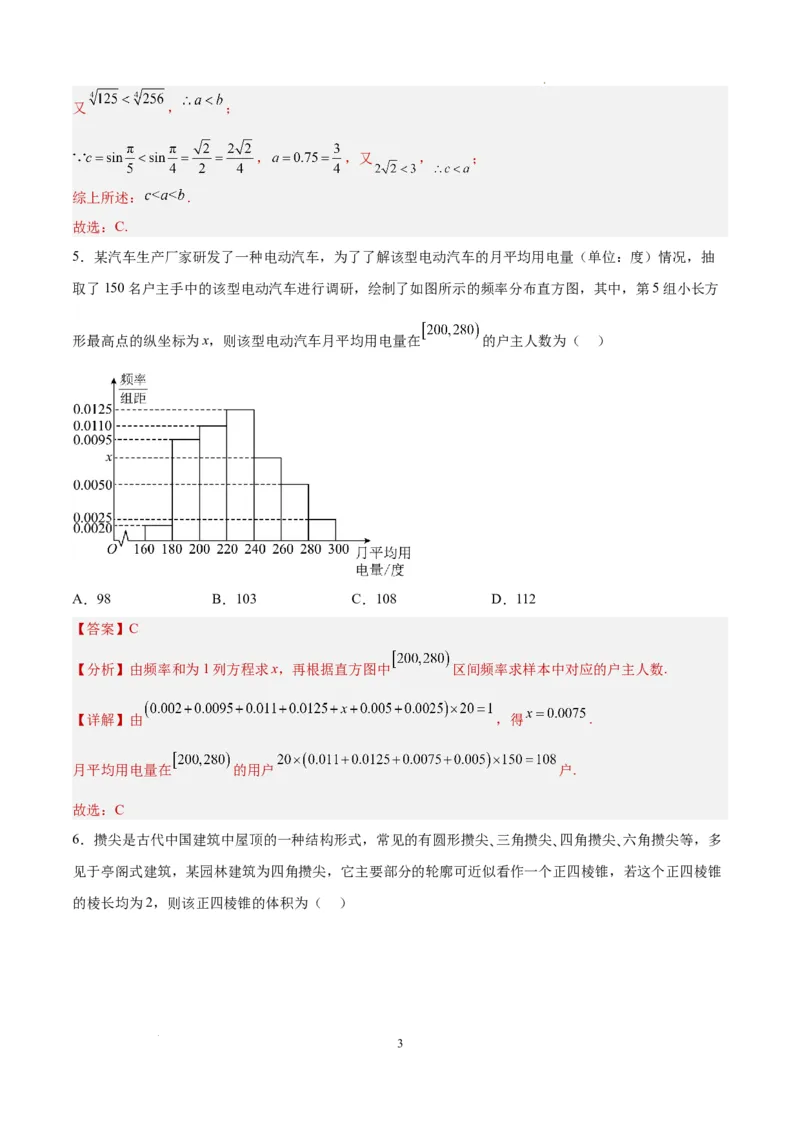
5.某汽车生产厂家研发了一种电动汽车,为了了解该型电动汽车的月平均用电量(单位:度)情况,抽
取了150名户主手中的该型电动汽车进行调研,绘制了如图所示的频率分布直方图,其中,第5组小长方
形最高点的纵坐标为x,则该型电动汽车月平均用电量在 的户主人数为( )
A.98 B.103 C.108 D.112
【答案】C
【分析】由频率和为1列方程求x,再根据直方图中 区间频率求样本中对应的户主人数.
【详解】由 ,得 .
月平均用电量在 的用户 户.
故选:C
6.攒尖是古代中国建筑中屋顶的一种结构形式,常见的有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,多
见于亭阁式建筑,某园林建筑为四角攒尖,它主要部分的轮廓可近似看作一个正四棱锥,若这个正四棱锥
的棱长均为2,则该正四棱锥的体积为( )
3
学科网(北京)股份有限公司A. B. C. D.
【答案】C
【分析】根据题意,结合正四棱锥的性质,即可求得 、 的长,根据椎体体积公式,即可得答案.
【详解】如图所示,正四棱锥 棱长均为2,连接AC、BD交于点O,连接PO
根据正四棱锥的性质,可得 平面ABCD.
所以 , ,
所以正四棱锥 的体积 .
故选:C
7.已知抛物线 的焦点为F,准线为l,过F且斜率为 的直线与C交于A,B两点,D
为AB的中点,且 于点M,AB的垂直平分线交x轴于点N,四边形DMFN的面积为 ,则
( )
A. B.4 C. D.
4
学科网(北京)股份有限公司【答案】A
【分析】设出直线AB的方程,联立抛物线方程,表达出 点坐标,作出辅助线,求出 ,
得到四边形DMFN为平行四边形,利用面积列出方程,求出 .
【详解】由题意知 ,直线AB的方程为 .
设 ,由 ,得 ,
所以 ,所以 ,
由 ,得 .
如图所示,作 轴于点E,则 .
因为 ,
故 , ,
又 ,故 ,
又 ,得四边形DMFN为平行四边形.
所以其面积为 ,解得 .
故选:A
5
学科网(北京)股份有限公司8.已知函数 ,以下说法中,正确的是()
①函数 关于点 对称;
②函数 在 上单调递增;
③当 时, 的取值范围为 ;
④将函数 的图像向右平移 个单位长度,所得图像对应的解折式为 .
A.①② B.②③④ C.①③ D.②
【答案】D
【分析】利用倍角公式和辅助角公式化简函数解析式,再利用正弦函数的性质,解决函数图像的对称中心、
单调区间、值域和平移问题.
【详解】由题意可得,微信搜索“高中试卷君”公众号 领取押题卷联考卷
,
由 ,则 ,所以 图像的对称中心为 ,说法①错误;
,则 , 是函数 单调递增区间,说法②正确;
当 时, , ,则 的取值范围为 ,说法③错误;
将函数 的图像向右平移 个单位长度,所得图像对应的解折式为
,说法④错误.
故选:D
6
学科网(北京)股份有限公司9.已知定义在 上的函数 是偶函数,当 时, ,若关于 的方程
,有且仅有6个不同实数根,则实数 的取值范围是( )
A. B.
C. D.
【答案】C
【分析】由偶函数性质可以画出函数 的图像,关于 的方程 有6个不
同的实数根,根据数形结合和韦达定理即可求得结果.
【详解】由题意可知,函数 的图像如下图所示:
根据函数图像,函数 在 上单调递增,在 上单调递减;
且 时取最大值2,在 时取最小值0, 是部分图像的渐近线.
令 ,则关于 的方程 即可写成
此时关于 的方程应该有两个不相等的实数根(其他情况不合题意),
设 为方程的两个实数根,
显然,有以下两种情况符合题意:
①当 时,此时 ,则
7
学科网(北京)股份有限公司②当 时,此时 ,则
综上可知,实数 的取值范围是 .
故选:C.
第Ⅱ卷
二、填空题:(本题共6小题,每小题5分,共30分。试题中包含两个空的,答对1个的给3分,全部答
对的给5分。)
10.【原创】已知复数 ( 是虚数单位),则复数 在复平面内对应的点位于第_____象限.
【答案】一
【解析】化简得到 ,得到复数对应象限.
【详解】 ,复数 在复平面内对应的点的坐标为 ,
故复数 在复平面内对应的点位于第一象限.
故答案为:一.
11.【原创】若 的展开式中所有项的系数和为 ,则展开式中 的系数为
__________.
【答案】
【分析】令 ,解出 ,进而通过二项展开式的通项公式即可求解;
【详解】令 ,得 ,解得 ,进而可得 的展开式为 ,令
,得 ,令 ,得 ,故 的系数为 .
故答案为:
12.【原创】已知 ,则 的最小值为____________.
8
学科网(北京)股份有限公司【答案】4
【分析】将 构造变形为 ,然后利用基本不等式即可求解;
【详解】由 ,当且仅当 ,
也即 时等号成立,故最小值为4.
故答案为:4
13.某项选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考试,否则即被淘汰.已
知某选手能正确回答第一、二、三轮的问题的概率分别为 , , ,且各轮问题能否正确回答互不影响,
则该选手被淘汰的概率为_________.
【答案】
【分析】设事件 表示“该选手能正确回答第 轮的问题”,选手被淘汰,考虑对立事件,代入
的值,可得结果;
【详解】记“该选手能正确回答第 轮的问题”为事件 ,则 .
该选手被淘汰的概率:
故答案为:
14.【原创】已知圆 与圆 外切,此时直线 被
圆 所截的弦长为__________.
【答案】
9
学科网(北京)股份有限公司【分析】由两圆外切关系求出 的值,进而代入公式即可求解;
【详解】由题意可得: ,即圆 的圆心为 ,半径为 ,即圆
心到直线 的距离为 ,故所截弦长为 .
故答案为:
15.窗花是贴在窗子或窗户上的剪纸,是中国古老的传统民间艺术之一,图1是一个正八边形窗花隔断,
图2是从窗花图中抽象出的几何图形的示意图.如图2,正八边形ABCDEFGH中,若
,则 的值为________ ;若正八边形ABCDEFGH的边长为2,P是正八边形
ABCDEFGH八条边上的动点,则 的最小值为______.
【答案】
【分析】以点 为坐标原点,分别以 所在直线为 轴,建立平面直角坐标系,由 ,
列出方程组,求得 ,从而得到 ;设 ,则 ,由 即可求得
的最小值.
【详解】
10
学科网(北京)股份有限公司,以点 为坐标原点,分别以 所在直线为 轴,建立平面直角坐标系,
正八边形内角和为 ,则 ,
所以, ,
,
因为 ,则 ,
所以 ,解得 ,
所以 ;
设 ,则 ,
,则 ,
所以,当点 在线段 上时, 取最小值 .
故答案为: , .
三、解答题(本题共5小题,共75分,解答应写出文字说明、证明过程或演算步骤。)
16.(本题14分)在 中,角 、 、 的对边分别为 、 、 ,已知
.
(1)求 的值;
11
学科网(北京)股份有限公司(2)若 ,
(ⅰ)求 的值;
(ⅱ)求 的值.
【答案】(1)
(2)(ⅰ) ;(ⅱ)
【分析】(1)利用正弦定理化简原式,直接利用余弦定理求 的值即可;
(2)(i)由(1)可得 ,再利用正弦定理求 的值,利用同角三角函数的基本关系和两角和
的正切公式即可求解;
(ii)由二倍角的正弦公式以及两角和的正弦公式可得结果.
【详解】(1)在 中,由正弦定理
可得: ,整理得 ,
由余弦定理,可得 ;
(2)(i)由(1)可得 ,又由正弦定理 ,
及已知 ,可得 ,
由已知 ,可得 ,故有 ,
为锐角,可得 , ,
则 ;
12
学科网(北京)股份有限公司(ii)由(i)可得 , ,
.
17.(本题15分)已知正三棱柱 中,侧棱长为 ,底面边长为2,D为AB的中点.
(1)证明: ;
(2)求二面角 的大小;
(3)求直线CA与平面 所成角的正弦值. 微信搜索“高中试卷君”公众号 领取押题卷联考卷
【答案】(1)证明见解析;
(2)
(3)
【分析】(1)由正三棱柱的性质可得 平面 ,再利用线面垂直的判定定理即可证明 平面
,即可得 ;(2)以 的中点 为坐标原点,建立空间直角坐标系利用空间向量与二面
角的几何关系即可求得二面角 的大小为 ;(3)根据(2)中结论,利用线面角与空间向量的
关系即可得直线CA与平面 所成角的正弦值为 .
【详解】(1)由 为正三棱柱可知, 平面 ,
13
学科网(北京)股份有限公司又 平面 ,所以 ,
由底面是边长为2的正三角形,D为AB的中点,所以 ;
又 , 平面 ,所以 平面 ;
又 平面 ,所以 ;
(2)取线段 的中点分别为 ,连接 ,
易知 两两垂直,以 为坐标原点,分别以 所在直线为 轴建立空间直角坐标
系 ,如下图所示;
由侧棱长为 ,底面边长为2可得,
,
由D为AB的中点可得 ,
所以 ,
设平面 的一个法向量为 ,
则 ,令 ,可得 ;
即 ;
14
学科网(北京)股份有限公司易得 即为平面 的一个法向量,
所以 ,
设二面角 的平面角为 ,由图可知 为锐角,
所以 ,即 ;
即二面角 的大小为 .
(3)由(2)可知 ,平面 的一个法向量为 ,
设直线CA与平面 所成的角为 ,
所以 ,
即直线CA与平面 所成角的正弦值为 .
18.(本题15分)已知数列 满足 ,其前8项的和为64;数列 是公比大于0的等比数列,
, .
(1)求数列 和 的通项公式;
(2)记 , ,求数列 的前 项和 ;
(3)记 ,求 .
【答案】(1) ,
15
学科网(北京)股份有限公司(2)
(3)
【分析】(1)根据条件得到等差数列的公差,利用前 项和公式,求出首项,得到通项公式,设出公比,
得到方程,求出公比,写成通项公式;
(2)写出 的通项公式,利用裂项相消法求和;
(3)方法一:变形得到 ,其中 利
用错位相减法求和, 分 为偶数和 为奇数两种情况求解,最终求出 ;
方法二:变形后, 利用裂项相消法求和, 分 为偶数和 为奇数
两种情况求解,最终求出 .
【详解】(1)∵ ,
∴数列 是公差为 等差数列,且 ,
∴ ,解得 ,
∴ ;
设等比数列 的公比为 ( ),
∵ , ,
,即 ,
解得 (舍去)或 ,
∴
16
学科网(北京)股份有限公司(2)由(1)得
,
(3)方法一:
∵ ,
①
②
两式相减得,
17
学科网(北京)股份有限公司,
,
当 为偶数时,
,
当 为奇数时,
,
.
方法二:
当 为偶数时,
,
当 为奇数时,
18
学科网(北京)股份有限公司,
.
19.(本题15分)已知椭圆 的离心率为 ,左、右顶点分别为 、 ,点 、 为
椭圆上异于 、 的两点, 面积的最大值为 .
(1)求椭圆 的方程;
(2)设直线 、 的斜率分别为 、 ,且 .
①求证:直线 经过定点.
②设 和 的面积分别为 、 ,求 的最大值.
【答案】(1)
(2)①证明见解析;② 微信搜索“高中试卷君”公众号 领取押题卷联考卷
【分析】(1)根据题意可得出关于 、 、 的方程组,解出这三个量的值,即可得出椭圆 的方程;
(2)①分析可知直线 不与 轴垂直,设直线 的方程为 ,可知 ,设点 、
.将直线 的方程的方程与椭圆 的方程联立,列出韦达定理,利用 求出 的值,即可得
出直线 所过定点的坐标;
②写出 关于 的函数关系式,利用对勾函数的单调性可求得 的最大值.
【详解】(1)解:当点 为椭圆 短轴顶点时, 的面积取最大值,
且最大值为 ,
19
学科网(北京)股份有限公司由题意可得 ,解得 ,
所以,椭圆 的标准方程为 .
(2)解:①设点 、 .
若直线 的斜率为零,则点 、 关于 轴对称,则 ,不合乎题意.
设直线 的方程为 ,由于直线 不过椭圆 的左、右焦点,则 ,
联立 可得 ,
,可得 ,
由韦达定理可得 , ,则 ,
所以,
,解得 ,
即直线 的方程为 ,故直线 过定点 .
②由韦达定理可得 , ,
所以,
,
20
学科网(北京)股份有限公司,则 ,
因为函数 在 上单调递增,故 ,
所以, ,当且仅当 时,等号成立,
因此, 的最大值为 .
20.(本题16分)设函数 .
(1)求 的单调区间;
(2)已知 ,曲线 上不同的三点 处的切线都经过点 .证
明:
(ⅰ)若 ,则 ;
(ⅱ)若 ,则 .
(注: 是自然对数的底数)
【答案】(1) 的减区间为 ,增区间为 .
(2)(ⅰ)见解析;(ⅱ)见解析.
【分析】(1)求出函数的导数,讨论其符号后可得函数的单调性.
(2)(ⅰ)由题设构造关于切点横坐标的方程,根据方程有3个不同的解可证明不等式成立,(ⅱ)
, ,则题设不等式可转化为 ,结合零点满足的方程进一
21
学科网(北京)股份有限公司步转化为 ,利用导数可证该不等式成立.
【详解】(1) ,
当 , ;当 , ,
故 的减区间为 , 的增区间为 .
(2)(ⅰ)因为过 有三条不同的切线,设切点为 ,
故 ,
故方程 有3个不同的根,
该方程可整理为 ,
设 ,
则
,
当 或 时, ;当 时, ,
故 在 上为减函数,在 上为增函数,
因为 有3个不同的零点,故 且 ,
故 且 ,
整理得到: 且 ,
22
学科网(北京)股份有限公司此时 ,
设 ,则 ,
故 为 上的减函数,故 ,
故 .
(ⅱ)当 时,同(ⅰ)中讨论可得:
故 在 上为减函数,在 上为增函数,
不妨设 ,则 ,
因为 有3个不同的零点,故 且 ,
故 且 ,
整理得到: ,
因为 ,故 ,
又 ,
设 , ,则方程 即为:
即为 ,
记
则 为 有三个不同的根,
设 , ,
23
学科网(北京)股份有限公司要证: ,即证 ,
即证: ,
即证: ,
即证: ,
而 且 ,
故 ,
故 ,
故即证: ,
即证:
即证: ,
记 ,则 ,
设 ,则 ,所以 ,
,
故 在 上为增函数,故 ,
所以 ,
24
学科网(北京)股份有限公司记 ,
则 ,
所以 在 为增函数,故 ,
故 即 ,
故原不等式得证:微信搜索“高中试卷君”公众号 领取押题卷联考卷
25
学科网(北京)股份有限公司26
学科网(北京)股份有限公司