数学（广东专用01，新题型结构）（全解全析）_2024高考押题卷_62024学科网全系列_24学科网高考押题预测卷_2024年高考数学押题预测卷

2024年高考押题预测卷【广东专用01】 数学·全解全析 第一部分（选择题 共58分） 一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要 求的。 1．已知某地最近 天每天的最高气温（单位： ）分别为 ，则 天最高气 温的第 百分位数是（ ） A．15 B．21 C． D．22 【答案】C 【详解】将此组数据从小到大排列： ， 且共有 个数，因为 ，所以第 百分位数为 . 故选：C. 2．已知向量 ，若向量 满足 ，且 ，则 的值是（ ） A． B．12 C．20 D． 【答案】A 【详解】由 可设 ， 由 可得 ，解得 ， 所以 ，则 . 故选：A 3．已知数列 为等比数列， 为数列 的前 项和.若 成等差数列，则 （ ） A． B． C． D． 【答案】A 1 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司【详解】设等比数列 的公比为 ， 若 成等差数列，可得： ， 当 时，此时 恒成立， 即为 ，得 ，即 ，显然不成立； 当 时， 即为： ，其中 ， 得 ，得 或 （舍去）， ， 故选：A. 4．已知函数 ， ，那么“ ”是“ 在 上是增函数”的（ ） A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 【答案】A 【详解】当 ， , 单调递增. 则当 时， 是增函数, 当 时, 在 单调递增，可得 在 上是增函数； 当 时, 在 单调递增，可得 在 上是增函数； 反之，当 在 上是增函数时，由 ，可知，此时 ，即 不成 立. 2 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司所以“ ”是“ 在 上是增函数”的充分而不必要条件. 故选：A. 5．“142857”这一串数字被称为走马灯数，是世界上著名的几个数之一，当142857与1至6中任意1个数 字相乘时，乘积仍然由1，4，2，8，5，7这6个数字组成．若从1，4，2，8，5，7这6个数字中任选4 个数字组成无重复数字的四位数，则在这些组成的四位数中，大于5200的偶数个数是（ ） A．87 B．129 C．132 D．138 【答案】A 【详解】若千位数字是5，则百位数字不能是1，故共有 （个）； （①一个四位数为偶数，则其个位上的数字一定是偶数；②组成的四位数要大于5200，则其千位上的数字 是5，7或8） 若千位数字是7，则共有 （个）； 若千位数字是8，则共有 （个）． 故符合条件的四位数共有 （个）． 故选：A 6．如图，四棱锥 是棱长均为2的正四棱锥，三棱锥 是正四面体， 为 的中点，则 下列结论错误的是（ ） A．点 共面 B．平面 平面 C． D． 平面 【答案】D 【详解】选项A：如图，取 中点 ，连接 ， ， ， ， 3 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司因为 是正四棱锥， 是正四面体， 为 的中点， 所以 ， ， ， 因为 ， 平面 ，所以 平面 ， 因为 ， 平面 ，所以 平面 ， 所以 四点共面， 由题意知 ， ，所以四边形 是平行四边形， 所以 ，因为 ，所以 ，所以 四点共面，故A说法正确； 选项B：由选项A知 ，又 平面 ， 平面 ，所以 平面 ， 因为 ，且 平面 ， 平面 ，所以 平面 ， 又 平面 ， 平面 ，且 ，所以平面 平面 ，故B说法正确； C选项：由选项A可得 平面 ，又 平面 ，所以 ，故C说法正确； D选项：假设 平面 ，因为 平面 ，则 ， 由选项A知四边形 是平行四边形，所以四边形 是菱形， 与 ， 矛盾，故D说法错误; 故选：D 7．已知函数 对 均满足 ，其中 是 的导数，则下列 不等式恒成立的是（ ） A． B． C． D． 4 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司【答案】A 【详解】 ，令 ，求导得： ， 当 时 ，当 时 ，因此函数 在 上单调递增，在 上单调递减， 对于A， ，则 ，即 ，A正确； 对于B， ，则 ，即 ，B错误； 对于C， ，则 ，即 ，C错误； 对于D， ，则 ，即 ，D错误． 故选：A 8．已知椭圆 的左焦点为 ，过 作圆 的一条切线 交椭圆 于 ， 两 点，若 ，则椭圆 的离心率为（ ） A． B． C． D． 【答案】B 【详解】设直线 ，与椭圆 联立，化简得 ， 设 ， ，则由根与系数的关系得 ①， 又 ，所以 ，代入①得 ②， 5 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司又直线 与圆 相切，所以 ，即 ，代入②整理得 ， 得 ，因此椭圆 的离心率 ，故B正确. 故选：B． 【点睛】将直线与椭圆联立后结合根与系数的关系及几何关系，从而求解. 二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部 选对的得6分，部分选对的得部分分，有选错的得0分． 9．已知复数 ，则下列命题正确的是（ ） A．若 ，则 B．若 ，则 C．若 是非零复数，且 ，则 D．若 是非零复数，则 【答案】BC 【详解】对于A项，若 ， ，显然满足 ，但 ，故A项错误； 对于B项，设 ，则 ， ，故 而 ，故B项正确； 对于C项，由 可得： ，因 是非零复数，故 ，即 ，故C 项正确； 6 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司对于D项，当 时， 是非零复数，但 ，故D项错误. 故选：BC. 10．在 中，角 所对的边分别为 ，且 ，则下列结论正确的有（ ） A． B．若 ，则 为直角三角形 C．若 为锐角三角形， 的最小值为1 D．若 为锐角三角形，则 的取值范围为 【答案】ABD 【详解】对于 中，由正弦定理得 ， 由 ，得 ，即 ， 由 ，则 ，故 ，所以 或 ， 即 或 （舍去），即 ，A正确； 对于B，若 ，结合 和正弦定理知 ， 又 ，所以可得 ，B正确； 对于 ，在锐角 中， ，即 . 故 ，C错误； 对于 ，在锐角 中，由 ， ， 7 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司令 ，则 ， 易知函数 单调递增，所以可得 ，D正确； 故选：ABD. 11．已知函数 的定义域和值域均为 ，对于任意非零实数 ，函数 满足： ，且 在 上单调递减， ，则下列结论错误的是 （ ） A． B． C． 在定义域内单调递减 D． 为奇函数 【答案】BC 【详解】对于 ，令 ，则 ， 因 ，故得 ，故A正确； 对于 由 ， 令 ，则 ， 则 ，即 ， 故 是以 为首项，2为公比的等比数列， 于是 ，故B错误； 8 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司对于 ，由题意，函数 的定义域为 ，关于原点对称， 令 ，则 ①， 把 都取成 ，可得 ②， 将②式代入①式，可得 ， 化简可得 即 为奇函数，故D正确； 对于C， 在 上单调递减，函数为奇函数，可得 在 上单调递减， 但是不能判断 在定义域上的单调性，例如 ，故C错误. 故选：BC. 【点睛】关键点点睛：本题解题的关键在于对已知的函数抽象表达式的处理，一般以赋值化简为主，根据 选项信息对自变量进行针对性赋值，求出函数值，或者推导出递推式，或者构造出 的关系式即 可判断奇偶性等. 第二部分（非选择题 共92分） 三、填空题：本题共3小题，每小题5分，共15分。 12．已知集合 ，则 . 【答案】 【详解】 ，解得 ，故 ； ，解得 ，故 ，故 . 故答案为： 9 原创精品资源学科网独家享有版权，侵权必究！ 学科网（北京）股份有限公司13．若 的展开式中有理项的系数和为2，则展开式中 的系数为 ． 【答案】1 【详解】 时为有理项， ， 由 系数： , 故答案为：1. 14．如图，将正四面体每条棱三等分，截去顶角所在的小正四面体，余下的多面体就成为一个半正多面体， 亦称“阿基米德体”．点A，B，M是该多面体的三个顶点，点N是该多面体表面上的动点，且总满足 ，若 ，则该多面体的表面积为 ，点N轨迹的长度为 ． 【答案】 【详解】根据题意该正四面体的棱长为 ，点 分别是正四面体棱的三等分点． 该正四面体的表面积为 ， 该多面体是正四面体截去顶角所在的小正四面体， 每个角上小正四面体的侧面面积为 ， 每个角上小正四面体的底面面积为 ， 所以该多面体的表面积为： ． 如图设点 为该多面体的一个顶点， 为 所在棱的顶点，则 ， 1 原创精品资源学科网独家享有版权，侵权必究！ 0 学科网（北京）股份有限公司在 中， ， 则 ，所以 ， 得 ，即 ； 同理 ， ， 由 ， 平面 ，所以 平面 ． 由点 是该多面体表面上的动点，且总满足 ， 则点 的轨迹是线段 ， 所以点 轨迹的长度为： ． 故答案为： ； 四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步棸。 f xxaexba,bR 1,1 f x x0 15．（13分）已知函数 的图象经过点 ，且 是 的极值点. f x (1)求函数 的解析式； f x (2)求函数 的单调区间和最值. f xx1ex1 【答案】(1) (0,) (,0) 0 (2)增区间为 ，减区间为 ，最小值为 ，无最大值 f xxaexb fxxa1ex 【详解】（1）解：由函数 ，可得 ，....................................1分 f x 1,1 f x x0 因为函数 过点 ，且 是 的极值点， 1 原创精品资源学科网独家享有版权，侵权必究！ 1 学科网（北京）股份有限公司f 11aeb1  可得 f01a0 ，解得a1,b1，......................................................................................3分 经检验符合题意；..........................................................................................................................................5分 f x f xx1ex1 所以函数 的解析式为 ..........................................................................................6分 fxxex （2）解：由（1）知 ， fx0 fx0 x0 x0 令 ，解 ；令 ，解 ，......................................................................................8分 f x (0,) (,0) 所以函数 在 上单调递增，在 上单调递减，.............................................................10分 f x f 00 x0 所以，当 时，函数 取得最小值，最小值为 ，无最大值.........................................12分 f x (0,) (,0) 0 即函数 的增区间为 ，减区间为 ，最小值为 ，无最大值.....................................13分 ABC AB4 D,E AC,AB DE 16．（15分）如图1，在等边三角形 中， ，点 分别是 的中点.如图2，以 为折 VADE A A BCDE AB,AC 痕将 折起，使点A到达点 的位置（ 平面 ），连接 . (1)证明：平面ABE 平面ABC； AB 10 AB ACD (2)当 时，求直线 与平面 所成角的正弦值. 【答案】(1)证明见解析； 2 6 (2) 5 . 1 原创精品资源学科网独家享有版权，侵权必究！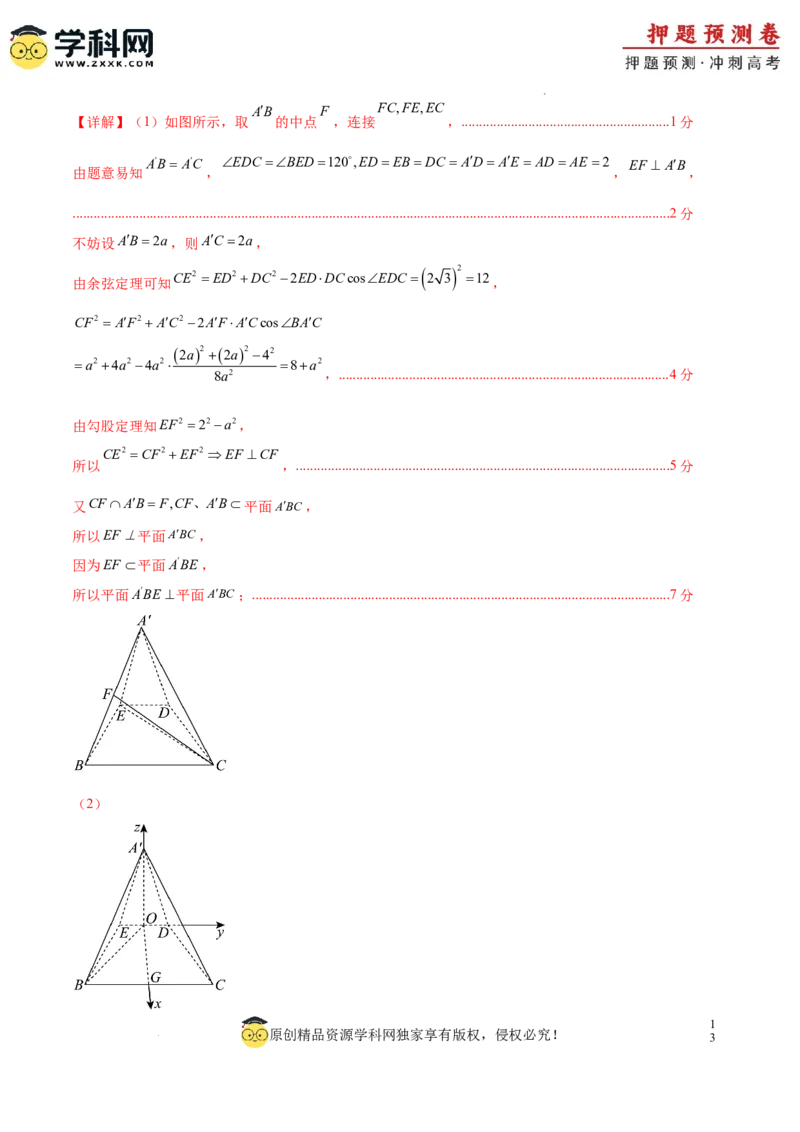 2 学科网（北京）股份有限公司AB F FC,FE,EC 【详解】（1）如图所示，取 的中点 ，连接 ，...........................................................1分 AB AC EDC BED120,EDEBDC  AD AE AD AE 2 EF  AB 由题意易知 ， ， ， ..........................................................................................................................................................................2分 不妨设AB2a，则AC 2a，  2 CE2 ED2DC22EDDCcosEDC  2 3 12 由余弦定理可知 ， CF2  AF2AC22AFACcosBAC 2a2 2a2 42 a24a24a2 8a2 8a2 ，..............................................................................................4分 由勾股定理知EF2 22a2， CE2 CF2EF2 EF CF 所以 ，..........................................................................................................5分 又CFABF,CF、AB平面ABC， 所以EF平面ABC， 因为EF 平面ABE， 所以平面ABE 平面ABC；.......................................................................................................................7分 （2） 1 原创精品资源学科网独家享有版权，侵权必究！ 3 学科网（北京）股份有限公司DE、BC O、G AO,BO 分别取 中点 ，连接 ，............................................................................................8分 由余弦定理可知OB2 2212221cos120 7，而AO2 2212 3， 显然AB2 OB2AO2，则AO⊥OB， 易知AODE，GODE， 又DEOBO,ED、OB平面DEBC， AO DEBC 所以 平面 ，...............................................................................................................................9分 因为OG平面DEBC，所以AOOG，则AO,OG,DE两两垂直， A  0,0, 3  ,D0,1,0,C  3,2,0  ,B  3,2,0  建立如图所示的空间直角坐标系，则 ， (cid:3) (cid:3) (cid:3)       AD 0,1, 3 ,AC  3,2, 3 ,AB 3,2, 3 所以 ， (cid:3) (cid:3)  nAD y 3z0 设平面 ADC 的一个法向量为 n (cid:3) x,y,z，则有  n (cid:3)   A (cid:3)   c 3x2y 3z0 ， (cid:3)   n 1, 3,1 取y 3z1,x1，即 ，...........................................................................................12分 设直线AB与平面ACD所成角为， (cid:3) (cid:3) n (cid:3)   A (cid:3)   B 2 6 则 sin cosn,AB  (cid:3) (cid:3)  ，...................................................................................................14分 n  AB 5 2 6 所以直线AB与平面ACD所成角的正弦值为 5 .................................................................................15分 N  220,202 17．（15分）已知某种机器的电源电压U（单位：V）服从正态分布 ．其电压通常有3种状态： ①不超过200V；②在200V~240V之间③超过240V．在上述三种状态下，该机器生产的零件为不合格品的 概率分别为0.15，0.05，0.2． (1)求该机器生产的零件为不合格品的概率； n2 p p (2)从该机器生产的零件中随机抽取n（ ）件，记其中恰有2件不合格品的概率为 n，求 n取得最大 值时n的值． 1 原创精品资源学科网独家享有版权，侵权必究！ 4 学科网（北京）股份有限公司Z ~ N  ,2 PZ 0.68 P2Z 20.95 附：若 ，取 ， ． 【答案】(1)0.09； (2)n22. 【详解】（1）记电压“不超过200V”、“在200V~240V之间”、“超过240V”分别为事件A，B，C， “该机器生产的零件为不合格品”为事件D．..........................................................................................1分 1PZ  10.68 因为U ~ N  220,202，所以PAPU 200  0.16， 2 2 PBP200U 240PZ 0.68 ， 1PZ  10.68 PCPU 240  0.16．............................................................4分 2 2 PDPAPD|APBPD|BPCPD|C 所以 0.160.150.680.050.160.20.09，..............................................................................................6分 所以该机器生产的零件为不合格品的概率为0.09．..................................................................................7分 X ~Bn,0.09 （2）从该机器生产的零件中随机抽取n件，设不合格品件数为X，则 ，...................9分 p PX 2C20.91n20.092 所以 n n ．...................................................................................................10分 p C2 0.91n10.092 n1 191 n1  n1  0.911 2n 由 p C20.91n20.092 n1 ，解得 9 ．...........................................................13分 n n 2n21 p  p 所以当 时， n n1； n22 p  p p 当 时， n n1；所以 22最大． n22 p 因此当 时， n最大．.......................................................................................................................15分 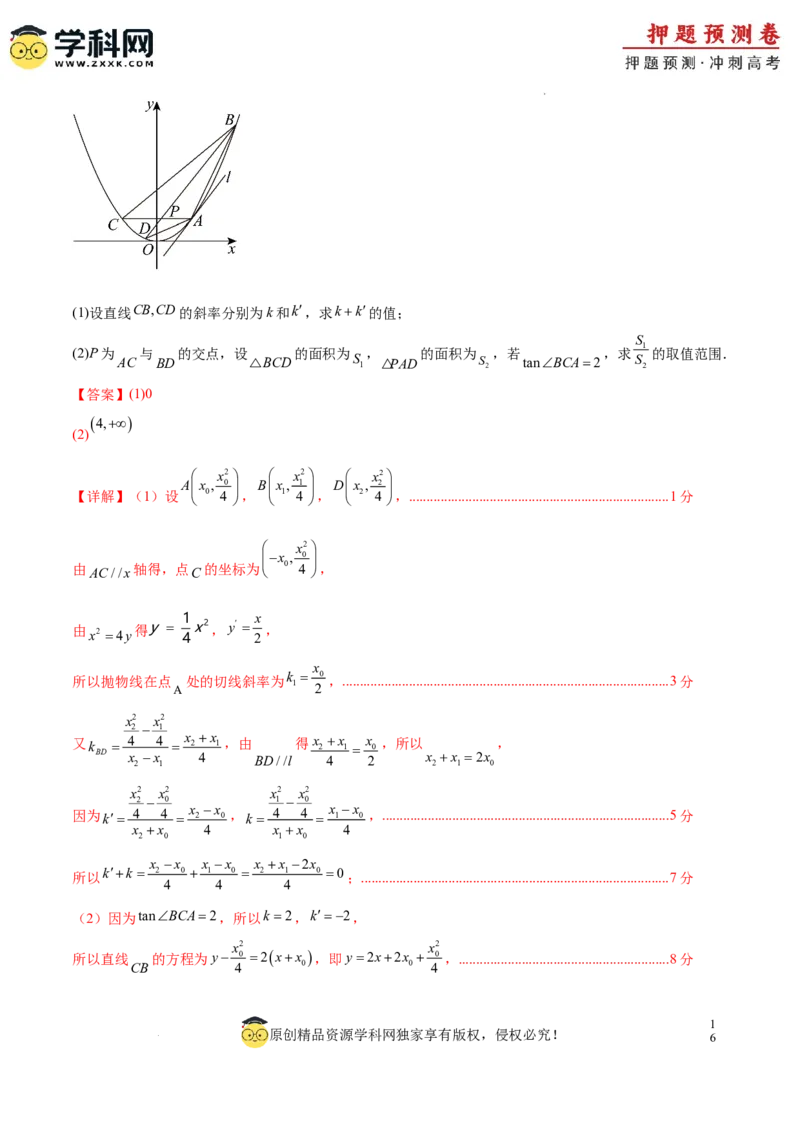ABCD x2 4y AC//x 18．（17分）如图，已知四边形 的四个顶点都在抛物线 上，且A，B在第一象限， 轴，抛物线在点A处的切线为l，且BD//l． 1 原创精品资源学科网独家享有版权，侵权必究！ 5 学科网（北京）股份有限公司(1)设直线CB,CD的斜率分别为k和k，求kk的值； S 1 (2)P为 与 的交点，设 的面积为 ， 的面积为 ，若 ，求 的取值范围． AC BD △BCD S 1 PAD S 2 tanBCA2 S 2 【答案】(1)0 4, (2)  x2   x2   x2  Ax , 0  Bx, 1  Dx , 2  【详解】（1）设  0 4 ，  1 4 ，  2 4 ，..........................................................................1分  x2 x , 0  由 AC//x 轴得，点C的坐标为 0 4 ， 1 x 由 x2 4y 得y  4 x2 ，y  2 ， x 所以抛物线在点 处的切线斜率为k  0 ，.............................................................................................3分 A 1 2 x2 x2 2  1 又k  4 4  x 2 x 1 ，由 得x 2 x 1  x 0 ，所以 ， BD x x 4 BD//l 4 2 x x 2x 2 1 2 1 0 x2 x2 x2 x2 2  0 1  0 因为k 4 4  x 2 x 0 ，k  4 4  x 1 x 0 ，..................................................................................5分 x x 4 x x 4 2 0 1 0 x x x x x x 2x 所以kk  2 0  1 0  2 1 0 0；........................................................................................7分 4 4 4 （2）因为tanBCA2，所以k 2，k2， x2 x2 所以直线 的方程为y 0 2xx  ，即y2x2x  0 ，............................................................8分 CB 4 0 0 4 1 原创精品资源学科网独家享有版权，侵权必究！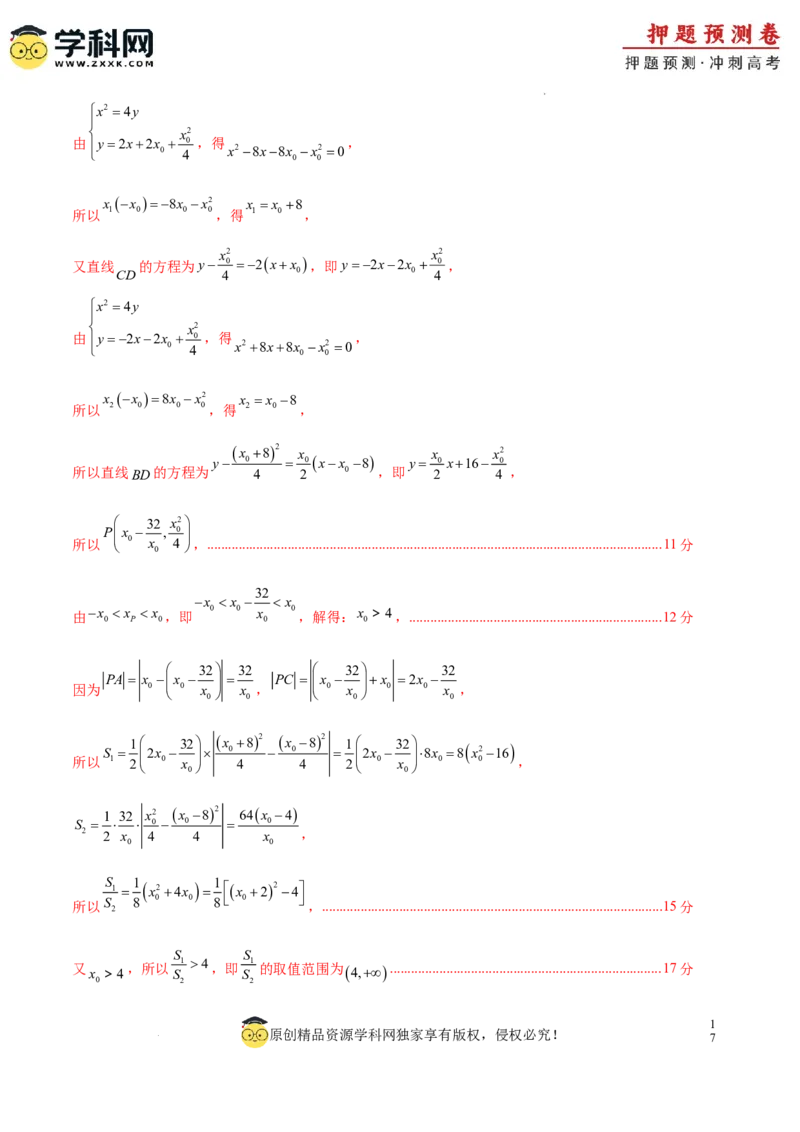 6 学科网（北京）股份有限公司x2 4y   x2 由  y2x2x 0  4 0 ，得 x28x8x x2 0 ， 0 0 x x 8x x2 x x 8 所以 1 0 0 0，得 1 0 ， x2 x2 又直线 的方程为y 0 2xx ，即y2x2x  0 ， CD 4 0 0 4 x2 4y   x2 由  y2x2x 0  4 0 ，得 x28x8x x2 0 ， 0 0 x x 8x x2 x x 8 所以 2 0 0 0，得 2 0 ， x 82 x x x2 y 0  0xx 8 y 0 x16 0 所以直线BD的方程为 4 2 0 ，即 2 4 ，  32 x2  Px  , 0  所以  0 x 4 ，..................................................................................................................................11分 0 32 x  x   x 由x x x ，即 0 0 x 0 ，解得：x >4，........................................................................12分 0 P 0 0 0  32 32  32 32 PA  x x    PC  x  x 2x  因为 0  0 x  x ，  0 x  0 0 x ， 0 0 0 0 1 32 x 82 x 82 1 32 S  2x   0  0  2x  8x 8  x216  所以 1 2 0 x  4 4 2 0 x  0 0 ， 0 0 1 32 x2 x 82 64x 4 S    0  0  0 2 2 x 4 4 x ， 0 0 S 1 1 1   x24x   x 224 所以S 8 0 0 8 0  ，.................................................................................................15分 2 S S 1 4 1 又 x >4 ，所以 S ，即 S 的取值范围为4,.............................................................................17分 0 2 2 1 原创精品资源学科网独家享有版权，侵权必究！ 7 学科网（北京）股份有限公司【点睛】关键点点睛：本题的关键是建立用解析思想解决几何问题，用点A的坐标表示B,C,D的坐标，从 而达到解决几何问题的目的. 19．（17分）已知数列 a n  的前 n 项和为 S n，若数列 a n  满足：①数列 a n  项数有限为 N ；② S N 0 ；③ N  a 1 i a  i1 ，则称数列 n 为“N 阶可控摇摆数列”. a 1n10 a  (1)若等比数列 n 为“10阶可控摇摆数列”，求 n 的通项公式； a  1n2m,mN* a a a  (2)若等差数列 n 为“2m阶可控摇摆数列”，且 m m1，求数列 n 的通项公式； N  a 2S a  i m S  (3)已知数列 n 为“N 阶可控摇摆数列”，且存在1mN ，使得 i1 ，探究：数列 n 能否为 “N 阶可控摇摆数列”，若能，请给出证明过程；若不能，请说明理由. 1 1 【答案】(1)a  (1)n11n10 或a  (1)n1n10 n 10 n 10 2n2m1 (2)a   1n2m,mN* n 2m2 (3)不能，理由见解析 10  a 0 【详解】（1）若q1，则 S 10a 0 ，解得 a 0 ，则 i ，与题设矛盾，舍去；............1分 10 1 1 i1 a  1q10 S  1 0 若q1，则 10 1q ，得 q1 ， 10 1 1  a 10 a 1 a  a  而 i 1 ，解得 1 10或 1 10，.........................................................................................3分 i1 1 1 a  (1)n11n10 a  (1)n1n10 故 或 ...........................................................................4分 n 10 n 10 a,a ,a ,,a m1 （2）设等差数列 1 2 3 2m 的公差为 d ， 2ma a  因为 ，则 1 2m 0，则 ，...............6分 a a a a 0 2 a a a a 0,a a 1 2 3 2m 1 2m m m1 m m1 1 原创精品资源学科网独家享有版权，侵权必究！ 8 学科网（北京）股份有限公司a a d 0,a 0,a 0 由 m m1，得 m m1 ， 2m 1 1  a 1 a a a a  ,a a a a  而 i ，故 1 2 3 m 2 m1 m2 m3 2m 2，..........................................8分 i1 1 d  两式相减得 ，即 ， m2d 1 m2 mm1 1 2m1 又am d  ，得a  ， 1 2 2 1 2m2 a a n1d  2m1 n1   1   2n2m1  1n2m,mN* 所以 n 1 2m2  m2  2m2 ...............................10分 a 1 ,a 2 ,a 3 ,,a N A B （3）记 中所有非负项之和为 ，负项之和为 ， AB0, 1 1 因为数列 a n  为“N 阶可控摇摆数列”，则  AB1,得 A 2 ,B 2，.......................................11分 1 1 1 故  BS  A n1,2,3,,N ，所以 S  . 2 n 2 n 2 N 1 若存在 ，使得  a 2S ，即S  ， 1mN i m m 2 i1 a 0,a 0,,a 0,a 0,a 0,,a 0 则 1 2 m m1 m2 N ， 1 且 a a a  .........................................................................................................................12分 m1 m2 N 2 假设数列 S n  也为“ N 阶可控摇摆数列”，记数列 S n  的前 n 项和为 T n， 1 则T S S S S  , m 1 2 3 m 2 1 S  因为 m 2 ，所以S S S S 0...........................................................................................13分 1 2 3 m1 1 所以a a a a 0,a  ； 1 2 3 m1 m 2 1 又 a m1 a m2 a N  2 ，则S ,S ,,S 0...............................................................................15分 m1 m2 N 1 原创精品资源学科网独家享有版权，侵权必究！ 9 学科网（北京）股份有限公司S  S  S  S S S S S 所以 1 2 3 N 1 2 3 N； S S S S 0 S  S  S  S 1 即 1 2 3 N 与 1 2 3 N 不能同时成立. S  故数列 n 不为“ N 阶可控摇摆数列”...................................................................................................17分 2 原创精品资源学科网独家享有版权，侵权必究！ 0 学科网（北京）股份有限公司