文档内容
2024年高考押题预测卷【广东专用03】
数学·全解全析
第一部分(选择题 共58分)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
1 2 3 4 5 6 7 8
D A B C C C A D
1.【答案】D
【解析】因为 ,
所以 可以是 ,共8个,
故选:D
2.【答案】A
【解析】因为 ,所以 ,即 ,
所以点 的轨迹是直径为2的圆.
故选:A.
3.【答案】B
【解析】由条件可得四片瓦的体积 ( )
所以500名学生,每人制作4片瓦共需粘土的体积为 ( ),
又 ,
所以共需粘土的体积为约为 ,
故选:B.
4.【答案】C
【解析】不考虑限制条件则共有 种方法,
若甲分到 编号子任务,有两种情况:
甲分到一个子任务(即只有 编号子任务),此时共有 种方法;
1
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司甲分到两个子任务(即包含 编号子任务),此时共有 种方法;
则所求的分配方法共有 种.
故选:C.
5.【答案】C
【解析】由图可知 的图象关于原点对称,则 为奇函数,
对于A : 定义域为 ,
当 时 , ,所以 ,不符合题意,故A错误;
对于B: 定义域为 ,
且 ,
所以 为非奇非偶函数,不符合题意,故B错误;
对于D: 定义域为 ,
且 ,
所以 为非奇非偶函数,不符合题意,故D错误;
对于C: 定义域为 , ,
所以 为奇函数,
且当 时 , ,所以 ,符合题意,故C正确;
故选:C
6.【答案】C
【解析】依题意, ,则 .
故选:C
2
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司7.【答案】A
【解析】设题图②中第 行白心圈的个数为 ,黑心圈的个数为 ,
依题意可得 ,且有 ,
故有 ,
所以 是以 为首项,3为公比的等比数列,
为常数数列,且 ,
所以 是以 为首项,1为公比的等比数列,
故 故 所以 .
故选:A.
8.【答案】D
【解析】
由题意可知点 , 分别为椭圆的左右顶点,所以 , ,
设点 在第一象限,设点 ,所以 ,
,
3
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司所以 , .
故选: .
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部
选对的得6分,部分选对的得部分分,有选错的得0分.
9 10 11
BC ABD BC
9.【答案】BC
【解析】对A,由于 共10个数据,且 ,
故第40百分位数为第4,5个数据的平均数为 ,故A错误;
对B,设数据 的平均数为 ,方差为
,
则数据 的平均数为
,
方差为
,所以
,故B正确;
对C, 则 ,即 ,由正
态分布 的性质可得 ,故C正确;
对D,在独立性检验中,零假设为 :分类变量 和 独立.基于小概率值 的独立性检验规则是:当
4
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司时,我们就推断 不成立,即认为 和 不独立,该推断犯错误的概率不超过 ;当 时,
我们没有充分证据推断 不成立,可以认为 和 独立.故D错误.
故选:BC
10.【答案】ABD
【解析】对于选项A,令 ,得 ,解得 或 ,
当 时,令 ,则 ,则 ,这与 不恒为零矛盾,所以 ,
故选项A正确,
对于选项B,令 ,则 ,即 ,
即 为偶函数,所以选项B正确,
对于选项C,取 ,满足题意,此时 不是 的极小值点,所以选项C错误,
对于选项D,令 ,得 ,
若 ,则 ,则 ,
则 ,所以选项D正确,
故选:ABD.
11.【答案】BC
【解析】对于A,由于MN与平面 的所成角大小为30°,所以点 到平面 的距离 ,
故半径为 的球面在平面 上截面圆的半径为 ,故截痕长为 ,A错误,
对于B,由于平面 ,所以以 为 ,在平面 内过 作 ,平面 内作 ,建立如
图所示的空间直角坐标系,
则 ,
5
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司设 ,则 ,
化简得 ,故P到点M和点N的距离相等,则点P的轨迹是一条直线,B正确,
,所以P到直线MN的距离为 ,化
简可得 ,
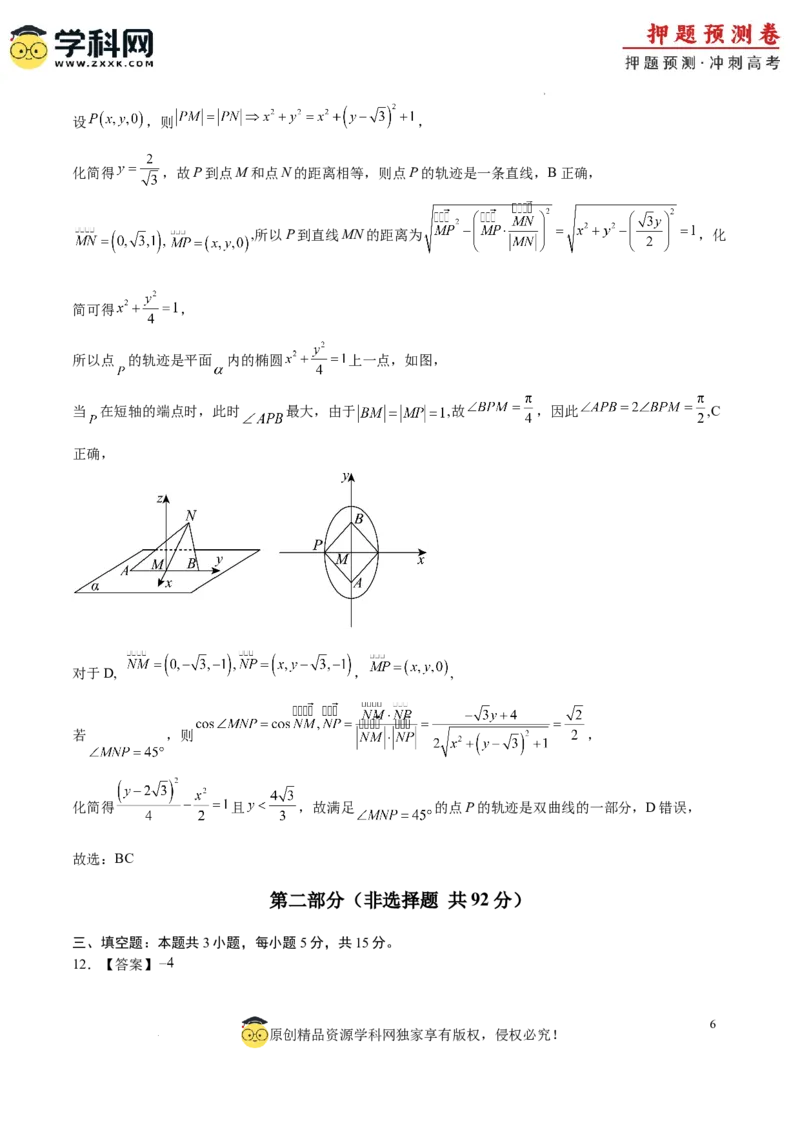
所以点 的轨迹是平面 内的椭圆 上一点,如图,
当 在短轴的端点时,此时 最大,由于 ,故 ,因此 ,C
正确,
对于D, , ,
若 ,则 ,
化简得 且 ,故满足 的点P的轨迹是双曲线的一部分,D错误,
故选:BC
第二部分(非选择题 共92分)
三、填空题:本题共3小题,每小题5分,共15分。
12.【答案】
6
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司【解析】因为 // ,所以 ,解得 ,
所以 .
故答案为:
13.【答案】
【解析】在 中,由余弦定理可得 ,
即 ,解得 ,
所以 , ,
在 中,由余弦定理可得
,
所以 .
故答案为: .
14.【答案】6
【解析】设 ,由题意 , , ,
可知 ,
故当 时, ,
当 时, ,
当 , ,
当 时, ,
当 时, ,
轨迹方程的图形如图,
7
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司图形的面积为: .
故答案为:6.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步棸。
15.【解析】(1)该比赛三局定胜负意味着甲、乙两人前面三局有一人连赢,
则该比赛三局定胜负的概率为 .
(2)依题意, 的可能取值为2,3,4,
则 , ,
,
则 的分布列为
2 3 4
故 .
16.【解析】(1)证明:由于 垂直下底面圆 ,
故 ,
平面 , 平面 ,所以 平面
又 ,所以 ,
平面 , 平面 ,所以 平面
8
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司平面 ,所以平面 平面
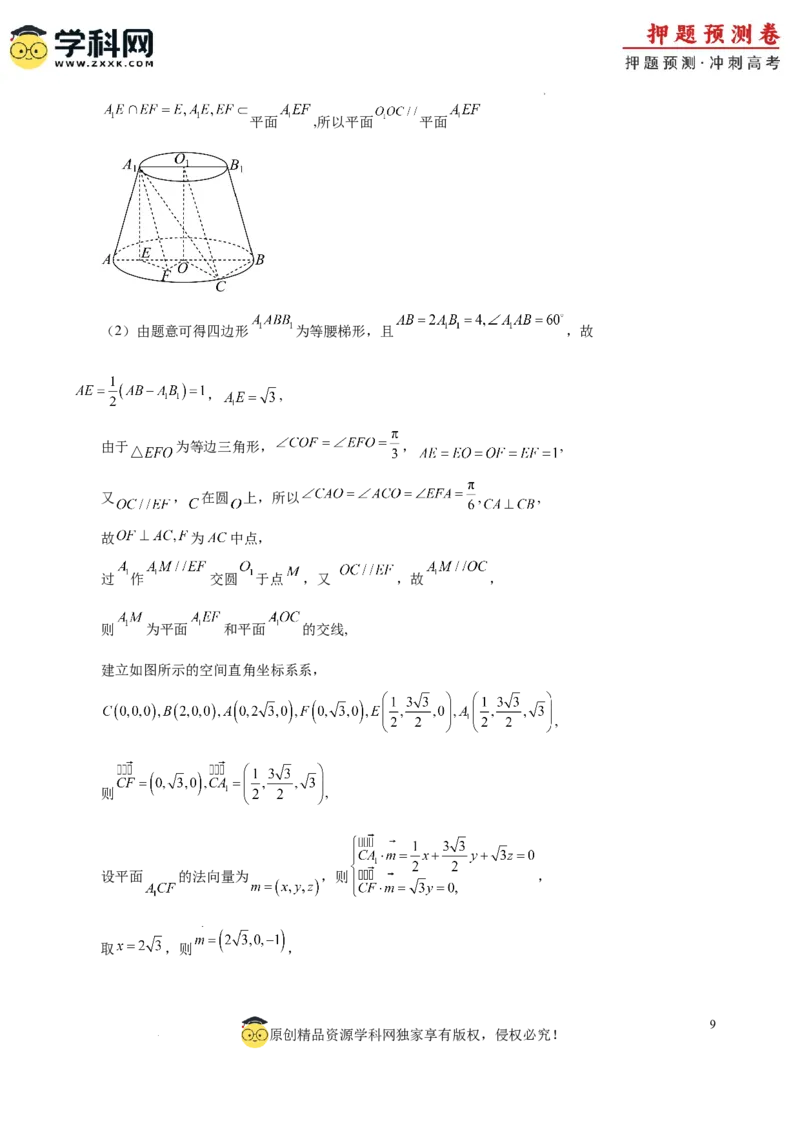
(2)由题意可得四边形 为等腰梯形,且 ,故
, ,
由于 为等边三角形, , ,
又 , 在圆 上,所以 , ,
故 为 中点,
过 作 交圆 于点 ,又 ,故 ,
则 为平面 和平面 的交线,
建立如图所示的空间直角坐标系系,
,
则 ,
设平面 的法向量为 ,则 ,
取 ,则 ,
9
原创精品资源学科网独家享有版权,侵权必究!
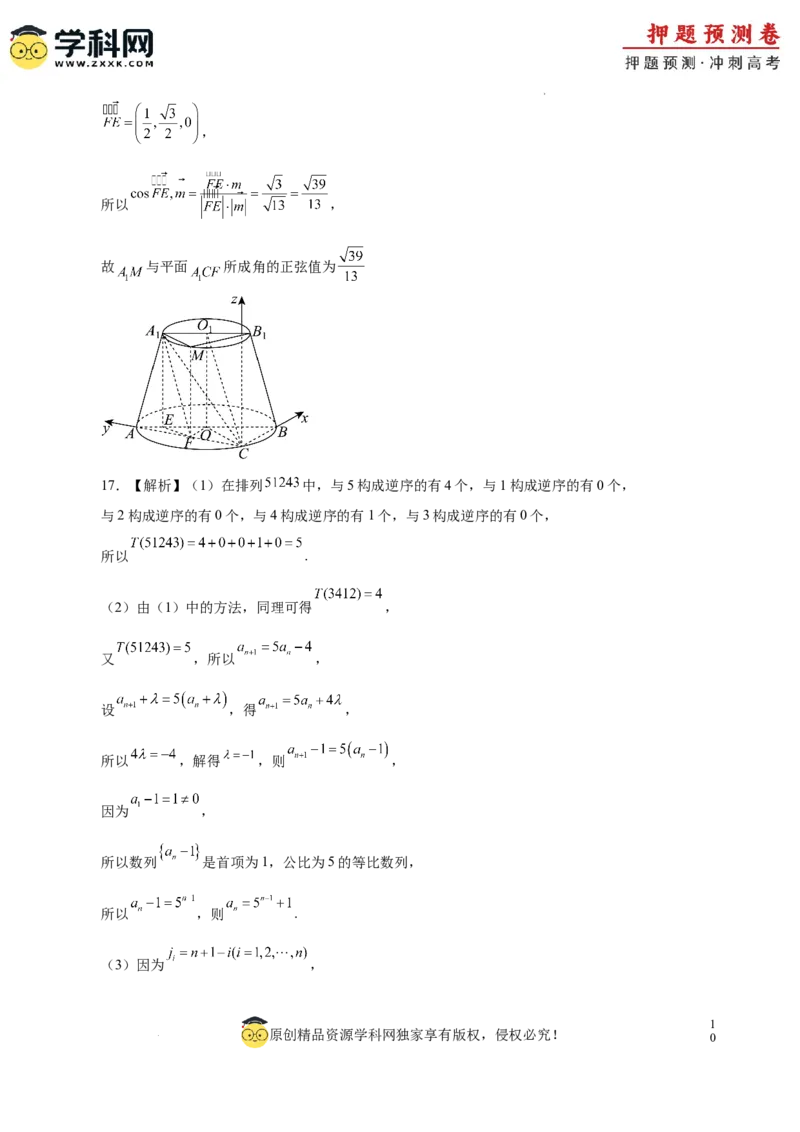
学科网(北京)股份有限公司,
所以 ,
故 与平面 所成角的正弦值为
17.【解析】(1)在排列 中,与5构成逆序的有4个,与1构成逆序的有0个,
与2构成逆序的有0个,与4构成逆序的有1个,与3构成逆序的有0个,
所以 .
(2)由(1)中的方法,同理可得 ,
又 ,所以 ,
设 ,得 ,
所以 ,解得 ,则 ,
因为 ,
所以数列 是首项为1,公比为5的等比数列,
所以 ,则 .
(3)因为 ,
1
原创精品资源学科网独家享有版权,侵权必究!
0
学科网(北京)股份有限公司所以 ,
所以 ,
所以 .
18.【解析】(1)由已知得 ,解得 ,
所以 的方程为 .
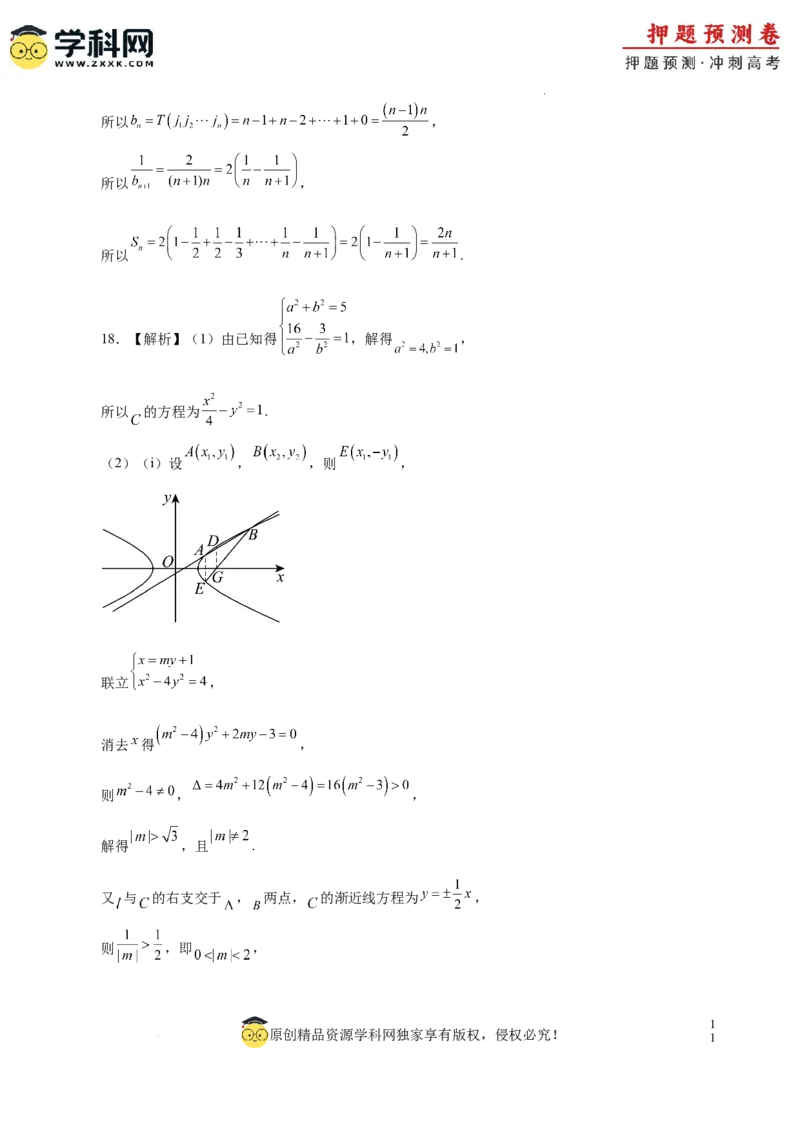
(2)(i)设 , ,则 ,
联立 ,
消去 得 ,
则 , ,
解得 ,且 .
又 与 的右支交于 , 两点, 的渐近线方程为 ,
则 ,即 ,
1
原创精品资源学科网独家享有版权,侵权必究!
1
学科网(北京)股份有限公司所以| 的取值范围为 .
(ii)由(i)得 , ,
又点 在 轴上的投影为 ,所以 , ,
所以 ,
,
所以 ,
又 , 有公共点 ,所以 , , 三点共线,所以直线 过点 .
19.【解析】(1)当 时,
所以切线方程为: 即
(2)(ⅰ)
即 ,
设
又 是 的一个必要条件,即
下证 时,满足
又 ,
设 在 上单调递减,
1
原创精品资源学科网独家享有版权,侵权必究!
2
学科网(北京)股份有限公司所以 ,
又 即 在 单调递增.
时, ;
下面证明 时不满足 ,
,
令 ,
则 ,
,
∴ 在 为增函数,
令 满足 ,
则 ,
又 ∴ ,使得 ,
当 时, ,
∴此时 在 为减函数,
当 时, ,
∴ 时,不满足 恒成立.
综上 .
(ⅱ)设
1
原创精品资源学科网独家享有版权,侵权必究!
3
学科网(北京)股份有限公司由(ⅰ)知 ,
在 上单调递增, 即
1
原创精品资源学科网独家享有版权,侵权必究!
4
学科网(北京)股份有限公司