文档内容
2024年高考押题预测卷【新高考卷】
数学·参考答案
第一部分(选择题 共58分)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
1 2 3 4 5 6 7 8
B D B C A B C D
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部
选对的得6分,部分选对的得部分分,有选错的得0分.
9 10 11
AB AD BD
第二部分(非选择题 共92分)
三、填空题:本题共3小题,每小题5分,共15分。
13. 14. 15.①③④
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步棸。
15.(13分)
【解析】(1) 的定义域为R, ,
当 时, , 单调递减;
当 时,令 ,得 , (3分)
当 时, , 单调递减;
当 时, , 单调递增.
1
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司综上,当 时, 在R 上单调递减;
当 时, 在 单调递减; 在 上单调递增. (7分)
(2)由(1)知, ,
设切点 为,则 ,
易知 ,故 . (10分)
又 ,即 ,将 代入,得 .
设 ,则 .
令 ,即 ,解得 ,
当 时, , 单调递增,
当 时, , 单调递减,
所以 ,
综上, . (15分)
16.(15分)
【解析】(1)将所给数据进行整理,得到如下列联表:
短视频
游客 合计
收看 未看
南方游
200 100 300
客
北方游
80 120 200
客
2
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司合计 280 220 500
零假设 :南北方游客来此景点旅游与短视频无关联. (4分)
根据小概率值 的独立性检验,我们推断 不成立,
即认为南北方游客来此景点旅游与收看短视频有关联,此推断犯错误的概率不大于0.001 (7分)
(2)(i)设经过 次传递后回到甲的概率为 ,
, ,
又 ,
所以 是首项为 ,公比为 的等比数列,
所以 . (10分)
(ii)(方法一)
设第 次传递时甲接到球的次数为 ,则 服从两点分布, ,
设前 次传递中球传到甲的次数为 ,
,
3
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司因为 ,所以 . (15分)
(方法二)
设第 次传递时,乙接到球的概率和次数分别为 与 ,则 服从两点分布,
,由题可知 , ,
又 ,所以 ,所以 是首项为 ,公比为 的等比数列,
, ,
,
故 . (15分)
17.(15分)
【解析】(1)取 中点 ,连接 分别为 的中点,
, 底面四边形 是矩形, 为棱 的中点,
,
故四边形 是平行四边形, ,
又 平面 平面 , //平面 . (6分)
4
原创精品资源学科网独家享有版权,侵权必究!
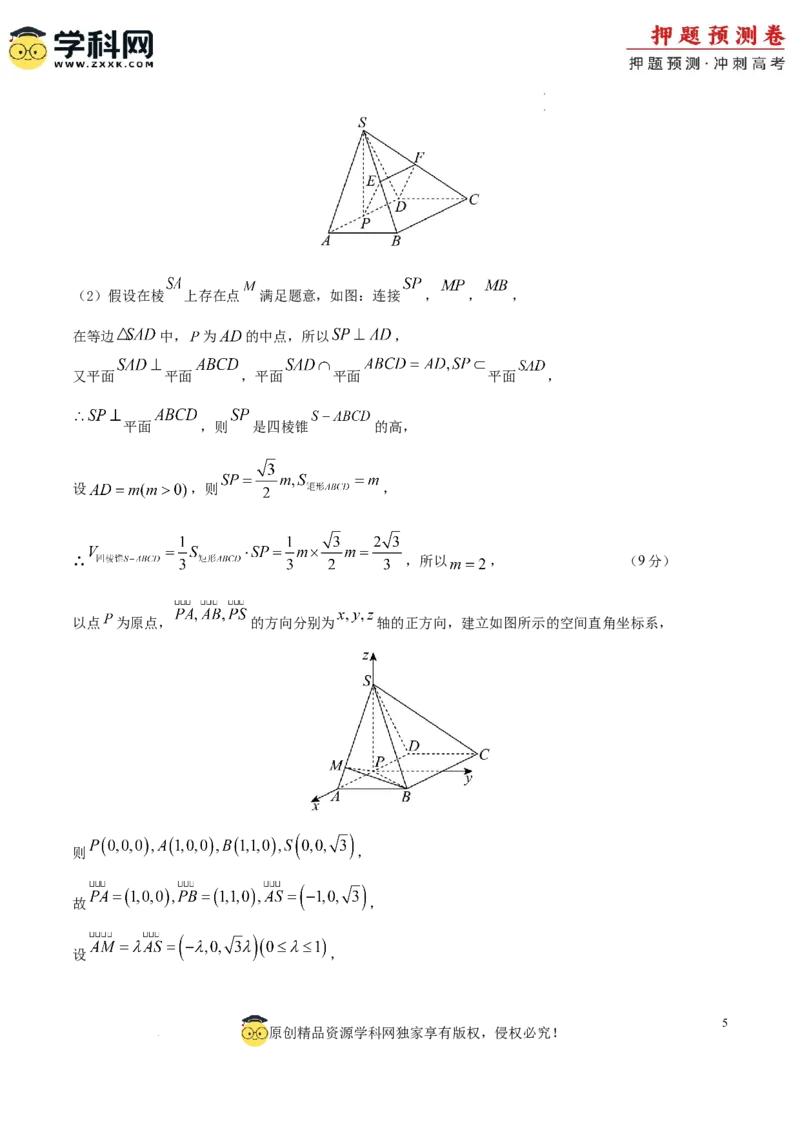
学学科科网网((北北京京))股股份份有有限限公公司司(2)假设在棱 上存在点 满足题意,如图:连接 , , ,
在等边 中, 为 的中点,所以 ,
又平面 平面 ,平面 平面 平面 ,
平面 ,则 是四棱锥 的高,
设 ,则 ,
∴ ,所以 , (9分)
以点 为原点, 的方向分别为 轴的正方向,建立如图所示的空间直角坐标系,
则 ,
故 ,
设 ,
5
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司.
设平面 的一个法向量为 ,
则 所以可取 .
易知平面 的一个法向量为 , (12分)
, ,
故存在点 满足题意. (15分)
18.(17分)
【解析】(1)设点 ,由题意可知 ,
即 ,经化简,得 的方程为 ,
当 时,曲线 是焦点在 轴上的椭圆;
当 时,曲线 是焦点在 轴上的双曲线. (3分)
(2)设点 ,其中 且 ,
(ⅰ)由(1)可知 的方程为 ,
因为 ,所以 ,
6
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司因此, 三点共线,且 , (6
分)
(法一)设直线 的方程为 ,联立 的方程,得 ,
则 ,
由(1)可知 ,
所以
,
所以 为定值1; (9分)
(法二)设 ,则有 ,解得 ,
同理由 ,解得 ,
所以 ,
所以 为定值1; (12分)
7
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司由椭圆定义 ,得 ,
,
解得 ,同理可得 ,
所以
.
因为 ,所以 的周长为定值 . (9分)
(ⅱ)当 时,曲线 的方程为 ,轨迹为双曲线,
根据(ⅰ)的证明,同理可得 三点共线,且 ,
(法一)设直线 的方程为 ,联立 的方程,
得 ,
8
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司,(*)
因为 ,
所以
,
将(*)代入上式,化简得 , (13分)
(法二)设 ,依条件有 ,解得 ,
同理由 ,解得 ,
所以 . (13分)
由双曲线的定义 ,得 ,
9
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司根据 ,解得 ,
同理根据 ,解得 ,
所以
,
由内切圆性质可知, ,
当 时, (常数).
因此,存在常数 使得 恒成立,且 . (17分)
19.(17分)【解析】(1)可求得 ,设 ,则 , ,
设点 , ,
10
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司故
.
所以
(7分)
(2)设 , ,则 , , ,
故
所以坐标变换公式为 ,
该变换所对应的二阶矩阵为 (9分)
(3)设矩阵 ,向量 , ,则 .
,
对应变换公式为: ,
,
所以
11
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司故对应变换公式同样为
所以 得证. (17分)
12
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司