文档内容
四川省乐山市 2021 年中考数学试卷
一、选择题:本大题共10个小题,每小题3分,共30分.
1. 如果规定收入为正,那么支出为负,收入2元记作 ,支出5元记作( ).
A. 5元 B. 元 C. 元 D. 7元
2. 在一次心理健康教育活动中,张老师随机抽取了40名学生进行了心理健康测试,并将测试结果按“健
康、亚健康、不健康”绘制成下列表格,其中测试结果为“健康”的频率是( ).
类型 健康 亚健康 不健康
数据(人) 32 7 1
A. 32 B. 7 C. D.
3. 某种商品 千克的售价为 元,那么这种商品8千克的售价为( )
A. (元) B. (元) C. (元) D. (元)
4. 如图,已知直线 、 、 两两相交,且 .若 ,则 的度数为( )
A. B. C. D.
5. 如图,已知直线 与坐标轴分别交于 、 两点,那么过原点 且将 的面积平分
的直线 的解析式为( )A. B. C. D.
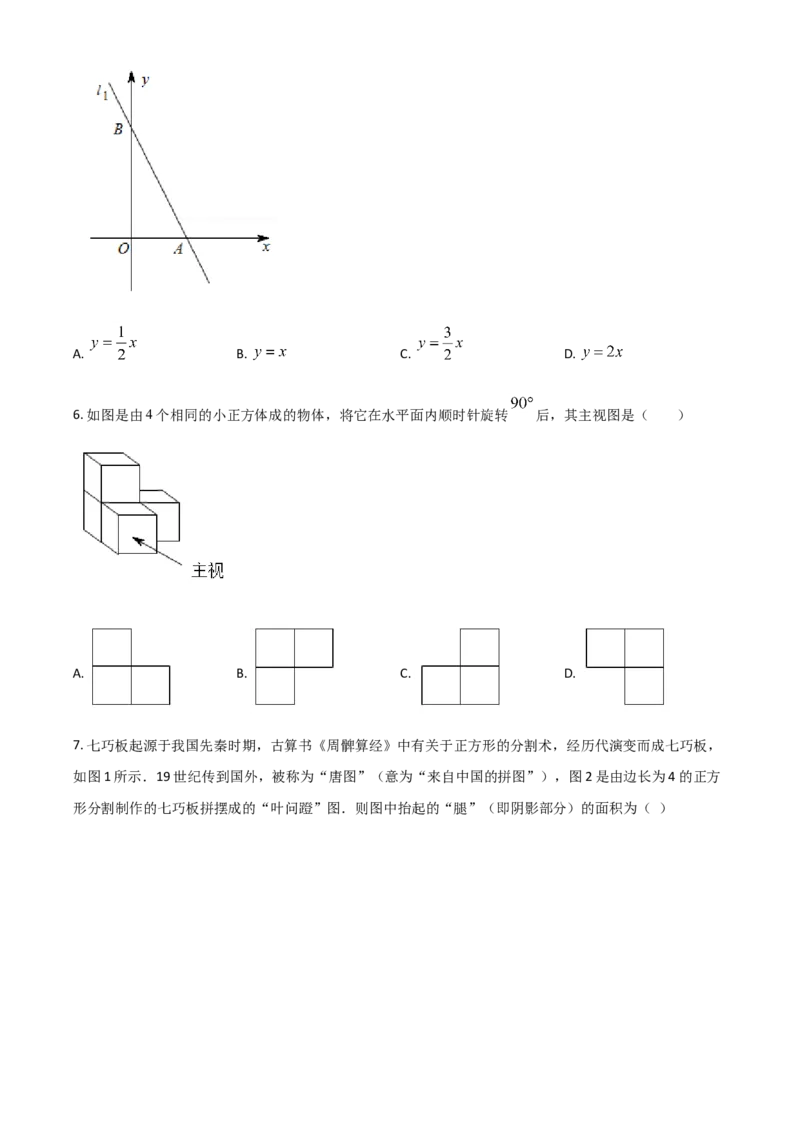
6. 如图是由4个相同的小正方体成的物体,将它在水平面内顺时针旋转 后,其主视图是( )
A. B. C. D.
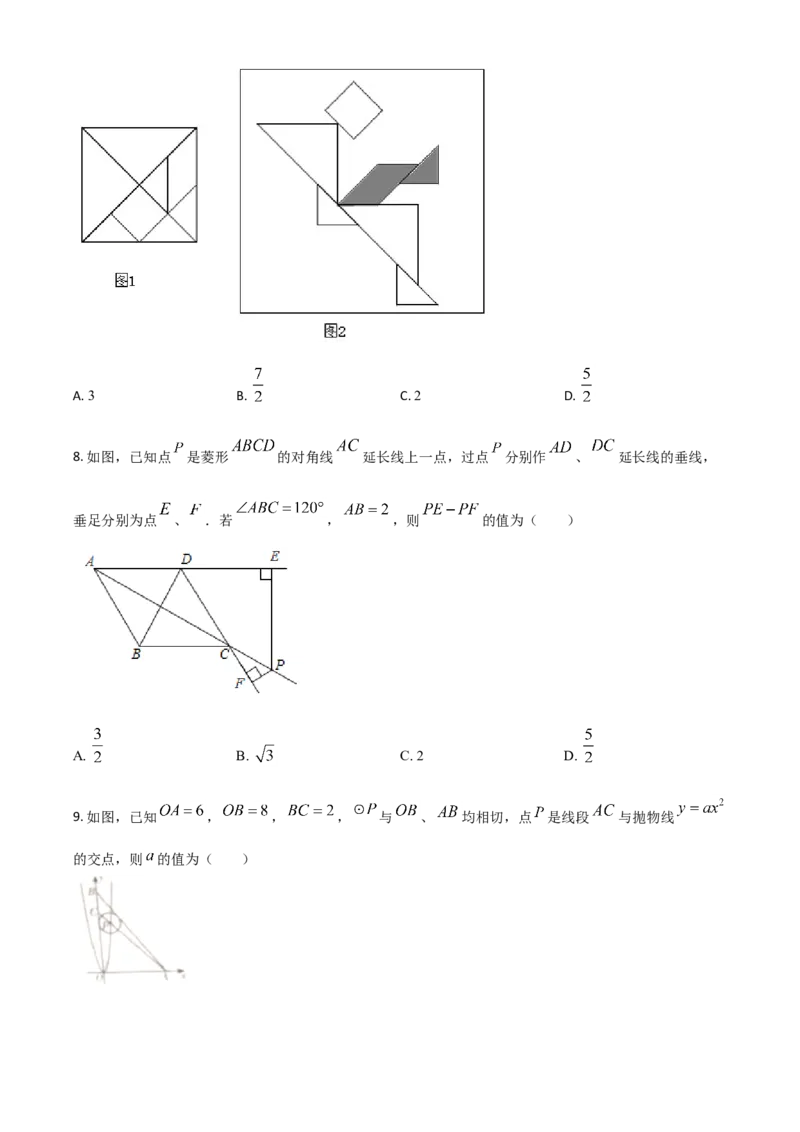
7. 七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板,
如图1所示.19世纪传到国外,被称为“唐图”(意为“来自中国的拼图”),图2是由边长为4的正方
形分割制作的七巧板拼摆成的“叶问蹬”图.则图中抬起的“腿”(即阴影部分)的面积为( )A. 3 B. C. 2 D.
8. 如图,已知点 是菱形 的对角线 延长线上一点,过点 分别作 、 延长线的垂线,
垂足分别为点 、 .若 , ,则 的值为( )
A. B. C. 2 D.
9. 如图,已知 , , , 与 、 均相切,点 是线段 与抛物线
的交点,则 的值为( )A. 4 B. C. D. 5
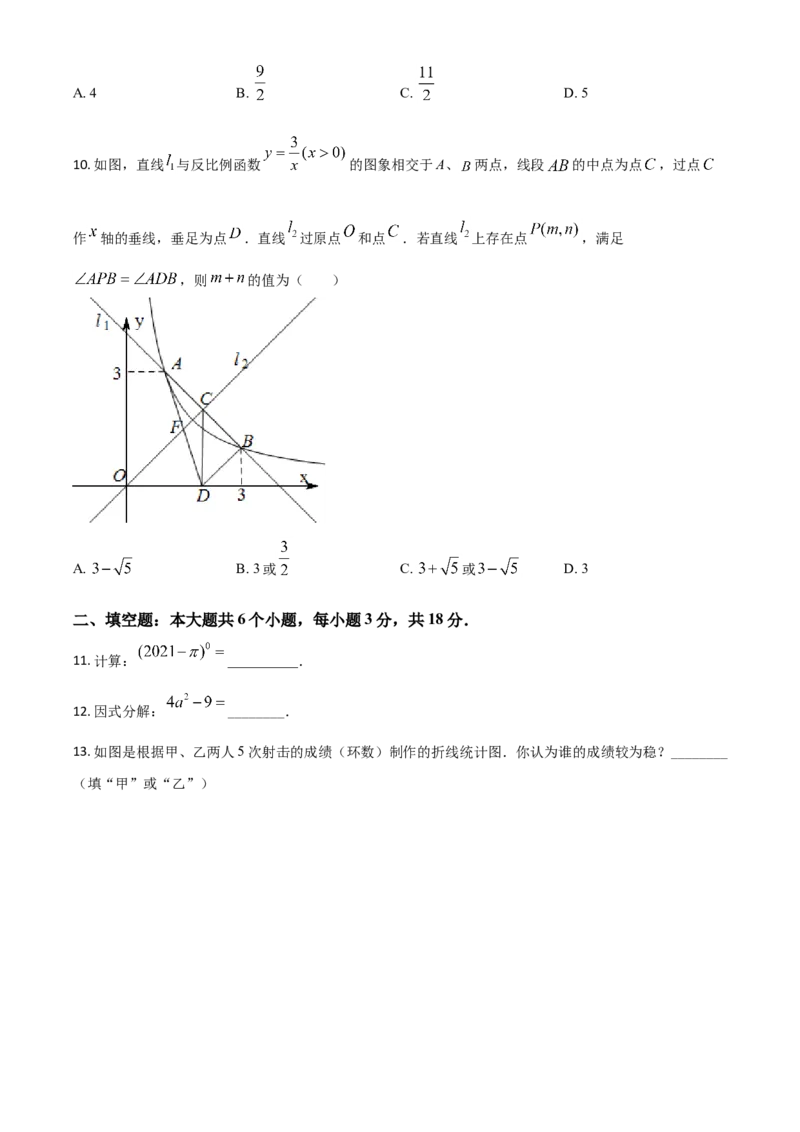
10. 如图,直线 与反比例函数 的图象相交于A、 两点,线段 的中点为点 ,过点
作 轴的垂线,垂足为点 .直线 过原点 和点 .若直线 上存在点 ,满足
,则 的值为( )
A. B. 3或 C. 或 D. 3
二、填空题:本大题共6个小题,每小题3分,共18分.
11. 计算: __________.
12. 因式分解: ________.
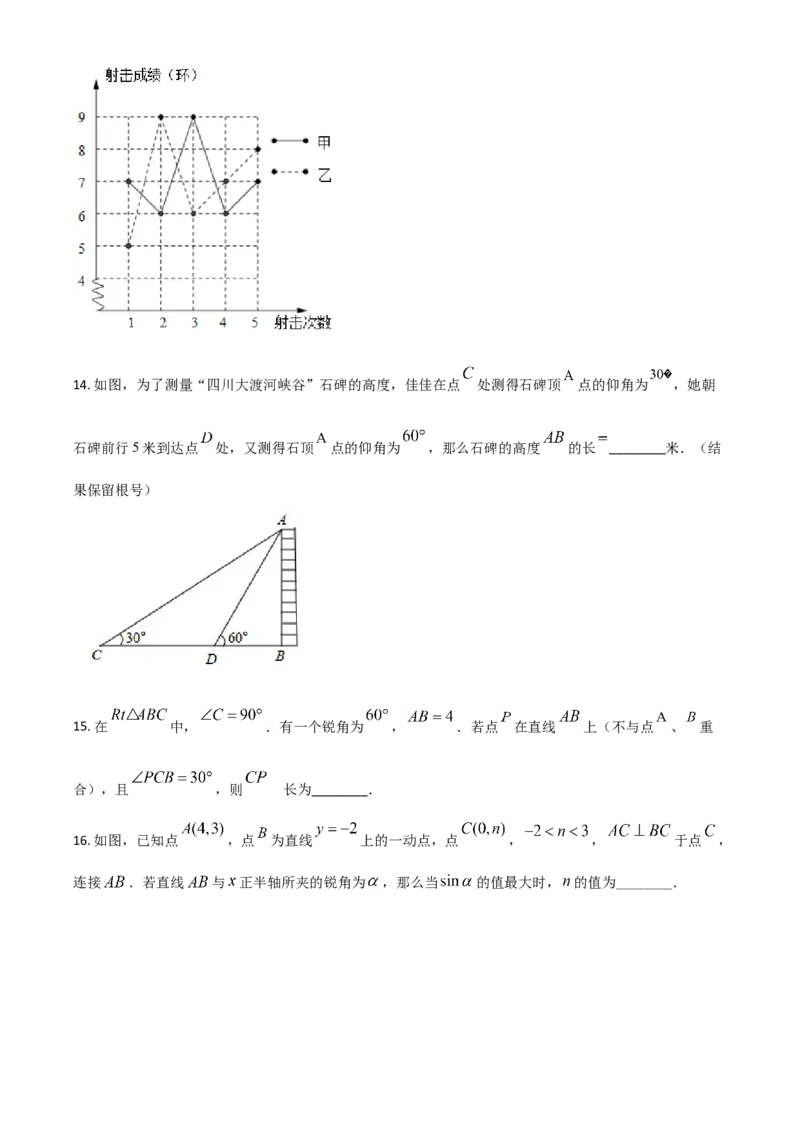
13. 如图是根据甲、乙两人5次射击的成绩(环数)制作的折线统计图.你认为谁的成绩较为稳?________
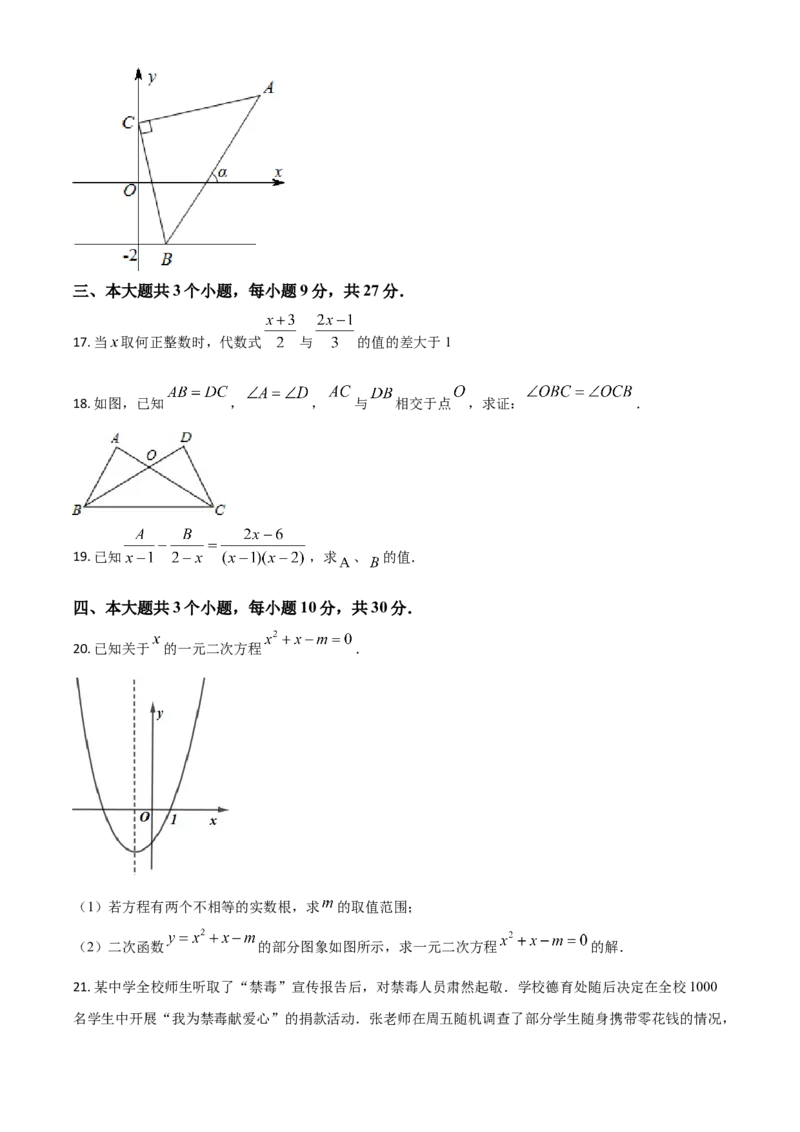
(填“甲”或“乙”)14. 如图,为了测量“四川大渡河峡谷”石碑的高度,佳佳在点 处测得石碑顶 点的仰角为 ,她朝
石碑前行5米到达点 处,又测得石顶 点的仰角为 ,那么石碑的高度 的长 ________米.(结
果保留根号)
15. 在 中, .有一个锐角为 , .若点 在直线 上(不与点 、 重
的
合),且 ,则 长为________.
16. 如图,已知点 ,点 为直线 上的一动点,点 , , 于点 ,
连接 .若直线 与 正半轴所夹的锐角为 ,那么当 的值最大时, 的值为________.三、本大题共3个小题,每小题9分,共27分.
17. 当 取何正整数时,代数式 与 的值的差大于1
18. 如图,已知 , , 与 相交于点 ,求证: .
19. 已知 ,求 、 的值.
四、本大题共3个小题,每小题10分,共30分.
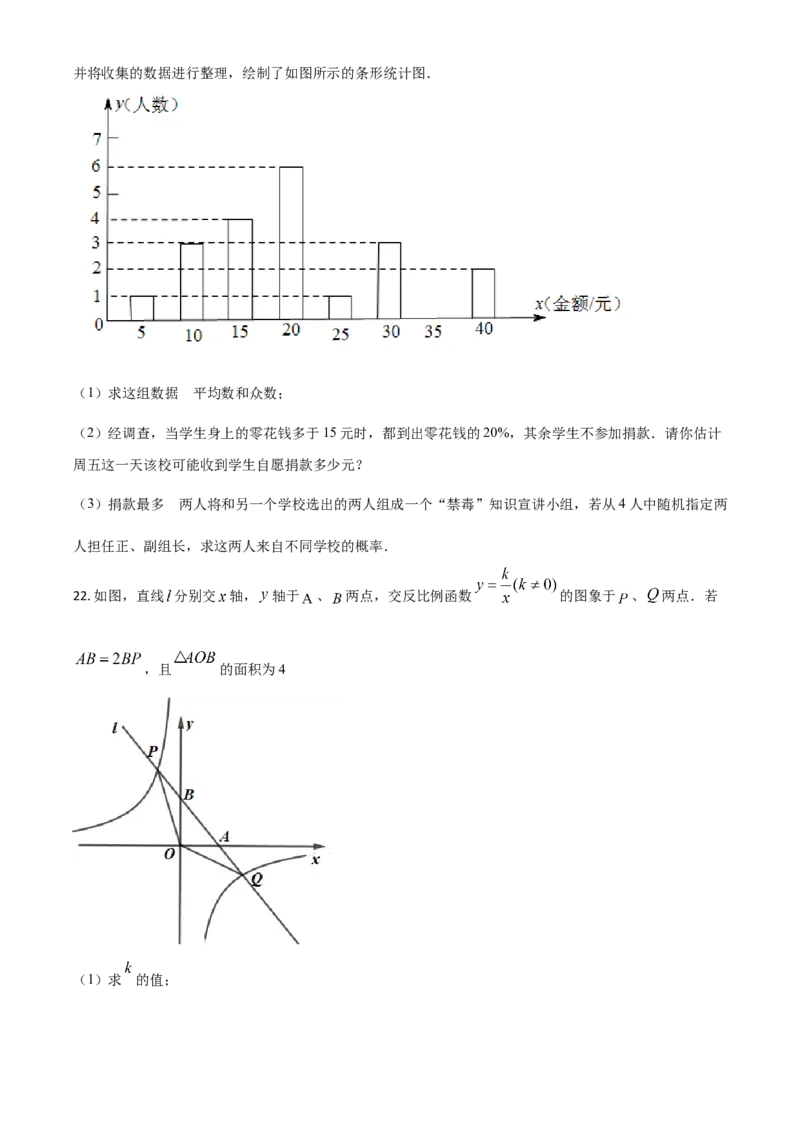
20. 已知关于 的一元二次方程 .
(1)若方程有两个不相等的实数根,求 的取值范围;
(2)二次函数 的部分图象如图所示,求一元二次方程 的解.
21. 某中学全校师生听取了“禁毒”宣传报告后,对禁毒人员肃然起敬.学校德育处随后决定在全校1000
名学生中开展“我为禁毒献爱心”的捐款活动.张老师在周五随机调查了部分学生随身携带零花钱的情况,并将收集的数据进行整理,绘制了如图所示的条形统计图.
的
(1)求这组数据 平均数和众数;
(2)经调查,当学生身上的零花钱多于15元时,都到出零花钱的20%,其余学生不参加捐款.请你估计
周五这一天该校可能收到学生自愿捐款多少元?
的
(3)捐款最多 两人将和另一个学校选出的两人组成一个“禁毒”知识宣讲小组,若从4人中随机指定两
人担任正、副组长,求这两人来自不同学校的概率.
22. 如图,直线 分别交 轴, 轴于 、 两点,交反比例函数 的图象于 、 两点.若
,且 的面积为4
(1)求 的值;(2)当点 的横坐标为 时,求 的面积.
五、本大题共2个小题,每小题10分,共20分.
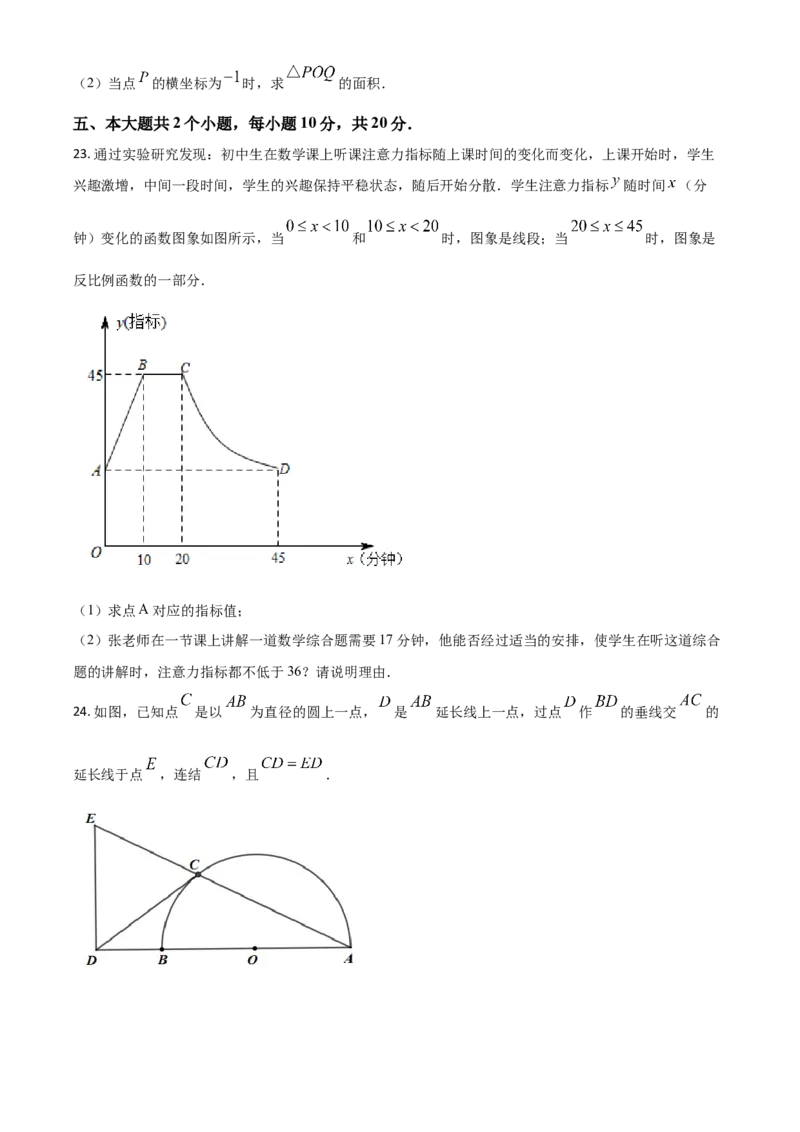
23. 通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生
兴趣激增,中间一段时间,学生的兴趣保持平稳状态,随后开始分散.学生注意力指标 随时间 (分
钟)变化的函数图象如图所示,当 和 时,图象是线段;当 时,图象是
反比例函数的一部分.
(1)求点 对应的指标值;
(2)张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合
题的讲解时,注意力指标都不低于36?请说明理由.
24. 如图,已知点 是以 为直径的圆上一点, 是 延长线上一点,过点 作 的垂线交 的
延长线于点 ,连结 ,且 .(1)求证: 是 的切线;
的
(2)若 , ,求 半径.
六、本大题共2个小题,第25题12分,第26题13分,共25分.
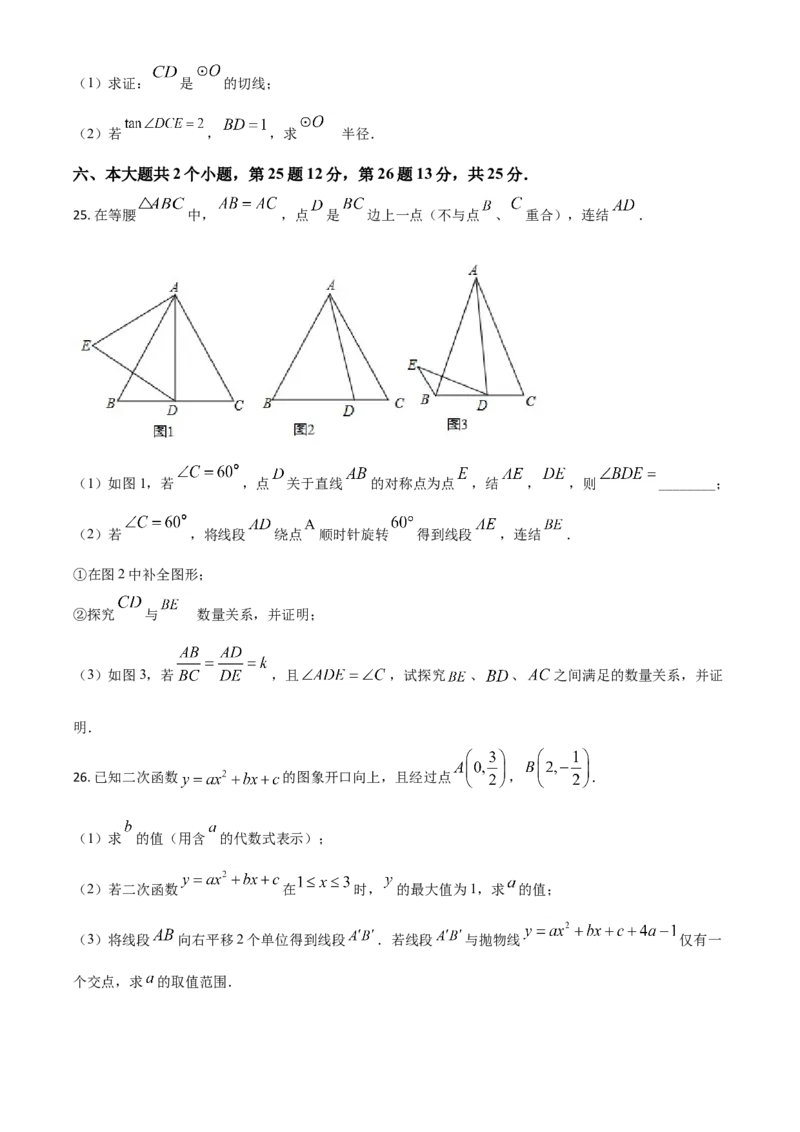
25. 在等腰 中, ,点 是 边上一点(不与点 、 重合),连结 .
(1)如图1,若 ,点 关于直线 的对称点为点 ,结 , ,则 ________;
(2)若 ,将线段 绕点 顺时针旋转 得到线段 ,连结 .
①在图2中补全图形;
的
②探究 与 数量关系,并证明;
(3)如图3,若 ,且 ,试探究 、 、 之间满足的数量关系,并证
明.
26. 已知二次函数 的图象开口向上,且经过点 , .
(1)求 的值(用含 的代数式表示);
(2)若二次函数 在 时, 的最大值为1,求 的值;
(3)将线段 向右平移2个单位得到线段 .若线段 与抛物线 仅有一
个交点,求 的取值范围.