四川省南充市2019年中考数学真题试题_中考真题_2.数学中考真题2015-2024年_2019年全国中考数学206份

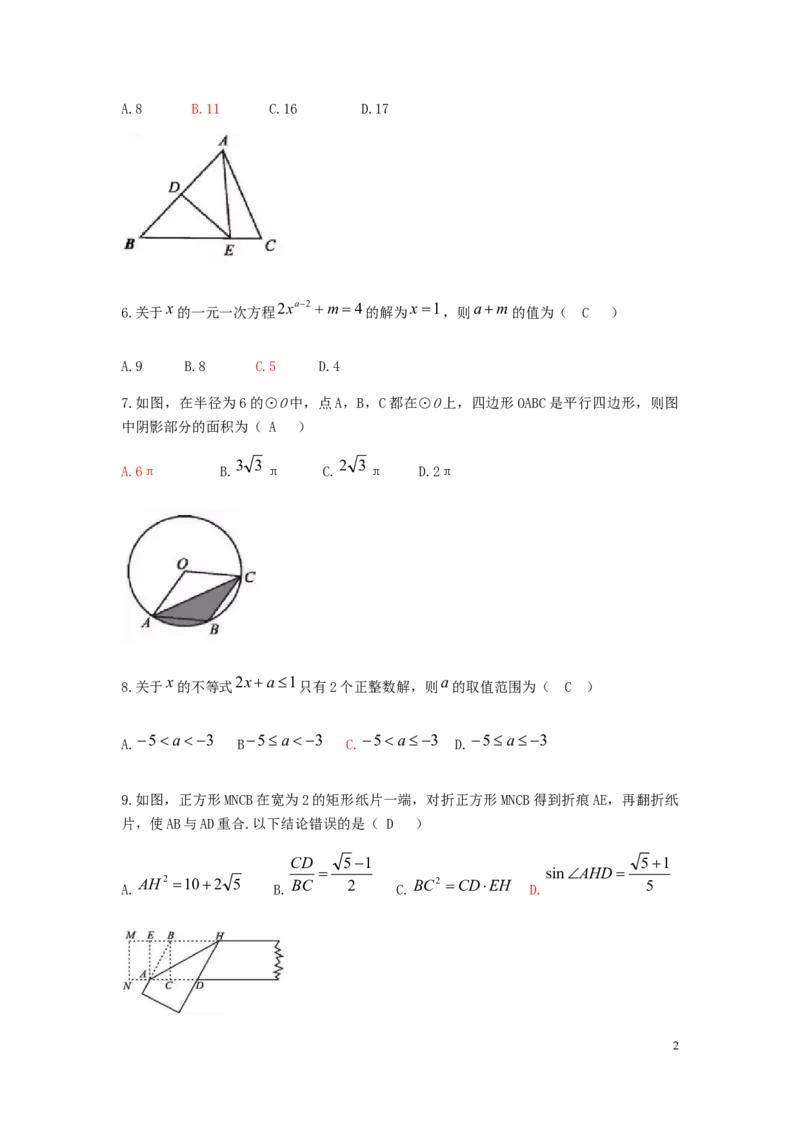
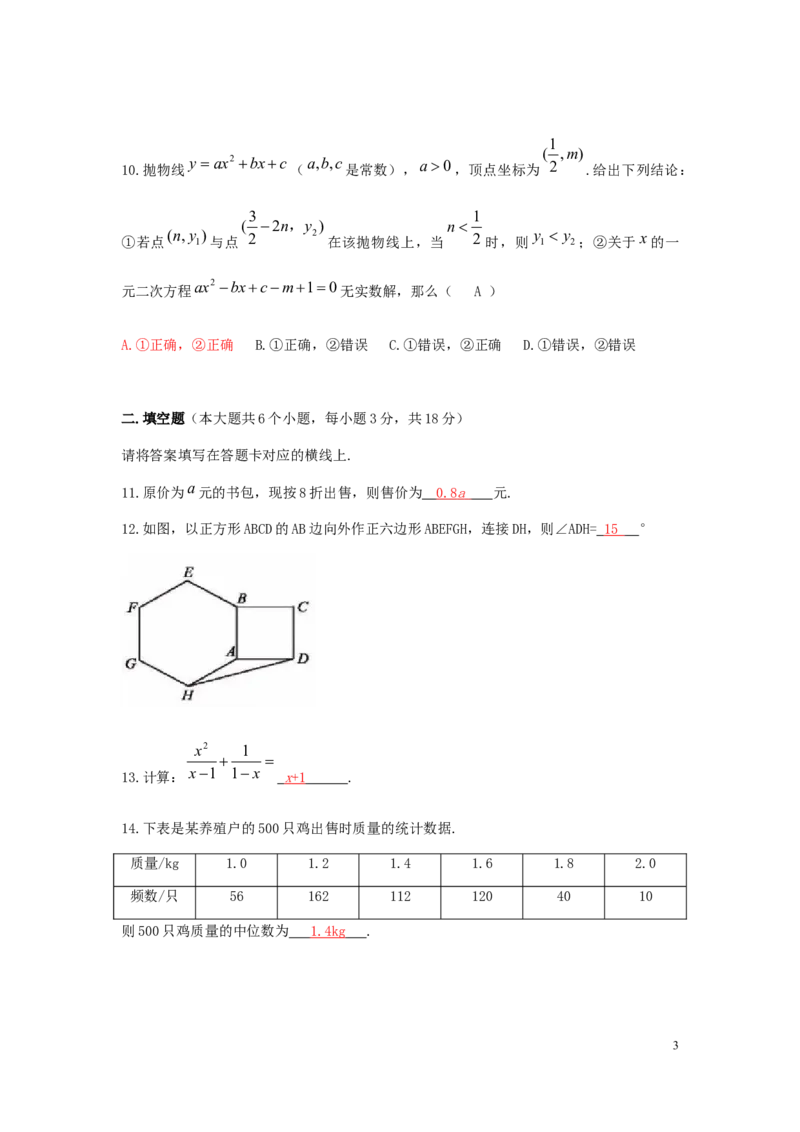
2019年南充中考数学试题 考试时间：120分钟 满分：120分 一.选择题（本大题共10个小题，每小题3分，共30分） 每小题都有代号为A、B、C、D四个答案选项，其中只有一个是正确的. 6a 1 a 1.如果 ，那么 的值为（ B ） 1 1  A.6 B.6 C.-6 D. 6 2.下列各式计算正确的是（ D ） xx2  x3 (x2)3  x5 x6 x2  x3 xx2  x3 A. B. C. D. 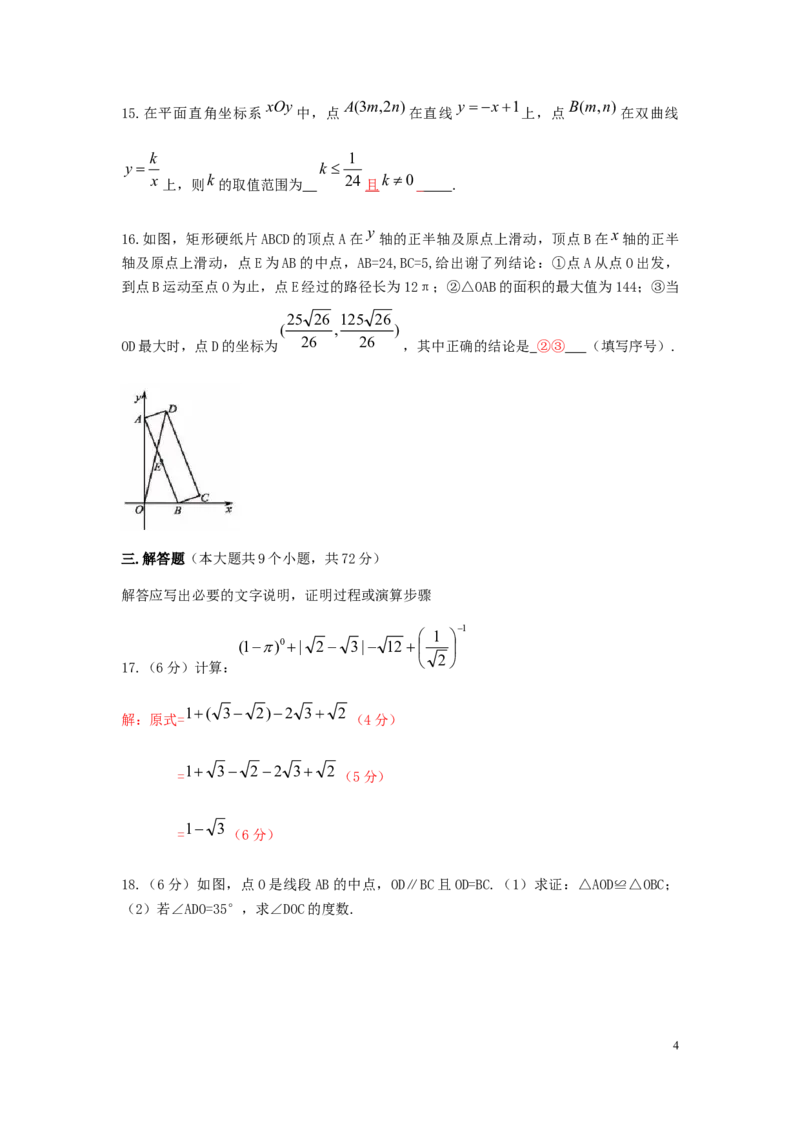3.如图是一个几何体的表面展开图，这个几何体是（ C ） A B C D 4.在2019年南充市初中毕业升学体育与健康考试中，某校九年级（1）班体育委员对本班 50名同学参加球类自选项目做了统计，制作出扇形统计图（如图），则该班选考乒乓球人 数比羽毛球人数多（ B ） A.5人 B.10人 C.15人 D.20人 5.如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，若BC=6，AC=5，则 △ACE的周长为（ B ） 1A.8 B.11 C.16 D.17 x 2xa2 m4 x1 am 6.关于 的一元一次方程 的解为 ，则 的值为（ C ） A.9 B.8 C.5 D.4 7.如图，在半径为6的⊙O中，点A，B，C都在⊙O上，四边形OABC是平行四边形，则图 中阴影部分的面积为（ A ） 3 3 2 3 A.6π B. π C. π D.2π x 2xa1 a 8.关于 的不等式 只有2个正整数解，则 的取值范围为（ C ） 5a3 5a3 5a3 5a3 A. B C. D. 9.如图，正方形MNCB在宽为2的矩形纸片一端，对折正方形 MNCB得到折痕AE，再翻折纸 片，使AB与AD重合.以下结论错误的是（ D ） CD 51 51  sinAHD A. AH2 102 5 B. BC 2 C. BC2 CDEH D. 5 21 ( ,m) 10.抛物线 y ax2 bxc （ a,b,c 是常数）， a0 ，顶点坐标为 2 .给出下列结论： 3 1 ( 2n，y ) n ①若点 (n,y 1 ) 与点 2 2 在该抛物线上，当 2 时，则 y 1  y 2；②关于 x 的一 ax2 bxcm10 元二次方程 无实数解，那么（ A ） A.①正确，②正确 B.①正确，②错误 C.①错误，②正确 D.①错误，②错误 二.填空题（本大题共6个小题，每小题3分，共18分） 请将答案填写在答题卡对应的横线上. a 11.原价为 元的书包，现按8折出售，则售价为 0. 8a 元. 12.如图，以正方形ABCD的AB边向外作正六边形ABEFGH，连接DH，则∠ADH= 15 ° x2 1   13.计算： x1 1x x + 1 . 14.下表是某养殖户的500只鸡出售时质量的统计数据. 质量/kg 1.0 1.2 1.4 1.6 1.8 2.0 频数/只 56 162 112 120 40 10 则500只鸡质量的中位数为 1.4k g . 3xOy A(3m,2n) y x1 B(m,n) 15.在平面直角坐标系 中，点 在直线 上，点 在双曲线 k 1 y  k  x 上，则 k 的取值范围为 24 且 k 0 . y x 16.如图，矩形硬纸片ABCD的顶点A在 轴的正半轴及原点上滑动，顶点B在 轴的正半 轴及原点上滑动，点E为AB的中点，AB=24,BC=5,给出谢了列结论：①点A从点O出发， 到点B运动至点O为止，点E经过的路径长为12π；②△OAB的面积的最大值为144；③当 25 26 125 26 ( , ) OD最大时，点D的坐标为 26 26 ，其中正确的结论是 ②③ （填写序号）. 三.解答题（本大题共9个小题，共72分） 解答应写出必要的文字说明，证明过程或演算步骤 1  1  (1)0| 2 3| 12   2 17.（6分）计算： 1( 3 2)2 3 2 解：原式= （4分） 1 3 22 3 2 = （5分） 1 3 = （6分） 18.（6分）如图，点O是线段AB的中点，OD∥BC且OD=BC.（1）求证：△AOD≌△OBC； （2）若∠ADO=35°，求∠DOC的度数. 4（1）证明：∵点O线段AB的中点，∴AO=BO（1分） ∵OD∥BC，∴∠AOD=∠OBC（2分） AO  BO  AOD OBC  OD  BC  在△AOD和△OBC中， ，∴△AOD≌△OBC（SAS）（4分） （2）解：∵△AOD≌△OBC，∴∠ADO=∠OCB=35°（5分） ∵OD∥BC，∴∠DOC=∠OCB=35°（6分） 19.（6分）现有四张完全相同的不透明卡片，其正面分别写有数字-2，-1,0,2，把这四张 卡片背面朝上洗匀后放在桌面上.（1）随机抽取一张卡片，求抽取的卡片上的数字为负数 的概率；（2）先随机抽取卡片，其上的数字作为点A的横坐标；然后放回并洗匀，再随机 抽取一张卡片，其上的数字作为点A的纵坐标，试用画树状图或列表的方法求出点A在直 线y=2x上的概率. 2 1  解：（1）∵抽取的负数可能为-2，-1，∴抽取出数字为负数的概率为P=4 2 （2分） （2）列表如下 （4分） ∵共有16种等可能结果，其中点A在直线y=2x上的结果有2种（5分） 2 1 P  ∴点A在直线y=2x上的概率为 16 8（6分） 5x x2 (2m1)xm2 30 20.（8分）已知关于 的一元二次方程 有实数根.（1）求实数 x ,x (x2 2x )(x2 4x 2) m的取值范围；（2）当m=2时，方程的根为 1 2，求代数式 1 1 2 2 的值. 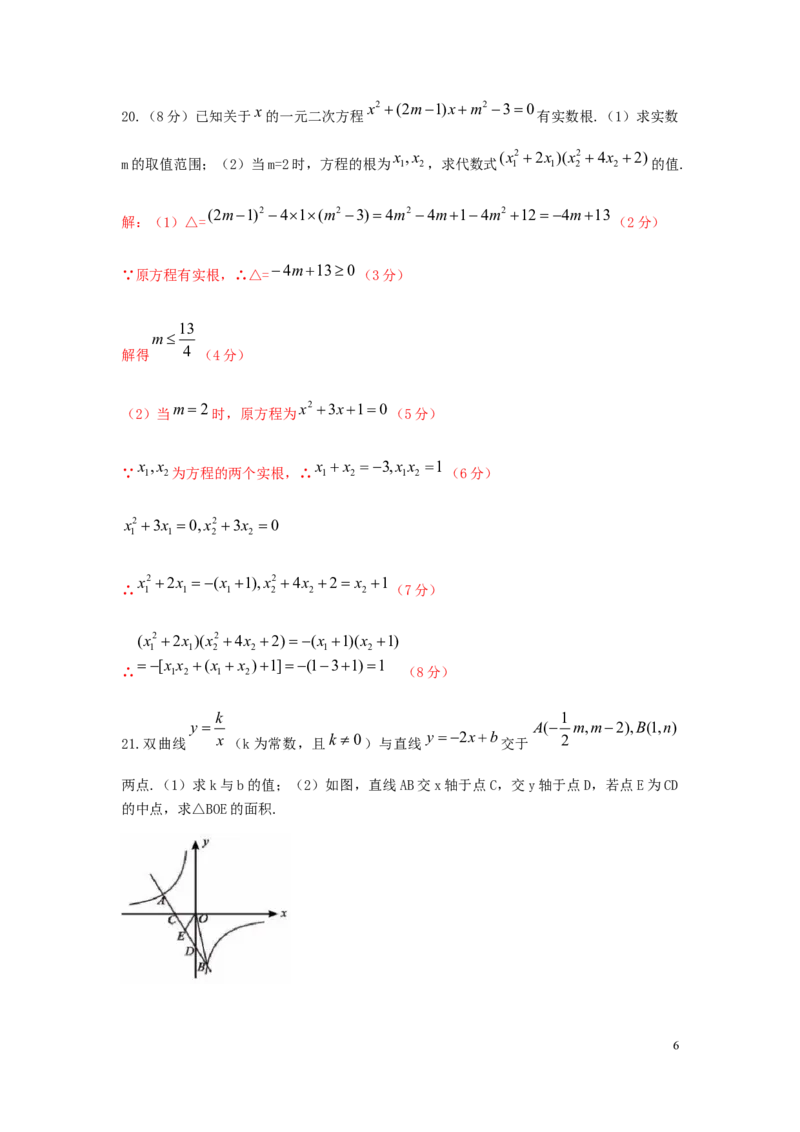(2m1)2 41(m2 3)4m2 4m14m2 124m13 解：（1）△= （2分） 4m130 ∵原方程有实根，∴△= （3分） 13 m 解得 4 （4分） m2 x2 3x10 （2）当 时，原方程为 （5分） x ,x x x 3,x x 1 ∵ 1 2为方程的两个实根，∴ 1 2 1 2 （6分） x2 3x 0,x2 3x 0 1 1 2 2 x2 2x (x 1),x2 4x 2 x 1 ∴ 1 1 1 2 2 2 （7分） (x2 2x )(x2 4x 2)(x 1)(x 1) 1 1 2 2 1 2 [x x (x x )1](131)1 ∴ 1 2 1 2 （8分） k 1 y  A( m,m2),B(1,n) 21.双曲线 x （k为常数，且 k 0 ）与直线 y 2xb 交于 2 两点.（1）求k与b的值；（2）如图，直线AB交x轴于点C，交y轴于点D，若点E为CD 的中点，求△BOE的面积. 61 A( m,m2) 解：（1）∵点 2 在直线 y 2xb 上， 1 2( m)bm2,b2 ∴ 2 （2分） y 2x2 y 2x2 n2124 ∴ ，∵点B（1，n）在直线 上，∴ （3分） k y  ∴B（1，-4），∵B（1，-4）在双曲线 x 上，∴ k 1(4)4 （4分） y 2x2 （2）直线 交x轴于C（-1,0），交y轴于D（0，-2）（5分） 1 |1||2|1 ∴S =2 △COD 1 1 ∵点E为CD的中点，∴S =2 S =2 （6分） △COE △COD 1 |1||4|2 ∵S =2 （7分） △COB 1 3  ∴S =S -S =2-2 2 .（8分） △BOE △COB △COE 22.（8分）如图，在△ABC中，以AC为直径的⊙O交AB于点D，连接CD，∠BCD=∠A. （1）求证：BC是⊙O的切线；（2）若BC=5，BD=3，求点O到CD的距离. 7（1）证明：∵AC是⊙O的直径，∴∠ADC=90°（1分） ∠A+∠ACD=90°，∵∠BCD=∠A，∴∠BCD+∠ACD=90°（2分） ∴OC⊥BC，∵OC是⊙O的半径，∴BC是⊙O的切线.（3分） （2）解：过点O作OE⊥CD于点E，如图所示（4分） 在Rt△BCD中，∵BC=5，BD=3，∴CD=4（5分） ∵∠ADC=∠CDB=90°，∠BCD=∠A. CD BD 3 16   AD ∴Rt△BDC∽Rt△CDA.∴ AD CD 4 ，∴ 3 （6分） ∵OE⊥CD，∴E为CD的中点（7分） 1 8 AD 又∵点O是AC的中点，∴OE=2 3（8分） 23.（10分）在“我为祖国点赞”征文活动中，学校计划对获得一、二等奖的学生分别奖 励一支钢笔，一本笔记本.已知购买2支钢笔和3个笔记本共38元，购买4支钢笔和5个笔 记本共70元.（1）钢笔、笔记本的单价分别为多少元？（2）经与商家协商，购买钢笔超 过30支时，每增加一支，单价降低0.1元；超过50支，均按购买50支的单价销售.笔记 本一律按原价销售.学校计划奖励一、二等奖学生共计100人，其中一等奖的人数不少于 30人，且不超过60人，这次奖励一等学生多少人时，购买奖品金额最少，最少为多少元？ 2x3y 38  x y 4x5y 70 解：（1）设钢笔、笔记本的单价分别为 、 元.根据题意可得 （2分） x10  y 6 解得： （4分）.答：钢笔、笔记本的单价分别为10元，6元. a （2）设钢笔单价为 元，购买数量为b支，支付钢笔和笔记本总金额为W元. 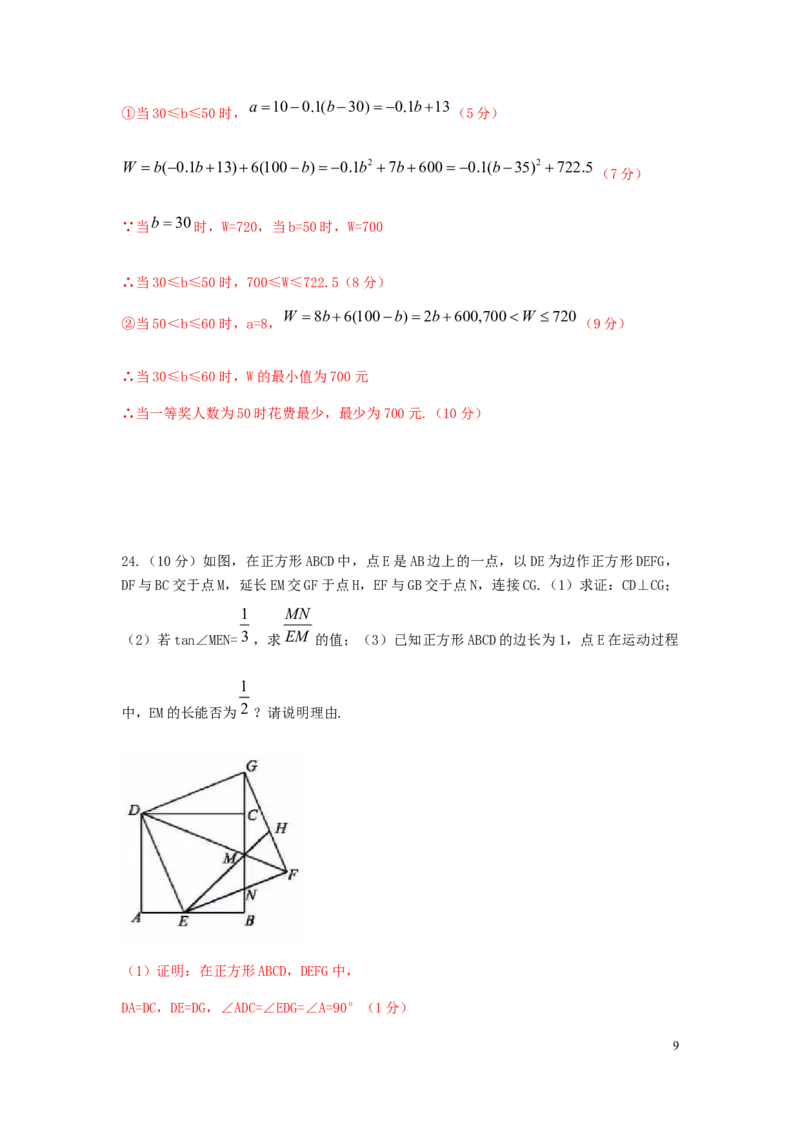8a 100.1(b30)0.1b13 ①当30≤b≤50时， （5分） W b(0.1b13)6(100b)0.1b2 7b6000.1(b35)2 722.5 （7分） b30 ∵当 时，W=720，当b=50时，W=700 ∴当30≤b≤50时，700≤W≤722.5（8分） W 8b6(100b)2b600,700W 720 ②当50＜b≤60时，a=8， （9分） ∴当30≤b≤60时，W的最小值为700元 ∴当一等奖人数为50时花费最少，最少为700元.（10分） 24.（10分）如图，在正方形ABCD中，点E是AB边上的一点，以DE为边作正方形DEFG， DF与BC交于点M，延长EM交GF于点H，EF与GB交于点N，连接CG.（1）求证：CD⊥CG； 1 MN （2）若tan∠MEN=3，求 EM 的值；（3）已知正方形ABCD的边长为1，点E在运动过程 1 中，EM的长能否为2 ？请说明理由. （1）证明：在正方形ABCD，DEFG中， DA=DC，DE=DG，∠ADC=∠EDG=∠A=90°（1分） 9∴∠ADC-∠EDC=∠EDG-∠EDC，即∠ADE=∠CDG，∴△ADE≌△CDG（SAS）（2分） ∴∠DCG=∠A=90°，∴CD⊥CG（3分） （2）解：∵CD⊥CG，DC⊥BC，∴G、C、M三点共线 ∵四边形DEFG是正方形，∴DG=DE，∠EDM=∠GDM=45°，又∵DM=DM ∴△EDM≌△GDM，∴∠DME=∠DMG（4分） 又∠DMG=∠NMF，∴∠DME=∠NMF，又∵∠EDM=∠NFM=45° MN FM  ∴△DME∽△FMN，∴ ME DM （5分） HF FM MN HF   又∵DE∥HF，∴ ED DM ，又∵ED=EF，∴ ME EF （6分） HF 1 MN 1   在Rt△EFH中，tan∠HEF= EF 3 ，∴ ME 3（7分） （3）设AE=x，则BE=1-x，CG=x，设CM=y，则BM=1-y，EM=GM=x+y（8分） 在Rt△BEM中，BE2 BM2  EM2 ，∴ (1x)2 (1 y)2 (x y)2 ， 1x y  解得 x1（9分） x2 1 1 x2 1 1 EM  x y  EM   ∴ x1 ，若 2，则 x1 2 ， 1 化简得： 2x2 x10 ，△=-7＜0，∴方程无解，故EM长不可能为2 . 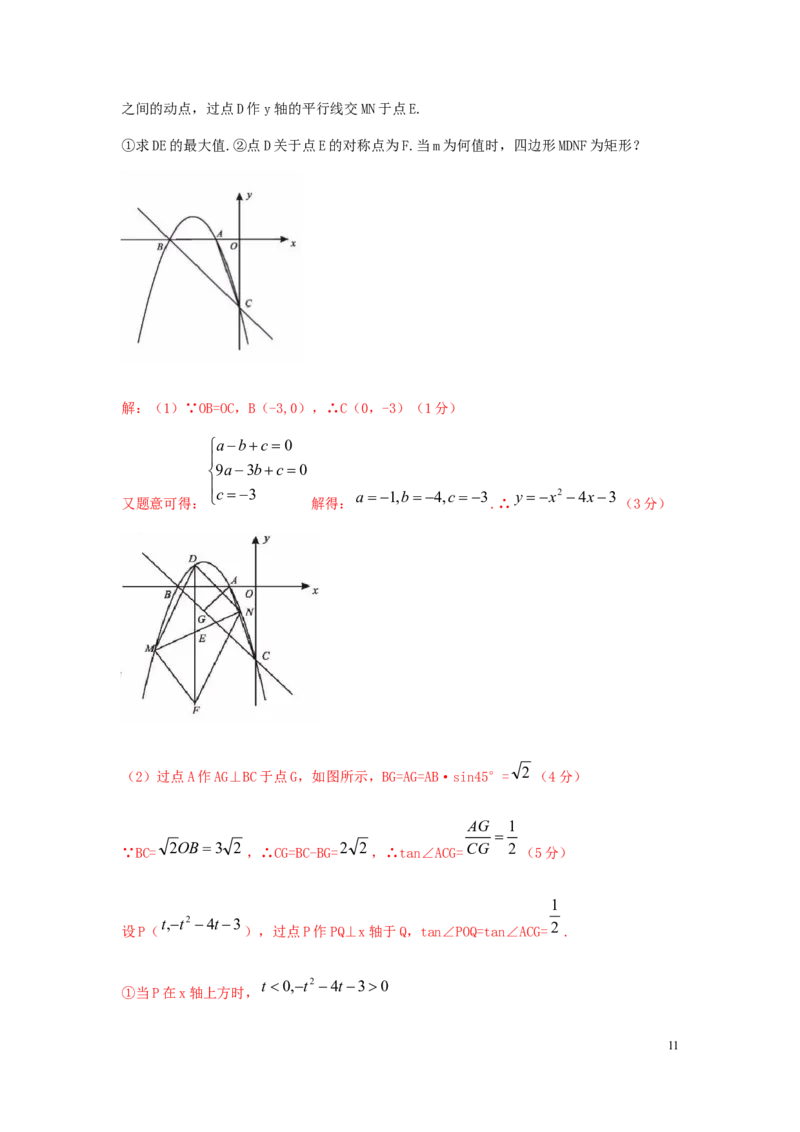y ax2 bxc x 25.（10分）如图，抛物线 与 轴交于点A（-1，0），点B（-3,0），且 OB=OC.（1）求抛物线的解析式；（2）点P在抛物线上，且∠POB=∠ACB，求点P的坐标； （3）抛物线上两点M，N，点M的横坐标为m，点N的横坐标为m+4.点D是抛物线上M，N 10之间的动点，过点D作y轴的平行线交MN于点E. ①求DE的最大值.②点D关于点E的对称点为F.当m为何值时，四边形MDNF为矩形？ 解：（1）∵OB=OC，B（-3,0），∴C（0，-3）（1分） abc0  9a3bc0   c3 a 1,b4,c3 y x2 4x3 又题意可得： 解得： .∴ （3分） 2 （2）过点A作AG⊥BC于点G，如图所示，BG=AG=AB·sin45°= （4分） AG 1  ∵BC= 2OB 3 2 ，∴CG=BC-BG= 2 2 ，∴tan∠ACG=CG 2（5分） 1 设P（ t,t2 4t3 ），过点P作PQ⊥x轴于Q，tan∠POQ=tan∠ACG=2 . t 0,t2 4t30 ①当P在x轴上方时， 11PQ t2 4t3 1   ,2t2 7t60 t2 4t3,OQt OQ t 2 则PQ= ，tan∠POQ= 3 3 3 t 2,t  P(2,1),P ( , ) 解得 1 2 2 ，∴ 1 2 2 4 （6分） t2 4y3 1  ,2t2 9t60 t 2 ②当点P在第三象限时， ， 9 33 9 33 t  ,t  解得： 3 4 4 4 9 33 9 33 9 33 9 33 P( , ),P ( , ) ∴ 3 4 8 4 4 8 （7分） ③当点P在第四象限时，∠POB＞90°，而∠ACB＜90°，∴点P不在第四象限 3 3 9 33 9 33 9 33 9 33 ( , ) ( , ) ( , ) 故点P坐标为 (2,1), 或 2 4 或 4 8 或 4 8 M(m,m2 4m3),N(m4,(m4)2 4(m4)3) （3）①由已知， N(m4,m2 12m35) y kxn 即 ，设直线MN为 kmnm2 4m3 k 2m8    k(m4)nm2 12m35 nm2 4m3 得： 解得： y (m8)x(m2 4m3) 故MN为 （8分） D(t,t2 4t3) E(t,(2m8)t(m2 4m3)) 设 ， (t2 4t3) [(2m8)t(m2 4m3)] ∴DE= t2 2(m2)t(m2 4m)  t(m2) 2 4 = ， 12t m2 当 时，DE最大值为4（9分） E(m2,m2 8m19) ②当DE最大时，点 为MN的中点. 由已知，点E为DF的中点，∴当DE最大时，四边形MDNF为平行四边形. MN2  DF2 4DE2, 42 (8m32)2 442 如果□MDNF为矩形，则 故 ， 3 3 (m4)2  m4 化简得， 4 ，故 2 . 3 3 m4 4 当 2 或 2 时，四边形MDNF为矩形（10分） 1314