文档内容
数学试题部分
(本卷满分150分 共4页 考试时间120分钟)
一、单选题(本题共8小题 每小题5分 共40分)
1. 已知集合 , , ,则M、N、P
的关系满足( ).
A. B.
C. D.
【答案】B
【解析】
【分析】先将集合 化简变形成统一形式,然后分析判断即可.
【详解】因为 ,
所以 .
故选:B.
2. 已知集合 ,若集合 有15个真子集,则实数 的取值范围为( )
A. B. C. D.
【答案】D【解析】
【分析】根据真子集的定义,推断出集合 含有4个元素,即不等式 的解集中有且仅有4个
整数解,由此进行分类讨论,列式算出实数 的取值范围.
【详解】若集合 有15个真子集,则 中含有4个元素,
结合 ,可知 ,即 ,且区间 , 中含有4个整数,
①当 时, , 的区间长度 ,此时 , 中不可能含有4个整数;
②当 时, , , ,其中含有4、5、6、7共4个整数,符合题意;
③当 时, , 的区间长度大于3,
若 , 的区间长度 ,即 .
若 是整数,则区间 , 中含有4个整数,根据 ,可知 , ,
此时 , , ,其中含有5、6、7、8共4个整数,符合题意.
若 不是整数,则区间 , 中含有5、6、7、8这4个整数,则必须 且 ,
解得 ;
若 时, , , ,其中含有5、6、7、8、9共5个整数,不符合题意;
当 时, , 的区间长度 ,此时 , 中只能含有6、7、8、9这4个整数,
故 ,即 ,结合 可得 .
综上所述, 或 或 ,即实数 的取值范围是 , , .
故选:D.【点睛】关键点点睛:由真子集的个数可得 ,且区间 , 中含有4个整数,结合区间长度 ,
即可对 讨论求解.
3. 设集合 , ,则 ( )
A. B.
C. D.
【答案】D
【解析】
【分析】利用最小公倍数排除A,B,利用奇数和偶数排除C,求解即可.
【详解】易知集合 , ,
则 中 前面的系数应为 的最小公倍数,故排除A,B,
对于C,当 时,集合 为 ,
而令 ,可得 不为整数,故 不含有7,
可得 中不含有7,故C错误,
故选:D
4. 已知命题“ ”为真命题,则实数 的取值范围是( )
A. B. C. D.
【答案】C
【解析】
【分析】根据命题是真命题的意思求解即可.
【详解】因为命题“ ”为真命题,
所以命题“ ”为真命题,
所以 时, .因 ,
为
所以当 时, ,此时 .
所以 时, ,即实数 的取值范围是 .
故选:C.
5. 如果对于任意实数 , 表示不超过 的最大整数.例如 , .那么“ ”是“
”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】B
【解析】
【分析】根据所给定义以及充分条件与必要条件的定义推导即可.
【详解】如果 ,比如 ,则有 ,
根据定义, ,
即“ ”不是“ ”的充分条件,
如果 ,则有 ,
,所以“ ”是“ ”的必要条件;
故“ ”是“ ”的必要而不充分条件.
故选:B.
6. 已知实数 ,且 ,则以下说法正确的是( )
A. B. 的值为4或8 C. D. 的值为【答案】B
【解析】
【分析】由 ,且 可得 或 ,后验证各选项即可得答案.
【详解】因 ,则 ,又 ,
则 或 .
则 或 ,结合 ,得 或 .
A选项,当 时, ;当 时, ,故A错
误;
B选项,当 时, ;当 时, ,故B正确;
C选项,当 时, ;当 时, ,故C错误;
D选项,当 时, ;当 时, ,故D错误.
故选:B
7. “喊泉”是一种地下水的毛细现象.在合适的条件下,人们在泉口吼叫或发出其他声响时,声波传入泉洞内
的储水池,进而产生一系列物理声学作用.已知声音越大,涌起的泉水越高,声强 与参考声强 之比的常用对数称作声强的声强级,记作 (单位:分贝),即 .若某处“喊泉”的声强级 (单位:分
贝)与喷出的泉水高度 (单位:分米)满足关系式 , 两人分别在这处“喊泉”大喊一声,若
“喊泉”喷出泉水的高度比 “喊泉”喷出的泉水高度高5分米,则 “喊泉”的声强是 “喊泉”声强的(
)
A. 5倍 B. 10倍 C. 20倍 D. 100倍
【答案】D
【解析】
【分析】根据对数的运算性质可求.
【详解】设 的声强分别为 “喊泉”喷出泉水的高度分别为 ,
则 ,即 ,
从而 ,即 ,所以 .
故 “喊泉”的声强是 “喊泉”声强的100倍.
故选:D
8. 已知 , ,且 ,则 的最小值为( )
A. 1 B. 2 C. 4 D. 8
【答案】C
【解析】
【分析】先得出 ,再利用基本不等式求解即可.
【详解】因为 ,
所以 ,所以 ,所以 ,
当且仅当 时取等号,
所以 的最小值为 .
故选:C.
二、多选题(本题共4小题 每小题5分 满分20分)
9. 设 ,若 ,则实数a的值为( )
A. B. C. D. 0
【答案】ABD
【解析】
【分析】分 、 两种情况讨论,分别确定集合 ,即可求出参数 的值.
【详解】因为 ,且 ,
当 时, ,符合题意;
当 时, ,又 ,所以 或 ,解得 或 ,
综上, 或 或 .
故选:ABD
10. 当两个集合中一个集合为另一个集合的子集时,称这两个集合构成“全食”;当两个集合有公共元素,
但互不为对方子集时,称这两个集合成“偏食”.对于集合 , ,
若 与B构成“全食”或“偏食”,则实数 的取值可以是( )
A. -2 B. C. 0 D. 1
【答案】BCD【解析】
【分析】考虑 时, , 时, ,依次将各个选项中的数据带入,计算集合 ,
再判断 和 之间的关系得到答案.
【详解】当 时, ,
当 时, ,
对选项A:若 , ,此时 ,不满足;
对选项B:若 , ,此时 ,满足;
对选项C:若 , ,此时 ,满足;
对选项D:若 , ,此时 ,满足;
故选:BCD.
11. 下列说法正确的有( )
A. 是 的必要不充分条件
B. “ ”是‘ ’成立的充分条件
C. 命题 ,则
D. 为无理数是 为无理数的既不充分也不必要条件
【答案】BD
【解析】
【分析】根据充分条件和必要条件的定义判断ABD,根据全称量词命题的否定为特称量词命题的否定判断
C.
【详解】对于A,若 ,则 ,但由 不能推出 ,所以 是 的充分不必要条件,故A错误;
对于B, 时, 一定成立,
所以 是 成立的充分条件,故B正确;
对于C,命题 ,则 ,故C错误;
对于D,当 时, ,
当 时, 为无理数,
所以 为无理数是 为无理数的既不充分也不必要条件,故D正确.
故选:BD.
12. ,运算“ ”为 ,则( )
A. B.
C. D. 若 ,则
【答案】ABCD
【解析】
【分析】由运算“ ”的定义分别计算判断A、B、C,用分析法分别从条件和结论出发证明得到D.
【详解】对于A, ,故A正确;
对于B, ,故B正确;
对于C, ,,
所以 ,故C正确;
对于D,若 ,则 , ,
要证 ,只需要证 ,即证 ,
即证 ,即证 ,即证 ,
因为 , ,所以上式成立,所以 ,故D正确.
故选:ABCD.
三、填空题(本题共4小题 每小题5分 满分20分)
13. 设 、 是非空集合,定义 且 .已知 ,
,则 ________.
【答案】 或
【解析】
【分析】先求出 ,再求出 ,从而可求 。
【详解】∵ 、 是非空集合, 且 ,
而 , ,∴ , ,
故 或 .
故答案为: 或 .
14. 已知集合 , ,若 ,则实数 的取值范围是
______.【答案】
【解析】
【分析】可求出集合 ,然后根据 ,得到 ,从而求出实数 的取值范围.
【详解】由 ,可得 ,
由于 ,且 ,则 ,
所以 ,则实数 的取值范围是 ,
为
故答案 :
15. 已知命题“ : , ”,若 是假命题,则实数 的取值范围是___________.
【答案】
【解析】
【分析】由特称量词与全称量词得出命题的否定,再由一元二次不等式恒成立得出实数 的取值范围.
【详解】若 是假命题,则 , ,
当 时,代入不等式得 成立;
当 时, ,
综上可得实数 的取值范围是 .
故答案为:
16. 设正实数 满足 ,且 ,则 的最小值为__________.
【答案】 ##
【解析】【分析】化简 ,利用基本不等式得
.
可得答案
【详解】 ,
由于 是正实数,且 ,
所以
,
当且仅当 ,即 ,所以 时等号成立,
则 的最小值为2,所以
,
当且仅当 ,即 时等号成立,
则 最小值为 .
故答案为: .
四、解答题(本题共6小题 第17题10分 第18-22题12分 满分70分)17. 设 为全集,集合 , .
(1)若 ,求 , ;
(2)若 ,求实数 的取值范围.
【答案】(1) ;
(2)
【解析】
【分析】(1)先求出集合 , ,然后结合集合的交集及补集运算即可求解;
(2)由已知结合集合的包含关系对集合 是否为空集进行分类讨论即可求解.
【小问1详解】
(1)由题意可得 ,
当 时, ,
所以 ,
因为 ,
所以
【小问2详解】
由(1)知, ,
若 ,即 ,解得 ,此时满足 ;
若 ,要使 ,则 ,解得 ,
综上,若 ,所求实数 的取值范围为18. 已知集合 , .
(1)若 ,求实数 的取值范围;
(2)若将题干中的集合 改为 ,是否有可能使命题 :“ ,都有
”为真命题,请说明理由.
【答案】(1)
(2)不可能,理由见解析
【解析】
【分析】(1)直接根据 列不等式求解;
(2)先得到 ,再根据包含关系列不等式求解.
【小问1详解】
因为 ,
所以 或 或 ,
解得 或 或 ,
所以 ;
【小问2详解】
若 , ,
对 ,都有 ,则 ,所以 ,该不等式组无解,
故命题 :“ ,都有 ”为真命题不可能.
19. 已知集合 , .
(1)若 ,求 ;
(2)若存在正实数m,使得“ ”是“ ”成立的充分不必要条件,求正实数m的取值范围.
【答案】(1)
(2)
【解析】
【分析】(1)解指数不等式,一元二次不等式化简集合 ,然后由交集定义计算;
(2)根据充分不必要条件的定义得不等式组求解;
【小问1详解】
因 ,则 .
当 时, ,所以 .
【小问2详解】
的
因“ ”是“ ”成立 充分不必要条件,则A是B的真子集.
所以 ,经检验“=”满足.
所以实数m的取值范围是 .20. (1)计算: ;
(2)已知 ,求 的值.
【答案】(1)9;(2)1
【解析】
【分析】(1)根据对数的运算性质和分数指数幂的运算性质求解;
(2)由 求出 ,然后代入 中化简计算即可.
【详解】(1)
;
(2)∵ ,
∴ , ,
∴.
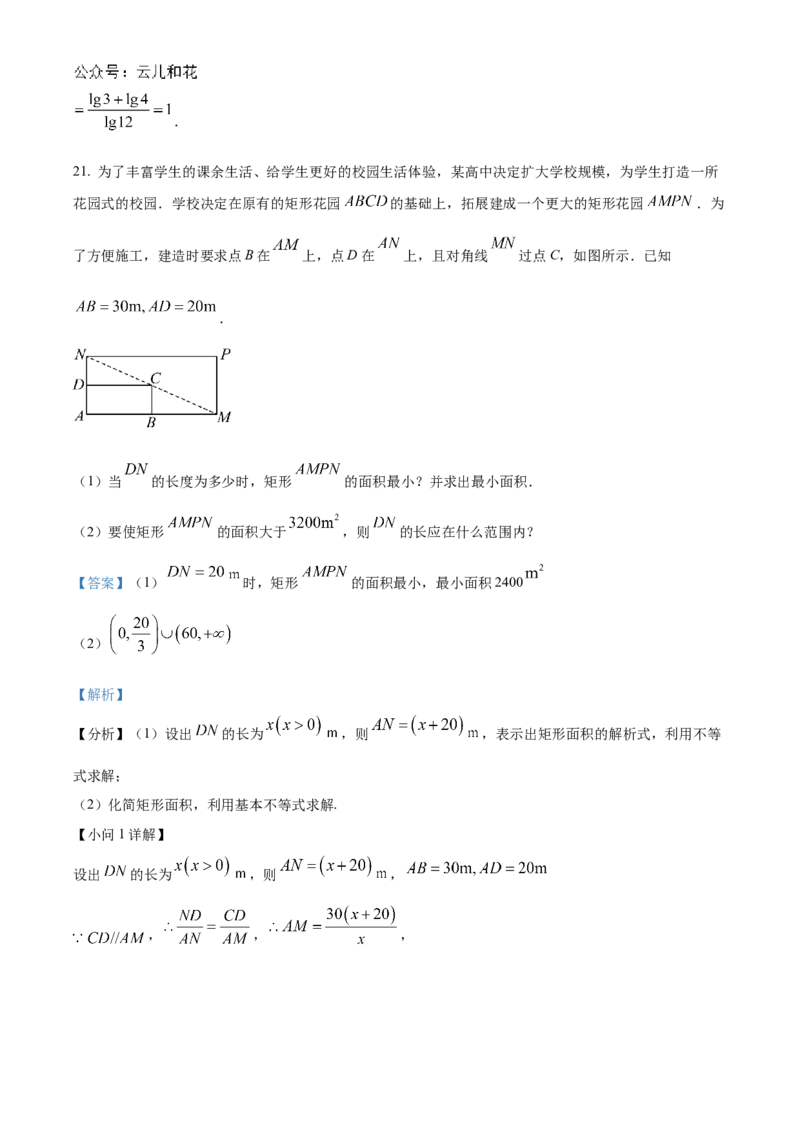
21. 为了丰富学生的课余生活、给学生更好的校园生活体验,某高中决定扩大学校规模,为学生打造一所
花园式的校园.学校决定在原有的矩形花园 的基础上,拓展建成一个更大的矩形花园 .为
了方便施工,建造时要求点B在 上,点D在 上,且对角线 过点C,如图所示.已知
.
(1)当 的长度为多少时,矩形 的面积最小?并求出最小面积.
(2)要使矩形 的面积大于 ,则 的长应在什么范围内?
【答案】(1) 时,矩形 的面积最小,最小面积2400
(2)
【解析】
【分析】(1)设出 的长为 ,则 ,表示出矩形面积的解析式,利用不等
式求解;
(2)化简矩形面积,利用基本不等式求解.
【小问1详解】
设出 的长为 ,则 ,
, , ,∴矩形 的面积 ,
由基本不等式得: ,
当且仅当 时,取“=”, 当 ,即 时, ;
【小问2详解】
由(1)得 ,即 ,
∴ ,
∴ 或 ,
的范围在 .
22. 已知整数 ,集合 , , ,满足 ,
对任意的 ,都有 且 .记 .
(1)若 ,写出两组满足条件的集合 , 并写出相应的 ;
(2)证明: ;
(3)求 的所有可能取值.
【答案】(1)答案见解析;
(2)证明见解析; (3) .
【解析】
【分析】(1)根据 中的元素递增, 中元素递减,即可列举求解,(2)根据 和 两种情况,结合 中的元素递增, 中元素递减,即可分类求解,
(3)根据 , ,可得 ,根据
,可得 , ,…, 是 ,…, 的排列,即可由
求解.
【小问1详解】
(共6组,任写2组即可)
, , . , , .
, , . , , .
, , . , , .
【小问2详解】
由题设可得 ,
若 ,则 ,而 , , ,…, ,
所以 ,
若 ,由于 即 ,由于 ,
故 ,由于 ,
而 需要有 个不同的元素,故矛盾,因此 , ,结论成立.
若 ,则由 且 , ,…, 互不相同的正整数,知 ,
若 ,由于 即 ,由于 ,
故 ,由于 ,而 需要有 个不同的元素,故 ,而 ,
故此时 不符合要求,
故 ,所以 ,结论成立.
【小问3详解】
设 ,则 , ,
两个 中,其中一个取等号,另一个不取等号,所以 比 中至少 个数大,
因此 ,即 , ,…, ,而 , ,…, 两两不同,
所以 , ,…, 恰好是 ,…, 的一个排列.
再设 ,则 , ,…, ,
, ,…, 恰好是 ,…, 的一个排列,
所以 , ,…, 是 ,…, 的排列,故有:
【点睛】方法点睛:对于以集合为背景的新定义问题的求解策略:
1、紧扣新定义,首先分析新定义的特点,把心定义所叙述的问题的本质弄清楚,应用到具体的解题过程
中;
2、用好集合的性质,解题时要善于从试题中发现可以使用的集合的性质的一些因素.
3、涉及有交叉集合的元素个数问题往往可采用维恩图法,基于课标要求的,对于集合问题,要熟练基本
的概念,数学阅读技能、推理能力,以及数学抽象和逻辑推理能力.