江西2025年高考全国一卷数学高考真题解析_1.高考2025全国各省真题+答案_2.高考数学试题及答案

2025 年普通高等学校招生全国统一考试（新 1 卷） 祝大家学习生活愉快 ★ ★ 注意事项： 1.答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号，试室号， 座位号填写在答题卡上.用2B 铅笔将试卷类型和考生号填涂在答题卡相应位置 上. 2.选择题每小题选出答案后，用 2B 铅笔把答题卡上对应的题目选项的答案信息 点涂黑：如需改动，用橡皮擦干净后，再填涂其他答案.答案不能答在试卷上. 3.非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指 定区域内相应位置上：如需改动，先划掉原来的答案，然后再写上新的答案， 不准使用铅笔和涂改液.不按以上要求作答的答案无效. 一、选择题：本大题共 8小题，每小题 5分，共计 40分.每小题给出的四个选项 中，只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上. 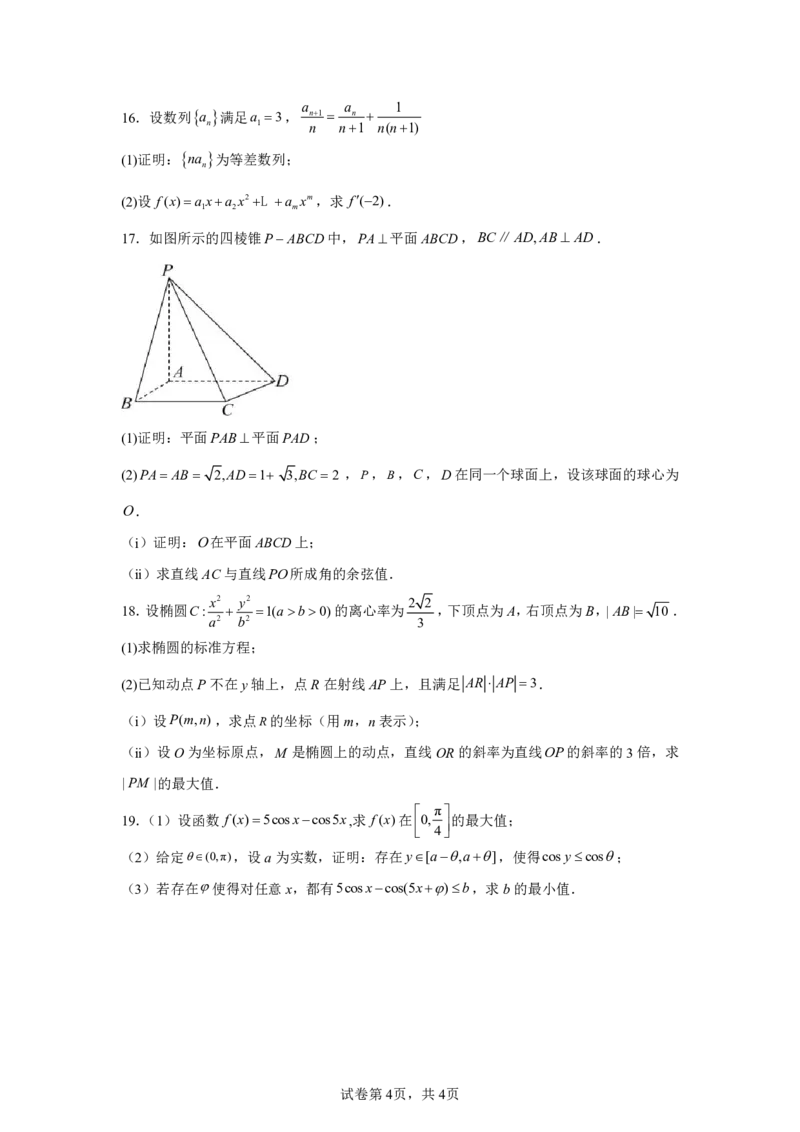1．(15i)i的虚部为（ ） A．1 B．0 C．1 D．6 2．设全集U   x x是小于9的正整数 ，集合A{1,3,5}，则ð A中元素个数为（ ） U A．0 B．3 C．5 D．8 3．若双曲线C的虚轴长为实轴长的 7倍，则C的离心率为（ ） A． 2 B．2 C． 7 D．2 2  π 4．若点(a,0)(a0)是函数y2tanx 的图象的一个对称中心，则a的最小值为（ ）  3 π π π 4π A． B． C． D． 6 3 2 3  3 5．设 f(x)是定义在R上且周期为2的偶函数，当2 x3时，f(x)52x，则 f  （ ）  4 1 1 1 1 A． B． C． D． 2 4 4 2 6．帆船比赛中，运动员可借助风力计测定风速的大小和方向，测出的结果在航海学中称为 视风风速，视风风速对应的向量，是真风风速对应的向量与船行风速对应的向量之和，其中 船行风速对应的向量与船速对应的向量大小相等，方向相反.图1给出了部分风力等级、名 试卷第1页，共4页称与风速大小的对应关系.已知某帆船运动员在某时刻测得的视风风速对应的向量与船速对 应的向量如图2（风速的大小和向量的大小相同），单位（m/s），则真风为（ ） 等级 风速大小m/s 名称 2 1.1~3.3 轻风 3 3.4~5.4 微风 4 5.5~7.9 和风 5 8.0~10.1 劲风 A．轻风 B．微风 C．和风 D．劲风 7．若圆x2(y2)2 r2(r0)上到直线y 3x2的距离为1的点有且仅有2个，则r的 取值范围是（ ） A．(0,1) B．(1,3) C．(3,) D．(0,) 8．若实数x，y，z满足2log x3log y5log z，则x，y，z的大小关系不可能是（ ） 2 3 5 A．x y z B．xz y C．y x z D．yzx 二、选择题：本题共3小题，每小题 6分，共18分.在每小题给出的选项中，有 多项符合题目要求.全部选对的得 6分，部分选对的得部分分，有选错的得0分. 9．在正三棱柱ABCABC 中，D为BC中点，则（ ） 1 1 1 A．AD AC B．BC平面AAD 1 1 C．CC //平面AAD D．AD//AB 1 1 1 1 10．设抛物线C: y2 6x的焦点为F，过F的直线交C于A、B，过F且垂直于AB的直线 试卷第2页，共4页3 交l:x 于E，过点A作准线l的垂线，垂足为D，则（ ） 2 A．|AD||AF| B．|AE||AB| C．|AB|6 D．|AE||BE|18 1 1 11．已知V ABC的面积为 ，若cos2Acos2B2sinC 2,cosAcosBsinC  ，则（ ） 4 4 A．sinCsin2 Asin2B B．AB 2 6 C．sinAsinB D．AC2BC2 3 2 三、填空题：本大题共 3小题，每小题 5分，共计 15分. 12．若直线y2x5是曲线yexxa的切线，则a . 13．若一个等比数列的前4项和为4，前8项和为68，则该等比数列的公比为 . 14．一个箱子里有5个相同的球，分别以1~5标号，若每次取一颗，有放回地取三次，记至 少取出一次的球的个数X，则数学期望E(X) . 四、解答题：本题共 5小题，共77分.解答应写出文字说明、证明过程或演算步 骤. 15．为研究某疾病与超声波检查结果的关系，从做过超声波检查的人群中随机调查了1000 人，得到如下列联表： 超声波检查结果组别 正常 不正常 合计 患该疾病 20 180 200 未患该疾病 780 20 800 合计 800 200 1000 (1)记超声波检查结果不正常者患该疾病的概率为P，求P的估计值； (2)根据小概率值0.001的独立性检验，分析超声波检查结果是否与患该疾病有关. n(ad bc)2 附2  ， (ab)(cd)(ac)(bd) P  x2k  0.005 0.010 0.001 k 3.841 6.635 10.828 试卷第3页，共4页a a 1 16．设数列a 满足a 3， n1  n  n 1 n n1 n(n1) (1)证明：na 为等差数列； n (2)设 f(x)a xa x2L a xm，求 f(2)． 1 2 m 17．如图所示的四棱锥PABCD中，PA平面ABCD，BC∥AD,AB AD． (1)证明：平面PAB平面PAD； (2)PAAB 2,AD1 3,BC  2 ，P，B，C，D在同一个球面上，设该球面的球心为 O． （i）证明：O在平面ABCD上； （ⅱ）求直线AC与直线PO所成角的余弦值． x2 y2 2 2 18．设椭圆C:  1(ab0)的离心率为 ，下顶点为A，右顶点为B，|AB| 10． a2 b2 3 (1)求椭圆的标准方程； (2)已知动点P不在y轴上，点R在射线AP上，且满足 AR  AP 3． （i）设P(m,n)，求点R的坐标（用m，n表示）； （ⅱ）设O为坐标原点，M 是椭圆上的动点，直线OR的斜率为直线OP的斜率的3倍，求 |PM |的最大值．  π 19．（1）设函数 f(x)5cosxcos5x,求 f(x)在  0,  的最大值；  4 （2）给定(0,π)，设a为实数，证明：存在y[a,a]，使得cosycos； （3）若存在使得对任意x，都有5cosxcos(5x)b，求b的最小值． 试卷第4页，共4页1．C 【分析】根据复数代数形式的运算法则以及虚部的定义即可求出. 【详解】因为15iii5i2 5i，所以其虚部为1， 故选：C. 2．C 【分析】根据补集的定义即可求出． 【详解】因为U 1,2,3,4,5,6,7,8，所以ð A2,4,6,7,8， ð A中的元素个数为5， U U 故选：C． 3．D 【分析】由题可知双曲线中a,b的关系，结合a2b2 c2和离心率公式求解 【详解】设双曲线的实轴，虚轴，焦距分别为2a,2b,2c， 由题知，b 7a， 于是a2b2 c2 a27a2 8a2，则c2 2a， c 即e 2 2. a 故选：D 4．B 【分析】根据正切函数的对称中心的结论求解. π π kπ 【详解】根据正切函数的性质，y2tan(x ) 的对称中心横坐标满足x  ,kZ， 3 3 2 π π kπ  即y2tan(x )的对称中心是  ,0,kZ， 3 3 2  π kπ 即a  ,kZ， 3 2 π 又a0，则k 0时a最小，最小值是 ， 3 π 即a . 3 故选：B 5．A 【分析】根据周期性和奇偶性把待求自变量转化为[2,3]的范围中求解. 【详解】由题知 f(x) f(x), f(x2) f(x)对一切xR成立， 答案第1页，共26页3 3 11 11 1 于是 f( ) f( ) f( )52  . 4 4 4 4 2 故选：A 6．A 【分析】结合题目条件和图2写出视风风速对应的向量和船行风速对应的向量，求出真风风 速对应的向量，得出真风风速的大小，即可由图1得出结论. 【详解】由题意及图得，  视风风速对应的向量为：n0,23,33,1， 视风风速对应的向量，是真风风速对应的向量与船行风速对应的向量之和， 船速方向和船行风速的向量方向相反，   设真风风速对应的向量为n ，船行风速对应的向量为n ， 1 2     ∴nn n ，船行风速：n   3,32,0  1,3， 1 2 2    ∴n nn 3,11,3 2,2， 1 2  n  2222 2 22.828 ， 1 ∴由表得，真风风速为轻风， 故选：A. 7．B 【分析】先求出圆心E0,2到直线y 3x2的距离，然后结合图象，即可得出结论. 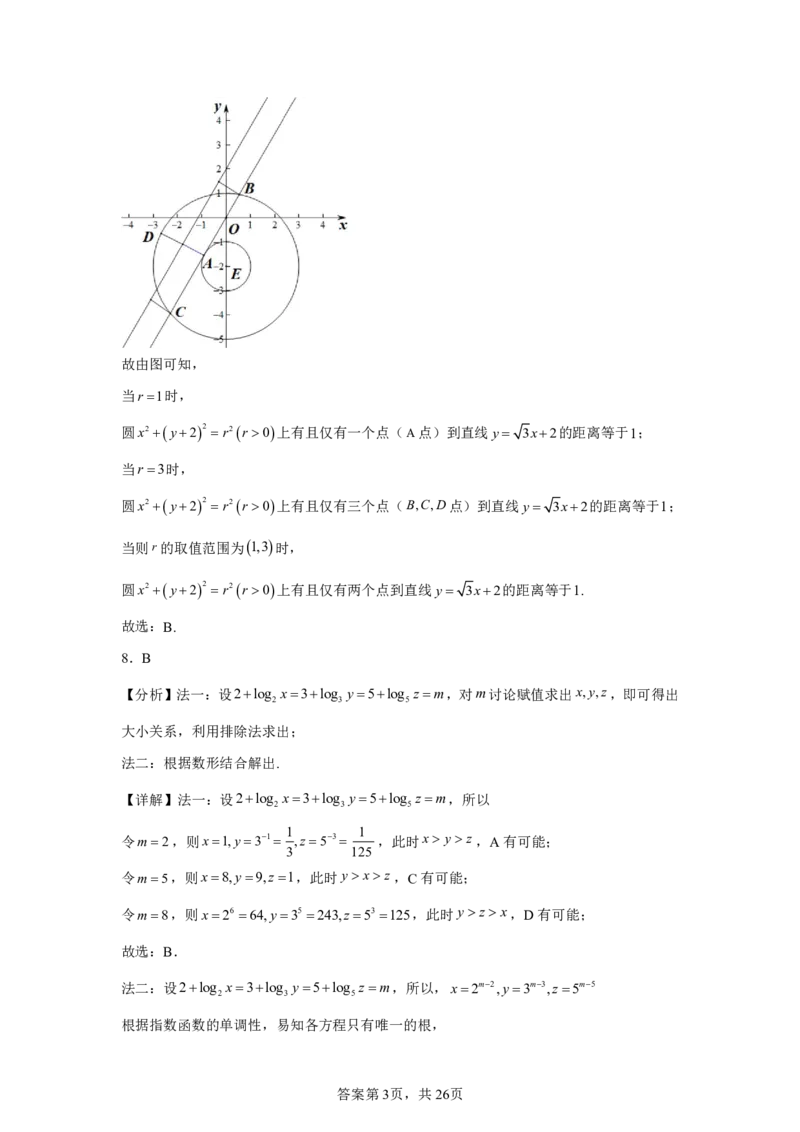【详解】由题意， 在圆x2y22 r2r 0中，圆心E0,2，半径为r， 到直线y 3x2的距离为1的点有且仅有 2个， 0 3212 ∵圆心E0,2到直线y 3x2的距离为：d  2，  3 2 12 答案第2页，共26页故由图可知， 当r 1时， 圆x2y22 r2r 0上有且仅有一个点（A点）到直线y 3x2的距离等于1； 当r3时， 圆x2y22 r2r 0上有且仅有三个点（B,C,D点）到直线y 3x2的距离等于1； 当则r的取值范围为1,3时， 圆x2y22 r2r 0上有且仅有两个点到直线y 3x2的距离等于1. 故选：B. 8．B 【分析】法一：设2log x3log y5log zm，对m讨论赋值求出x,y,z，即可得出 2 3 5 大小关系，利用排除法求出； 法二：根据数形结合解出. 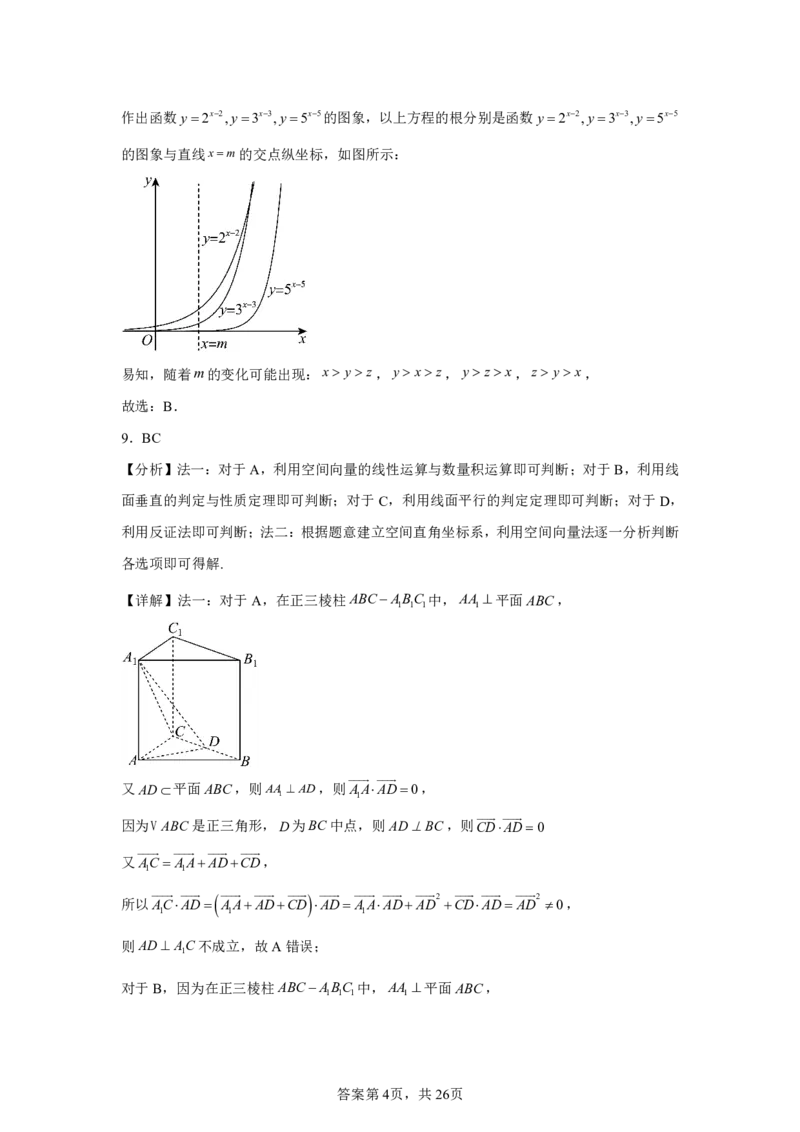【详解】法一：设2log x3log y5log zm，所以 2 3 5 1 1 令m2，则x1,y31 ,z53 ，此时x y z，A有可能； 3 125 令m5，则x8,y9,z1，此时y x z，C有可能； 令m8，则x26 64,y35 243,z53 125，此时yzx，D有可能； 故选：B． 法二：设2log x3log y5log zm，所以，x2m2,y3m3,z5m5 2 3 5 根据指数函数的单调性，易知各方程只有唯一的根， 答案第3页，共26页作出函数y2x2,y3x3,y5x5的图象，以上方程的根分别是函数y2x2,y3x3,y5x5 的图象与直线xm的交点纵坐标，如图所示： 易知，随着m的变化可能出现：x y z，y x z，yzx，z y x， 故选：B． 9．BC 【分析】法一：对于A，利用空间向量的线性运算与数量积运算即可判断；对于B，利用线 面垂直的判定与性质定理即可判断；对于C，利用线面平行的判定定理即可判断；对于D， 利用反证法即可判断；法二：根据题意建立空间直角坐标系，利用空间向量法逐一分析判断 各选项即可得解. 【详解】法一：对于A，在正三棱柱ABCABC 中，AA 平面ABC， 1 1 1 1   又AD平面ABC，则AA  AD，则AAAD0， 1 1   因为V ABC是正三角形，D为BC中点，则ADBC，则CDAD0     又AC AAADCD， 1 1               2 2 所以ACAD AAADCD AD AAADAD CDAD AD 0， 1 1 1 则AD AC不成立，故A错误； 1 对于B，因为在正三棱柱ABCABC 中，AA 平面ABC， 1 1 1 1 答案第4页，共26页又BC 平面ABC，则AA BC， 1 因为V ABC是正三角形，D为BC中点，则ADBC， 又AA AD A,AA,AD平面AAD， 1 1 1 所以BC 平面AAD，故B正确； 1 对于C，因为在正三棱柱ABCABC 中，CC //AA 1 1 1 1 1 又AA 平面AAD,CC  平面AAD，所以CC //平面AAD，故C正确； 1 1 1 1 1 1 对于D，因为在正三棱柱ABCABC 中，AB //AB， 1 1 1 1 1 假设AD// AB，则AD//AB，这与ADAB A矛盾， 1 1 所以AD// AB不成立，故D错误； 1 1 故选：BC. 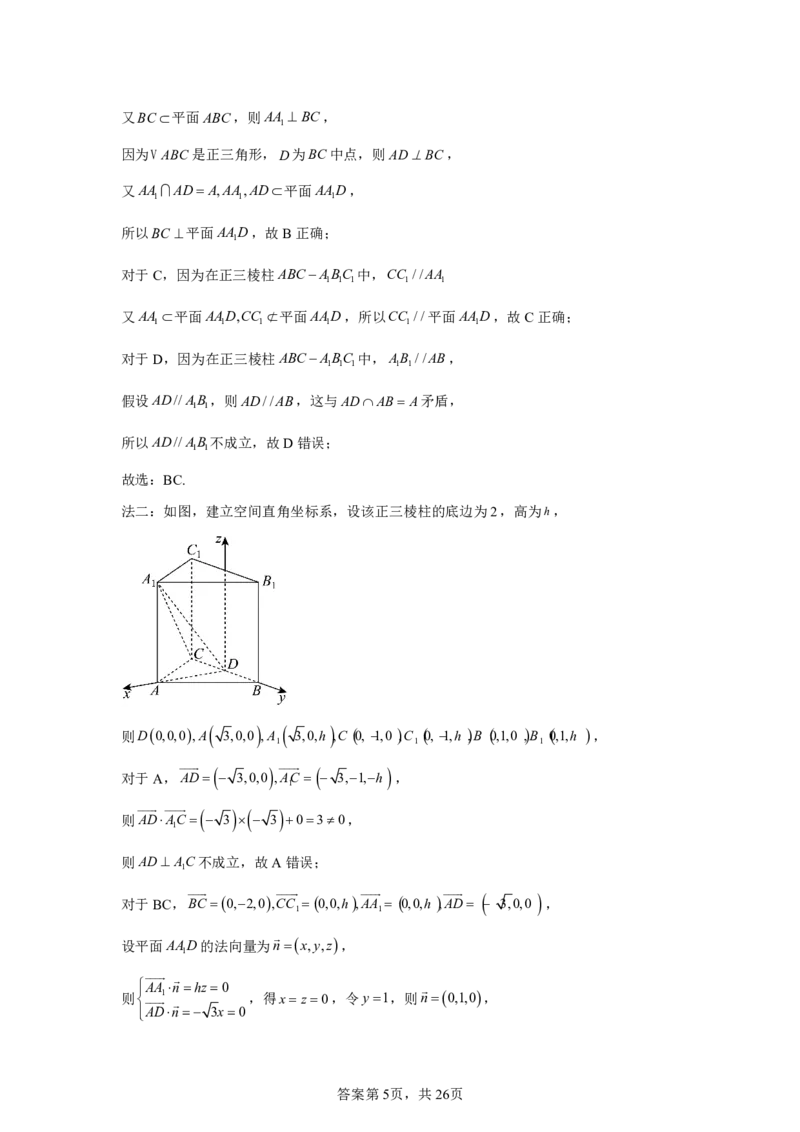法二：如图，建立空间直角坐标系，设该正三棱柱的底边为2，高为h， 则D0,0,0,A  3,0,0  ,A  3,0,h  ,C 0, 1,0 ,C 0, 1,h ,B 0,1,0 ,B 0,1,h ， 1 1 1       对于A，AD  3,0,0 ,AC   3,1,h ， 1       则ADAC   3   3 030， 1 则AD AC不成立，故A错误； 1     对于BC，BC 0,2,0,CC  0,0,h,AA  0,0,h ,AD   3,0,0  ， 1 1  设平面AAD的法向量为nx,y,z， 1    AA n hz 0  则 1  ，得x z0，令y1，则n0,1,0， ADn  3x0 答案第5页，共26页所以  B  C  0,2,02n  ，C uu C ur n r 0， 1 则BC 平面AAD，CC //平面AAD，故BC正确； 1 1 1       对于D，AD  3,0,0 ,AB   3,1,0 ， 1 1  3 0 则  ，显然AD// AB不成立，故D错误； 1 1  3 1 故选：BC. 10．ACD 3 【分析】对于A，先判断得直线l:x 为抛物线的准线，再利用抛物线的定义即可判断； 2 对于B，利用三角形相似证得AEB 90，进而得以判断；对于C，利用直线的反设法（法 一）与正设法（法二），联立直线AB与抛物线方程，结合韦达定理与焦点弦公式可判断C； 利用利用三角形相似证得 AE 2  AF  AB ， BE 2  BF  AB ，结合焦半径公式可判断D. 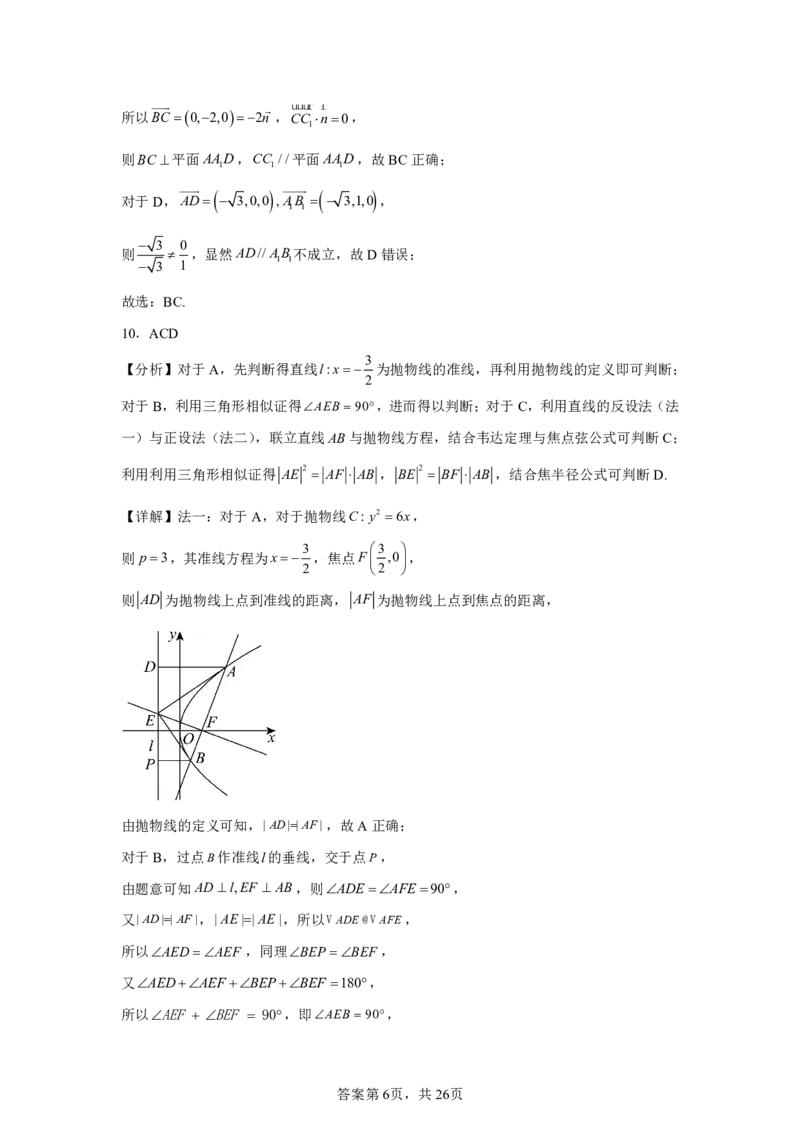【详解】法一：对于A，对于抛物线C: y2 6x， 3 3  则 p3，其准线方程为x ，焦点F ,0， 2 2  则 AD 为抛物线上点到准线的距离， AF 为抛物线上点到焦点的距离， 由抛物线的定义可知，|AD||AF|，故A正确； 对于B，过点B作准线l的垂线，交于点P， 由题意可知ADl,EF  AB，则ADEAFE90， 又|AD||AF|，|AE||AE|，所以VADE@VAFE， 所以AEDAEF ，同理BEPBEF， 又AEDAEFBEPBEF 180， 所以AEF  BEF  90，即AEB 90， 答案第6页，共26页显然AB为ABE的斜边，则|AE||AB|，故B错误； 对于C，易知直线AB的斜率不为0， 设直线AB的方程为xmy 3 ，Ax ,y ,Bx ,y ， 2 1 1 2 2  3 xmy 联立 2，得y26my90，  y2 6x 易知0，则y y 6m,y y 9， 1 2 1 2 3 3 又x my  ，x my  ， 1 1 2 2 2 2 所以|AB| x x  p my  y 33 6m26 6 ， 1 2 1 2 当且仅当m0时取等号，故C正确； 对于D，在Rt△ABE与RtAEF 中，BAE EAF， AE AF 所以RtABERtAEF，则  ，即 AE 2  AF  AB ， AB AE 同理 BE 2  BF  AB ，  3 3 又 AF  BF x  x  my 3my 3  1 2 2 2 1 2 m2y y 3my  y 99m218m299  m21  ， 1 2 1 2 AB 6m266  m21  ， 所以 AE 2 BE 2  BF  AF  AB 2 9  m21  36  m21 2， 1 3 则 AE  BE 3  m21  26  m21  18  m21  2 18 ，故D正确. 故选：ACD. 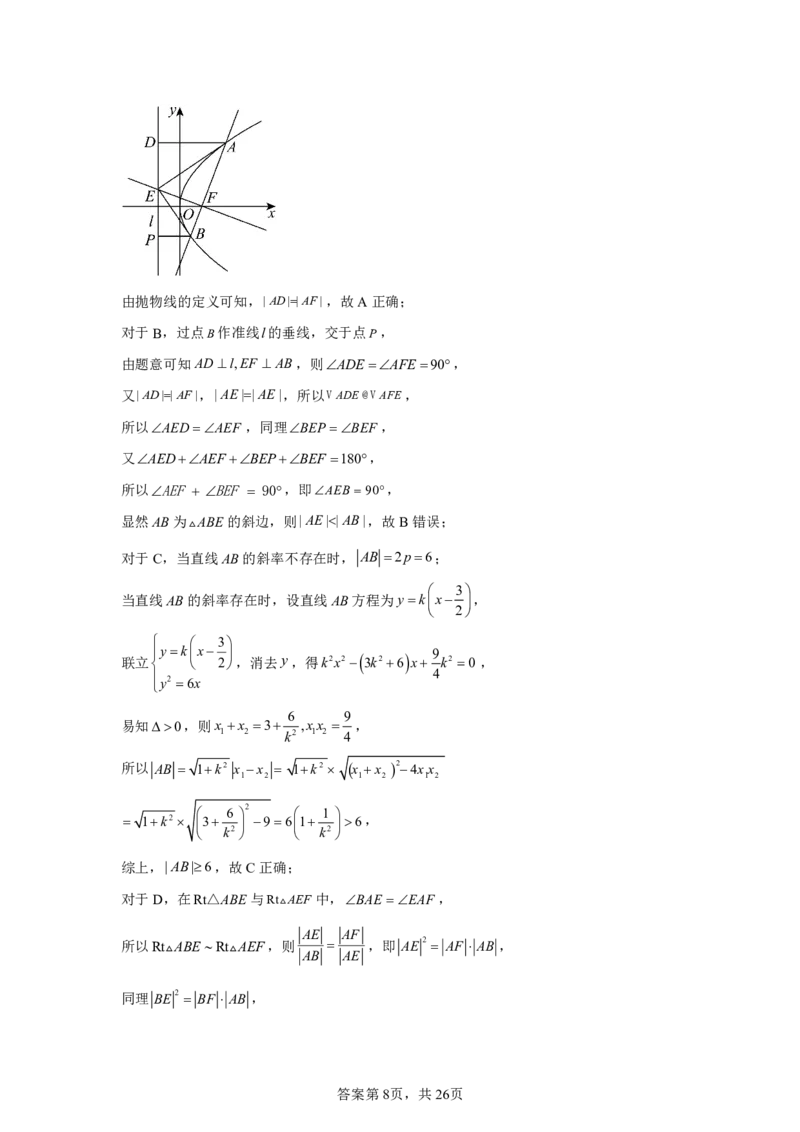法二：对于A，对于抛物线C: y2 6x， 3 3  则 p3，其准线方程为x ，焦点F ,0， 2 2  则 AD 为抛物线上点到准线的距离， AF 为抛物线上点到焦点的距离， 答案第7页，共26页由抛物线的定义可知，|AD||AF|，故A正确； 对于B，过点B作准线l的垂线，交于点P， 由题意可知ADl,EF  AB，则ADEAFE90， 又|AD||AF|，|AE||AE|，所以VADE@VAFE， 所以AEDAEF ，同理BEPBEF， 又AEDAEFBEPBEF 180， 所以AEF  BEF  90，即AEB 90， 显然AB为ABE的斜边，则|AE||AB|，故B错误； 对于C，当直线AB的斜率不存在时， AB 2p6；  3 当直线AB的斜率存在时，设直线AB方程为ykx ，  2   3 联立   yk  x 2  ，消去y，得k2x2   3k2 6  x 9 k2 0 ，  4 y2 6x 6 9 易知0，则x x 3 ,xx  ， 1 2 k2 1 2 4 所以 AB  1k2 x x  1k2 x x 24xx 1 2 1 2 1 2 2  6   1   1k2  3  9 61 6，  k2   k2  综上，|AB|6，故C正确； 对于D，在Rt△ABE与RtAEF 中，BAE EAF， AE AF 所以RtABERtAEF，则  ，即 AE 2  AF  AB ， AB AE 同理 BE 2  BF  AB ， 答案第8页，共26页1 当直线AB的斜率不存在时， AB 6， AF  BF  AB 3； 2 所以 AE 2 BE 2  BF  AF  AB 2 3362，即 AE  BE 18；  1  当直线AB的斜率存在时， AB 61 ，  k2   3 3 3 9 AF BF x  x  xx  x x   1 2 2 2 1 2 2 1 2 4 9 3 6  9  1    3  91  ， 4 2 k2 4  k2 2  1   1  所以 AE 2BE 2  BF  AF  AB 2  91  361  ，  k2  k2 1 3 则 AE  BE 3  1 1   2 6  1 1  18  1 1   2 18 ；  k2  k2  k2 综上， AE  BE 18，故D正确. 故选：ACD. 11．ABC 【分析】对cos2Acos2B2sinC2由二倍角公式先可推知A选项正确，然后分情况比较 π π AB和 的大小，亦可使用正余弦定理讨论解决，结合正弦函数的单调性可推出C  ， 2 2 1 然后利用cosAcosBsinC  算出A,B取值，最后利用三角形面积求出三边长，即可判断每 4 个选项. 【详解】cos2Acos2B2sinC2，由二倍角公式，12sin2 A12sin2B2sinC 2， 整理可得，sinCsin2 Asin2B，A选项正确； 由诱导公式，sin(AB)sinπCsinC， 展开可得sinAcosBsinBcosAsin2 Asin2B， 即sinA(sinAcosB)sinB(sinBcosA)0， π 若AB ，则sinAcosB,sinBcosA可知等式成立； 2 π π 若AB ，即A B，由诱导公式和正弦函数的单调性可知，sinAcosB，同理 2 2 sinBcosA， 又sinA0,sinB0，于是sinA(sinAcosB)sinB(sinBcosA)0， 答案第9页，共26页π 与条件不符，则AB 不成立； 2 π π 若AB ，类似可推导出sinA(sinAcosB)sinB(sinBcosA) 0，则则AB 不成 2 2 立. π π 综上讨论可知，AB ，即C  . 2 2 方法二：sinCsin2 Asin2B时，由C(0,π)，则sinC(0,1]， 于是1sinC sin2 Asin2Bsin2C， 由正弦定理，a2b2 c2， π 由余弦定理可知，cosC0，则C(0, ]， 2 π π 1 若C(0, )，则AB ，注意到cosAcosBsinC ，则cosAcosB0， 2 2 4  π 于是cosA0,cosB0 （两者同负会有两个钝角，不成立），于是A,B0, ，  2 π π π π  结合AB  A B ，而A, B都是锐角，则sinAsin BcosB0， 2 2 2 2  于是sinC sin2 Asin2Bcos2Bsin2B1，这和sinC1相矛盾， π π 故C(0, )不成立，则C  2 2 1 π 1 由cosAcosBsinC  cosAcosB ，由AB ，则cosBsinA，即sinAcosA ， 4 2 4 1 1 则sin2A ，同理sin2B ，注意到A,B是锐角，则2A,2B(0,π)， 2 2 π 5π π 5π 不妨设AB，则2A ,2B ，即A ,B ， 6 6 12 12 π 5π 6 2 6 2 6 由两角和差的正弦公式可知sin sin    ，C选项正确 12 12 4 4 2 5π 由两角和的正切公式可得，tan 2 3， 12     设BC t,AC  2 3 t ，则AB 2 6 t ， 2 1 1 42 3  31 31 由S  (2 3)t2  ，则t2     ，则t  ， ABC 2 4 4   2   2 于是AB( 6 2)t  2 ，B选项正确，由勾股定理可知，AC2BC2  2，D选项错误. 答案第10页，共26页故选：ABC 12．4 【分析】法一：利用导数的几何性质与导数的四则运算求得切点，进而代入曲线方程即可得 解；法二：利用导数的几何性质与导数的四则运算得到关于切点x ,y 与a的方程组，解 0 0 之即可得解. 【详解】法一：对于yexxa，其导数为yex 1， 因为直线y2x5是曲线的切线，直线的斜率为2， 令yex12，即ex 1，解得x0， 将x0代入切线方程y2x5，可得y2055， 所以切点坐标为(0,5)， 因为切点(0,5)在曲线yexxa上， 所以5e00a，即51a，解得a4. 故答案为：4. 法二：对于yexxa，其导数为yex 1， 假设y2x5与yexxa的切点为x ,y ， 0 0 ex0 12  则y 2x 5 ，解得a4. 0 0   y 0 ex0 x 0 a 故答案为：4. 13．2 【分析】法一：利用等比数列的求和公式作商即可得解；法二：利用等比数列的通项公式与 前n项和的定义，得到关于q的方程，解之即可得解；法三：利用等比数列的前n项和性质 得到关于q的方程，解之即可得解. 【详解】法一：设该等比数列为a ，S 是其前n项和，则S 4,S 68， n n 4 8 答案第11页，共26页设a 的公比为q， n 当q1时，S 4a 4，即a 1，则S 8a 868，显然不成立，舍去； 4 1 1 8 1 a  1q4 a  1q8  当q1时，则S  1  4,S  1  68， 4 1q 8 1q 1q8 68  1q4 1q4 两式相除得  ，即 17， 1q4 4 1q4 则1q4 17，解得q2， 所以该等比数列公比为2. 故答案为：2. 法二：设该等比数列为a ，S 是其前n项和，则S 4,S 68， n n 4 8 设a 的公比为q， n 所以S a a a a 4， 4 1 2 3 4 S a a a a a a a a 8 1 2 3 4 5 6 7 8 a a a a aq4a q4a q4a q4 1 2 3 4 1 2 3 4 a a a a  1q4 68， 1 2 3 4 所以4  1q4 68，则1q4 17，解得q2， 所以该等比数列公比为2. 故答案为：2. 法三：设该等比数列为a ，S 是其前n项和，则S 4,S 68， n n 4 8 设a 的公比为q， n 因为S S a a a a a a a a q4 68464， 8 4 5 6 7 8 1 2 3 4 又S a a a a 4， 4 1 2 3 4 S S 64 所以 8 4 q4  16，解得q2， S 4 4 所以该等比数列公比为2. 故答案为：2. 答案第12页，共26页61 14． ##2.44 25 【分析】法一：根据题意得到X 的可能取值，再利用分步乘法原理与古典概型的概率公式 求得X 的分布列，从而求得E(X)；法二，根据题意假设随机变量X ，利用对立事件与独立 i 事件的概率公式求得E(X )，进而利用数学期望的性质求得E(X). i 【详解】法一：依题意，X 的可能取值为1、2、3， 总的选取可能数为53 125， 其中X 1：三次抽取同一球，选择球的编号有5种方式， 5 1 故P(X 1)  ， 125 25 X 2：恰好两种不同球被取出（即一球出现两次，另一球出现一次）， 选取出现两次的球有5种方式，选取出现一次的球有4种方式， 其中选取出现一次球的位置有3种可能，故事件X 2的可能情况有54360种， 60 12 故P(X 2)  ， 125 25 X 3：三种不同球被取出， 由排列数可知事件X 3的可能情有况54360种， 60 12 故P(X 3)  ， 125 25 所以EX1PX 12PX 23PX 3 5 12 12 61 1 2 3  . 125 25 25 25 61 故答案为： . 25 法二：依题意，假设随机变量X ，其中i1,2,3,4,5： i 1,这3次选取中,球i至少被取出一次 5 其中X  ，则X X ， i 0,这3次选取中,球i一次都没被取出 i1 i 由于球的对称性，易知所有E  X 相等， i  5  5 则由期望的线性性质，得E[X]E X  E  X 5E  X ， i i i   i1 i1 4 由题意可知，球i在单次抽取中未被取出的概率为 ， 5 答案第13页，共26页3 4 64 由于抽取独立，三次均未取出球i的概率为PX 0   ， i 5 125 64 61 因此球i至少被取出一次的概率为：PX 11  ， i 125 125 61 故EX  ， i 125 61 61 所以E[X]5EX 5  . i 125 25 61 故答案为： . 25 9 15．(1) 10 (2)有关 【分析】（1）根据古典概型的概率公式即可求出； （2）根据独立性检验的基本思想,求出2,然后与小概率值0.001对应的临界值10.828比 较,即可判断. 【详解】（1）根据表格可知，检查结果不正常的200人中有180人患病，所以 p的估计值为 180 9  ； 200 10 （2）零假设为H ：超声波检查结果与患病无关， 0 100020207801802 根据表中数据可得，2   765.625 10.828 x ， 800200800200 0.001 根据小概率值0.001的2独立性检验，我们推断H 不成立，即认为超声波检查结果与患 0 该病有关，该推断犯错误的概率不超过0.001. 16．(1)证明见解析； 7 3m72m (2) f2  9 9 a a 1 【分析】（1）根据题目所给条件 n n1  n n 1  nn1 化简，即可证明结论； （2）先求出a 的通项公式，代入函数并求导，函数两边同乘以x，作差并利用等比数列 n 前n项和得出导函数表达式，即可得出结论. 【详解】（1）由题意证明如下，nN*， a a 1 在数列a 中，a 3， n1  n  ， n 1 n n1 nn1 答案第14页，共26页∴n1a na 1，即n1a na 1， n1 n n1 n ∴na 是以a 3为首项，1为公差的等差数列. n 1 （2）由题意及（1）得，nN*， 在数列na 中，首项为3，公差为1， n 2 ∴na 31n1，即a 1 ， n n n 在 f xaxa x2a xm中， 1 2 m  2 f x3x2x21 xm， fx34xm2xm1  m fx34xm2xm1 ∴ ， xfx3x4x2m2xm 当x1且x0时， x  1xm1 ∴1x fx3xx2xm1m2xm 3 m2xm， 1x 3 x  1xm1 m2xm ∴ fx   1x 1x2 1x ∴ f2 3  2   12m1   m22m 12  12  2 1 2  2  12m1  m22m 1  9 3 2 2m m22m 1   9 9 3 7 3m72m   . 9 9 17．(1)证明见解析； (2)（i）证明见解析； 2 （ii） . 3 【分析】（1）通过证明AP AB，APAD，得出AB平面PAD，即可证明面面垂直； （2）（i）法一：建立空间直角坐标系并表达出各点的坐标，假设P,B,C,D在同一球面O上， 答案第15页，共26页在平面xAy中，得出点O坐标，进而得出点O在空间中的坐标，计算出 OP  OB  OC  OD ，即可证明结论； 法二：作出△BCD的边BC和CD的垂直平分线，找到三角形的外心O ，求出PO ，求出出 1 1 外心O 到P，B，C，D的距离相等，得出外心O 即为P，B，C，D所在球的球心，即 1 1 可证明结论； （ii）法一：写出直线AC和PO的方向向量，即可求出余弦值. 法二：求出AC的长，过点O作AC的平行线，交BC的延长线为C ，连接AC ，PC ，利用 1 1 1 勾股定理求出AC 的长，进而得出PC 的长，在△POC 中由余弦定理求出cosPOC ，即可 1 1 1 1 求出直线AC与直线PO所成角的余弦值. 【详解】（1）由题意证明如下， 在四棱锥PABCD中，PA⊥平面ABCD，ABAD， AB平面ABCD，AD平面ABCD， ∴AP AB，APAD， ∵AP平面PAD，AD平面PAD，APADA， ∴AB平面PAD， ∵AB平面PAB， ∴平面PAB平面PAD. 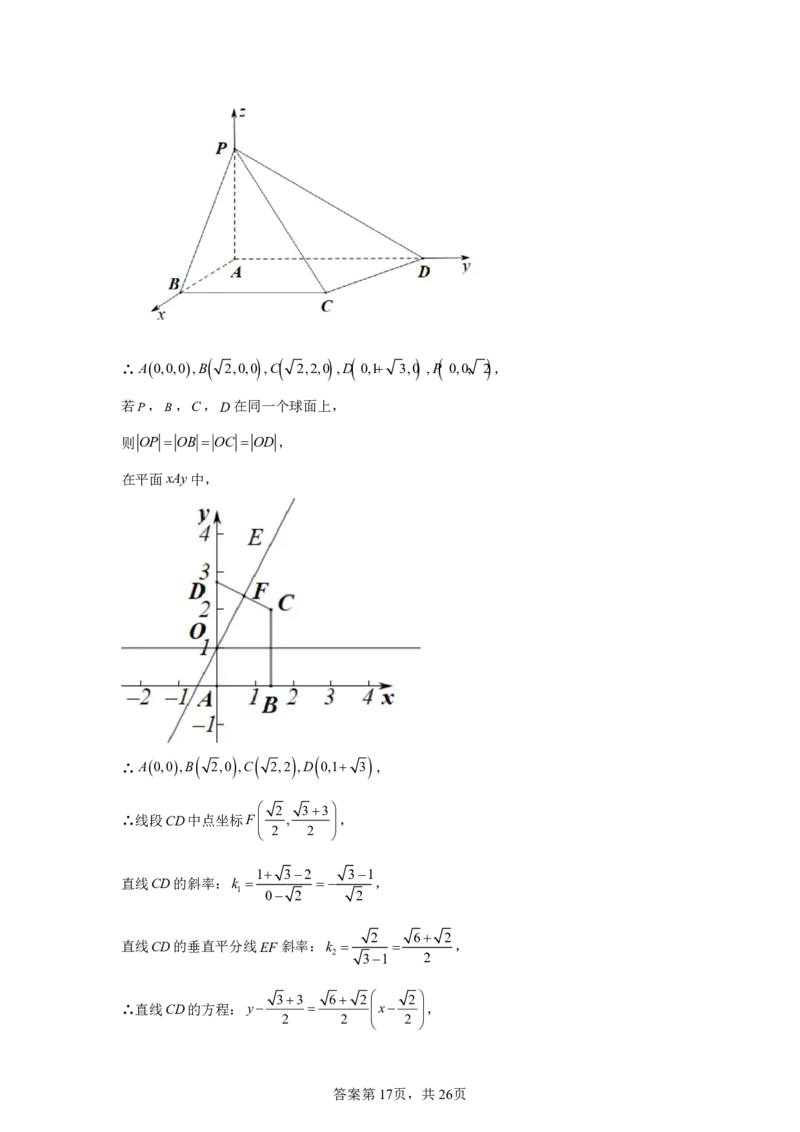（2）（i）由题意及（1）证明如下， 法一： 在四棱锥PABCD中，AP AB，APAD，ABAD ，BC∥AD， PAAB 2 ，AD1 3， 建立空间直角坐标系如下图所示， 答案第16页，共26页∴A0,0,0,B  2,0,0  ,C  2,2,0  ,D  0,1 3,0  ,P  0,0, 2  ， 若P，B，C，D在同一个球面上， 则 OP  OB  OC  OD ， 在平面xAy中， ∴A0,0,B  2,0  ,C  2,2  ,D  0,1 3  ，  2 33 ∴线段CD中点坐标F , ，    2 2  1 32 31 直线CD的斜率：k   ， 1 0 2 2 2 6 2 直线CD的垂直平分线EF斜率：k   ， 2 31 2 33 6 2 2 ∴直线CD的方程：y  x ，   2 2  2  答案第17页，共26页6 2 2 33 即y x  ，   2  2  2 6 2 2 33 当y1时，1 x   ，解得：x 0， 2   O 2   2 O ∴O0,1 在立体几何中，O0,1,0，   2 OP  0212 0 2    2 OB  0 2 1202  ∵  OC   0 2 2 12202    2 OD  02 11 3 02  解得： OP  OB  OC  OD  3， ∴点O在平面ABCD上. 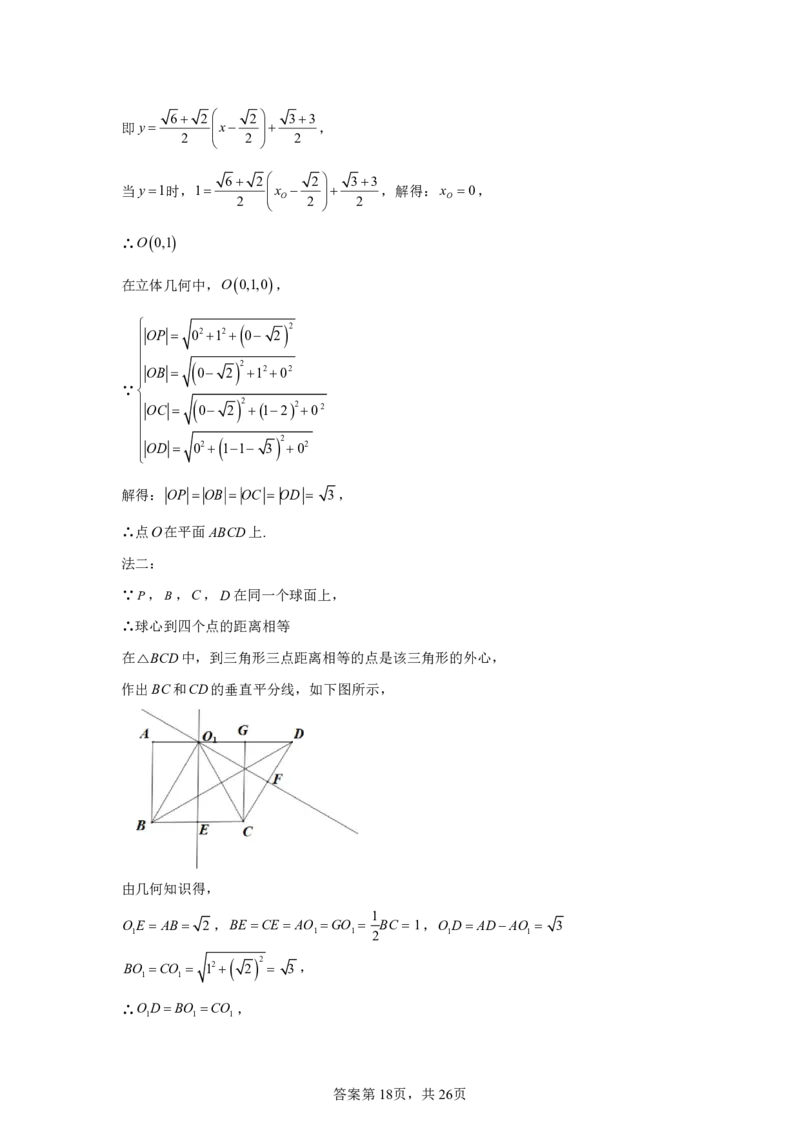法二： ∵P，B，C，D在同一个球面上， ∴球心到四个点的距离相等 在△BCD中，到三角形三点距离相等的点是该三角形的外心， 作出BC和CD的垂直平分线，如下图所示， 由几何知识得， 1 OE  AB 2，BE CE AO GO  BC  1，ODADAO  3 1 1 1 2 1 1  2 BO CO  12 2  3 ， 1 1 ∴ODBO CO ， 1 1 1 答案第18页，共26页∴点O 是△BCD的外心， 1 在RtAOP中，APAD，AP 2， 由勾股定理得，  2 PO  AP2AO2  2 12  3 1 1 ∴PO  BO CO OD 3， 1 1 1 1 ∴点O 即为点P，B，C，D所在球的球心O， 1 此时点O在线段AD上，AD平面ABCD， ∴点O在平面ABCD上. 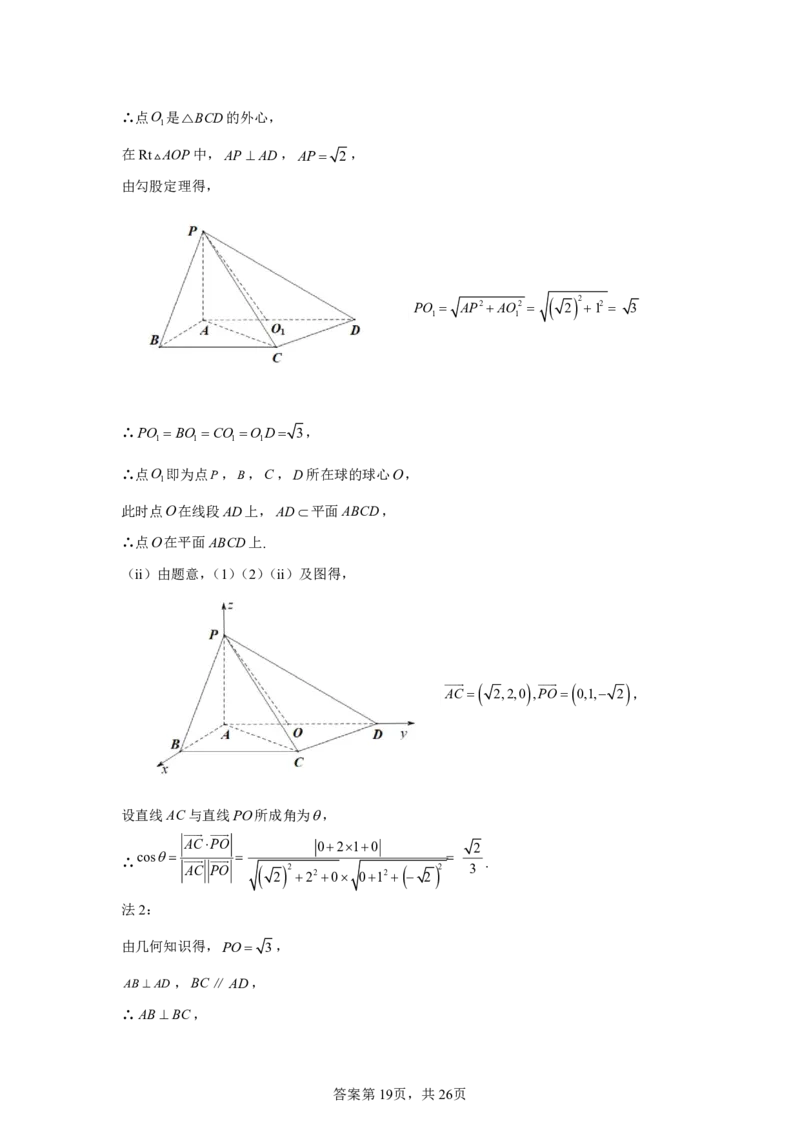（ii）由题意，（1）（2）（ii）及图得，       AC  2,2,0 ,PO 0,1, 2 ， 设直线AC与直线PO所成角为，   ACPO 0210 2 ∴cos     . 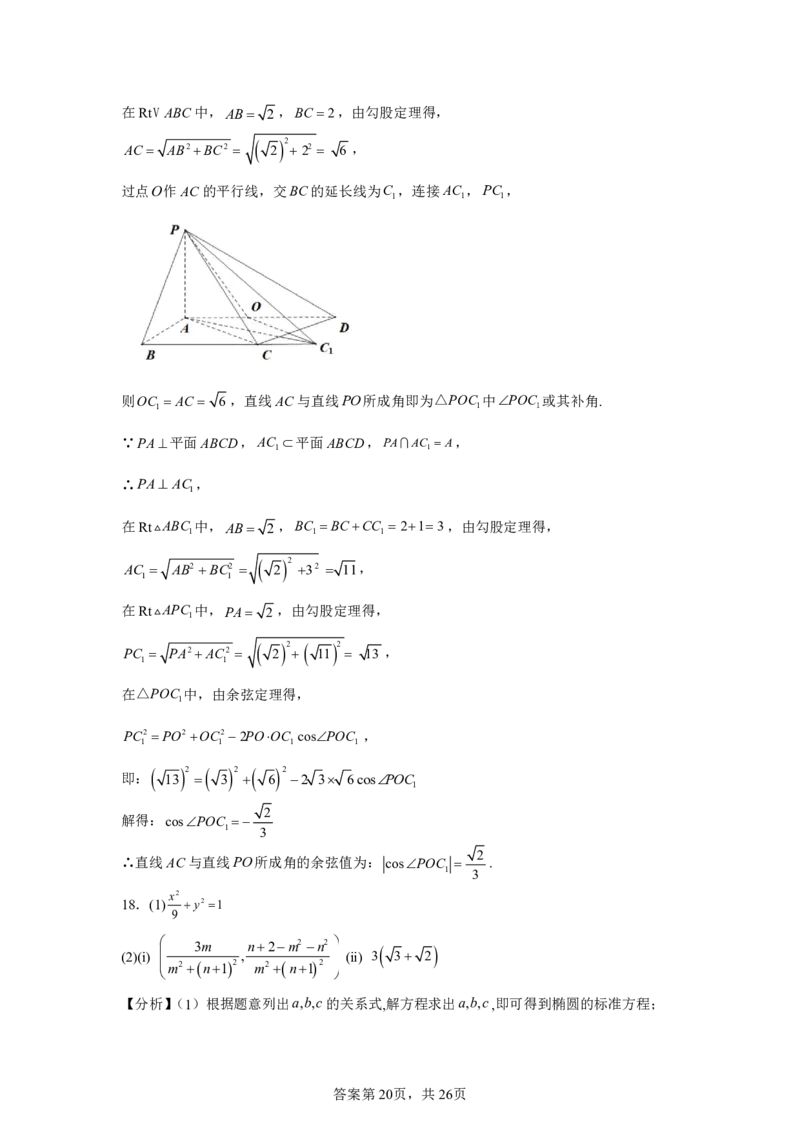AC PO  2  2 3 2 220 012  2 法2： 由几何知识得，PO 3， ABAD ，BC∥AD， ∴ABBC， 答案第19页，共26页在RtV ABC中，AB 2，BC 2，由勾股定理得，  2 AC  AB2BC2  2  22  6 ， 过点O作AC的平行线，交BC的延长线为C ，连接AC ，PC ， 1 1 1 则OC AC  6 ，直线AC与直线PO所成角即为△POC 中POC 或其补角. 1 1 1 ∵PA平面ABCD，AC 平面ABCD，PAAC A， 1 1 ∴PA AC ， 1 在RtABC 中，AB 2，BC BCCC  21 3，由勾股定理得， 1 1 1  2 AC  AB2 BC2  2 32  11， 1 1 在RtAPC 中，PA 2，由勾股定理得， 1  2  2 PC  PA2AC2  2  11  13 ， 1 1 在△POC 中，由余弦定理得， 1 PC2 PO2OC22POOC cosPOC ， 1 1 1 1  2  2  2 即： 13  3  6 2 3 6cosPOC 1 2 解得：cosPOC  1 3 2 ∴直线AC与直线PO所成角的余弦值为： cosPOC  . 1 3 x2 18．(1) y21 9  3m n2m2 n2    (2)(ⅰ)  ,  (ⅱ) 3 3 2  m2n12 m2n12   【分析】（1）根据题意列出a,b,c的关系式,解方程求出a,b,c,即可得到椭圆的标准方程； 答案第20页，共26页（2）(ⅰ)设Rx ,y  ,根据斜率相等以及题目条件列式,化简即可求出或者利用数乘向量求出； 0 0 (ⅱ) 根据斜率关系可得到点P的轨迹为圆（除去两点），再根据点与圆的最值求法结合三角 换元或者直接运算即可解出. 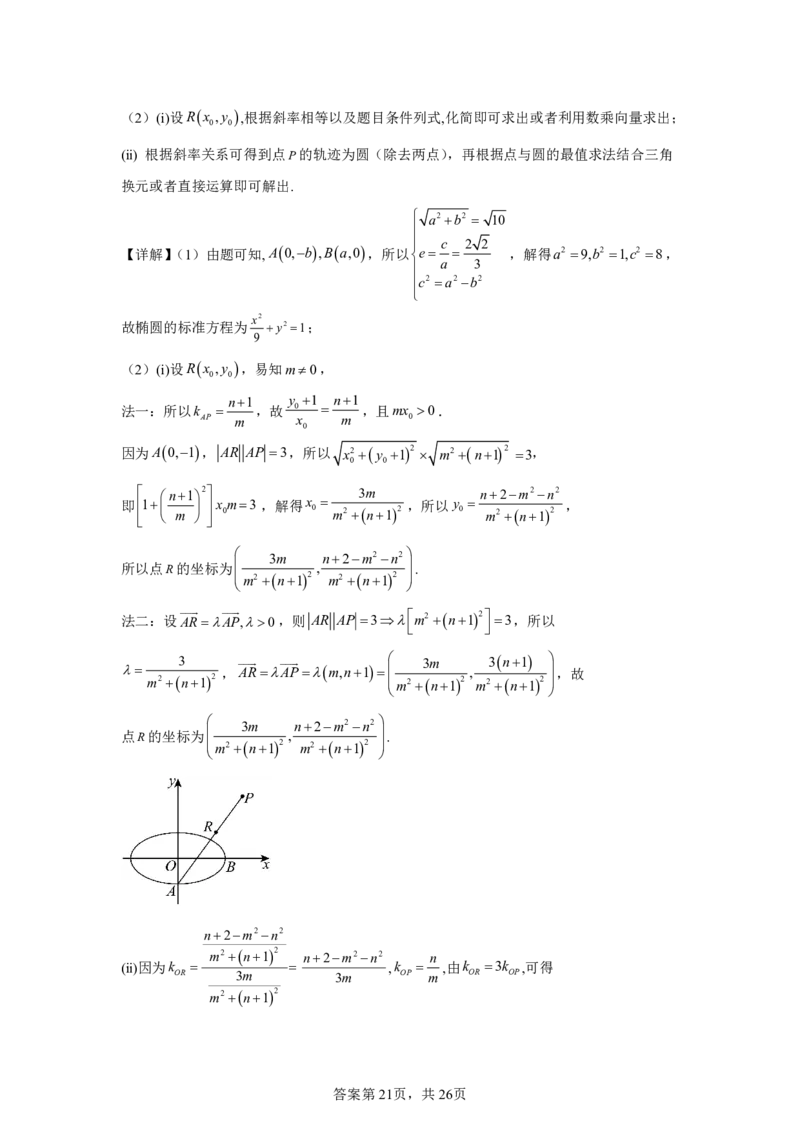 a2b2  10   c 2 2 【详解】（1）由题可知,A0,b,Ba,0，所以e  ，解得a2 9,b2 1,c2 8，  a 3 c2 a2b2  x2 故椭圆的标准方程为 y21； 9 （2）(ⅰ)设Rx ,y ，易知m0， 0 0 n1 y 1 n1 法一：所以k  ，故 0  ，且mx 0． AP m x m 0 0 因为A0,1， AR AP 3，所以 x2y 12  m2n12 3， 0 0  n1 2 3m n2m2n2 即  1  m     x 0 m3 ，解得x 0  m2n12 ，所以y 0  m2n12 ，  3m n2m2n2  所以点R的坐标为 , .  m2n12 m2n12     法二：设ARAP,0，则 AR AP 3 m2n123，所以   3    3m 3n1   ，ARAPm,n1 , ，故 m2n12  m2n12 m2n12    3m n2m2n2  点R的坐标为 , .  m2n12 m2n12   n2m2n2 m2n12 n2m2n2 n (ⅱ)因为k   ,k  ,由k 3k ,可得 OR 3m 3m OP m OR OP m2n12 答案第21页，共26页3n n2m2n2  ,化简得m2n28n20,即m2n42 18m0, m 3m 所以点P在以N0,4为圆心,3 2为半径的圆上（除去两个点）, PM 为M 到圆心N的距离加上半径, max 法一：设M3cos,sin ,所以 MN 2 3cos2sin42 9cos2sin28sin16 8cos218sin16 8  1sin2  8sin17 8sin28sin25  1 2 1 8sin  2727,当且仅当sin 时取等号,  2 2   所以 PM  273 23 3 2 . max 法二：设Mx ,y ，则 x M 2 y2 1， M m 9 M MN 2  x2 y 42 99y2  y2 8y 168y2 8y 25 M M M M M M M  1 2 1 8  y M  2   2727 ，当且仅当y M  2 时取等号,   故 PM  27 3 2 3 3 2 . max 19．(1)3 3 (2)证明见解析 (3)3 3 【分析】（1）利用导数结合三角变换得导数零点，讨论导数的符号后得单调性，从而可求最 大值；或者利用均值不等式可求最大值. （2）利用反证法可证三角不等式有解； （3）先考虑t 0,π时b的范围，对于t0,π时，可利用（2）中的结论结合特值法求得b3 3， 从而可得b的最小值；或者先根据函数解析特征得b0，再结合特值法可得b3 3，结合 （1）的结果可得b的最小值. 答案第22页，共26页【详解】（1）法1： fx5sinx5sin5x10cos3xsin2x，  π  π 因为x0, ，故2x0, ，故sin2x0，  4  2 π 当0 x 时，cos3x0即 fx0， 6 当 π x π 时，cos3x0即 fx0， 6 4  π π π 故 f x在0, 上为增函数，在 , 为减函数，  6 6 4  π π π 5π 故 f x在0, 上的最大值为 f  5cos cos 3 3.  4 6 6 6 法2：我们有cos5xcosx4xcosxcos4xsinxsin4x cosx  2cos22x1  sinx2sin2xcos2x   cosx 2  2cos2x1 2 1 sinx22sinxcosxcos2x cosx  8cos4x8cos2x1  4cosxcos2xsin2x 8cos5x8cos3xcosx4cosx  2cos2x1  1cos2x  16cos5x20cos3x5cosx. 所以： f x5cosxcos5x5cosx  16cos5x20cos3x5cosx  20cos3x16cos5x 4cos3x  54cos2x  4cosx 3 54cosx 2 4cosx 3 52cosx  52cosx  32 153  153    cosx cosx cosx  52cosx  52cosx    3  4 4  5 32  1 153  153      cosx  cosx  cosx  52cosx  52cosx     3  5 4 4  5 32 3    3 3.   3  2  π π 5π 这得到 f x3 3，同时又有 f  5cos cos 3 3， 6 6 6  π 故 f x在0, 上的最大值为3 3，在R上的最大值也是3 3.  4 （2）法1：由余弦函数的性质得cosxcos的解为 2kπ,2kπ2π，kZ， 答案第23页，共26页若任意 2kπ,2kπ+2π ,kZ与 a,a交集为空， 则a2kπ2π且a2kπ2π，此时a无解， 矛盾，故无解；故存在kZ，使得2kπ,2kπa,a， 法2：由余弦函数的性质知cosycos的解为 2kπ,2k1π  kZ， 若每个 2kπ,2k1π  与 a,a交集都为空， 则对每个kZ，必有2k1πa或2kπa之一成立. a a  a a  此即k 1或k  ，但长度为1的闭区间  1,  上必有一整数k，该整数k不满足 2π 2π 2π 2π 条件，矛盾. 故存在ya,a，使得cosycos成立. （3）法1：记h(x)5cosxcos5xt， 因为h(x2π)5cosx2πcos5x10π+thx， 故hx为周期函数且周期为2π,故只需讨论x 0,2π  ,t 0,π 的情况. 当t  π时，h(x)5cosxcos5xπ6cosx6， 当t 0时，h(x)5cosxcos5x， 此时hx5sinx5sin5x10cos3xsin2x,x0,2π， π π 5π 7π 3π 11π 令h(x)0，则x , , ,π, , , ， 6 2 6 6 2 6 π 11π π 3π 5π 7π 而h( )h( )3 3,h( )h( )0,h( )h( )3 3,h(π)4， 6 6 2 2 6 6 π 11π h(0)h(2π)4，故h(x) h( )h( )3 3， max 6 6 当t0,π，在（2）中取at，则存在yt,t，使得cosycos， 5π 3 yt    yt    取 ，则cosy ，取x  , 即x  , ， 6 2 5  5 5 5  6 6 故5cosx 5 3 ，故5cosxcos5xt3 3 ， 2 π 综上b3 3，可取x ，t 0使得等号成立. 6 综上，b 3 3. min 答案第24页，共26页法2：设g x5cosxcos5xt . t ①一方面，若存在t，使得g x5cosxcos5xtb对任意x恒成立，则对这样的t，同 t 样有g xg xπb. t t 所以 g x b对任意x恒成立，这直接得到b0. t t π 设  m，则根据 g x b恒成立，有 6 6 t  t π  t π t 5π t π t π t π b g     5cos  cos    5cos  cos    6cos   6cosm t 6 6  6 6 6 6  6 6 6 6 6 6  t π  t π t 5π t π t π t π  π b g     5cos  cos    5cos  cos    6cos   6cosm  t 6 6  6 6 6 6  6 6 6 6 6 6  3  t π  t π t 5π t π t π t π  π b g     5cos  cos    5cos  cos    6cos   6cosm  t 6 2  6 2 6 2  6 2 6 2 6 2  3  π  π  b 所以 cosm ,cosm  ,cosm 均不超过 ，  3  3 6 再结合cos2x2cosx 21，  2π  2π b 2 b2 就得到cos2m,cos2m ,cos2m 均不超过2  1 1.  3   3  6 18  2 假设b3 3，则b2 1 3 3 1 1 ， 18 18 2  2π  2π  1 故cos2m,cos2m ,cos2m   1, .  3   3   2 2π 2π 但这是不可能的，因为三个角2m,2m ,2m 和单位圆的交点将单位圆三等分，这三个 3 3 1 点不可能都在直线x 左侧. 2 所以假设不成立，这意味着b3 3. ②另一方面，若b3 3，则由（1）中已经证明 f x3 3， 知存在t 0，使得 答案第25页，共26页5cosxcos5xt5cosxcos5x f x 3 3 b . 从而b3 3满足题目要求. 综合上述两个方面，可知b的最小值是3 3. 答案第26页，共26页