文档内容
数学试题
一、选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一
项是符合要求的.
1. 下列实数中,无理数是( )
A. B. 0 C. D.
【答案】D
【解析】
【分析】无理数就是无限不循环小数,理解无理数的概念,一定要同时理解有理数的概念,有理数是整数
与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数,由此即可判定选择
项.
本题主要考查了无理数的定义,其中初中范围内学习的无理数有: 等;开方开不尽的数;以及像
,等数.
【详解】根据无理数的定义可得:无理数是
故选:D.
2. 据《人民日报》3月12日电,世界知识产权组织近日公布数据显示,2023年,全球 (《专利合作
条约》)国际专利申请总量为27.26万件,中国申请量为69610件,是申请量最大的来源国.数据69610
用科学记数法表示为( )
A. B. C. D.
【答案】C
【解析】
【分析】根据科学记数法的定义解答,科学记数法的表示形式为 的形式,其中 为整
数,确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
当原数绝对值 时,n是正数;当原数的绝对值 时,n是负数.
本题考查了科学记数法,熟悉科学记数法概念是解题 关键.
【详解】
故选:C.
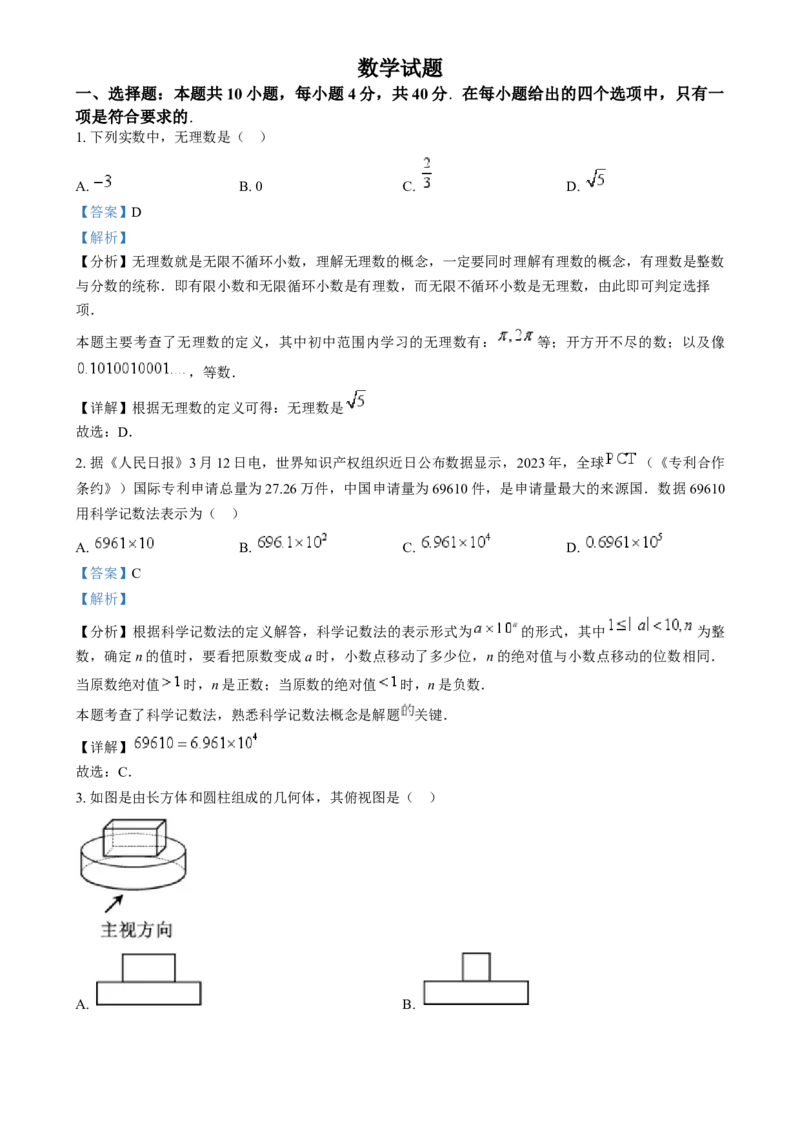
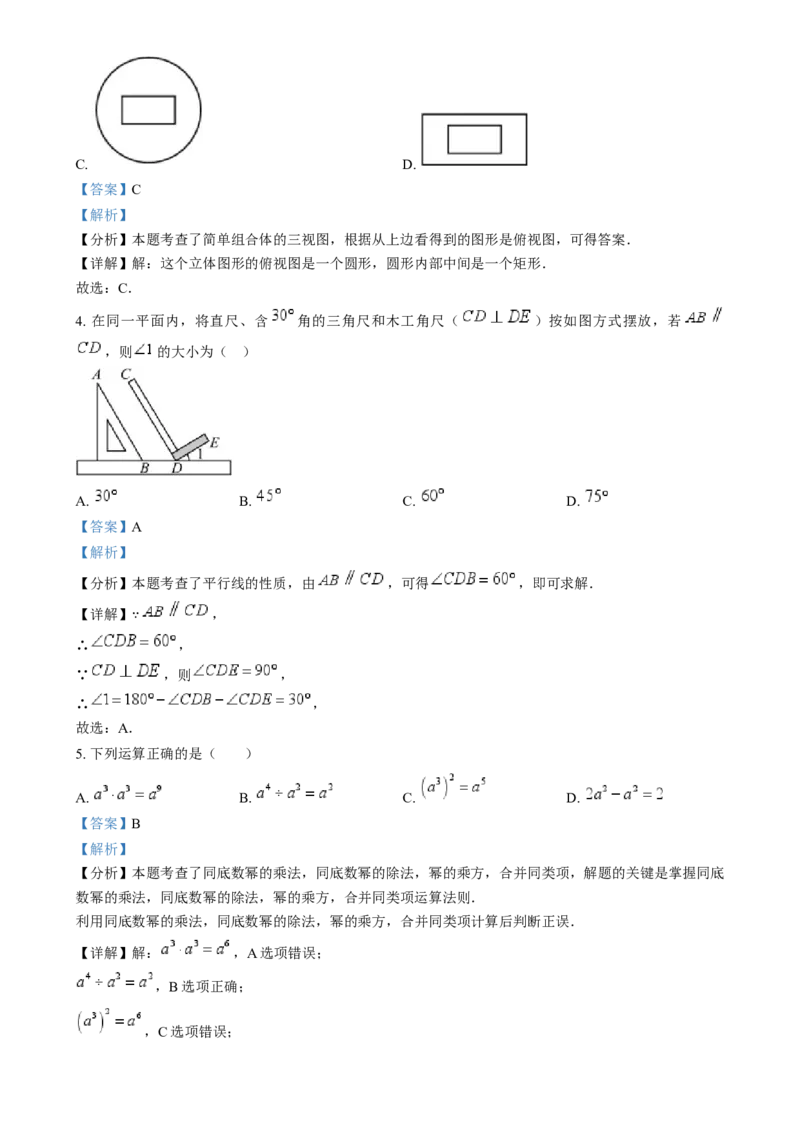
3. 如图是由长方体和圆柱组成的几何体,其俯视图是( )
A. B.C. D.
【答案】C
【解析】
【分析】本题考查了简单组合体的三视图,根据从上边看得到的图形是俯视图,可得答案.
【详解】解:这个立体图形的俯视图是一个圆形,圆形内部中间是一个矩形.
故选:C.
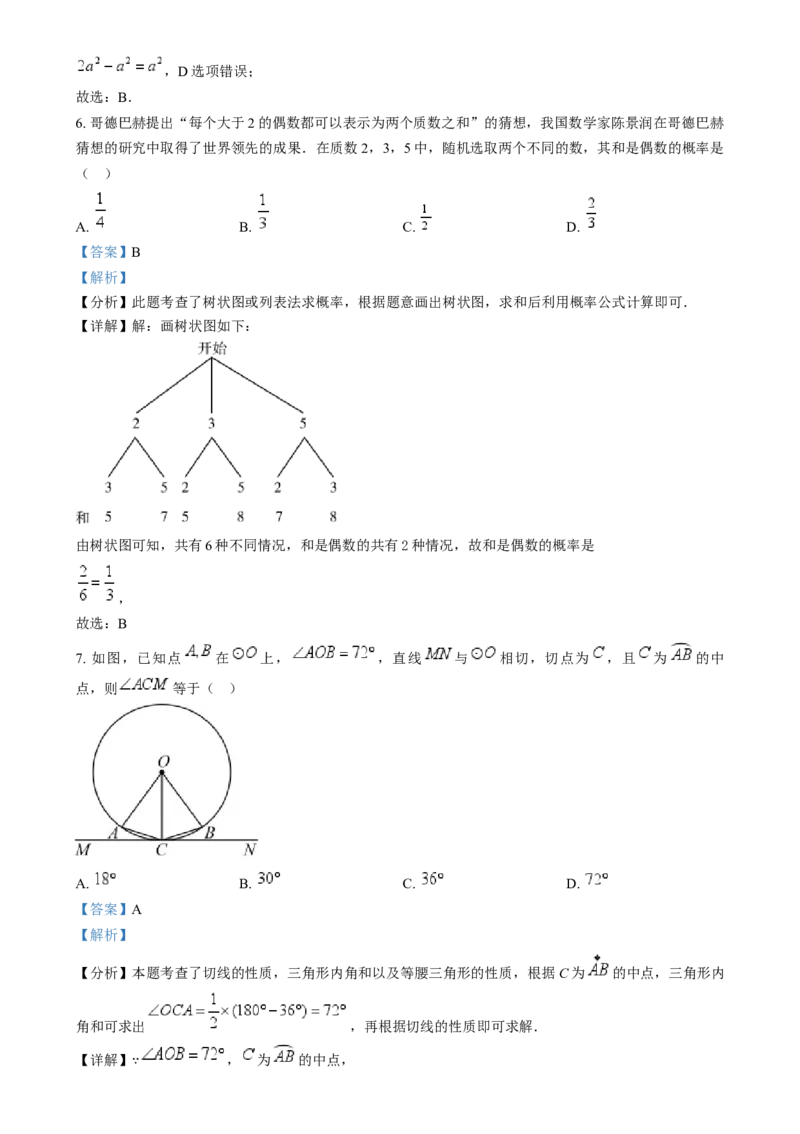
4. 在同一平面内,将直尺、含 角的三角尺和木工角尺( )按如图方式摆放,若
,则 的大小为( )
A. B. C. D.
【答案】A
【解析】
【分析】本题考查了平行线的性质,由 ,可得 ,即可求解.
【详解】 ,
∴ ∵ ,
∵ ,则 ,
∴ ,
故选:A.
5. 下列运算正确的是( )
A. B. C. D.
【答案】B
【解析】
【分析】本题考查了同底数幂的乘法,同底数幂的除法,幂的乘方,合并同类项,解题的关键是掌握同底
数幂的乘法,同底数幂的除法,幂的乘方,合并同类项运算法则.
利用同底数幂的乘法,同底数幂的除法,幂的乘方,合并同类项计算后判断正误.
【详解】解: ,A选项错误;
,B选项正确;
,C选项错误;,D选项错误;
故选:B.
6. 哥德巴赫提出“每个大于2的偶数都可以表示为两个质数之和”的猜想,我国数学家陈景润在哥德巴赫
猜想的研究中取得了世界领先的成果.在质数2,3,5中,随机选取两个不同的数,其和是偶数的概率是
( )
A. B. C. D.
【答案】B
【解析】
【分析】此题考查了树状图或列表法求概率,根据题意画出树状图,求和后利用概率公式计算即可.
【详解】解:画树状图如下:
由树状图可知,共有6种不同情况,和是偶数的共有2种情况,故和是偶数的概率是
,
故选:B
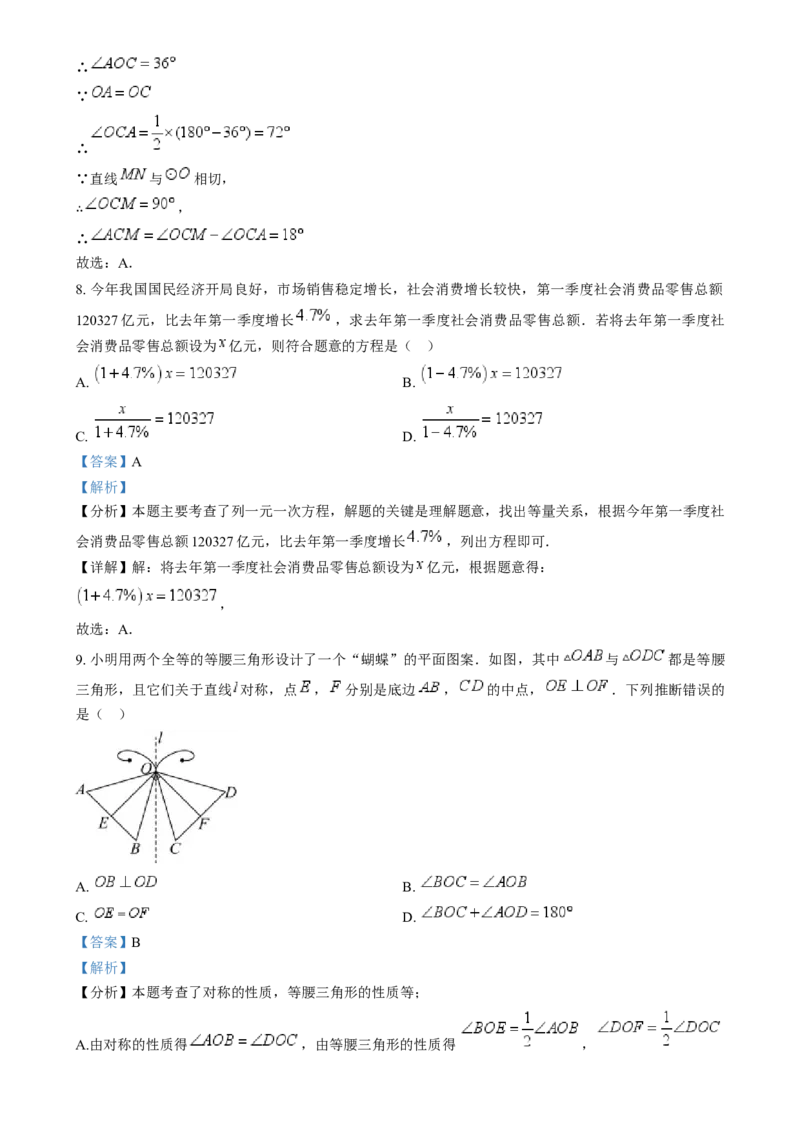
7. 如图,已知点 在 上, ,直线 与 相切,切点为 ,且 为 的中
点,则 等于( )
A. B. C. D.
【答案】A
【解析】
【分析】本题考查了切线的性质,三角形内角和以及等腰三角形的性质,根据C为 的中点,三角形内
角和可求出 ,再根据切线的性质即可求解.
【详解】 , 为 的中点,
∵∴
∵
∴
∵直线 与 相切,
,
∴∴
故选:A.
8. 今年我国国民经济开局良好,市场销售稳定增长,社会消费增长较快,第一季度社会消费品零售总额
120327亿元,比去年第一季度增长 ,求去年第一季度社会消费品零售总额.若将去年第一季度社
会消费品零售总额设为 亿元,则符合题意的方程是( )
A. B.
C. D.
【答案】A
【解析】
【分析】本题主要考查了列一元一次方程,解题的关键是理解题意,找出等量关系,根据今年第一季度社
会消费品零售总额120327亿元,比去年第一季度增长 ,列出方程即可.
【详解】解:将去年第一季度社会消费品零售总额设为 亿元,根据题意得:
,
故选:A.
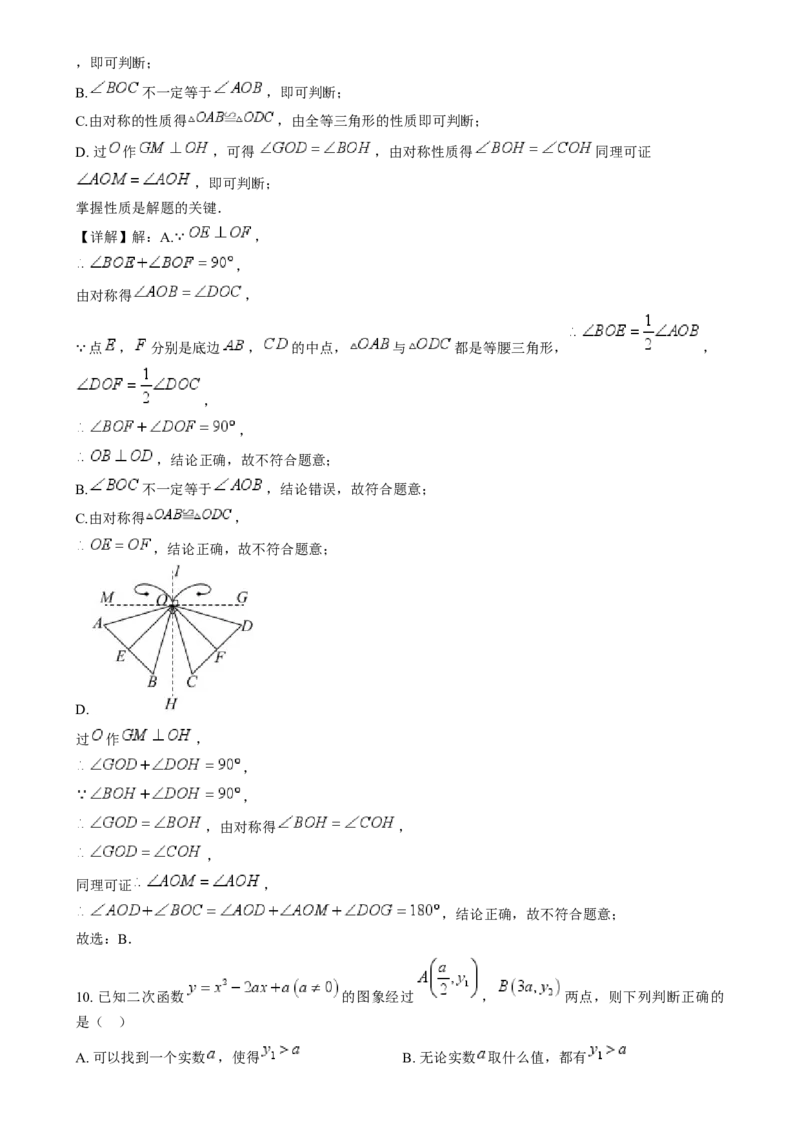
9. 小明用两个全等的等腰三角形设计了一个“蝴蝶”的平面图案.如图,其中 与 都是等腰
三角形,且它们关于直线 对称,点 , 分别是底边 , 的中点, .下列推断错误的
是( )
A. B.
C. D.
【答案】B
【解析】
【分析】本题考查了对称的性质,等腰三角形的性质等;
A.由对称的性质得 ,由等腰三角形的性质得 ,,即可判断;
B. 不一定等于 ,即可判断;
C.由对称的性质得 ,由全等三角形的性质即可判断;
D. 过 作 ,可得 ,由对称性质得 同理可证
,即可判断;
掌握性质是解题的关键.
【详解】解:A. ,
,
由对称得 ,
点 , 分别是底边 , 的中点, 与 都是等腰三角形, ,
,
,
,结论正确,故不符合题意;
B. 不一定等于 ,结论错误,故符合题意;
C.由对称得 ,
,结论正确,故不符合题意;
D.
过 作 ,
,
,
,由对称得 ,
,
同理可证 ,
,结论正确,故不符合题意;
故选:B.
10. 已知二次函数 的图象经过 , 两点,则下列判断正确的
是( )
A. 可以找到一个实数 ,使得 B. 无论实数 取什么值,都有C. 可以找到一个实数 ,使得 D. 无论实数 取什么值,都有
【答案】C
【解析】
【分析】本题考查二次函数的图象和性质,根据题意得到二次函数开口向上,且对称轴为
,顶点坐标为 ,再分情况讨论,当 时,当 时, , 的大小情况,即可解题.
【详解】解: 二次函数解析式为 ,
二次函数开口向上,且对称轴为 ,顶点坐标为 ,
当 时, ,
,
当 时, ,
,
故A、B错误,不符合题意;
当 时, ,
由二次函数对称性可知, ,
当 时, ,由二次函数对称性可知, ,不一定大于 ,
故C正确符合题意;D错误,不符合题意;
故选:C.
二、填空题:本题共6小题,每小题4分,共24分.
11. 因式分解:x2+x=_____.
【答案】
【解析】
【分析】要将一个多项式分解因式的一般步骤是首先看各项有没有公因式,若有公因式,则把它提取出
来,之后再观察是否是完全平方公式或平方差公式,若是就考虑用公式法继续分解因式.因此,直接提取
公因式x即可.
【详解】解:
12. 不等式 的解集是______.
【答案】
【解析】
【分析】本题考查的是解一元一次不等式,通过移项,未知数系数化为1,求解即可解.
【详解】解: ,
,,
故答案为: .
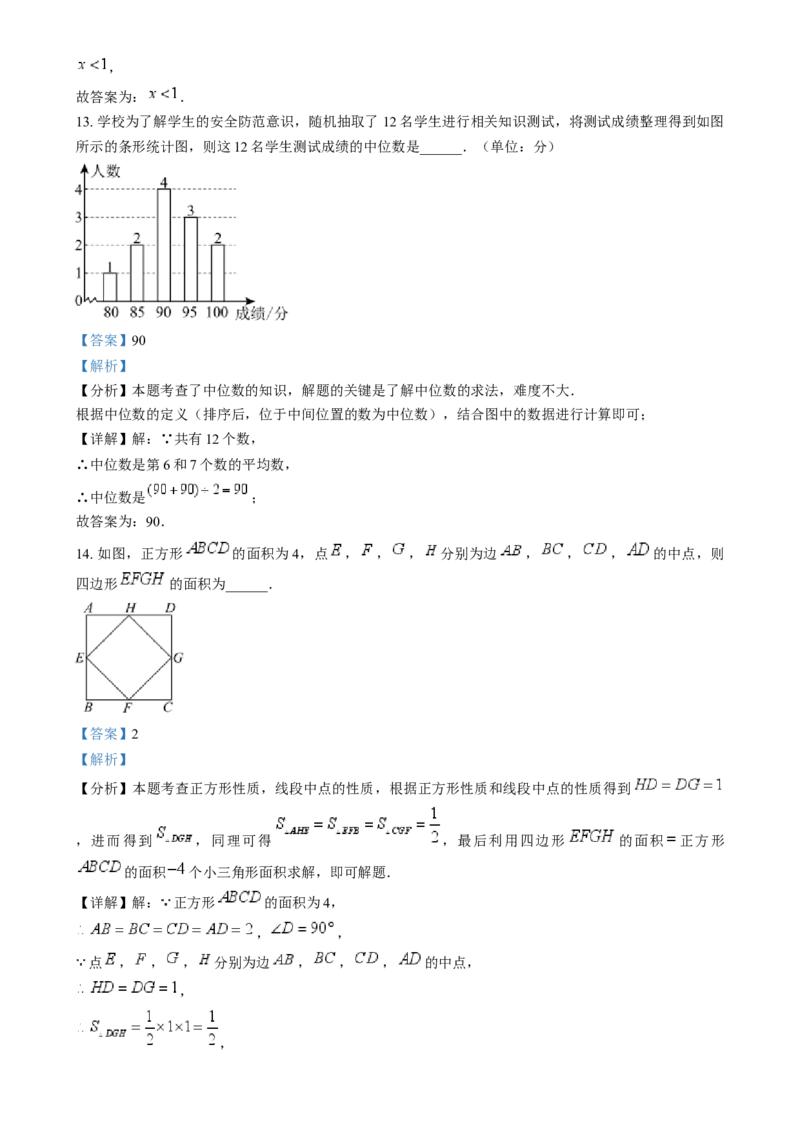
13. 学校为了解学生的安全防范意识,随机抽取了12名学生进行相关知识测试,将测试成绩整理得到如图
所示的条形统计图,则这12名学生测试成绩的中位数是______.(单位:分)
【答案】90
【解析】
【分析】本题考查了中位数的知识,解题的关键是了解中位数的求法,难度不大.
根据中位数的定义(排序后,位于中间位置的数为中位数),结合图中的数据进行计算即可;
【详解】解:∵共有12个数,
∴中位数是第6和7个数的平均数,
∴中位数是 ;
故答案为:90.
14. 如图,正方形 的面积为4,点 , , , 分别为边 , , , 的中点,则
四边形 的面积为______.
【答案】2
【解析】
【分析】本题考查正方形性质,线段中点的性质,根据正方形性质和线段中点的性质得到
,进而得到 ,同理可得 ,最后利用四边形 的面积 正方形
的面积 个小三角形面积求解,即可解题.
【详解】解: 正方形 的面积为4,
, ,
点 , , , 分别为边 , , , 的中点,
,
,同理可得 ,
四边形 的面积为 .
故答案为:2.
15. 如图,在平面直角坐标系 中,反比例函数 的图象与 交于 两点,且点 都在第
一象限.若 ,则点 的坐标为______.
【答案】
【解析】
【分析】本题考查了反比例函数的性质以及勾股定理,完全平方公式的应用,先根据 得出
, 设 , 则 , 结 合 完 全 平 方 公 式 的 变 形 与 应 用 得 出
,结合 ,则 ,即可作答.
详解】解:如图:连接
∵反比例函数 的图象与 交于 两点,且
∴
设 ,则
∵
∴
则∵点 在第一象限
∴
把 代入得
∴
经检验: 都是原方程的解
∵
∴
故答案为:
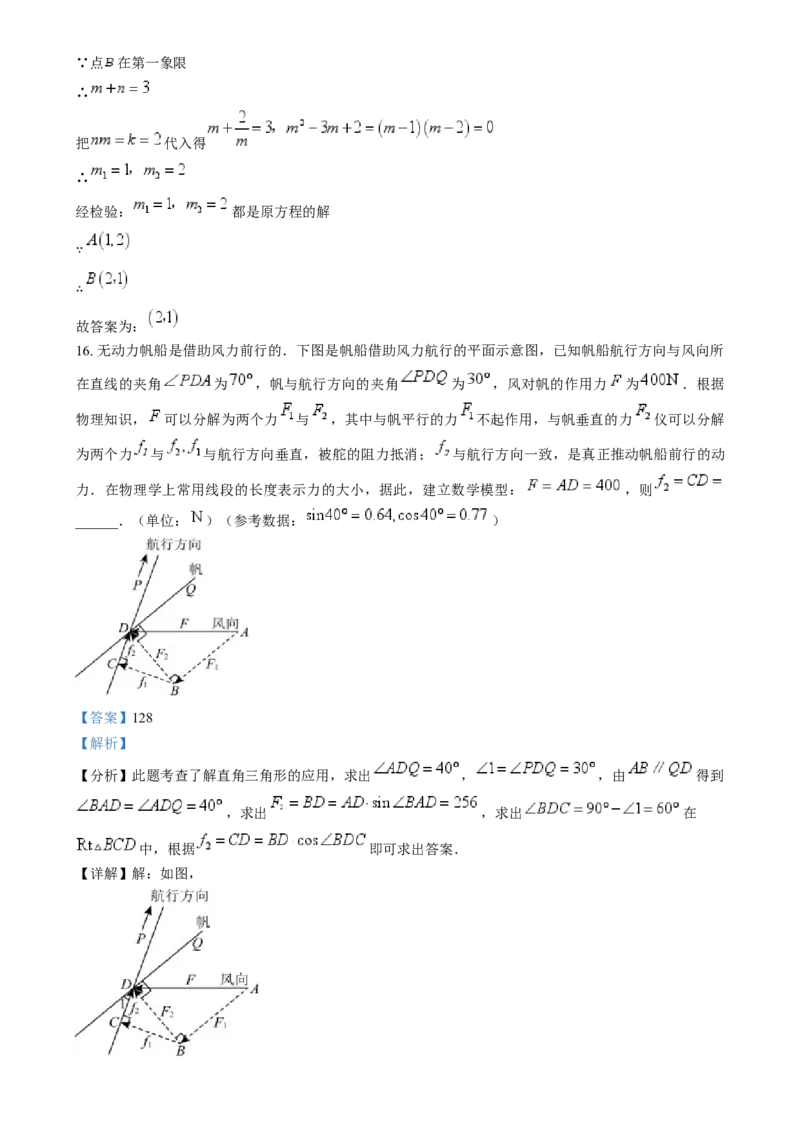
16. 无动力帆船是借助风力前行的.下图是帆船借助风力航行的平面示意图,已知帆船航行方向与风向所
在直线的夹角 为 ,帆与航行方向的夹角 为 ,风对帆的作用力 为 .根据
物理知识, 可以分解为两个力 与 ,其中与帆平行的力 不起作用,与帆垂直的力 仪可以分解
为两个力 与 与航行方向垂直,被舵的阻力抵消; 与航行方向一致,是真正推动帆船前行的动
力.在物理学上常用线段的长度表示力的大小,据此,建立数学模型: ,则
______.(单位: )(参考数据: )
【答案】128
【解析】
【分析】此题考查了解直角三角形的应用,求出 , ,由 得到
,求出 ,求出 在
中,根据 即可求出答案.
【详解】解:如图,帆船航行方向与风向所在直线的夹角 为 ,帆与航行方向的夹角 为 ,
∵ , ,
∴ ,
∵ ,
∴在 中, , ,
,
∴由题意可知, ,
,
∴
∴在 中, ,
∴ ,
故答案为:
三、解答题:本题共9小题,共86分。解答应写出文字说明、证明过程或演算步骤。
17. 计算: .
【答案】4
【解析】
【分析】本小题考查零指数幂、绝对值、算术平方根等基础知识,考查运算能力.
根据零指数幂、绝对值、算术平方根分别计算即可;
【详解】解:原式 .
18. 如图,在菱形 中,点 分别在 边上, ,求证: .
【答案】见解析
【解析】
【分析】本题考查菱形的性质、全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解答的关
键.根据菱形的性质证得 , ,再根据全等三角形的判定证明
即可.
【详解】证明: 四边形 是菱形,
, ,
,
,.
19. 解方程: .
【答案】 .
【解析】
【分析】本题考查解分式方程,掌握解分式方程的步骤和方法,将分式方程化为整式方程求解,即可解
题.
【详解】解: ,
方程两边都乘 ,得 .
去括号得: ,
解得 .
经检验, 是原方程的根.
20. 已知A、B两地都只有甲、乙两类普通高中学校.在一次普通高中学业水平考试中,A地甲类学校有
考生3000人,数学平均分为90分:乙类学校有考生2000人,数学平均分为80分.
(1)求A地考生的数学平均分;
(2)若B地甲类学校数学平均分为94分,乙类学校数学平均分为82分,据此,能否判断B地考生数学
平均分一定比A地考生数学平均分高?若能,请给予证明:若不能,请举例说明.
【答案】(1)86; (2)不能,举例见解析.
【解析】
【分析】本小题考查加权平均数等基础知识,
(1)根据平均数的概念求解即可;
(2)根据平均数的意义求解即可.
【小问1详解】
由题意,得A地考生的数学平均分为 .
【小问2详解】
不能.
举例如下:如B地甲类学校有考生1000人,乙类学校有考生3000人,则B地考生的数学平均分为
.
因为 ,
所以不能判断B地考生数学平均分一定比 地考生数学平均分高.
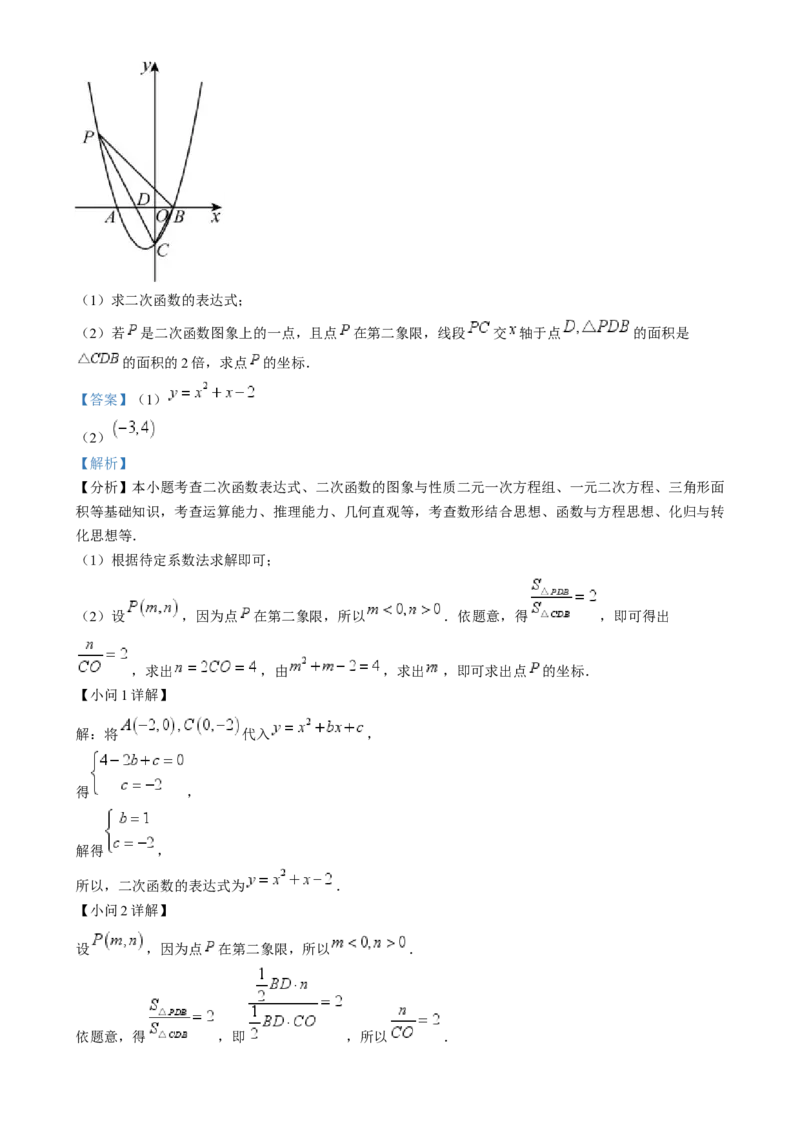
21. 如图,已知二次函数 的图象与 轴交于 两点,与 轴交于点 ,其中
.(1)求二次函数的表达式;
(2)若 是二次函数图象上的一点,且点 在第二象限,线段 交 轴于点 的面积是
的面积的2倍,求点 的坐标.
【答案】(1)
(2)
【解析】
【分析】本小题考查二次函数表达式、二次函数的图象与性质二元一次方程组、一元二次方程、三角形面
积等基础知识,考查运算能力、推理能力、几何直观等,考查数形结合思想、函数与方程思想、化归与转
化思想等.
(1)根据待定系数法求解即可;
(2)设 ,因为点 在第二象限,所以 .依题意,得 ,即可得出
,求出 ,由 ,求出 ,即可求出点 的坐标.
【小问1详解】
解:将 代入 ,
得 ,
解得 ,
所以,二次函数的表达式为 .
【小问2详解】
设 ,因为点 在第二象限,所以 .
依题意,得 ,即 ,所以 .由已知,得 ,
所以 .
由 ,
解得 (舍去),
所以点 坐标为 .
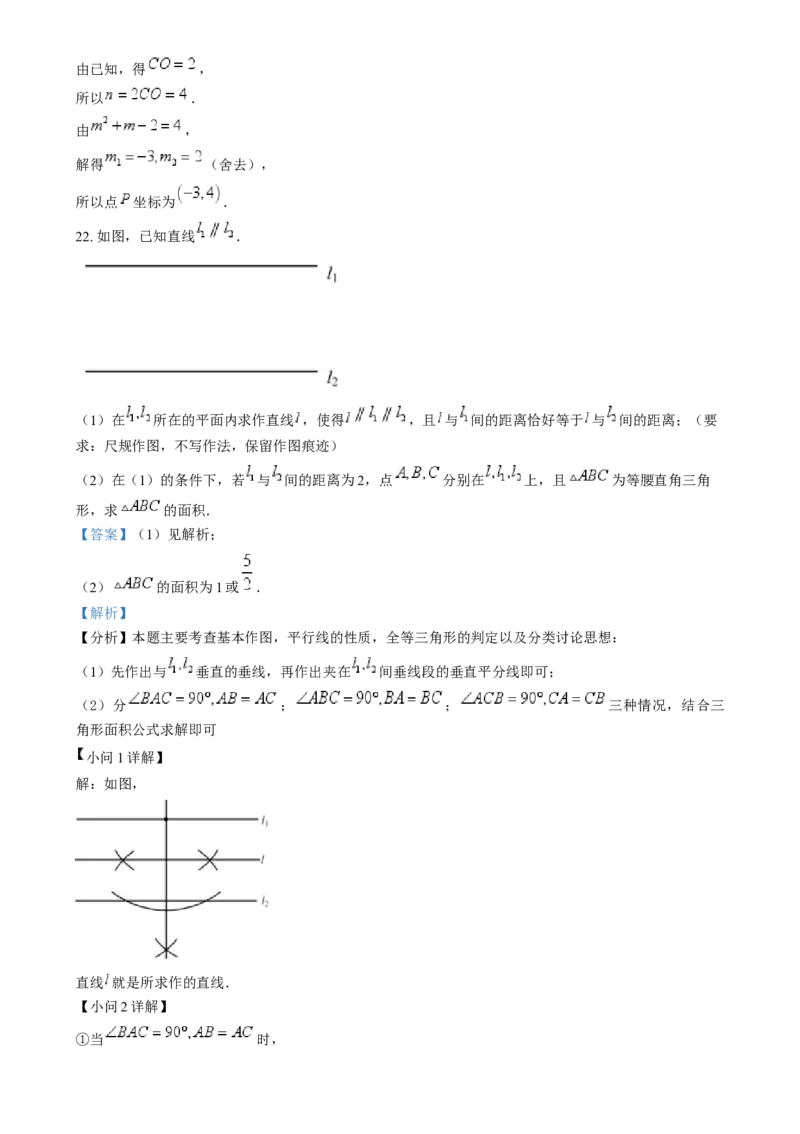
22. 如图,已知直线 .
(1)在 所在的平面内求作直线 ,使得 ,且 与 间的距离恰好等于 与 间的距离;(要
求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,若 与 间的距离为2,点 分别在 上,且 为等腰直角三角
形,求 的面积.
【答案】(1)见解析;
(2) 的面积为1或 .
【解析】
【分析】本题主要考查基本作图,平行线的性质,全等三角形的判定以及分类讨论思想:
(1)先作出与 垂直的垂线,再作出夹在 间垂线段的垂直平分线即可;
(2)分 ; ; 三种情况,结合三
角形面积公式求解即可
小问1详解】
解:如图,
直线 就是所求作的直线.
【小问2详解】
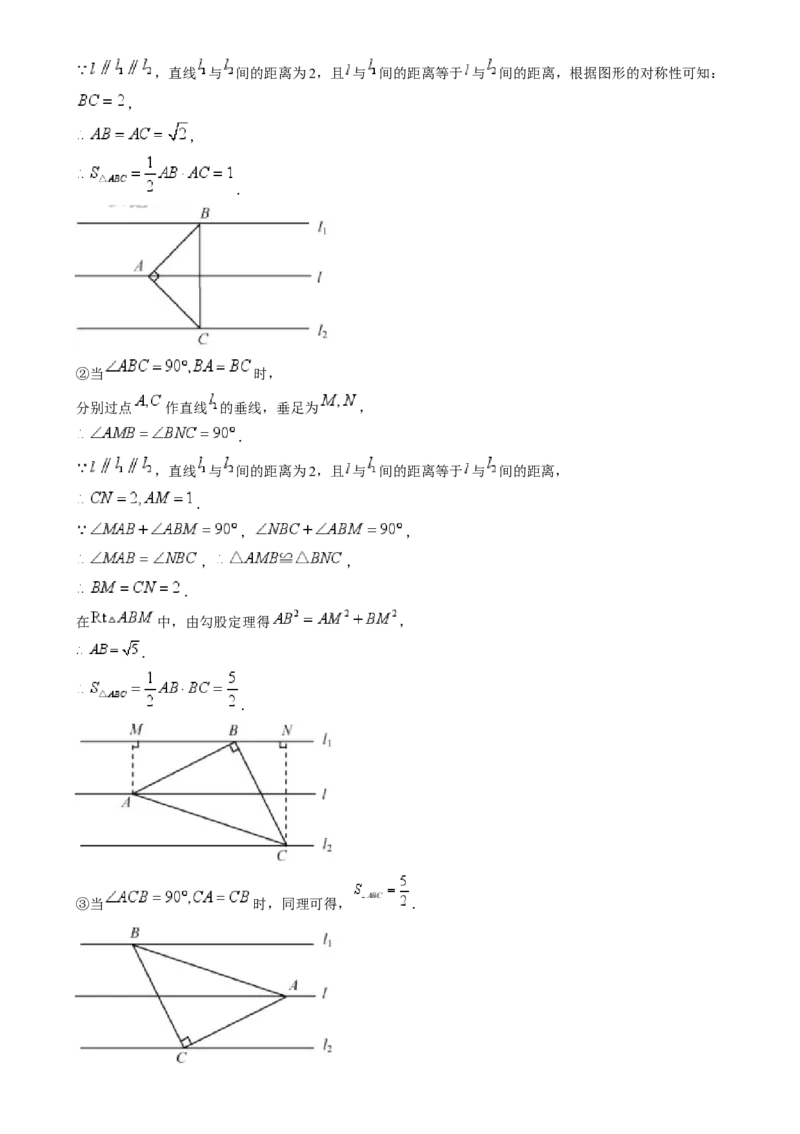
①当 时,,直线 与 间的距离为2,且 与 间的距离等于 与 间的距离,根据图形的对称性可知:
,
,
.
②当 时,
分别过点 作直线 的垂线,垂足为 ,
.
,直线 与 间的距离为2,且 与 间的距离等于 与 间的距离,
.
, ,
, ,
.
在 中,由勾股定理得 ,
.
.
③当 时,同理可得, .综上所述, 面积为1或 .
23. 已知实数 满足 .
(1)求证: 为非负数;
(2)若 均为奇数, 是否可以都为整数?说明你的理由.
【答案】(1)证明见解析;
(2) 不可能都为整数,理由见解析.
【解析】
【分析】(1)根据题意得出 ,进而计算 ,根据非负数的性质,即可求
解;
(2)分情况讨论,① 都为奇数;② 为整数,且其中至少有一个为偶数.
【小问1详解】
解:因为 ,
所以 .
则
.
因为 是实数,所以 ,
所以 为非负数.
【小问2详解】
不可能都为整数.
理由如下:若 都为整数,其可能情况有:① 都为奇数;② 为整数,且其中至少有一个为偶
数.
①当 都为奇数时,则 必为偶数.
又 ,所以 .
因为 为奇数,所以 必为偶数,这与 为奇数矛盾.
②当 为整数,且其中至少有一个为偶数时,则 必为偶数.
又因为 ,所以 .
因为 为奇数,所以 必为偶数,这与 为奇数矛盾.综上所述, 不可能都为整数.
【点睛】本小题考查整式的运算、因式分解、等式的性质等基础知识:考查运算能力、推理能力、创新意
识等,考查综合应用所学知识分析、解决问题的能力:考查化归与转化思想、分类与整合思想等.
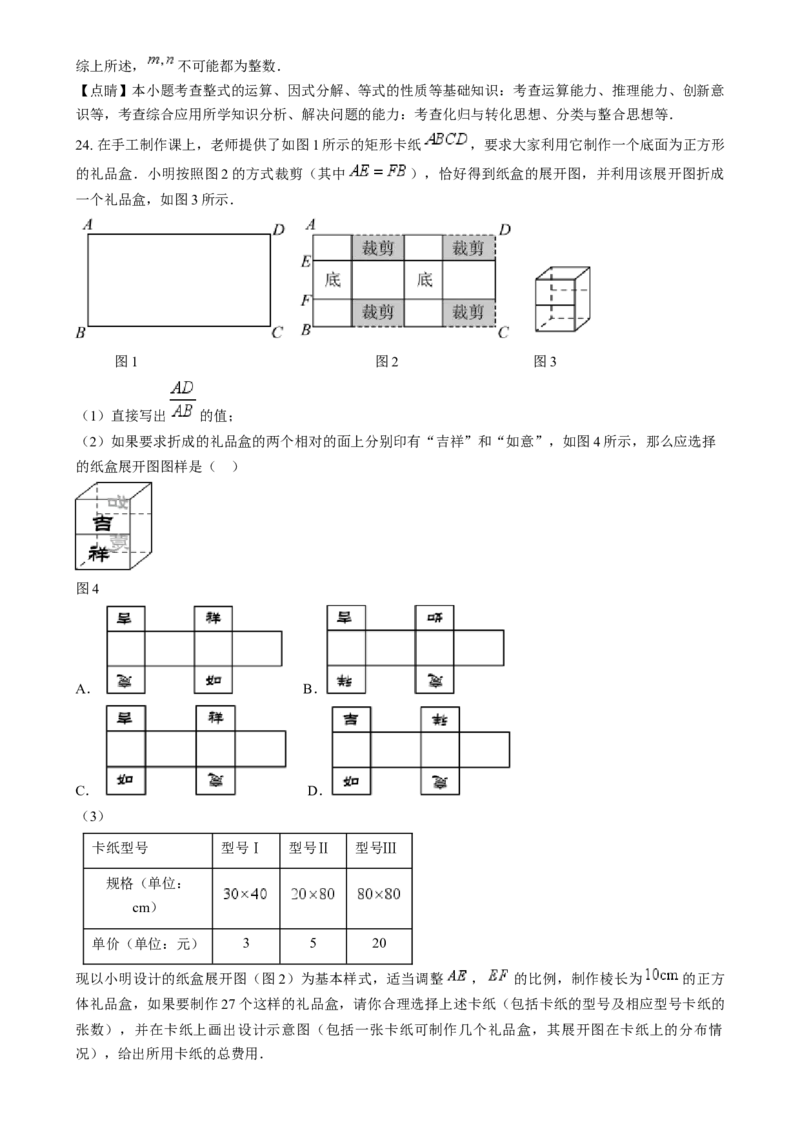
24. 在手工制作课上,老师提供了如图1所示的矩形卡纸 ,要求大家利用它制作一个底面为正方形
的礼品盒.小明按照图2的方式裁剪(其中 ),恰好得到纸盒的展开图,并利用该展开图折成
一个礼品盒,如图3所示.
图1 图2 图3
(1)直接写出 的值;
(2)如果要求折成的礼品盒的两个相对的面上分别印有“吉祥”和“如意”,如图4所示,那么应选择
的纸盒展开图图样是( )
图4
A. B.
C. D.
(3)
卡纸型号 型号Ⅰ 型号Ⅱ 型号Ⅲ
规格(单位:
cm)
单价(单位:元) 3 5 20
现以小明设计的纸盒展开图(图2)为基本样式,适当调整 , 的比例,制作棱长为 的正方
体礼品盒,如果要制作27个这样的礼品盒,请你合理选择上述卡纸(包括卡纸的型号及相应型号卡纸的
张数),并在卡纸上画出设计示意图(包括一张卡纸可制作几个礼品盒,其展开图在卡纸上的分布情
况),给出所用卡纸的总费用.(要求:①同一型号 卡纸如果需要不止一张,只要在一张卡纸上画出设计方案;②没有用到的卡纸,不
要在该型号的卡纸上作任何设计;③所用卡纸的数量及总费用直接填在答题卡的表格上;④本题将综合考
虑“利用卡纸的合理性”和“所用卡纸的总费用”给分,总费用最低的才能得满分;⑤试卷上的卡纸仅供
作草稿用)
【答案】(1)2; (2)C;
(3)见解析.
【解析】
【分析】本题考查了几何体的展开与折叠,空间观念、推理能力、模型观念、创新意识等知识,掌握相关
知识是解题的关键.
(1)由折叠和题意可知, , ,四边形 是正方形,得到 ,
即 ,即可求解;
(2)根据几何体的展开图即可求解;
(3)由题意可得,每张型号 卡纸可制作10个正方体,每张型号 卡纸可制作2个正方体,每张型号
卡纸可制作1个正方体,即可求解.
【小问1详解】
解:如图:
上述图形折叠后变成:由折叠和题意可知, , ,
∵四边形 是正方形,
∴ ,即 ,
∴ ,即 ,
∵ ,
∴ ,
∴ 的值为: .
【小问2详解】
解:根据几何体的展开图可知,“吉”和“如”在对应面上,“祥”和“意”在对应面上,而对应面上的
字中间相隔一个几何图形,且字体相反,
∴C选项符合题意,
故选:C.
【小问3详解】
解:
卡纸型号 型号 型号 型号
需卡纸的数量(单位:张) 1 3 2
所用卡纸总费用(单位:元) 58
根据(1)和题意可得:卡纸每格的边长为 ,则要制作一个边长为 的正方体的展开图形为:
∴型号 卡纸,每张卡纸可制作10个正方体,如图:型号 卡纸,每张这样的卡纸可制作2个正方体,如图:
型号 卡纸,每张这样的卡纸可制作1个正方体,如图:
∴可选择型号 卡纸2张,型号 卡纸3张,型号 卡纸1张,则
(个),
∴所用卡纸总费用为:
(元).
25. 如图,在 中, ,以 为直径的 交 于点 , ,垂
足为 的延长线交 于点 .
(1)求 的值;
(2)求证: ;
(3)求证: 与 互相平分.【答案】(1)
(2)证明见解析 (3)证明见解析
【解析】
【分析】(1)先证得 ,再在 中, .在 中,
,可得 ,再证得结果;
(2)过点 作 ,交 延长线于点 ,先证明 ,可得
,再证得 ,再由相似三角形的判定可得结论;
( 3 ) 如 图 , 连 接 , 由 ( 2 ) , 可 得
, 从 而 得 出 , 从 而 得 出
, 得出 ,再上平行线判定得出 ,再证得 ,
从而得出四边形 是平行四边形,最后由平行四边形的性质可得结果.
【小问1详解】
,且 是 的直径,
.
,
在 中, .
,
在 中, .
,
;
【小问2详解】
过点 作 ,交 延长线于点 .
.,
,
.
,
,
,
, ,
.
,
,
,
.
【小问3详解】
如图,连接 .
是 的直径,
.
,
.
由(2)知, ,
,
,
.
.
,
.
由(2)知, ,
.,
,
,
四边形 是平行四边形,
与 互相平分.
【点睛】本小题考查等腰三角形及直角三角形的判定与性质、锐角三角函数、全等三角形的判定与性质、
相似三角形的判定与性质、平行线的判定与性质、平行四边形的判定与性质、圆的基本性质等基础知识,
考查推理能力、几何直观、运算能力、创新意识等,考查化归与转化思想等.