文档内容
二○二四年齐齐哈尔市初中学业考试
数学试卷
考生注意:
1.考试时间120分钟
2.全卷共三道大题,总分120分
3.使用答题卡的考生,请将答案填写在答题卡的指定位置
一、选择题(每小题只有一个正确答案,每小题3分,满分30分)
1. 实数 的相反数是( )
A. 5 B. C. D.
2. 下列美术字中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3. 下列计算正确的是( )
A. B.
C. D.
4. 将一个含 角的三角尺和直尺如图放置,若 ,则 的度数是( )
A. B. C. D.
5. 如图,若几何体是由5个棱长为1的小正方体组合而成的,则该几何体左视图与俯视图的面积和是(
)
1A. 6 B. 7 C. 8 D. 9·
6. 如果关于 的分式方程 的解是负数,那么实数 的取值范围是( )
A. 且 B. C. D. 且
7. 六月份,在“阳光大课间”活动中,某校设计了“篮球、足球、排球、羽毛球”四种球类运动项目,且
每名学生在一个大课间只能选择参加一种运动项目,则甲、乙两名学生在一个大课间参加同种球类运动项
目的概率是( )
A. B. C. D.
8. 校团委开展以“我爱读书”为主题的演讲比赛活动,为奖励表现突出的学生,计划拿出200元钱全部用
于购买单价分别为8元和10元的两种笔记本(两种都要购买)作为奖品,则购买方案有( )
A. 5种 B. 4种 C. 3种 D. 2种
9. 如图,在等腰 中, , ,动点E,F同时从点A出发,分别沿射线
和射线 的方向匀速运动,且速度大小相同,当点E停止运动时,点F也随之停止运动,连接 ,以
为边向下做正方形 ,设点E运动的路程为 ,正方形 和等腰
重合部分的面积为下列图像能反映y与x之间函数关系的是( )
2A. B. C. D.
10. 如图,二次函数 的图象与 轴交于 , ,其中 .结合图
象给出下列结论:
① ;② ;
③当 时, 随 的增大而减小;
④关于 的一元二次方程 的另一个根是 ;
⑤ 的取值范围为 .其中正确结论的个数是( )
A. B. C. D.
二、填空题(每小题3分,满分21分)
11. 共青团中央发布数据显示:截至2023年12月底,全国共有共青团员 万名.将 万用科学
记数法表示为______.
12. 如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴正半轴于点M,交y轴正半轴
于点N,再分别以点M,N为圆心,大于 的长为半径画弧,两弧在第一象限交于点H,画射线 ,
3若 ,则 ______.
13. 在函数 中,自变量 的取值范围是______.
14. 若圆锥的底面半径是1cm,它的侧面展开图的圆心角是直角,则该圆锥的高为______cm.
15. 如图,反比例函数 的图象经过平行四边形 的顶点 , 在 轴上,若点
, ,则实数 的值为______.
16. 已知矩形纸片 , , ,点P在边 上,连接 ,将 沿 所在的直线
折叠,点B的对应点为 ,把纸片展平,连接 , ,当 为直角三角形时,线段 的长为
______.
17. 如图,数学活动小组在用几何画板绘制几何图形时,发现了如“花朵”形的美丽图案,他们将等腰三
角形 OBC 置于平面直角坐标系中,点 O 的坐标为 ,点 B 的坐标为 ,点 C 在第一象限,
.将 沿x轴正方向作无滑动滚动,使它的三边依次与x轴重合,第一次滚动后,点
4O的对应点为 ,点C的对应点为 , 与 的交点为 ,称点 为第一个“花朵”的花心,点
为第二个“花朵”的花心;……;按此规律, 滚动2024次后停止滚动,则最后一个“花朵”的
花心的坐标为______.
三、解答题(本题共7道大题,共69分)
.
18 (1)计算:
(2)分解因式:
19. 解方程:x2﹣5x+6=0
20. 为提高学生的环保意识,某校举行了“爱护环境,人人有责”环保知识竞赛,对收集到的数据进行了
整理、描述和分析.
【收集数据】随机抽取部分学生的竞赛成绩组成一个样本.
【整理数据】将学生竞赛成绩的样本数据分成 四组进行整理.
(满分 分,所有竞赛成绩均不低于 分)如下表:
组别
成绩(
/分)
人数
(人)
【描述数据】根据竞赛成绩绘制了如下两幅不完整的统计图.
【分析数据】根据以上信息,解答下列问题:
5(1)填空: ______, ______;
(2)请补全条形统计图;
(3)扇形统计图中, 组对应的圆心角的度数是______ ;
(4)若竞赛成绩 分以上(含 分)为优秀,请你估计该校参加竞赛的 名学生中成绩为优秀的人数.
的
21. 如图, 内接于 , 为 直径, 于点D,将 沿 所在的直线翻折,
得到 ,点D的对应点为E,延长 交 的延长线于点F.
(1)求证: 是 的切线;
(2)若 , ,求图中阴影部分的面积.
22. 领航无人机表演团队进行无人机表演训练,甲无人机以a米/秒的速度从地面起飞,乙无人机从距离地
面20米高的楼顶起飞,甲、乙两架无人机同时匀速上升,6秒时甲无人机到达训练计划指定的高度停止上
升开始表演,完成表演动作后,按原速继续飞行上升,当甲、乙无人机按照训练计划准时到达距离地面的
高度为96米时,进行了时长为t秒的联合表演,表演完成后以相同的速度大小同时返回地面.甲、乙两架
无人机所在的位置距离地面的高度y(米)与无人机飞行的时间x(秒)之间的函数关系如图所示.请结合图象
解答下列问题:
(1) ______米/秒, ______秒;
6(2)求线段 所在直线的函数解析式;
(3)两架无人机表演训练到多少秒时,它们距离地面的高度差为12米?(直接写出答案即可)
23. 综合与实践:如图1,这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为
“赵爽弦图”,受这幅图的启发,数学兴趣小组建立了“一线三直角模型”.如图2,在 中,
,将线段 绕点 顺时针旋转 得到线段 ,作 交 的延长线于点 .
的
(1)【观察感知】如图2,通过观察,线段 与 数量关系是______;
(2)【问题解决】如图3,连接 并延长交 的延长线于点 ,若 , ,求 的
面积;
(3)【类比迁移】在(2)的条件下,连接 交 于点 ,则 ______;
(4)【拓展延伸】在(2)的条件下,在直线 上找点 ,使 ,请直接写出线段 的长
度.
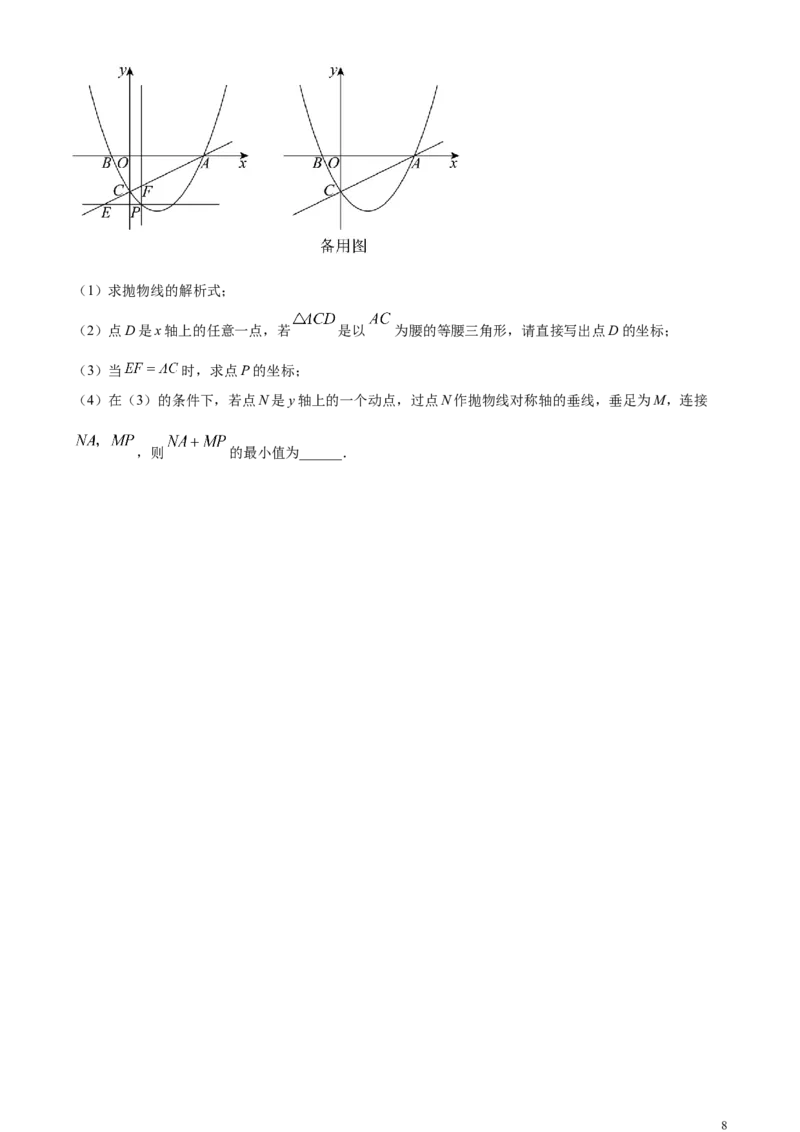
24. 综合与探究:如图,在平面直角坐标系中,已知直线 与x轴交于点A,与y轴交于点C,过
A,C两点的抛物线 与x轴的另一个交点为点 ,点P是抛物线位于第四象
限图象上的动点,过点P分别作x轴和y轴的平行线,分别交直线 于点E,点F.
7(1)求抛物线的解析式;
(2)点D是x轴上的任意一点,若 是以 为腰的等腰三角形,请直接写出点D的坐标;
(3)当 时,求点P的坐标;
(4)在(3)的条件下,若点N是y轴上的一个动点,过点N作抛物线对称轴的垂线,垂足为M,连接
,则 的最小值为______.
8