附件资料分析计算公式整理_26吉林考备考资料包_04行测资料包（笔记图推导图等）_34资料分析必备公式

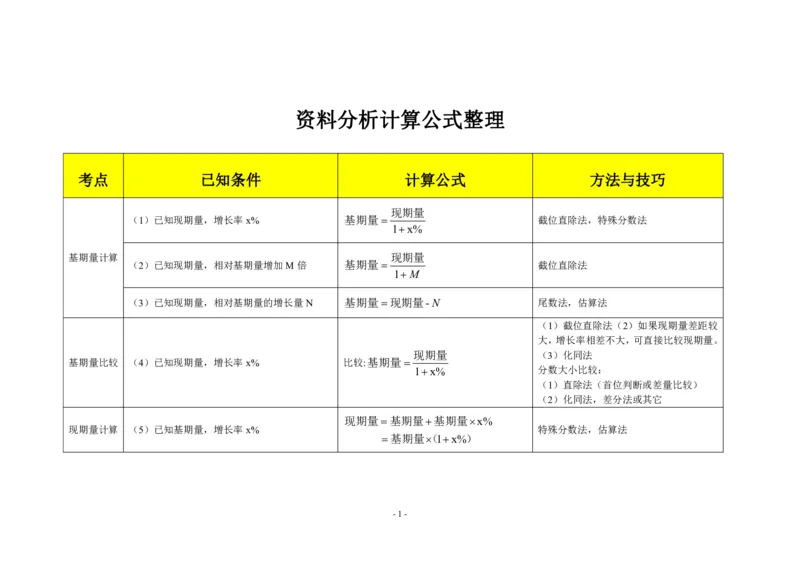
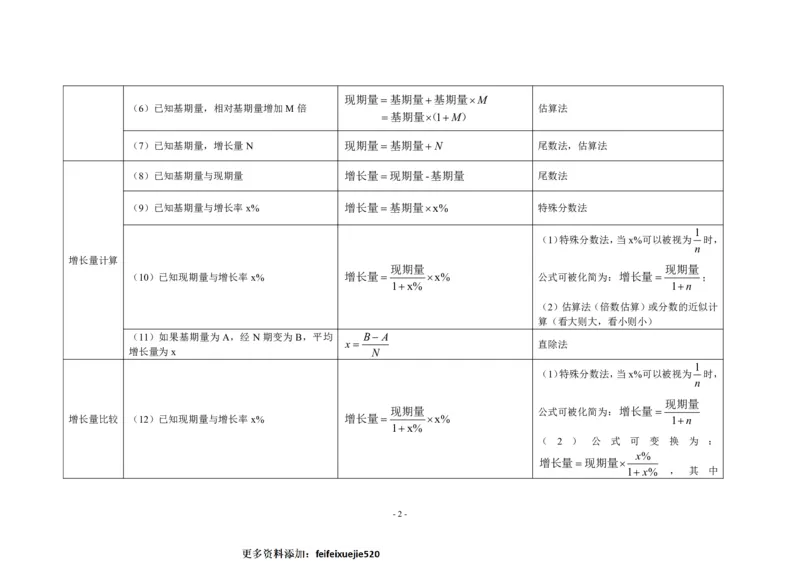
资料分析计算公式整理 考点 已知条件 计算公式 方法与技巧 现期量 （1）已知现期量，增长率x% 基期量 截位直除法，特殊分数法 1x% 基期量计算 现期量 （2）已知现期量，相对基期量增加M倍 基期量 截位直除法 1M （3）已知现期量，相对基期量的增长量N 基期量现期量-N 尾数法，估算法 （1）截位直除法（2）如果现期量差距较 大，增长率相差不大，可直接比较现期量。 现期量 （3）化同法 基期量比较 （4）已知现期量，增长率x% 比较:基期量 1x% 分数大小比较： （1）直除法（首位判断或差量比较） （2）化同法，差分法或其它 现期量基期量基期量x% 现期量计算 （5）已知基期量，增长率x% 特殊分数法，估算法 基期量（1x%） -1-现期量基期量基期量M （6）已知基期量，相对基期量增加M倍 估算法 基期量（1M） （7）已知基期量，增长量N 现期量基期量 N 尾数法，估算法 （8）已知基期量与现期量 增长量现期量-基期量 尾数法 （9）已知基期量与增长率x% 增长量基期量x% 特殊分数法 1 （1）特殊分数法，当x%可以被视为 时， n 增长量计算 现期量 现期量 （10）已知现期量与增长率x% 增长量 x% 公式可被化简为：增长量 ； 1x% 1n （2）估算法（倍数估算）或分数的近似计 算（看大则大，看小则小） （11）如果基期量为A，经N期变为B，平均 B A x 直除法 增长量为x N 1 （1）特殊分数法，当x%可以被视为 时， n 现期量 现期量 公式可被化简为：增长量 增长量比较 （12）已知现期量与增长率x% 增长量 x% 1n 1x% （ 2 ） 公 式 可 变 换 为 ： x% 增长量现期量 1x% ， 其 中 -2-x% 为增函数，所以现期量大，增长率 1x% 大的情况下，增长量一定大。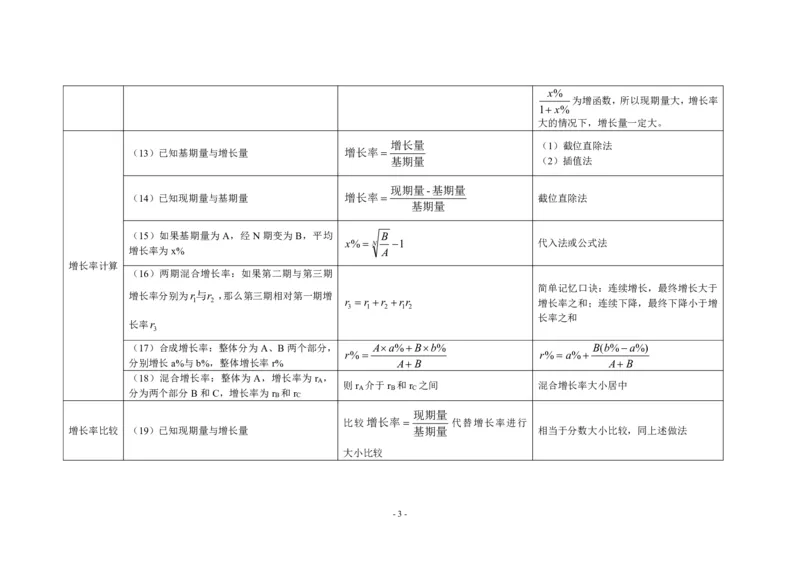 增长量 （1）截位直除法 （13）已知基期量与增长量 增长率 基期量 （2）插值法 现期量-基期量 （14）已知现期量与基期量 增长率 截位直除法 基期量 （15）如果基期量为A，经N期变为B，平均 B x% N 1 代入法或公式法 增长率为x% A 增长率计算 （16）两期混合增长率：如果第二期与第三期 简单记忆口诀：连续增长，最终增长大于 增长率分别为r与r ，那么第三期相对第一期增 1 2 r r r rr 增长率之和；连续下降，最终下降小于增 3 1 2 1 2 长率之和 长率r 3 （17）合成增长率：整体分为A、B两个部分， Aa%Bb% B(b%a%) r% r%a% 分别增长a%与b%，整体增长率r% AB AB （18）混合增长率：整体为A，增长率为r ， A 则r 介于r 和r 之间 混合增长率大小居中 分为两个部分B和C，增长率为r 和r A B C B C 现期量 比较增长率  代替增长率进行 增长率比较 （19）已知现期量与增长量 基期量 相当于分数大小比较，同上述做法 大小比较 -3-现期量 （1）截位直除法 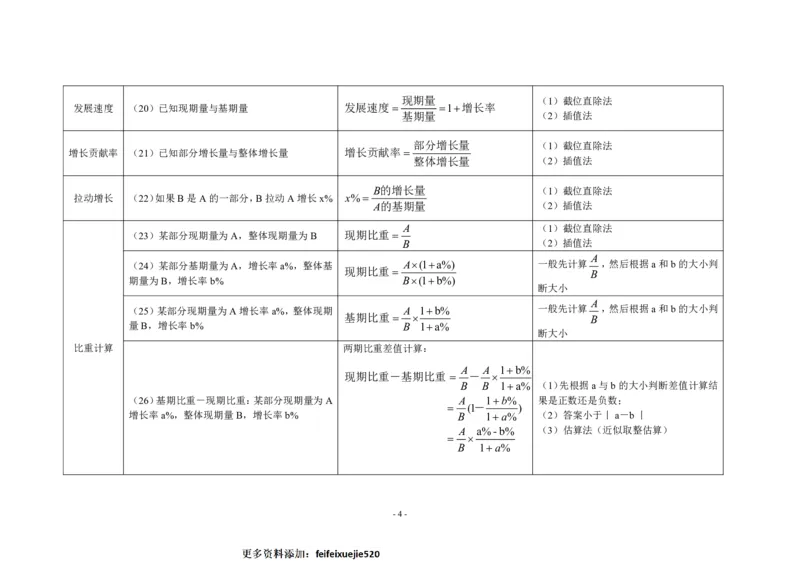发展速度 （20）已知现期量与基期量 发展速度 1增长率 基期量 （2）插值法 部分增长量 （1）截位直除法 增长贡献率 （21）已知部分增长量与整体增长量 增长贡献率  整体增长量 （2）插值法 B的增长量 （1）截位直除法 拉动增长 （22）如果B是A的一部分，B拉动A增长x% x% A的基期量 （2）插值法 A （1）截位直除法 （23）某部分现期量为A，整体现期量为B 现期比重 B （2）插值法 A （24）某部分基期量为A，增长率a%，整体基 A(1a%) 一般先计算 ，然后根据a和b的大小判 现期比重 B 期量为B，增长率b% B(1b%) 断大小 A （25）某部分现期量为A增长率a%，整体现期 A 1b% 一般先计算 ，然后根据a和b的大小判 基期比重  B 量B，增长率b% B 1a% 断大小 比重计算 两期比重差值计算： A A 1b% 现期比重－基期比重  －  B B 1a% （1）先根据a与b的大小判断差值计算结 （26）基期比重－现期比重：某部分现期量为A A 1b% 果是正数还是负数；  (1－ ) 增长率a%，整体现期量B，增长率b% B 1a% （2）答案小于丨a－b丨 A a%-b% （3）估算法（近似取整估算）   B 1a% -4-A （27）某部分现期量为A，整体现期量为B 现期比重 相当于分数大小比较，同上述做法 B 比重比较 （28）基期比重与现期比重比较：某部分现期 A(1b%) 当部分增长率大于整体增长率，则现期比 量为A，增长率a%，整体现期量为B，增长率 基期比重  B(1a%) 重大于基期比重。（方法为“看”增长率） b% n n n 平均数计算 （29）已知N个量的值，求平均数 平均数 1 2 N 凑整法 N （30）方法：读题做标记，辅助工具（直尺） 直接读数类 （31）四项基本原则：题干短原则，不计算原 综合分析题 则（时间与材料时间一致），信息易得原则，简 单计算原则 -5-