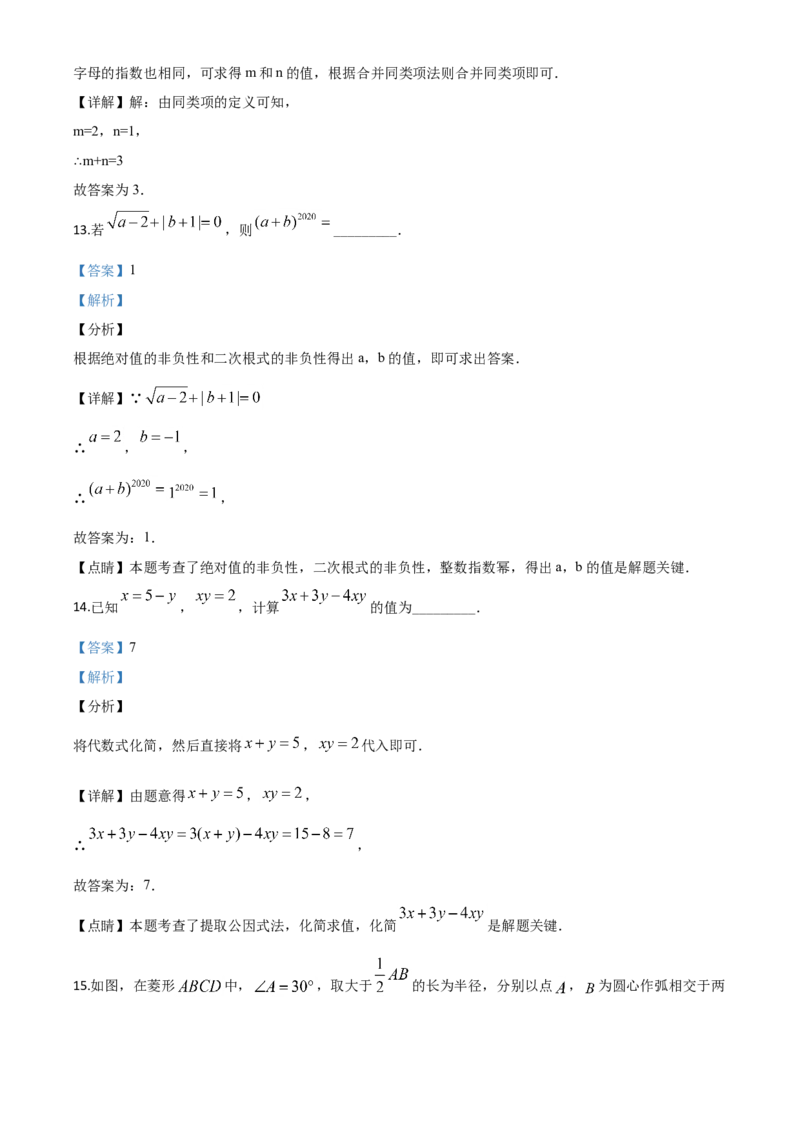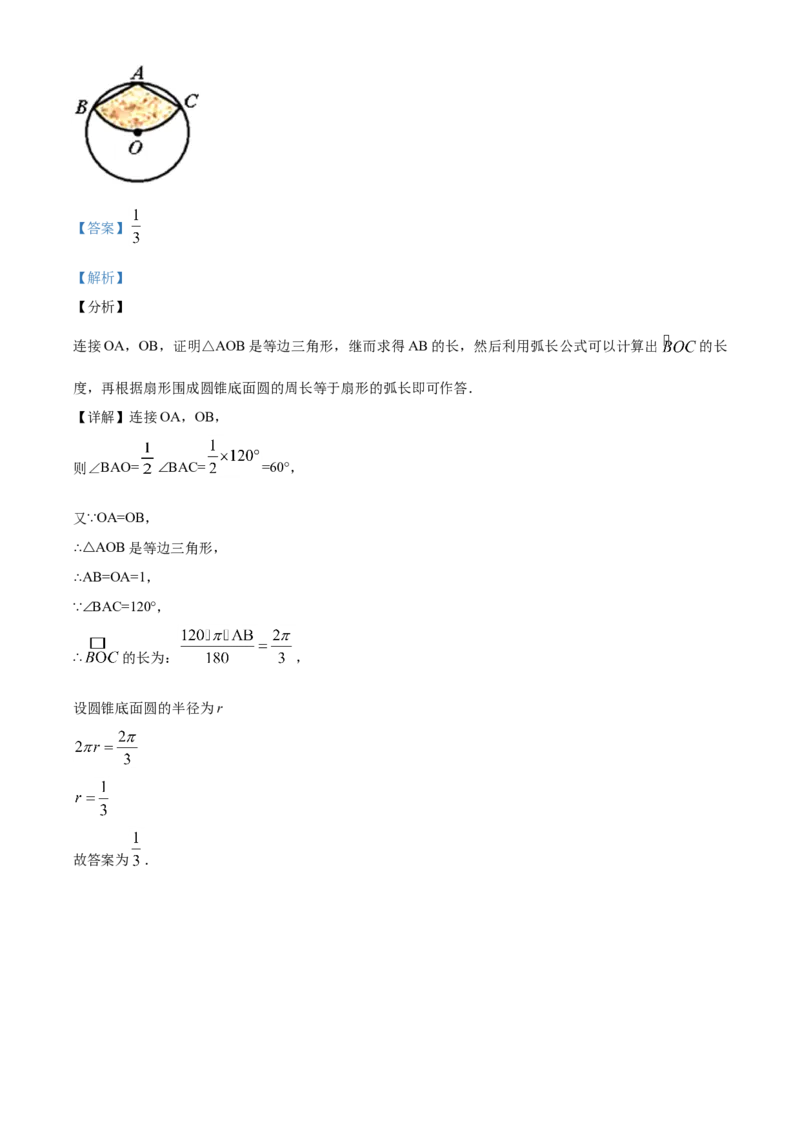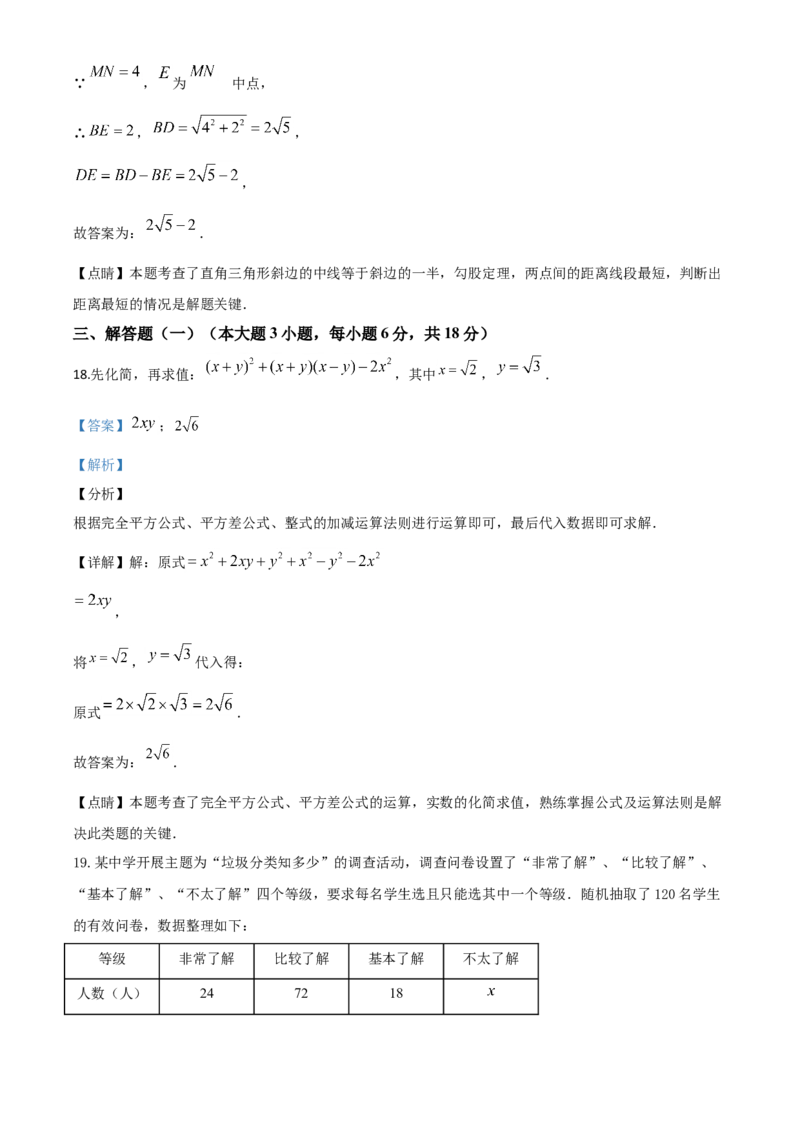文档内容
2020 年广东省初中学业水平考试
数学
一、选择题(本大题10小题,每小題3分,共30分)在每小题列出的四个选项中,只有一
个是正确的,请把答题卡上对应题目所选的选项涂黑.
1.9的相反数是( )
A. B. C. D.
【答案】B
【解析】
根据相反数的定义:“只有符号不同的两个数互为相反数”可知,9的相反数是-9.
故选B.
2.一组数据2,4,3,5,2的中位数是( )
A. 5 B. 35 C. 3 D. 25
【答案】C
【解析】
【分析】
把这组数据从小到大的顺序排列,取最中间位置的数就是中位数.
【详解】把这组数据从小到大的顺序排列:2,2,3,4,5,处于最中间位置的数是3,
∴这组数据的中位数是3,
故选:C.
【点睛】本题考查了求中位数,熟练掌握中位数的求法是解答的关键.
3.在平面直角坐标系中,点 关于 轴对称的点的坐标为( )
A. B. C. D.
【答案】D
【解析】
【分析】
利用关于x轴对称的点坐标特征:横坐标不变,纵坐标互为相反数解答即可.
【详解】点 关于 轴对称的点的坐标为(3,-2),
故选:D.【点睛】本题主要考查了关于坐标轴对称的点的坐标特征,熟练掌握关于坐标轴对称的点的坐标特征是解
答的关键.
4.若一个多边形的内角和是540°,则该多边形的边数为( )
A. 4 B. 5 C. 6 D. 7
【答案】B
【解析】
【分析】
根据内角和公式即可求解.
【详解】设这个多边形的边数为n,
∴(n-2)×180°=540°
解得n=5
故选B.
【点睛】此题主要考查多边形的内角和,解题的关键是熟知内角和公式.
5.若式子 在实数范围内有意义,则 的取值范围是( )
A. B. C. D.
【答案】B
【解析】
【分析】
根据二次根式里面被开方数 即可求解.
【详解】解:由题意知:被开方数 ,
解得: ,
故选:B.
【点睛】本题考查了二次根式有意义的条件,必须保证被开方数大于等于0.
6.已知 的周长为16,点 , , 分别为 三条边的中点,则 的周长为( )
A. 8 B. C. 16 D. 4
【答案】A
【解析】
【分析】
由 , , 分别为 三条边的中点,可知DE、EF、DF为 的中位线,即可得到 的周长.
【详解】解:如图,
∵ , , 分别为 三条边的中点,
∴ , , ,
∵ ,
∴ ,
故选:A.
【点睛】本题考查了三角形的中位线,熟练掌握三角形的中位线平行于第三边且是第三边的一半是解题的
关键.
7.把函数 的图象向右平移1个单位长度,平移后图象的函数解析式为( )
A. B.
C. D.
【答案】C
【解析】
【分析】
抛物线在平移时开口方向不变,a不变,根据图象平移的口诀“左加右减、上加下减”即可解答.
【详解】把函数 的图象向右平移1个单位长度,平移后图象的函数解析式为
,
故选:C.
【点睛】本题考查了二次函数图象与几何变换,解答的重点在于熟练掌握图象平移时函数表达式的变化特点.
8.不等式组 的解集为( )
A. 无解 B. C. D.
【答案】D
【解析】
【分析】
分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定
不等式组的解集.
【详解】解:解不等式2−3x≥−1,得:x≤1,
解不等式x−1≥−2(x+2),得:x≥−1,
则不等式组的解集为−1≤x≤1,
故选:D.
【点睛】本题考查 的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小
取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
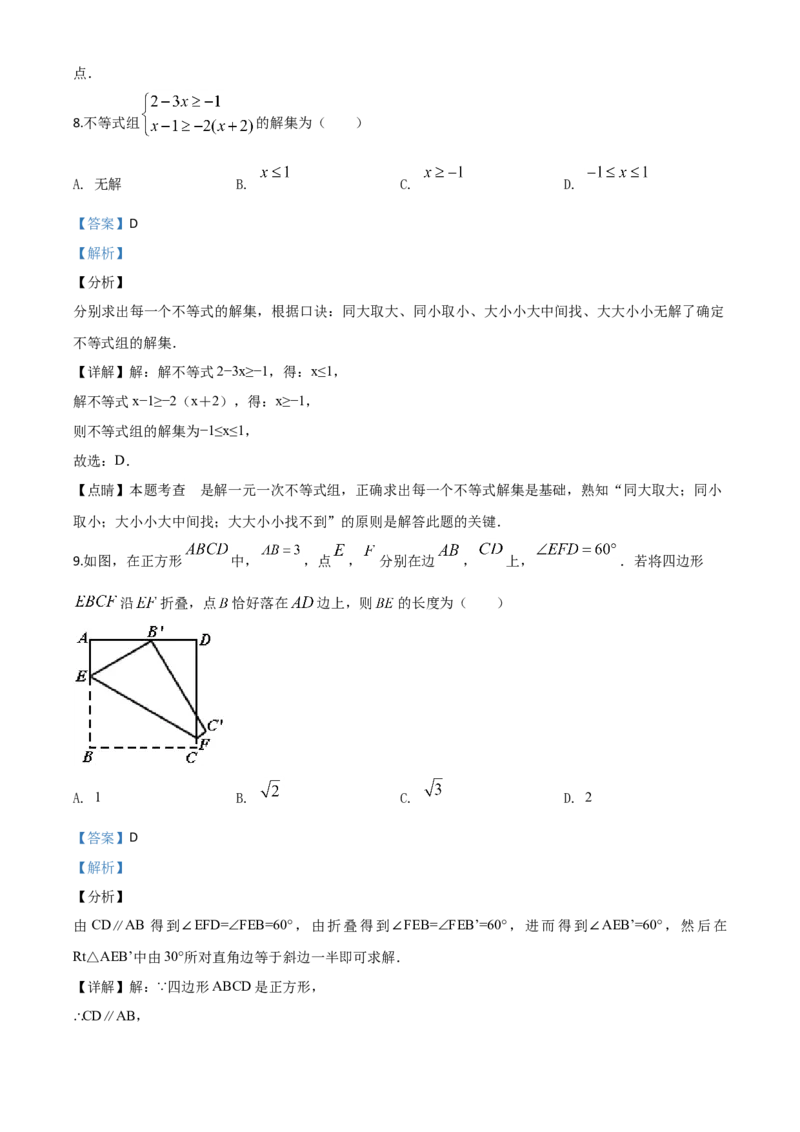
9.如图,在正方形 中, ,点 , 分别在边 , 上, .若将四边形
沿 折叠,点 恰好落在 边上,则 的长度为( )
A. 1 B. C. D. 2
【答案】D
【解析】
【分析】
由 CD∥AB 得到∠EFD=∠FEB=60°,由折叠得到∠FEB=∠FEB’=60°,进而得到∠AEB’=60°,然后在
Rt△AEB’中由30°所对直角边等于斜边一半即可求解.
【详解】解:∵四边形ABCD是正方形,
∴CD∥AB,∴∠EFD=∠FEB=60°,
由折叠前后对应角相等可知:∠FEB=∠FEB’=60°,
∴∠AEB’=180°-∠FEB-∠FEB’=60°,
∴∠AB’E=30°,
设AE=x,则BE=B’E=2x,
∴AB=AE+BE=3x=3,
∴x=1,
∴BE=2x=2,
故选:D.
的
【点睛】本题借助正方形考查了折叠问题,30°角所对直角边等于斜边 一半等知识点,折叠问题的性质包
括折叠前后对应边相等,对应角相等,折叠产生角平分线,由此即可解题.
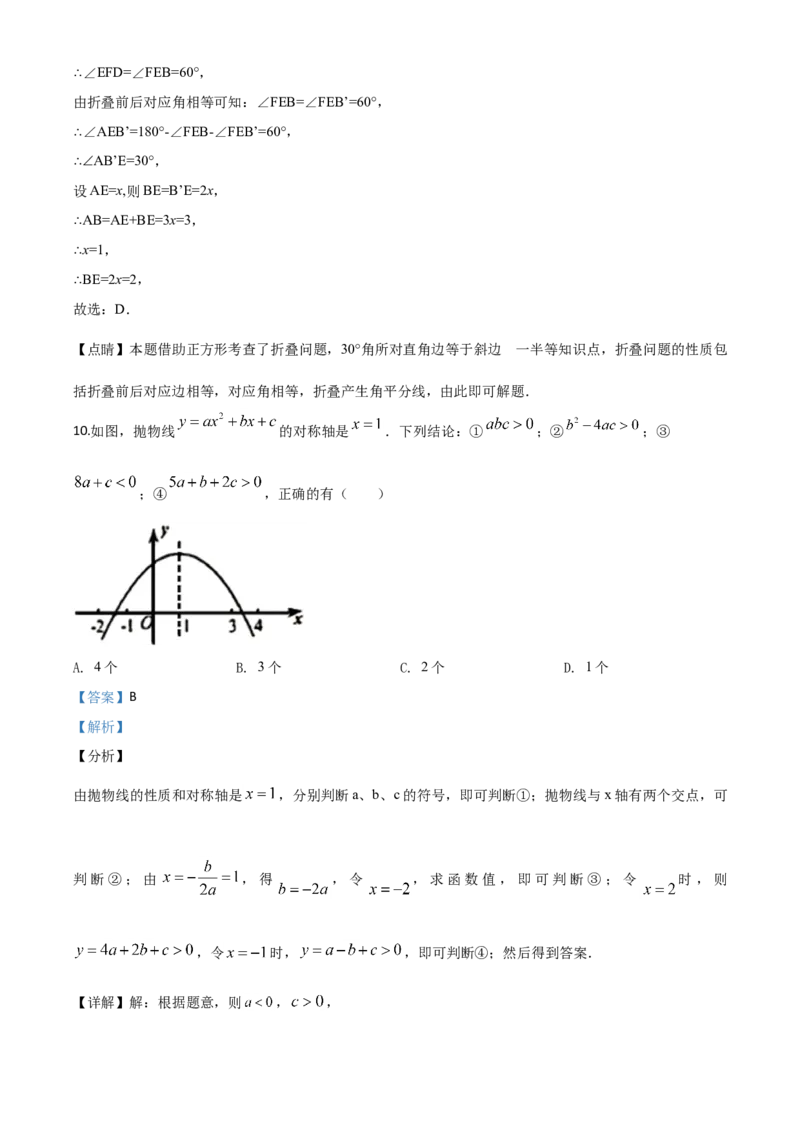
10.如图,抛物线 的对称轴是 .下列结论:① ;② ;③
;④ ,正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
【答案】B
【解析】
【分析】
由抛物线的性质和对称轴是 ,分别判断a、b、c的符号,即可判断①;抛物线与x轴有两个交点,可
判断②;由 ,得 ,令 ,求函数值,即可判断③;令 时,则
,令 时, ,即可判断④;然后得到答案.
【详解】解:根据题意,则 , ,∵ ,
∴ ,
∴ ,故①错误;
由抛物线与x轴有两个交点,则 ,故②正确;
∵ ,
令 时, ,
∴ ,故③正确;
在 中,
令 时,则 ,
令 时, ,
由两式相加,得 ,故④正确;
∴正确的结论有:②③④,共3个;
故选:B.
【点睛】本题考查了二次函数的图像和性质,解题的关键是熟练掌握二次函数的性质,熟练判断各个式子
的符号.
二、填空题(本大题7小題,每小题4分,共28分)请将下列各题的正确答案填写在答题卡
相应的位置上.
11.分解因式:xy―x=_____________.
【答案】x(y-1)
【解析】
试题解析:xy―x=x(y-1)
12.若 与 是同类项,则 ___________.
【答案】3
【解析】
【分析】
本题考查同类项的定义,所含字母相同且相同字母的指数也相同的项是同类项,根据同类项的定义中相同字母的指数也相同,可求得m和n的值,根据合并同类项法则合并同类项即可.
【详解】解:由同类项的定义可知,
m=2,n=1,
∴m+n=3
故答案为3.
13.若 ,则 _________.
【答案】1
【解析】
【分析】
根据绝对值的非负性和二次根式的非负性得出a,b的值,即可求出答案.
【详解】∵
∴ , ,
∴ ,
故答案为:1.
【点睛】本题考查了绝对值的非负性,二次根式的非负性,整数指数幂,得出a,b的值是解题关键.
14.已知 , ,计算 的值为_________.
【答案】7
【解析】
【分析】
将代数式化简,然后直接将 , 代入即可.
【详解】由题意得 , ,
∴ ,
故答案为:7.
【点睛】本题考查了提取公因式法,化简求值,化简 是解题关键.
15.如图,在菱形 中, ,取大于 的长为半径,分别以点 , 为圆心作弧相交于两点,过此两点的直线交 边于点 (作图痕迹如图所示),连接 , ,则 的度数为
_________.
【答案】45°
【解析】
【分析】
根据题意知虚线为线段 AB 的垂直平分线,得 AE=BE,得 ;结合 °,
,可计算 的度数.
【详解】
∵
∴
∴
故答案为:45°.
【点睛】本题考查了菱形的性质,及垂直平分线的性质,熟知以上知识点是解题的关键.
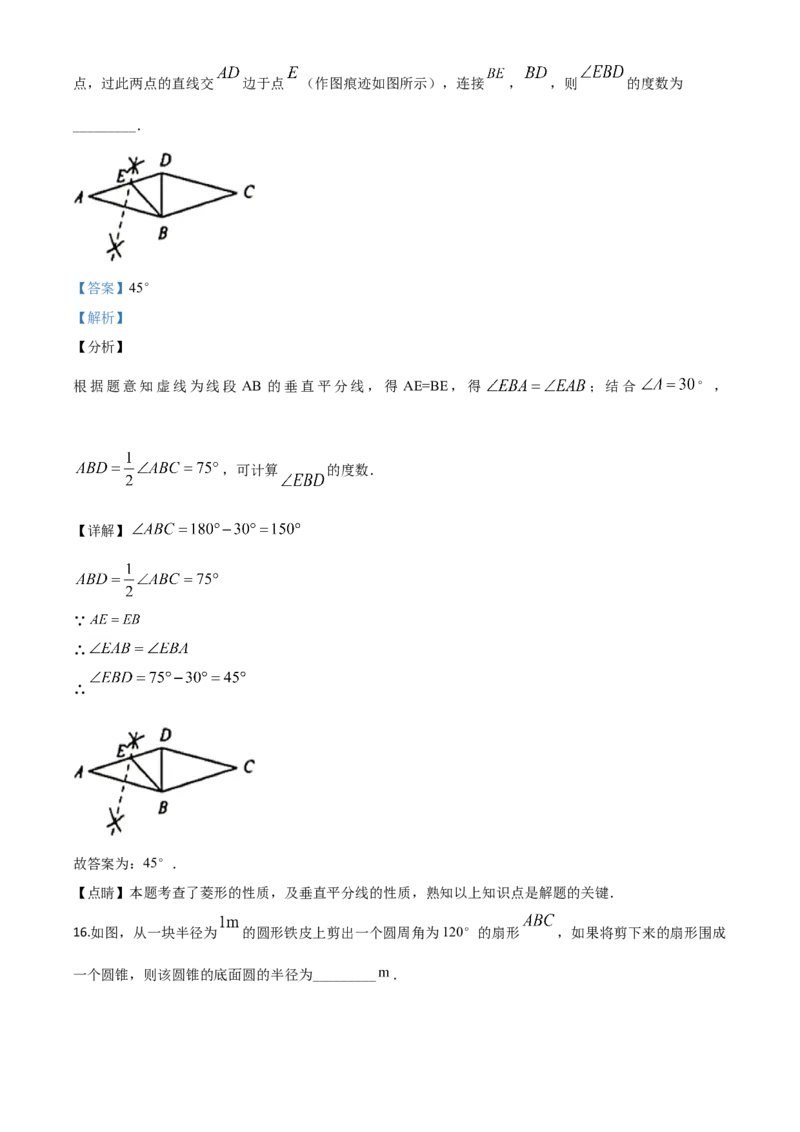
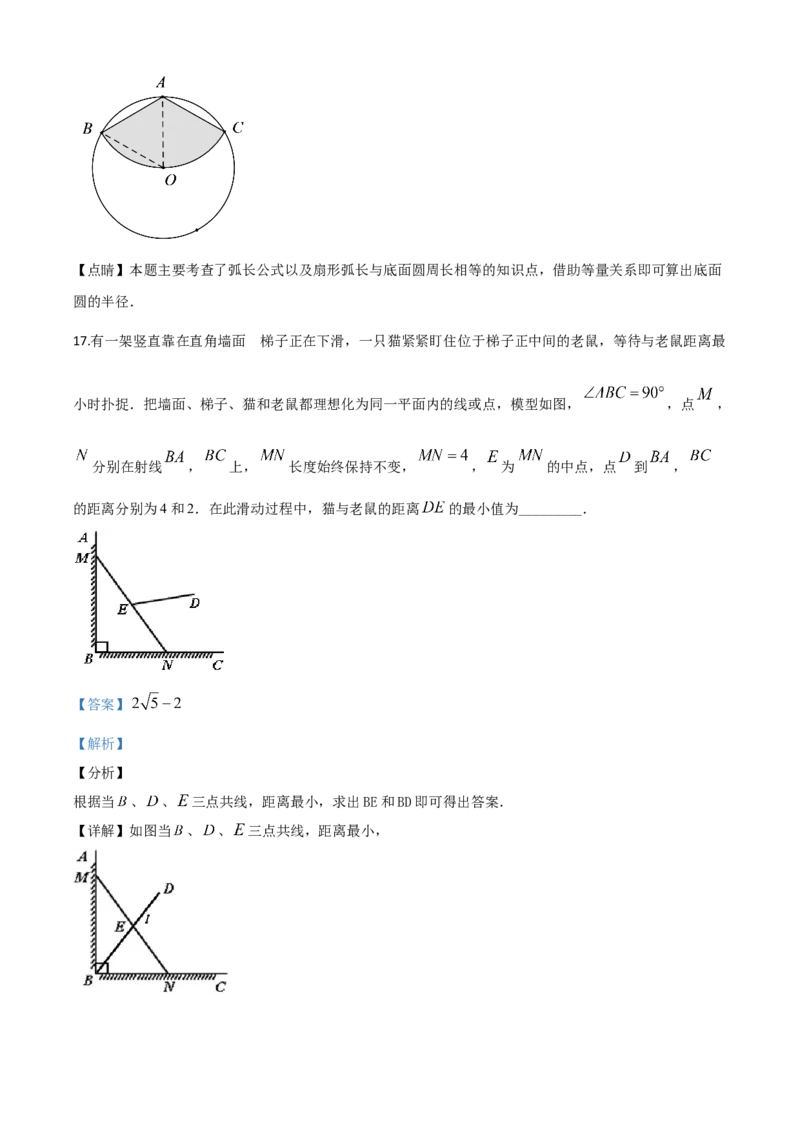
16.如图,从一块半径为 的圆形铁皮上剪出一个圆周角为120°的扇形 ,如果将剪下来的扇形围成
一个圆锥,则该圆锥的底面圆的半径为_________ .【答案】
【解析】
【分析】
连接OA,OB,证明△AOB是等边三角形,继而求得AB的长,然后利用弧长公式可以计算出 的长
度,再根据扇形围成圆锥底面圆的周长等于扇形的弧长即可作答.
【详解】连接OA,OB,
则∠BAO= ∠BAC= =60°,
又∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=1,
∵∠BAC=120°,
∴ 的长为: ,
设圆锥底面圆的半径为r
故答案为 .【点睛】本题主要考查了弧长公式以及扇形弧长与底面圆周长相等的知识点,借助等量关系即可算出底面
圆的半径.
的
17.有一架竖直靠在直角墙面 梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最
小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图, ,点 ,
分别在射线 , 上, 长度始终保持不变, , 为 的中点,点 到 ,
的距离分别为4和2.在此滑动过程中,猫与老鼠的距离 的最小值为_________.
【答案】
【解析】
【分析】
根据当 、 、 三点共线,距离最小,求出BE和BD即可得出答案.
【详解】如图当 、 、 三点共线,距离最小,的
∵ , 为 中点,
∴ , ,
,
故答案为: .
【点睛】本题考查了直角三角形斜边的中线等于斜边的一半,勾股定理,两点间的距离线段最短,判断出
距离最短的情况是解题关键.
三、解答题(一)(本大题3小题,每小题6分,共18分)
18.先化简,再求值: ,其中 , .
【答案】 ;
【解析】
【分析】
根据完全平方公式、平方差公式、整式的加减运算法则进行运算即可,最后代入数据即可求解.
【详解】解:原式
,
将 , 代入得:
原式 .
故答案为: .
【点睛】本题考查了完全平方公式、平方差公式的运算,实数的化简求值,熟练掌握公式及运算法则是解
决此类题的关键.
19.某中学开展主题为“垃圾分类知多少”的调查活动,调查问卷设置了“非常了解”、“比较了解”、
“基本了解”、“不太了解”四个等级,要求每名学生选且只能选其中一个等级.随机抽取了120名学生
的有效问卷,数据整理如下:
等级 非常了解 比较了解 基本了解 不太了解
人数(人) 24 72 18(1)求 的值;
(2)若该校有学生1800人,请根据抽样调查结果估算该校“非常了解”和“比较了解”垃圾分类知识的
学生共有多少人?
【答案】(1)6 (2)1440人
【解析】
【分析】
(1)根据四个等级的人数之和为120求出x的值;
(2)用总人数乘以样本中“非常了解”和“比较了解”垃圾分类知识的学生占被调查人数的比例即可求出结果.
【详解】(1)解:由题意得:
解得
(2)解: (人)
答:估算“非常了解”和“比较了解”垃圾分类知识的学生有1440人.
【点睛】本题主要考查了用样本估计总体,属于基础题目,审清题意,找到对应数据是解题的关键.
20.如图,在 中,点 , 分别是 、 边上的点, , , 与
相交于点 ,求证: 是等腰三角形.
【答案】见解析
【解析】
【分析】
先证明 ,得到 , ,进而得到 ,故可求解.
【详解】证明:在 和 中∴
∴
∴
又∵
∴
即
∴ 是等腰三角形.
【点睛】此题主要考查等腰三角形的判定,解题的关键是熟知全等三角形的判定与性质.
四、解答题(二)(本大题3小题,每小题8分,共24分)
21.已知关于 , 的方程组 与 的解相同.
(1)求 , 的值;
(2)若一个三角形的一条边的长为 ,另外两条边的长是关于 的方程 的解.试判断该
三角形的形状,并说明理由.
【答案】(1) ; (2)等腰直角三角形,理由见解析
【解析】
【分析】
(1)关于x,y的方程组 与 的解相同.实际就是方程组
的解,可求出方程组的解,进而确定a、b的值;(2)将a、b的值代入关于x的方程x2+ax+b=0,求出方程的解,再根据方程的两个解与 为边长,
判断三角形的形状.
【详解】解:由题意列方程组:
解得
将 , 分别代入 和
解得 ,
∴ ,
(2)
解得
这个三角形是等腰直角三角形
理由如下:∵
∴该三角形是等腰直角三角形.
【点睛】本题考查一次方程组、一元二次方程的解法以及等腰直角三角形的判定,掌握一元二次方程的解
法和勾股定理是得出正确答案的关键.
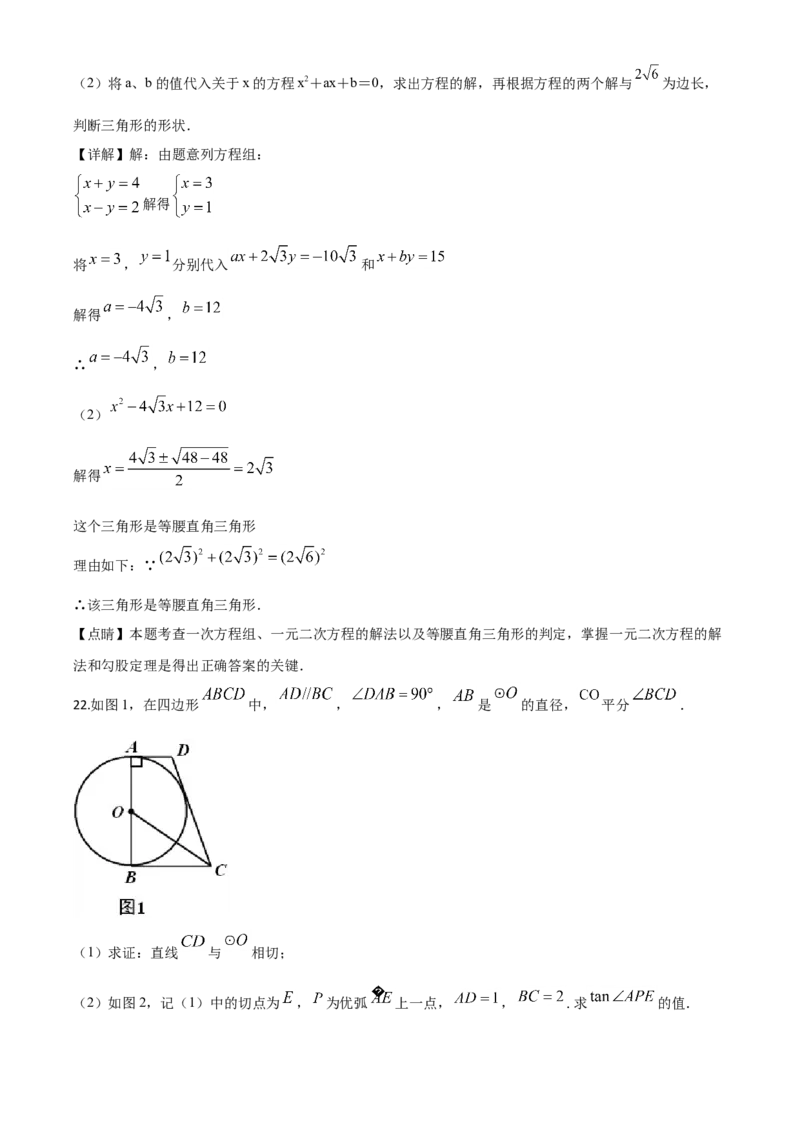
22.如图1,在四边形 中, , , 是 的直径, 平分 .
(1)求证:直线 与 相切;
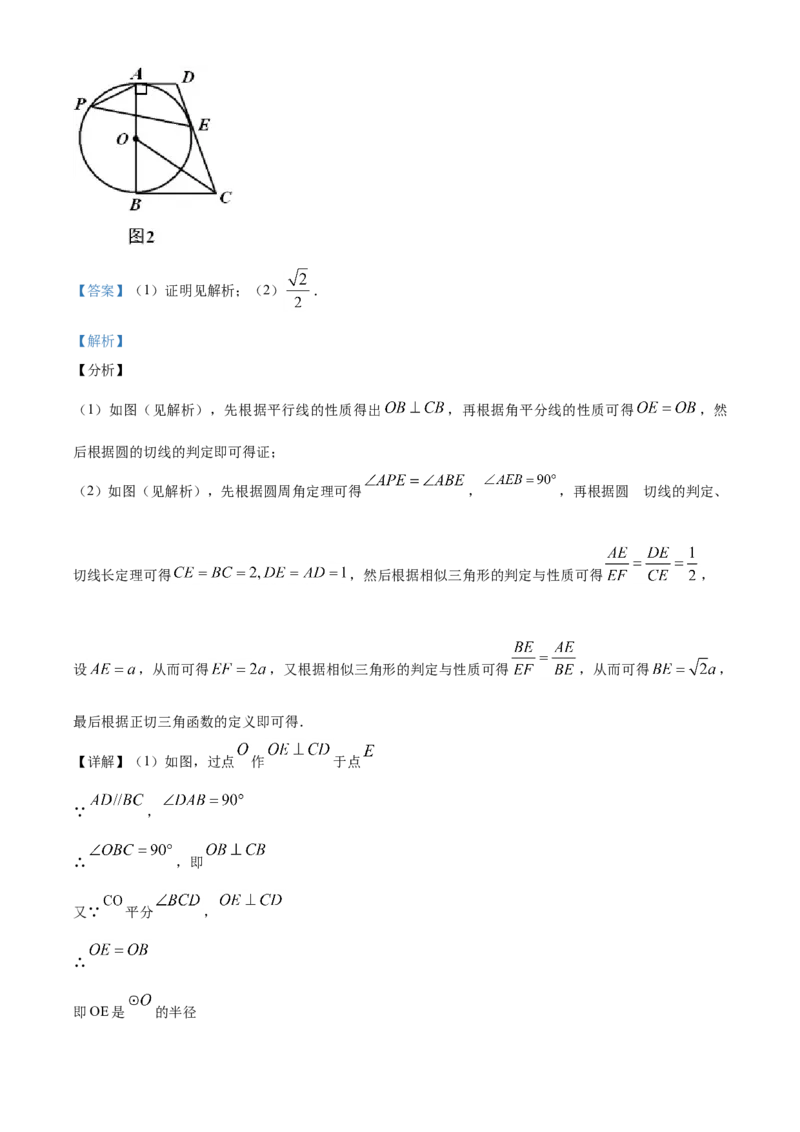
(2)如图2,记(1)中的切点为 , 为优弧 上一点, , .求 的值.【答案】(1)证明见解析;(2) .
【解析】
【分析】
(1)如图(见解析),先根据平行线的性质得出 ,再根据角平分线的性质可得 ,然
后根据圆的切线的判定即可得证;
的
(2)如图(见解析),先根据圆周角定理可得 , ,再根据圆 切线的判定、
切线长定理可得 ,然后根据相似三角形的判定与性质可得 ,
设 ,从而可得 ,又根据相似三角形的判定与性质可得 ,从而可得 ,
最后根据正切三角函数的定义即可得.
【详解】(1)如图,过点 作 于点
∵ ,
∴ ,即
又∵ 平分 ,
∴
即OE是 的半径∴直线 与 相切;
(2)如图,连接 ,延长 交 延长线于点
由圆周角定理得: ,
是 的直径, ,
AD、BC都是 的切线
由切线长定理得:
∵
∴
在 和 中,
∴
∴
设 ,则
在 和 中,,即
解得
在 中,
则 .
【点睛】本题考查了圆的切线的判定与性质、圆周角定理、切线长定理、相似三角形的判定与性质、正切
三角函数等知识点,较难的是题(2),通过作辅助线,构造相似三角形是解题关键.
23.某社区拟建 , 两类摊位以搞活“地摊经济”,每个 类摊位的占地面积比每个 类摊位的占地面
积多2平方米,建 类摊位每平方米的费用为40元,建 类摊位每平方米的费用为30元,用60平方米建
类摊位的个数恰好是用同样面积建 类摊位个数的 .
(1)求每个 , 类摊位占地面积各为多少平方米?
(2)该社拟建 , 两类摊位共90个,且 类摊位的数量不少于 类摊位数量的3倍.求建造这90个摊
位的最大费用.
【答案】(1)5平方米;3平方米 (2)10520元
【解析】
【分析】
(1)设 类摊位占地面积 平方米,则 类占地面积 平方米,根据同等面积建立A类和B类的倍
数关系列式即可;(2)设建 类摊位 个,则 类 个,设费用为 ,由(1)得A类和B类摊位的建设费用,列出
总费用的表达式,根据一次函数的性质进行讨论即可.
【详解】解:(1)设每个 类摊位占地面积 平方米,则 类占地面积 平方米
由题意得
解得 ,
∴ ,经检验 为分式方程的解
∴每个 类摊位占地面积5平方米, 类占地面积3平方米
(2)设建 类摊位 个,则 类 个,费用为
∵
∴
,
∵110>0,
∴z随着a的增大而增大,
又∵a为整数,
∴当 时z有最大值,此时
∴建造90个摊位的最大费用为10520元
【点睛】本题考查了一次函数的实际应用问题,熟练的掌握各个量之间的关系进行列式计算,是解题的关
键.
五、解答题(三)(本大题2小题,每小题10分,共20分)
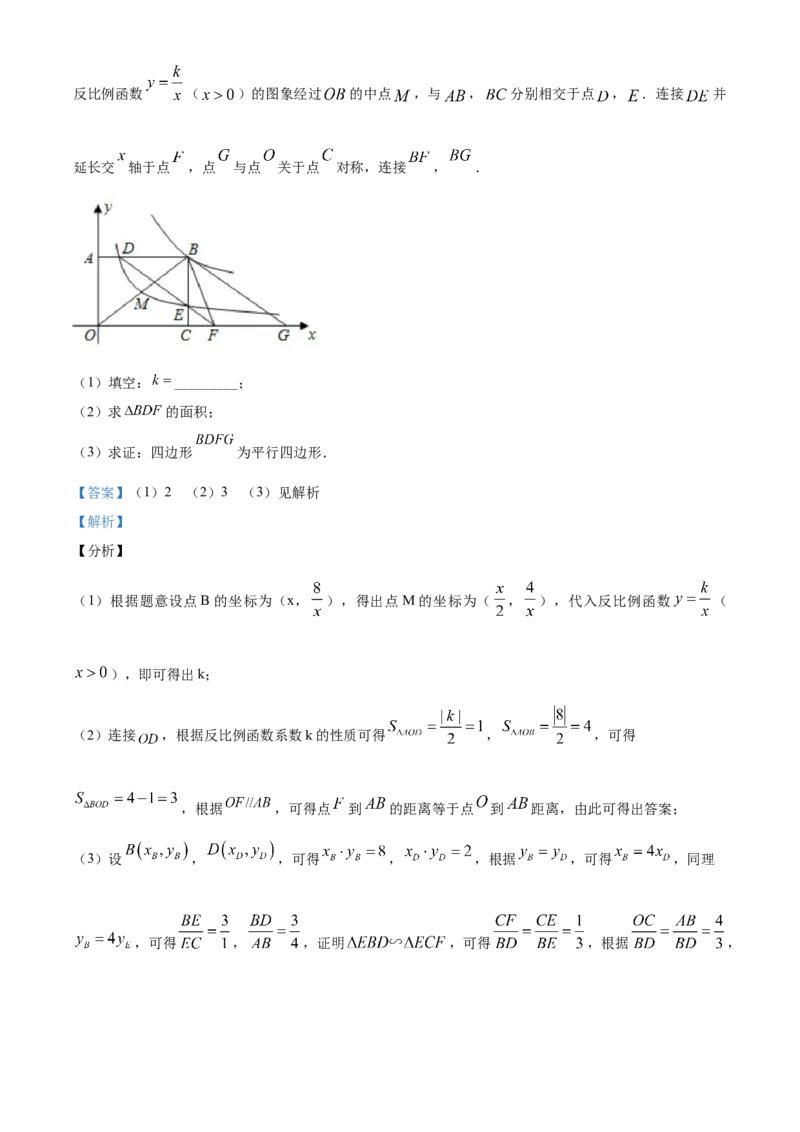
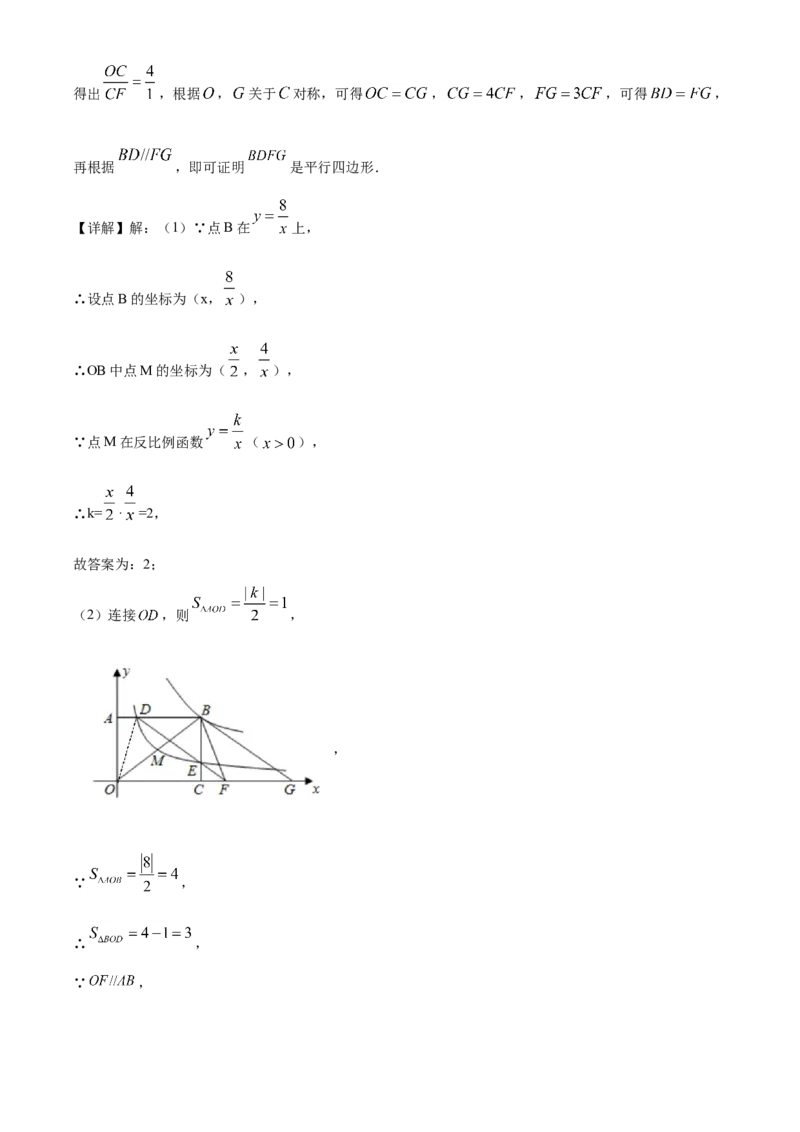
24.如图,点 是反比例函数 ( )图象上一点,过点 分别向坐标轴作垂线,垂足为 , ,反比例函数 ( )的图象经过 的中点 ,与 , 分别相交于点 , .连接 并
延长交 轴于点 ,点 与点 关于点 对称,连接 , .
(1)填空: _________;
(2)求 的面积;
(3)求证:四边形 为平行四边形.
【答案】(1)2 (2)3 (3)见解析
【解析】
【分析】
(1)根据题意设点B的坐标为(x, ),得出点M的坐标为( , ),代入反比例函数 (
),即可得出k;
(2)连接 ,根据反比例函数系数k的性质可得 , ,可得
,根据 ,可得点 到 的距离等于点 到 距离,由此可得出答案;
(3)设 , ,可得 , ,根据 ,可得 ,同理
,可得 , ,证明 ,可得 ,根据 ,得出 ,根据 , 关于 对称,可得 , , ,可得 ,
再根据 ,即可证明 是平行四边形.
【详解】解:(1)∵点B在 上,
∴设点B的坐标为(x, ),
∴OB中点M的坐标为( , ),
∵点M在反比例函数 ( ),
∴k= · =2,
故答案为:2;
(2)连接 ,则 ,
,
∵ ,
∴ ,
∵ ,∴点 到 的距离等于点 到 距离,
∴ ;
(3)设 , ,
, ,
又∵ ,
∴ ,
同理 ,
∴ , ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ , 关于 对称,
∴ ,
∴ ,
∴ ,
又∵ ,∴ ,
又∵ ,
∴ 是平行四边形.
【点睛】本题考查了反比例函数系数的性质,相似三角形的判定和性质,平行四边形的判定,平行线的性
质,灵活运用知识点是解题关键.
25.如图,抛物线 与 轴交于 , 两点,点 , 分别位于原点的左、右两侧,
,过点 的直线与 轴正半轴和抛物线的交点分别为 , , .
(1)求 , 的值;
(2)求直线 的函数解析式;
(3)点 在抛物线的对称轴上且在 轴下方,点 在射线 上,当 与 相似时,请直接写
出所有满足条件的点 的坐标.
【答案】(1) ; (2) (3) , ,
,
【解析】
【分析】(1)根据 ,得出 , ,将A,B代入 得出关于b,c
的二元一次方程组求解即可;
(2)根据二次函数是 , , ,得出 的横坐标
为 ,代入抛物线解析式求出 ,设 得解析式为: ,将B,D代入求解即
可;
(3)由题意得tan∠ABD= ,tan∠ADB=1,由题意得抛物线的对称轴为直线x=1,设对称轴与x轴交
点为M,P(1,n)且n<0,Q(x,0)且x<3,分①当△PBQ∽△ABD时,②当△PQB∽△ABD时,③当
△PQB∽△DAB时,④当△PQB∽△ABD时四种情况讨论即可.
【详解】解:(1)∵ ,
∴ , ,
∴将A,B代入 得 ,
解得 ,
∴ , ;
(2)∵二次函数是 , , ,
∴ 的横坐标为 ,代入抛物线解析式得
∴ ,
设 得解析式为:
将B,D代入得 ,
解得 ,
∴直线 的解析式为 ;
(3)由题意得tan∠ABD= ,tan∠ADB=1,
由题意得抛物线的对称轴为直线x=1,设对称轴与x轴交点为M,P(1,n)且n<0,Q(x,0)且x<3,
①当△PBQ∽△ABD时,tan∠PBQ=tan∠ABD即 = ,
解得n= ,
tan∠PQB=tan∠ADB即 ,
解得x=1- ,此时Q的坐标为(1- ,0);
②当△PQB∽△ABD时,tan∠PBQ=tan∠ADB即 =1,
解得n=-2,
tan∠QPB=tan∠ABD即 = ,
解得x=1- ,
此时Q的坐标为(1- ,0);
③当△PQB∽△DAB时,tan∠PBQ=tan∠ABD即 = ,
解得n= ,
tan∠PQM=tan∠DAE即 ,
解得x= -1,
此时Q的坐标为( -1,0);
④当△PQB∽△ABD时,tan∠PBQ=tan∠ABD即 =1,
解得n=-2,
tan∠PQM=tan∠DAE即 ,
解得x=5- ,
Q的坐标为(5- ,0);综上:Q的坐标可能为 , , , .
【点睛】本题考查了二次函数,一次函数,相似三角形的判定和性质,锐角三角函数,掌握知识点灵活运
用是解题关键.本试卷的题干、答案和解析均由组卷网(http://zujuan.xkw.com)专业教师团队编校出品。
登录组卷网可对本试卷进行单题组卷、细目表分析、布置作业、举一反三等操作。
试卷地址:在组卷网浏览本卷
组卷网是学科网旗下的在线题库平台,覆盖小初高全学段全学科、超过900万精品解析试题。
关注组卷网服务号,可使用移动教学助手功能(布置作业、线上考试、加入错题本、错题训练)。
学科网长期征集全国最新统考试卷、名校试卷、原创题,赢取丰厚稿酬,欢迎合作。
钱老师 QQ:537008204 曹老师 QQ:713000635