文档内容
专题 06 任意角和弧度制、三角函数的概念、诱导公式
(4 种经典基础练+3 种优选提升练)
任意角(共10题)
一、单选题
1.(23-24高一上·江苏盐城·期末)若角 的终边与角 的终边关于 轴对称,则 的终边落在
( )
A. 轴的非负半轴 B.第一象限
C. 轴的非负半轴 D.第三象限
【答案】A
【知识点】轴线角、找出终边相同的角
【分析】由对称可知 ,得终边所在位置.
【详解】角 的终边与角 的终边关于 轴对称,则角 的终边与角 的终边相同,
得 ,则有 ,
所以 的终边落在 轴的非负半轴.
故选:A.
2.(23-24高一上·山东枣庄·期末)已知集合 钝角 , 第二象限角 , 小于 的
角 ,则( )
A. B.
C. D.
【答案】C
学科网(北京)股份有限公司【知识点】由已知角所在的象限确定某角的范围、判断两个集合的包含关系
【分析】根据钝角的范围,即可得出选项C正确,再由第二象限角的范围
,即可判断出选项ABD的正误,从而得出结果.
【详解】因为钝角大于 ,且小于 的角,一定是第二象限角,所以 ,故选项C正确,
又第二象限角的范围为 ,
不妨取 ,此时 是第二象限角,但 ,所以选项ABD均错误,
故选:C.
3.(23-24高一上·河北唐山·期末)已知 ,则 是( )
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
【答案】C
【知识点】确定已知角所在象限
【分析】 ,再根据终边相同的角的集合,判断 是第几象限角,即可求
出结果.
【详解】因为 ,又 是第三象限角,
所以 是第三象限角,
故选:C.
4.(23-24高一上·内蒙古·期末)若角 与角 的终边相同,则 可能是( )
A. B. C. D.
【答案】D
【知识点】找出终边相同的角
【分析】根据 观察选项得答案.
【详解】由已知
观察选项可得只有 ,所以 可能是 .
故选:D.
5.(22-23高一上·广东深圳·期末)概念是数学的重要组成部分,理清新旧概念之间的关系对学习
学科网(北京)股份有限公司数学十分重要.现有如下三个集合, {钝角}, {第二象限角}, {小于180°的角},则下列
说法正确的是( )
A. B. C. D.
【答案】C
【知识点】由已知角所在的象限确定某角的范围、确定已知角所在象限、判断两个集合的包含关系
【分析】利用钝角和第二象限角的定义即可判断.
【详解】钝角是大于 ,且小于 的角,一定是第二象限角,故 ;
第二象限角的范围是 ,即第二象限角不一定小于 ,
故ABD错误,C正确;
故选:C
二、多选题
6.(23-24高一上·湖北·期末)下列说法中正确的是( )
A.若函数 是R上的奇函数,则
B.函数 与 为同一个函数
C.命题“ , ”的否定是“ , ”
D.若 是第二象限角,则 是第一象限角
【答案】ABC
【知识点】全称命题的否定及其真假判断、判断两个函数是否相等、函数奇偶性的应用、确定n分
角所在象限
【分析】由奇函数的性质可判断A;根据函数的三要素是否相同判断B;根据含有一个量词的命题
的否定判断C;根据 的范围,可写出 的取值范围,即可判断D.
【详解】对于A,函数 是R上的奇函数,则有 ,故正确;
对于B,因为 定义域为R,且 ,
学科网(北京)股份有限公司的定义域为R,二者定义域相同,对应关系相同,值域均为 ,
所以 与 是同一函数,故正确;
对于C:命题“ , ”为全称量词命题,
则其否定为存在量词命题:“ , ”,正确;
对于D:由题知 是第二象限角,即 , ,
∴ , ,即 是第一或第三象限角,D不正确.
故选:ABC
7.(23-24高一上·湖南株洲·期末)下列各命题中正确的是( )
A. 与 ( 且 )互为反函数
B.函数 的定义域为
C.已知 为第一象限的角,则 是第一、三象限的角
D.时针转过4小时,则时针转过的弧度数为
【答案】AC
【知识点】确定n分角所在象限、任意角的概念、反函数的性质应用、具体函数的定义域
【分析】利用反函数的定义判断A;利用偶次根式被开方数大于等于0列不等式求解判断B;利用
象限角的范围列不等式求 的范围判断C,利用正负角的意义判断D.
【详解】对于A, 与 ( 且 )互为反函数,正确;
对于B,要使函数 有意义,则 ,解得 ,
所以函数 的定义域为 ,错误;
对于C,若 是第一象限角,则 ,得 ,
学科网(北京)股份有限公司为偶数时, 是第一象限角; 为奇数时, 是第三象限角,正确;
对于D,钟表的时针是顺时针旋转,所以经过4小时,时针转过的弧度数为 ,错误.
故选:AC
三、填空题
8.(23-24高一上·浙江台州·期末) 角是第 象限角.
【答案】二
【知识点】确定已知角所在象限
【分析】直接由象限角的概念得答案.
【详解】由象限角的定义可知, 的角是第二象限角.
故答案为:二.
9.(23-24高一上·天津河西·期末)已知角 ,则角 的终边落在第 象限.
【答案】三
【知识点】确定已知角所在象限、找出终边相同的角
【分析】
根据终边相同的角的表示,将 化为 ,即可判断答案.
【详解】由题意得 ,
由于 的终边在第三象限内,故角 的终边落在第三象限内,
故答案为:三
10.(22-23高一上·上海浦东新·期末)已知 ,若将角 的终边顺时针旋转 ,所得的角
的终边与角 的终边重合.则角 .
【答案】
【知识点】找出终边相同的角
【分析】角 的终边顺时针旋转 得到 ,根据终边相同的角的关系列出方程,根据
学科网(北京)股份有限公司求得 的值.
【详解】角 的终边顺时针旋转 得到 ,它与 边重合,所以 ,
所以 ,
又 ,所以只能令 , .
故答案为:
弧度制(共16题)
一、单选题
1.(23-24高一上·广东·期末)要在半径 厘米的圆形金属板上截取一块扇形板 ,使其
弧 的长为120厘米,则圆心角 ( )
A. B. C. D.
【答案】B
【知识点】弧度的概念
【分析】根据角弧度制的定义,可得答案.
【详解】设扇形弧长为 ,圆心角为 ,半径为 ,则 .
故选:B.
2.(23-24高一上·贵州六盘水·期末)达-芬奇的经典之作《蒙娜丽莎》举世闻名,画中女子神秘的
微笑,数百年来引无数观赏者对其进行研究.某业余爱好者对《蒙娜丽莎》的缩小影像作品进行粗
略测绘,将画中女子的嘴唇近似看作一段圆弧,并测得圆弧 所对的圆心角 为 ,弦 的
长为 ,根据测量得到的数据计算:《蒙娜丽莎》缩小影像作品中圆弧 的长为( )(单
位: )
学科网(北京)股份有限公司A. B. C. D.
【答案】C
【知识点】弧长的有关计算
【分析】根据扇形弧长公式 代入求解即可.
【详解】因为圆弧 所对的圆心角 ,所以 为等边三角形,
如图所示:
所以 ,即圆弧的半径 ,
所以圆弧 的长为 .
故选:C
3.(23-24高一上·安徽安庆·期末)第19届亚运会于2023年9月23日至10月8日在浙江省杭州市
举行,本届亚运会会徽“潮涌”的主体图形由扇面、钱塘江、钱江潮头、赛道、互联网符号及象征
亚奥理事会的太阳图形六个元素组成,其中扇面造型反映江南人文意蕴.已知扇面呈扇环形,内环
半径为1,外环半径为3,扇环所对圆心角为 ,则该扇面的面积为( )
学科网(北京)股份有限公司A. B. C. D.
【答案】B
【知识点】扇形面积的有关计算
【分析】根据给定条件,利用扇形面积公式计算即得.
【详解】依题意,该扇面的面积为 .
故选:B
4.(23-24高一上·福建龙岩·期末)已知扇形的周长为 ,圆心角为 ,则此扇形的面积是
( )
A. B. C. D.
【答案】B
【知识点】扇形面积的有关计算、扇形弧长公式与面积公式的应用
【分析】首先求出扇形的半径,再由面积公式计算可得.
【详解】设扇形的半径为 ,因为扇形的圆心角 ,扇形的周长为 ,
则 ,解得 ,
所以此扇形的面积 .
故选:B
5.(23-24高一上·山西·期末)已知扇形的圆心角为 ,半径为4,则扇形的弧长为( )
A. B.2 C.4 D.8
【答案】D
【知识点】弧长的有关计算
【分析】根据扇形弧长公式计算可得.
【详解】因为扇形的圆心角为 ,半径为4,
学科网(北京)股份有限公司所以由弧长公式得扇形的弧长为 .
故选:D
6.(23-24高一上·山东德州·期末)中国传统扇文化有着极其深厚的底蕴,一般情况下,折扇可看
作是从一个圆面中剪下的扇形制作而成;一个半径为 的扇形,它的周长是 ,则这个扇形所含
弓形的面积是( )
A. B. C. D.
【答案】C
【知识点】扇形弧长公式与面积公式的应用
【分析】通过扇形的周长,求出扇形的弧长,求出扇形的圆心角,然后求出扇形的面积,三角形的
面积,即可得到这个扇形所含弓形的面积.
【详解】
可得:扇形面积 ,
三角形面积 ,
可得弓形面积 ,
故选:C
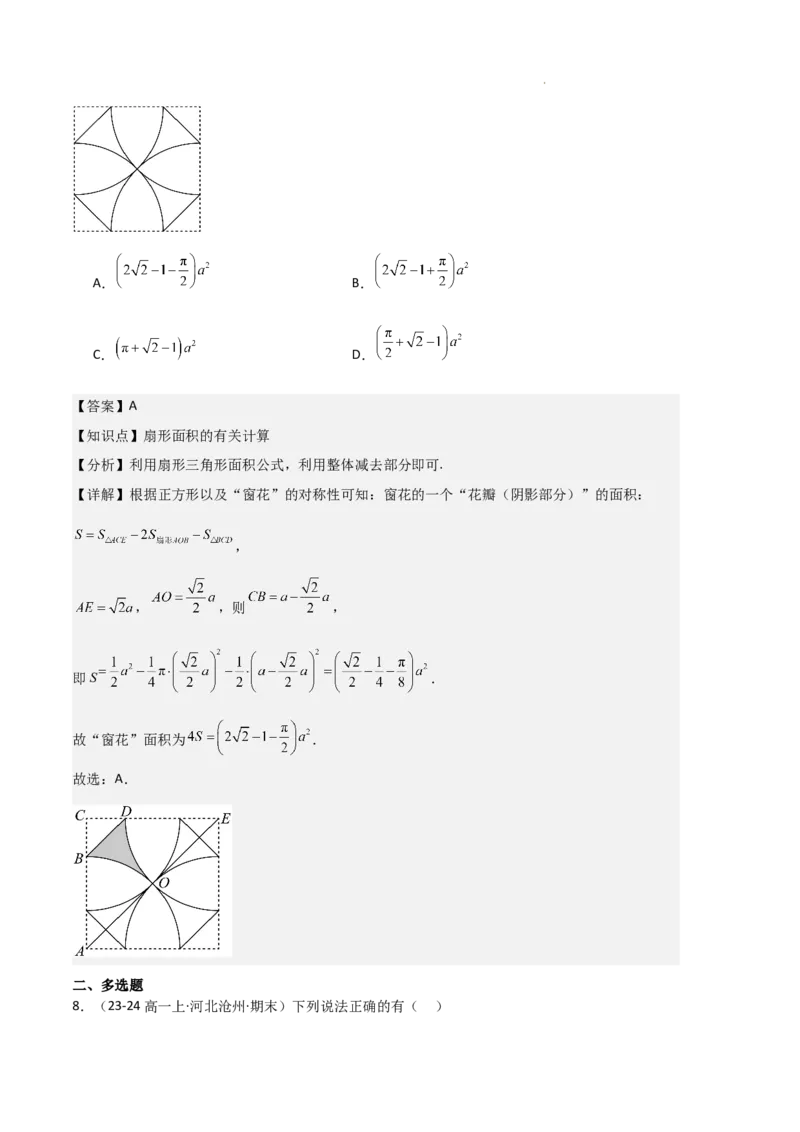
7.(23-24高一上·云南昆明·期末)窗花是贴在窗纸或窗户玻璃上的剪纸是中国古老的传统民间艺
术之一,它历史悠久,风格独特,深受国内外人士所喜爱.窗花是农耕文化的特色艺术,农村生活
的地理环境,农业生产特征以及社会的习俗方式,也使这种乡土艺术具有了鲜明的中国民俗情趣和
艺术特色.如图所示的四叶形窗花是由一些圆弧构成的旋转对称图形,若设外围虚线正方形的边长
为a,则窗花的面积为( )
学科网(北京)股份有限公司A. B.
C. D.
【答案】A
【知识点】扇形面积的有关计算
【分析】利用扇形三角形面积公式,利用整体减去部分即可.
【详解】根据正方形以及“窗花”的对称性可知:窗花的一个“花瓣(阴影部分)”的面积:
,
, ,则 ,
即S .
故“窗花”面积为 .
故选:A.
二、多选题
8.(23-24高一上·河北沧州·期末)下列说法正确的有( )
学科网(北京)股份有限公司A.若一个扇形弧长的值与面积的值都是5,则这个扇形圆心角的大小是
B.已知 ,则
C.函数 在其定义域上单调递减
D.若幂函数 的图象过点 ,则
【答案】AB
【知识点】对数的运算性质的应用、求幂函数的解析式、扇形面积的有关计算、根据解析式直接判
断函数的单调性
【分析】利用扇形的面积和弧长公式,计算圆心角判断选项A;由指数式与对数式的互化和对数式
的运算规则求值,判断选项B;由反比例函数的单调性判断选项C;由幂函数的定义判断选项D.
【详解】对于A,设这个扇形的圆心角为 ,半径为r,
其弧长的值与面积的值都是5, , ,解得 ,故A选项正确;
对于B, , , ,则 ,故B选项
正确;
对于C, , 其定义域为 ,
由反比例函数的单调性可知, 在 和 上都单调递减,但在定义域上不是单调递减
的,故C选项不正确;
对于D,幂函数 的图象过点 ,则有 ,
解得 ,故D选项不正确.
故选:AB.
9.(23-24高一上·吉林长春·期末)中国传统扇文化有着极其深厚的底蕴,一般情况下,折扇可看
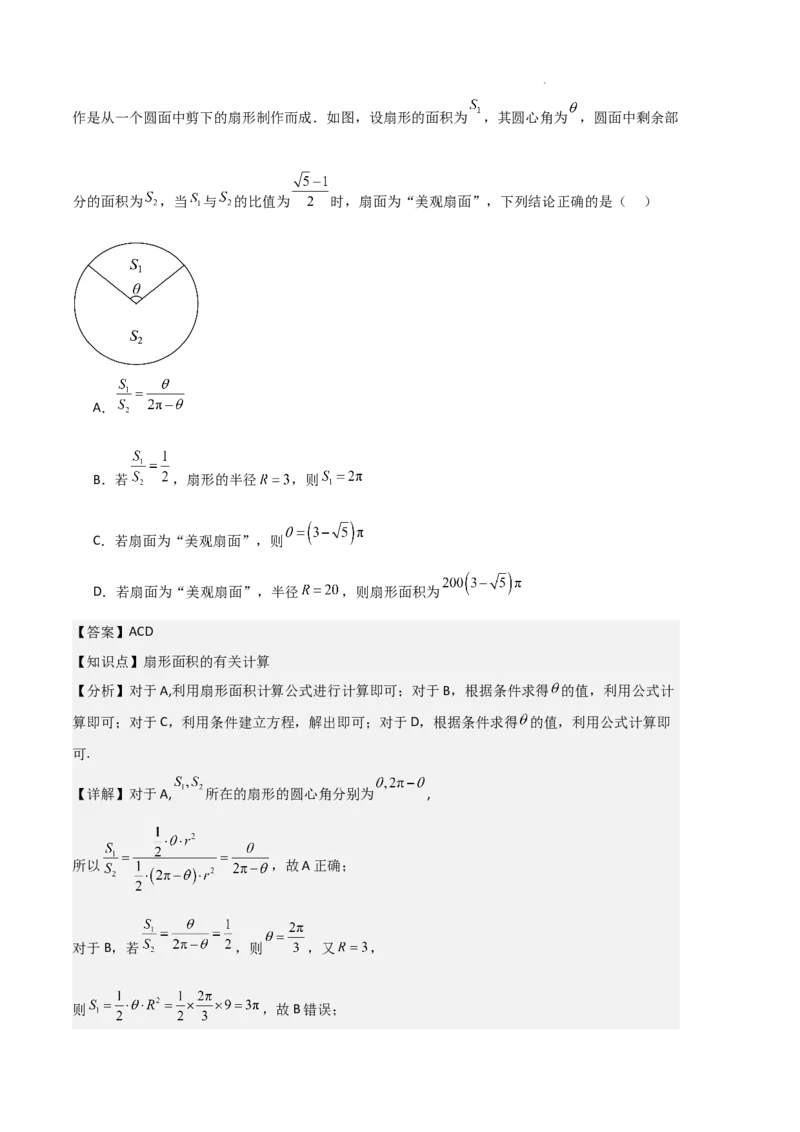
学科网(北京)股份有限公司作是从一个圆面中剪下的扇形制作而成.如图,设扇形的面积为 ,其圆心角为 ,圆面中剩余部
分的面积为 ,当 与 的比值为 时,扇面为“美观扇面”,下列结论正确的是( )
A.
B.若 ,扇形的半径 ,则
C.若扇面为“美观扇面”,则
D.若扇面为“美观扇面”,半径 ,则扇形面积为
【答案】ACD
【知识点】扇形面积的有关计算
【分析】对于A,利用扇形面积计算公式进行计算即可;对于B,根据条件求得 的值,利用公式计
算即可;对于C,利用条件建立方程,解出即可;对于D,根据条件求得 的值,利用公式计算即
可.
【详解】对于A, 所在的扇形的圆心角分别为 ,
所以 ,故A正确;
对于B,若 ,则 ,又 ,
则 ,故B错误;
学科网(北京)股份有限公司对于C,若 ,
所以 ,故C正确;
对于D,若 , ,又 ,
所以 ,
故D正确,
故选:ACD.
三、填空题
10.(23-24高一上·甘肃陇南·期末) 用弧度制表示为 .
【答案】 /
【知识点】角度化为弧度
【分析】利用弧度制与角度值的转化即可得到答案.
【详解】因为 弧度,所以 (弧度).
故答案为:
11.(23-24高一上·福建·期末)若扇形的周长为 ,面积为 ,则它的圆心角的弧度数为
.
【答案】
【知识点】弧长的有关计算、扇形面积的有关计算
【分析】
由扇形的面积公式和周长公式列方程,再由弧长公式解出即可.
【详解】设扇形的弧长为 ,半径为 ,
由题意可知 ,解得 ,
设扇形的圆心角为 ,则 .
学科网(北京)股份有限公司故答案为:
12.(23-24高一上·广西贺州·期末)已知扇形的面积为 ,圆心角弧度数为 ,则其弧长为
;
【答案】6
【知识点】弧长的有关计算、扇形面积的有关计算
【分析】
根据弧长公式以及扇形面积公式即可求解.
【详解】设弧长为 ,半径为 ,圆心角为 ,
故 ,
故 ,
故答案为:6
13.(23-24高一上·云南昆明·期末)已知某扇形的圆心角是 ,半径为 ,则该扇形的面积为
.
【答案】
【知识点】扇形面积的有关计算
【分析】根据题意,结合扇形的面积公式,准确计算,即可求解.
【详解】由扇形的圆心角是 ,半径为 ,则该扇形的面积为 .
故答案为: .
14.(23-24高一上·山东青岛·期末)如图,已知 是等腰直角三角形, , ,
在平面内 绕点 逆时针旋转到 ,使C,B, 在同一直线上,则图中阴影部分的面
积为 .
【答案】
【知识点】扇形面积的有关计算
学科网(北京)股份有限公司【分析】由图可知 ,分别计算即可.
【详解】如图:
由 是等腰直角三角形, , ,
所以 , ,
, ,
所以
.
故答案为:
15.(23-24高一上·山东临沂·期末)临沂一中校本部19、20班某数学兴趣小组在探究扇形时,发
现如下现象:如图所示,⊙B向⊙A靠近的过程,就像月亮被磨弯一样.已知在某一时刻,圆A和圆
B处于图1的状态,简化后如图2, , , .则S = .
阴影
【答案】
【知识点】扇形面积的有关计算、三角形面积公式及其应用
【分析】阴影部分的面积为 的半圆面积减去 中圆心角为 的弓形面积,利用已知数据计算
即可.
学科网(北京)股份有限公司【详解】 ,则 为⊙A的直径,连接 ,如图所示,
, ,则 为等边三角形, ,
的半径为2, 的半径为4,
阴影部分的面积为 的半圆面积减去 中圆心角为 的弓形面积,
则阴影部分的面积为 .
故答案为:
四、解答题
16.(23-24高一上·陕西西安·期末)某农户计划围建一块扇形的菜地,已知该农户围建菜地的篱
笆的长度为24米.
(1)若该扇形菜地的圆心角为4弧度,求该扇形菜地的面积;
(2)当该扇形菜地的圆心角为何值时,菜地的面积最大,最大值是多少?
【答案】(1) 平方米.
(2)该扇形菜地的圆心角为2弧度时,菜地的面积取得最大值36.
【知识点】弧长的有关计算、扇形面积的有关计算、扇形弧长公式与面积公式的应用
【分析】(1)根据弧长公式及扇形面积公式即可求解;
(2)结合扇形面积公式及二次函数的最值即可求解.
【详解】(1)设该扇形菜地的半径为 ,弧长为 ,
则 ,解得 ,
故该扇形菜地的面积 平方米.
(2)因为 ,所以 ,
则 .
学科网(北京)股份有限公司当 时, 取得最大值36,
此时 ,从而 .
故该扇形菜地的圆心角为2弧度时,菜地的面积取得最大值36.
三角函数的概念(共11题)
一、单选题
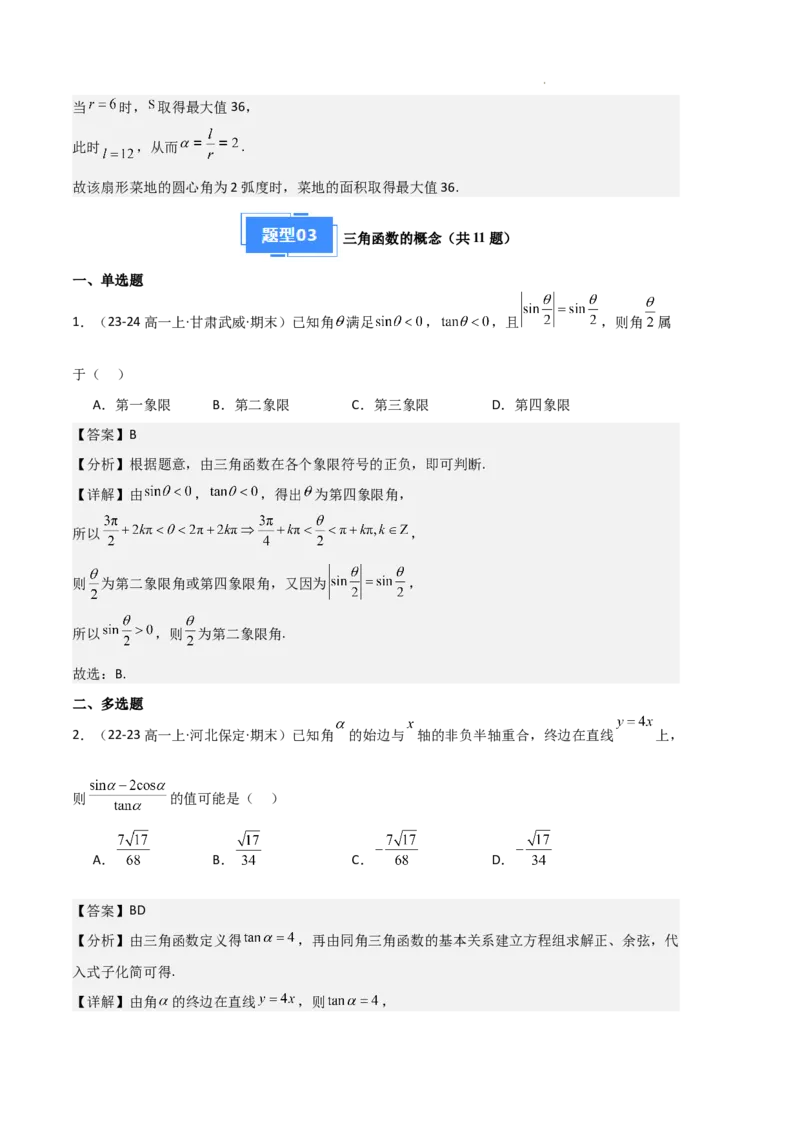
1.(23-24高一上·甘肃武威·期末)已知角 满足 , ,且 ,则角 属
于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】B
【分析】根据题意,由三角函数在各个象限符号的正负,即可判断.
【详解】由 , ,得出 为第四象限角,
所以 ,
则 为第二象限角或第四象限角,又因为 ,
所以 ,则 为第二象限角.
故选:B.
二、多选题
2.(22-23高一上·河北保定·期末)已知角 的始边与 轴的非负半轴重合,终边在直线 上,
则 的值可能是( )
A. B. C. D.
【答案】BD
【分析】由三角函数定义得 ,再由同角三角函数的基本关系建立方程组求解正、余弦,代
入式子化简可得.
【详解】由角 的终边在直线 ,则 ,
学科网(北京)股份有限公司联立 解得 或 ;
终边落在第一象限时, ,此时 ,
则 ;
终边落在第三象限时, ,此时 ,
则 ;
综上所述, 的值为 或 .
故选:BD.
三、填空题
3.(23-24高一上·云南昭通·期末) 为 终边上一点,则 .
【答案】 /0.8
【分析】由余弦的定义可直接求解.
【详解】 .
故答案为: .
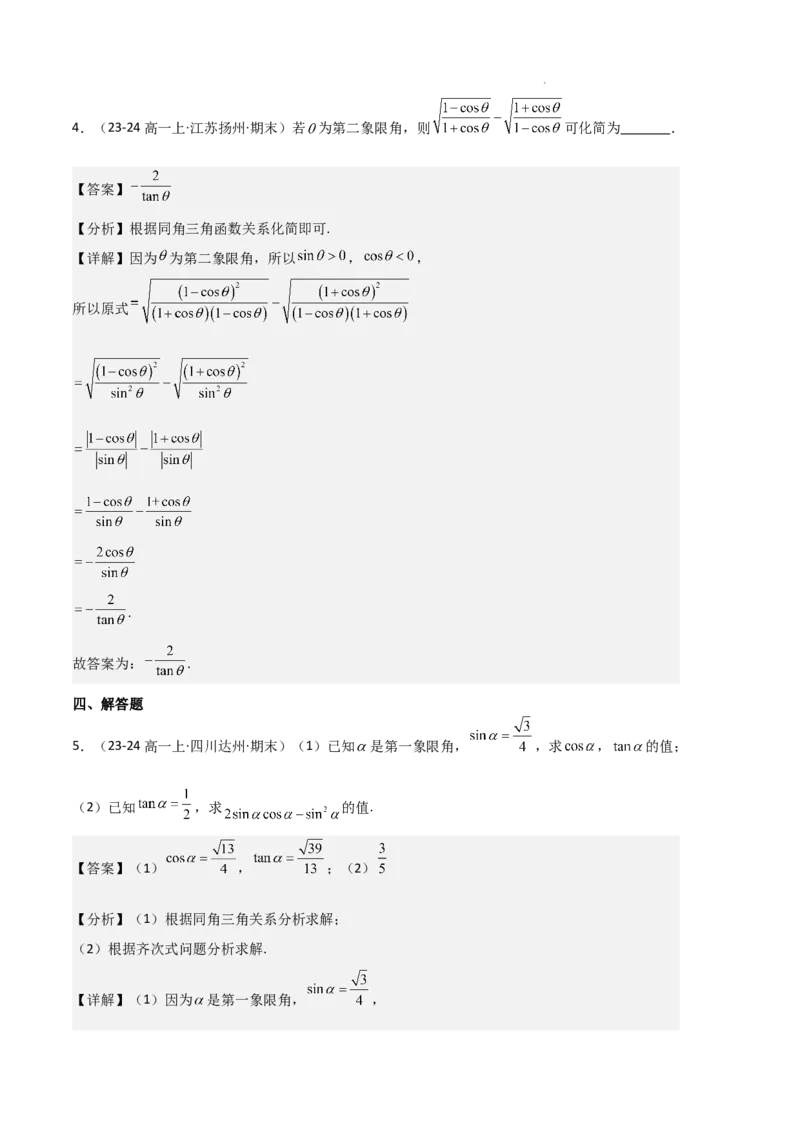
学科网(北京)股份有限公司4.(23-24高一上·江苏扬州·期末)若 为第二象限角,则 可化简为 .
【答案】
【分析】根据同角三角函数关系化简即可.
【详解】因为 为第二象限角,所以 , ,
所以原式
.
故答案为: .
四、解答题
5.(23-24高一上·四川达州·期末)(1)已知 是第一象限角, ,求 , 的值;
(2)已知 ,求 的值.
【答案】(1) , ;(2)
【分析】(1)根据同角三角关系分析求解;
(2)根据齐次式问题分析求解.
【详解】(1)因为 是第一象限角, ,
学科网(北京)股份有限公司所以 , ;
(2)因为 ,
所以 .
6.(23-24高一上·四川成都·期末)已知 .
(1)求 ;
(2)求 的值.
【答案】(1)
(2)
【分析】(1)上下同除 ,将正余弦化成正切即可计算;
(2)借助 ,将原式化为齐次分式后上下同除 ,将正余弦化成正切后借助
的值即可计算.
【详解】(1) , ,
解得 ;
(2)
.
7.(22-23高一上·黑龙江牡丹江·期末)已知 .
(1)求 的值;
学科网(北京)股份有限公司(2)求 的值.
【答案】(1)
(2)
【分析】(1)根据题意整理可得 ,进而可得结果;
(2)根据齐次式问题分析求解,注意“1”的转化.
【详解】(1)因为 ,整理得 ,
所以 ;
(2)因为 ,
所以
.
8.(23-24高一上·广东中山·期末)已知 ,求下列各式的值.
(1) ;
(2) .
【答案】(1)
(2)
【分析】(1)根据同角三角函数的基本关系式求得正确答案.
(2)利用“ 的代换”的方法,结合同角三角函数的基本关系式求得正确答案.
【详解】(1) .
(2)
学科网(北京)股份有限公司.
9.(23-24高一上·陕西西安·期末)已知 是第二象限角,且 .
(1)求 的值;
(2)求 的值.
【答案】(1)
(2) .
【分析】(1)根据同角三角函数的基本关系求解即可;
(2)根据诱导公式和同角三角函数的基本关系求解即可.
【详解】(1)因为 ,所以 ,
因为 ,所以 ,
因为 是第二象限角,所以 ,
则 .
(2)
.
10.(23-24高一上·广东深圳·期末)如图,在平面直角坐标系xoy中,锐角 的终边与单位圆交于
点 ,射线OA绕点O按逆时针方向旋转 后交单位圆于点B,点B的横坐标为 .
学科网(北京)股份有限公司(1)求 的表达式,并求 的值;
(2)若 , ,求 的值.
【答案】(1) ,
(2)
【分析】(1)由题意可知 ,结合任意角三角函数的定义分析求解;
(2)由题意可得 ,结合同角三角关系运算求解.
【详解】(1)因为锐角 的终边与单位圆交于点 ,
则 ,可知 ,
又因为射线OA绕点O按逆时针方向旋转 后交单位圆于点B,
所以 ,可得 .
(2)若 , ,则 ,
所以 .
11.(23-24高一上·江苏南京·期末)如图,有一条宽为 的笔直的河道(假设河道足够长),
学科网(北京)股份有限公司规划在河道内围出一块直角三角形区域(图中 )种植荷花用于观赏, 两点分别在两岸
上, ,顶点 到河两岸的距离 ,设 .
(1)若 ,求荷花种植面积(单位: )的最大值;
(2)若 ,且荷花的种植面积为 ,求 .
【答案】(1)
(2) 或 .
【分析】(1)表达出 ,表达出 ,结合 ,由
基本不等式求出最值,得到答案;
(2)求出 ,根据荷花的种植面积求出 ,结合同角三角函数关系得到
,所以 和 为一元二次方程 的两个实数根,求出答案.
【详解】(1) .
当 时, ,
所以 .
又因为 ,
学科网(北京)股份有限公司所以 ,当且仅当 时取等号.
所以荷花种植区域面积的最大值为 .
(2)因为 ,所以 ,
故 ,
从而 ,
所以 .
又因为 ,
所以 .
又因为 ,所以 ,
所以 和 为一元二次方程 的两个实数根,
解得 或 ,
故 为 或 .
诱导公式(共16题)
一、单选题
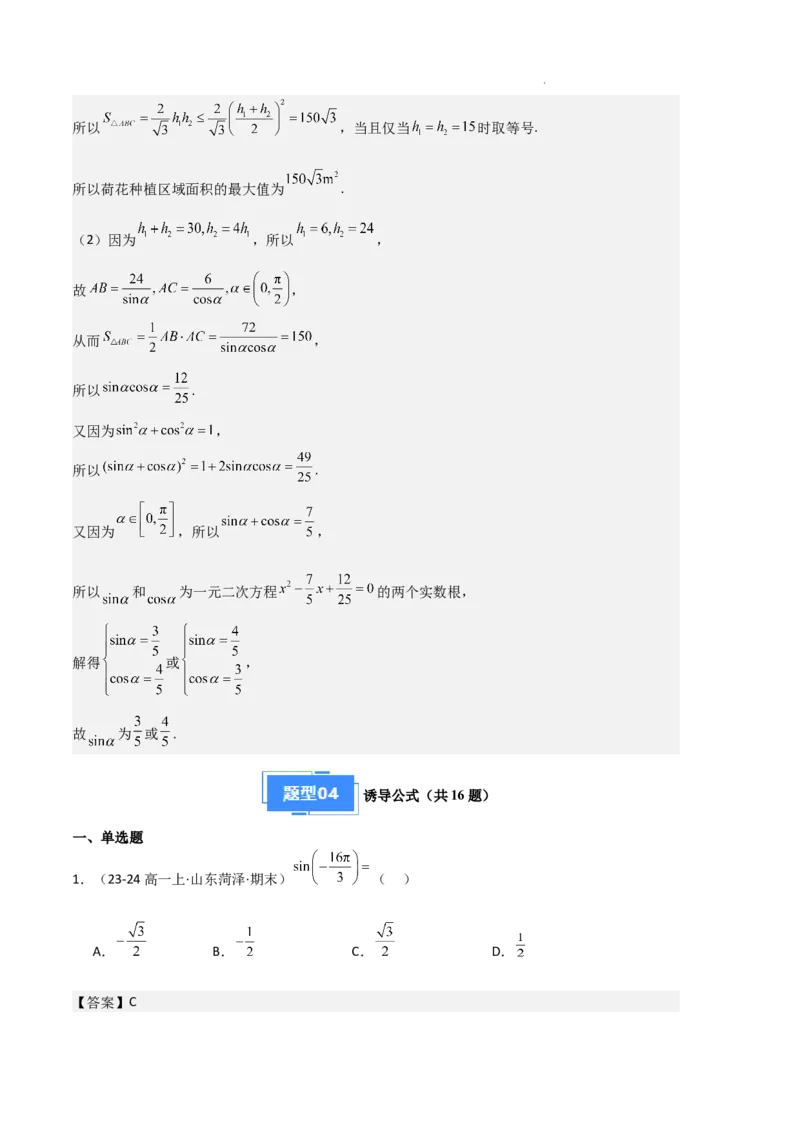
1.(23-24高一上·山东菏泽·期末) ( )
A. B. C. D.
【答案】C
学科网(北京)股份有限公司【分析】利用诱导公式化简可得出所求代数式的值.
【详解】 .
故选:C.
2.(23-24高一上·浙江嘉兴·期末)已知 ,则 ( )
A. B. C. D.
【答案】D
【分析】应用诱导公式 ,求解即可.
【详解】由诱导公式 ,且 ,
可得 ,即 .
故选:D.
二、多选题
3.(23-24高一上·安徽马鞍山·期末)若角 是 的三个内角,则下列结论中一定成立的
是( )
A. B.
C. D.
【答案】AD
【分析】结合三角形的内角与利用诱导公式逐项判断.
【详解】对于A: ,故A正确;
对于B: ,故B错误;
对于C: ,故C错误;
学科网(北京)股份有限公司对于D: ,故D正确.
故选:AD.
4.(23-24高一上·湖北荆门·期末)已知 ,则下列结论正确的是( )
A. B.
C. D.
【答案】AC
【分析】根据条件,逐一求出各选项的值,再进行判断.
【详解】由 .故A正确;
,故C正确;
,故D错误;
因为 ,所以 为第一或第三象限角.
若 为第一象限角,则 ,所以 ;
若 为第三象限角,则 ,所以 .
所以B错误.
故选:AC
三、填空题
学科网(北京)股份有限公司5.(23-24高一上·福建福州·期末)若 ,则 .
【答案】 /
【分析】利用诱导公式求解.
【详解】由 ,
所以 .
故答案为:
6.(23-24高一上·浙江杭州·期末)若 ,则 .
【答案】 /
【分析】利用角的变换结合诱导公式可求
【详解】因为 ,
所以
故答案为:
7.(23-24高一上·浙江丽水·期末)化简 .
【答案】1
【分析】利用诱导公式化简求值.
【详解】 .
学科网(北京)股份有限公司故答案为:1.
8.(23-24高一上·河南洛阳·期末)在平面直角坐标系中, 为坐标原点,点 ,线段
绕点 顺时针方向旋转 后,得到线段 ,则点 的坐标为 .
【答案】
【分析】先判断出以 为终边的角的大小,然后顺时针旋转 ,判断以 为终边的角的大小即
可得出答案.
【详解】因为 ,所以点 在单位圆 上,
且点 在 角的终边所在的直线上,
则点 的初始位置坐标 ,
线段 绕点 顺时针转动 后,点 在 角的终边所在的直线上,
所以点 所在位置的坐标为 .
故答案为: .
四、解答题
9.(23-24高一上·云南曲靖·期末)已知 ,且 为第三象限角.
(1)求 , 的值;
(2)求 的值.
学科网(北京)股份有限公司【答案】(1) ,
(2)
【分析】(1)利用同角三角函数的基本关系求解;
(2)利用诱导公式化简求值.
【详解】(1)因为 , ,
所以 ,又 为第三象限角,
所以 ,所以 ;
(2)由诱导公式化简得:
.
10.(23-24高一上·河南漯河·期末)(1)化简: ;
(2)化简: .
【答案】(1)17;(2)
【分析】(1)由指数、对数运算性质运算即可;(2)由诱导公式化简即可求解.
【详解】(1)
.
(2)
学科网(北京)股份有限公司.
11.(23-24高一上·江苏常州·期末)在平面直角坐标系 中,点 在角 的终边上.
(1)求 的值;
(2)求 的值.
【答案】(1)
(2)
【分析】(1)由三角函数定义求得 ,进而求出 ,再由
即可得出答案;
(2)由同角三角函数的基本关系求解即可.
【详解】(1)点 在角 的终边上, ,
, ,
所以 , ,
所以 .
(2) .
12.(23-24高一上·安徽阜阳·期末)(1)计算:
(2)若 ,求 的值.
【答案】(1) ;(2)2.
学科网(北京)股份有限公司【分析】(1)利用指数对数运算法则即可;
(2)先利用诱导公式求出 ,然后利用同角三角函数基本关系式即可.
【详解】(1)原式 .
(2) , ,
所以 .
13.(23-24高一上·河北承德·期末)已知角 的终边经过点 .
(1)求 的值;
(2)若 ,求 的值.
【答案】(1)
(2)
【分析】(1)根据三角函数的定义,即可求解;
(2)首先利用诱导公式化简,再转化为正切表示的式子,即可求解.
【详解】(1)由三角函数的定义可知 ,解得 .
所以 .
(2)原式
学科网(北京)股份有限公司.
14.(23-24高一上·湖南娄底·期末)已知 .
(1)若 是第三象限角,求 , 的值;
(2)先化简再求值: .
【答案】(1)
(2)
【分析】(1)由平方关系、商数关系结合 是第三象限角即可求解.
(2)由诱导公式化简并化成关于 的齐次式,代入即可求解.
【详解】(1)因为 , ,若 是第三象限角,
则解得 .
(2)由题意 ,
若 ,则原式 .
15.(23-24高一上·安徽马鞍山·期末)计算下列各式的值:
(1) ;
(2) .
【答案】(1)
(2)
【分析】(1)由对数运算法则、指数以及分数指数幂的运算法则求解即可;
学科网(北京)股份有限公司(2)由诱导公式以及特殊三角函数值即可求解.
【详解】(1) .
(2) .
16.(23-24高一上·贵州毕节·期末)已知 ,α是第三象限角,求:
(1) 的值;
(2) 的值.
【答案】(1)2
(2)
【分析】(1)利用同角三角函数的基本关系求解;
(2)利用诱导公式化简求值.
【详解】(1)因为 ,α是第三象限角,
则 ,
所以tan ;
(2) .
学科网(北京)股份有限公司扇形中的最值问题(共8题)
1.(23-24高一上·江苏南京·期末)已知扇形的半径为 ,弧长为 .若其周长的数值为面积的数值
的2倍,则下列说法正确的是( )
A.该扇形面积的最小值为8
B.当扇形周长最小时,其圆心角为2
C. 的最小值为9
D. 的最小值为
【答案】BCD
【知识点】基本不等式求和的最小值、扇形面积的有关计算
【分析】由题意,知 ,则 ,对于选项ABC利用基本不等式可判断,对于
选项D利用二次函数可解.
【详解】由题意,知 ,则 ,
所以扇形面积
,
当且仅当 ,即 时,等号成立,选项A错误;
扇形周长为
,
当且仅当 ,即 时,等号成立,
此时,圆心角为 ,选项B正确;
学科网(北京)股份有限公司,
当且仅当 ,即 时,等号成立,选项C正确;
,
当 时,上式取得最小值为 ,选项D正确.
故选:BCD.
2.(22-23高一上·吉林·期末)如图,在扇形OPQ中,半径 ,圆心角 ,C是扇形
弧PQ上的动点,矩形 内接于扇形,记 .则下列说法正确的是( )
A.弧PQ的长为
B.扇形OPQ的面积为
C.当 时,矩形 的面积为
D.矩形 的面积的最大值为
【答案】ACD
【知识点】三角恒等变换的化简问题、求含sinx(型)函数的值域和最值、扇形面积的有关计算、弧
长的有关计算
【分析】根据弧长公式可判断A;根据扇形的面积公式可判断B;解直角三角形求得 的长,
学科网(北京)股份有限公司即可求出矩形 的面积的表达式,结合三角函数的恒等变换化简求值,可判断C,D.
【详解】由题意知,在扇形OPQ中,半径 ,圆心角 ,
故弧PQ的长为 ,A正确;
扇形OPQ的面积为 ,B错误;
在 中, ,
在 中, ,
则 的面积
,
当 时,又 ,故 ,
则 ,
则 ,
则 ,
即矩形 的面积为 ,C正确;
由C的分析可知矩形 的面积 ,
当 ,即 时,矩形 的面积取最大值 ,D正确,
故选:ACD
【点睛】关键点睛:解答本题的关键C,D选项的判断,解答时要结合解直角三角形,表示出边
学科网(北京)股份有限公司的长,从而表示出矩形 的面积,再结合三角函数的恒等变换,即可判断这两个选项
的正误.
3.(23-24高一上·北京东城·期末)如图,在平面直角坐标系 中,点 , ,
角 的顶点与坐标原点 重合,始边为 轴的非负半轴,终边与单位圆 交于点 ,则阴影区域的
面积的最大值为 .
【答案】
【知识点】扇形面积的有关计算、由终边或终边上的点求三角函数值、求15°等特殊角的正弦、圆
上点到定直线(图形)上的最值(范围)
【分析】连接 ,当点 距离直线 最远时,阴影区域的面积的最大值,利用三角形的面积公
式和扇形面积公式计算即可.
【详解】连接 ,当点 距离直线 最远时,阴影区域的面积的最大值,根据圆的几何特征可
得此时 且 ,如图:
设 是 的终边,则 ,所以 ,则 ,
又 ,
所以阴影区域的面积的最大值为 .
学科网(北京)股份有限公司故答案为: .
4.(23-24高一上·重庆·期末)南朝乐府民歌《子夜四时歌》之夏歌曰:“叠扇放床上,企想远风
来;轻袖佛华妆,窈窕登高台”,中国传统折扇有着极其深厚的文化底蕴.如图所示,展开的折扇
可看作是从一个扇形,某艺术节展示活动中,小李同学打算利用一条2米长的紫色丝带围成一个扇
形展示框,则该展示框的面积最大值为 .
【答案】 /
【知识点】扇形面积的有关计算、求二次函数的值域或最值
【分析】设该扇形的半径为 ,弧长为 ,面积为 ,由已知可得 , ,利用扇形面
积公式结合二次函数求最值即可.
【详解】设该扇形的半径为 ,弧长为 ,面积为 ,
由已知 ,则 , ,
所以 ,
所以当 时, 有最大值 .
故答案为: .
三、解答题
5.(22-23高一上·湖南长沙·期末)如图所示,有一块扇形钢板 ,面积是 平方米,其所在圆
学科网(北京)股份有限公司的半径为1米.
(1)求扇形圆心角的大小;
(2)现在钢板 上裁下一块平行四边形钢板 ,要求使裁下的钢板面积最大.设 ,
试问如何确定 的位置,才能使裁下的钢板符合要求?最大面积为多少?
【答案】(1)
(2) 是 的中点, 平方米
【知识点】扇形面积的有关计算、辅助角公式、cos2x的降幂公式及应用、三角形面积公式及其应
用
【分析】(1)利用扇形面积公式列方程,从而求得扇形圆心角的大小.
(2)连接 ,设 ,将裁下的钢板的面积用 来表示,结合三角函数的性质求得面积的
最大值以及此时 点的位置.
【详解】(1)依题意, ,
设 ,则 , ,
即扇形圆心角的大小为 .
(2)连接 ,设 ,过 作 ,垂足为 ,
在 中, ,
所以 ,
设四边形 的面积为 ,
学科网(北京)股份有限公司则
,
由于 , , ,
所以当 , 时, 取得最大值为 (平方米).
所以当 是 的中点时,裁下的钢板符合要求,最大面积为 平方米.
6.(23-24高一上·湖南株洲·期末)在半径为 的半圆形空地上,某小区准备设计三个矩形地块栽
种一种花草,三个扇形 , , 的圆心角均为 ,且矩形的地块具有对称性,按如图
所示的方案,矩形分别内接于对应的扇形,分别求扇形 和 内接矩形的最大值.
【答案】 ;
【知识点】辅助角公式、求含sinx(型)函数的值域和最值、扇形面积的有关计算
【分析】利用锐角三角函数定义,结合矩形面积公式分别表示两个矩形面积,根据正弦二倍角公式、
辅助角公式、降幂公式,结合正弦型函数的性质进行求解即可.
【详解】在扇形 中,其内接矩形为 ,如图1:
学科网(北京)股份有限公司设 ,在直角 中,由 ,可得 , .
又 ,
所以
.
当 ,即 时,扇形 内接矩形 的面积最大,最大值为 .
在扇形 中,其内接矩形为 ,取圆弧 的中点为 ,连接 ,
设 , , ,如图2:
则 ,于是 ,
又 ,
所以
学科网(北京)股份有限公司,
当 时,即 时,扇形 内接矩形 的面积最大,最大值为 .
7.(23-24高一上·江苏南通·期末)如图,在半径为4、圆心角为 的扇形 中; 分别为
的中点,点 在圆弧 上且 ·
(1)若 ,求梯形 的高;
(2)求四边形 面积的最大值.
【答案】(1)
(2)
【知识点】扇形中的最值问题、任意角的概念
【分析】(1)作出梯形 的高后结合题意计算即可得;
(2)四边形 面积为 ,设 ,结合
,即可求出面积关于 的表达式,即可得最大值.
【详解】(1)连接 ,过点 作 于点 ,交 于点 ,
由 , ,扇形半径为4, 分别为 的中点,
故 , , , ,
学科网(北京)股份有限公司则 ,故 为等边三角形,
则 , ,
故梯形 的高为 ;
(2)设 ,则 ,
且此时 ,四边形 面积为:
,
∴ 时, 取最大值 .
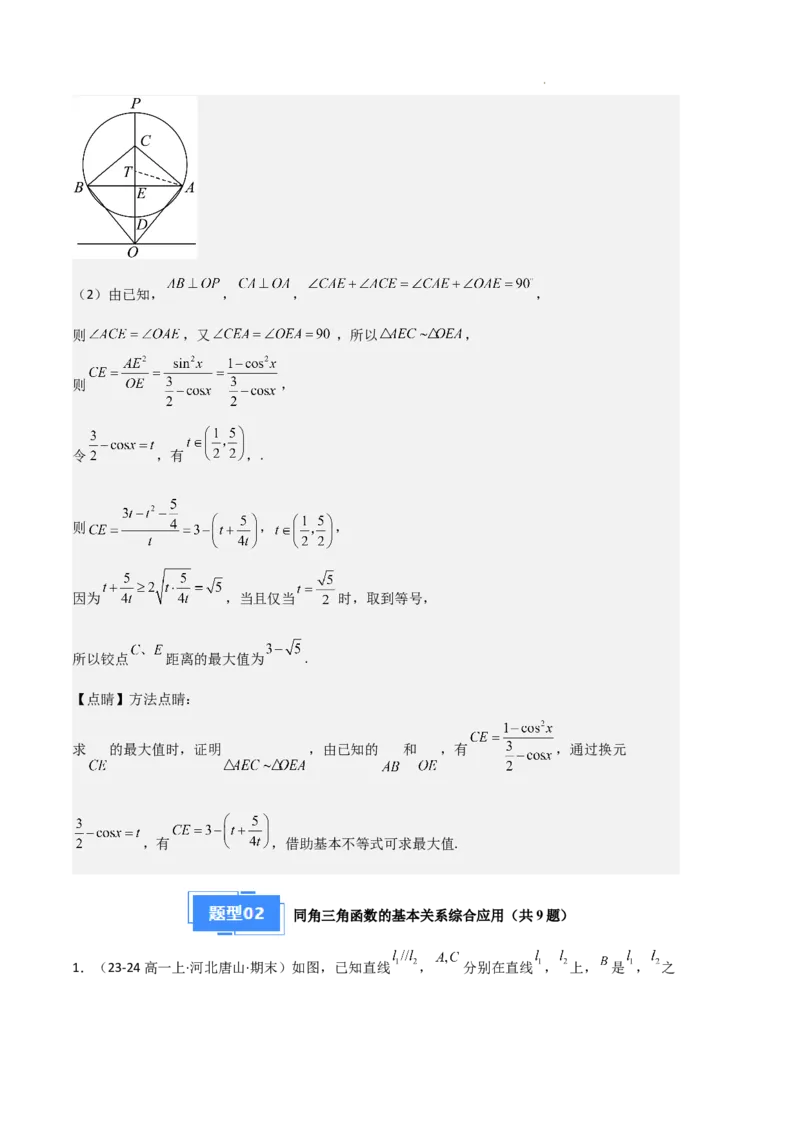
8.(23-24高一上·浙江台州·期末)如图是一种升降装置结构图,支柱 垂直水平地面,半径为1
的圆形轨道固定在支柱 上,轨道最低点 , , .液压杆 、 ,牵引杆 、
,水平横杆 均可根据长度自由伸缩,且牵引杆 、 分别与液压杆 、 垂直.当液压杆
、 同步伸缩时,铰点 在圆形轨道上滑动,铰点 在支柱 上滑动,水平横杆
作升降运动(铰点指机械设备中铰链或者装置臂的连接位置,通常用一根销轴将相邻零件连接起来,
学科网(北京)股份有限公司使零件之间可围绕铰点转动).
(1)设劣弧 的长为 ,求水平横杆 的长和 离水平地面的高度 (用 表示);
(2)在升降过程中,求铰点 距离的最大值.
【答案】(1) ;
(2)
【知识点】基本(均值)不等式的应用、三角函数在生活中的应用、弧长的有关计算
【分析】(1)轨道圆心为 ,圆的半径为1,劣弧 的长为 时,有 ,由三角函数表
示出 和 的长;
(2)证明出 ,则 ,通过换元利用基本不等式求出最
大值.
【详解】(1)记轨道圆心为 ,则 ,
设劣弧 的长为 ,则 ,
得 ,
.
学科网(北京)股份有限公司(2)由已知, , , ,
则 ,又 ,所以 ,
则 ,
令 ,有 ,.
则 , ,
因为 ,当且仅当 时,取到等号,
所以铰点 距离的最大值为 .
【点睛】方法点睛:
求 的最大值时,证明 ,由已知的 和 ,有 ,通过换元
,有 ,借助基本不等式可求最大值.
同角三角函数的基本关系综合应用(共9题)
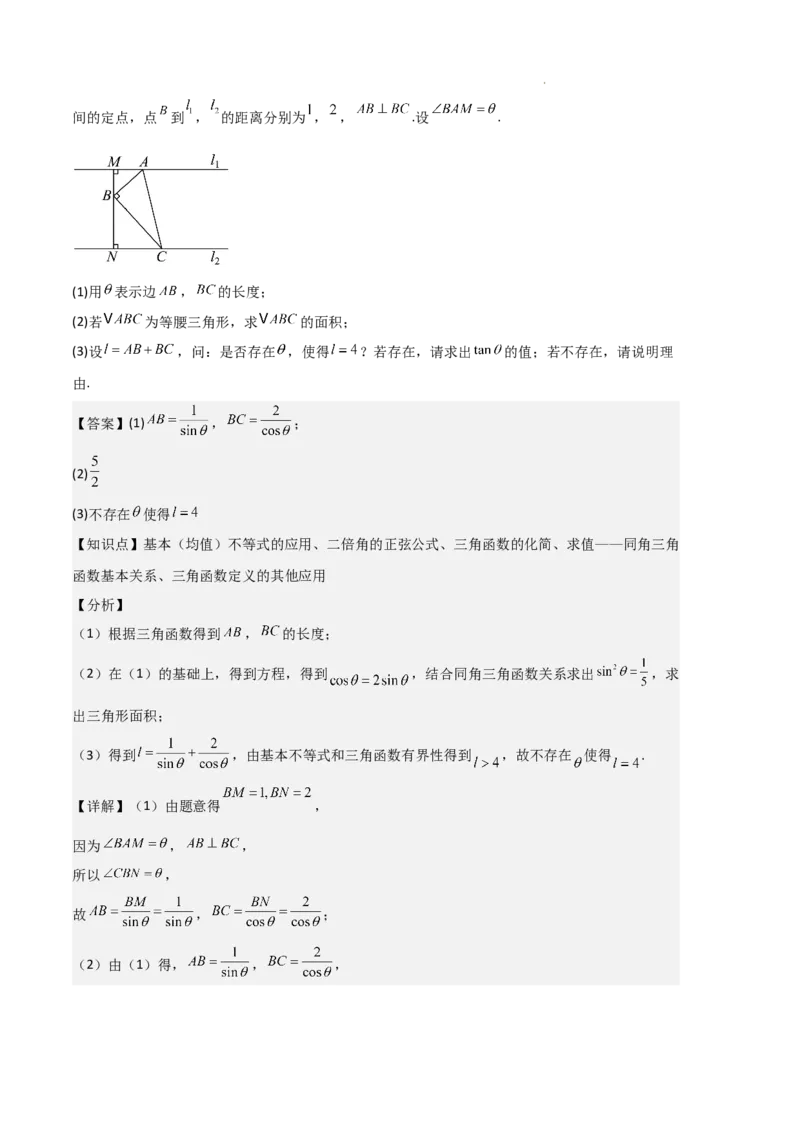
1.(23-24高一上·河北唐山·期末)如图,已知直线 , 分别在直线 , 上, 是 , 之
学科网(北京)股份有限公司间的定点,点 到 , 的距离分别为 , , .设 .
(1)用 表示边 , 的长度;
(2)若 为等腰三角形,求 的面积;
(3)设 ,问:是否存在 ,使得 ?若存在,请求出 的值;若不存在,请说明理
由.
【答案】(1) , ;
(2)
(3)不存在 使得
【知识点】基本(均值)不等式的应用、二倍角的正弦公式、三角函数的化简、求值——同角三角
函数基本关系、三角函数定义的其他应用
【分析】
(1)根据三角函数得到 , 的长度;
(2)在(1)的基础上,得到方程,得到 ,结合同角三角函数关系求出 ,求
出三角形面积;
(3)得到 ,由基本不等式和三角函数有界性得到 ,故不存在 使得 .
【详解】(1)由题意得 ,
因为 , ,
所以 ,
故 , ;
(2)由(1)得, , ,
学科网(北京)股份有限公司故 ,即 ,
又 ,所以 ,即 ,
所以 ;
(3)由(1)得, , ,
故 ,
当且仅当 ,即 时,等号成立,
又 ,当且仅当 时,等号成立,
显然 与 不会同时成立,
故 ,不存在 使得 .
【点睛】三角函数的思想方法常常用来解决一些与角度有关的实际问题,原因是三角函数的有界性,
且三角函数的公式众多,比如和差公式,倍角公式,半角公式等,可以很好的表达相关量的关系,
利用相关工具,解决问题
2.(23-24高一上·山西长治·期末)已知 .
(1)若 为锐角,求 的值;
(2)求 的值.
【答案】(1)
(2)3
【知识点】正、余弦齐次式的计算、三角函数的化简、求值——同角三角函数基本关系、用和、差
角的余弦公式化简、求值、二倍角的正弦公式
【分析】(1)化简 得 ,结合平方关系求出 ,再利用两角差
学科网(北京)股份有限公司的余弦公式,即可求得答案;
(2)由(1)可得 ,化简 为 ,利用齐次式法求值,
即可得答案.
【详解】(1)由 ,得 ,
因为 锐角, ,所以 ,
可得 ;
(2)由 得 ,
则
.
3.(23-24高一上·河南省直辖县级单位·期末)如图,在平面直角坐标系中,锐角 的顶点与原点
重合,始边与x轴的正半轴重合,终边和单位圆交于A点,将 绕点O按逆时针方向旋转角 后,
终边在第二象限和单位圆交于B点.点A的横坐标为 ,点B的横坐标为 .
(1)求 的值;
学科网(北京)股份有限公司(2)求 的值;
(3)求 的值.
【答案】(1) ;
(2) ;
(3) .
【知识点】二倍角的余弦公式、已知两角的正、余弦,求和、差角的余弦、三角函数的化简、求值
——同角三角函数基本关系、由终边或终边上的点求三角函数值
【分析】(1)利用三角函数定义,同角三角函数的平方关系及诱导公式计算即可;
(2)利用诱导公式,二倍角公式计算即可;
(3)利用三角函数定义,同角三角函数的平方关系及商数关系结合余弦的差角公式计算即可.
【详解】(1)由题意及三角函数定义可知 , ,所以 ,
由诱导公式可知 ;
(2)由(1)及二倍角公式可知
,
又 ,所以 ,故 (负值舍去);
(3)由题意可知 , 为第二象限角,
所以 ,
所以
学科网(北京)股份有限公司,
因为 , 为第二象限角, ,
则 为第二象限角,即 ,
所以
4.(23-24高一上·广东广州·期末)已知函数 .
(1)求函数 的最小正周期;
(2)若 ,求 的值.
【答案】(1)
(2)
【知识点】辅助角公式、求正弦(型)函数的最小正周期、三角函数的化简、求值——同角三角函
数基本关系
【分析】(1)由辅助角公式化简后结合正弦型函数的性质即可得;
(2)由题意结合象限可得 、 ,借助二倍角公式即可得 的值.
【详解】(1) ,
则 ,即函数 的最小正周期为 ;
(2) ,
故 ,又 ,故 ,
学科网(北京)股份有限公司.
5.(23-24高一上·四川广安·期末)已知 .
(1)求 和 的值;
(2)若 为第四象限角,当 时,求函数 的最小值.
【答案】(1) ;
(2)
【知识点】三角恒等变换的化简问题、二倍角的正切公式、三角函数的化简、求值——同角三角函
数基本关系、求二次函数的值域或最值
【分析】(1)利用两角和的正弦与余弦公式展开化简已知等式得 ,由同角三角函
数关系得 ,再由二倍角正切公式可得 ;
(2)由 为第四象限,可得 的值,确定二次函数 ,按对称轴是否在区间内分类讨
论求最小值即可.
【详解】(1)由 得,
,
所以有 ,
化简整理得 .
若 ,则 ,这与 矛盾,
故 ,所以有 ,
学科网(北京)股份有限公司则 ;
(2)由 为第四象限角,得 ,
故联立 ,可得 ,
所以 ,
二次函数 的图象开口向上,对称轴为 ,
由 , ,则 .
当 时, , 在 上单调递减,在 单调递增,
则 ;
当 时, 在 单调递增,
则 .
综上所述, .
6.(23-24高一上·江苏常州·期末)已知 .
(1)若 为奇函数,求 的值,并解方程 ;
(2)解关于 的不等式 .
【答案】(1)
(2)答案见解析
【知识点】由奇偶性求参数、解含有参数的一元二次不等式、三角函数的化简、求值——同角三角
学科网(北京)股份有限公司函数基本关系、对数的运算性质的应用
【分析】(1)由 为奇函数,可令 ,求出 的值,并根据对数运算求出
,即得方程的解集;
(2)将不等式代入化简为 ,即 ,分别在
三种情况下分类讨论即可.
【详解】(1) 的定义域为R,
因为 为奇函数,则 ,
解得 ,故 ,
又 ,即 ,
所以函数 为奇函数,故 .
又 ,即 ,
解得 ,即 .
(2)因为 , , ,
关于 的不等式 可转化为 ,
即 ,
①当 时, ;
②当 时, ,解得 ,
学科网(北京)股份有限公司③当 时, 或 ,解得 或 , ,
综上,当 时,原不等式的解集为 ,
当 时,原不等式的解集为 ,
当 时,原不等式的解集为 .
7.(23-24高一上·山西太原·期末)已知 ,且 .
(1)求 的值;
(2)求 的值.
【答案】(1)
(2)
【知识点】三角函数的化简、求值——同角三角函数基本关系、用和、差角的余弦公式化简、求值、
二倍角的正弦公式、给值求值型问题
【分析】(1)借助二倍角公式与三角函数基本关系将弦化为切计算即可得;
(2)结合三角函数基本关系与三角恒等变换计算即可得.
【详解】(1) ,且 ,
则 ;
(2) ,
,
, , ,
则 ,即 , ,
学科网(北京)股份有限公司.
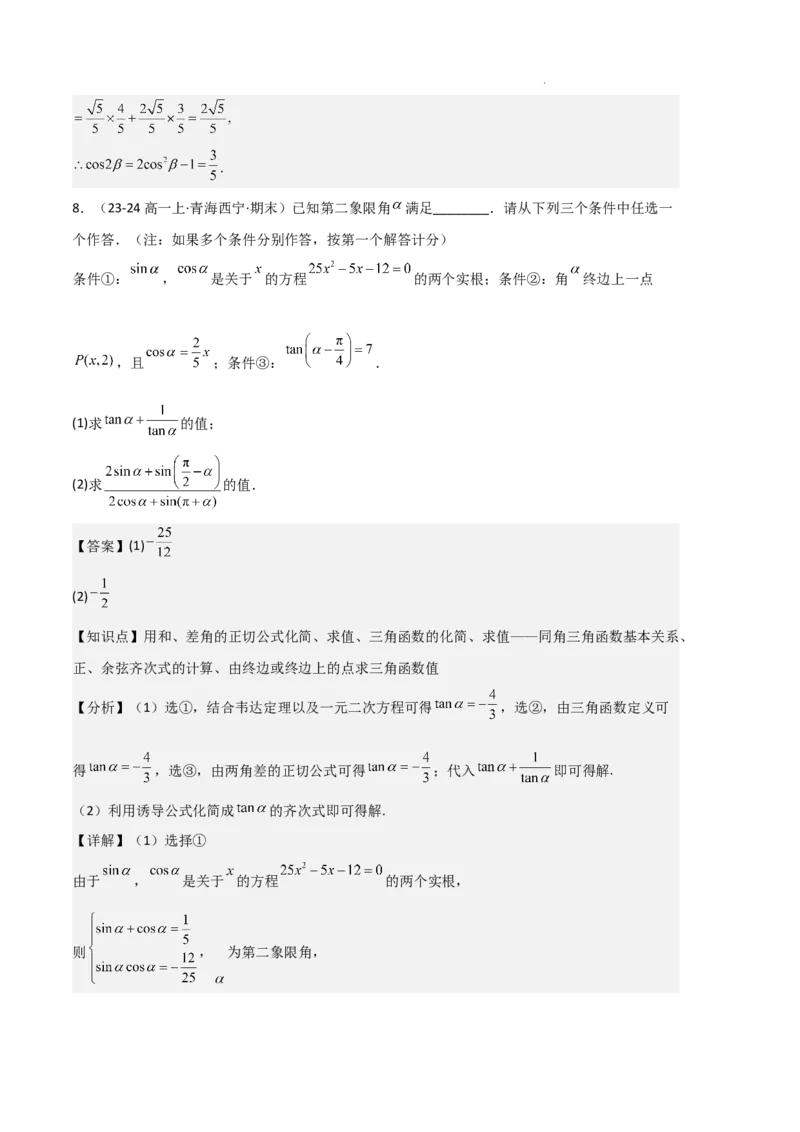
8.(23-24高一上·青海西宁·期末)已知第二象限角 满足________.请从下列三个条件中任选一
个作答.(注:如果多个条件分别作答,按第一个解答计分)
条件①: , 是关于 的方程 的两个实根;条件②:角 终边上一点
,且 ;条件③: .
(1)求 的值;
(2)求 的值.
【答案】(1)
(2)
【知识点】用和、差角的正切公式化简、求值、三角函数的化简、求值——同角三角函数基本关系、
正、余弦齐次式的计算、由终边或终边上的点求三角函数值
【分析】(1)选①,结合韦达定理以及一元二次方程可得 ,选②,由三角函数定义可
得 ,选③,由两角差的正切公式可得 ;代入 即可得解.
(2)利用诱导公式化简成 的齐次式即可得解.
【详解】(1)选择①
由于 , 是关于 的方程 的两个实根,
则 , 为第二象限角,
学科网(北京)股份有限公司解得 , ;
则 ,
选②
因为角 终边上一点 ,且 ,
所以 ,且 为第二象限角,解得 ,
则点 ;
所以 ,
选③
因为 ,
所以 ,
解得 ,
所以 .
(2) .
9.(23-24高一上·湖南长沙·期末)已知 , .
(1)求 的值;
(2)若 ,且 ,求 的值.
学科网(北京)股份有限公司【答案】(1)
(2)
【知识点】二倍角的正弦公式、用和、差角的正切公式化简、求值、三角函数的化简、求值——同
角三角函数基本关系
【分析】(1)利用两角差正切公式求得 ,然后化弦为切及二倍角公式,结合“1”的代换
化弦为切求解即可;
(2)先利用同角三角函数关系求得 ,然后利用两角和正切公式求值,最后根据角的范围
确定角的大小.
【详解】(1)因为 , ,
所以 ,解得 ,
所以
;
(2)因为 ,且 ,所以 ,所以 .
所以 ,
又因为 , ,所以 ,所以 .
诱导公式综合应用(共25题)
学科网(北京)股份有限公司1.(23-24高一上·山西长治·期末)已知 ,则下列说法正
确的是( )
A. B.
C.若 ,则 D.若 ,则
【答案】BCD
【知识点】正、余弦齐次式的计算、三角函数的化简、求值——同角三角函数基本关系、三角函数
的化简、求值——诱导公式、二倍角的正弦公式
【分析】利用诱导公式化简 的表达式,可判断A,B;利用齐次式法求值,可判断C;化
为 ,求值,即可判断D.
【详解】由题意得 ,A错误,B正确;
当 时, ,C正确;
若 ,则 ,D正确.
故选:BCD.
2.(23-24高一上·安徽芜湖·期末)已知 ,则下列结论正确的是( )
A. B.
C. D.
【答案】ACD
学科网(北京)股份有限公司【知识点】二倍角的余弦公式、诱导公式五、六、三角函数的化简、求值——同角三角函数基本关
系
【分析】利用诱导公式整体求值判断A,同角三角函数基本关系判断B,利用二倍角余弦公式判断CD.
【详解】已知 ,则 ,A正确;
因为 ,则 ,故 ,故B错误;
,C正确;
,故 ,D正确.
故选:ACD
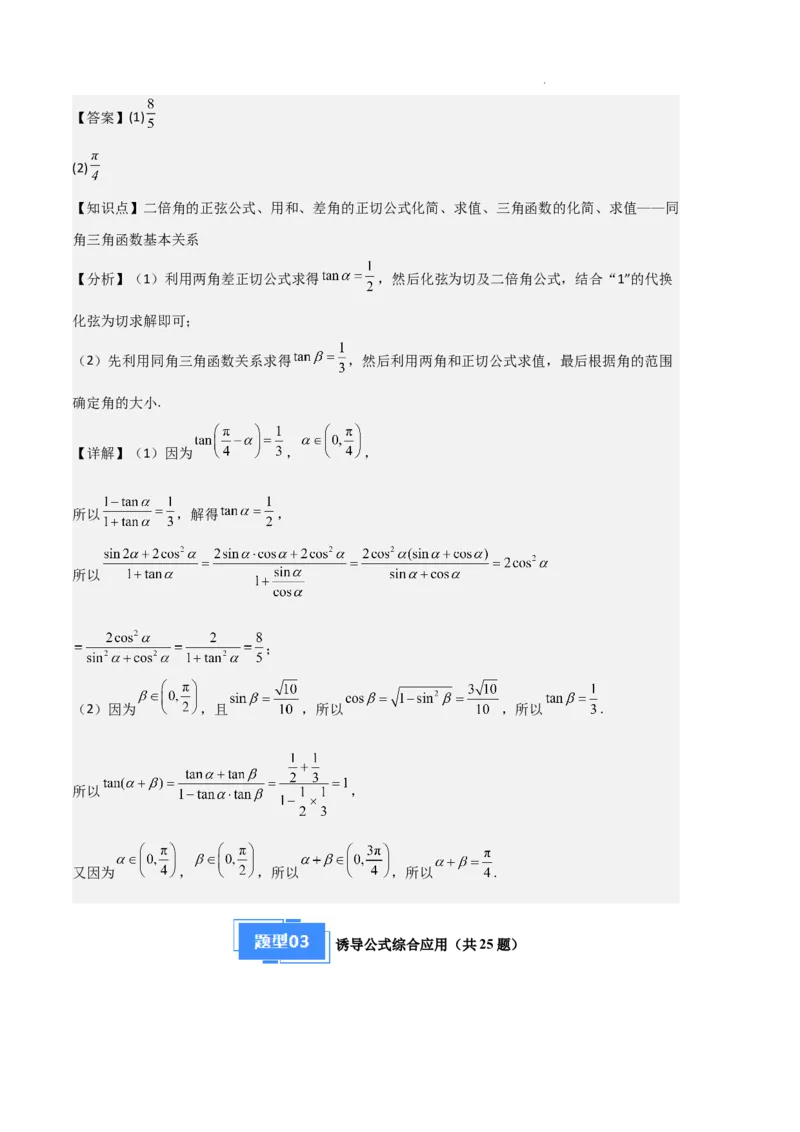
3.(23-24高一上·广东惠州·期末)已知函数 的部分图
象如图所示, 图象经过点 和点 ,且 在区间 上单调,则( )
A. B.
C. D.
【答案】BCD
【知识点】由正(余)弦函数的性质确定图象(解析式)、利用正弦型函数的单调性求参数、三角
学科网(北京)股份有限公司函数的化简、求值——诱导公式
【分析】根据图象先确定出 的值,然后根据图象所过的点以及单调性结合分类讨论确定出 的
值,则AB选项可判断;求出 的解析式,代入计算可判断出C选项;计算并化简
,即可判断出D选项.
【详解】由图象可知: ,所以 ,
因为 的图象过 ,所以 ,
因为 ,所以 或 ,
因为 在区间 上单调,所以 ,所以 ,
①当 时, ,
因为 图象过 ,所以 ,所以 ,
所以 , ,又 ,所以 ,
此时 ,显然 在 附近单调递增,这与图象矛盾,故B错误;
②当 时, ,
因为 图象过 ,所以 ,所以 ,
所以 , ,又 ,所以 ,
所以 ,当 时,令 ,
此时 在 上单调递减,故A正确;
因为 ,故C正确;
学科网(北京)股份有限公司因为 ,
,
所以 ,故D正确;
故选:BCD.
【点睛】关键点点睛:本题考查正弦函数的图象与性质的综合运用,对学生的分析与计算能力要求
较高,难度较大.解答本题的关键在于:分析出 取值并结合单调性求解出 的值后,要根据图象
对所得结果进行检验,排除一组 的取值,由此才可继续分析剩余选项.
4.(23-24高一上·福建龙岩·期末)在①角 的终边与单位圆的交点为 ;②
;③ 这三个条件中任选一个,补充在下面的横线上,并解答
问题.
已知 ,且 ,_________.
(1)求 的值;
(2)求 的值.
【答案】(1)
(2)
【知识点】用和、差角的正弦公式化简、求值、三角函数的化简、求值——诱导公式、三角函数的
化简、求值——同角三角函数基本关系
【分析】(1)选条件①:根据 满足单位圆方程求解;选条件②:根据正弦的二倍角公式,
结合同角三角函数的关系求解;选条件③:根据同角三角函数的关系求解;均可得
的值,再根据诱导公式化简即可;
学科网(北京)股份有限公司(2)根据题意可得 ,再根据 ,展开后根据同角三角函数的关
系结合角度范围分别求解正余弦值,从而求得 ,进而根据角度范围可得 .
【详解】(1)选条件①:因为角 的终边与单位圆的交点为 ,
可得 ,又 为锐角,所以 ,
所以由三角函数的定义可得
选条件②:
因为 , 为锐角,所以 ;
又因为 ,得 .
选条件③:因为 , ,
所以 得 ,
又因为 为锐角,所以 , , .
故
;
(2) ,
由(1) , ,
学科网(北京)股份有限公司.
.
5.(23-24高一上·河北沧州·期末)已知角 的终边经过点 .
(1)求 的值;
(2)求 的值.
【答案】(1)
(2)
【知识点】由终边或终边上的点求三角函数值、正、余弦齐次式的计算、三角函数的化简、求值
——同角三角函数基本关系、三角函数的化简、求值——诱导公式
【分析】(1)由三角函数定义得 ,进一步结合诱导公式化简求值即可;
(2)由平方关系、商数关系化成关于 的齐次式即可求解.
【详解】(1)由条件知 ,
.
(2)
.
6.(23-24高一上·江苏常州·期末)在平面直角坐标系xOy中,角 的始边为 轴的非负半轴,终
学科网(北京)股份有限公司边经过第四象限内的点 ,且 .
(1)求 的值;
(2)求 的值.
【答案】(1)
(2)
【知识点】由终边或终边上的点求三角函数值、三角函数的化简、求值——同角三角函数基本关系、
诱导公式二、三、四、诱导公式五、六
【分析】(1)利用角 的始边为x轴的非负半轴,终边经过第四象限内的点 ,得出
,求解 即可;
(2)利用诱导公式转化为 ,结合三角函数定义即可求值.
【详解】(1)因为角 的始边为x轴的非负半轴,终边经过第四象限内的点 ,
,
所以 ,且 ,
解得
(2)
因为 ,
学科网(北京)股份有限公司所以 ,
所以原式
7.(23-24高一上·湖北武汉·期末)已知函数 .
(1)化简 的解析式;
(2)若 ,且 , ,求 .
【答案】(1) ;
(2) .
【知识点】用和、差角的正弦公式化简、求值、三角函数的化简、求值——诱导公式、三角函数的
化简、求值——同角三角函数基本关系
【分析】(1)直接利用三角函数的诱导公式求出结果;
(2)利用三角函数的值和角的恒等变换求出结果.
【详解】(1)
(2)由于 ,
故 ,
所以 ,
由于 ,
故 , , ,
所以 , ,
学科网(北京)股份有限公司故 , ,
故
,
所以 .
8.(23-24高一上·安徽安庆·期末)(1)求 的值;
(2)已知 , ,求 的值.
【答案】(1) ;(2)
【知识点】诱导公式五、六、三角函数的化简、求值——同角三角函数基本关系、对数的运算性质
的应用、对数的运算
【分析】(1)根据对数的运算法则及指数的运算法则计算即可;
(2)由已知条件可得 ,再利用诱导公式及同角的商数关系化简原不等式即可得答案.
【详解】(1)
(2)因为 ,
所以 ,
所以 ,
所以 或 ,即 或 ,
又 , 为第二象限角,所以 ,所以 ;
学科网(北京)股份有限公司所以 .
9.(23-24高一上·山东青岛·期末)如图,平面直角坐标系 中,角 的终边 与单位圆交于
点 .
(1)求 , 的值;
(2)求 的值.
【答案】(1) ,
(2)
【知识点】三角函数的化简、求值——诱导公式、三角函数的化简、求值——同角三角函数基本关
系、由终边或终边上的点求三角函数值
【分析】(1)利用三角函数的定义即可求解.
(2)利用诱导公式化简即可求解.
【详解】(1)由三角函数的定义知:
因为 ,所以 ,
所以 .
(2)因为 , ,
学科网(北京)股份有限公司,
所以 .
10.(23-24高一上·广西柳州·期末)已知 ,
(1)求 的值
(2) .
【答案】(1)
(2)
【知识点】三角函数的化简、求值——诱导公式、三角函数的化简、求值——同角三角函数基本关
系
【分析】(1)利用同角三角函数的关系结合诱导公式求解即可.
(2)利用同角三角函数的关系求解即可.
【详解】(1)因为 ,
又因为 ,所以 .
(2)
11.(23-24高一上·山东济宁·期末)在平面直角坐标系xoy中,角 与 的顶点均为坐标原点O,
学科网(北京)股份有限公司始边均为x轴的非负半轴.若角 的终边OP与单位圆交于点 ,将OP绕原点O
按逆时针方向旋转 后与角 的终边OQ重合.
(1)求 的值;
(2)求 的值.
【答案】(1)
(2)
【知识点】三角函数的化简、求值——诱导公式、三角函数的化简、求值——同角三角函数基本关
系、正、余弦齐次式的计算、由单位圆求三角函数值
【分析】(1)根据任意角三角函数的定义结合同角三角关系可得 , ,进而
结合诱导公式运算求解;
(2)根据题意利用诱导公式结合齐次式问题运算求解.
【详解】(1)由题意可知: , ,
因为 ,即 ,且 ,解得 ,
即 , .
又因为 ,
可得 ,
学科网(北京)股份有限公司.
所以 .
(2)由(1)知 ,
所以 .
12.(23-24高一上·江苏宿迁·期末)已知函数 , .
(1)若角 顶点在坐标原点,始边为 正半轴,终边与单位圆交点的横坐标为 ,求 的值;
(2)若 ,求 的值.
【答案】(1)
(2)
【知识点】三角函数的化简、求值——诱导公式、三角函数的化简、求值——同角三角函数基本关
系、已知正(余)弦求余(正)弦、由终边或终边上的点求三角函数值
【分析】(1)利用同角三角函数的平方关系化简函数 的解析式,由已知条件求出 的值,
结合同角三角函数的基本关系可求得 的值;
(2)利用诱导公式结合同角三角函数的基本关系可求得 的值.
【详解】(1)解:由
,
学科网(北京)股份有限公司因为 , , ,
所以 ,
因为角 的终边与单位圆交点的横坐标为 ,且 ,
由三角函数的定义可得 ,则 ,
因此, .
(2)解:因为 ,
所以 ,
所以
.
13.(23-24高一上·江苏盐城·期末)如图,在平面直角坐标系 中,锐角 和钝角 的顶角与
坐标原点重合,始边与 轴的非负半轴重合,终边分别与单位圆交于 两点,且 .
(1)求 的值;
学科网(北京)股份有限公司(2)若 ,求 的值.
【答案】(1)
(2)
【知识点】三角函数的化简、求值——同角三角函数基本关系、诱导公式二、三、四、诱导公式五、
六
【分析】(1)依题意 ,利用诱导公式化简可得 ;
(2)由 可得 ,由同角三角函数之间的基本关系可得结果.
【详解】(1)由题意可知钝角 ,
所以 .
(2)由 可得 ,
即 ,可得 ,
即 ,所以 ;
可得 ,即 ,
解得 或 .
而 为钝角,且 ,故 ,故 ,
故 .
14.(23-24高一上·湖北恩施·期末)(1)已知 ,求
学科网(北京)股份有限公司的值;
(2)已知 为第二象限角, ,求 的值.
【答案】(1) ;(2)
【知识点】三角函数的化简、求值——诱导公式、三角函数的化简、求值——同角三角函数基本关
系、正、余弦齐次式的计算、sinα±cosα和sinα·cosα的关系
【分析】(1)利用诱导公式化简,可得 ,然后把原式化成齐次式,利用以求的正切函数求值;
(2)利用同角的三角函数的基本关系求值.
【详解】解:(1)∵ ,
∴由诱导公式化简得: ,
∴ ,
∴
.
(2)∵ ,∴ ,
∴ ,
∴ ,
又∵ 为第二象限角,∴ ,
∴ ,∴ .
15.(23-24高一上·江苏连云港·期末)求值
(1)已知 是第三象限角,且 ,求 的值;
(2)已知 ,求 的值.
学科网(北京)股份有限公司【答案】(1)
(2)
【知识点】已知正(余)弦求余(正)弦、已知弦(切)求切(弦)、诱导公式五、六、三角函数
的化简、求值——诱导公式
【分析】(1)根据条件,利用平方关系得到 ,再利用诱导公式即可求出结果;
(2)根据条件得到 ,从而得到 ,通过求出 ,联立
,求出 ,即可求出结果.
【详解】(1)因为 是第三象限角,且 ,
所以 ,
又 ,所以 .
(2)因为 ①,得到 ,即 ,
又 ,所以 ,由 ,
得到 ②,联立①②得到 ,
所以 .
16.(23-24高一上·陕西宝鸡·期末)已知 .
(1)求 的值;
(2)求 的值.
【答案】(1)
学科网(北京)股份有限公司(2) 或
【知识点】已知正(余)弦求余(正)弦、正、余弦齐次式的计算、三角函数的化简、求值——同
角三角函数基本关系、三角函数的化简、求值——诱导公式
【分析】(1)利用三角函数的诱导公式结合同角三角函数关系化简已知等式,即可求得答案;
(2)判断角所在象限,分类讨论,根据同角三角函数关系求出 的值,即可求得答案.
【详解】(1)由题意得
.
得 ,即 ;
(2)由 ,知 ,则 为第一象限角或第三象限角,
代入 ,得 ,
当 为第一象限角时, , ,
所以
当 为第三象限角时, , ,
所以
综上所述, 或
17.(23-24高一上·河北石家庄·期末)(1)计算:
:
学科网(北京)股份有限公司(2)已知 是第三象限角,且
①求 的值;
②求 的值.
(3)化简: .
【答案】(1) ;(2)① ;② ;(3) .
【知识点】对数的运算性质的应用、正、余弦齐次式的计算、三角函数的化简、求值——诱导公式、
二倍角的余弦公式
【分析】(1)运用对数换底公式、对数的运算性质、指数幂的运算性质化简计算即得;
(2)①利用三角诱导公式和同角的基本关系式化简已知式求得 ,再根据角的象限确定
值;②将所求的弦的二次齐次式通过构造分母化弦为切即得;
(3)利用二倍角公式化单角为半角,再逆用二倍角公式,最后根据角的范围去掉根号,化简即得.
【详解】(1)
.
(2)由题意可得:①
,
即 是第三象限角, .
② 是第三象限角, ,
学科网(北京)股份有限公司(3)由
,
原式 .
18.(23-24高一上·云南昭通·期末)已知
.
(1)化简 ;
(2)若 ,且 ,求 的值.
【答案】(1)
(2)
【知识点】二倍角的余弦公式、二倍角的正弦公式、用和、差角的正弦公式化简、求值、三角函数
的化简、求值——诱导公式
【分析】(1)利用诱导公式化简即可;
(2)先由 求得 ,再结合二倍角公式以及两角和与差的正弦公式即可求得答
案.
学科网(北京)股份有限公司【详解】(1)∵ ,
∴ ,
∴ .
(2)∵ ,∴ .
又 ,∴ ,
∴ , ,
∴ .
19.(23-24高一上·重庆·期末)化简或计算下列各式:
(1) ;
(2)
【答案】(1)18
(2)
【知识点】三角函数的化简、求值——诱导公式、对数的运算性质的应用、指数幂的运算
【分析】(1)由指数函数和对数函数的运算性质得到结果.
(2)由半角和全角公式化简得到结果.
【详解】(1)
学科网(北京)股份有限公司(2)
20.(23-24高一上·福建莆田·期末)(1)化简求值
(2)已知 为锐角,且满足 求 的值;
【答案】(1) ;(2)
【知识点】三角函数的化简、求值——诱导公式、正、余弦齐次式的计算、对数的运算性质的应用、
对数的运算
【分析】(1)根据对数的运算法则,即可求得答案;
(2)解方程求出 ,利用诱导公式化简 ,结合齐次式法求值,即可得
答案.
【详解】(1)
;
(2)因为 为锐角,且满足 ,
解得 ,(负值舍),
故 .
21.(23-24高一上·陕西西安·期末)(1)证明差角的余弦公式
学科网(北京)股份有限公司(2)若 ,求 的值.
【答案】(1)证明见解析;(2)
【知识点】三角函数的化简、求值——诱导公式、利用平方关系求参数、由三角函数值求终边上的
点或参数
【分析】(1)在单位圆中作角 ,利用三角函数定义写出相应点的坐标,再由
关系利用两点间的距离公式代入整理可证;
(2)根据整体角间的关系利用诱导公式求解可得.
【详解】(1)不妨令 .
如图,
设单位圆与 轴的正半轴相交于点 ,
以 轴非负半轴为始边作角 ,
则它们的终边分别与单位圆相交于点 , , .
连接 .若把扇形 绕着点 旋转 角,
则点 分别与点 重合.
学科网(北京)股份有限公司根据圆的旋转对称性可知, 与 重合,
从而 = ,∴ .
根据两点间的距离公式,得:
,
化简得:
当 时,上式仍然成立.
∴对于任意角 有: .
(2)由 ,
则 ;
且 ;
,
故 .
22.(23-24高一上·宁夏石嘴山·期末)已知角 为第四象限角,且角 的终边与单位圆交于点
.
(1)求 的值;
(2)求 的值.
学科网(北京)股份有限公司【答案】(1)
(2)
【知识点】三角函数的化简、求值——诱导公式、由终边或终边上的点求三角函数值
【分析】(1)将点代入单位圆后结合任意角三角函数定义求解即可.
(2)利用诱导公式化简求值即可.
【详解】(1)在单位圆中 ,解得 ,
因为 第四象限角,所以
(2) 第四象限角
.
23.(23-24高一上·江苏常州·期末)已知集合 .
(1)判断元素 , 与集合 的关系,并说明理由;
(2)求 .
【答案】(1) , .
(2)
【知识点】三角函数的化简、求值——诱导公式、交集的概念及运算、判断元素与集合的关系
【分析】(1)由元素与集合的关系求解即可;
(2)由 结合诱导公式求出 ,再由交集的定义求解即可.
【详解】(1)令 ,解得: ,故 ;
学科网(北京)股份有限公司令 ,解得: ,故 ;
故 , .
(2)因为 , ,
当 为偶数,则 ,
当 为奇数,则 ,
所以 ,所以 .
24.(23-24高一上·山东聊城·期末)在平面直角坐标系中,角 的顶点与坐标原点重合,始边与
轴非负半轴重合,终边过点 .
(1)求 的值;
(2)已知 为锐角, ,求 .
【答案】(1)
(2)
【知识点】给值求角型问题、三角函数的化简、求值——诱导公式、正、余弦齐次式的计算、由终
边或终边上的点求三角函数值
【分析】(1)利用三角函数的定义求出 的值,利用诱导公式以及弦化切可求得所求代数式的
值;
(2)求出 的值,利用两角差的正弦公式求出 的值,结合角 的范围可求得角 的
值.
【详解】(1)解:因为角 的终边过点 ,所以 ,
学科网(北京)股份有限公司则 , , .
.
(2)解:因为角 的终边过点 ,所以 为第四象限角,即 ,
又因为 为锐角,则 ,可得 ,
因为 ,则 ,
因为 ,所以 .
则
.
所以 .
25.(22-23高一上·陕西榆林·期末)筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,
所以至今还在农业生产中被使用.如图,假定在水流稳定的情况下,一个直径为10米的筒车开启后
按逆时针方向匀速旋转,转一周需要1分钟,筒车的轴心O距离水面的高度为 米.以盛水筒P刚
浮出水面时开始计算时间,设筒车开始旋转t秒后盛水筒P到水面的距离为h米(规定:若盛水筒
P在水面下,则h为负数).
学科网(北京)股份有限公司(1)写出h(单位:米)关于t(单位:秒)的函数解析式 (其中 , ,
);
(2)若盛水筒P在 , 时刻距离水面的高度相等,求 的最小值.
【答案】(1) ,
(2)40
【知识点】几何中的三角函数模型、由正(余)弦函数的性质确定图象(解析式)、三角函数的化
简、求值——诱导公式
【分析】(1)根据图形,利用几何知识和三角函数求解函数解析式;
(2)根据正弦方程,求解 的关系,通过分类讨论得到 的最小值.
【详解】(1)如图,过O作 交PB于点C,设筒车与水面的交点为M,N,连接OM.
因为筒车转一周需要1分钟,所以筒车每秒钟转 ,则 .
又因为 , ,所以 ,
则 .
, ,
即 , .
学科网(北京)股份有限公司(2)不妨设 ,由题意得 ,
故 ,
① , ,解得 , ,故 ,当且
仅当 , 时,等号成立,
② , ,解得 ,显然当 时, 取得最小
值,最小值为 .
综上, 的最小值为40.
【点睛】思路点睛:几何中的三角函数模型, 一般应按下面几个步骤进行:一是要认真分析题意,
借助已知或画出的示意图,弄清已知量和未知量,二是找出有关的数学模型,找出直角三角形或通
过添加辅助线构造有关的直角三角形,把问题转化为求直角三角形的边或角有关问题,三是选择合
适的三角函数表示出相应的角或线段,建立起函数模型.
学科网(北京)股份有限公司