文档内容
2024 年高考数学终极押题猜想
(高分的秘密武器:终极密押+押题预测)
押题猜想一 函数性质(奇偶性、对称性、周期性、单调性)的综合应用..........................................................1
押题猜想二 导数中的零点问题................................................................................................................................6
押题猜想三 三角恒等变换求值问题......................................................................................................................16
押题猜想四 解三角形中的范围与最值问题..........................................................................................................20
押题猜想五 外接球、内切球、棱切球..................................................................................................................26
押题猜想六 立体几何中的不规则图形..................................................................................................................32
押题猜想七 条件概率背景下概率与实际生活密切联系......................................................................................42
押题猜想八 圆锥曲线的离心率..............................................................................................................................53
押题猜想九 圆锥曲线中的面积问题......................................................................................................................58
押题猜想十 数列新定义..........................................................................................................................................69
押题猜想一 函数性质(奇偶性、对称性、周期性、单调性)的综合应用
已知函数 的定义域为R,对于任意实数x,y满足 ,且 ,
则下列结论错误的是( )
A. B. 为偶函数
C. 是周期函数 D.
【答案】C
【解析】令 ,得 ,因为 ,所以 ,A正确;
令 ,则 ,所以 ,则 为偶函数,B正确;
令 ,得 ,即 ,所以 不是周期函数,C错误;
当x取正整数n时, ,则 ,D正确.
故选:C.
押题解读
从近五年的高考情况来看,本部分多以选择题的压轴题呈现,函数的单调性、奇偶性、周期性是高考的必
1
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司考内容,重点关注单调性、奇偶性结合在一起,与函数图像、函数零点和不等式相结合进行考查,解题时
要充分运用转化思想、数形结合思想和通过合理的赋值解决,抽象函数问题是今年高考的热点之一.
1.已知函数 ,则不等式 的解集为( )
A. B. C. D.
【答案】D
【解析】因为 ,
所以 ,
所以 ,即 的图像关于点 中心对称.
(当且仅当
时等号成立).
因为 ,所以 ,所以 在 上单调递增.
由 ,得 .
由 可得 ,即 ,
所以 ,解得 .
故选:D.
2.(多选题)已知函数 为偶函数,且 ,当 时, ,则
( )
A. 的图象关于点 对称 B. 的图象关于直线 对称
C. 的最小正周期为2 D.
【答案】ABD
【解析】对A:因为 为偶函数,则 ,
即 ,所以 是奇函数,
所以 的图象关于点 对称,故A正确;
2
原创精品资源学科网独家享有版权,侵权必究!对B:因为 ,所以 的图象关于直线 对称,故B正确;
对C:因为 , ,
则 ,则 ,
所以 的最小正周期为 ,故C错误;
对D:因为当 时, ,所以 , ,
因为 的图象既关于点 对称,又关于直线 对称,
所以 , ,
因为 的最小正周期为4,
所以 ,所以 ,
所以
,故D正确.
故选:ABD.
3.(多选题)已知定义城为R的函数 .满足 ,且 ,
,则( )
A. B. 是偶函数
C. D.
【答案】ABC
【解析】对于A项,由 ,
令 ,则 ,故A项正确;
对于B项,令 ,则 ,
因 ,故 ,
令 ,则 ①,
所以函数 关于点 成中心对称,
令 ,则 ,
令 ,则 ②,
3
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司由①可得: ③,由②③可知: ,
且函数 的定义域为 ,则函数 是偶函数,故B项正确;
对于C项,令 ,则 ,
因为 , , ,代入上式中得,
故得: ,故C项正确;
对于D项,由上可知: ,则 ,
故函数 的一个周期为4,故 ,
令 ,则 ,
所以 ,
则 ,故D项错误.
故选:ABC.
4.(多选题)已知定义在R上的函数 的导函数分别为 ,且 ,
,则( )
A. 关于直线 对称 B.
C. 的周期为4 D.
【答案】ACD
【解析】由 ,得 ①,
②,得 ③,
由①②③,得 ,所以函数 图象关于直线 对称,故A正确;
由 ,得 ,令 ,得 ;
由 ,得 ,
令 ,得 ,
∴ ④,
又 ⑤,令 ,得 ,故B错误;
④⑤两式相加,得 ,得 ,
所以 ,即函数 的周期为4,故C正确;
由 ,令 ,得 ,所以 ,
4
原创精品资源学科网独家享有版权,侵权必究!所以 ,故D正确.
故选:ACD
5.(多选题)已知函数 的定义域为 ,且 ,都有 ,
, , ,当 时, ,则下列说法正确的
是( )
A.函数 的图象关于点 对称
B.
C.
D.函数 与函数 的图象有8个不同的公共点
【答案】ABD
【解析】由 得函数 关于 对称,A正确;
由 得函数 关于 对称,
所以 , ,
所以 ,即 ,
所以 ,故函数 的周期为 ,
由 知 , ,
又 时, ,所以 ,解得 ,
所以 时, ,
所以 ,B正确;
,C错误;
画出函数 和函数 的图象,如图:
,观察图象可得函数 与函数 的图像有8个不同的公共点,D正确.
故选:ABD.
5
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司押题猜想二 导数中的零点问题
已知函数 , .
(1)若 与 的图象有且仅有两个不同的交点,求实数 的取值范围;
(2)若 , 是 的导函数,方程 有两个不相等的实数解 , ,求证:
.
【解析】(1)法一:由已知 与 的图象有且仅有两个不同的交点,
则方程 ,即 有且仅有两个不同的实数解,
令 ,
则原问题可转化为函数 的图象与直线 有两个不同的交点.
,
令 ,得 ,令 ,得 ,
故 在 上单调递增,在 上单调递减,
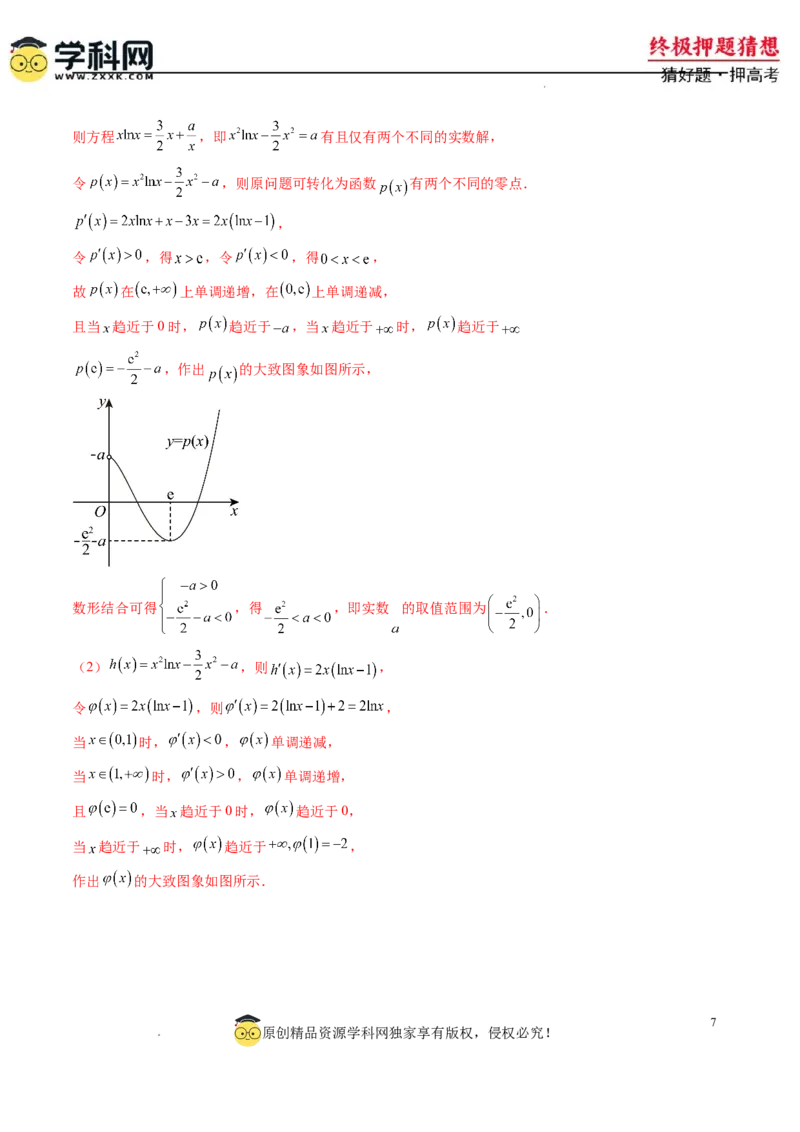
且当 趋近于0时, 趋近于0,当 趋近于 时, 趋近于 ,
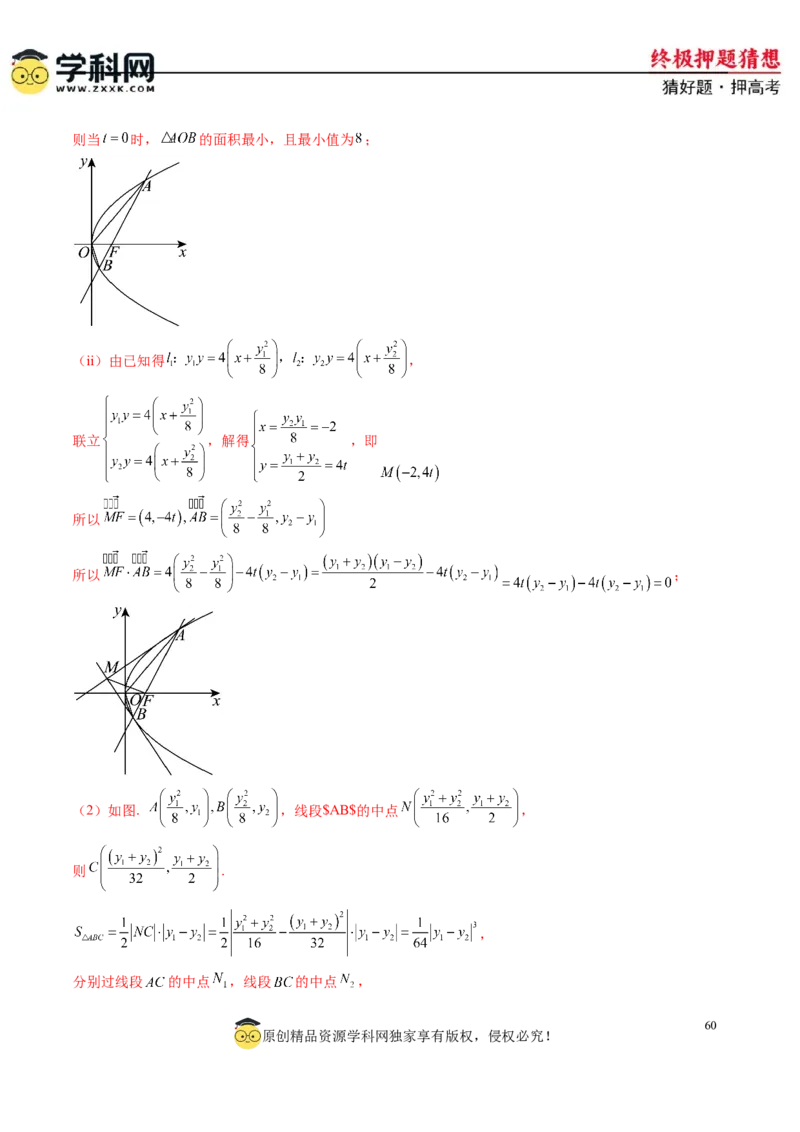
,作出 与 的大致图象如图所示,
数形结合可得 ,即实数 的取值范围为 .
解法二:若 与 的图象有且仅有两个不同的交点,
6
原创精品资源学科网独家享有版权,侵权必究!则方程 ,即 有且仅有两个不同的实数解,
令 ,则原问题可转化为函数 有两个不同的零点.
,
令 ,得 ,令 ,得 ,
故 在 上单调递增,在 上单调递减,
且当 趋近于0时, 趋近于 ,当 趋近于 时, 趋近于
,作出 的大致图象如图所示,
数形结合可得 ,得 ,即实数 的取值范围为 .
(2) ,则 ,
令 ,则 ,
当 时, , 单调递减,
当 时, , 单调递增,
且 ,当 趋近于0时, 趋近于0,
当 趋近于 时, 趋近于 ,
作出 的大致图象如图所示.
7
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司不妨令 ,则由 ,得 ,
令 , ,
则
当 时, ,所以 , 单调递减,
所以 ,所以 , .
因为 ,所以 ,
又 ,故 ,
又 , ,且 在 上单调递增,故 ,即 .
押题解读
本部分多以解答题呈现,导数压轴题以零点问题为主,重点关注由函数的零点生成的各类问题(结合不等
式、双变量问题、恒成立与有解问题、极值点偏移问题等)的求解思路,本质是如何构造函数以及变形函
数求解难题,导数中的零点问题与不等式结合是今年高考的热点之一
1.已知 ,函数 的图象在点 处的切线方程为 .
(1)求a,b的值;
(2)若方程 (e为自然对数的底数)有两个实数根 ,且 ,证明:
【解析】(1)因为 ,所以 ,
由题意知 ,所以 ,
8
原创精品资源学科网独家享有版权,侵权必究!联立方程组 ,解得 .
(2)由(1)可知 , ,
,设 ,
,
所以 即 在 上单调递增.
又 ,所以存在 ,使得 ,
故 在 上单调递减,在 上单调递增,
设 ,令 ,
则 ,
因为 在 上单调递增,
所以 在 上单调递增.
又 ,所以当 时, ,当 时, .
所以 在 上单调递减,在 上单调递增.
故 ,即 ,当且仅当 时,等号成立.
因为方程 有两个实数根 ,且 ,
也就是 ,且注意到 在 上单调递增,
所以 ,
所以 ,即 .
设 的根为: ,则 ,
又 在 上单调递增,所以 ,
故 ①.
易知 的图象在坐标原点处的切线方程为 ,
9
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司令 ,
则 ,
因为 在 上单调递增,
所以 在 上单调递增.
又 ,
所以当 时, ,当 时, ,
所以 在 上单调递减,在 上单调递增.
所以 , ,当且仅当 时,等号成立.
因为 ,所以 ,即 .
设 的根为 ,则 ,
又 在 上单调递减,
所以 ,所以 ,
从而 ②.
由①②可知: .
2.已知函数 .
(1)当 时,求曲线 在点 处的切线方程;
(2)设 ,求函数 的极大值;
(3)若 ,求函数 的零点个数.
【解析】(1)当 时, , ,
则 ,
所以曲线 在点 处的切线方程为 ,即 ;
(2) ,则 ,
则 ,
10
原创精品资源学科网独家享有版权,侵权必究!当 时, ,此时函数 无极值;
当 时,令 ,则 或 ,令 ,则 ,
所以函数 在 上单调递增,在 上单调递减,
所以 的极大值为 ;
当 时,令 ,则 或 ,令 ,则 ,
所以函数 在 上单调递增,在 上单调递减,
而函数 的定义域为 ,
所以此时函数 无极值.
综上所述,当 时,函数 无极大值;
当 时, 的极大值为 ;
(3)令 ,则 ,
当 时, ,
所以 时,函数 无零点;
当 时,由 ,得 ,所以 ,
则 时,函数 零点的个数即为函数 图象交点的个数,
令 ,则 ,
当 时, ,当 时, ,
所以函数 在 上单调递增,在 上单调递减,
所以 ,
又当 时, 且 ,当 时, ,
如图,作出函数 的大致图象,
11
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司又 ,由图可知,所以函数 的图象只有 个交点,
即当 时,函数 只有 个零点;
综上所述,若 ,函数 有 个零点.
3.已知函数 .
(1)讨论 的单调性;
(2)若关于 的不等式 无整数解,求 的取值范围.
【解析】(1) ,
当 ,得 ,
当 时, 时, , 单调递增,
时, , 单调递减,
当 时, 时, , 单调递减,
时, , 单调递增,
当 时, ,函数 在 上单调递增,
综上可知, 时,函数 的单调递增区间是 ,单调递减区间是 ,
时,函数 的单调递减区间是 ,单调递增区间是 ,
时,函数 的增区间是 ,无减区间.
(2)不等式 ,即 ,
12
原创精品资源学科网独家享有版权,侵权必究!设 , ,
设 , ,所以 单调递增,
且 , ,
所以存在 ,使 ,即 ,
当 时, , 单调递减,当 时, , 单调递增,
所以 ,
因为 ,所以 ,
当 时, ,当 时, ,
不等式 无整数解,即 无整数解,
若 时,不等式恒成立,有无穷多个整数解,不符合题意,
若 时,即 ,因为函数 在 上单调递减,在 上单调递增,
所以 时, ,所以 无整数解,符合题意,
当 时,因为 ,显然 是 的两个整数解,不符合题意,
综上可知, .
4.已知函数 .
(1)讨论函数 的单调性;
(2)求函数 在 上的零点个数.
【解析】(1)∵ ,故 ,
令 ,
所以 在 上单调递减,在 上单调递增;
(2)因为 , ,
则 .
13
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司①当 时,因为 ,
所以 在 上单调递减.所以 .
所以 在 上无零点.
②当 时,因为 单调递增,且 , ,
所以存在 ,使 .
当 时, ;当 时, .
所以 在 上单调递减,在 上单调递增,且 .
所以 .设 , ,
由(1)知 在 上单调递减,在 上单调递增.
所以 .
所以 ,得 .
所以 .所以 在 上存在一个零点.
所以 在 有2个零点.
③当 时, ,
所以 在 上单调递增.因为 ,所以 在 上无零点.
综上所述, 在 上的零点个数为2.
5.已知函数 .
(1)讨论 的单调性.
(2)已知 是函数 的两个零点 .
14
原创精品资源学科网独家享有版权,侵权必究!(ⅰ)求实数 的取值范围.
(ⅱ) 是 的导函数.证明: .
【解析】(1) .
①当 时, 在 上单调递增.
②当 时,令 得 ,即 在 上单调递增;
同理,令 得 ,即 在 上单调递减.
(2)(ⅰ)由(1)可知当 时, 在 上单调递增,不可能有两个零点.
当 时, 在 上单调递增,在 上单调递减,
若使 有两个零点,则 ,即 ,解得 ,
且 ,当 时, ,则有 ,
所以 的取值范围为 .
(ⅱ) 是函数 的两个零点,则有 ①, ②,
①-②得 ,即 ,
,
因为 有两个零点,所以 不单调,
因为 ,得 ,
所以 .
若要证明 成立,
只需证 ,
15
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司即证 ,令 ,则 ,
则不等式只需证 ,
即证 ,
令 ,
,令 ,
令 ,因为 ,得 在 上单调递减,
得 ,得 ,即 在 上单调递减,
得 ,得 ,即 在 上单调递减,
所以有 ,
故有 ,不等式得证.
押题猜想三 三角恒等变换求值问题
己知 , ,则 ( )
A. B. C. D.
【答案】B
【解析】因为 ,
所以 ,
所以 ,
所以 ,
16
原创精品资源学科网独家享有版权,侵权必究!所以 ,
因为 ,所以 ,
所以 ,所以 ,
所以 .
故选:B.
押题解读
在近几年的高考中,本部分多以选择题或者填空题形式呈现,三角恒等变换是三角函数部分考查频率最高
的一个知识点,考查题目灵活多变。在学习时,公式特别多,难度非常大,学好的首要条件是熟练掌握三
角函数诱导公式,然后主要是理解掌握两角差的余弦公式的推导过程,进而推导出两角和与差的正弦、余
弦、正切公式。在三角函数求值题目当中,常常会出现已知条件中给出两个或者一个三角函数值,求问题
中的三角函数值,解决此类问题的关键在于用“已知角”来表示“未知角”,因此三角恒等变换求值问题
是今年高考的热点之一.
1. ( )
A. B. C. D.
【答案】A
【解析】由
.
故选:A.
2.已知 ,则 ( )
A. B. C. D.
【答案】A
【解析】由已知可得, ,显然 ,
17
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司两边同时乘以 可得, ,
整理可得 ,
所以, ,
两边同时平方可得 ,
即 ,解得 或 .
当 时, ,此时 ,不满足题意,舍去.
所以, .
故选:A.
3.已知 , ,则 ( )
A. B. C. D.
【答案】B
【解析】因为 ,所以 ,
又因为 ,所以 ,
从而 , ,
所以 .
故选:B.
4.已知 , , ,则 ( )
A. B. C. D.
【答案】A
【解析】因为 , ,
18
原创精品资源学科网独家享有版权,侵权必究!所以 ,
解得 ,
所以 ,
又 ,所以 ,所以 .
故选:A
5.在 中,已知 .若 ,则 ( )
A.无解 B.2 C.3 D.4
【答案】A
【解析】由 ,即 ,则 ,
由 ,知 ,
则 ,则 ,
又 ,
故 ,设 ,则 ,
有 ,即 , ,
即该方程无解,故不存在这样三角形,即 无解.
故选:A.
6.已知 ,则 ( )
A. B. C. D.
【答案】A
【解析】由题意知, , ,
19
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司由 ,得 ,
整理,得 ,解得 或 ,
又 ,则 ,所以 .
所以
.
故选:A
押题猜想四 解三角形中的范围与最值问题
记锐角 的内角 , , 的对边分别为 , , ,已知 .
(1)证明: ;
(2)求 的取值范围.
【解析】(1)证明:由 ,
得 ,
即 ,
由正弦定理可得 ,即 ,
由余弦定理可得 ,故 ,
又 ,故 ,由 ,
故 ;
(2)由正弦定理可得:
,
又锐角 中,有 , ,解得 ,
20
原创精品资源学科网独家享有版权,侵权必究!即 ,即 ,
故 .
押题解读
本部分多以解答题或者填空题呈现,解三角形问题是高考高频考点,命题多位于解答题第一题,主要利用
三角形的内角和定理,正、余弦定理、三角形面积公式等知识解题,解题时要灵活利用三角形的边角关系
进行“边转角”、“角转边”.解决“最值与范围问题”的基本方法:①利用正弦定理,边转角,转化为
关于角的三角函数.②利用余弦定理,角转边,转化为关于边的函数,通过代入消元或基本不等式求解最
值.③若条件中包含“锐角三角形”,则一般转角.④通过画图寻找思路,以及检查结果.
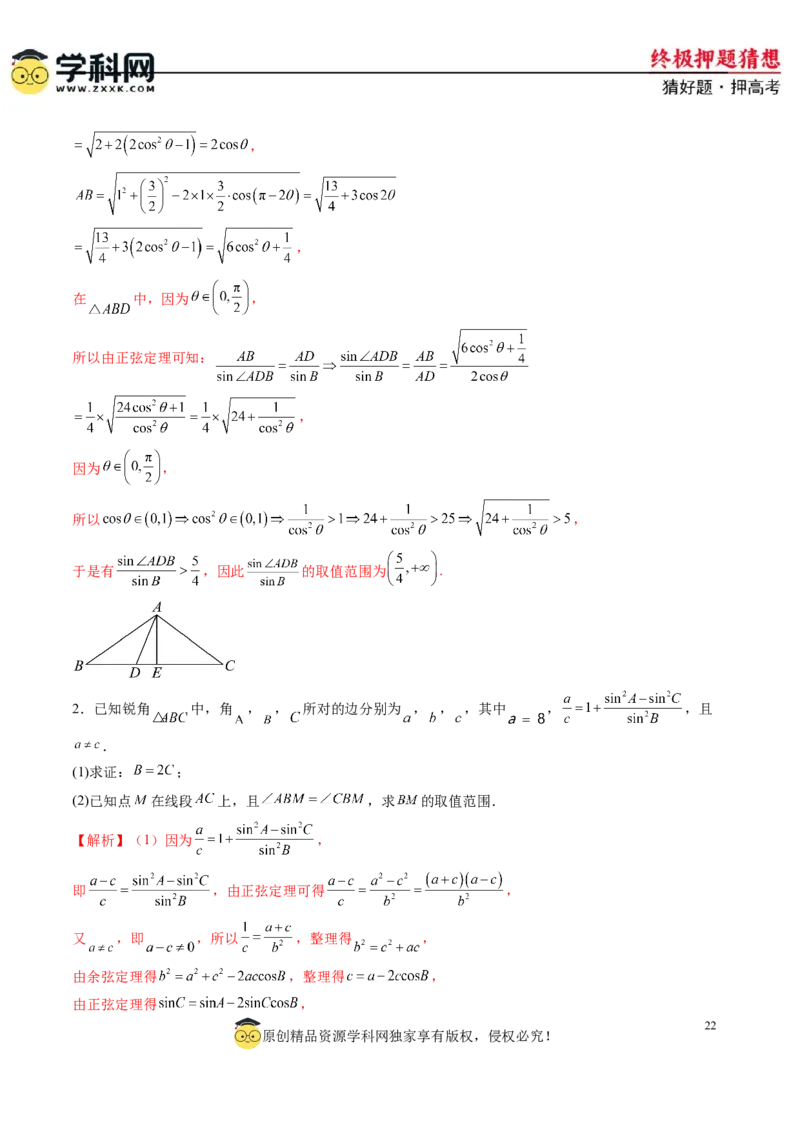
1.在 中, 为 边上一点, ,且 面积是 面积的2倍.
(1)若 ,求 的长;
(2)求 的取值范围.
【解析】(1)设 边上的高为 ,垂足为 ,
因为 面积是 面积的2倍,
所以有 ,
设 ,
由余弦定理可知:
,
解得 或 舍去,即 ;
(2)由(1)可知 ,
设 ,由 且 ,
由余弦定理可得:
21
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司,
,
在 中,因为 ,
所以由正弦定理可知:
,
因为 ,
所以 ,
于是有 ,因此 的取值范围为 .
2.已知锐角 中,角 , , 所对的边分别为 , , ,其中 , ,且
.
(1)求证: ;
(2)已知点 在线段 上,且 ,求 的取值范围.
【解析】(1)因为 ,
即 ,由正弦定理可得 ,
又 ,即 ,所以 ,整理得 ,
由余弦定理得 ,整理得 ,
由正弦定理得 ,
22
原创精品资源学科网独家享有版权,侵权必究!故 ,
即 ,
整理得 ,
又因为 为锐角三角形,则 ,可得 ,
所以 ,即 .
(2)因为点 在线段 上,且 ,即 平分 ,
又 ,所以 ,则 ,
在 中,由正弦定理得 ,
所以 ,
因为 为锐角三角形,且 ,所以 ,解得 .
故 ,所以 .
因此线段 长度的取值范围 .
3. 中, 为 边的中点, .
23
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司(1)若 的面积为 ,且 ,求 的值;
(2)若 ,求 的取值范围.
【解析】(1)因为 为 边的中点,所以 ,
又 ,即 ,解得 ,
在 中由余弦定理 ,
即 ,所以 ,
在 中由正弦定理 ,即 ,解得 .
(2)设 , ,
在 中由余弦定理 ,
即 ,
在 中由余弦定理 ,
即 ,
在 中由余弦定理 ,
因为 ,所以 ,则 ,
所以 ,
所以 ,
所以 ,即 .
4.已知平面四边形 中, .
(1)若 ,求 ;
(2)若 的面积为 ,求四边形 周长的取值范围.
【解析】(1)在 中,由余弦定理得 ,
24
原创精品资源学科网独家享有版权,侵权必究!在 中,由余弦定理得 ,
因为 ,
所以 ,
即 ,
解得 .
(2)由已知 ,得 ,
在 中, ,由余弦定理得
,则 ,
设 ,在 中,由余弦定理得
,
则 ,得 ,
所以 ,当且仅当 时取等号,
又 ,
所以四边形 周长的取值范围为 .
5. 的内角 的对边分别为 ,已知 .
(1)求 ;
(2)若 为锐角三角形,且 ,求 面积的取值范围.
【解析】(1)因为 中, ,即 ,
而 ,故 ,
25
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司故 ,又 ,
则 ;
(2)由(1)以及题设可得 ;
由正弦定理得
,
因为 为锐角三角形, , ,
则 ,
则 ,则 ,
即 ,则 ,
即 面积的取值范围为 .
押题猜想五 外接球、内切球、棱切球
已知体积为 的球O与正四面体 的四个面均相切,且与正四面体 的六条棱均相切,
则正四面体 与 的表面积的比值为( )
A.6 B. C. D.3
【答案】D
【解析】设球O的半径为R,因为球O的体积为 ,所以 ,得 .
设正四面体 的棱长为a,则该正四面体的高 ,所以该正四面体的体积
26
原创精品资源学科网独家享有版权,侵权必究!,又 ,
所以 ,解得 ,即正四面体 的棱长为 .
将正四面体 放到正方体中,如图,易知该正方体的内切球即与正四面体 的六条棱均
相切的球O.
因为 ,所以该正方体的棱长为6,则正四面体 的棱长为 ,
所以 ,
故选:D.
押题解读
纵观近几年高考对于组合体的考查,与球相关的外接与内切问题是高考命题的热点之一.高考命题小题综
合化倾向尤为明显,要求学生有较强的空间想象能力和准确的计算能力,才能顺利解答.从近几年全国高
考命题来看,这部分内容以选择题、填空题为主,大题很少见,此部分是重点也是一个难点,属于中等难
度.
1.(多选题)在三棱锥 中, 与 是全等的等腰直角三角形,平面 平面
为线段 的中点.过点 作平面截该三棱锥的外接球所得的截面面积可能是( )
A. B. C. D.
【答案】AB
【解析】由题意可知,满足条件的三棱锥有五种情况,如图.
由于图(1)(2)(3)(4)将三棱锥 补成正方体,其外接球球心为正方体中心,
点 到球心 的距离相等,因此只考虑一种情况.
以图(1)为例,其外接球半径 .
当 垂直于截面时,截面圆的半径取最小值 ,此时其面积为 ;
27
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司当截面过球心时,截面圆的半径取最大值 ,此时其面积为 .
因此截面圆的面积的取值范围为 .
若三棱锥为图(5), 时,
则球心 与 重合,此时 ,截面圆的面积为 .
故选:AB.
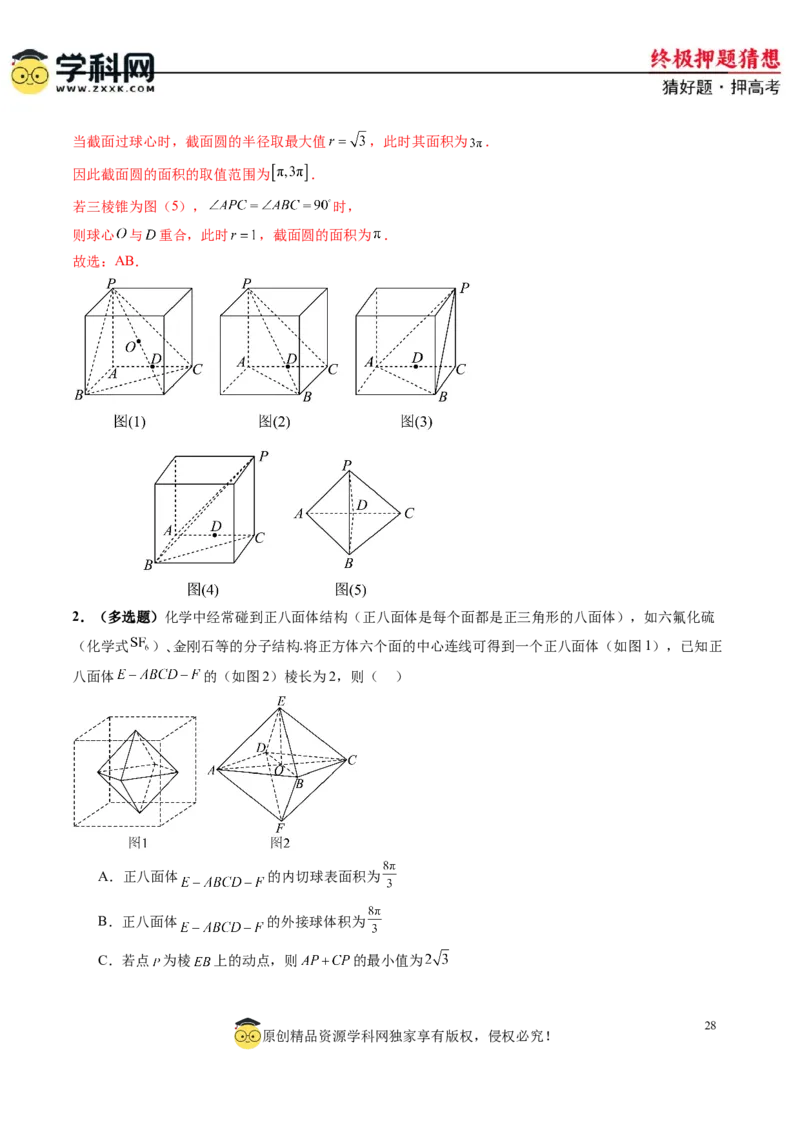
2.(多选题)化学中经常碰到正八面体结构(正八面体是每个面都是正三角形的八面体),如六氟化硫
(化学式 )、金刚石等的分子结构.将正方体六个面的中心连线可得到一个正八面体(如图1),已知正
八面体 的(如图2)棱长为2,则( )
A.正八面体 的内切球表面积为
B.正八面体 的外接球体积为
C.若点 为棱 上的动点,则 的最小值为
28
原创精品资源学科网独家享有版权,侵权必究!D.若点 为棱 上的动点,则三棱锥 的体积为定值
【答案】ACD
【解析】对于 A 项,设该正八面体内切球的半径为 ,由内切球的性质可知正八面体的体积
,
解得 ,故它的内切球表面积为 ,故A项正确;
对 于 B 项 , 设 该 正 八 面 体 外 接 球 的 半 径 为 , 由 图 知 , 是 正 方 形 ,
,
在 中, ,利用对称性知 ,故点 为正八面体外接球的球心,则
,
所以正八面体外接球的体积为 ,故 项错误;
对于C项,如图,因 与 是边长为2的全等的正三角形,可将 翻折到 ,使其与
共面,从而得到一个菱形 .
连接 与 相交于点 ,此时 , ,则 取得最小值为 ,
故 项正确;
对于D项,易知 ,因为 平面 平面 ,所以 //平面 ,
所以 ,故D项正确.
故选:ACD.
3.在四面体 中, ,且 与 所成的角为 .若四面体 的体
积为 ,则它的外接球半径的最小值为 .
29
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司【答案】3
【解析】依题意,可将四面体 补形为如图所示的直三棱柱 ,因为 与 所成的角为
,
所以 或 ,设 ,外接球半径记为 ,
外接球的球心如图点 .
易知 平面 ,所以点 到平面 的距离等于点 到平面 的距离,
,得 ,
在 中, ,
在 中,由余弦定理得 ,
所以当 时,外接球的半径会更小.
所以 ,
所以 ,
所以 .
故答案为:3.
4.如图,棱长为 的正方体 的内切球为球 , , 分别是棱 , 的中点, 在
棱 上移动,则( )
30
原创精品资源学科网独家享有版权,侵权必究!A.对于任意点 , 平面
B.直线 被球 截得的弦长为
C.过直线 的平面截球 所得的所有截面圆中,半径最小的圆的面积为
D.当 为 的中点时,过 , , 的平面截该正方体所得截面的面积为
【答案】C
【解析】
对于A,根据已知条件圆 为以 为圆心,半径 的圆; 在棱 上移动,
当 与点 重合时,平面 即为平面 ,因为 在直线 上,
所以 平面 ,所以 与平面 相交,A错误;
对于B,以 点为坐标原点, 、 、 所在直线分别为 、 、 轴建立如图所示的空间直角坐标
系,
则 、 、 、 ,
则 , , ,
设直线 与直线 夹角为 ,则 ,
由此可知 ,连结 ,过 作直线 的垂线,垂足为 ,
31
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司则在 中,有 ,解得 ,
设直线 被球O截得的弦长为 ,则 ,B错误;
对于C,过直线 的平面截球O所得的所有截面圆半径最小时,有 垂直于过 的平面,
此时圆的半径为 ,圆的面积为 ,C正确;
对于D,根据题意当 为 的中点时,
过 , , 的平面截该正方体所得截面为正六边形 , ,
在 中, ,所以边长 ,
所以截面面积为 ,D错误.
故选:C
5.在正四棱台 中, ,若球 与上底面A B C D 以及棱
1 1 1 1
均相切,则球 的表面积为( )
A. B. C. D.
【答案】C
【解析】设棱台上下底面的中心为 ,连接 ,
则 ,
所以棱台的高 ,
设球半径为 ,根据正四棱台的结构特征可知:球 与上底面A B C D 相切于 ,与棱 均相切
1 1 1 1
于各边中点处,
设 中点为 ,连接 ,
所以 ,解得 ,
所以球 的表面积为 ,
故选:C
32
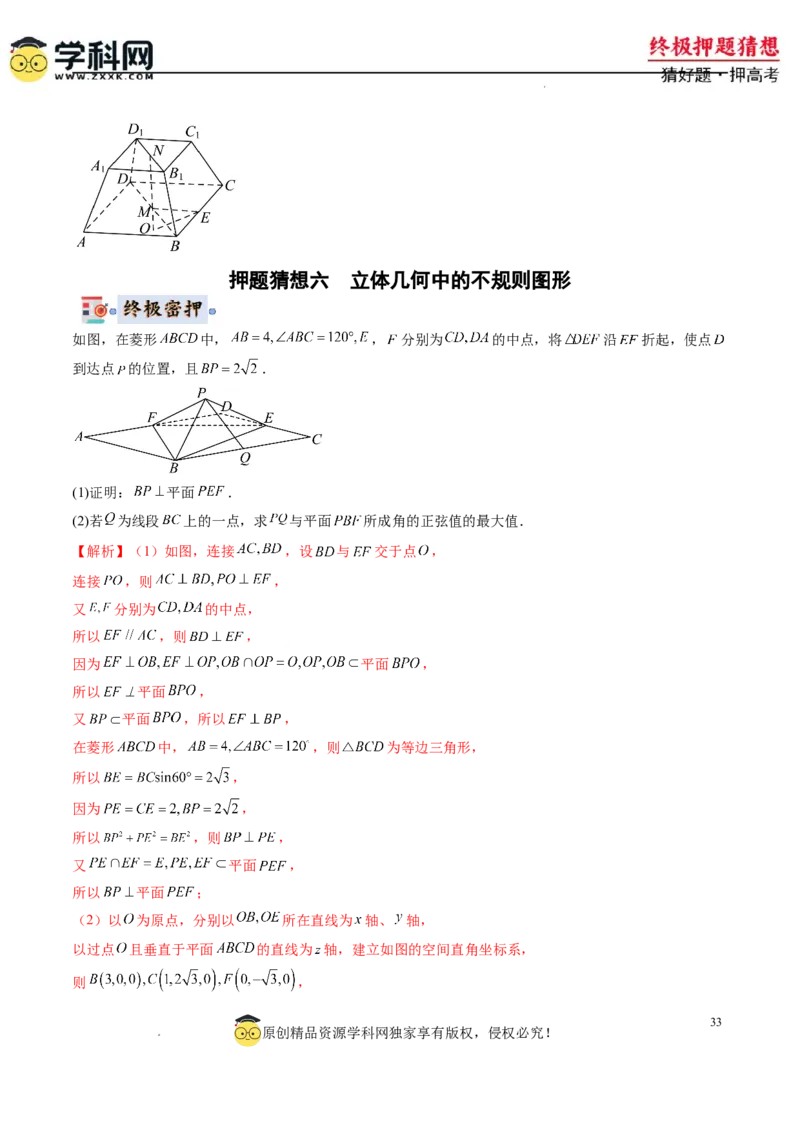
原创精品资源学科网独家享有版权,侵权必究!押题猜想六 立体几何中的不规则图形
如图,在菱形 中, , 分别为 的中点,将 沿 折起,使点
到达点 的位置,且 .
(1)证明: 平面 .
(2)若 为线段 上的一点,求 与平面 所成角的正弦值的最大值.
【解析】(1)如图,连接 ,设 与 交于点 ,
连接 ,则 ,
又 分别为 的中点,
所以 ,则 ,
因为 平面 ,
所以 平面 ,
又 平面 ,所以 ,
在菱形 中, ,则 为等边三角形,
所以 ,
因为 ,
所以 ,则 ,
又 平面 ,
所以 平面 ;
(2)以 为原点,分别以 所在直线为 轴、 轴,
以过点 且垂直于平面 的直线为 轴,建立如图的空间直角坐标系,
则 ,
33
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司由(1)可知 平面 ,
又 平面 ,所以平面 平面 ,
因为 ,
所以 ,即 .
在 中,点 到 的距离为 ,
又 ,故 ,
所以 ,
设平面 的法向量为 ,
则有 ,即 ,
令 ,则 ,所以 ,
设 ,
则 ,
设 与平面 所成的角为 ,
显然当 时, ,不符合题意,
则 ,所以 ,
所以
,
当 ,即 时, 取得最大值,为 .
34
原创精品资源学科网独家享有版权,侵权必究!押题解读
本部分多以解答题呈现,立体几何中的不规则图形问题是一个由抽象到直观,由直观到抽象的过程.高考
中,立体几何中的不规则图形常与空间中的平行、垂直、空间角及距离相结合命题.因此,关注立体几何
中的不规则图形问题是非常有必要的,也是今年高考的热点之一.
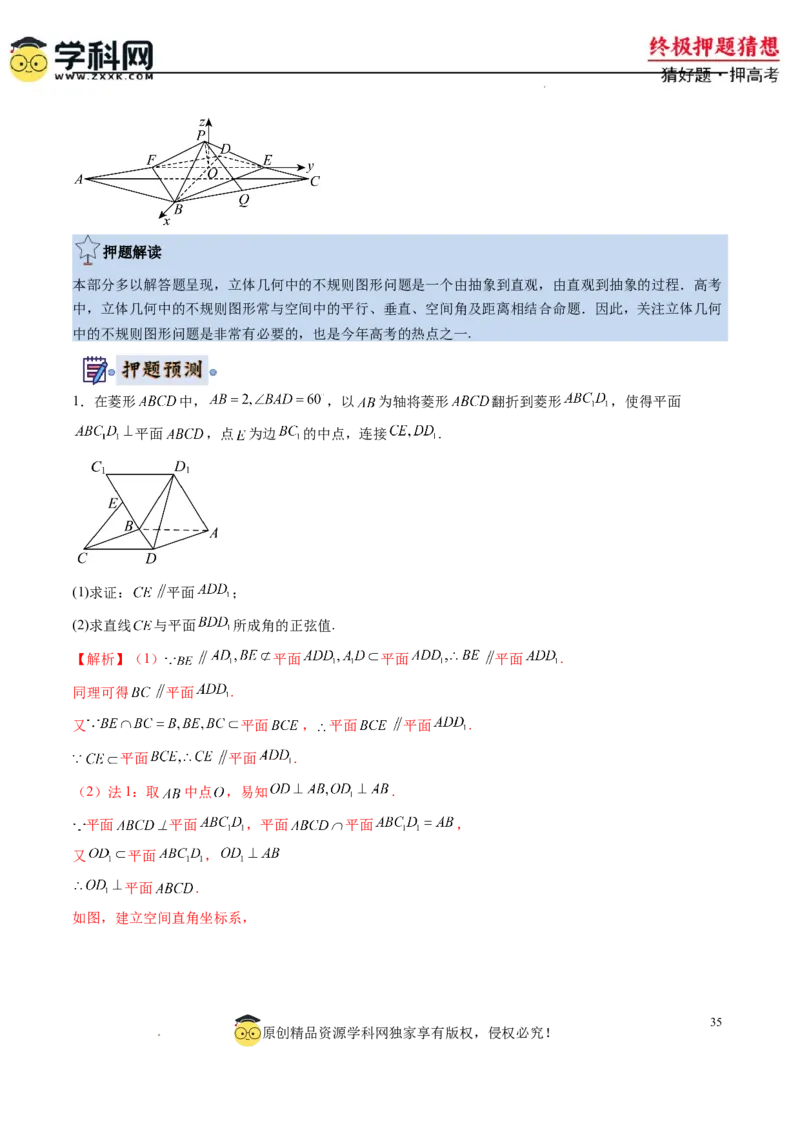
1.在菱形 中, ,以 为轴将菱形 翻折到菱形 ,使得平面
平面 ,点 为边 的中点,连接 .
(1)求证: 平面 ;
(2)求直线 与平面 所成角的正弦值.
【解析】(1) 平面 平面 平面 .
同理可得 平面 .
又 平面 , 平面 平面 .
平面 平面 .
(2)法1:取 中点 ,易知 .
平面 平面 ,平面 平面 ,
又 平面 ,
平面 .
如图,建立空间直角坐标系,
35
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司则 .
从而 ,得 .
又 ,设平面 的法向量 ,
有 ,得 ,解得 ,取 ,故 ,
设直线 与平面 所成角为 ,则
,
所以直线 与平面 所成角的正弦值为 .
法2:取 中点 ,则 是平行四边形,所以 .
从而 与平面 所成角即为 与平面 所成角,设为 .
过 作 交 于 ,过 作 交 于 ,
过 作 交 于 .
因为平面 平面 ,平面 平面 ,
又 平面 ,
36
原创精品资源学科网独家享有版权,侵权必究!所以 平面 ,又 平面 ,
所以 ,又 , 平面 ,
从而 平面 ,因为 平面 ,
所以 ,又 , 平面 ,
从而 平面 .
所以 的长即为 到平面 的距离.
由 ,可得 .
又 ,所以 到平面 的距离设为 即为 到平面 的距离,即 .
又 ,可得 .
在 中, ,所以 ,得 .
所以 ,
所以直线 与平面 所成角的正弦值为 .
2.如图,在圆台 中, 为轴截面, 为下底面圆周上一点, 为下
底面圆 内一点, 垂直下底面圆 于点 .
(1)求证:平面 平面 ;
(2)若 为等边三角形,求平面 和平面 的交线 与平面 所成角的正弦值.
【解析】(1)证明:由于 垂直下底面圆 ,
故 ,
平面 , 平面 ,所以 平面
又 ,所以 ,
37
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司平面 , 平面 ,所以 平面
平面 ,所以平面 平面
(2)由题意可得四边形 为等腰梯形,且 ,故 ,
,
由于 为等边三角形, , ,
又 , 在圆 上,所以 , ,
故 为 中点,
过 作 交圆 于点 ,又 ,故 ,
则 为平面 和平面 的交线,
建立如图所示的空间直角坐标系系,
,
则 ,
设平面 的法向量为 ,则 ,
取 ,则 ,
,
所以 ,
38
原创精品资源学科网独家享有版权,侵权必究!故 与平面 所成角的正弦值为
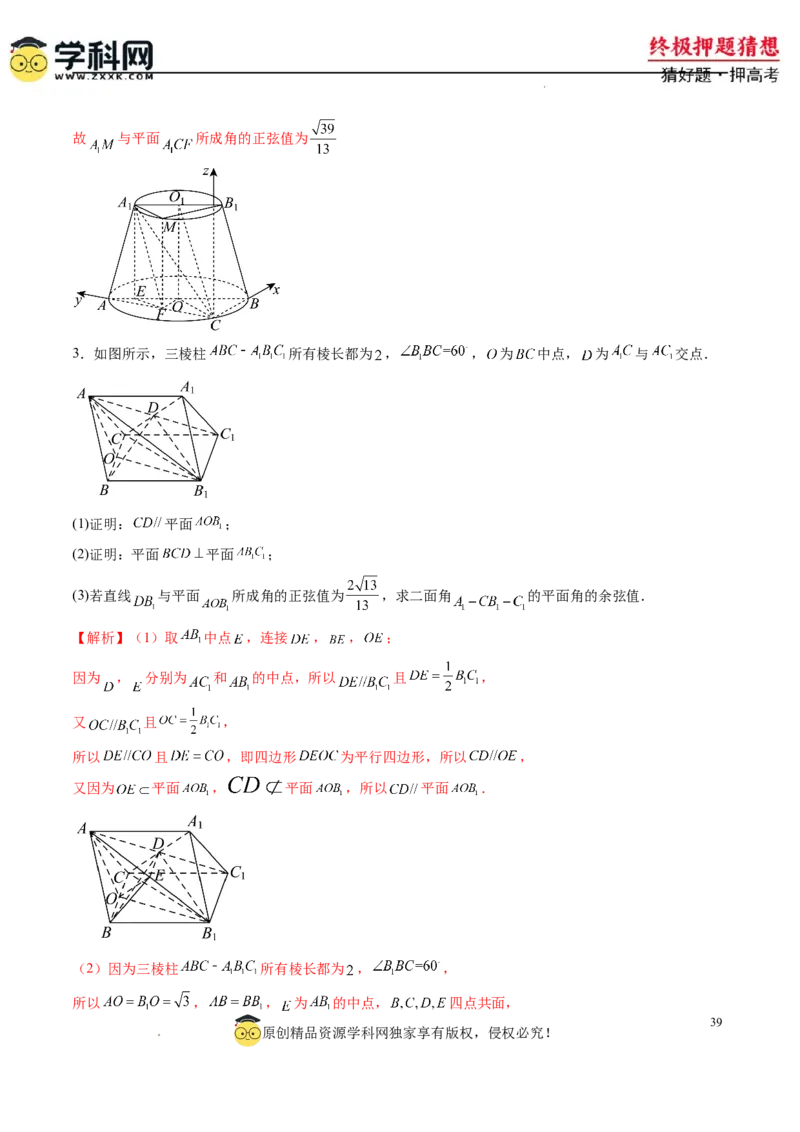
3.如图所示,三棱柱 所有棱长都为 , , 为 中点, 为 与 交点.
(1)证明: 平面 ;
(2)证明:平面 平面 ;
(3)若直线 与平面 所成角的正弦值为 ,求二面角 的平面角的余弦值.
【解析】(1)取 中点 ,连接 , , ;
因为 , 分别为 和 的中点,所以 且 ,
又 且 ,
所以 且 ,即四边形 为平行四边形,所以 ,
又因为 平面 , 平面 ,所以 平面 .
(2)因为三棱柱 所有棱长都为 , ,
所以 , , 为 的中点, 四点共面,
39
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司所以 ,且 , , 平面 , ,所以 平面 ,
又 平面 ,所以平面 平面 .
(3)由题意知, ,且 , , 平面 , ,
所以 平面 ,又 ,所以 平面 ,
所以 为直线 与平面 所成角,
又 ,所以 ,
因为 ,所以 平面 , 平面 ,所以 ,
所以 为直角三角形,所以 ,所以 ,
在 中, ,所以 ,
以 为原点,作 平面 ,以 , , 方向为 , , 轴正方向,建立空间直角坐标系,
如图所示:
则 , , , ,由 ,所以 ,
所以 , ,
设平面 的一个法向量为 ,则 ,即 ,
令 ,解得 ,所以平面 的一个法向量为 ,
记二面角 的平面角为 ,由图可得 为锐角,
则 ,
即二面角 的平面角的余弦值为 .
40
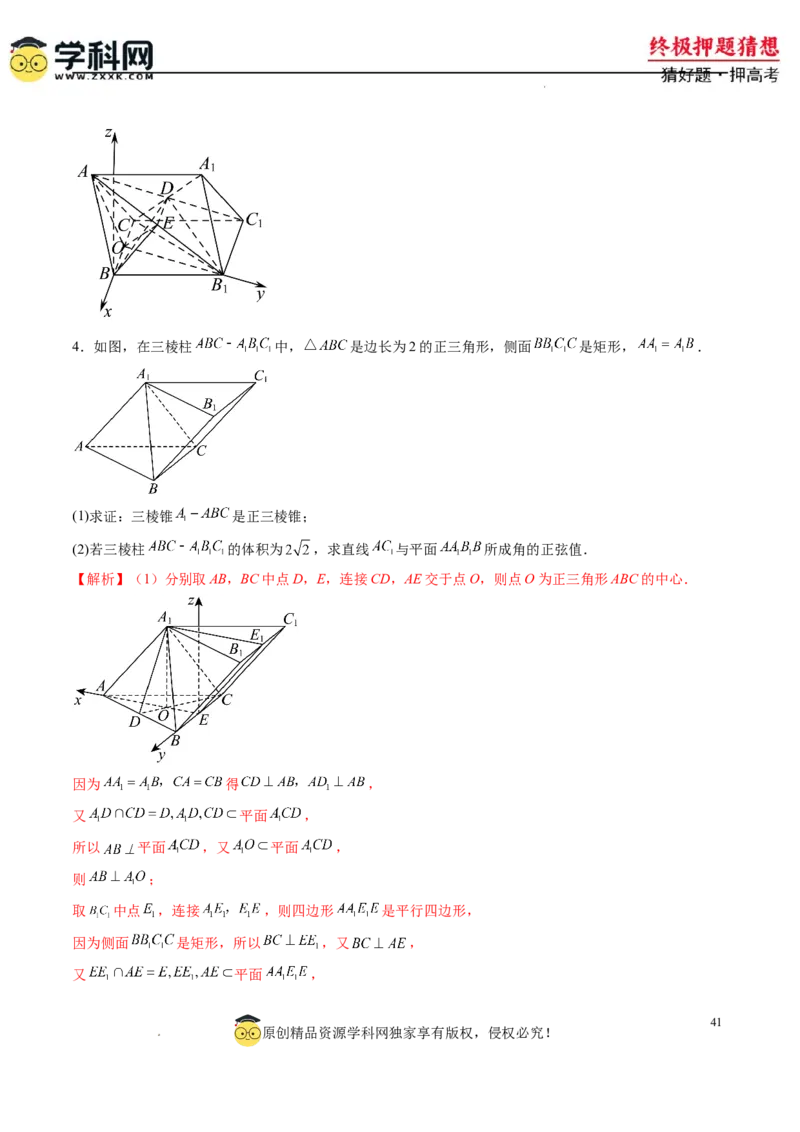
原创精品资源学科网独家享有版权,侵权必究!4.如图,在三棱柱 中, 是边长为2的正三角形,侧面 是矩形, .
(1)求证:三棱锥 是正三棱锥;
(2)若三棱柱 的体积为 ,求直线 与平面 所成角的正弦值.
【解析】(1)分别取AB,BC中点D,E,连接CD,AE交于点O,则点O为正三角形ABC的中心.
因为 得 ,
又 平面 ,
所以 平面 ,又 平面 ,
则 ;
取 中点 ,连接 ,则四边形 是平行四边形,
因为侧面 是矩形,所以 ,又 ,
又 平面 ,
41
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司所以 平面 ,又 平面 ,则 ;
又 , 平面 ,所以 平面 ,
所以三棱锥 是正三棱锥.
(2)因为三棱柱 的体积为 ,底面积为 ,所以高 ,
以E为坐标原点,EA为x轴正方向,EB为y轴正方向,过点E且与 平行的方向为z轴的正方向建立空
间直角坐标系,
则 ,
设平面 的法向量 ,因为 .
则 ,取 ,可得 ,
又 ,
设直线 与平面 所成角为θ,
所以 .
5.如图 是由两个三角形组成的图形,其中 , , , .将三
角形 沿 折起,使得平面 平面 ,如图 .设 是 的中点, 是 的中点.
(1)求直线 与平面 所成角的大小;
(2)连接 ,设平面 与平面 的交线为直线 ,判别 与 的位置关系,并说明理由.
【解析】(1)过 作 于 ,连接 ,
∵平面 平面 ,且平面 平面 , ,
42
原创精品资源学科网独家享有版权,侵权必究!∴ 平面 ,∴ 为直线 与平面 所成角.
∵ ,不妨设 ,
在 中,由正弦定理得 .
易知 ,
,
∴在 中, , ,
∴直线 与平面 所成角的大小为 .
(2)∵ 是 的中点, 是 的中点,∴DO∥PC;
又∵ , ,∴DO∥平面PBC;
又∵平面 平面 ,∴ ∥ ,
∴ ∥ .
押题猜想七 条件概率背景下概率与实际生活密切联系
流感病毒是一种 病毒,大致分为甲型、乙型、丙型三种,其中甲流病毒传染性最强,致死率最高,危
害也最大.某药品科技研发团队针对甲流病毒的特点,研发出预防甲流药品 和治疗甲流药品 ,根据研
发前期对动物试验所获得的相关有效数据作出统计,随机选取其中的100个样本数据,得到如下2×2列联
表:
甲流病毒
预防药品 合计
感染 未感染
未使用 24 21 45
使用 16 39 55
合计 40 60 100
43
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司(1)根据 的独立性检验,分析预防药品 对预防甲流的有效性;
(2)用频率估计概率,从已经感染的动物中,采用随机抽样方式每次选出1只,用治疗药品 对该动物进行
治疗,已知治疗药品 的治愈数据如下:对未使用过预防药品 的动物的治愈率为0.5,对使用过预防药
品 的动物的治愈率为0.75,若共选取3只已感染动物,每次选取的结果相互独立,记选取的3只已感染
动物中被治愈的动物只数为 ,求 的分布列与数学期望.
附: .
0.050 0.010 0.001
3.841 6.635 10.828
【解析】(1)假设 :使用预防药品 与对预防甲流无效果,
由列联表可知 ,
根据小概率值 的独立性检验,推断 不成立,
即认为使用预防药品 与对预防甲流有效果,此推断犯错误的概率不大于0.05.
(2)设事件 表示使用治疗药品 并且治愈,事件 表示未使用过预防药品 ,事件 表示使用过预防
药品 ,
由题意可得 ,
且 ,
则 ,
治疗药品 的治愈概率 ,
则 ,
所以 , ,
, ,
所以,随机变量 的分布列为
0 1 2 3
44
原创精品资源学科网独家享有版权,侵权必究!.
押题解读
回顾近几年的高考试题,可以看出概率统计解答题,大多紧密结合社会实际,以现实生活为背景设置试题,
注重知识的综合应用与实际应用,作为考查实践能力的重要载体,命题者要求考生会收集,整理、分析数
据,能从大量数据中抽取对研究问题有用的信息,建立数学模型,再应用数学原理和数学工具解决实际问
题,是高考常用的考查形式.
1.某企业监控汽车零件的生产过程,现从汽车零件中随机抽取100件作为样本,测得质量差(零件质量与
标准质量之差的绝对值)的样本数据如下表:
质量差(单位:
54 57 60 63 66
)
件数(单位:件) 5 21 46 25 3
(1)求样本质量差的平均数 ;假设零件的质量差 ,其中 ,用 作为 的近似值,求
的值;
(2)已知该企业共有两条生产汽车零件的生产线,其中全部零件的 来自第1条生产线.若两条生产线的废品
率分别为0.016和0.012,且这两条生产线是否产出废品是相互独立的.现从该企业生产的汽车零件中随机抽
取一件.
(i)求抽取的零件为废品的概率;
(ii)若抽取出的零件为废品,求该废品来自第1条生产线的概率.
参考数据:若随机变量 ,则
.
【解析】(1)由题意可知 ,
则 ,
所以
;
(2)(i)设事件 表示“随机抽取一件该企业生产的该零件为废品”,
45
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司事件 表示“随机抽取一件零件为第1条生产线生产”,
事件 表示“随机抽取一件零件为第2条生产线生产”,
则 , , , ,
所以 ;
(ii)因为 ,
所以 ,
所以 .
2.2023年10月10日,习近平总书记来到九江市考察调研,特别关注生态优先,绿色发展.某生产小型污
水处理设备企业甲,原有两条生产线,其中1号生产线生产的产品优品率为0.85,2号生产线生产的产品
优品率为0.8.为了进一步扩大生产规模,同时响应号召,助力长江生态恢复,该企业引进了一条更先进、
更环保的生产线,该生产线(3号)生产的产品优品率为0.95.所有生产线生产的产品除了优品,其余均为
良品.引进3号生产线后,1,2号生产线各承担20%的生产任务,3号生产线承担60%的生产任务,三条生
产线生产的产品都均匀放在一起,且无区分标志.
(1)现产品质检员,从所有产品中任取一件进行检测,求取出的产品是良品的概率;
(2)现某企业需购进小型污水处理设备进行污水处理,处理污水时,需几台同型号的设备同时工作.现有两种
方案选择:方案一,从甲企业购进设备,每台设备价格30000元,可先购进2台设备.若均为优品,则2台
就可以完成污水处理工作;若其中有良品,则需再购进1台相同型号设备才能完成污水处理工作.方案二,
从乙企业购进设备,每台23000元.需要三台同型号设备同时工作,才能完成污水处理工作.从购买费用期望
角度判断应选择哪个方案,并说明理由.
【解析】(1)设 “任取一件产品为优品”,
“产品为第 号生产线生产” ,
由全概率公式得:
则从所有产品中任取一件是良品的概率为:
.
(2)选择方案一,理由如下:
设从甲企业购进设备的费用为 元,
46
原创精品资源学科网独家享有版权,侵权必究!则 可取: , ,
由(1)知:
所以 .
设从乙企业购进设备的费用为 元,
则 ,
因为 ,
故选择方案一比较合适.
3.甲、乙两人进行知识问答比赛,共有 道抢答题,甲、乙抢题的成功率相同.假设每题甲乙答题正确的
概率分别为 和 ,各题答题相互独立.规则为:初始双方均为0分,答对一题得1分,答错一题得﹣1分,
未抢到题得0分,最后累计总分多的人获胜.
(1)若 , ,求甲获胜的概率;
(2)若 ,设甲第 题的得分为随机变量 ,一次比赛中得到 的一组观测值 ,如下表.
现利用统计方法来估计 的值:
①设随机变量 ,若以观测值 的均值 作为 的数学期望,请以此求出 的估计
值 ;
②设随机变量 取到观测值 的概率为 ,即 ;
在一次抽样中获得这一组特殊观测值的概率应该最大,随着 的变化,用使得 达到最大时 的取值
作为参数 的一个估计值.求 .
题目 1 2 3 4 5 6 7 8 9 10
得分 1 0 0 ﹣1 1 1 ﹣1 0 0 0
1 1 1
题目 11 12 14 15 17 19 20
3 6 8
﹣
得分 0 1 1 ﹣1 0 0 0 1 0
1
表1:甲得分的一组观测值.
47
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司附:若随机变量 , 的期望 , 都存在,则 .
【解析】(1)记甲获胜为事件 ,甲抢到3道题为事件 ,甲抢到2道题为事件 ,甲抢到1道题为事
件 ,甲抢到0道题为事件 ,
则 , ,
, ,
而 ,
,
,
,
所以
.
(2)① , , ,
所以 ;
因为 ,
由表中数据可知 ,
所以 , .
②因为 取值相互独立,
所以
,
48
原创精品资源学科网独家享有版权,侵权必究!所以 ;
令 得 ,
又 ,
所以当 时, , 单调递增;
当 时, , 单调递减;
即当 时 取到最大值,从而 .
4.为保护森林公园中的珍稀动物,采用某型号红外相机监测器对指定区域进行监测识别.若该区域有珍稀
动物活动,该型号监测器能正确识别的概率(即检出概率)为 ;若该区域没有珍稀动物活动,但监测器
认为有珍稀动物活动的概率(即虚警概率)为 .已知该指定区域有珍稀动物活动的概率为0.2.现用2台该
型号的监测器组成监测系统,每台监测器(功能一致)进行独立监测识别,若任意一台监测器识别到珍稀
动物活动,则该监测系统就判定指定区域有珍稀动物活动.
(1)若 .
(i)在该区域有珍稀动物活动的条件下,求该监测系统判定指定区域有珍稀动物活动的概率;
(ii)在判定指定区域有珍稀动物活动的条件下,求指定区域实际没有珍稀动物活动的概率(精确到
0.001);
(2)若监测系统在监测识别中,当 时,恒满足以下两个条件:①若判定有珍稀动物活动时,该
区域确有珍稀动物活动的概率至少为0.9;②若判定没有珍稀动物活动时,该区域确实没有珍稀动物活动
的概率至少为0.9.求 的范围(精确到0.001).
(参考数据: )
【解析】(1)记事件 为“监测系统判定指定区域有珍稀动物活动”,事件 为“监测区域实际上有珍稀
动物活动”,
(i) ;
(ii)
49
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司,
则
;
(2) ,
,
由题意可得 ,即 ,
令 , ,得 , ,故 , ,
即 ,即 ,则 ,
因为 ,所以 ,所以 ,
故 ,即 ,所以 ,
故 .
5.入冬以来,东北成为全国旅游和网络话题的“顶流”.南方的小土豆们纷纷北上体验东北最美的冬天,
这个冬天火的不只是东北的美食、东北人的热情,还有东北的洗浴中心,拥挤程度堪比春运,南方游客直
接拉着行李箱进入.东北某城市洗浴中心花式宠“且”,为给顾客更好的体验,推出了 和 两个套餐服
务,顾客可自由选择 和 两个套餐之一,并在App平台上推出了优惠券活动,下表是该洗浴中心在App
平台10天销售优惠券情况.
日期 1 2 3 4 5 6 7 8 9 10
销售量 (千张) 1.9 1.98 2.2 2.36 2.43 2.59 2.68 2.76 2.7 0.4
50
原创精品资源学科网独家享有版权,侵权必究!经计算可得: , , .
(1)因为优惠券购买火爆,App平台在第10天时系统出现异常,导致当天顾客购买优惠券数量大幅减少,
现剔除第10天数据,求 关于 的经验回归方程(结果中的数值用分数表示);
(2)若购买优惠券的顾客选择 套餐的概率为 ,选择 套餐的概率为 ,并且 套餐可以用一张优惠券,
套餐可以用两张优惠券,记App平台累计销售优惠券为 张的概率为 ,求 ;
(3)记(2)中所得概率 的值构成数列 .
①求 的最值;
②数列收敛的定义:已知数列 ,若对于任意给定的正数 ,总存在正整数 ,使得当 时,
,( 是一个确定的实数),则称数列 收敛于 .根据数列收敛的定义证明数列 收敛.
参考公式: , .
【解析】(1)剔除第10天数据的 ,
,
, ,
所以 ,
故 ,所以 .
(2)由题意可知 ,
其中 ,
所以 ,
51
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司又 ,
所以 是首项为 的常数列,故 ,
所以 ,又 ,
所以 是以首项为 ,公比为 的等比数列,
故 ,即 .
(3)①当 为偶数时, 单调递减,最大值为 ;
当 为奇数时, 单调递增,最小值为 ;
综上:数列 的最大值为 ,最小值为 .
②证明:对任意 总存在正整数 ,(其中 表示取整函数),
当 时, ,
所以数列 收敛.
6.某商场举办摸球赢购物券活动.现有完全相同的甲、乙两个小盒,每盒中有除颜色外形状和大小完全相
同的10个小球,其中甲盒中有8个黑球和2个白球,乙盒中有3个黑球和7个白球.参加活动者首次摸球,
可从这两个盒子中随机选择一个盒子,再从选中的盒子中随机摸出一个球,若摸出黑球,则结束摸球,得
300元购物券;若摸出的是白球,则将摸出的白球放回原来盒子中,再进行第二次摸球.第二次摸球有如
下两种方案:方案一,从原来盒子中随机摸出一个球;方案二,从另外一个盒子中随机摸出一个球.若第
二次摸出黑球,则结束摸球,得200元购物券;若摸出的是白球,也结束摸球,得100元购物券.用X表
示一位参加活动者所得购物券的金额.
(1)在第一次摸出白球的条件下,求选中的盒子为甲盒的概率.
(2)①在第一次摸出白球的条件下,通过计算,说明选择哪个方案第二次摸到黑球的概率更大;
②依据以上分析,求随机变量 的数学期望的最大值.
【解析】(1)设试验一次,“取到甲盒”为事件 ,“取到乙盒”为事件 ,
“第一次摸出黑球”为事件 ,“第一次摸出白球”为事件 ,
52
原创精品资源学科网独家享有版权,侵权必究!,
所以 ,
所以选中的盒子为甲盒的概率为 .
(2)① ,
所以方案一中取到黑球的概率为: ,
方案二中取到黑球的概率为: ,
因为 ,所以方案二中取到黑球的概率更大.
②随机变量 的值为 ,
依据以上分析,若采用方案一:
,
,
,
,
若采用方案二:
,
,
,
,
所以随机变量 的数学期望的最大值 .
53
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司押题猜想八 圆锥曲线的离心率
如图,已知双曲线 : ( , )的右焦点为 ,点 是双曲线 的渐近线上的一点,
点 是双曲线 左支上的一点.若四边形 是一个平行四边形,且 ,则双曲线 的离心率是
( )
A. B.2 C. D.3
【答案】A
【解析】因为四边形 是一个平行四边形,且 ,可得 ,即 ,
由双曲线 ,可得 ,渐近线方程为 ,即 ,
可得 ,且 ,
因为直线 ,可得 ,
又因为 ,所以 即 ,
代入双曲线 方程,可得 ,整理得 ,
所以 ,可得 ,即 ,
所以离心率 .
故选:A.
54
原创精品资源学科网独家享有版权,侵权必究!押题解读
圆锥曲线的离心率问题是高考中的一个难点和热点.因为离心率是刻画圆锥曲线形状的一个基本量,能考
查考生对圆锥曲线形状最本质的理解,考查数学抽象、数学建模、数学运算等数学核心素养,灵活多变,
综合性强.求椭圆或双曲线的离心率、与双曲线的渐近线有关的问题,多以选择、填空题的形式考查,难
度中等,是高考常用的考查形式.双曲线的离心率是今年高考的热点之一.
1.已知 , 分别是双曲线 的左、右焦点.若双曲线右支上存在一点 ,使
,则双曲线 的离心率的取值范围为( )
A. B. C. D.
【答案】B
【解析】依题意可得 ,
代入 并整理,得 ,解得 ,
所以 ,即 ,所以 .
因为双曲线上的点到焦点的距离的最小值为 ,
所以要满足双曲线右支上存在一点 ,使 ,则 ,
即 ,所以 ,
所以双曲线 的离心率的取值范围为 .
故选:B.
2.已知点A,B,C都在双曲线 : 上,且点A,B关于原点对称, .过
A作垂直于x轴的直线分别交 , 于点M,N.若 ,则双曲线 的离心率是( )
55
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司A. B. C.2 D.
【答案】B
【解析】
不妨设 ,由 且 轴,
所以 ,所以 ,
从而 ,即 ,
设点 ,且它在双曲线上,
,
即 ,其中 , ,
从而 , .
故选:B.
3.已知双曲线 的左,右顶点分别为 是双曲线上不同于 , 的一点,设直
线 的斜率分别为 ,则当 取得最小值时,双曲线 的离心率为( )
A. B. C. D.2
【答案】A
【解析】设 为双曲线 上异于 、 两点的任意一点,则 ,
又 , ,所以:
56
原创精品资源学科网独家享有版权,侵权必究!所以 ,
设 ,则 ( ),
因为 ,
所以 在 上单调递减,在 上单调递增,所以当 时,函数取得最小值.
即 时, 取得最小值.
此时: .
故选:A
4.已知 , 分别为双曲线 的左、右焦点,过 的直线与双曲线C左支相交于
A,B两点,若 , ,则双曲线C的离心率为( )
A. B. C. D.
【答案】C
【解析】如图,
由 , ,
结合正弦定理得 , ,
由双曲线的定义得 ,
所以 ,
57
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司在 中,由余弦定理,得 .
又因为 ,于是在 中,由余弦定理
得 ,整理得 ,
所以 .
故选:C.
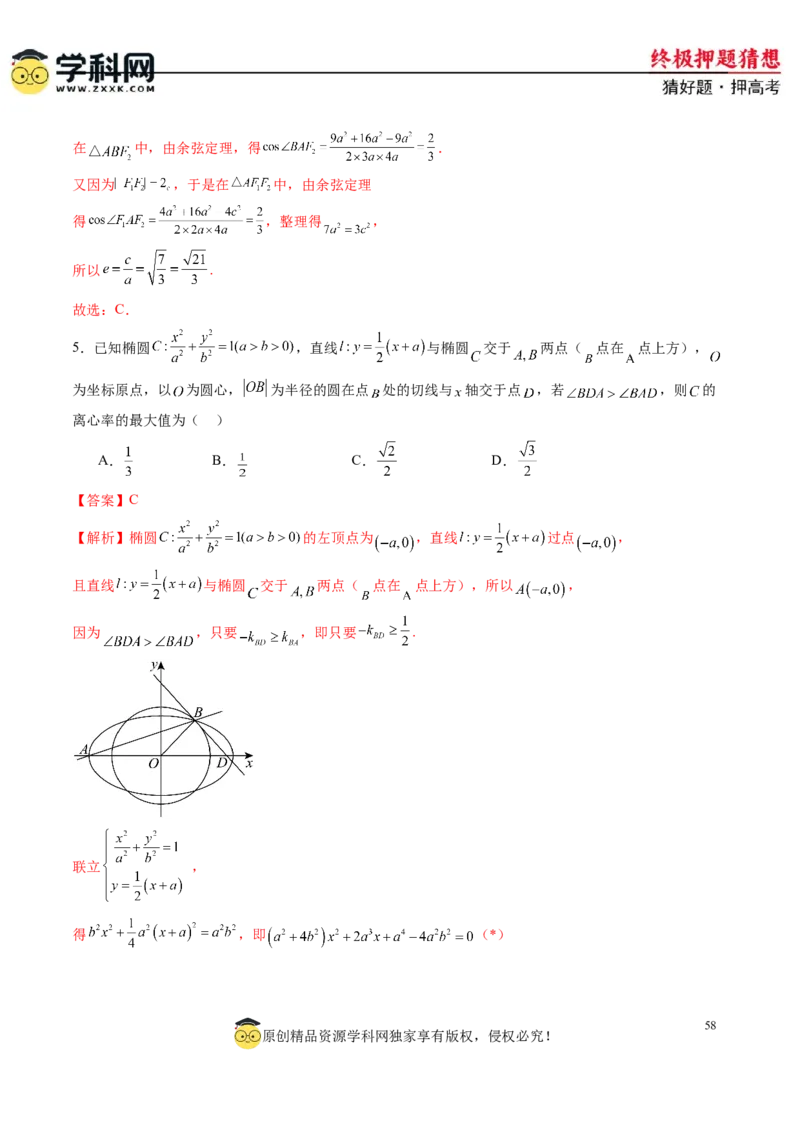
5.已知椭圆 ,直线 与椭圆 交于 两点( 点在 点上方),
为坐标原点,以 为圆心, 为半径的圆在点 处的切线与 轴交于点 ,若 ,则 的
离心率的最大值为( )
A. B. C. D.
【答案】C
【解析】椭圆 的左顶点为 ,直线 过点 ,
且直线 与椭圆 交于 两点( 点在 点上方),所以 ,
因为 ,只要 ,即只要 .
联立 ,
得 ,即 (*)
58
原创精品资源学科网独家享有版权,侵权必究!注意到 为方程(*)的一个根,故 ,
则 ,
所以点 ,可得 ,
由于 ,故 ,
令 ,得 ,
即 ,所以离心率的取值范围是 ,则 的离心率的最大值为 .
故选:C
押题猜想九 圆锥曲线中的面积问题
某校数学问题研究小组的同学利用电脑对曲线 进行了深人研究.已知点 在曲线 上,
曲线 在点 处的切线方程为 .请同学们研究以下问题,并作答.
(1)问题1:过曲线 的焦点 的直线与曲线 交于 两点,点 在第一象限.
(i)求 ( 为坐标原点)面积的最小值;
(ii)曲线 在点 处的切线分别为 ,两直线 相交于点 ,证明 .
(2)问题2:若 是曲线 上任意两点,过 的中点 作 轴的平行线交曲线 于点 ,记线段 与
曲线 围成的封闭区域为 ,研究小组的同学利用计算机经过多次模拟实验发现 是个定值,请
求出这个定值.
【解析】(1)(i)明显直线 的斜率不为零,设直线 的方程为 , ,
联立 ,消去 得 ,
则 ,
又 ,
59
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司则当 时, 的面积最小,且最小值为 ;
(ii)由已知得 ,
联立 ,解得 ,即
所以
所以 ;
(2)如图. ,线段$AB$的中点 ,
则 .
,
分别过线段 的中点 ,线段 的中点 ,
60
原创精品资源学科网独家享有版权,侵权必究!作 轴的平行线交抛物线分别于 两点,连接 .
同理可得 .
,(分子的上标均省略了文字“的面积”)
又由于 的面积 的面积 的面积 ,
所以 ,解得 .
押题解读
本部分多以解答题呈现,圆锥曲线面积问题的题目思路会比较顺畅,重点会在计算上面设置障碍,要利用
几何关系转换所求的面积,复习过程中要关注如何简化计算和转化思想.抛物线的面积问题是今年高考的
热点之一.
1.已知椭圆C: 短轴长为2,左、右焦点分别为 , ,过点 的直线l与椭圆C
交于M,N两点,其中M,N分别在x轴上方和下方, , ,直线 与直线MO交于点
,直线 与直线NO交于点 .
(1)若 的坐标为 ,求椭圆C的方程;
(2)在(1)的条件下,过点 并垂直于x轴的直线交C于点B,椭圆上不同的两点A,D满足 , ,
61
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司成等差数列.求弦AD的中垂线的纵截距的取值范围;
(3)若 ,求实数a的取值范围.
【解析】(1)依题意, ,故椭圆C: ;
易知点 为 的重心,则 ,故 ,
代入椭圆方程得 ∴椭圆C的方程为 ;
(2)
∵ , , 成等差数列,.∴ .
设 , ,AD中点 . ,
由弦长公式
,
∵ ,∴ ,
同理 ,代入可得 ,
①当AB斜率存在时 两式作差可得 , ,
∴ ,
62
原创精品资源学科网独家享有版权,侵权必究!∴弦AD的中垂线方程为 ,
当 时, ,即AD的中垂线的纵截距.
∵ 在椭圆C内,∴ ,得 ,且 .
②当AB斜率不存在时,此时AD: , .
∴综上所述 ,即弦AD的中垂线的纵截距的取值范围为 .
(3)解法一:易知点 , 分别为 , 的重心,设 , ,设点
, ,则根据重心性质及面积公式得 ,
,
而 ∴ ,
∴ ,∴ , ,
设直线l: ,则联立椭圆方程得
消元化简得, , ,
∴ , ,
∴ ,
∴ 对任意的t恒成立,
即 ,故实数a的取值范围为 .
解法二:易知点 为 的重心, ,
63
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司∴, , ,
此时,设点 , , , ,则根据重心的性质可得 ,
∴ , , ,
∴ , ;
;
而 ,∴ ,
∴ , ;
设直线l: ,则联立椭圆方程得
消元化简得, , ,
∴ , ,
∴ ,
∴ 对任意的t恒成立,
即 ,故实数a的取值范围为 .
2.如图,已知椭圆 和抛物线 , 的焦点 是 的上顶点,过 的直线
交 于 、 两点,连接 、 并延长之,分别交 于 、 两点,连接 ,设 、 的
面积分别为 、 .
64
原创精品资源学科网独家享有版权,侵权必究!(1)求 的值;
(2)求 的值;
(3)求 的取值范围.
【解析】(1)椭圆 的上顶点坐标为 ,
则抛物线 的焦点为 ,故 .
(2)若直线 与 轴重合,则该直线与抛物线 只有一个公共点,不符合题意,
所以直线 的斜率存在,设直线 的方程为 ,点 、 ,
联立 可得 , 恒成立,则 ,
.
(3)设直线 、 的斜率分别为 、 ,其中 , ,
联立 可得 ,解得 ,
点 在第三象限,则 ,
点 在第四象限,同理可得 ,
且
,
65
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司当且仅当 时,等号成立.
的取值范围为 .
3.已知椭圆 : 的上顶点为 ,离心率 ,过点 的直线 与椭圆
交于 , 两点,直线 、 分别与 轴交于点 、 .
(1)求椭圆 的方程;
(2)已知命题“对任意直线 ,线段 的中点为定点”为真命题,求 的重心坐标;
(3)是否存在直线 ,使得 ?若存在,求出所有满足条件的直线 的方程;若不存在,请说明
理由.(其中 、 分别表示 、 的面积)
【解析】(1)依题意 , ,又 ,
解得 ,所以椭圆 的方程为 ;
(2)因为命题“对任意直线 ,线段 的中点为定点”为真命题,
可以取直线 为 ,由 ,解得 或 ,
所以 , ,
则 ,所以 , ,所以 ,
设 的重心为 ,则 , ,
所以 ,即 的重心坐标为 .
(3)依题意可得直线 的斜率存在、不为 且斜率为负数,
66
原创精品资源学科网独家享有版权,侵权必究!设直线 , , ,
则直线 : ,令 ,得 ,同理可得: ;
所以
设直线 与 轴交于 点,则 ,所以 , ,
,
因为 ,故得 ①,
由 ,
则 , ,
代入①得 ,解得 ,
所以 ,故直线 的方程为 .
4.已知O为坐标原点,抛物线 ,过点 的直线交抛物线于A,B两点,
.
(1)求抛物线C的方程;
(2)若点 ,连接AD,BD,证明: ;
(3)已知圆G以G为圆心,1为半径,过A作圆G的两条切线,与y轴分别交于点M,N且M,N位于x轴
两侧,求 面积的最小值.
【解析】(1)设直线 的方程为 ,
由 ,得 ,
67
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司设 , ,
则 , ,
从而 ,解得 ,
所以抛物线C的方程为 ;
(2)要证 ,即证DG平分 ,即证 ,
由(1)可知 , ,
则
,
故 ;
(3)记AM,AN分别与圆G切于点T,F,连接TG,MG,NG,
由题意,得 ,
由切线长定理,知 , , ,
所以 ,
又
,解得 ,
所以 ,
当且仅当 ,即 时,取等号,
68
原创精品资源学科网独家享有版权,侵权必究!故 面积的最小值为8.
5.已知双曲线 的虚轴长为4,渐近线方程为 .
(1)求双曲线 的标准方程;
(2)过右焦点 的直线 与双曲线 的左、右两支分别交于点 ,点 是线段 的中点,过点 且与 垂
直的直线 交直线 于点 ,点 满足 ,求四边形 面积的最小值.
【解析】(1)由题意可知 ,
又浙近线方程为 ,所以 ,
易知双曲线的标准方程为 .
(2)
设 ,联立方程 得
,
且 ,
69
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司由 三点共线得 ①,
由 得 ,即 ②,
由①②解得 .
由 可知,四边形 是平行四边形,所以 ,
,
,
所以 ,
令 ,则 ,
令 ,则 ,
所以 在 上单调递减, 上单调递增,所以 ,
所以 ,当且仅当 ,即 时取等号.
押题猜想十 数列新定义
定义:若对 恒成立,则称数列 为“上凸数列”.
(1)若 ,判断 是否为“上凸数列”,如果是,给出证明;如果不是,请说明理由.
(2)若 为“上凸数列”,则当 时, .
(ⅰ)若数列 为 的前 项和,证明: ;
(ⅱ)对于任意正整数序列 ( 为常数且 ),若
70
原创精品资源学科网独家享有版权,侵权必究!恒成立,求 的最小值.
【解析】(1) 是“上凸数列”,理由如下:
因为 ,
令 ,
则 .
当 时, ,
所以 ,
所以 在区间 上单调递减,
所以 ,
所以 ,
所以 是“上凸数列”.
(2)(ⅰ)证明:因为 是“上凸数列”,由题意可得对任意 ,
,
所以 ,
所以 .
(ⅱ)令 ,
由(1)可得当 时, 是“上凸数列”,
由题意可知,当 时, .
因为 ,
即
.
所以
71
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司,
当且仅当 时等号成立,
所以 .
综上所述, 的最小值为 .
押题解读
继九省联考结束后,各省相继发布高考新命题结构通知,往年的新高考没出现这类题型,由于题型上的变
动较大,所以都会引起大部分考生的焦虑心态.回顾往年高考历程,创新题北京卷几乎每年都考,其它地
区每年都有,但不是“跳板式”的新,而是循序渐进式的新,因为高考出题非常重视高考卷的区分度,因
此在最后的备考阶段要踏踏实实地总结复习,多做、多想、多悟真题.本部分多以解答题压轴题形式呈现,
数列新定义是今年高考的热点之一
1.已知 为非零常数, ,若对 ,则称数列 为 数列.
(1)证明: 数列是递增数列,但不是等比数列;
(2)设 ,若 为 数列,证明: ;
(3)若 为 数列,证明: ,使得 .
【解析】(1) ,
故 为公差为 的等差数列,所以 ,
若 ,则当 时, ,不合题意,
若 ,则 ,满足要求,
,
因为 ,所以 ,故 ,故数列 为递增数列,
,由于 为递增数列,故 不是常数,
不是常数,故 数列是递增数列,但不是等比数列;
72
原创精品资源学科网独家享有版权,侵权必究!(2)因为 为 数列,所以 ,故 ,
因为 ,
所以 ,
因为 ,
当且仅当 时,等号成立,所以 ;
(3)因为 为 数列,
所以 ,
所以 ,
令 ,则 ,解得 ,
所以 ,使得 .
2.已知数列 的各项均为正整数,设集合 , ,记 的元
素个数为 .
(1)若数列A:1,3,5,7,求集合 ,并写出 的值;
(2)若 是递减数列,求证:“ ”的充要条件是“ 为等差数列”;
(3)已知数列 ,求证: .
【解析】(1)由题意,数列 ,
可得 ,
所以集合 ,所以 .
(2)证明:充分性:若 为等差数列,且 是递减数列,则 的公差为 ,
当 时, ,所以 ,
则 ,故充分性成立.
必要性:若 是递减数列, ,则 为等差数列,
因为 是递减数列,所以 ,
73
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司所以 ,且互不相等,
所以 ,
又因为 ,
所以 且互不相等,
所以 ,
所以 ,
所以 为等差数列,必要性成立.
所以若 是递减数列,“ ”的充要条件是“ 为等差数列”.
(3)证明:由题意集合 中的元素个数最多为 个,
即 ,
对于数列 ,此时 ,
若存在 ,则 ,其中 ,
故 ,
若 ,不妨设 ,则 ,而 ,
故 为偶数, 为奇数,矛盾,
故 ,故 ,故由 得到的 彼此相异,所以 .
3. 表示正整数a,b的最大公约数,若 ,且 ,
,则将k的最大值记为 ,例如: , .
(1)求 , , ;
(2)已知 时, .
(i)求 ;
(ii)设 ,数列 的前n项和为 ,证明: .
【解析】(1)依题可得 表示所有不超过正整数m,且与m互质的正整数的个数,
因为与2互质的数为1,所以 ;
74
原创精品资源学科网独家享有版权,侵权必究!因为与3互质的数为1,2,所以 ;
因为与6互质的数为1,5,所以 .
(2)(i)因为 中与 互质的正整数只有奇数,
所以 中与 互质的正整数个数为 ,所以 ,
又因为 中与 互质的正整数只有 与 两个,
所以 中与 互质的正整数个数为 ,
所以 ,所以 ,
(ii)解法一:因为 ,
所以 ,所以 ,
令 ,因为 ,
所以数列 是以 为首项, 为公比的等比数列,
所以数列 的前n项和 ,
所以 ,
又因为 ,所以 ,
解法二:因为 ,所以 ,
又因为 ,
所以 ,
75
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司所以 ,
所以 ,所以
因为 ,所以 ,
4.在 个数码 构成的一个排列 中,若一个较大的数码排在一个较小的数码的
前面,则称它们构成逆序(例如 ,则 与 构成逆序),这个排列的所有逆序的总个数称为这个排
列的逆序数,记为 ,例如, ,
(1)计算 ;
(2)设数列 满足 ,求 的通项公式;
(3)设排列 满足 ,求 ,
【解析】(1)在排列 中,与5构成逆序的有4个,与1构成逆序的有0个,
与2构成逆序的有0个,与4构成逆序的有1个,与3构成逆序的有0个,
所以 .
(2)由(1)中的方法,同理可得 ,
又 ,所以 ,
设 ,得 ,
所以 ,解得 ,则 ,
因为 ,
所以数列 是首项为1,公比为5的等比数列,
所以 ,则 .
(3)因为 ,
所以 ,
所以 ,
所以 .
76
原创精品资源学科网独家享有版权,侵权必究!5.若数列 满足:存在等差数列 ,使得集合 元素的个数为不大于 ,则称
数列 具有 性质.
(1)已知数列 满足 , .求证:数列 是等差数列,
且数列 有 性质;
(2)若数列 有 性质,数列 有 性质,证明:数列 有 性质;
(3)记 为数列 的前n项和,若数列 具有 性质,是否存在 ,使得数列 具有 性
质?说明理由.
【解析】(1)由 ,
故 ,
即 ,
又 ,故数列 是以 为首项, 为公差的等差数列,
则 ,即 ,
故存在等差数列 ,使 ,
由 ,故数列 有 性质;
(2)设对数列 ,存在等差数列 ,使 ,
对数列 ,存在等差数列 ,使 ,
则对数列 ,存在等差数列 ,
使 的值为 ,
这样的 最多有 个,即数列 有 性质;
(3)设对数列 ,存在等差数列 ,且其公差为 ,使得 ,
当 时,有
,
77
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司由 ,
故当 时, ,
当 时, ,当 时, 可能有 种,
故这样的 最多有 个,
即存在等差数列 ,使 ,
的元素个数不超过 个,
故一定存在 ,使得数列 具有 性质.
78
原创精品资源学科网独家享有版权,侵权必究!