文档内容
2013年全国统一高考数学试卷(文科)(新课标Ⅰ)
参考答案与试题解析
一、选择题共12小题.每小题5分,共60分.在每个小题给出的四个选项中,
只有一项是符合题目要求的一项.
1.(5分)已知集合A={1,2,3,4},B={x|x=n2,n∈A},则A∩B=( )
A.{1,4} B.{2,3} C.{9,16} D.{1,2}
【考点】1E:交集及其运算.
菁优网版权所有
【专题】5J:集合.
【分析】由集合A中的元素分别平方求出x的值,确定出集合B,找出两集合的公
共元素,即可求出交集.
【解答】解:根据题意得:x=1,4,9,16,即B={1,4,9,16},
∵A={1,2,3,4},
∴A∩B={1,4}.
故选:A.
【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.
2.(5分) =( )
A.﹣1﹣ i B.﹣1+ i C.1+ i D.1﹣ i
【考点】A5:复数的运算.
菁优网版权所有
【专题】11:计算题.
【分析】利用分式的分母平方,复数分母实数化,运算求得结果.
【解答】解: = = = =﹣1+ i.
故选:B.
【点评】本题考查复数代数形式的混合运算,复数的乘方运算,考查计算能力
.
第1页 | 共23页3.(5分)从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2
的概率是( )
A. B. C. D.
【考点】CC:列举法计算基本事件数及事件发生的概率.
菁优网版权所有
【专题】5I:概率与统计.
【分析】本题是一个等可能事件的概率,试验发生包含的事件是从4个不同的数
中随机的抽2个,共有C 2种结果,满足条件的事件是取出的数之差的绝对值
4
等于2的有两种,得到概率.
【解答】解:由题意知本题是一个等可能事件的概率,
试验发生包含的事件是从4个不同的数中随机的抽2个,共有C 2=6种结果,
4
满足条件的事件是取出的数之差的绝对值等于2,有2种结果,分别是(1,3)
,(2,4),
∴要求的概率是 = .
故选:B.
【点评】本题考查等可能事件的概率,是一个基础题,本题解题的关键是事件
数是一个组合数,若都按照排列数来理解也可以做出正确的结果.
4.(5分)已知双曲线C: (a>0,b>0)的离心率为 ,则C的渐
近线方程为( )
A.y= B.y= C.y=±x D.y=
【考点】KC:双曲线的性质.
菁优网版权所有
【专题】5D:圆锥曲线的定义、性质与方程.
【分析】由离心率和abc的关系可得b2=4a2,而渐近线方程为y=± x,代入可得
第2页 | 共23页答案.
【解答】解:由双曲线C: (a>0,b>0),
则离心率e= = = ,即4b2=a2,
故渐近线方程为y=± x= x,
故选:D.
【点评】本题考查双曲线的简单性质,涉及的渐近线方程,属基础题.
5.(5分)已知命题p:∀x∈R,2x<3x;命题q:∃x∈R,x3=1﹣x2,则下列命题
中为真命题的是( )
A.p∧q B.¬p∧q C.p∧¬q D.¬p∧¬q
【考点】2E:复合命题及其真假.
菁优网版权所有
【专题】21:阅读型;5L:简易逻辑.
【分析】举反例说明命题p为假命题,则¬p为真命题.引入辅助函数f(x)=x3+
x2﹣1,由函数零点的存在性定理得到该函数有零点,从而得到命题q为真命
题,由复合命题的真假得到答案.
【解答】解:因为x=﹣1时,2﹣1>3﹣1,所以命题p:∀x∈R,2x<3x为假命题,则
¬p为真命题.
令f(x)=x3+x2﹣1,因为f(0)=﹣1<0,f(1)=1>0.所以函数f(x)=x3+x2
﹣1在(0,1)上存在零点,
即命题q:∃x∈R,x3=1﹣x2为真命题.
则¬p∧q为真命题.
故选:B.
【点评】本题考查了复合命题的真假,考查了指数函数的性质及函数零点的判
断方法,解答的关键是熟记复合命题的真值表,是基础题.
6.(5分)设首项为1,公比为 的等比数列{a }的前n项和为S ,则( )
n n
第3页 | 共23页A.S =2a ﹣1 B.S =3a ﹣2 C.S =4﹣3a D.S =3﹣2a
n n n n n n n n
【考点】89:等比数列的前n项和.
菁优网版权所有
【专题】54:等差数列与等比数列.
【分析】由题意可得数列的通项公式,进而可得其求和公式,化简可得要求的
关系式.
【解答】解:由题意可得a =1× = ,
n
∴S = =3﹣ =3﹣2 =3﹣2a ,
n n
故选:D.
【点评】本题考查等比数列的求和公式和通项公式,涉及指数的运算,属中档
题.
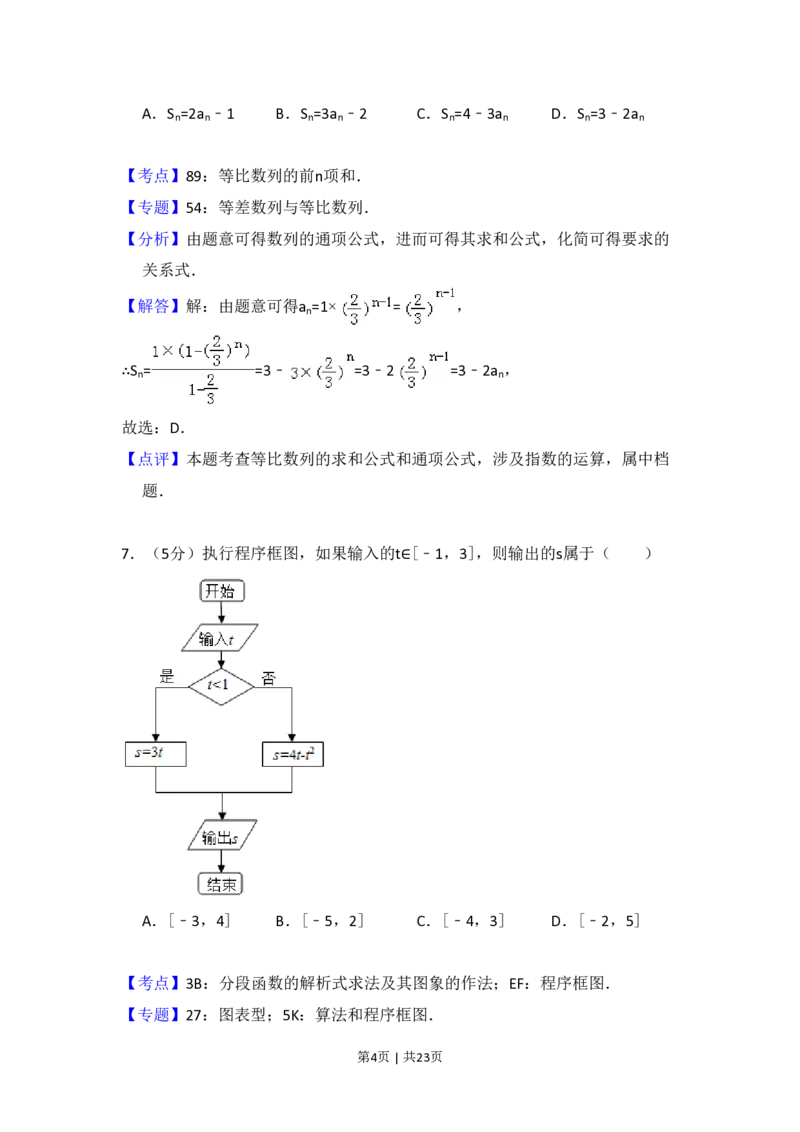
7.(5分)执行程序框图,如果输入的t∈[﹣1,3],则输出的s属于( )
A.[﹣3,4] B.[﹣5,2] C.[﹣4,3] D.[﹣2,5]
【考点】3B:分段函数的解析式求法及其图象的作法;EF:程序框图.
菁优网版权所有
【专题】27:图表型;5K:算法和程序框图.
第4页 | 共23页【分析】本题考查的知识点是程序框图,分析程序中各变量、各语句的作用,
再根据流程图所示的顺序,可知:该程序的作用是计算一个分段函数的函数
值,由条件为t<1我们可得,分段函数的分类标准,由分支结构中是否两条
分支上对应的语句行,我们易得函数的解析式.
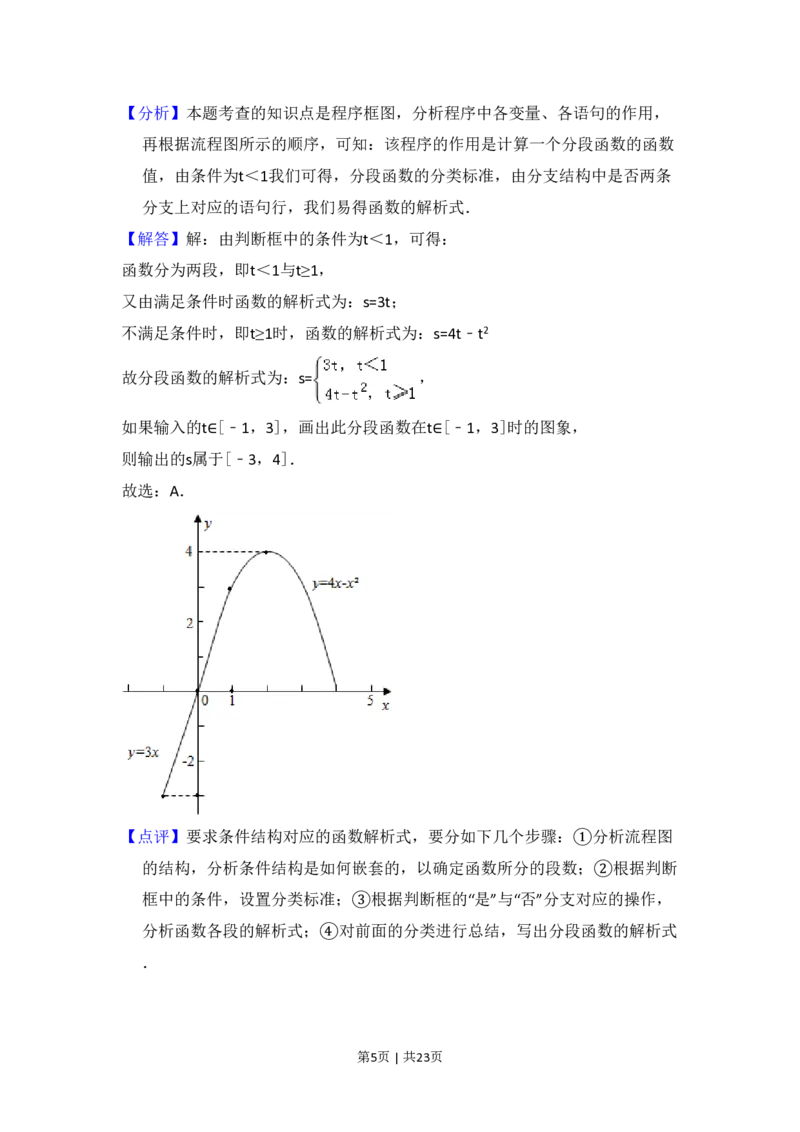
【解答】解:由判断框中的条件为t<1,可得:
函数分为两段,即t<1与t≥1,
又由满足条件时函数的解析式为:s=3t;
不满足条件时,即t≥1时,函数的解析式为:s=4t﹣t2
故分段函数的解析式为:s= ,
如果输入的t∈[﹣1,3],画出此分段函数在t∈[﹣1,3]时的图象,
则输出的s属于[﹣3,4].
故选:A.
【点评】要求条件结构对应的函数解析式,要分如下几个步骤:①分析流程图
的结构,分析条件结构是如何嵌套的,以确定函数所分的段数;②根据判断
框中的条件,设置分类标准;③根据判断框的“是”与“否”分支对应的操作,
分析函数各段的解析式;④对前面的分类进行总结,写出分段函数的解析式
.
第5页 | 共23页8.(5分)O为坐标原点,F为抛物线C:y2=4 x的焦点,P为C上一点,若|PF|
=4 ,则△POF的面积为( )
A.2 B.2 C.2 D.4
【考点】K8:抛物线的性质.
菁优网版权所有
【专题】11:计算题;5D:圆锥曲线的定义、性质与方程.
【分析】根据抛物线方程,算出焦点F坐标为( ).设P(m,n),由抛
物线的定义结合|PF|=4 ,算出m=3 ,从而得到n= ,得到△POF的
边OF上的高等于2 ,最后根据三角形面积公式即可算出△POF的面积.
【解答】解:∵抛物线C的方程为y2=4 x
∴2p=4 ,可得 = ,得焦点F( )
设P(m,n)
根据抛物线的定义,得|PF|=m+ =4 ,
即m+ =4 ,解得m=3
∵点P在抛物线C上,得n2=4 ×3 =24
∴n= =
∵|OF|=
∴△POF的面积为S= |OF|×|n|= =2
故选:C.
【点评】本题给出抛物线C:y2=4 x上与焦点F的距离为4 的点P,求△POF的
第6页 | 共23页面积.着重考查了三角形的面积公式、抛物线的标准方程和简单几何性质等
知识,属于基础题.
9.(5分)函数f(x)=(1﹣cosx)sinx在[﹣π,π]的图象大致为( )
A. B.
C. D.
【考点】3A:函数的图象与图象的变换.
菁优网版权所有
【专题】51:函数的性质及应用.
【分析】由函数的奇偶性可排除B,再由x∈(0,π)时,f(x)>0,可排除A,
求导数可得f′(0)=0,可排除D,进而可得答案.
【解答】解:由题意可知:f(﹣x)=(1﹣cosx)sin(﹣x)=﹣f(x),
故函数f(x)为奇函数,故可排除B,
又因为当x∈(0,π)时,1﹣cosx>0,sinx>0,
故f(x)>0,可排除A,
又f′(x)=(1﹣cosx)′sinx+(1﹣cosx)(sinx)′
=sin2x+cosx﹣cos2x=cosx﹣cos2x,
故可得f′(0)=0,可排除D,
故选:C.
【点评】本题考查三角函数的图象,涉及函数的奇偶性和某点的导数值,属基
础题.
10.(5分)已知锐角△ABC的内角A,B,C的对边分别为a,b,c,23cos2A+cos
2A=0,a=7,c=6,则b=( )
A.10 B.9 C.8 D.5
第7页 | 共23页【考点】HR:余弦定理.
菁优网版权所有
【专题】58:解三角形.
【分析】利用二倍角的余弦函数公式化简已知的等式,求出cosA的值,再由a与
c的值,利用余弦定理即可求出b的值.
【解答】解:∵23cos2A+cos2A=23cos2A+2cos2A﹣1=0,即cos2A= ,A为锐角,
∴cosA= ,
又a=7,c=6,
根据余弦定理得:a2=b2+c2﹣2bc•cosA,即49=b2+36﹣ b,
解得:b=5或b=﹣ (舍去),
则b=5.
故选:D.
【点评】此题考查了余弦定理,二倍角的余弦函数公式,熟练掌握余弦定理是
解本题的关键.
11.(5分)某几何体的三视图如图所示,则该几何体的体积为( )
A.16+8π B.8+8π C.16+16π D.8+16π
【考点】L!:由三视图求面积、体积.
菁优网版权所有
【专题】16:压轴题;27:图表型.
第8页 | 共23页【分析】三视图复原的几何体是一个长方体与半个圆柱的组合体,依据三视图
的数据,得出组合体长、宽、高,即可求出几何体的体积.
【解答】解:三视图复原的几何体是一个长方体与半个圆柱的组合体,如图,
其中长方体长、宽、高分别是:4,2,2,半个圆柱的底面半径为2,母线长
为4.
∴长方体的体积=4×2×2=16,
半个圆柱的体积= ×22×π×4=8π
所以这个几何体的体积是16+8π;
故选:A.
【点评】本题考查了几何体的三视图及直观图的画法,三视图与直观图的关系
,柱体体积计算公式,空间想象能力
12.(5分)已知函数f(x)= ,若|f(x)|≥ax,则a的取值范
围是( )
A.(﹣∞,0] B.(﹣∞,1] C.[﹣2,1] D.[﹣2,0]
【考点】7E:其他不等式的解法.
菁优网版权所有
【专题】16:压轴题;59:不等式的解法及应用.
【分析】由函数图象的变换,结合基本初等函数的图象可作出函数y=|f(x)|
的图象,和函数y=ax的图象,由导数求切线斜率可得l的斜率,进而数形结合
可得a的范围.
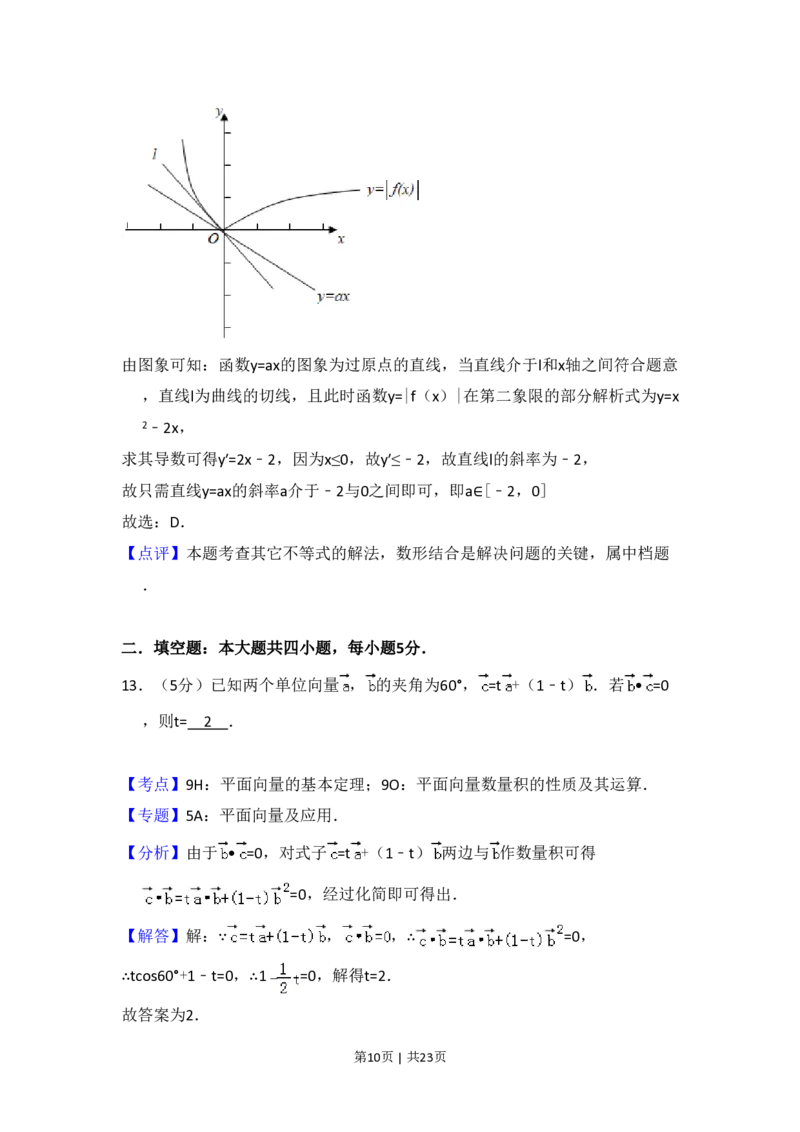
【解答】解:由题意可作出函数y=|f(x)|的图象,和函数y=ax的图象,
第9页 | 共23页由图象可知:函数y=ax的图象为过原点的直线,当直线介于l和x轴之间符合题意
,直线l为曲线的切线,且此时函数y=|f(x)|在第二象限的部分解析式为y=x
2﹣2x,
求其导数可得y′=2x﹣2,因为x≤0,故y′≤﹣2,故直线l的斜率为﹣2,
故只需直线y=ax的斜率a介于﹣2与0之间即可,即a∈[﹣2,0]
故选:D.
【点评】本题考查其它不等式的解法,数形结合是解决问题的关键,属中档题
.
二.填空题:本大题共四小题,每小题5分.
13.(5分)已知两个单位向量 , 的夹角为60°, =t +(1﹣t) .若 • =0
,则t= 2 .
【考点】9H:平面向量的基本定理;9O:平面向量数量积的性质及其运算.
菁优网版权所有
【专题】5A:平面向量及应用.
【分析】由于 • =0,对式子 =t +(1﹣t) 两边与 作数量积可得
=0,经过化简即可得出.
【解答】解:∵ , ,∴ =0,
∴tcos60°+1﹣t=0,∴1 =0,解得t=2.
故答案为2.
第10页 | 共23页【点评】熟练掌握向量的数量积运算是解题的关键.
14.(5分)设x,y满足约束条件 ,则z=2x﹣y的最大值为 3 .
【考点】7C:简单线性规划.
菁优网版权所有
【专题】59:不等式的解法及应用.
【分析】先根据约束条件画出可行域,再利用几何意义求最值,z=2x﹣y表示直
线在y轴上的截距,只需求出可行域直线在y轴上的截距最大值即可.
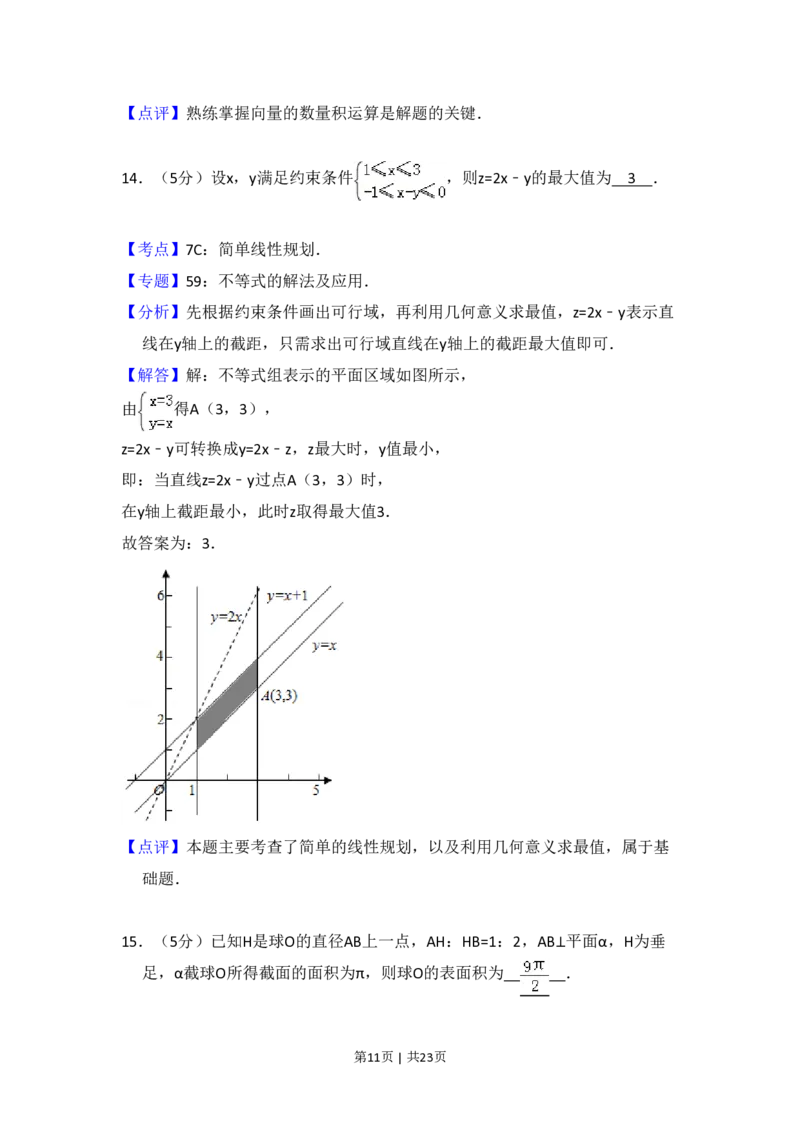
【解答】解:不等式组表示的平面区域如图所示,
由 得A(3,3),
z=2x﹣y可转换成y=2x﹣z,z最大时,y值最小,
即:当直线z=2x﹣y过点A(3,3)时,
在y轴上截距最小,此时z取得最大值3.
故答案为:3.
【点评】本题主要考查了简单的线性规划,以及利用几何意义求最值,属于基
础题.
15.(5分)已知H是球O的直径AB上一点,AH:HB=1:2,AB⊥平面α,H为垂
足,α截球O所得截面的面积为π,则球O的表面积为 .
第11页 | 共23页【考点】LG:球的体积和表面积.
菁优网版权所有
【专题】16:压轴题;5F:空间位置关系与距离.
【分析】本题考查的知识点是球的表面积公式,设球的半径为R,根据题意知由
与球心距离为 R的平面截球所得的截面圆的面积是π,我们易求出截面圆的
半径为1,根据球心距、截面圆半径、球半径构成直角三角形,满足勾股定
理,我们易求出该球的半径,进而求出球的表面积.
【解答】解:设球的半径为R,∵AH:HB=1:2,∴平面α与球心的距离为 R,
∵α截球O所得截面的面积为π,
∴d= R时,r=1,
故由R2=r2+d2得R2=12+( R)2,∴R2=
∴球的表面积S=4πR2= .
故答案为: .
【点评】若球的截面圆半径为r,球心距为d,球半径为R,则球心距、截面圆半
径、球半径构成直角三角形,满足勾股定理,即R2=r2+d2
16.(5分)设当x=θ时,函数f(x)=sinx﹣2cosx取得最大值,则cosθ= ﹣
.
【考点】GP:两角和与差的三角函数;H4:正弦函数的定义域和值域.
菁优网版权所有
【专题】16:压轴题;56:三角函数的求值.
【分析】f(x)解析式提取 ,利用两角和与差的正弦函数公式化为一个角的
正弦函数,由x=θ时,函数f(x)取得最大值,得到sinθ﹣2cosθ= ,与sin2θ
+cos2θ=1联立即可求出cosθ的值.
【解答】解:f(x)=sinx﹣2cosx= ( sinx﹣ cosx)= sin(x﹣α)(
其中cosα= ,sinα= ),
∵x=θ时,函数f(x)取得最大值,
第12页 | 共23页∴sin(θ﹣α)=1,即sinθ﹣2cosθ= ,
又sin2θ+cos2θ=1,
联立得(2cosθ+ )2+cos2θ=1,解得cosθ=﹣ .
故答案为:﹣
【点评】此题考查了两角和与差的正弦函数公式,同角三角函数间的基本关系
,以及正弦函数的定义域与值域,熟练掌握公式是解本题的关键.
三.解答题:解答应写出文字说明,证明过程或演算步骤.
17.(12分)已知等差数列{a }的前n项和S 满足S =0,S =﹣5.
n n 3 5
(Ⅰ)求{a }的通项公式;
n
(Ⅱ)求数列{ }的前n项和.
【考点】84:等差数列的通项公式;8E:数列的求和.
菁优网版权所有
【专题】54:等差数列与等比数列.
【分析】(Ⅰ)设出等差数列{a }的首项和公差,直接由S =0,S =﹣5列方程组
n 3 5
求出,然后代入等差数列的通项公式整理;
(Ⅱ)把(Ⅰ)中求出的通项公式,代入数列{ }的通项中进行列项
整理,则利用裂项相消可求数列{ }的前n项和.
【解答】解:(Ⅰ)设数列{a }的首项为a ,公差为d,则 .
n 1
由已知可得 ,即 ,解得a =1,d=﹣1,
1
故{a }的通项公式为a =a +(n﹣1)d=1+(n﹣1)•(﹣1)=2﹣n;
n n 1
(Ⅱ)由(Ⅰ)知 .
从而数列{ }的前n项和
S =
n
第13页 | 共23页= .
【点评】本题考查了等差数列的通项公式,考查了裂项相消法求数列的和,是
中档题.
18.(12分)为了比较两种治疗失眠症的药(分别成为A药,B药)的疗效,随
机地选取20位患者服用A药,20位患者服用B药,这40位患者服用一段时间后
,记录他们日平均增加的睡眠时间(单位:h)实验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5
2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4
服用B药的20位患者日平均增加的睡眠时间:
3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4
1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5
(Ⅰ)分别计算两种药的平均数,从计算结果看,哪种药的疗效更好?
(Ⅱ)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?
【考点】BA:茎叶图;BB:众数、中位数、平均数.
菁优网版权所有
【专题】5I:概率与统计.
【分析】(Ⅰ)利用平均数的计算公式即可得出,据此即可判断出结论;
(Ⅱ)利用已知数据和茎叶图的结构即可完成.
【解答】解:(Ⅰ)设A药观测数据的平均数据的平均数为 ,设B药观测数据
的平均数据的平均数为 ,
则 = ×(0.6+1.2+2.7+1.5+2.8+1.8+2.2+2.3+3.2+3.5+2.5+2.6+1.2+2.7+1.5+2.9+3.0
+3.1+2.3+2.4)=2.3.
第14页 | 共23页×(3.2+1.7+1.9+0.8+0.9+2.4+1.2+2.6+1.3+1.4+1.6+0.5+1.8+0.6+2.1+1.1+2.5+
1.2+2.7+0.5)=1.6.
由以上计算结果可知: .由此可看出A药的效果更好.
(Ⅱ)根据两组数据得到下面茎叶图:
从以上茎叶图可以看出,A药疗效的试验结果有 的叶集中在2,3上.而B药疗
效的试验结果由 的叶集中在0,1上.由此可看出A药的疗效更好.
【点评】熟练掌握平均数的计算公式和茎叶图的结果及其功能是解题的关键.
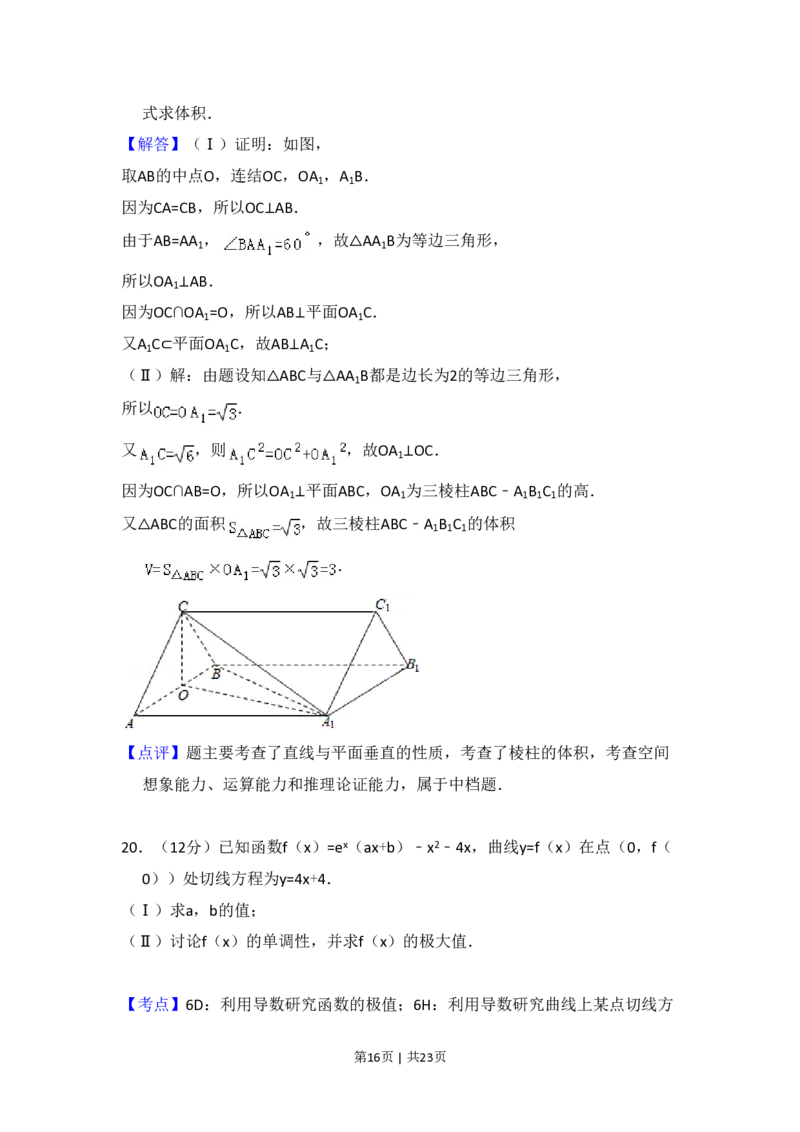
19.(12分)如图,三棱柱ABC﹣A B C 中,CA=CB,AB=AA ,∠BAA =60°
1 1 1 1 1
(Ⅰ)证明:AB⊥A C;
1
(Ⅱ)若AB=CB=2,A C= ,求三棱柱ABC﹣A B C 的体积.
1 1 1 1
【考点】LF:棱柱、棱锥、棱台的体积;LW:直线与平面垂直.
菁优网版权所有
【专题】5F:空间位置关系与距离.
【分析】(Ⅰ)由题目给出的边的关系,可想到去AB中点O,连结OC,OA ,可
1
通过证明AB⊥平面OA C得要证的结论;
1
(Ⅱ)在三角形OCA 中,由勾股定理得到OA ⊥OC,再根据OA ⊥AB,得到OA 为
1 1 1 1
三棱柱ABC﹣A B C 的高,利用已知给出的边的长度,直接利用棱柱体积公
1 1 1
第15页 | 共23页式求体积.
【解答】(Ⅰ)证明:如图,
取AB的中点O,连结OC,OA ,A B.
1 1
因为CA=CB,所以OC⊥AB.
由于AB=AA , ,故△AA B为等边三角形,
1 1
所以OA ⊥AB.
1
因为OC∩OA =O,所以AB⊥平面OA C.
1 1
又A C⊂平面OA C,故AB⊥A C;
1 1 1
(Ⅱ)解:由题设知△ABC与△AA B都是边长为2的等边三角形,
1
所以 .
又 ,则 ,故OA ⊥OC.
1
因为OC∩AB=O,所以OA ⊥平面ABC,OA 为三棱柱ABC﹣A B C 的高.
1 1 1 1 1
又△ABC的面积 ,故三棱柱ABC﹣A B C 的体积
1 1 1
.
【点评】题主要考查了直线与平面垂直的性质,考查了棱柱的体积,考查空间
想象能力、运算能力和推理论证能力,属于中档题.
20.(12分)已知函数f(x)=ex(ax+b)﹣x2﹣4x,曲线y=f(x)在点(0,f(
0))处切线方程为y=4x+4.
(Ⅰ)求a,b的值;
(Ⅱ)讨论f(x)的单调性,并求f(x)的极大值.
【考点】6D:利用导数研究函数的极值;6H:利用导数研究曲线上某点切线方
第16页 | 共23页程.
菁优网版权所有
【专题】16:压轴题;53:导数的综合应用.
【分析】(Ⅰ)求导函数,利用导数的几何意义及曲线y=f(x)在点(0,f(0
))处切线方程为y=4x+4,建立方程,即可求得a,b的值;
(Ⅱ)利用导数的正负,可得f(x)的单调性,从而可求f(x)的极大值.
【解答】解:(Ⅰ)∵f(x)=ex(ax+b)﹣x2﹣4x,
∴f′(x)=ex(ax+a+b)﹣2x﹣4,
∵曲线y=f(x)在点(0,f(0))处切线方程为y=4x+4
∴f(0)=4,f′(0)=4
∴b=4,a+b=8
∴a=4,b=4;
(Ⅱ)由(Ⅰ)知,f(x)=4ex(x+1)﹣x2﹣4x,f′(x)=4ex(x+2)﹣2x﹣4=4
(x+2)(ex﹣ ),
令f′(x)=0,得x=﹣ln2或x=﹣2
∴x∈(﹣∞,﹣2)或(﹣ln2,+∞)时,f′(x)>0;x∈(﹣2,﹣ln2)时,f′(x
)<0
∴f(x)的单调增区间是(﹣∞,﹣2),(﹣ln2,+∞),单调减区间是(﹣2,
﹣ln2)
当x=﹣2时,函数f(x)取得极大值,极大值为f(﹣2)=4(1﹣e﹣2).
【点评】本题考查导数的几何意义,考查函数的单调性与极值,考查学生的计
算能力,确定函数的解析式是关键.
21.(12分)已知圆M:(x+1)2+y2=1,圆N:(x﹣1)2+y2=9,动圆P与圆M外
切并与圆N内切,圆心P的轨迹为曲线C.
(Ⅰ)求C的方程;
(Ⅱ)l是与圆P,圆M都相切的一条直线,l与曲线C交于A,B两点,当圆P的半
径最长时,求|AB|.
第17页 | 共23页【考点】J3:轨迹方程;J9:直线与圆的位置关系.
菁优网版权所有
【专题】5B:直线与圆.
【分析】(I)设动圆的半径为R,由已知动圆P与圆M外切并与圆N内切,可得|
PM|+|PN|=R+1+(3﹣R)=4,而|NM|=2,由椭圆的定义可知:动点P的轨迹
是以M,N为焦点,4为长轴长的椭圆,求出即可;
(II)设曲线C上任意一点P(x,y),由于|PM|﹣|PN|=2R﹣2≤4﹣2=2,所以R
≤2,当且仅当⊙P的圆心为(2,0)R=2时,其半径最大,其方程为(x﹣2)
2+y2=4.分①l的倾斜角为90°,此时l与y轴重合,可得|AB|.②若l的倾斜角
不为90°,由于⊙M的半径1≠R,可知l与x轴不平行,设l与x轴的交点为Q,根
据 ,可得Q(﹣4,0),所以可设l:y=k(x+4),与椭圆的方程联
立,得到根与系数的关系利用弦长公式即可得出.
【解答】解:(I)由圆M:(x+1)2+y2=1,可知圆心M(﹣1,0);圆N:(x
﹣1)2+y2=9,圆心N(1,0),半径3.
设动圆的半径为R,
∵动圆P与圆M外切并与圆N内切,∴|PM|+|PN|=R+1+(3﹣R)=4,
而|NM|=2,由椭圆的定义可知:动点P的轨迹是以M,N为焦点,4为长轴长的
椭圆,
∴a=2,c=1,b2=a2﹣c2=3.
∴曲线C的方程为 (x≠﹣2).
(II)设曲线C上任意一点P(x,y),
由于|PM|﹣|PN|=2R﹣2≤3﹣1=2,所以R≤2,当且仅当⊙P的圆心为(2,0)R=
2时,其半径最大,其方程为(x﹣2)2+y2=4.
①l的倾斜角为90°,则l与y轴重合,可得|AB|= .
②若l的倾斜角不为90°,由于⊙M的半径1≠R,可知l与x轴不平行,
设l与x轴的交点为Q,则 ,可得Q(﹣4,0),所以可设l:y=k(x+4)
,
由l于M相切可得: ,解得 .
第18页 | 共23页当 时,联立 ,得到7x2+8x﹣8=0.
∴ , .
∴|AB|= = =
由于对称性可知:当 时,也有|AB|= .
综上可知:|AB|= 或 .
【点评】本题综合考查了两圆的相切关系、直线与圆相切问题、椭圆的定义及
其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、弦长公
式等基础知识,需要较强的推理能力和计算能力及其分类讨论的思想方法.
请考生在第22、23、24三题中任选一题作答。注意:只能做所选定的题目。如
果多做,则按所做的第一个题目计分,作答时请用2B铅笔在答题卡上将所选
题号后的方框涂黑。
22.(10分)(选修4﹣1:几何证明选讲)
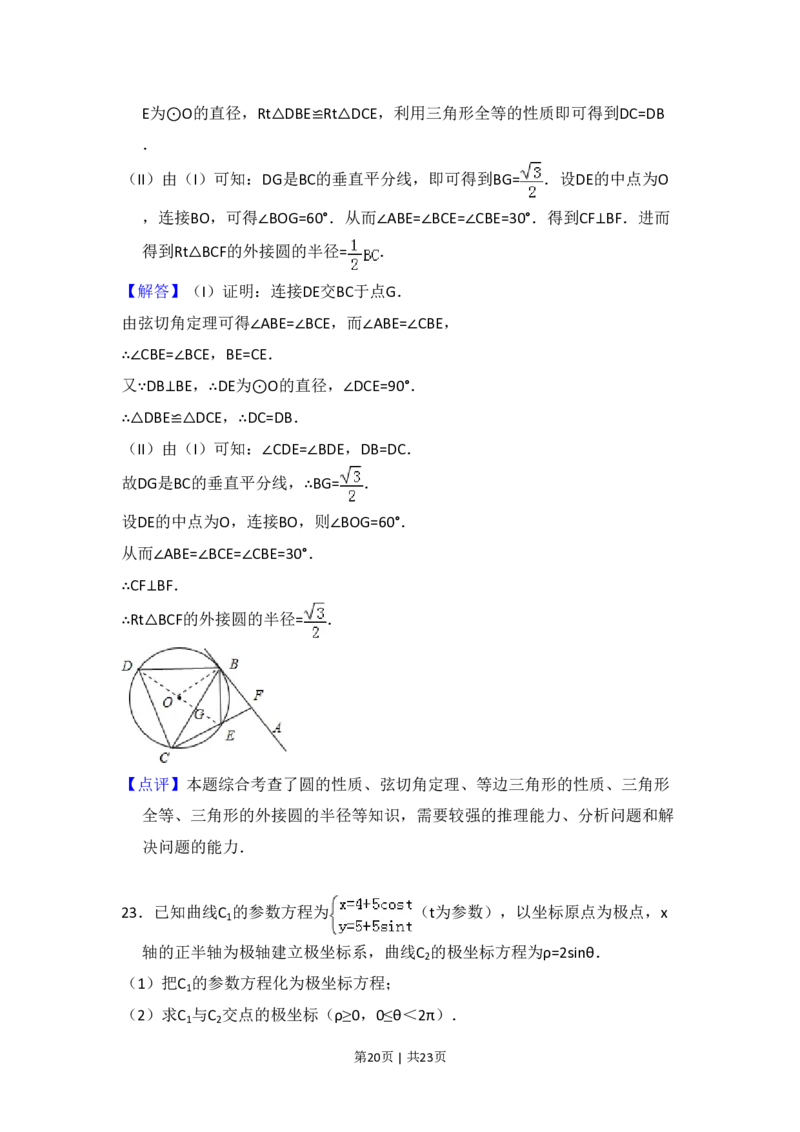
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点
E,DB垂直BE交圆于D.
(Ⅰ)证明:DB=DC;
(Ⅱ)设圆的半径为1,BC= ,延长CE交AB于点F,求△BCF外接圆的半径.
【考点】NC:与圆有关的比例线段.
菁优网版权所有
【专题】5B:直线与圆.
【分析】(I)连接DE交BC于点G,由弦切角定理可得∠ABE=∠BCE,由已知角平
分线可得∠ABE=∠CBE,于是得到∠CBE=∠BCE,BE=CE.由已知DB⊥BE,可知D
第19页 | 共23页E为⊙O的直径,Rt△DBE≌Rt△DCE,利用三角形全等的性质即可得到DC=DB
.
(II)由(I)可知:DG是BC的垂直平分线,即可得到BG= .设DE的中点为O
,连接BO,可得∠BOG=60°.从而∠ABE=∠BCE=∠CBE=30°.得到CF⊥BF.进而
得到Rt△BCF的外接圆的半径= .
【解答】(I)证明:连接DE交BC于点G.
由弦切角定理可得∠ABE=∠BCE,而∠ABE=∠CBE,
∴∠CBE=∠BCE,BE=CE.
又∵DB⊥BE,∴DE为⊙O的直径,∠DCE=90°.
∴△DBE≌△DCE,∴DC=DB.
(II)由(I)可知:∠CDE=∠BDE,DB=DC.
故DG是BC的垂直平分线,∴BG= .
设DE的中点为O,连接BO,则∠BOG=60°.
从而∠ABE=∠BCE=∠CBE=30°.
∴CF⊥BF.
∴Rt△BCF的外接圆的半径= .
【点评】本题综合考查了圆的性质、弦切角定理、等边三角形的性质、三角形
全等、三角形的外接圆的半径等知识,需要较强的推理能力、分析问题和解
决问题的能力.
23.已知曲线C 的参数方程为 (t为参数),以坐标原点为极点,x
1
轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρ=2sinθ.
2
(1)把C 的参数方程化为极坐标方程;
1
(2)求C 与C 交点的极坐标(ρ≥0,0≤θ<2π).
1 2
第20页 | 共23页【考点】Q4:简单曲线的极坐标方程;QH:参数方程化成普通方程.
菁优网版权所有
【专题】11:计算题;35:转化思想;4R:转化法;5S:坐标系和参数方程.
【分析】(1)曲线C 的参数方程消去参数t,得到普通方程,再由
1
,能求出C 的极坐标方程.
1
(2)曲线C 的极坐标方程化为直角坐标方程,与C 的普通方程联立,求出C 与
2 1 1
C 交点的直角坐标,由此能求出C 与C 交点的极坐标.
2 1 2
【解答】解:(1)将 ,消去参数t,化为普通方程(x﹣4)2+(y﹣
5)2=25,
即C :x2+y2﹣8x﹣10y+16=0,
1
将 代入x2+y2﹣8x﹣10y+16=0,
得ρ2﹣8ρcosθ﹣10ρsinθ+16=0.
∴C 的极坐标方程为ρ2﹣8ρcosθ﹣10ρsinθ+16=0.
1
(2)∵曲线C 的极坐标方程为ρ=2sinθ.
2
∴曲线C 的直角坐标方程为x2+y2﹣2y=0,
2
联立 ,
解得 或 ,
∴C 与C 交点的极坐标为( )和(2, ).
1 2
【点评】本题考查曲线极坐标方程的求法,考查两曲线交点的极坐标的求法,
考查极坐标方程、直角坐标方程、参数方程的互化等基础知识,考查推理论
证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题
.
24.已知函数f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.
(Ⅰ)当a=﹣2时,求不等式f(x)<g(x)的解集;
(Ⅱ)设a>﹣1,且当x∈[﹣ , ]时,f(x)≤g(x),求a的取值范围.
第21页 | 共23页【考点】R5:绝对值不等式的解法.
菁优网版权所有
【分析】(Ⅰ)当a=﹣2时,求不等式f(x)<g(x)化为|2x﹣1|+|2x﹣2|﹣x
﹣3<0.设y=|2x﹣1|+|2x﹣2|﹣x﹣3,画出函数y的图象,数形结合可得结
论.
(Ⅱ)不等式化即
1+a≤x+3,故x≥a﹣2对x∈[﹣ , ]都成立,分析可得﹣ ≥a﹣2,由此解得a
的取值范围.
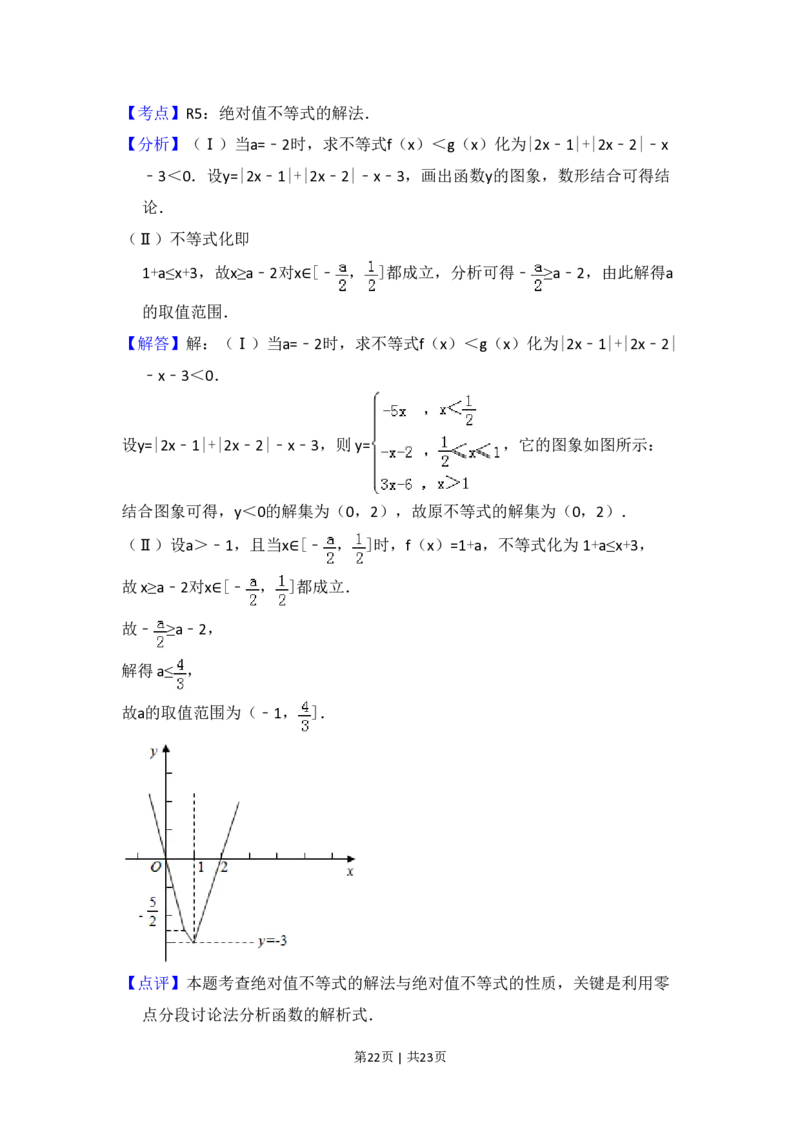
【解答】解:(Ⅰ)当a=﹣2时,求不等式f(x)<g(x)化为|2x﹣1|+|2x﹣2|
﹣x﹣3<0.
设y=|2x﹣1|+|2x﹣2|﹣x﹣3,则 y= ,它的图象如图所示:
结合图象可得,y<0的解集为(0,2),故原不等式的解集为(0,2).
(Ⅱ)设a>﹣1,且当x∈[﹣ , ]时,f(x)=1+a,不等式化为 1+a≤x+3,
故 x≥a﹣2对x∈[﹣ , ]都成立.
故﹣ ≥a﹣2,
解得 a≤ ,
故a的取值范围为(﹣1, ].
【点评】本题考查绝对值不等式的解法与绝对值不等式的性质,关键是利用零
点分段讨论法分析函数的解析式.
第22页 | 共23页第23页 | 共23页